Significance
T cells are essential components of vertebrate immune systems, but the mechanisms by which they are maintained are still poorly defined. Existing methods infer cell lifetimes and division rates using DNA labeling of dividing cells, but do not resolve heterogeneity in population dynamics well. We present a novel experimental system that, when combined with mathematical models, yields kinetic parameters and allows us to measure the effect of a cell’s age on its ability to survive and divide. Our approach quantifies lymphocyte dynamics over a year of a mouse’s life and reveals a first-in, last-out structure in which subpopulations of naive T cells generated early in life persist with slower kinetics and resist displacement by newer specificities.
Keywords: T-cell homeostasis, mathematical modeling, Ki67, kinetic heterogeneity
Abstract
Understanding how our T-cell compartments are maintained requires knowledge of their population dynamics, which are typically quantified over days to weeks using the administration of labels incorporated into the DNA of dividing cells. These studies present snapshots of homeostatic dynamics and have suggested that lymphocyte populations are heterogeneous with respect to rates of division and/or death, although resolving the details of such heterogeneity is problematic. Here we present a method of studying the population dynamics of T cells in mice over timescales of months to years that reveals heterogeneity in rates of division and death with respect to the age of the host at the time of thymic export. We use the transplant conditioning drug busulfan to ablate hematopoetic stem cells in young mice but leave the peripheral lymphocyte compartments intact. Following their reconstitution with congenically labeled (donor) bone marrow, we followed the dilution of peripheral host T cells by donor-derived lymphocytes for a year after treatment. Describing these kinetics with mathematical models, we estimate rates of thymic production, division and death of naive CD4 and CD8 T cells. Population-averaged estimates of mean lifetimes are consistent with earlier studies, but we find the strongest support for a model in which both naive T-cell pools contain kinetically distinct subpopulations of older host-derived cells with self-renewing capacity that are resistant to displacement by naive donor lymphocytes. We speculate that these incumbent cells are conditioned or selected for increased fitness through homeostatic expansion into the lymphopenic neonatal environment.
Normal adaptive immunity depends on maintaining populations of naive CD4 and CD8 T cells of sufficient sizes and diversities of antigen receptors. Mature naive cells are generated by the thymus and, once in the periphery, divide slowly and are lost either to death or differentiation into effector cells. It is known qualitatively how both cytokine (1–7) and T-cell receptor (TCR) (4, 8, 9) signals influence their survival and self-renewal through division, but we still lack a quantitative understanding of the rules that govern the development and persistence of our naive T-cell repertoires.
To develop our understanding of lymphocyte homeostasis, much effort has been directed at defining the kinetics of T cells under normal physiological conditions. Division and death are normally quantified by following the accumulation and loss of cells labeled in vivo with BrdU or deuterium from heavy water or deuterated glucose, taken up by dividing cells during administration of label and diluted following its withdrawal (10–20). These experiments are typically performed over days to weeks and collectively have revealed that cell populations initially assumed to be homogenous may in fact comprise multiple subpopulations dividing and dying at different rates (kinetic heterogeneity) and/or that cells that are quiescent or have recently divided may have different susceptibilities to death (temporal heterogeneity). Discriminating between these scenarios with labeling alone is difficult (16), and the parameter estimates inferred from in vivo labeling are also sensitive to the assumed nature of heterogeneity (15, 16, 20), the duration of labeling (14, 20), and assumptions regarding the relative contributions of input of cells from external sources and self-renewal through division (11, 21).
With the exception of a study that distinguished recent thymic emigrants and mature naive cells (22), heterogeneity has also been left as a rather general concept in labeling studies and not tied firmly to any other variables or identifiable subsets of cells. Average T-cell lifetimes in both mice and humans appear to vary with age (18), and so it seems plausible that turnover may be heterogeneous with respect to cell age, measured by the time since export from the thymus. However, without stratifying cells by their residence histories, labeling provides only host age-specific, cross-sectional snapshots of population dynamics. Thus, we need more information to build a unified description of T-cell homeostasis from birth into old age that will allow us to explain how the phenotypic composition and TCR repertoires of lymphocyte compartments evolve over an individual’s lifetime.
In this study, we quantify the homeostatic dynamics and probe the age structure of the naive CD4 and CD8 T-cell compartments over a year of a mouse’s life, using what we term a “temporal fate mapping” approach. Hematopoetic stem cells of young adult mice were specifically replaced with congenically labeled stem cells while leaving the peripheral T-cell compartment intact. We monitored the replacement of host T cells with de novo-generated donor T cells. Although a simple model of homogeneous dynamics is able to describe the total naive CD4 and CD8 compartment sizes over the course of a year, this model and even extremely general extensions of it were unable to simultaneously explain the changes in total naive T-cell numbers over time and the kinetics of replacement of host by donor cells. Instead, the data and modeling pointed strongly to the presence of a long-lived, self-renewing population of host naive T cells (which we term “incumbents”) generated in the first few weeks after birth and resistant to replacement by newer, “displaceable” cells. Using the rate of dilution of host by donor cells in conjunction with measurements of the proportions of cells undergoing division, we were able to infer the mean residence and interdivision times of incumbent and displaceable cells within both the naive CD4 and CD8 T-cell populations. Our study reveals, for the first time to our knowledge, the age-dependent population dynamics of the naive T-cell pools and unexpected heterogeneity within them.
Methods
Busulfan Chimeras.
WT CD45.1 mice aged 8–10 wk were treated with 20 mg/kg busulfan (Busilvex; Pierre Faber), delivered as two i.p. injections of 10 mg/kg diluted in PBS, allowing 24 h for recovery between injections. This dose is sufficient to deplete bone marrow (BM) cells without immediately impacting the peripheral T-cell compartment (23, 24). Donor BM was harvested from the femurs of age- and sex-matched congenic WT CD45.2 mice and depleted of T cells by immunomagnetic selection, using biotinylated antibodies to CD3 and TCR-β chain (eBioscience) and streptavidin-coupled Dynabeads (Life Technologies). Busulfan-treated mice received 10–20 million T cell-depleted BM cells by i.v. injection, 24 h after the final injection of busulfan. Chimeras were killed for analysis at the indicated times after BM transplantation (BMT), and cells from the thymus, spleen, and lymph nodes (LNs) were analyzed by flow cytometry. Mice were bred and maintained in a conventional pathogen-free colony at the National Institute for Medical Research (London, UK), and all experiments were performed in accordance with UK Home Office regulations.
Flow Cytometry.
The following monoclonal antibodies and cell dyes were used: CD45.1 FITC, CD45.2 AlexaFluor700, CD45.2 FITC, TCR-β APC, CD4 PerCP-eFluor710, CD44 APC-eFluor780, CD25 PE-Cy7, l-selectin eFluor450, and CD122 biotin (all eBioscience); CD8 Pacific orange, streptavidin PE-Texas Red, and LIVE/DEAD blue (all Invitrogen); CD45.1 brilliant violet 650, CD4 brilliant violet 711, and TCR-β PerCP-Cy5.5 (all BioLegend); and Ki67 PE (BD Pharmingen). Where Ki67 staining was performed, cells were first fixed and permeabilized using the eBioscience FoxP3/transcription factor staining buffer set. Samples were acquired on LSR-II, LSRFortessa, or Fortessa ×20 flow cytometers (BD), and analysis was performed with FlowJo software (Treestar). Gating strategies for defining naive cells are detailed in SI Appendix S1.
Models.
Model fitting was performed by first solving the equations analytically where possible or using Mathematica and/or R where required to solve them numerically. For all model fitting, the functions of interest are the time courses of total cell counts and the percentage of naive cells that are donor derived. Both are described with a single model, and therefore the maximization of the log-likelihood is equivalent to minimization of the product of the residual sum of squares for each time course (SI Appendix S2). Minimizations were performed both in Mathematica using its simulated annealing and random search algorithms, and in R using the GenSA package. In the latter, the maximum number of iterations was set at , and initial temperatures varying over five orders of magnitude yielded no discernible differences in parameter estimates. To normalize residuals, total cell counts and donor fractions were log- and arcsin-squareroot transformed, respectively. Confidence intervals were computed using bootstrapping of residuals with 500 replicates.
Results
The Fate of Newly Generated T Cells Can Be Monitored Over Time in Busulfan-Treated Chimeras.
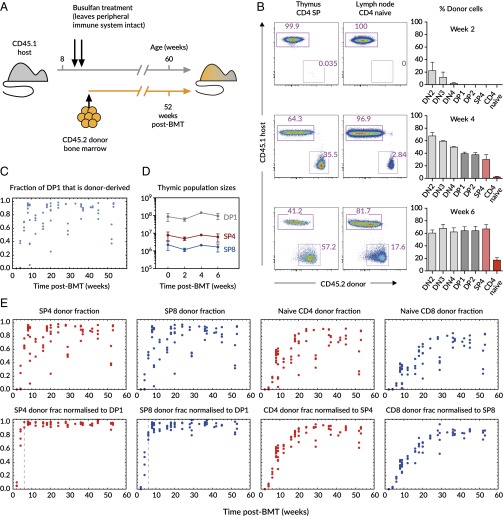
To investigate the cellular mechanisms responsible for maintaining the peripheral naive T-cell compartment, we analyzed busulfan bone marrow chimeric mice as described previously (25). Busulfan is a conditioning drug (26) that specifically depletes hematopoetic stem cells (HSCs), but leaves mature hematopoetic cells unaffected. Groups of 8- to 10-wk-old young adult CD45.1 C57Bl6/J host mice were treated with two injections of busulfan, and their HSC compartments were reconstituted via injection with 107 T cell-depleted BM cells from CD45.2 C57Bl6/J donors (Fig. 1A). Donor cells could be detected in the CD4 CD8 double negative (DN) compartment by as early as 2 wk (Fig. 1B). By 4 wk, donor cells were present in the CD4 CD8 double positive (DP) and single positive (SP) compartments, but had not reached equilibrium, as representation was still greatest at the more immature DN stages of development. However, by 6 wk, reconstitution was complete and reached a maximum at all stages of thymic development, and donor cells could be observed in the peripheral lymphoid compartments (Fig. 1B, Lower). Because host-derived thymocytes were still present after equilibration of the thymic compartments, it was evident that busulfan conditioning allowed partial replacement of host HSCs. Using the donor fraction in DP1 as a proxy, we observed variable levels of replacement of host HSCs (median, 89%; range, 5–98.3%; Fig. 1C). Therefore, after reconstitution, the thymi of mice produced new T cells that were a mixture of donor and host, typically 90% donor. Analyzing the thymi of hosts after transplantation revealed that thymus size was unaffected during the course of reconstitution (Fig. 1D). The fraction of mature naive T cells that were donor derived was normalized to the level of chimerism in the relevant single-positive compartment of each animal, revealing the time course of replacement of the peripheral compartments up to a year after thymic reconstitution (Fig. 1E).
Fig. 1.
Experimental setup and the kinetics of host-donor chimerism. (A) Host CD45.1 mice aged 8–10 wk were treated with two doses of 10 mg/kg busulfan, followed by injection of T cell-depleted bone marrow cells from CD45.2 donors. The numbers of donor and host cells in the thymus and peripheral lymphocyte compartments were evaluated by flow cytometry at various time points up to 1 y after BMT. (B) Representative flow cytometry plots show expression of CD45.1 (host) and CD45.2 (donor) on CD4 single positive thymocytes (CD4+CD8−; Left) and naive CD4 cells from lymph nodes (TCRβ+CD4+ and CD44loCD25−; Center). Numbers indicate the percentage of cells in each gate. Graphs (Right) show the percentage of cells that are of donor origin, i.e., CD45.2+, within the indicated thymic populations and in naive CD4 cells from lymph nodes. Data are from two to four mice per time point at 2, 4, and 6 wk after BMT. (C) The percentage of cells that were of donor origin within the DP1 compartment in the thymus was assessed by flow cytometry. (D) Treatment has no substantial effect on total (host+donor) sizes of thymocyte populations (error bars show SD for four mice per time point). (E) (Upper) Percentage of cells that were donor derived within the indicated thymic (CD4 and CD8 single positive) and peripheral naive (lymph node + spleen CD4 or CD8) populations, against the time after BMT. Each point represents a single mouse. (Lower) Same populations normalized to the donor-derived fraction within the appropriate precursor population (DP1 for SP cells, and SP for peripheral naive cells) for each individual. The vertical dashed lines indicate 6 wk after BMT, which we took to be the point at which reconstitution of the thymus was complete: that is, the donor fraction at all stages of thymic development had stabilized.
Quantifying Lymphocyte Dynamics.
The compositions of the naive T-cell compartments are determined by the interplay of export from the thymus, production through division in the periphery, and loss either through cell death or onward differentiation. To quantify naive T-cell population dynamics and infer the rules of replacement of older (host) T cells by newer (donor) cells, we used a mathematical modeling approach. Considering the periphery as the lymph nodes and spleen combined, we began with a simple and widely used model of the production and loss of a kinetically homogeneous peripheral T-cell population that is exported from the thymus
| [1] |
where is an age-dependent rate of thymic output, ρ is a constant per-cell rate of peripheral cell division, and δ is a constant per-cell rate of loss from the naive compartment through death or differentiation. Without specific measurements of death and division, this model does not distinguish these two parameters separately but instead contains the net per-capita rate of loss of cells from the periphery: .
There are some inconsistencies in terminology in the literature relating to lymphocyte dynamics. “Turnover” is generally understood to refer to the flux of individuals through a population that is at or close to equilibrium. Total naive cell numbers N change slowly, and so in this simple model the total rate of loss of cells, , is approximately balanced by input from the thymus and division in the periphery. We therefore define turnover to be the loss rate δ. In a population in quasi-equilibrium sustained by peripheral division and not supplemented by cells from the thymus, the rate of turnover is then also the division rate ρ, and the net loss rate in the periphery is zero.
If we assume host and donor-derived cells in treated mice are kinetically identical, with this model the changes in naive T-cell numbers of host () and donor () origin is described by
| [2] |
| [3] |
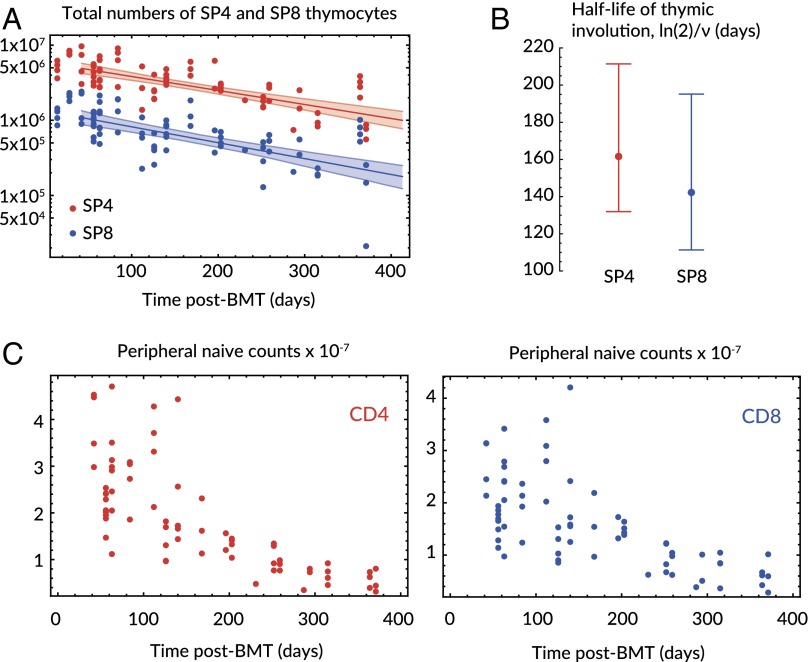
Quantifying naive T-cell population dynamics with this model requires knowledge of the production terms and . Single-positive (SP4 and SP8) cells are in the last stage of development in the thymus and therefore their numbers are proxies for the rates of export of naive CD4 and CD8 T cells, respectively. Thymic output declines with age in healthy mice (27, 28), and in keeping with this, we found that total (host + donor) numbers of SP4 and SP8 thymocytes declined exponentially and in tandem from the time of treatment at 8 wk of age (Fig. 2A), with half-lives of 159 d (95% CI: 128, 208) for SP4 and 143 (95% CI: 111, 199) days for SP8 (Fig. 2B). These figures are consistent with an estimate of 169 d (95% CI: 157, 182) derived from the decline in total thymocyte numbers with age (28).
Fig. 2.
Kinetics of thymic involution and total peripheral naive CD4 and CD8 numbers after transplant. (A) The decline in total SP4 (red) and SP8 (blue) cells with age, with fitted exponential decay from 42 d after treatment and envelopes spanned by the 95% CI on the decay constant, ν. (B) Associated estimates of the half-life of thymic involution, . (C) Total numbers of naive CD4 and CD8 T cells (recovered from spleen and lymph nodes) decline over a year after transplant.
With this information, we use the following equations to describe the dynamics of peripheral naive CD4 or CD8 T cells from time days after treatment, when the chimerism between DP1 and the SP stages at all stages of thymic development had equilibrated at a (mouse-specific) level χ, defined as the proportion of cells at SP4 or SP8 that were donor-derived (Fig. 1E):
| [4] |
| [5] |
Here, ν is the estimated rate of thymic involution, is the total (host + donor) rate of export of naive CD4 or CD8 T cells from the thymus at time , and within each population (CD4 or CD8), host- and donor-derived cells were assumed to have identical net loss rates λ. The following quantity is independent of chimerism:
| [6] |
| [7] |
which is obtained by solving Eqs. 4 and 5 directly. Here time t is measured from onward, and is the total naive T-cell compartment size at . We expect the ratio to be only weakly dependent on chimerism and body mass, because thymic output might reasonably be assumed to scale positively with the sizes of peripheral naive populations across different animals. We therefore assumed the normalized donor fraction depends only on parameters common across mice. The levels of chimerism at the DP1 and SP stages in each mouse were closely comparable, and using the donor fraction at DP1 stage to define χ yielded very similar time courses (SI Appendix S3) and for the models considered in this study yielded indistinguishable qualities of fit, parameter estimates, and degrees of relative support.
Eq. 7 tells us that the rate at which donor cells replace host cells is determined by the difference between the net loss rate and the rate of involution of the thymus, . This result means, perhaps unintuitively, that the rate of replacement of host cells by donor cells in the periphery is not necessarily the rate of turnover, δ.
Replacement Kinetics Cannot Be Explained by Models of Homogeneous Turnover.
This model predicts that if the net loss rate of cells in the periphery is faster than the rate of thymic involution (), the normalized donor fraction approaches 1 over time (Eq. 7); that is, the donor/host chimerism in the naive T-cell compartments eventually reflects that in the BM and thymus. However, the donor cells consistently failed to populate the periphery to this extent, reaching a normalized donor fraction of 0.87 (95% CI: 0.84, 0.91) and 0.83 (95% CI: 0.80, 0.85) for naive CD4 and CD8 T cells, respectively (Fig. 1E). These values were calculated using data from 100 d.
The model represented by Eq. 7 can explain this observation only if thymic output declines faster than the net loss rate; that is, if the supply of donor-derived cells dwindles too rapidly for peripheral chimerism to catch up with that in the BM. However, without fitting this model to the data, we can see with a simple argument that it is insufficient to describe the incomplete replacement. Peripheral naive CD4 and CD8 numbers declined continuously with age (Fig. 2C), requiring that the net rate of loss λ be positive. [λ > 0 is a weak constraint; for cell counts to be declining at all times, λ must be greater than at all times.] In this model, peripheral chimerism approaches stability at the rate , which is at most the rate of thymic involution ν (i.e., when the net rate of loss, λ, is zero), but chimerism stabilizes by roughly 200 d (Fig. 1E), by which time thymic output has fallen only by 60% (half-life of involution 150 d; Fig. 2B). Thus, the homogeneous model with a constant, positive net loss rate λ (Eqs. 4 and 5) is not able to explain the saturation kinetics.
To explore this issue further, we generalized the homogeneous model to allow for completely arbitrary time-dependent rates of division and/or death. This generalization also effectively includes models in which rates of division or loss are functions of cell numbers and not time. We found, surprisingly, that even using this extremely broad class of models, the constraints imposed by the measured rate of thymic involution and continuously declining peripheral cell counts mean that is impossible to reproduce the kinetics of both the normalized donor fraction and total counts (SI Appendix S4).
Heterogeneity in Naive T-Cell Population Dynamics.
The inadequacy of models assuming homogeneous naive populations strongly suggested that host and donor-derived cells do not obey the same kinetics after treatment and/or that heterogeneity exists within one or both subpopulations. To explore these possibilities, we first made a simple extension to the model in which the underrepresentation of donor naive cells in the periphery derives from a host-derived population that is resistant to displacement. We began with the simplest assumption that these incumbent cells were established before treatment and were not supplemented from the thymus after treatment. The dynamics of displaceable and incumbent host-derived cells and donor-derived cells (assumed to be all displaceable) are then described by
| [8] |
| [9] |
| [10] |
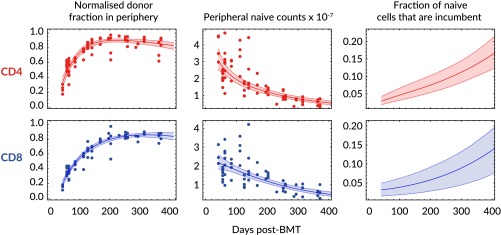
where we allow the net rates of loss of incumbent and displaceable cells, and λ, respectively, to differ. As in the homogeneous case, the normalized donor fraction can be calculated in this model (SI Appendix S5) and again represents a quantity that is conserved across animals, allowing us to describe the kinetics of reconstitution of mice with different levels of chimerism with a single prediction curve. This model was fitted simultaneously to the total peripheral naive counts and the normalized donor fraction (see SI Appendix S5 for details) and was able to describe the year-long time courses of both quantities for both naive CD4 and CD8 T cells (Fig. 3, Left and Center). There was only marginal statistical support for nonzero loss rates of incumbents [CD4, = 0.0052 (0, 0.059), AIC = 2.13; CD8, (0, 0.070), AIC = 2.18] and therefore we inferred that both CD4 and CD8 incumbents were stable, self-renewing populations (). This numerical stability, combined with declining total naive T-cell numbers, means that incumbent cells are predicted to occupy increasing fractions of the naive CD4 and CD8 compartments with age (Fig. 3, Right). The phenotypes of the host-derived naive CD4 and CD8 cells were confirmed as CD62LhiCD122lo naive (SI Appendix S6).
Fig. 3.
Fits of the heterogeneous (incumbent/displaceable) model to kinetics of host and donor-derived naive T cells. We fitted the model simultaneously to the normalized donor fraction (Eq. 7; Left) and the total numbers (Eqs. 8–10; Center) for naive CD4 and CD8 T cells. (Right) Estimated proportions of the naive CD4 and CD8 pools occupied by incumbent cells over time. Shaded regions on the fitted curves (Left and Center) are uncertainty envelopes defined by the 95% CI on parameter estimates. Shaded regions on the Right represent 95% CIs on the estimated fraction of naive cells that are incumbent.
Models of Kinetics Varying with Cell Age, or with Continual Production of Incumbents, Provide Inferior Descriptions of the Data.
The analysis above assumes heterogeneity in cells’ behavior with respect to the age of the host at the time of thymic export. An alternative possibility is that cells’ net rate of loss decreases with their time spent in the periphery. This mechanism is a generalization of one used recently to explain crashes in naive CD4 T-cell diversity in the elderly, in which slowly accumulated mutations lead to a sudden increase in fitness and subsequent outgrowth of clonal populations (29). Allowing division or death rates to vary with cell age reflects an alternative, continuous form of kinetic heterogeneity, and is also able to describe the data (SI Appendix S7). Despite having only three fitted parameters compared with five in the incumbent model, the best age-dependent model gives poorer fits and has significantly less statistical support than the incumbent-displaceable model (CD4, ; CD8, ). Further, an extension of the incumbent-displaceable model to allow posttreatment generation of both host and donor incumbents also yielded poorer descriptions of the data (AIC for both CD4 and CD8 cells). Collectively these results support the conclusion that the persistent naive population is established early in life.
Estimating the Mean Interdivision and Lifetimes of Naive CD4 and CD8 T Cells.
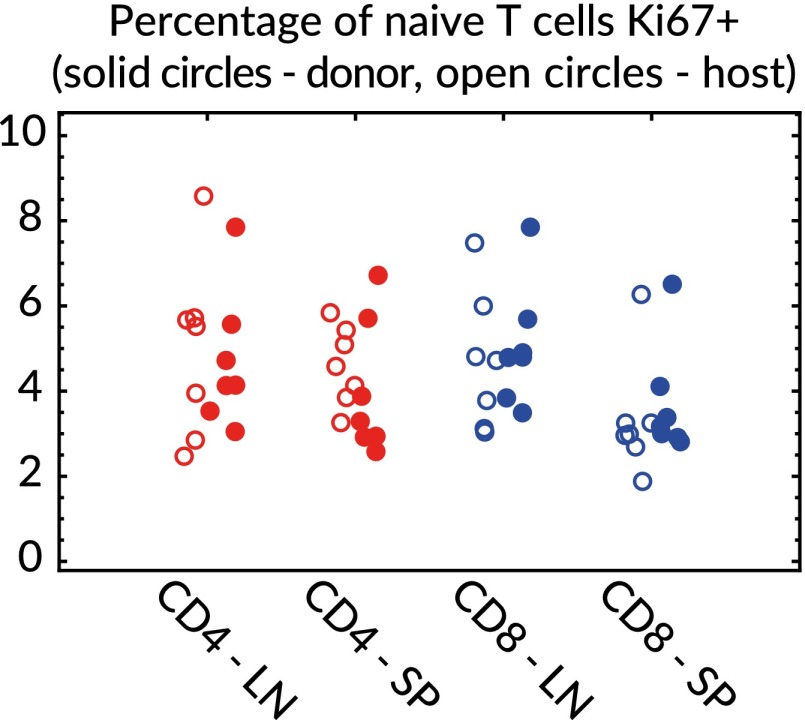
Applying the model to the data yielded the net loss rate λ, but the quantities of biological interest are the rates of division (ρ) and turnover (δ). These rates can be obtained with additional information regarding the proportion of cells in division at any time. A marker of division status is the nuclear antigen Ki67, which is expressed on entry into the cell cycle, is readily detectable in lymphocytes, and persists for roughly 4 d after mitosis (18, 30). In SI Appendix S8 we show that the division and death rates can be extracted from λ using the proportion of cells that are Ki67hi, the mean duration of Ki67 expression, and the relative susceptibility to death of Ki67hi over Ki67lo cells, σ. We measured the proportions of cells that were Ki67hi at 36 and 53 wk after treatment (Fig. 4) and found no significant differences between host and donor populations within or between these time points. Within the framework of our model, this observation implies that there were no detectable differences in the Ki67hi fraction between displaceable and incumbent cells. However, this observation does not necessarily imply that the two populations have the same division rates, because unlike incumbents, the displaceable population has an additional source of Ki67hi cells from the thymus (SI Appendix S8).
Fig. 4.
Ki67 expression at 36 and 53 wk after BMT (pooled) in host/donor/4/8/LN/spleen.
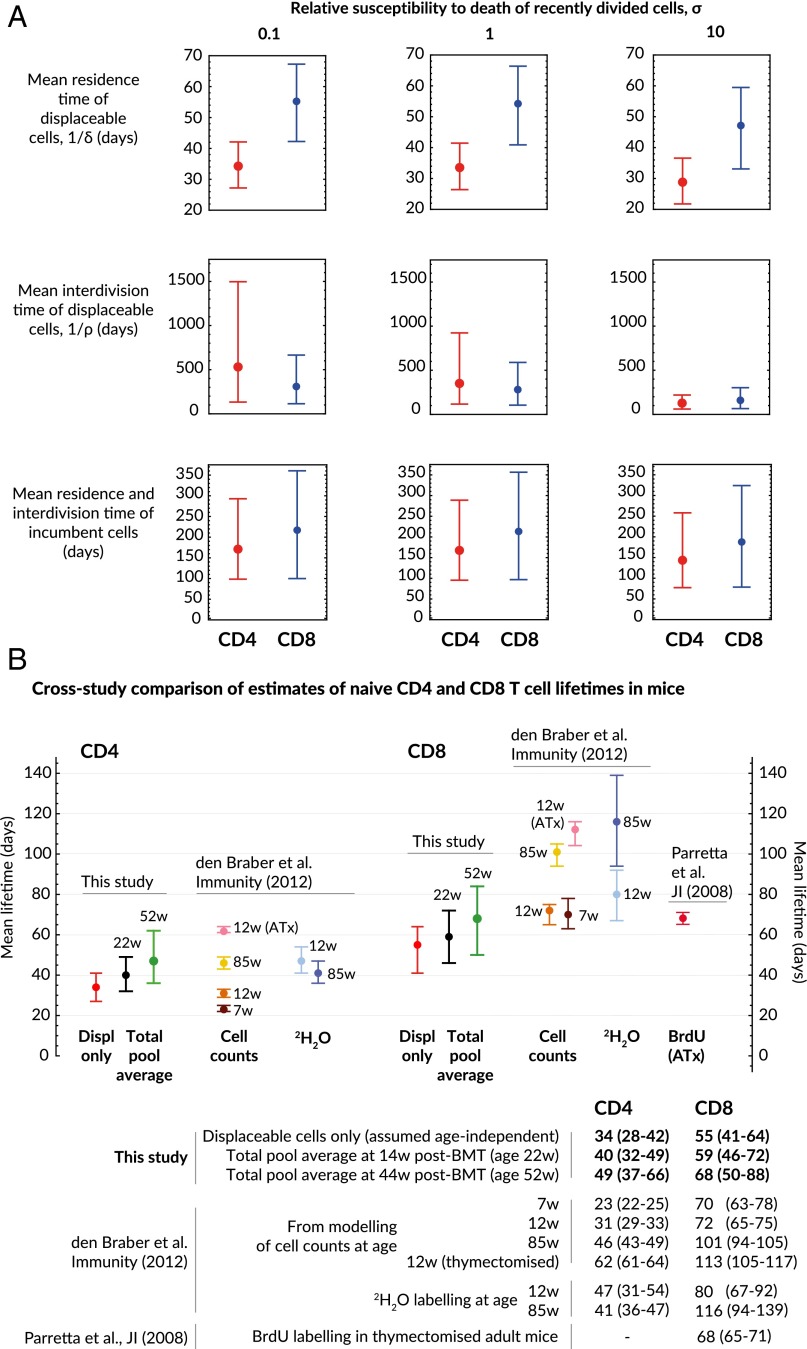
The kinetic parameters estimated using the incumbent-displaceable model are shown in Table 1 and Fig. 5A. Conservative confidence intervals on ρ and δ were generated using a hybrid bootstrap/Monte Carlo approach; empirical distributions of parameter estimates were obtained by repeatedly fitting to datasets obtained by resampling residuals and simultaneously sampling values of (i) the thymic involution rate ν from bootstrap replicates, (ii) the proportion of cells that were Ki67hi from the data (pooled host+donor for displaceables, host only for incumbents), and (iii) the Ki67 lifetime from a lognormal distribution with mean 4 d (18, 30) and SD of 0.5 d. We assume that 20% of thymically produced cells are Ki67hi, but our estimates of turnover rates are insensitive to this value (SI Appendix S8). The relative susceptibility to death of recently divided and resting naive cells, σ, is unknown, and so we quote parameter estimates for , and 10. Because the proportion of cells in division at any point is low, σ has little effect on the estimates of mean residence times, but has a stronger influence on the mean interdivision time. Our pool-wide estimates of the mean CD4 and CD8 residence times are comparable to those obtained by labeling methods (Fig. 5B), but these population averages mask considerable differences in the rates of turnover of displaceable and incumbent cells (Fig. 5A).
Table 1.
| Quantity | Parameter | Relative loss rate Ki67hi/Ki67lo | Naive CD4 | Naive CD8 |
| Proportion incumbent at 6 wk after BMT | — | 0.030 (0.020,0.044) | 0.032 (0.018,0.048) | |
| Daily thymic output 6 wk after BMT | — | 4.74 (3.64, 6.07) | 2.37 (1.99,2.81) | |
| Daily thymic output as proportion of peripheral numbers 6 wk after BMT | — | 0.016 (0.012, 0.021) | 0.011 (0.009, 0.013) | |
| Expected residence time of displaceables (d) | 0.1 | 34 (28, 42) | 55 (42, 65) | |
| 1 | 34 (26, 41) | 55 (41,66) | ||
| 10 | 29 (22, 37) | 46 (33, 57) | ||
| Expected interdivision time of displaceables (d) | 0.1 | 530 (134, 1496) | 309 (112, 665) | |
| 1 | 350 (117, 923) | 280 (105, 588) | ||
| 10 | 127 (61, 219) | 159 (65, 302) | ||
| Expected residence and interdivision time of incumbents (d) | 0.1 | 171 (98, 292) | 217 (100, 359) | |
| 1 | 167 (95, 288) | 213 (97, 355) | ||
| 10 | 143 (77, 257) | 187 (78, 323) | ||
| Expected residence time of pooled population at 14 wk after BMT (age 22 wk), | 0.1 | 41 (32, 50) | 61 (47, 73) | |
| 1 | 40 (32, 49) | 59 (46, 72) | ||
| 10 | 34 (26, 43) | 52 (37, 64) | ||
| Expected residence time of pooled population at 44 wk after BMT (age 52 wk) | 0.1 | 50 (37, 66) | 70 (52, 90) | |
| 1 | 49 (37, 65) | 68 (50, 88) | ||
| 10 | 42 (31, 57) | 60 (41, 79) | ||
| Expected interdivision time of pooled population at 14 wk after BMT (age 22 wk) | 0.1 | 514 (134, 1440) | 306 (115, 648) | |
| 1 | 342 (119, 886) | 278 (106, 575) | ||
| 10 | 128 (63, 217) | 161 (68, 229) | ||
| Expected interdivision time of pooled population at 44 wk after BMT (age 52 wk) | 0.1 | 490 (134, 1349) | 301 (118, 626) | |
| 1 | 330 (120, 863) | 275 (110, 560) | ||
| 10 | 129 (66, 213) | 162 (72, 293) |
Figures in bold reflect the situation in which resting and recently divided cells have identical death rates.
Fig. 5.
Estimates of parameters governing naive CD4 and CD8 T-cell population dynamics. (A) Mean residence times (lifetimes) and interdivision times of naive T cells; only the estimates of interdivision times are sensitive to the (unknown) relative susceptibility to death of recently divided and quiescent cells, the parameter σ. The mean lifetime of incumbent cells is statistically indistinguishable from the mean interdivision time. The division and death rates of displaceables and incumbents are assumed independent of age. (B) Comparison of naive T-cell lifetime estimates with those from labeling studies (95% confidence intervals shown in parentheses). In our model the shifting host/donor composition of the pool leads to an increase in the relative abundance of incumbents with age, and hence an increase in the pool-averaged naive CD4 and CD8 T-cell lifetimes with age.
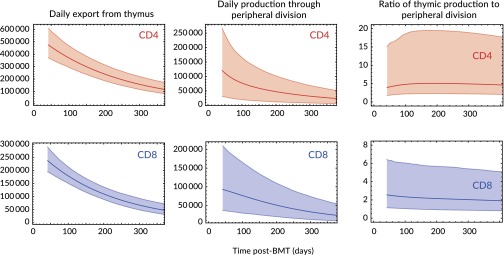
Finally, combining the estimates of the total rate of thymic export at 6 wk after BMT (), the rate of thymic involution (ν), and the division rates of incumbent and displaceable cells (ρ and ), we estimated the total daily production of cells, partitioned into cells exported from the thymus and those generated by division of mature naive cells (Fig. 6), confirming that the bulk of naive T-cell production in mice up to 1 y in age derives from thymic export, most markedly for CD4 T cells.
Fig. 6.
Estimates of rates of production of cells per day through thymic export and peripheral division. Shaded regions represent uncertainty envelopes generated by 95% CIs on fitted parameters. Uncertainty in the second and third columns stems largely from uncertainty in the division rate, ρ.
Discussion
Although it is recognized that memory T-cell populations are heterogeneous in phenotype, turnover, and recirculation patterns, to date, the canonical view of the mature naive T-cell pool is a homogeneous population of undifferentiated precursors that all follow the same rules of replacement. However, this assumption has not previously been examined in detail. Here, by following the development and integration of new T cells into replete peripheral CD4 and CD8 compartments, we find evidence of heterogeneity within both. Subsets of older cells appear to have a competitive advantage, being self-renewing and resistant to replacement by cells exported from the thymus later in life. We explored two explanatory models of this process: one in which an advantage is conferred to a subpopulation of naive cells generated during gestation or in the first few weeks of life and the other, a continuum age-structured model in which naive T cells gradually increase their competitive fitness the longer they survive in the periphery. Although both are able to explain the data, the former had clearly stronger statistical support.
Previous estimates of the average lifespans of naive T cells in mice are ∼20–60 d for CD4 (31) and between 70 and 120 d for CD8 T cells (31, 32) (Fig. 5B). Our population-averaged estimates are consistent with these for CD4 and lie slightly lower than those for CD8, but we argue these numbers conceal quite considerable heterogeneity. Displaceable CD4 and CD8 cells turn over relatively rapidly with mean residence times of 34 and 55 d, respectively. In contrast, incumbent CD4 and CD8 cells, which we assume are not renewed from the thymus, have estimated lifetimes of roughly 170 and 210 d, respectively, and in 1-y-old mice may comprise roughly 15% of the naive T-cell population (Fig. 3). Incumbents appear to be stable in numbers, and so their lifetimes are also their mean interdivision times. Inferring division rates from Ki67 expression requires knowledge of the relative susceptibility to death of resting and recently divided cells, which is unknown. If this quantity is 1 (that is, survival and division are not linked), the mean interdivision times of displaceable CD4 and CD8 cells are both roughly 1 y (Table 1). If recently divided cells are 10 times as susceptible to death as resting cells, the estimated interdivision time for both populations falls by 50%. Therefore, as observed elsewhere (18), some kinetic parameters are very sensitive to model assumptions.
Recent thymic emigrants are a phenotypically distinct transitional subpopulation of peripheral naive T cells, and it has been proposed that they preferentially displace mature cells (22, 33). A question is then whether the conclusions we draw based on total peripheral naive numbers derive from differences in the dynamics of recent thymic emigrant (RTE) and mature naive cells. However, this scenario corresponds to a model of homeostatic fitness varying with respect to cell age (time after export from the thymus), and we found much stronger evidence for heterogeneity in kinetics and resistance to displacement with respect to the age of the host at which naive cells were generated. Further, the conclusion that RTEs are preferentially incorporated into the mature pool under replete conditions suggests their intrinsic lifespan (distinct from their rate of maturation) is longer than that of mature cells, a difference that is opposite to that required for the age-structured model to explain the data. We also explored a model in which the efficiency with which RTEs are incorporated into the mature pool declines with the age of the individual. Such a process would effectively increase the rate of thymic involution and therefore may overcome the constraint that ruled out homogeneous models. This model lacked statistical support compared with the incumbent model, with AIC = 8.5 and 8.8 for CD4 and CD8, respectively (fits shown in SI Appendix S9). Further, declining rates of RTE maturation are at odds with the observation that the frequency of RTE scales with the size of the thymus (34). It has also been inferred from a small dataset that RTE in humans may themselves be kinetically heterogeneous and include a subset of exceptionally long-lived veteran cells that retain immature status (35). This possibility corresponds to an extension to the model in which throughout life a constant fraction of both donor and host RTE are destined to become incumbents. These fractions were estimated to be close to zero, meaning this addition to the model had no impact on the quality of fit but incurred the cost of additional parameters (AIC = 4.4 for both CD4 and CD8 cells). In summary, then, by parsimony, we find the strongest support for a model in which only a subset of host cells generated pretreatment had incumbent properties.
The busulfan system allows us to examine the impact of the timing of export from thymus on T cells’ competitive fitness within the peripheral pool. In addition it further validates the use of random birth-death models that have been used to describe lymphocyte turnover. Various studies measuring lymphocyte kinetics using in vivo labeling yield results that are consistent with slow homeostatic division as a simple Poisson process, with each cell having an equal probability of dividing within any given time interval, irrespective of its division history, both in the many labeling studies performed in lymphoreplete mice or humans and in lymphopenic mice (36). The kinetic of death or loss of cells is difficult to quantify in these systems, however. Were mature T cells to have a narrow distribution of lifespans/residencies, as described (for example) for red blood cells (37), or for thymocytes that progress through development in a roughly linear, conveyor-belt fashion (38), we would have anticipated a linear replacement of existing cells with new thymic emigrants. Instead, replacement occurred with a kinetic consistent with both cell lifetimes and interdivision times being exponentially distributed (Fig. 3).
We assume that the persisting incumbent population is fully formed in young adult mice by 6–8 wk of age and is not supplemented from the thymus thereafter. This conclusion draws on parsimony; formally we can’t exclude the possibility that these cells continue to be exported from the thymus later in life. However, there are possible biological explanations for such a conclusion. The peripheral lymphoid compartment of neonates is T lymphopenic, and new T cells emerging into this environment undergo lymphopenia-induced proliferation (LIP) (39). We speculate that incumbent naive T cells are generated early in ontogeny and that either the lymphopenic environment or the process of LIP increases their average fitness relative to cells that develop subsequently into a full compartment, perhaps through epigenetic modifications or by magnifying natural variation in homeostatic fitness through multiple rounds of proliferation. Consistent with this view, naive T cells from lymphopenic hosts have greater competitive fitness than those from replete hosts (40). The impact of this long-lived population on immune function is not known, but our analysis suggests that its representation increases with host age (Fig. 3). If a similar population exists in adult humans, in whom thymic output plays a lesser role in generating and maintaining the peripheral naive compartment (31), our experiments predict that incumbents would progressively form an even larger fraction of the human naive compartment than they do than in (relatively short-lived) mice. Given that estimates of the lifespans of human naive CD4 and CD8 T cells range from roughly 5 mo to 10 y (see ref. 18 for a summary), it is entirely possible that substantial fractions of naive T cells generated in the first years of life can persist into midlife. Future studies will address the functional capacity of these cells. However, given that incumbents are maintained throughout life without further input from thymus, the diversity of their TCR repertoire can only decrease with time. Whether and at what stage this compromises immunity remain to be determined.
Supplementary Material
Acknowledgments
We thank Jose Borghans and Rob de Boer for useful discussions. This work was supported by the National Institutes of Health (R01AI093870), Arthritis Research UK, and the Medical Research Council (U117573801).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1517246112/-/DCSupplemental.
References
- 1.Polic B, Kunkel D, Scheffold A, Rajewsky K. How alpha beta T cells deal with induced TCR alpha ablation. Proc Natl Acad Sci USA. 2001;98(15):8744–8749. doi: 10.1073/pnas.141218898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Witherden D, et al. Tetracycline-controllable selection of CD4(+) T cells: Half-life and survival signals in the absence of major histocompatibility complex class II molecules. J Exp Med. 2000;191(2):355–364. doi: 10.1084/jem.191.2.355. [DOI] [PubMed] [Google Scholar]
- 3.Labrecque N, et al. How much TCR does a T cell need? Immunity. 2001;15(1):71–82. doi: 10.1016/s1074-7613(01)00170-4. [DOI] [PubMed] [Google Scholar]
- 4.Seddon B, Zamoyska R. TCR and IL-7 receptor signals can operate independently or synergize to promote lymphopenia-induced expansion of naive T cells. J Immunol. 2002;169(7):3752–3759. doi: 10.4049/jimmunol.169.7.3752. [DOI] [PubMed] [Google Scholar]
- 5.Berard M, Brandt K, Bulfone-Paus S, Tough DF. IL-15 promotes the survival of naive and memory phenotype CD8+ T cells. J Immunol. 2003;170(10):5018–5026. doi: 10.4049/jimmunol.170.10.5018. [DOI] [PubMed] [Google Scholar]
- 6.Park JH, et al. Suppression of IL7Ralpha transcription by IL-7 and other prosurvival cytokines: A novel mechanism for maximizing IL-7-dependent T cell survival. Immunity. 2004;21(2):289–302. doi: 10.1016/j.immuni.2004.07.016. [DOI] [PubMed] [Google Scholar]
- 7.Fry TJ, Mackall CL. The many faces of IL-7: From lymphopoiesis to peripheral T cell maintenance. J Immunol. 2005;174(11):6571–6576. doi: 10.4049/jimmunol.174.11.6571. [DOI] [PubMed] [Google Scholar]
- 8.Goldrath AW, Bevan MJ. Low-affinity ligands for the TCR drive proliferation of mature CD8+ T cells in lymphopenic hosts. Immunity. 1999;11(2):183–190. doi: 10.1016/s1074-7613(00)80093-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Seddon B, Zamoyska R. TCR signals mediated by Src family kinases are essential for the survival of naive T cells. J Immunol. 2002;169(6):2997–3005. doi: 10.4049/jimmunol.169.6.2997. [DOI] [PubMed] [Google Scholar]
- 10.Bonhoeffer S, Mohri H, Ho D, Perelson AS. Quantification of cell turnover kinetics using 5-bromo-2′-deoxyuridine. J Immunol. 2000;164(10):5049–5054. doi: 10.4049/jimmunol.164.10.5049. [DOI] [PubMed] [Google Scholar]
- 11.Asquith B, Debacq C, Macallan DC, Willems L, Bangham CR. Lymphocyte kinetics: the interpretation of labelling data. Trends Immunol. 2002;23(12):596–601. doi: 10.1016/s1471-4906(02)02337-2. [DOI] [PubMed] [Google Scholar]
- 12.De Boer RJ, Mohri H, Ho DD, Perelson AS. Estimating average cellular turnover from 5-bromo-2′-deoxyuridine (BrdU) measurements. Proc Biol Sci. 2003;270(1517):849–858. doi: 10.1098/rspb.2002.2316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Macallan DC, et al. Measurement and modeling of human T cell kinetics. Eur J Immunol. 2003;33(8):2316–2326. doi: 10.1002/eji.200323763. [DOI] [PubMed] [Google Scholar]
- 14.Borghans JAM, de Boer RJ. Quantification of T-cell dynamics: From telomeres to DNA labeling. Immunol Rev. 2007;216:35–47. doi: 10.1111/j.1600-065X.2007.00497.x. [DOI] [PubMed] [Google Scholar]
- 15.Ganusov VV, Borghans JAM, De Boer RJ. Explicit kinetic heterogeneity: Mathematical models for interpretation of deuterium labeling of heterogeneous cell populations. PLOS Comput Biol. 2010;6(2):e1000666. doi: 10.1371/journal.pcbi.1000666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.De Boer RJ, Perelson AS, Ribeiro RM. Modelling deuterium labelling of lymphocytes with temporal and/or kinetic heterogeneity. J R Soc Interface. 2012;9(74):2191–2200. doi: 10.1098/rsif.2012.0149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ganusov VV, De Boer RJ. A mechanistic model for bromodeoxyuridine dilution naturally explains labelling data of self-renewing T cell populations. J R Soc Interface. 2013;10(78):20120617. doi: 10.1098/rsif.2012.0617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.De Boer RJ, Perelson AS. Quantifying T lymphocyte turnover. J Theor Biol. 2013;327:45–87. doi: 10.1016/j.jtbi.2012.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Schittler D, Allgöwer F, De Boer RJ. A new model to simulate and analyze proliferating cell populations in BrdU labeling experiments. BMC Syst Biol. 2013;7(Suppl 1):S4. doi: 10.1186/1752-0509-7-S1-S4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Westera L, et al. Closing the gap between T-cell life span estimates from stable isotope-labeling studies in mice and humans. Blood. 2013;122(13):2205–2212. doi: 10.1182/blood-2013-03-488411. [DOI] [PubMed] [Google Scholar]
- 21.Mohri H, et al. Increased turnover of T lymphocytes in HIV-1 infection and its reduction by antiretroviral therapy. J Exp Med. 2001;194(9):1277–1287. doi: 10.1084/jem.194.9.1277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Vrisekoop N, et al. Sparse production but preferential incorporation of recently produced naive T cells in the human peripheral pool. Proc Natl Acad Sci USA. 2008;105(16):6115–6120. doi: 10.1073/pnas.0709713105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Westerhof GR, et al. Comparison of different busulfan analogues for depletion of hematopoietic stem cells and promotion of donor-type chimerism in murine bone marrow transplant recipients. Cancer Res. 2000;60(19):5470–5478. [PubMed] [Google Scholar]
- 24.Andersson G, et al. Nonmyeloablative conditioning is sufficient to allow engraftment of EGFP-expressing bone marrow and subsequent acceptance of EGFP-transgenic skin grafts in mice. Blood. 2003;101(11):4305–4312. doi: 10.1182/blood-2002-06-1649. [DOI] [PubMed] [Google Scholar]
- 25.Hsieh MM, et al. Low-dose parenteral busulfan provides an extended window for the infusion of hematopoietic stem cells in murine hosts. Exp Hematol. 2007;35(9):1415–1420. doi: 10.1016/j.exphem.2007.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Seddon BM, Cassoni AM, Galloway MJ, Rees JH, Whelan JS. Fatal radiation myelopathy after high-dose busulfan and melphalan chemotherapy and radiotherapy for Ewing’s sarcoma: A review of the literature and implications for practice. Clin Oncol (R Coll Radiol) 2005;17(5):385–390. doi: 10.1016/j.clon.2005.03.004. [DOI] [PubMed] [Google Scholar]
- 27.Sempowski GD, Gooding ME, Liao HX, Le PT, Haynes BF. T cell receptor excision circle assessment of thymopoiesis in aging mice. Mol Immunol. 2002;38(11):841–848. doi: 10.1016/s0161-5890(01)00122-5. [DOI] [PubMed] [Google Scholar]
- 28.Hsu HC, et al. Age-related thymic involution in C57BL/6J x DBA/2J recombinant-inbred mice maps to mouse chromosomes 9 and 10. Genes Immun. 2003;4(6):402–410. doi: 10.1038/sj.gene.6363982. [DOI] [PubMed] [Google Scholar]
- 29.Johnson PLF, Yates AJ, Goronzy JJ, Antia R. Peripheral selection rather than thymic involution explains sudden contraction in naive CD4 T-cell diversity with age. Proc Natl Acad Sci USA. 2012;109(52):21432–21437. doi: 10.1073/pnas.1209283110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pitcher CJ, et al. Development and homeostasis of T cell memory in rhesus macaque. J Immunol. 2002;168(1):29–43. doi: 10.4049/jimmunol.168.1.29. [DOI] [PubMed] [Google Scholar]
- 31.den Braber I, et al. Maintenance of peripheral naive T cells is sustained by thymus output in mice but not humans. Immunity. 2012;36(2):288–297. doi: 10.1016/j.immuni.2012.02.006. [DOI] [PubMed] [Google Scholar]
- 32.Parretta E, et al. Kinetics of in vivo proliferation and death of memory and naive CD8 T cells: Parameter estimation based on 5-bromo-2′-deoxyuridine incorporation in spleen, lymph nodes, and bone marrow. J Immunol. 2008;180(11):7230–7239. doi: 10.4049/jimmunol.180.11.7230. [DOI] [PubMed] [Google Scholar]
- 33.Berzins SP, Boyd RL, Miller JF. The role of the thymus and recent thymic migrants in the maintenance of the adult peripheral lymphocyte pool. J Exp Med. 1998;187(11):1839–1848. doi: 10.1084/jem.187.11.1839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hale JS, Boursalian TE, Turk GL, Fink PJ. Thymic output in aged mice. Proc Natl Acad Sci USA. 2006;103(22):8447–8452. doi: 10.1073/pnas.0601040103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bains I, Yates AJ, Callard RE. Heterogeneity in thymic emigrants: Implications for thymectomy and immunosenescence. PLoS One. 2013;8(2):e49554. doi: 10.1371/journal.pone.0049554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Yates A, Saini M, Mathiot A, Seddon B. Mathematical modeling reveals the biological program regulating lymphopenia-induced proliferation. J Immunol. 2008;180(3):1414–1422. doi: 10.4049/jimmunol.180.3.1414. [DOI] [PubMed] [Google Scholar]
- 37.Franco RS. Measurement of red cell lifespan and aging. Transfus Med Hemother. 2012;39(5):302–307. doi: 10.1159/000342232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Yates AJ. Theories and quantification of thymic selection. Front Immunol. 2014;5:13. doi: 10.3389/fimmu.2014.00013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Min B, et al. Neonates support lymphopenia-induced proliferation. Immunity. 2003;18(1):131–140. doi: 10.1016/s1074-7613(02)00508-3. [DOI] [PubMed] [Google Scholar]
- 40.Pearson C, Silva A, Saini M, Seddon B. IL-7 determines the homeostatic fitness of T cells by distinct mechanisms at different signalling thresholds in vivo. Eur J Immunol. 2011;41(12):3656–3666. doi: 10.1002/eji.201141514. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.