The Generalized Roy Model and the Cost-Benefit Analysis of Social Programs

Abstract

The literature on treatment effects focuses on gross benefits from program participation. We extend this literature by developing conditions under which it is possible to identify parameters measuring the cost and net surplus from program participation. Using the generalized Roy model, we nonparametrically identify the cost, benefit, and net surplus of selection into treatment without requiring the analyst to have direct information on the cost. We apply our methodology to estimate the gross benefit and net surplus of attending college.

1 Introduction

The traditional approach to the evaluation of public policy compares the benefits and costs of policies. Measures of net surplus are used to determine whether policies should be undertaken (see Hotelling, 1938; Tinbergen, 1956; Harberger and Jenkins, 2002; and Chetty, 2009). The recent literature on program evaluation, or “treatment effects”, focuses on gross benefits of policies and considers neither the marginal costs nor the perceived surplus associated with the programs being evaluated.¹

We extend this literature using the generalized Roy model. In it, agents choose treatment if their expected surplus from doing so is positive, so the benefit outweighs the subjective cost. We present conditions under which we can use the economics of the model to identify cost and surplus parameters even without direct information on the costs of treatment. Information on revealed choices creates a simple relationship between the cost and benefit parameters: for individuals who are indifferent towards treatment participation, the benefit equals the cost and the surplus is zero. Building on existing identification results for benefit parameters, we show how to identify surplus and cost parameters by varying the margin of indifference. Our identification analysis applies traditional exclusion restrictions that separately shift costs and benefits from treatment. We use cost shifters to identify the benefit of treatment, and benefit shifters to vary the margin of indifference and thus to identify the cost of the treatment.

Our analysis complements and extends the work by Björklund and Moffitt (1987) who first noted the duality between cost and benefit parameters in the generalized Roy model. They estimate marginal gains and surpluses for policies within a parametric normal generalized Roy model. They use structural econometric methods to identify the components of the cost and benefit functions. This paper extends their analysis to a more general setting. It develops and applies a nonparametric identification analysis of benefits, costs, and surpluses without the need to identify all of the ingredients of a fully specified structural model. This approach implements Marschak’s Maxim (Heckman, 2010) by directly estimating the cost, benefit, and surplus parameters rather then constructing them from the estimates of a full structural model.

We present ex ante and ex post analyses of costs and benefits. Applying our methods to the data on ex post gross benefits analyzed by Carneiro et al. (2011), we find that heterogeneity in benefits, and not costs, is the main driver of the variability in the decision to attend college.

Our analysis is reminiscent of the Heckman (1974) model of female labor supply. In that analysis, the econometrician observes the offered wage only for the agents who choose to work. The economist does not observe the reservation wage of any agent. Yet, his analysis identifies the parameters of the offered wage equation and the reservation wage equation by using the implication of the underlying economic model that agents decide to work if the offered wage exceeds the reservation wage.² In our analysis, we observe program outcomes for agents who select into treatment, and we observe the no treatment outcome for the agents who do not select into treatment. We do not observe the cost of treatment for any agent. Yet, using the economics of the model, we are able to identify the average benefit and average cost of treatment parameters by exploiting the agent’s decision rule of selecting into treatment if the benefit exceeds the cost.

Our analysis is very different from analyses using randomized experiments to infer treatment effects. In commonly implemented randomizations, it is not possible to identify the choice probability (Heckman, 1992; Heckman and Smith, 1995). Instead of using randomization to bypass problems of self-selection, we exploit the information that agents self-select into treatment and infer information on the cost of the treatment that cannot be recovered by standard randomized experiments.

The paper unfolds in the following way. Section 2 introduces the generalized Roy model. Section 3 reviews the average benefit of treatment parameters from Heckman and Vytlacil (1999, 2005, 2007), and develops and analyzes the dual cost parameters that match the benefit parameters. Section 4 presents our identification analysis of the cost and surplus parameters. Section 5 extends our analysis to allow agents to have imperfect foresight about future outcomes. We apply our analysis to study the decision to attend college in Section 6. Section 7 concludes.

2 The Generalized Roy Model

Suppose there are two potential outcomes (Y₀, Y₁), and a choice indicator D with D = 1 if the agent selects into treatment so that Y₁ is observed and D = 0 if the agent does not select into treatment so that Y₀ is observed. Anticipating our empirical analysis, Y₁ is the annualized flow of income from college, and Y₀ is the annualized flow of income from high school. The observed outcome Y can be written in switching regression form (Quandt, 1958, 1972):

$$Y=D{Y}_1+(1-D)Y_0,$$ (2.1)

where E(Y_j | X) = μ_j and

$$Y_j={\mu }_j(X)+U_j$$ (2.2)

for j = 0, 1. X is a vector of regressors observed by the economist while (U₀, U₁) are not. Combining Equations (2.1) and (2.2),

$$Y={\mu }_0(X)+\{[{\mu }_1(X)-{\mu }_0(X)]+U_1-U_0\}D+U_0.$$

The individual gross benefit of treatment associated with moving an otherwise identical person from state “0” to “1” is B = Y₁ − Y₀ and is defined as the causal effect on Y of a ceteris paribus move from “0” to “1”. Defining E(C | Z) = μ_C(Z), the subjective cost of choosing treatment as perceived by the agent is

$$C={\mu }_C(Z)+U_C,$$ (2.3)

where Z is an observed random vector of cost shifters and U_C is a random variable unobserved by the econometrician. Individuals choose treatment if the perceived benefit from treatment is greater than the subjective cost:

$$D=1\text{if}S\ge 0;D=0\text{otherwise},$$ (2.4)

where S is the surplus, i.e. the net benefit, from treatment:

$$\begin{array}{l}S=(Y_1-Y_0)-C\\ =\{[{\mu }_1(X)-{\mu }_0(X)]-{\mu }_C(Z)\}-[U_C-(U_1-U_0)]\\ ={\mu }_S(X,Z)-V,\end{array}$$

with μ_S(X, Z) = [μ₁(X) − μ₀(X)] − μ_C(Z) and V = U_C − (U₁ − U₀). Our identification analysis of cost and surplus parameters does not assume particular functional forms for μ₀, μ₁, and μ_C, nor does it assume that the distributions of U₀, U₁, and U_C are of a known parametric form.

The original Roy (1951) model assumes that there are no observed regressors, X, that the cost of treatment is identically zero (i.e. μ_C = 0, U_C = 0), and that (U₀, U₁) ~ N(0, Σ). Heckman and Honoré (1990) present an identification analysis for a nonparametric version of the Roy model using variation in regressors and making no parametric assumption on the distribution of (U₀, U₁). Their version of the Roy model also imposes the condition that the cost of treatment is identically zero. In contrast, we allow for nonzero cost of treatment. In fact, for our identification analysis we require nondegenerate cost of treatment and observed cost shifters.³ From the point of view of the observing economist, (X, Z) is observed and (U₁, U₀, U_C) is unobserved. This model assumes that agents know the gross benefit, B = Y₁ − Y₀, of treatment. We show in Section 5 that our results extend to a broader class of models, where agents only have imperfect foresight about the benefits of treatment. This model also supposes that there is no other aspect of the benefit of treatment than Y₁ − Y₀. Implicitly, any subjective benefits of the program are incorporated into the costs of treatment, i.e. the cost function includes the subjective benefits of the treatment. For example, if job training allows the individual to work in a job with preferred amenities, this is modeled as a (negative) contribution to the subjective cost of treatment. The classification of effects in either positive benefits or negative subjective cost (or vice versa) does not affect the definition of the surplus. To simplify the exposition, we suppose that Z and X do not contain any common elements. Thus, all of our analysis can be seen as implicitly conditioning on all common elements of X and Z.

We make the following technical assumptions:

(A-1) (U₀, U₁, U_C) is independent of (X, Z).

(A-2) The distribution of μ_C(Z) conditional on X is absolutely continuous with respect to Lebesgue measure.

(A-3) The distribution of V = U_C − (U₁ − U₀) is absolutely continuous with respect to Lebesgue measure and has a cumulative distribution function that is strictly increasing.

(A-4) The population means E|Y₁|, E|Y₀| and E|C| are finite.

Assumption (A-1) assumes that (U₀, U₁, U_C) is independent of (X, Z). Thus, D is endogenous but all other regressors in both the treatment equation and the outcome equation are exogenous. We implicitly condition on any regressors that enter both the outcome equations and the cost equation. Thus, this condition should be interpreted as an independence assumption for the error terms with regard to the unique elements of X and Z conditional on the regressors that enter both equations. No independence condition is required for the common elements. We also do not impose any restrictions on the dependence among the unobservables. (A-2) requires that there exists at least one continuous component of Z conditional on X. This assumption will only be required for our identification analysis, and is not needed for our definition or analysis of the cost and surplus parameters. (A-3) is a regularity condition. It allows for the possibility that U_C is degenerate (costs do not vary conditional on Z) or that U₁ − U₀ is degenerate (benefits do not vary conditional on X), though not both. Assumption (A-4) is required for the mean benefit and cost parameters to be well defined. An implication of our model with Assumptions (A-1) and (A-3) is that 0 < Pr(D = 1 | X, Z) < 1 w.p.1, so that there is a treated group and a control group for almost all (X, Z). Note that this restriction still allows the support of the distribution of Pr(D = 1|X, Z) to be the full unit interval.

Let P(X, Z) denote the probability of selecting into treatment given (X, Z). Statisticians call this the “propensity score” P(X, Z) ≡ Pr(D = 1 | X, Z) = F_V(μ_S(X, Z)), where F_V(·) denotes the distribution of V.⁴ We sometimes denote P(X, Z) by P, suppressing the (X, Z) argument. We also work with U_S, a uniform random variable (U_S ~ Unif[0, 1]) defined by U_S = F_V(V). Different values of U_S denote different quantiles of V. Given our previous assumptions, F_V is strictly increasing, and P(X, Z) is a continuous random variable conditional on X.

The generalized Roy model presented in this paper is a special case of the model of Heckman and Vytlacil (1999, 2005). Under Assumptions (A-1)–(A-4), the model of Equations (2.1)–(2.4) implies the model and assumptions of Heckman and Vytlacil (1999, 2005). From the analysis of Vytlacil (2002), the more general model is equivalent to the conditions that justify the Local Average Treatment Effect (LATE) model of Imbens and Angrist (1994). We impose more restrictions here. In particular, we impose the generalized Roy model and the corresponding assumptions that will allow us to exploit its structure for identification of subjective cost parameters. As in the conventional Roy model (Heckman and Sedlacek, 1985), we assume additive separability in the outcome equations. Additive separability is not required in Heckman and Vytlacil (1999, 2005), but is required by our analysis in order to obtain additive separability in the latent index equation consistent with the generalized Roy model.⁵ Thus our assumptions are most appropriate for continuous outcome variables, and we exclude discrete outcomes from our analysis. We also assume conditions on X that are not required in Heckman and Vytlacil (1999, 2005) to identify the gross benefit parameters. Their analysis conditions on X, and thus does not need to assume that X is independent of the error vector. In contrast, in order to use the generalized Roy model to recover subjective cost parameters, we require that the unique elements X are independent of the error vector.⁶

3 Benefit, Cost, and Surplus Parameters

This section defines and analyzes the benefit, cost, and surplus parameters. We maintain the model of Equations (2.1)–(2.4), and invoke Assumptions (A-1) and (A-3)–(A-4). We do not require Assumption (A-2) for the definition of the parameters, but do require it for our identification analysis.

Standard treatment effect analyses identify averaged parameters of the gross benefit of treatment, B = Y₁ − Y₀. The most commonly studied treatment effect parameter is the average benefit of treatment B^ATE(x) ≡ E(Y₁ − Y₀ | X = x) = μ₁(x) − μ₀(x). This is the effect of assigning treatment randomly to everyone of type X = x assuming full compliance, and ignoring any general equilibrium effects. Another commonly used parameter is the average benefit of treatment on persons who actually take the treatment, referred to as the benefit of treatment on the treated: B^TT(x) ≡ E(Y₁ − Y₀ | X = x, D = 1) = μ₁(x) − μ₀(x) + E(U₁ − U₀|X = x, D = 1). Heckman and Vytlacil (1999, 2005) unify a broad class of treatment effect parameters including the B^ATE(x) and B^TT(x) through the marginal benefit of treatment, defined as B^MTE(x, u_S) ≡ E(Y₁ − Y₀|X = x, U_S = u_S) = μ₁(x) − μ₀(x) + E(U₁ − U₀|U_S = u_S). B^MTE(x, u_S) is the treatment effect parameter that conditions on the unobserved desire to select into treatment.

The conventional analysis of treatment effects does not define, identify, or estimate any aspect of the cost of the treatment. We define a set of cost parameters parallel to the benefit parameters, where cost is the subjective cost as perceived by the agent. Thus, we define the average cost of treatment, the average cost of treatment on the treated, and the marginal cost of treatment as follows:

$$\begin{array}{lllll}{C}^{\mathit{ATE}}(z)\hfill & =\hfill & E(C\mid Z=z)\hfill & =\hfill & {\mu }_C(z)\hfill \\ C^{TT}(z)\hfill & =\hfill & E(C\mid Z=z,D=1)\hfill & =\hfill & {\mu }_C(z)+E(U_C\mid Z=z,D=1)\hfill \\ C^{\mathit{MTE}}(z,u_S)\hfill & =\hfill & E(C\mid Z=z,U_S=u_S)\hfill & =\hfill & {\mu }_C(z)+E(U_C\mid U_S=u_S).\hfill \end{array}$$

Recalling that S = B − C = μ_S(X, Z) − V, where μ_S(X, Z) = [μ₁(X) − μ₀(X)] − μ_C(Z) and V = U_C − (U₁ − U₀), we can define the corresponding surplus parameters:

$$\begin{array}{lllll}{S}^{\mathit{ATE}}(x,z)\hfill & =\hfill & E(S\mid X=x,Z=z)\hfill & =\hfill & {\mu }_S(x,z)\hfill \\ S^{\mathit{MTE}}(x,z,u_S)\hfill & =\hfill & E(S\mid X=x,Z=z,U_S=u_S)\hfill & =\hfill & {\mu }_S(x,z)-E(V\mid U_S=u_S)\hfill \end{array}$$

and

$$\begin{array}{lllll}{S}^{TT}(x,z)\hfill & =\hfill & E(S\mid X=x,Z=z,D=1)\hfill & =\hfill & {\mu }_S(x,z)-E(V\mid X=x,Z=z,D=1).\hfill \end{array}$$

With these parameters, we can answer questions not only about the outcome change from treatment, but also about the subjective cost of treatment and the net surplus as well. As the surplus from treatment participation S^TT(x, z) is always positive among the treated, it follows immediately that B^TT(x) > C^TT(z) holds as well. Following Heckman and Vytlacil (1999, 2005), we can represent the average treatment effects and treatment on the treated as averaged versions of the marginal effects of treatment:

$$\begin{array}{lll}{B}^{\mathit{ATE}}(x)\hfill & =\hfill & {\int }_0^1{B}^{\mathit{MTE}}(x,u_S){du}_S\hfill \\ B^{TT}(x)\hfill & =\hfill & {\int }_0^1{B}^{\mathit{MTE}}(x,u_S)\frac{1-F_{P\mid X}(u_S\mid x)}{{\int }_0^1(1-F_{P\mid X}(t\mid x))dt}{du}_S.\hfill \end{array}$$ (3.1)

Following the same line of argument as used by Heckman and Vytlacil (1999, 2005),

$$\begin{array}{lll}{C}^{\mathit{ATE}}(z)\hfill & =\hfill & {\int }_0^1{C}^{\mathit{MTE}}(z,u_S){du}_S\hfill \\ C^{TT}(z)\hfill & =\hfill & {\int }_0^1{C}^{\mathit{MTE}}(z,u_S)\frac{1-F_{P\mid Z}(u_S\mid z)}{{\int }_0^1(1-F_{P\mid Z}(t\mid z))dt}{du}_S,\hfill \end{array}$$ (3.2)

and

$$\begin{array}{lll}{S}^{\mathit{ATE}}(x,z)\hfill & =\hfill & {\int }_0^1{S}^{\mathit{MTE}}(x,z,u_S){du}_S\hfill \\ S^{TT}(x,z)\hfill & =\hfill & \frac{1}{P(x,z)}{\int }_0^{P(x,z)}{S}^{\mathit{MTE}}(x,z,u_S){du}_S.\hfill \end{array}$$ (3.3)

We now establish relationships among these parameters. First, consider the marginal surplus parameter. Recall that U_S = F_V(V) with F_V strictly increasing. Thus U_S = u_S is equivalent to $V=F_V^{-1}(u_S)$, and

$$S^{\mathit{MTE}}(x,z,u_S)={\mu }_S(x,z)-E(V\mid V=F_V^{-1}(u_S))={\mu }_S(x,z)-F_V^{-1}(u_S).$$

$F_V^{-1}$ is strictly increasing, and thus S^MTE(x, z, u_S) is strictly decreasing in u_S. Individuals with low u_S want to enter the program the most and are those with the highest surplus from the program, while individuals with high u_S want to enter the program the least and have the smallest surplus from the program. Using the fact that F_V is strictly increasing and that P(X, Z) = F_V(μ_S(X, Z)), conditioning on u_s = P(x, z) is equivalent to conditioning on V = μ_S(x, z). Thus

$$S^{\mathit{MTE}}(x,z,P(x,z))={\mu }_S(x,z)-E(V\mid V={\mu }_S(x,z))=0.$$

An individual with u_S = P(x, z) is an individual who is indifferent between being treated and untreated if assigned X = x and Z = z. Since S^MTE(x, z, u_S) is strictly decreasing in u_S, S^MTE(x, z, u_S) is positive for u_S < P(x, z), is equal to zero at u_S = P(x, z), and is negative if u_S > P(x, z). If we instead fix evaluation point u_S and consider how S^MTE(x, z, u_S) varies with (x, z), S^MTE(x, z, u_S) will be positive for all (x, z) such that P(x, z) > u_S and will be negative for all (x, z) such that P(x, z) < u_S.

We have thus far discussed only the marginal surplus function. Using the relationship S^MTE(x, z, u_S) = B^MTE(x, u_S)−C^MTE(z, u_S), we can translate statements about S^MTE(x, z, u_S) into inequalities about the marginal benefit and marginal cost functions:

$$\begin{array}{lllll}{B}^{\mathit{MTE}}(x,u_S)\hfill & >\hfill & C^{\mathit{MTE}}(z,u_S)\hfill & \forall \hfill & (x,z,u_S)\text{s.t.}P(x,z)>u_S\hfill \\ B^{\mathit{MTE}}(x,u_S)\hfill & =\hfill & C^{\mathit{MTE}}(z,u_S)\hfill & \forall \hfill & (x,z,u_S)\text{s.t.}P(x,z)=u_S\hfill \\ B^{\mathit{MTE}}(x,u_S)\hfill & <\hfill & C^{\mathit{MTE}}(z,u_S)\hfill & \forall \hfill & (x,z,u_S)\text{s.t.}P(x,z)<u_S.\hfill \end{array}$$

The benefit and cost parameters coincide when evaluated at u_S = P(x, z), because at this point the marginal cost equals the marginal benefit. We exploit this equality at the margin of indifference in the next section to achieve identification of the cost parameters.

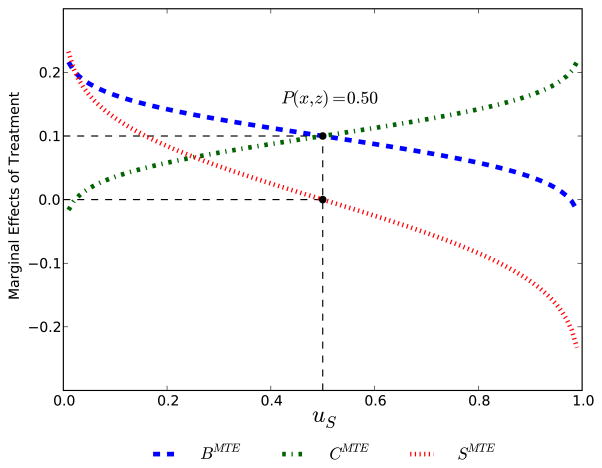
To fix ideas, in Figure 1 we display the full set of marginal effects for a numerical example. We plot the marginal effect functions for fixed values of (x, z), where it happens that P(x, z) = 0.50. Individuals at that margin, u_S = 0.50, have their benefit of treatment just offset by their subjective cost and are thus indifferent between participation in treatment and nonparticipation. The benefits are positive, but so are the costs. Overall, the surplus is zero. For u_S < 0.50, the marginal benefit function lies above the marginal cost function and thus the marginal surplus is strictly positive. The reverse is true for u_S > 0.50.

Figure 1.

Marginal Effects of Treatment

This example is constructed to have intuitive properties, with the marginal benefit of treatment B^MTE(x, u_S) decreasing in u_S and the marginal cost of treatment C^MTE(z, u_S) increasing in u_S. Agents with the greatest unobserved desire to select into treatment not only have higher benefits, but also have lower costs. These properties, while intuitive, need not hold in general—individuals with lower values of u_S (and thus a greater unobserved desire to take treatment) must necessarily have higher net surplus than those with higher values of u_S, but they need not have higher benefits and lower costs. It is possible, for example, that benefits and costs are so strongly positively correlated that those with the greatest unobserved desire to participate have either the smallest benefits and the lowest costs or the largest benefits and the highest costs. In Appendix A, we establish sufficient conditions for intuitive properties on B^MTE(x, u_S) and C^MTE(z, u_S) to hold, as well as testable implications of those conditions.

4 Identifying the Surplus and Benefit Functions Nonparametrically

Heckman and Vytlacil (1999, 2005) show that local instrumental variables (LIV) identify the marginal benefit of treatment:

$$\frac{\partial E(Y\mid X=x,P=p)}{\partial p}=B^{\mathit{MTE}}(x,p).$$ (4.1)

We can identify E(Y|X = x, P = p) and its derivative for all (x, p) ∈ Supp(X, P), where Supp(X, P) denotes the support of (X, P(X, Z)).⁷ We can thus identify B^MTE(x, u_S) for all values of (x, u_S) ∈ Supp(X, P). For a fixed x, we can identify B^MTE(x, u_S) for u_S ∈ Supp(P|X = x). The more variation in propensity scores P conditional on X = x, the larger the set of evaluation points u_S for which we identify B^MTE(x, u_S). Variation in propensity scores conditional on X is driven by variation in Z, the cost shifters. Thus, if we observe regressors that produce large variations in costs, we will be able to identify B^MTE(x, u_S) on a larger set.

We can identify B^ATE(x) and B^TT(x) by identifying B^MTE(x, u_S) over the appropriate support and then integrating the latter with the appropriate weights, which are known given data on X and Z. By Equation (3.1), we identify B^ATE(x) if Supp(P|X = x) = [0, 1]. For fixed X = x, this requires that there be enough variation in the cost shifters Z to drive the probabilities P(x, Z) all the way to zero and to one. In other words, holding fixed the regressors that enter the outcome equation, we must observe cost shifters such that conditional on some values of those cost shifters, the cost to the agent is so low that the agent will select into treatment with probability arbitrarily close to one, and, conditional on other values of the cost shifters, the cost to the agent is so high that the agent will select into treatment with probability arbitrarily close to zero. Likewise, we identify B^TT(x) if $\text{Supp}(P\mid X=x)=[0,p_x^{\mathit{max}}]$ where $p_x^{\mathit{max}}$ is the supremum of Supp(P|X = x). This support requirement in turn requires that, for fixed X = x, there be enough variation in the cost shifters Z to drive the selection probability arbitrarily close to zero.⁸

Using Equation (4.1) and the relationship for people on the margin of choice that B^MTE(x, P(x, z)) = C^MTE(z, P(x, z)), we have

$${\frac{\partial E(Y\mid X=x,P=p)}{\partial p}|}_{p=P(x,z)}=C^{\mathit{MTE}}(z,P(x,z)).$$ (4.2)

Using this relationship, we identify C^MTE(z, u_S) for all values of (z, u_S) ∈ Supp(Z, P). We thus identify the marginal cost parameter without direct information on the cost of treatment by using the structure of the Roy model and by identifying the marginal benefit of treatment for individuals at the margin of participation. For a fixed z, we identify C^MTE(z, u_S) for u_S ∈ Supp(P|Z = z). The greater the variation in propensity scores conditional on Z = z, the larger the set of evaluation points for which we identify C^MTE(z, u_S). Variation in propensity scores conditional on Z = z is driven by variation in X, the regressors that affect the potential outcomes and thus that drive the benefit of treatment. If we observe X regressors that cause large variations in benefits, we will be able to identify C^MTE(z, u_S) at a larger set of u_S evaluation points. In contrast, if there are no X regressors, then P only depends on Z and we can only identify C^MTE(z, u_S) for u_S = P(z).

From Equation (3.2), we can identify C^ATE(z) if Supp(P|Z = z) = [0, 1]. This requires, for fixed Z = z, for there to be enough variation in the outcome shifters X to drive the probabilities P(X, Z) all the way to zero and to one. In other words, holding fixed the regressors that enter the cost equation, we must observe outcome shifters such that conditional on some values of those outcome shifters, the benefit to the agent is so high that the agent will select into treatment with probability arbitrarily close to one; conditional on other values of the outcome shifters, the benefit to the agent is so low that the agent will select into treatment with probability arbitrarily close zero. Likewise, we identify C^TT(x) if $\text{Supp}(P\mid Z=z)=[0,p_z^{\mathit{max}}]$ where $p_z^{\mathit{max}}$ is the supremum of Supp(P|Z = z). This support requirement in turn requires that, for fixed Z = z, there is sufficient variation in the outcome shifters X to drive the probabilities arbitrarily close to zero.

Finally, consider identification of the surplus parameters. Using the fact that

$$S^{\mathit{MTE}}(x,z,u_S)=B^{\mathit{MTE}}(x,u_S)-C^{\mathit{MTE}}(z,u_S),$$

we can identify the marginal surplus parameter at (x, z, u_S) such that (x, u_S) ∈ Supp(X, P) and (z, u_S) ∈ Supp(Z, P). By Equation (3.3), we can integrate S^MTE(x, z, u_S) using the appropriate weights (which are identified from the data on X and Z) to identify S^ATE(x, z) and S^TT(x, z) under the appropriate support conditions. For example, we identify S^ATE(x, z) if Supp(P|X = x) = [0, 1] and Supp(P|Z = z) = [0, 1].

Thus, for identification of the treatment parameters we need sufficient variation in cost shifters conditional on the outcome shifters. For identification of the cost parameters, we need sufficient variation in the outcome shifters conditional on the cost shifters. For identification of the surplus parameters we need sufficient variation in both sets of regressors. We can thus identify the marginal cost, the average cost, and the cost of treatment without direct information on the cost. Consequently, we can also identify the corresponding surplus parameters as well. Our ability to do so is directly related to the extent of variation in observed regressors that shift the benefit of the treatment.

We summarize our discussion in the form of a theorem:

Theorem 1

Assume that Equations (2.1)–(2.4) and our Assumptions (A-1)–(A-4) hold.

1. B^MTE(x, u_S) is identified for (x, u_S) ∈ Supp(X, P); C^MTE(z, u_S) is identified for (z, u_S) ∈ Supp(Z, P); and S^MTE(x, z, u_S) is identified for (x, z, u_S) such that (x, u_S) ∈ Supp(X, P) and (z, u_S) ∈ Supp(Z, P).

2. B^ATE(x) is identified if Supp(P|X = x) = [0, 1]; C^ATE(z) is identified if Supp(P|Z = z) = [0, 1]; S^ATE(x, z) is identified if Supp(P|X = x) = [0, 1] and Supp(P|Z = z) = [0, 1].

3. B^TT(x) is identified if $\mathit{Supp}(P\mid X=x)=[0,p_x^{\mathit{max}}]$; C^TT(z) is identified if $\mathit{Supp}(P\mid Z=z)=[0,p_z^{\mathit{max}}]$; S^TT(x, z) is identified if $\mathit{Supp}(P\mid X=x)=[0,p_x^{\mathit{max}}]$ and $\mathit{Supp}(P\mid Z=z)=[0,p_z^{\mathit{max}}]$.

Our results allow for unobserved heterogeneity in costs and benefits conditional on the observed regressors. If there is no unobserved (by the economist) heterogeneity in the costs of treatment, U_C = 0, then C^MTE(z, u_S) = C^TT(z) = C^ATE(z) and thus we can identify the cost of treatment on the treated and average cost parameters without the additional support conditions. Likewise, if we impose that there is no unobserved heterogeneity in the benefits of treatment, U₁ − U₀ = 0, we have B^MTE(z, u_S) = B^TT(z) = B^ATE(z) and can thus identify all of the benefit parameters without additional support conditions.

We establish identification of the marginal effect parameters within the conditional support of P. However, exploiting additive separability, we are able to extend the margin of identification to the unconditional support of P by a chaining argument. We illustrate the reasoning behind this for the B^MTE(x, u_S), but the analogous result applies to the marginal cost and surplus functions as well.

Recall that B^MTE(x, u_S) = μ₁(x) − μ₀(x) + E(U₁ − U₀|U_S = u_S) is identified for all (x, u_S) ∈ Supp(X, P). How B^MTE(x, u_S) varies with x does not depend on the point of evaluation of u_S, and how B^MTE(x, u_S) varies with u_S does not depend on the point of evaluation of x. This insight is helpful in securing identification of B^MTE(x, u_S) for other (x, u_S) pairs.

For example, consider two potential values of X, x₀ and x₁, and suppose that there exists some p^* such that p^* ∈ Supp(P|X = x₀) ∩ Supp(P|X = x₁) so that B^MTE(x₀, p^*) and B^MTE(x₁, p^*) are both identified by Theorem 1. B^MTE(x, u_S) is additively separable in x and u_S. As a consequence of additive separability, it follows directly that

$$B^{\mathit{MTE}}(x_0,u_S)-B^{\mathit{MTE}}(x_0,p^{\ast })=B^{\mathit{MTE}}(x_1,u_S)-B^{\mathit{MTE}}(x_1,p^{\ast }).$$ (4.3)

If u_S ∈ Supp(P|X = x₁), we identify B^MTE(x₁, u_S) by Theorem 1. We can solve Equation (4.3) to identify B^MTE(x₀, u_S) even if u_S ∉ Supp(P|X = x₀). Alternatively, if u_S ∈ Supp(P|X = x₀), we identify B^MTE(x₀, u_S) by Theorem 1 and can now solve Equation (4.3) to identify B^MTE(x₁, u_S) even if u_S ∉ Supp(P|X = x₁). Thus, if there exists some p^* such that p^* ∈ Supp(P|X = x₀) ∩ Supp(P|X = x₁), we can chain together identification of B^MTE(x₀, u_S) for u_S ∈ Supp(P|X = x₀) and identification of B^MTE(x₁, u_S) for u_S ∈ Supp(P|X = x₁) to obtain identification of B^MTE(x₀, u_S) and B^MTE(x₁, u_S) for all u_S ∈ Supp(P|X = x₀) ∪ Supp(P|X = x₁). One can iterate to further increase the range of values for which B^MTE(x, u_S) is identified. Under an additional rank condition, we can use this strategy to identify B^MTE(x, u_S) for all (x, u_S) ∈ Supp(X) × Supp(P). In particular, we consider the following assumption:

(A-5) X and P(X, Z) are measurably separated; i.e., any function of X that almost surely equals a function of P(X, Z) must be almost surely equal to a constant.

Measurable separability between X and P is a rank condition. A necessary condition for measurable separability between X and P(X, Z) is for P(X, Z) to be nondegenerate conditional on X, as implied by P(X, Z) = F_V(μ_S(X, Z)) along with Assumptions (A-2) and (A-3). In Theorem 5 in Appendix A, we build on Theorem 2 of Florens et al. (2008) to provide sufficient conditions on our model for measurable separability between X and P(X, Z). As shown by that theorem, strengthened versions of Assumptions (A-2) and (A-3), along with an additional support condition, are sufficient for measurable separability between X and P(X, Z).

Using Assumption (A-5), we obtain the following identification result:

Theorem 2

Assume that Equations (2.1)–(2.4) and our Assumptions (A-1)–(A-5) hold. Then, for x ∈ Supp(X) and z ∈ Supp(Z),

1. B^MTE(x, u_S), C^MTE(z, u_S) and S^MTE(x, z, u_S) are identified for u_S ∈ Supp(P).

2. B^ATE(x), C^ATE(z) and S^ATE(x, z) are identified if Supp(P) = [0, 1], and

3. B^TT(x), C^TT(z) and S^TT(x, z) are identified if Supp(P) = [0, p^max].

The proof of Theorem 2 is in Appendix B. The theorem shows that, under our maintained assumptions and condition (A-5), identification of the treatment parameters depends on the marginal support of P, not on the support of P conditional on X or Z.

5 Extension to the Case of Limited Information by the Agent

Thus far, our analysis has assumed choice Equation (2.4), i.e., that D = 1[S ≥ 0] where S = (Y₁ − Y₀) − C. This implicitly assumes that agents have perfect foresight about their net benefit. In this section, we extend the choice model of Equation (2.4) to allow for limited information on the part of the agents, while maintaining the model for latent outcomes (Y₀, Y₁) and cost C of Equations (2.2) and (2.3). We assume that agents form valid expectations about their outcomes and costs given the information that they have at the time of their treatment choice and that they select into treatment if the expected surplus is positive. We allow agents to know only some elements of (X, Z), and possibly to have incomplete knowledge of (U₀, U₁, U_C) and hence their own idiosyncratic benefit and cost of treatment. We now show that the preceding analysis goes through with minor modifications, though it is now important to distinguish conditioning sets: what is known to the agent at the time of treatment choice (which might include some information not known to the econometrician), what is known to the econometrician (which might include some information not known to the agent at the time of treatment choice), and what is realized ex post. The essential change in our procedure in the case of incomplete information is that the marginal benefit of treatment identified by LIV must be projected onto the agent’s information set when selecting treatment to form the expected marginal benefit of treatment conditional on the information available to the agent. This coarsened version of B^MTE is used to identify the marginal cost parameter. In addition, only components of X that are known to the agent at the time of treatment choice can aid in identification of the cost parameters. The exclusion restrictions for identification of the cost parameter are variables in X that are not in Z and that are known to the agent at the time of choosing treatment.

Let (X_I, Z) denote components of (X, Z) that are observed by the agent when choosing whether to select into treatment.⁹ Suppose that the agent’s information set is (X_I, Z, U_I).¹⁰ U_I is the private information of the agent relevant to his or her own benefits and cost of treatment, and is not observed by the econometrician.

We revise assumption (A-1) in the following way:

(A-1′) (U₀, U₁, U_C, U_I) is independent of (X, Z), and X is independent of Z conditional on X_I.

Assumption (A-1′) imposes the requirement that the private information of the agent is independent of the observed regressors. Note that, under this independence assumption, (U₀, U₁, U_C, U_I) ⫫ (X_I, Z), and

$$E(V\mid X,Z,U_I)=E(V\mid X_I,Z,U_I)=E(V\mid U_I),$$

using the definition V = U_C − (U₁ − U₀).

Assumption (A-1′) implies that (X, Z) ⫫ U_I | (X_I, Z), so that U_I does not help the agent predict elements of (X, Z) that are not contained in (X_I, Z). Thus, we allow the agents to have private information about their own idiosyncratic benefits (U₁ − U₀) and costs U_C, though we impose the restriction that the only information known by the agent that is useful for predicting X is (X_I, Z). Furthermore, Assumption (A-1′) requires that, conditional on the components of X known to the agent at the time of selecting into treatment, Z does not help to predict those elements of X not known at the time of treatment selection. This restriction is only imposed for notational convenience and can be easily relaxed.

We restate Assumption (A-3) as:

(A-3′) The distribution of Ṽ = E(V|U_I) is absolutely continuous with respect to Lebesgue measure, and the cumulative distribution function of Ṽ is strictly increasing.

An implication of (A-3′) is that E(V|U_I) is a nondegenerate random variable, and thus that agents have some nontrivial information about their own idiosyncratic cost or benefit from treatment when deciding whether to select into treatment. We maintain Assumptions (A-2) and (A-4) as before.

Define ${\mu }_j^I(X_I)=E(Y_j\mid X_I)$ for j = 0, 1, and ${\mu }_C^I(Z)=E(C\mid Z)$, and note that given our independence assumptions and the law of iterated expectations, ${\mu }_j^I(X_I)=E({\mu }_j(X)\mid X_I),{\mu }_C^I(Z)=E({\mu }_C(Z)\mid Z)$. Define ${\mu }_S^I(X_I,Z)=E(S\mid X_I,Z)$. Under our assumptions,

$$E(S\mid X_I,Z,U_I)={\mu }_S^I(X_I,Z)-\stackrel{\sim }{V}={\mu }_1^I(X_I)-{\mu }_0^I(X_I)-{\mu }_C^I(Z)-\stackrel{\sim }{V}.$$

The decision rule becomes

$$D=1\text{if}E(S\mid X_I,Z,U_I)\ge 0;D=0\text{otherwise},$$ (5.1)

where E(S|X_I, Z, U_I) is the expected surplus from treatment, with the expectation conditional on the agents information set. We thus have

$$D=\mathbf{1}[{\mu }_S^I(X_I,Z)-\stackrel{\sim }{V}\ge 0],$$

where our independence assumptions imply Ṽ ⫫ (X_I, Z), and thus the selection model is of the same form as that used by Heckman and Vytlacil (1999), which allows us to use LIV to identify B^MTE(x, u_S). Redefining U_S = F_Ṽ(Ṽ) and $P(X_I,Z)=Pr[D=1\mid X_I,Z]=F_{\stackrel{\sim }{V}}({\mu }_S^I(X_I,Z))$, we have

$$D=\mathbf{1}[P(X_I,Z)-U_S\ge 0],$$

with U_S distributed unit uniform and independent of (X, Z) and thus independent of (X_I, Z).

Define $B_I^{\mathit{MTE}}(x_I,u_S)\equiv E(Y_1-Y_0\mid X_I=x_I,U_S=u_S),C_I^{\mathit{MTE}}(z,u_S)\equiv E(C\mid Z=z,U_S=u_S)$, and $S_I^{\mathit{MTE}}(x_I,z,u_S)\equiv B_I^{\mathit{MTE}}(x_I,u_S)-C_I^{\mathit{MTE}}(z,u_S)$, the marginal benefit, cost, and net surplus of treatment conditional on the agent’s information set, where again by the law of iterated expectations and our independence assumptions

$$\begin{array}{lllll}{B}_I^{\mathit{MTE}}(x_I,u_S)\hfill & =\hfill & E(B^{\mathit{MTE}}(X,u_S)\mid X_I=x_I,U_S=u_S)\hfill & =\hfill & E(B^{\mathit{MTE}}(X,u_S)\mid X_I=x_I)\hfill \\ C_I^{\mathit{MTE}}(z,u_S)\hfill & =\hfill & E(C^{\mathit{MTE}}(Z,u_S)\mid Z=z,U_S=u_S)\hfill & =\hfill & E(C^{\mathit{MTE}}(Z,u_S)\mid Z=z).\hfill \end{array}$$

Evaluating $S_I^{\mathit{MTE}}(x_I,z,u_S)$ at u_S = P(x_I, z), we obtain

$$\begin{array}{l}{S}_I^{\mathit{MTE}}(x_I,z,P(x_I,z))={\mu }_S^I(x_I,z)-E(V\mid U_S=P(x_I,z))\\ ={\mu }_S^I(x_I,z)-E(V\mid \stackrel{\sim }{V}={\mu }_S^I(x_I,z))\\ ={\mu }_S^I(x_I,z)-E(V\mid E(V\mid U_I)={\mu }_S^I(x_I,z))\\ ={\mu }_S^I(x_I,z)-E(E(V\mid U_I)\mid E(V\mid U_I)={\mu }_S^I(x_I,z))\\ ={\mu }_S^I(x_I,z)-{\mu }_S^I(x_I,z)\\ =0,\end{array}$$

where the second equality is obtained by plugging in the definition of U_S, the third equality is obtained by plugging in the definition of Ṽ, and the fourth equality is obtained using the law of iterated expectations and the fact that E(V|U_I) is degenerate given U_I. Since $S_I^{\mathit{MTE}}(x_I,z,u_S)=B_I^{\mathit{MTE}}(x_I,u_S)-C_I^{\mathit{MTE}}(z,u_S)$, we have

$$B_I^{\mathit{MTE}}(x_I,u_S)=C_I^{\mathit{MTE}}(z,u_S)\text{for}{u}_S\text{such}\text{that}{u}_S=P(x_I,z).$$

Thus, identification of $B_I^{\mathit{MTE}}(x_I,P(x_I,z))$ provides identification of $C_I^{\mathit{MTE}}(z,P(x_I,z))$.

Since our model is a special case of Heckman and Vytlacil (1999), we can follow them in using LIV to identify B^MTE(x, u_S) for (x, u_S) in the support of (X, P(X_I, Z)). It is important to note that LIV does not identify the B^MTE(x, u_S) that is relevant to the agent’s decision problem. LIV identifies B^MTE(x, u_S) = E(Y₁ − Y₀|X = x, U_S = u_S), not $B_I^{\mathit{MTE}}(x_I,u_S)=E(Y_1-Y_0\mid X_t=x_I,U_S=u_S)$. However, we can project the B^MTE(x, u_S) identified by LIV on the information known to the agent at the time of selecting into treatment and coarsen the set used to define and identify B^MTE(x, u_S), to identify the $B_I^{\mathit{MTE}}(x_I,u_S)$ relevant to the agent’s decision problem. It is the latter that is relevant for identifying the cost functions. By the law of iterated expectations, we obtain

$$B_I^{\mathit{MTE}}(x_I,u_S)=E(B^{\mathit{MTE}}(X,u_S)\mid X_I=x_I)=\int B^{\mathit{MTE}}(x,u_S)d{F}_x(x\mid X_I=x_I),$$ (5.2)

where F_X(·|X_I = x_I) is the cumulative distribution function of X conditional on X_I = x_I. We directly identify F_X(·|X_I = x_I), and thus, for given u_S, obtain identification of B^MTE(x, u_S) for all x ∈ Supp(X|X_I = x_I) implies identification of $B_I^{\mathit{MTE}}(x_I,u_S)$. Since, for a given x, we identify B^MTE(x, u_S) if u_S ∈ Supp(P(X_I, Z)|X = x), we thus identify $B_I^{\mathit{MTE}}(x_I,u_S)$ if

$$u_S\in \underset{x\in \text{Supp}(X\mid X_I=x_I)}{\cap }\text{Supp}(P(X_I,Z)\mid X=x).$$

In other words, to identify ex ante $B_I^{\mathit{MTE}}(x_I,u_S)$, we need to identify ex post B^MTE(x, u_S) for every value x that X can take given X_I = x_I, and thus we need for u_S to be an element of Supp(P(X_I, Z)|X = x) for each value x that X can take given X_I = x_I. However, using the fact that X_I is a subvector of X and independence assumption (A-1′), it follows that Supp(P(X_I, Z)|X) = Supp(P(X_I, Z)|X_I), and thus using Equation (5.2) we identify $B_I^{\mathit{MTE}}(x_I,u_S)$ for (x_I, u_S) in the support of (X_I, P(X_I, Z)). Using the fact that $B_I^{\mathit{MTE}}(x_I,P(x_I,z))=C_I^{\mathit{MTE}}(z,P(x_I,z))$, we identify $C_I^{\mathit{MTE}}(z,u_S)$ for (z, u_S) in the support of (Z, P(X_I, Z)). We have thus identified the marginal cost parameter, and can integrate it to obtain other cost parameters. We can also combine it with the benefit parameters to identify net surplus parameters as before. The only elements of X that are useful for identifying the cost parameters are those elements that are in X, but not in Z, and which are known to the agent at the time of selection into treatment (i.e., are contained in X_I).

6 Estimating the Cost and Surplus from Educational Choices

We apply our methodology to an analysis of educational choice and estimate the marginal benefit, cost, and surplus from a college education. Carneiro et al. (2011) provide estimates of the marginal benefit of attending college. We extend their work by adding results for the subjective cost and surplus. Björklund and Moffitt (1987) provide fully parametric estimates of cost and surplus in the context of a manpower training program in Sweden. Application of their approach offers a useful benchmark to gauge our more flexible estimation strategy. Our nonparametric identification analysis follows Marschak (1953) who noted that for many policy analyses only combinations of structural parameters are required. We embrace Marschak’s Maxim (Heckman, 2010) and implement an estimation strategy with minimal assumptions and transparent sources of identification for the marginal effects of treatment.

We analyze a sample of 1,747 white males from the National Longitudinal Survey of Youth of 1979 (NLSY79).¹¹ The outcome variable is the log of the mean non-missing values of the hourly wage between 1989 and 1993, which we interpret as an estimate of the log hourly wage in 1991, and an approximation to the long-run wage. Schooling is measured in 1991 when individuals are between 28 and 34 years of age. We separate individuals into two groups: persons with no college (D = 0) and persons with at least some college (D = 1). We present annualized returns to education, obtained by dividing all our estimates by four which is the average difference in years of schooling between those with D = 1 and those with D = 0.

To identify the $C_I^{\mathit{MTE}}(z,u_S)$, we require variables that do not affect the cost of attending college, but that change future wages and are known to the agent at college entry (benefit shifters). We measure long-run labor market conditions by permanent local wages and compute average earnings between 1973 and 2000 for each location of residence at 17 as a proxy. Since we will also condition on current labor market conditions at the time of potential enrollment, these regressors should only affect the schooling decision through their effect on agent’s expected future wages and thus the expected benefit of treatment. We assume that the main benefits to a higher education are through earnings. Any other subjective benefits, such as allowing access to jobs with preferred amenities, are implicitly included (as a negative contribution) in costs. The validity of our exclusion restriction would be threatened if our measure of permanent local wages affects the subjective benefit of education.

We identify B^MTE(x, u_S) and $B_I^{\mathit{MTE}}(x_I,u_S)$ using variables that do not affect future wages, but only the cost of attending college (cost shifters). We use current fluctuations in local labor market conditions such as local wages at the time of the educational decision, which shift the opportunity cost of schooling. They should not help to predict the agent’s expected future wages as we also control for permanent local labor market conditions. Effectively, we use only the innovations in local wages as cost shifters. We also include tuition cost, a dummy variable indicating urban residence at age 14, and distance to college as shifters that affect the direct cost of attending college.

Table 1 presents the covariates used in our empirical analysis. We highlight the two different types of exclusion restrictions. Variables that affect benefits as well as costs of treatment (common elements) include the Armed Forces Qualifying Test (AFQT) scores, mother’s education, number of siblings, and cohort dummies. In what follows, we keep this set of observables in the background to ease notation. X and Z continue to denote the benefit and cost shifters respectively. X_I is the subvector of X which is known to the agent at the college entry decision. We include two variables in X not included in X_I : years of experience and wages in the county of residence. The excluded variables are measured approximately 12 years after the agent’s college entry decision and thus not in the individual’s information set at the time of the treatment decision. We follow the analysis of Section 5 and allow agents to have imperfect foresight about the realizations of these variables. They form expectations about their future wages, but do not have perfect information. In line with our exposition, we assume that Z does not help to predict the ex post realization of X conditional on X_I and denote the agent’s information about their idiosyncratic cost and benefit from treatment as Ṽ = E (V | U_I).

Table 1.

Specification

	X	XI	Z	Common
Years of Experience (in 1991)	✓
Current Local Wages (in 1991)	✓
Permanent Local Wages	✓	✓
AFQT Scores				✓
Mother’s Education				✓
Number of Siblings				✓
Cohort Dummies				✓
Urban Residence			✓
Local Presence of Public College (age 14)			✓
Local Tuition at Public College (age 17)			✓
Local Wages (age 17)			✓

Notes: Our main specification includes years of experience (linear and squared), current local wages (linear), permanent local wages (linear and squared), AFQT scores (linear and squared), mother’s education (linear and squared), number of siblings (linear and squared), urban residence (linear), cohort dummies (linear), local presence of public colleges (linear), local tuition of public college (linear), and local wages (linear). All exclusions from the benefit equation are interacted with AFQT scores, mother’s education, and number of siblings.

We specify a linear version of the generalized Roy model. Define potential outcomes:

$$Y_1=X{\beta }_1+U_1\text{and}{Y}_0=X{\beta }_0+U_0.$$

The choice equation is:

$$D=\mathbf{1}\left[X_I({\alpha }_1-{\alpha }_0)-Z\gamma >\stackrel{\sim }{V}\right],$$

where we assume that agents form valid expectations about their own outcomes so that E (X(β₁ − β₀) | X_I) = X_I (α₁ − α₀) holds. Note that X_I does not only affect the returns to education directly, but also helps to predict the ex post realization of those elements of X not contained in X_I.

We first implement the traditional structural approach and explicitly estimate all components of the generalized Roy model and combine them to form the marginal effect parameters (Björklund and Moffitt, 1987). We impose normality for the unobservables and fit the model by maximum-likelihood. As the participation decision is based on the net surplus and X does not affect the cost of treatment, this implies a cross-equation restriction between the coefficients on X in the outcome equations and X_I in the choice equation. We account for agents’ imperfect foresight and set $({\alpha }_1-{\alpha }_0)={({\overline{X}}_I^{\prime }{\overline{X}}_I)}^{-1}{\overline{X}}_I^{\prime }\overline{X}({\beta }_1-{\beta }_0)$, where (X̄, X̄_I) denote the matrices with the outcome shifters of the whole sample. We estimate the whole model in one step. In a standard Probit model, the coefficients can only be identified up to a factor of proportionality. However, as the wage gain (α₁ − α₀)X_I appears with a coefficient of one in the choice equation, we do not need to normalize the variance of Ṽ and estimate it instead. We can then construct the marginal effects of treatment based on the results:

$$\begin{array}{lllll}{B}^{\mathit{MTE}}(x,u_S)\hfill & =\hfill & x({\beta }_1-{\beta }_0)\hfill & +\hfill & \left(\frac{{\sigma }_{U_1-U_0,\stackrel{\sim }{V}}}{{\sigma }_{\stackrel{\sim }{V}}^2}\right){\mathrm{\Phi }}_{{\sigma }_{\stackrel{\sim }{V}}}^{-1}(u_S)\hfill \\ B_I^{\mathit{MTE}}(x_I,u_S)\hfill & =\hfill & x_I({\alpha }_1-{\alpha }_0)\hfill & +\hfill & \left(\frac{{\sigma }_{U_1-U_0,\stackrel{\sim }{V}}}{{\sigma }_{\stackrel{\sim }{V}}^2}\right){\mathrm{\Phi }}_{{\sigma }_{\stackrel{\sim }{V}}}^{-1}(u_S)\hfill \\ C_I^{\mathit{MTE}}(z,u_S)\hfill & =\hfill & z\gamma \hfill & +\hfill & \left(\frac{{\sigma }_{U_C,\stackrel{\sim }{V}}}{{\sigma }_{\stackrel{\sim }{V}}^2}\right){\mathrm{\Phi }}_{{\sigma }_{\stackrel{\sim }{V}}}^{-1}(u_S)\hfill \\ S_I^{\mathit{MTE}}(x_I,z,u_S)\hfill & =\hfill & x_I({\alpha }_1-{\alpha }_0)-z\gamma \hfill & -\hfill & {\mathrm{\Phi }}_{{\sigma }_{\stackrel{\sim }{V}}}^{-1}(u_S),\hfill \end{array}$$

where σ_U1−U0,Ṽ and σ_UCṼ denote the covariance between (U₁ − U₀, Ṽ) and (U_C, Ṽ) respectively. ${\mathrm{\Phi }}_{{\sigma }_{\stackrel{\sim }{V}}}^{-1}$ indicates the inverse of a normal cumulative distribution function with standard deviation σ_Ṽ.

The sign of the slope of the marginal effect parameters is determined by σ_UCṼ and σ_U1−U0Ṽ as ${\sigma }_{\stackrel{\sim }{V}}^2>0$. We present our results for these parameters in Table 2. The estimate for σ_U1−U0Ṽ is negative and thus the marginal benefits of treatment decrease when moving along the margins of Ṽ. The opposite is true for σ_UCṼ and so the marginal cost increases in u_S. However, only σ_U1−U0Ṽ is significantly different from zero at the 10% level.

Table 2.

Slope Parameters

Parameter	Estimate	90% Confi.	p -val.
σ(U1−U0),Ṽ	−0.042	−0.216 / 0.001	0.06
σUC,Ṽ	0.015	−0.020 / 0.579	0.29
${\sigma }_{\stackrel{\sim }{V}}^2$	0.058	0.005 / 0.769	0.00

Notes: Confi. = Confidence Interval, p - val. = p -values.

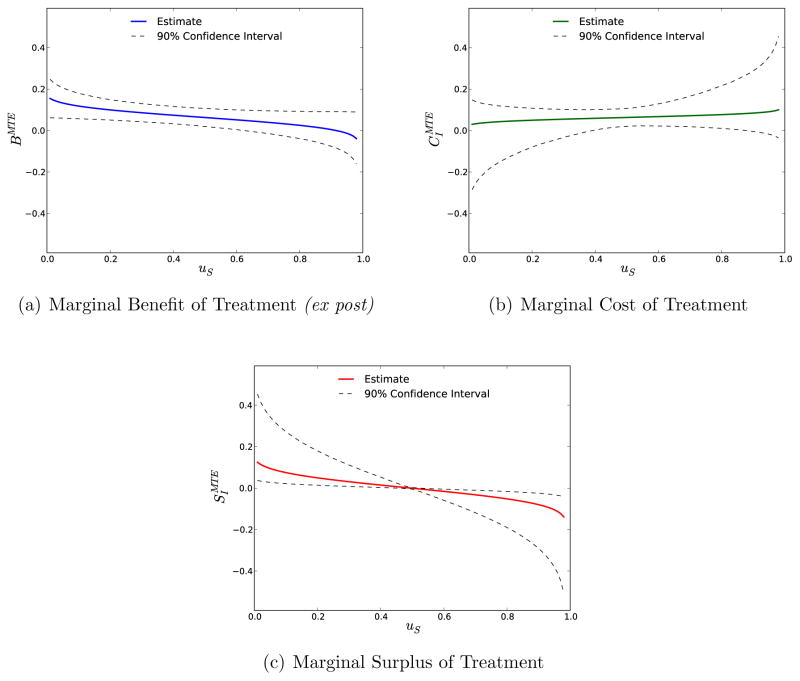
Figure 2 presents our fully parametric results for the ex post marginal benefit and ex ante cost and surplus parameters. We plot them as a function of u_S and evaluate them at the sample mean of (X_I, Z). As agents are assumed to form valid expectations about their future benefits, the ex ante and ex post marginal benefits are identical. Individuals with a high unobserved desire for treatment (low u_S) have the highest benefit, strictly decreasing from +16% to −4%. The estimated surplus is positive for low values of u_S and decreases when moving along the margins of Ṽ. The opposite holds for the marginal cost, which is always positive and slightly increasing. The cost is lowest for individuals with low values of u_S and ranges from +3% to +10%. In summary, the benefit is highest and cost lowest for those most likely to pursue a higher education. However, the estimates are not precisely determined. The marginal benefit of treatment is significantly different from zero for roughly half of the individuals. Along all margins of Ṽ, the marginal cost of a college education does not significantly differ from zero. By construction, the marginal surplus is strictly positive for all those individuals who participate in the treatment and negative for those that do not. Conditional on the observables set to their sample mean, individuals are indifferent towards treatment when u_S = 0.51.

Figure 2.

Marginal Effects of Treatment, Parametric

Figure 2 presents the marginal effect parameters over the full unit interval from the structural model. The distributional assumptions on (U₁, U₀, Ṽ) expand the margins for which we can identify the marginal effects of treatment. As we assume full independence between all observables and unobservables, we identify the marginal effects of treatment over the unconditional common support of P (X_I, Z). In our sample, this support ranges between 0.03 and 0.98. Adding joint normality, we can extrapolate even further and cover the full unit interval.

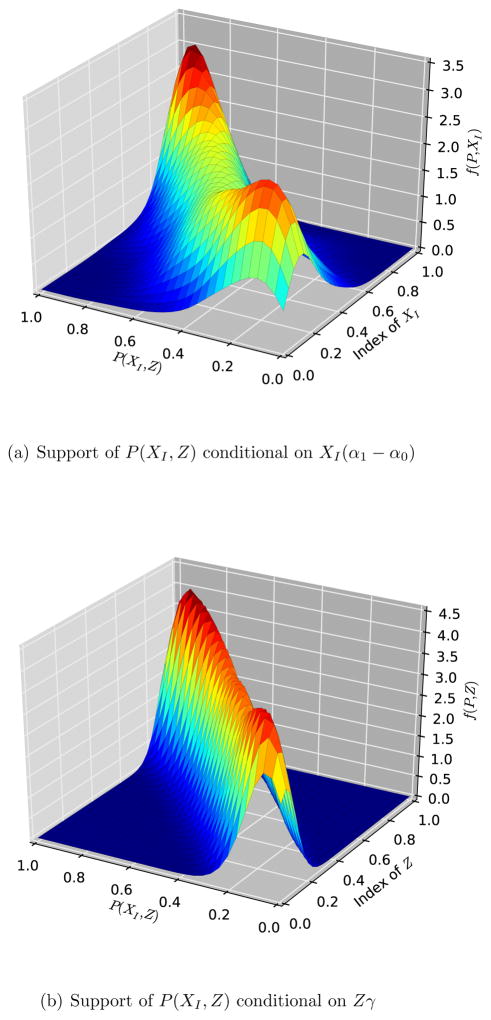
However, our formal analysis demonstrates that in a fully nonparametric setting we are only able to identify the $B_I^{\mathit{MTE}}(x_I,u_S)$ over the support of P (X_I, Z) conditional on X_I = x_I and the $C_I^{\mathit{MTE}}(z,u_S)$ over the support of P (X_I, Z) conditional on Z = z. We identify the $S_I^{\mathit{MTE}}(x_I,z,u_S)$ over the intersection of the two supports. In Figure 3 we plot the conditional densities of P (X_I, Z) in our data. As X_I and Z are both multidimensional, we condition on the decile of the relevant index, i.e. on X_I (α₁ − α₀) for the $B_I^{\mathit{MTE}}(x_I,u_S)$ and Zγ for the $C_I^{\mathit{MTE}}(z,u_S)$.¹² The support is very limited and thus the results of a fully parametric implementation rely heavily on extrapolation based on the distributional assumptions.

Figure 3.

Conditional Support

We now develop a semiparametric estimation strategy that relies on fewer assumptions and provides more transparent sources of identification. We apply Marschak’s Maxim, estimating only those combinations of structural parameters needed for the marginal effect parameters. To fix ideas, consider the estimation of the B^MTE(x, u_S), where the conditional expectation of (U₁ − U₀) along the margins of Ṽ is a key element. In the fully parametric normal-theory approach, it is directly constructed from estimates of (σ_U1,Ṽ, σ_U0,Ṽ) and ${\sigma }_{\stackrel{\sim }{V}}^2$:

$$E(U_1-U_0\mid U_S=u_S)=\left(\frac{{\sigma }_{U_1-U_0,\stackrel{\sim }{V}}}{{\sigma }_{\stackrel{\sim }{V}}^2}\right){\mathrm{\Phi }}_{{\sigma }_{\stackrel{\sim }{V}}}^{-1}(u_S).$$

Instead, in what follows, we directly obtain E (U₁ − U₀ | U_S = u_S) without having to estimate all structural components. We will also carefully recognize the relevant conditional support of P for each parameter and thus present a data-sensitive structural analysis (Heckman, 2010).

We determine the support of P by building on an estimator of the joint support of the distribution of (X, Z):

$${\widehat{S}}_{X,Z}=\{(x,z):\Vert (X_i,Z_i)-(x,z)\Vert \le \epsilon \text{for}\text{some}i\},$$

where || · || corresponds to the Euclidean norm and i denotes a generic observation in our data.¹³ Then, letting x_I (x) indicate the appropriate subvector of x, our resulting estimator for the support of (X_I, Z) is:

$${\widehat{S}}_{X_I,Z}=\{(x_I^{\ast },z^{\ast }):\exists (x,z)\in {\widehat{S}}_{X,Z}\text{such}\text{that}(x_I(x),z)=(x_I^{\ast },z^{\ast })\}.$$

We can use these estimates to construct our desired support for the marginal cost and benefit parameters:

$$\begin{array}{lll}\hfill {\widehat{S}}_{X,P}=\{(x^{\ast },p^{\ast }):\exists (x,z)\in {\widehat{S}}_{X,Z}& \text{such}\text{that}\hfill & (x,P(x_I(x),z))=(x^{\ast },p^{\ast })\}\hfill \\ \hfill {\widehat{S}}_{X_I,P}=\{(x_I^{\ast },p^{\ast }):\exists (x_I,z)\in {\widehat{S}}_{X_I,Z}& \text{such}\text{that}\hfill & (x_I,P(x_I,z))=(x_I^{\ast },p^{\ast })\}\hfill \\ \hfill {\widehat{S}}_{Z,P}=\{(z^{\ast },p^{\ast }):\exists (x_I,z)\in {\widehat{S}}_{X_I,Z}& \text{such}\text{that}\hfill & (z,P(x_I,z))=(z^{\ast },p^{\ast })\}.\hfill \end{array}$$

Note, that the variation in p for a given x and x_I (x) is the same in Ŝ_X,P and Ŝ_{X_I,P}. Thus we can identify the B^MTE(x, u_S) and $B_I^{\mathit{MTE}}(x_I(x),u_S)$ over the same margins. Finally, for the marginal surplus parameter, we collect in Ŝ_{X_I,Z,P} all (x_I, z, p) where the relevant subsets in Ŝ_{X_I,P} and Ŝ_Z,P overlap in p. We only report estimates for the margins within these sets and thus acknowledge the limitations of the data.

We estimate the B^MTE(x, u_S) using the method of local instrumental variables (LIV) proposed in Heckman and Vytlacil (1999, 2001b, 2005). They show that under our conditions the B^MTE(x, u_S) is identified by differentiating the conditional expectation of observed outcomes:

$${\frac{\partial E(Y\mid X=x,P=p)}{\partial p}|}_{p=u_S}=B^{\mathit{MTE}}(x,u_S).$$ (6.1)

Applied to sample data, this is the LIV estimator of Heckman and Vytlacil (1999).¹⁴ As noted in Carneiro et al. (2011), it is empirically very difficult to apply the LIV estimator while conditioning on all variables in the outcome equations. Thus we proceed by invoking the stronger assumption that in addition to the variables in X, all elements common to outcome and choice equations are independent of (U₁, U₀, Ṽ) as well. Because our generalized Roy model is also linear, the conditional expectation of Y simplifies to:

$$\begin{array}{l}E(Y\mid X=x,P=p)=E(D{Y}_1+(1-D)Y_0\mid X=x,P=p)\\ =x{\beta }_0+px({\beta }_1-{\beta }_0)+K(p),\end{array}$$ (6.2)

where K(p) = E(U₁ − U₀ | D = 1, P = p) can be estimated nonparametrically. We determine the parameters of Equation (6.1) by a partially linear regression of Y on X and P. We proceed in two steps. The first step is the construction of P, and the second step is the estimation of β₁ and β₀ using the estimated P. We carry out the first step using a Probit regression of D on (X_I, Z). In the second step we use Robinson (1988)’s method for estimating partially linear models as extended in Heckman et al. (1997a).¹⁵ Next, consider the estimation of K(P). Equation (6.2) implies that E(Ỹ) = K(p), where Ỹ = Y − xβ₀ − px(β₁ − β₀) is the residualized observed outcome. We thus use a local quadratic regression of Ỹ on P to estimate K(P) and its partial derivative with respect to P.¹⁶ We construct the ex post marginal benefit of treatment B^MTE(x, u_S) based on these estimates:

$$B^{\mathit{MTE}}(x,p)=x({\beta }_1-{\beta }_0)+\frac{\partial K(p)}{\partial p}\forall (x,p)\in {\widehat{S}}_{X,P}.$$

For the ex ante marginal benefit of treatment, we account for the agents’ imperfect foresight about the future realization of components of X. As agents form valid expectations, we calculate $({\alpha }_1-{\alpha }_0)={({\overline{X}}_I^{\prime }{\overline{X}}_I)}^{-1}{\overline{X}}_I^{\prime }\overline{X}({\beta }_1-{\beta }_0)$¹⁷ and then construct the $B_I^{\mathit{MTE}}(x_I,u_S)$ as follows:

$$B_I^{\mathit{MTE}}(x_I,p)=x_I({\alpha }_1-{\alpha }_0)+\frac{\partial K(p)}{\partial p}\forall (x_I,p)\in {\widehat{S}}_{X_I,P}.$$

We can identify the $C_I^{\mathit{MTE}}(z,u_S)$ using the equality of the marginal cost and benefit parameter at the margin of indifference:

$$C_I^{\mathit{MTE}}(z,p)=B_I^{\mathit{MTE}}(x_I,p)\forall (z,p)\in {\widehat{S}}_{Z,P}.$$ (6.3)

This step directly mirrors Equation (4.2) from our nonparametric identification analysis. We obtain an estimate for the marginal cost of treatment using only information on the marginal benefits. We do not exploit any additional distributional assumptions such as joint normality of the unobservables.

We finally determine the $S_I^{\mathit{MTE}}(x_I,z,u_S)$ by taking the difference between benefits and costs:

$$S_I^{\mathit{MTE}}(x_I,z,p)=B_I^{\mathit{MTE}}(x_I,p)-C_I^{\mathit{MTE}}(z,p)\forall (x_I,z,p)\in {\widehat{S}}_{X_I,Z,P}.$$ (6.4)

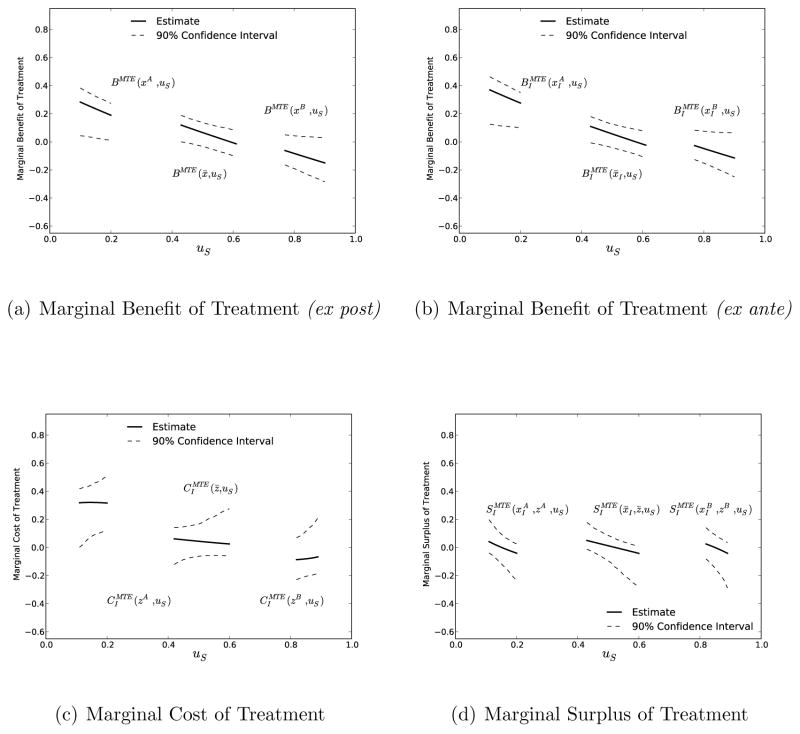
Figure 4 presents our semiparametric results for the ex ante benefit, cost and surplus parameters as well as the ex post benefit. We calculate the marginal effects at the mean values in the sample (x̄, z̄) and at two additional points of evaluation (x^A, z^A) and (x^B, z^B). We plot them as a function of u_S within the relevant conditional support and compute the 90% confidence bands using the bootstrap.¹⁸

Figure 4.

Marginal Effects of Treatment, Semiparametric

Our estimates show that individuals with a high unobserved desire for treatment (low u_S) have high benefits as well as high costs from participation. When moving up the margins of u_S the benefits fall more quickly than the costs as the surplus decreases. The $B_I^{\mathit{MTE}}(x_I,x_S)$ ranges from +37% within the support of x^A to as low as −12% within the support of x^B. The $C_I^{\mathit{MTE}}(z,u_S)$ varies between +32% and −6% overall, but within each margin of support the variation is limited to about 4% in absolute value. We can calculate the $S_I^{\mathit{MTE}}(x_I,z,u_S)$ which ranges from +5% to −5% as the difference between ex ante benefits and costs within the overlap of the support. Note that the estimates for the marginal benefits at x^B are all negative. However, costs are as well and so the surplus is still positive at the lower end of the conditional support. After conditioning on observables, it is unobservable heterogeneity in benefits and not costs that is driving the college entry decision. However, all estimates are rather imprecise, precision is highest at the mean values in the sample.

The conditional support is limited as shown in Figure 3. The location and range of the support depends on the point of evaluation. In general, we can identify B^MTE(x, u_S) and $B_I^{\mathit{MTE}}(x_I,x_S)$ over longer stretches of u_S than the $C_I^{\mathit{MTE}}(z,u_S)$ function. In fact, for all x_I, z evaluation points considered, the values of u_S for which we identify $C_I^{\mathit{MTE}}(z,u_S)$ is a subset of the values of u_S for which we identify $B_I^{\mathit{MTE}}(x_I,x_S)$. Hence, for the x_I, z evaluation points considered, we can identify $S_I^{\mathit{MTE}}(x_I,z,u_S)$ only over the set of u_S values corresponding to the smaller set of u_S values for which we identify $C_I^{\mathit{MTE}}(z,u_S)$. The conditional variation in P is largest at x̄_I where we can identify the longest stretch for the $B_I^{\mathit{MTE}}({\overline{x}}_I,x_S)$ with u_S ∈ (0.42, 0.61), while it is smallest for $C_I^{\mathit{MTE}}(z^B,x_S)$ with u_S ∈ (0.81, 0.89). Note that we identify all marginal effect parameters around the margin of indifference at $S_I^{\mathit{MTE}}(x_I,z,u_S)=0$.

We can also assess the magnitude of the expectation errors due to the agents’ imperfect foresight about parts of their future benefits. Given our prediction model, the ex post and ex ante benefits coincide for the average individual (x̄, z̄). However, a comparison between realized and predicted benefits reveals that at x^A, ex post benefits are overestimated by about 9%, while at x^B the prediction is only off by 3%.

We can compare the results for the marginal effects of treatment between the two estimation approaches at (x̄, z̄) within the conditional support. The semiparametric approach indicates larger heterogeneity in benefits and costs due to the steeper slope of the marginal effect parameters. In both cases, benefits decrease considerably when moving along the margins of Ṽ while variation in costs is limited. Thus, it is heterogeneity in benefits that drives the college attendance decision. This is in line with the results by Björklund and Moffitt (1987), who also find that heterogeneity in rewards is more important than heterogeneity in costs for the participation decision in their context of a manpower training program in Sweden.

7 Summary and Conclusion

This paper extends the modern treatment effect literature by developing a framework for identifying both the marginal benefit and marginal cost of policies. The treatment effect literature focuses only on the benefit side, and does not address the question of the subjective cost of treatment as perceived by the agents attempting to take it. We build on the pioneering parametric analysis of Björklund and Moffitt (1987) by extending the nonparametric analysis of Heckman and Vytlacil (1999, 2005, 2007) to identify subjective cost and surplus functions. We provide identification results for the case of perfect foresight (as in the previous literature) as well as cases with imperfect foresight not previously considered. An analysis of college-going finds unobserved heterogeneity in the benefits as well as costs of attending college, with agents selecting into college based on both their idiosyncratic expected benefit and perceived cost of attending college. We find more heterogeneity in expected benefits than in perceived cost. Thus, the observed variability in college attendance is mainly driven by the variability in expected benefits.