Treatment Decisions Based on Scalar and Functional Baseline Covariates

Summary

The amount and complexity of patient-level data being collected in randomized controlled trials offers both opportunities and challenges for developing personalized rules for assigning treatment for a given disease or ailment. For example, trials examining treatments for major depressive disorder are not only collecting typical baseline data such as age, gender, or scores on various tests, but also data that measure the structure and function of the brain such as images from magnetic resonance imaging (MRI), functional MRI (fMRI), or electroencephalography (EEG). These latter types of data have an inherent structure and may be considered as functional data. We propose an approach that uses baseline covariates, both scalars and functions, to aid in the selection of an optimal treatment. In addition to providing information on which treatment should be selected for a new patient, the estimated regime has the potential to provide insight into the relationship between treatment response and the set of baseline covariates. Our approach can be viewed as an extension of “advantage learning” to include both scalar and functional covariates. We describe our method and how to implement it using existing software. Empirical performance of our method is evaluated with simulated data in a variety of settings and also applied to real data arising from the study of patients suffering from major depressive disorder from which baseline scalar covariates as well as functional data from EEG are available.

1. Introduction

Personalized medicine aims to provide a sound approach for making treatment decisions based on each individual’s clinical characteristics. These characteristics may include demographic information such as age, gender, or race, as well as more complex clinical information such as brain structure or function. The latter type of information may be viewed as functional data (Ramsay and Silverman, 2005). Developments in medical technology have begun to allow for the collection of such data on a scale that has never been seen before and there is growing interest in how best to use these data to guide clinicians in selecting targeted therapies that have the greatest chance to successfully combat a given disease or ailment.

One area of medical research that may substantially benefit from advances in personalized medicine is the development and assignment of treatment for major depressive disorder (MDD). It has been reported that fewer than 40% of patients find success (i.e., achieve remission) in using the first-line treatment that they are prescribed (Gaynes et al., 2009; Holtzheimer and Mayberg, 2011) even though a wide array of first-line treatments is available for patients suffering from MDD. This is especially troubling since selection of the “wrong” initial treatment may not only allow for MDD symptoms to persist but may also result in the worsening of those symptoms, additional suffering from treatment-related side effects, or heightened risk of suicide.

Considering the consequences of using an improper or ineffective first-line treatment for MDD, investigators have suggested that focus should shift to identifying baseline biological markers that can guide clinicians in treatment selection (McGrath et al., 2013). More specifically, it has been suggested that the search for these biomarkers should be among measures derived from neuroimaging modalities such as magnetic resonance imaging (MRI), functional MRI (fMRI), and electroencephalography (EEG), among others. Large clinical trials are now underway, EMBARC (NCT01407094) and iSPOT-D (NCT00693849), that have been designed to discover baseline clinical characteristics that modify the effect of treatment in MDD patients. In these studies, investigators are collecting large amounts of baseline information consisting of hundreds or thousands of scalar quantities as well as hundreds of 1-, 2-, and 3-dimensional brain images that can be regarded as functional data.

The statistical literature indicates that there is a growing interest in developing methods for using data from clinical settings to estimate strategies for providing treatment. While some investigators have focused on methods for making a treatment decision at one time point (Qian and Murphy, 2011; Zhao et al., 2012; Zhang et al., 2012; Lu et al., 2013), others have considered strategies consisting of a sequence of decisions often referred to as dynamic treatment regimes (Murphy, 2003; Robins, 2004; Zhao et al., 2009; Chakraborty et al., 2009; Moodie and Richardson, 2010; Laber et al., 2014).

Whether the focus has been on developing rules for one or multiple time points, the majority of the research has concentrated on using scalar covariates to guide treatment selection while decisions based on functional covariates or combinations of scalars and functions which account for the smooth nature of the functional covariates have remained unexplored. Oftentimes, when functional data are collected in clinical trials that involve an imaging component, these data are reduced to “expert-derived” scalar covariates which are used to develop treatment assignment strategies. Such large scale reduction in the data may explain why there has been relatively little success in identifying biomarkers for MDD treatment response based on imaging studies. Here we propose a method that overcomes the need to reduce functional data to scalar summaries but rather allows for functions and scalars to be used together to estimate a treatment decision rule and better understand heterogeneity in treatment response. Moreover, our approach can help investigators discover features of functional data that are most strongly associated with treatment response.

To our knowledge McKeague and Qian (2014) are the only ones to date who have taken a functional data approach to constructing treatment policies. They propose methods for estimating and evaluating treatment regimes based on one baseline functional covariate. With respect to estimation of a treatment policy, they discuss several approaches including (1) the FAME model of James and Silvermam (2005), (2) models based on a single component of the functional covariate (i.e., models that use only one value of the functional covariate at a specified time, location, etc.), and (3) an “area impact” model in which treatment selection is based on a localized region of the functional covariate.

We are interested in considering situations in which multiple functional covariates or combinations of scalar and functional covariates are available and can be used to estimate a treatment regime. We propose a method in which the task of estimating the optimal regime using scalar and functional predictors is cast as a loss-minimizing procedure where the loss function corresponds to a form of A-learning (Murphy, 2003; Robins, 2004; Blatt et al., 2004). Accordingly, we expect that the estimated regime is robust to certain types of mis-specification of the posited model for the response provided that the part of the model involving interactions between treatment and baseline covariates is correctly specified. We provide evidence of this via numerical investigations. Furthermore, our approach produces an estimated regime that can be used to better understand how the scalar and functional baseline covariates interact with treatment. This may provide important information about which patient-level characteristics are particularly important in guiding treatment selection and may also aid in understanding the etiology of the disease being treated. In contrast to McKeague and Qian (2014) our method (i) allows for both multiple scalars and multiple functions to be used in estimating a treatment regime and (ii) employs penalized functional regression (PFR) (Goldsmith et al., 2011) to incorporate the functional predictors.

The remainder of the paper is organized as follows. In Section 2 we discuss the framework of potential outcomes and treatment regimes in the setting where both scalar and functional baseline covariates are available. We follow this with a description of our approach for estimating a treatment decision rule. Our proposed approach is assessed via simulations in Section 3. In Section 4 we apply our method to a data set arising from a study of subjects with MDD from which baseline scalar covariates and baseline functional covariates derived from EEG measures were collected. We conclude with a discussion in Section 5. Additional information including a derivation, additional simulation results, and R code is available in the online appendix.

2. Framework and Methodology

2.1 Formal Framework

In what follows, we essentially restrict our discussion to data arising from a randomized controlled trial (RCT) where treatment is randomly assigned. However, we note that data from observational studies, where treatment is not randomly assigned, can be cast in the same framework and analyzed using the subsequently described methodology.

Suppose we have n subjects sampled from a patient population of interest. Each subject is randomly given one of two possible treatments. These treatments are assigned based on some pre-specified probabilities that are the same for all subjects. Let the variable A, corresponding to treatment assignment, take on the value of either 0 or 1. For each subject we observe a collection of baseline covariates consisting of scalar values and functions. Denote the set of baseline scalar covariates by a p-dimensional vector Z = (Z₁, …, Z_p)^⊤ and denote the set of baseline functional covariates by the q-element set of functions X = {X₁, …, X_q}. Here we assume that X₁, …, X_q are one-dimensional functional random variables (X_ℓ : D_ℓ ⊂ ℝ → ℝ, ℓ = 1, …, q) that are each square integrable on a compact support I ⊂ ℝ (i.e, ${\int }_I{X}_{\ell }^2(s)ds<\infty$, ℓ = 1, …, q). Although we present only one-dimensional functional predictors here, it is possible to extend our approach to higher dimensional functional random variables such as images. Lastly, let Y be the observed outcome of interest. Without loss of generality, we assume that larger values of Y are preferred. The observed data are given by (Y_i, A_i, Z_i, X_i), i = 1, …, n, which are independent and identically distributed with Z_i = (Z_1i, …, Z_pi), X_i = {X_1i, …, X_qi}, and X_ℓi(s) is the value of ith subject’s ℓth functional covariate at argument s.

We wish to use these data to construct a rule for assigning treatment, often referred to as a “treatment regime” (Zhang et al., 2012; Murphy, 2003), to future subjects in such a way that the selected treatment yields higher outcome values than the alternative treatment for these subjects. As in Zhang et al. (2012), we formalize the notion of an optimal treatment regime by defining the potential outcomes Y*(0) and Y*(1) to be the values of the outcome that would be observed if a subject was assigned treatment 0 or 1 respectively. We assume that Y = Y*(1)A + Y*(0)(1 − A) (i.e., for the treatment that is actually received, the observed and potential outcomes are the same (Rubin, 1978)), which is known as the consistency assumption. Furthermore, we assume that subjects do not interfere with one another and that an individual’s treatment assignment is independent of the potential outcomes conditional on the baseline covariates. This final assumption is satisfied in the context of a RCT where treatment is randomly assigned.

A treatment regime is a function, g, that maps the baseline covariates (Z, X) to {0, 1} such that a patient with baseline covariates (Z = z, X = x) will receive treatment 1 if g(z, x) = 1 and will receive treatment 0 if g(z, x) = 0. The “optimal treatment regime”, g^opt, is the function that maximizes the expected value of the response among some class of functions 𝒢, i.e., g^opt(Z, X) = argmax_g∈𝒢 E[Y*{g(Z, X)}].

With the framework and assumptions discussed above, we have that

$$E[Y^{*}\{g(\mathit{Z},\mathit{X})\}]=E_{(\mathit{Z},\mathit{X})}[E(Y|\mathit{Z},\mathit{X},A=1)g(\mathit{Z},\mathit{X})+E(Y|\mathit{Z},\mathit{X},A=0)\{1-g(\mathit{Z},\mathit{X})\}],$$

where E_(Z,X) (·) denotes expectation with respect to the joint distribution of (Z, X) and the optimal treatment regime is given by

$$g^{\mathit{\text{opt}}}(\mathit{Z},\mathit{X})=I\{E(Y|\mathit{Z},\mathit{X},A=1)>E(Y|\mathit{Z},\mathit{X},A=0)\}.$$ (1)

In the case where E(Y|Z, X, A = 1) = E(Y|Z, X, A = 0), one might employ a randomization procedure to select the treatment or use whichever treatment corresponds to the current standard of care if such a treatment is being considered.

A typical approach for deriving an optimal treatment regime is to assume some structure on E(Y|Z, X, A) and employ a regression model. Here we consider a semi-parametric model. Specifically, we propose to model the expected value as

$$E(Y|\mathit{Z},\mathit{X},A)=h_0(\mathit{Z},\mathit{X})+A\underset{f(\mathit{Z},\mathit{X})}{\underbrace{\{{\tilde{\mathit{Z}}}^{\top }\mathit{\beta }+\sum _{\ell =1}^q\int X_{\ell }(s){\omega }_{\ell }(s)ds\}}},$$ (2)

where h₀ is some “baseline” function that corresponds to the effects of the baseline covariates on the response for A = 0, Z̃ = (1, Z^⊤)^⊤, β = (β₀, …, β_p)^⊤, and {ω₁, …, ω_q} are smooth square integrable weight functions. In (2), f(Z, X) corresponds to the effect of the treatment A = 1 on the response, which is a function of the baseline covariates and is typically referred to as the “contrast.”When the conditional expectation of the response is modeled in this way, we see that f(Z, X) = E(Y|Z, X, A = 1)−E(Y|Z, X, A = 0) and so the optimal treatment regime corresponding to the model in (2) is given by g^opt(Z, X) = I{f(Z, X) > 0}. Since the optimal treatment regime depends only on the contrast, primary interest lies in obtaining estimates for the corresponding contrast parameters (i.e., β and ω = {ω₁, …, ω_q}).

2.2 Methodology

In order to develop an optimal treatment decision rule, we propose to take an approach that views the estimation of the contrast parameters as a loss-minimizing procedure in the framework of advantage learning (A-learning) (Murphy, 2003; Robins, 2004; Blatt et al., 2004). This approach parallels that taken in Lu et al. (2013) which considered only scalar baseline covariates in a high-dimensional setting. Given the observed data, (Y_i, A_i, Z_i, X_i), i = 1, …, n, we seek to minimize the loss function

$$L_{n,\varphi }(\mathit{\beta },\mathit{\omega })=\frac{1}{n}\sum _{i=1}^n{[Y_i-\varphi ({\mathit{Z}}_i,{\mathit{X}}_i)-\{{\tilde{\mathit{Z}}}_i^{\top }\mathit{\beta }+\sum _{\ell =1}^q\int X_{\ell i}(s){\omega }_{\ell }(s)ds\}\times \{A_i-\pi ({\mathit{Z}}_i,{\mathit{X}}_i)\}]}^2,$$ (3)

where ϕ(Z_i, X_i) is an arbitrary function of the baseline covariates which may or may not approximate h₀ from (2) well and π(Z_i, X_i) = P(A_i = 1|Z_i, X_i) is the propensity score which gives the probability that a subject with a specific covariate profile will receive treatment A = 1. For our purposes, we treat the propensity score as a known constant that is determined by trial protocols. In an observational study setting, one may posit a model for π (e.g., logistic model) that depends on all of or a subset of the baseline covariates and substitute the predicted propensity scores in (3).

In the case where there are only scalar baseline covariates, the estimating equations corresponding to (3) have been shown to provide consistent and asymptotically normal estimates for the contrast parameters of interest (Robins, 2004; Lu et al., 2013). This is advantageous in that even if h₀(Z, X) is mis-specified, the estimates of the contrast parameters can be consistently estimated, so long as the contrast is correctly specified and the propensity scores are known or can be estimated consistently.

Our setting is more complex since we have functional baseline covariates in addition to scalar ones. However, if we represent the functional covariates and their corresponding coefficient functions in terms of some suitably chosen set(s) of basis functions then we can view the loss function in (3) as wholly consisting of scalar quantities. This puts us back in a setting where we might expect the same benefit of consistent estimates for the contrast parameters.

There is a wide variety of basis functions from which to choose for representing the functional covariates and/or their corresponding coefficient functions including functional principal components, splines, and wavelets. We choose to employ the same representation used in Goldsmith et al. (2011) so that we can take advantage of existing software for obtaining estimates of the contrast parameters and ultimately of the treatment regime. We review this representation here. For ℓ ∈ {1, …, q} let $X_{\ell i}(s)={\sum }_{k=1}^{K_{\ell }}{c}_{\ell ik}{\psi }_{\ell k}(s)$ where ψ_ℓ(·) = {ψ_ℓk(·) : 1 ≤ k ≤ K_ℓ} are the first K_ℓ eigenfunctions of the smoothed estimated covariance operator Σ^X_ℓ(s₁, s₂) = cov{X_ℓ(s₁), X_ℓ(s₂)}. Each coefficient function can be expressed in terms of a truncated power series spline basis given by θ_ℓ = {θ₁, …, θ_Mℓ} such that ${\omega }_{\ell }(s)=b_{\ell 1}+b_{\ell 2}s+{\sum }_{m=3}^{M_{\ell }}{b}_{\ell m}{\theta }_m(s)$ where we have θ₁(s) = 1, θ₂(s) = s, θ_m(s) = (s−κ_m)₊ for m = 3, …, M_ℓ, and ${\{{\kappa }_m\}}_{m=3}^{M_{\ell }}$ are knots. Using these representations, the contrast can be written as ${\tilde{\mathit{Z}}}_i^{\top }\mathit{\beta }+{\sum }_{\ell =1}^q{\mathit{c}}_{\ell i}^{\top }{\mathit{J}}_{\ell }{\mathit{b}}_{\ell }$ where the functional principal component (FPC) scores for the ℓth functional predictor from the ith observation are given by c_ℓi = (c_ℓi1, …, c_ℓiKℓ)^⊤, the unknown spline coefficients for the ℓth coefficient function are b_ℓ = (b_ℓ1, …, b_ℓMℓ)^⊤, and J_ℓ is a K_ℓ × M_ℓ dimensional matrix with entry (u, υ) given by ∫ ψ_ℓu(s)θ_υ(s)ds. Letting ${\mathit{X}}_{\ell i}={\mathit{c}}_{\ell i}^{\top }{\mathit{J}}_{\ell }$ we have that (3) can be expressed as

$$L_{n,\varphi }(\mathit{\beta },{\mathit{b}}_1,\dots ,{\mathit{b}}_q)=\frac{1}{n}\sum _{i=1}^n{[Y_i-\varphi ({\mathit{Z}}_i,{\mathit{X}}_i)-\{{\tilde{\mathit{Z}}}_i^{\top }\mathit{\beta }+\sum _{\ell =1}^q{\mathit{X}}_{\ell i}{\mathit{b}}_{\ell }\}\times \{A_i-\pi ({\mathit{Z}}_i,{\mathit{X}}_i)\}]}^2,$$ (4)

which provides a loss function in the framework of A-learning. In Web Appendix A we show this loss function yields estimating equations corresponding to those associated with A-learning.

As noted above, a desirable consequence of using A-learning in our setting is that we expect the estimates of the contrast parameters to be robust to mis-specification of the h₀ function. Thus our approach is flexible in that it allows us to use any functional form for ϕ. Simulation studies conducted by Lu et al. (2013) and Schulte et al. (2014) show that if one happens to properly model the h₀ function, then one can expect good estimation accuracy and treatment selection performance with smaller sample sizes than if h₀ is mis-specified. Although it is not necessary to specify ϕ(z, x), it is common practice to employ some simple parametric form. One option is to use a linear model ${\varphi }_1(\mathit{z},\mathit{x})={\tilde{\mathit{z}}}^{\top }\mathit{\gamma }+{\sum }_{\ell =1}^q\int x_{\ell }(s){\alpha }_{\ell }(s)ds$, which, in practice, would require using similar representations for the functional components of ϕ as those involved in the contrast. As for each ω_ℓ, each α_ℓ, corresponds to a vector of unknown basis coefficients which we will denote by a_ℓ = (a_ℓ1, …, a_ℓVℓ)^⊤. As an alternative to using a function that is linear in the baseline predictors, one might choose to use a constant function for ϕ (i.e., ϕ₂(z, x) = γ).

For ϕ taking any parametric form, estimates of β and b₁, …, b_q (and therefore ω₁, …, ω_q) can be obtained using penalized functional regression (PFR) (Goldsmith et al., 2011). PFR allows for the functional covariates to be sparsely or densely sampled and also allows for them to be measured with or without error. Furthermore, PFR can be performed using existing software, pfr, contained in the R package refund (Crainiceanu et al., 2014). PFR takes account of the functional nature of ω₁, …, ω_q in order to provide smooth estimates. Smoothing is induced by assuming that ${\{b_{\ell m}\}}_{m=3}^{M_{\ell }}~N({\mathbf{0}}_{b_{\ell }},{\sigma }_{b_{\ell }}^2{\mathit{I}}_{b_{\ell }})$ for ℓ = 1, …, q, where 0_bℓ is a vector of zeros of length (M_ℓ − 2) and I_bℓ is an (M_ℓ − 2) × (M_ℓ − 2) identity matrix. If ϕ₁ is used for ϕ then we also have that ${\{a_{\ell m}\}}_{m=3}^{V_{\ell }}~N(\mathbf{0}{a}_{\ell },{\sigma }_{a_{\ell }}^2{\mathit{I}}_{a_{\ell }})$ for ℓ = 1, …, q, where 0_aℓ is a vector of zeros of length (V_ℓ − 2) and I_aℓ is a (V_ℓ − 2) × (V_ℓ − 2) identity matrix. (We note that if ϕ₂ is used for ϕ then there are no basis coefficients that need to be estimated in addition to those corresponding to the coefficient functions in the contrast.)

The basis coefficients are viewed as random effects in a mixed effects model. The variance components, ${\sigma }_{b_{\ell }}^2$ (and ${\sigma }_{a_{\ell }}^2$ if applicable), can be viewed as smoothing parameters and can be estimated via restricted maximum likelihood estimation (REML). The corresponding model for the response is

$$Y|\mathit{Z},\mathit{X}~N(\mu ,{\sigma }^2),\mu =\varphi (\mathit{Z},\mathit{X})-({\tilde{\mathit{Z}}}_i^{\top }\mathit{\beta }+\sum _{\ell =1}^q{\mathit{X}}_{\ell i}{\mathit{b}}_{\ell })\times \{A_i-\pi ({\mathit{Z}}_i,{\mathit{X}}_i)\},$$

$${\{b_{\ell m}\}}_{m=3}^{M_{\ell }}~N({\mathbf{0}}_{b_{\ell }},{\sigma }_{b_{\ell }}^2{\mathit{I}}_{b_{\ell }});\ell =1,\dots ,q,$$ (5)

$${\{a_{\ell m}\}}_{m=3}^{V_{\ell }}~N({\mathbf{0}}_{a_{\ell }},{\sigma }_{a_{\ell }}^2{\mathit{I}}_{a_{\ell }});\ell =1,\dots ,q,\text{if applicable},$$

which is a mixed model with ${\sum }_{\ell =1}^q(M_{\ell }+V_{\ell })-4q$ random effects in the case where ϕ = ϕ₁ or ${\sum }_{\ell =1}^q{M}_{\ell }-2q$ in the case where ϕ = ϕ₂. As noted in Goldsmith et al. (2011), maximizing the likelihood over the unknown parameters β, b₁, …, b_q, and any parameters related to ϕ, based on the data, is equivalent to minimizing

$$\frac{1}{{\sigma }^2}\sum _{i=1}^n{[Y_i-\varphi ({\mathit{Z}}_i,{\mathit{X}}_i)-({\tilde{\mathit{Z}}}_i^{\top }\mathit{\beta }+\sum _{\ell =1}^q{\mathit{X}}_{\ell i}{\mathit{b}}_{\ell })\times \{A_i-\pi ({\mathit{Z}}_i,{\mathit{X}}_i)\}]}^2+\sum _{\ell =1}^q\frac{1}{{\sigma }_{b_{\ell }}^2}{\mathit{b}}_{\ell }^{\top }{\mathit{D}}_{\ell }^b{\mathit{b}}_{\ell }+P_a,$$ (6)

where $P_a={\sum }_{\ell =1}^q\frac{1}{{\sigma }_{a_{\ell }}^2}{\mathit{a}}_{\ell }^{\top }{\mathit{D}}_{\ell }^a{\mathit{a}}_{\ell }$ if ϕ = ϕ₁ and P_a = 0 if ϕ = ϕ₂,

$${\mathit{D}}_{\ell }^b=\left[\begin{array}{cc}\hfill {\mathbf{0}}_{2\times 2}\hfill & \hfill {\mathbf{0}}_{2\times M_{\ell }}\hfill \\ \hfill {\mathbf{0}}_{M_{\ell }\times 2}\hfill & \hfill {\mathit{I}}_{M_{\ell }\times M_{\ell }}\hfill \end{array}\right]\text{and}{\mathit{D}}_{\ell }^a=\left[\begin{array}{cc}\hfill {\mathbf{0}}_{2\times 2}\hfill & \hfill {\mathbf{0}}_{2\times V_{\ell }}\hfill \\ \hfill {\mathbf{0}}_{V_{\ell }\times 2}\hfill & \hfill {\mathit{I}}_{V_{\ell }\times V_{\ell }}\hfill \end{array}\right].$$

Furthermore, minimizing (6) is equivalent to minimizing

$$L_{n,\varphi }(\mathit{\beta },{\mathit{b}}_1,\dots ,{\mathit{b}}_q)+\sum _{\ell =1}^q\frac{1}{{\sigma }_{b_{\ell }}^2}{\mathit{b}}_{\ell }^{\top }{\mathit{D}}_{\ell }^b{\mathit{b}}_{\ell }+P_a.$$

As noted above, the smoothing parameters can be automatically selected using REML. The tuning parameters that need to be selected by the user consist of the numbers of leading functional principal components used for representing each of the functional predictors and the numbers of spline basis functions used to represent each of the coefficient functions. Goldsmith et al. (2011) note that as long as the values of these tuning parameters are chosen “large enough,” then their specific values will have little impact on estimation. Alternatively, one can employ an objective data-driven procedure for selecting these tuning parameters such as cross-validation with the objective being to minimize (6). In practice, the sample size, n, sets upper limits on the values {M₁, …, M_q} (and {V₁, …, V_q} if applicable) as well as on the number of parameters corresponding to the scalar covariates that can be estimated. Specifically, if we choose to employ ϕ = ϕ₁ then there are $2+2p+{\sum }_{\ell =1}^q(M_{\ell }+V_{\ell })$ parameters to estimate whereas if we employ ϕ = ϕ₂ then there are $2+p+{\sum }_{\ell =1}^q{M}_{\ell }$ parameters to estimate.

3. Numerical Investigations

3.1 Numerical Investigation Setup

We assess the performance of our method with respect to estimation accuracy and selection of the optimal treatment regime on simulated data in various settings. We consider six scenarios that differ in the the number of baseline covariates available and in the true form of the baseline h₀ function. Each simulated observation consists of a treatment assignment indicator, a set of p scalar covariates (p = 2 in Scenarios 1 – 3, p = 15 in Scenarios 4 – 6), a set of q functional covariates (q = 2 in Scenarios 1 – 3, q = 15 in Scenarios 4 – 6), and a response.

The treatment assignment indicator, A, is generated such that π(Z, X) = 0.5. The vector of baseline scalar covariates, Z = (Z₁, …, Z_p)^⊤, is generated from a multivariate normal distribution with each component having mean 0 and variance 1. Correlation between the components is given by corr(Z_j, Z_k) = 0.5^|j−k|.

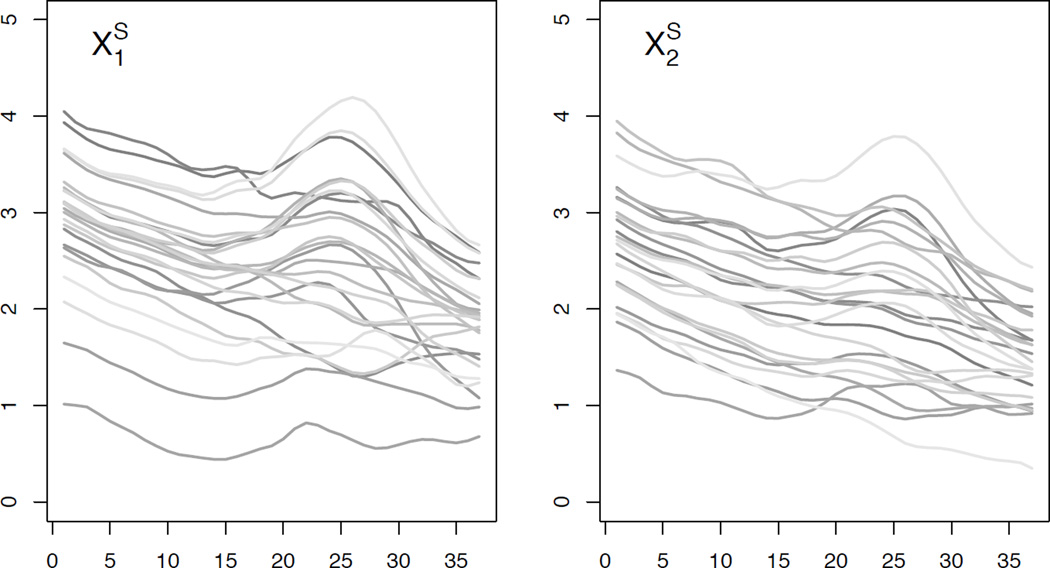
The functional baseline covariates, {X₁, …, X_q}, are generated to be similar to the EEG curves observed in the motivating data set discussed in Section 4. To simulate the baseline functional covariates, we take an approach similar to that used in Swihart et al. (2013). Specifically, to generate a new functional covariate, X_ℓ, we compute the first 5 observed (O) principal component basis functions $\{{\psi }_{\ell 1}^O,\dots ,{\psi }_{\ell 5}^O\}$, corresponding score variances, ${\mathit{\lambda }}^O={({\lambda }_{\ell 1}^O,\dots ,{\lambda }_{\ell 5}^O)}^{\top }$, and mean function, ${\mu }_{\ell }^O$, from a FPC decomposition of the collection of curves from the data set corresponding to the ℓth electrode from the cap worn during an EEG recording. To produce the ℓth simulated (S) full (F) functional covariate for the ith observation, we generate subject-specific PC loadings, ${\mathit{c}}_{\ell i}^S={(c_{\ell 1i}^S,\dots ,c_{\ell 5i}^S)}^{\top }$, from ${\mathit{c}}_{\ell i}^S~N(\mathbf{0},\text{diag}({\mathit{\lambda }}_{\ell }^O))$, let $X_{\ell i}^{SF}(s)={\mu }_{\ell }^O(s)+{\sum }_{j=1}^5{c}_{\ell ji}^S{\psi }_{\ell j}^O(s)$, and evaluate this function at 300 equally spaced values of s yielding, $X_{\ell i}^{SF}$, a vector of 300 values. The first value corresponds to the current source density (CSD) value, a measure derived from EEG, at the 0.25 Hz frequency and the 300th value corresponds to the CSD value at the 75 Hz frequency. To mirror the analysis that we perform in Section 4, we trim the full functional covariates to argument values roughly corresponding to the theta and alpha bands (4 – 13 Hz) of the EEG CSD curves, to form $X_{\ell i}^S$ which is a vector of 37 values. Figure 1 shows 25 simulated functional covariates for each of 2 different electrodes.

Figure 1.

Simulated functional predictors: (left) 25 $X_1^S$ and (right) 25 $X_2^S$ functional predictors from one simulated data set.

Responses are generated such that $Y=h_0(\mathit{Z},\mathit{X})+A\{{\tilde{\mathit{Z}}}^{\top }\mathit{\beta }+{\sum }_{\ell =1}^q\int X_{\ell }(s){\omega }_{\ell }(s)ds\}+\epsilon$. The error term, ε, follows a $N(0,{\sigma }_{\epsilon }^2)$ distribution where σ_ε is chosen such that R² = 0.85.

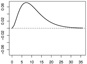
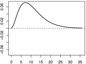
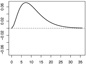
In Scenarios 1 – 3, in which p = q = 2, we have β = (β₀, β₁, β₂)^⊤ = (−0.65, 0.65,−0.65)^⊤, ω₁(s) = [1/{135 · 15² · Γ(3)}](s/36)²e^−10(s/36), and ω₂(s) = −[1/{135 · 15² · Γ(3)}]{(s − 36)/36}²e^{10{(s−36)/36}}. In Scenarios 4 – 6, in which p = q = 15, we have β = (β₀, …, β₁₅)^⊤ = (−0.65, 0.65,−0.65, 0₁₃)^⊤ (0_d is a zero-vector of length d), ω₁ and ω₂ are the same as in Scenarios 1 – 3, and ω₃ = …= ω₁₅ ≡ 0.

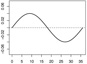
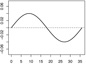
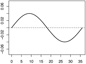
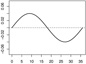
We consider three forms for h₀ that are composed of the functions h₀₁ and h₀₂. Let $h_{01}={\mathit{Z}}^{\top }{\gamma }_1+{\sum }_{\ell =1}^q\int X_{\ell }(s){\alpha }_{1,\ell }(s)ds$ and $h_{02}={\mathit{Z}}^{\top }{\gamma }_2+{\sum }_{\ell =1}^q\int X_{\ell }(s){\alpha }_{2,\ell }(s)ds$. In Scenarios 1 – 3 we have γ₁ = (γ_1,1, γ_1,2)^⊤ = (0.65, −0.65)^⊤, γ₂ = (γ_2,1, γ_2,2)^⊤ = (−0.65, 0.65)^⊤, α_1,1(s) = 0.04sin(2πs/36), α_1,2(s) = −0.04sin(2πs/36), ${\alpha }_{2,1}(s)=\{1/(10\sqrt{2\pi })\}{e}^{-50{(s/36-0.5)}^2}$, and ${\alpha }_{2,2}(s)=-\{1/(10\sqrt{2\pi })\}{e}^{-50{(s/36-0.75)}^2}$. In Scenarios 4 – 6 we have γ₁ = (γ_1,1, …, γ_1,15)^⊤ = (0.65, −0.65, 0₁₃)^⊤, γ₂ = (γ_2,1, …, γ_2,15)^⊤ = (−0.65, 0.65, 0₁₃)^⊤, {α_1,1, α_1,2, α_2,1, α_2,2} are the same as in Scenarios 1 – 3 and α_1,3 = … = α_1,15 = α_2,3 = …= α_2,15 ≡ 0. In Scenarios 1 and 4 we have h₀ = 1 + h₀₁, a linear function of the baseline covariates. In Scenarios 2 and 5 we have h₀ = 1 + 0.5h₀₁h₀₂, involving interactions among the baseline covariates. In Scenarios 3 and 6 we have $h_0=1+0.5\mathit{\text{sin}}(h_{01})+0.2h_{02}^2$, involving nonlinear functions of the baseline covariates. Table 1 shows the form of h₀ and all parameter values, including plots of the functional coefficients, used in each of the six scenarios. Note that scenario pairs 1 and 4, 2 and 5, and 3 and 6 are exactly the same except that Scenarios 4 – 6 include more baseline variables that are unrelated to the response.

Table 1.

Parameters for models generating responses in simulation Scenarios 1 – 6 and average treatment responses under these scenarios.

Parameter	Scenario 1	Scenario 2	Scenario 3	Scenario 4	Scenario 5	Scenario 6
Baseline Function
h0	1 + h01	1 + 0.5h01h02	$1+0.5\mathit{\text{sin}}(h_{01})+0.2h_{02}^2$	1 + h01	1 + 0.5h01h02	$1+0.5\mathit{\text{sin}}(h_{01})+0.2h_{02}^2$
γ1,1	0.65	0.65	0.65	0.65	0.65	0.65
γ1,2	−0.65	−0.65	−0.65	−0.65	−0.65	−0.65
γ1,3 − γ1,15	-	-	-	0	0	0
γ2,1	-	−0.65	−0.65	-	−0.65	−0.65
γ2,2	-	0.65	0.65	-	0.65	0.65
γ2,3 − γ2,15	-	-	-	-	0	0
α1,1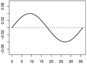
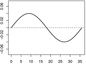α1,2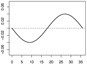
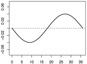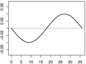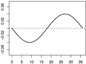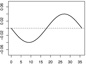α1,3 − α1,15	-	-	-	0	0	0
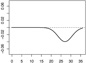
α2,1	-			-
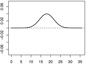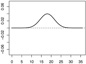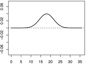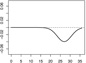
α2,2	-			-
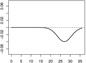α2,3 − α2,15	-	-	-	-	0	0
Contrast Function
β0	−0.65	−0.65	−0.65	−0.65	−0.65	−0.65
β1	0.65	0.65	0.65	0.65	0.65	0.65
β2	−0.65	−0.65	−0.65	−0.65	−0.65	−0.65
β3 − β15	-	-	-	0	0	0
ω1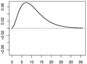
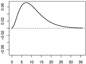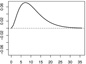ω2
β3 − β15	-	-	-	0	0	0
Average Treatment Response
E{Y*(0)}	0.93	0.77	1.09	0.93	0.77	1.09
E{Y*(1)}	0.82	0.66	0.97	0.82	0.66	0.97
E{Y*(gopt)}	1.31	1.16	1.47	1.31	1.16	1.47

A “-” indicates that the parameter is not applicable in the scenario.

We compare two different commonly employed working models for $\varphi :{\varphi }_1(\mathit{Z},\mathit{X})={\tilde{\mathit{Z}}}^{\top }\gamma +{\sum }_{\ell =1}^q\int X_{\ell }(s){\alpha }_{\ell }(s)ds$ and ϕ₂(Z, X) = γ.We consider four different sample sizes n = 75, 150, 300, and 600 for Scenarios 1 – 3 and two sample sizes n = 300 and 600 for Scenarios 4 – 6. (We do not fit models for Scenarios 4 – 6 with the smaller sample sizes because the number of parameters is too large in each case.) For each scenario and sample size combination, we generate 250 data sets and estimate a treatment regime for each. For each scenario we also generate a test set with N = 150, 000 independent observations that are used for evaluating treatment selection performance. Based on previous analyses, not discussed here, we chose to employ PFR using 8 B-spline basis functions since this provided a small but rich-enough set of functions to estimate the contrast coefficients well in all settings. We also used the first 10 observed functional principal components as we found that they accounted for over 99% of the variation in each of the functional predictors.

Estimation performance is evaluated separately for the scalar and functional parts of the models. For the scalar coefficients, we compute the mean squared error (MSE), ‖β̂ − β₀‖² where β₀ is the vector of true values for β, from each of the 250 estimated regimes and report the mean and corresponding standard error. For the functional coefficients, we compute the mean integrated mean squared error (MIMSE) for the estimated coefficient functions corresponding to the first two functional predictors, $\frac{1}{2L}{\sum }_{\ell =1}^2\int {\{{\hat{\omega }}_{\ell }(s)-{\omega }_{\ell }(s)\}}^{2}ds$ where L is the length of the interval over which the baseline covariate functions are observed, from each of the 250 estimated regimes and report the mean and corresponding standard error. We consider estimation error in only the first two coefficient functions in order to draw performance comparisons between the scenarios with no spurious covariates and the corresponding scenarios with spurious covariates.

We evaluate treatment assignment accuracy for each estimated regime on a test data set that is independent of the data used to fit the model. The model estimates are used to compute the treatment assignment $I\{{\tilde{\mathit{Z}}}_i^{\top }\hat{\mathit{\beta }}+{\sum }_{\ell =1}^q\int X_{\ell i}(s){\hat{\omega }}_{\ell }(s)ds>0\}$ for the ith test observation. For the entire set of test observations we compute the percent correct decision (PCD) given by

$$1-\frac{1}{N}\sum _{i=1}^N\left|I\right\{{\tilde{\mathit{Z}}}_i^{\top }\hat{\mathit{\beta }}+\sum _{\ell =1}^q\int X_{\ell i}(s){\hat{\omega }}_{\ell }(s)ds>0\}-I\{{\tilde{\mathit{Z}}}_i^{\top }{\mathit{\beta }}_0+\sum _{\ell =1}^q\int X_{\ell i}(s){\omega }_{\ell }(s)ds>0\left\}\right|,$$

and take the average of these accuracies over the 250 replications. We also evaluate the treatment selection performance by computing the the expected value of the response under the selected treatment in a test data set. When we constructed the test set for each scenario, we generated the response under each treatment so that we are able to calculate an approximation to the average treatment response under treatment 0 (E{Y*(0)}), under treatment 1 (E{Y*(1)}), and under the optimal treatment (E{Y*(g^opt)}). These values are provided in the bottom three rows of Table 1 for each scenario. We point out that in all scenarios, assigning treatment 0 to all subjects is favored over assigning treatment 1 since the average value of the response is larger, but assigning the optimal treatment results in even better (larger) average response. We use the baseline covariates from the test data to estimate treatment assignment from the estimated regimes in the 250 replications and compute the mean response on the selected treatment and then average over the 250 replicates. These values are denoted by 8 E{Y*(ĝ)}.

3.2 Numerical Investigation Results

Tables 2 and 3 summarize the estimation and treatment selection accuracy of our method based on the data generated under Scenarios 1 – 3 and Scenarios 4 – 6 respectively using either ϕ₁ or ϕ₂ as a working model for h₀ and based on varying sample sizes. In general we see that increased sample size yields improved estimation accuracy for both the scalar and functional parameter estimates. The results also suggest that using a richer linear working model for ϕ yields better estimation accuracy when compared with the simpler constant working model, even when h₀ is not truly linear in the baseline covariates. We further note that settings in which there are no spurious variables (Scenarios 1 – 3) generally show better estimation performance than the corresponding settings with spurious variables (Scenarios 4 – 6). A closer inspection of estimation performance with respect to the scalar and functional parts of the contrast is provided in Web Appendix C.

Table 2.

Estimation performance (se) and treatment selection performance for Scenarios 1, 2, and 3 for different working functions for h₀ (ϕ = ϕ₁ or ϕ₂) and for various sample sizes.

Scenario	ϕ	n	Scalar MSE	Functional MIMSE	PCD	Ê{Y*(ĝ)}
1	ϕ1	600	0.030 (0.042)	3.748 (1.408)	0.97	1.312 (0.001)
		300	0.062 (0.092)	4.891 (2.437)	0.95	1.310 (0.002)
		150	0.117 (0.135)	6.884 (6.401)	0.94	1.306 (0.005)
		75	0.242 (0.291)	11.498 (15.711)	0.91	1.297 (0.011)
	ϕ2	600	0.128 (0.150)	7.289 (6.133)	0.93	1.304 (0.006)
		300	0.271 (0.302)	10.104 (11.895)	0.91	1.295 (0.012)
		150	0.550 (0.666)	15.945 (19.385)	0.87	1.275 (0.028)
		75	1.195 (1.525)	40.839 (84.929)	0.82	1.243 (0.055)
2	ϕ1	600	0.031 (0.036)	3.633 (1.335)	0.97	1.154 (0.001)
		300	0.060 (0.071)	4.804 (2.393)	0.95	1.152 (0.003)
		150	0.115 (0.138)	6.845 (5.531)	0.93	1.146 (0.006)
		75	0.212 (0.258)	9.457 (9.847)	0.91	1.138 (0.013)
	ϕ2	600	0.067 (0.077)	5.256 (3.407)	0.95	1.151 (0.003)
		300	0.123 (0.130)	6.539 (4.570)	0.93	1.147 (0.006)
		150	0.232 (0.273)	9.132 (8.516)	0.91	1.139 (0.011)
		75	0.465 (0.565)	14.722 (20.344)	0.88	1.124 (0.023)
3	ϕ1	600	0.021 (0.029)	3.335 (1.242)	0.97	1.467 (0.001)
		300	0.043 (0.056)	4.218 (2.130)	0.96	1.465 (0.002)
		150	0.083 (0.091)	5.867 (4.874)	0.94	1.462 (0.004)
		75	0.160 (0.182)	8.420 (9.496)	0.92	1.455 (0.007)
	ϕ2	600	0.070 (0.085)	5.459 (2.942)	0.95	1.463 (0.003)
		300	0.143 (0.157)	7.545 (6.940)	0.93	1.458 (0.006)
		150	0.274 (0.340)	9.937 (9.884)	0.91	1.449 (0.013)
		75	0.570 (0.678)	19.008 (31.063)	0.87	1.431 (0.026)

Note that MIMSE values (se) are ×10⁻⁴.

Table 3.

Estimation performance (se) and treatment selection performance for Scenarios 4, 5, and 6 for different working functions for h₀ (ϕ = ϕ₁ or ϕ₂) and for various sample sizes.

Scenario	ϕ	n	Scalar MSE	Functional MIMSE	PCD	Ê{Y*(ĝ)}
4	ϕ1	600	0.037 (0.052)	0.922 (0.498)	0.92	1.302 (0.003)
		300	0.081 (0.112)	1.833 (2.756)	0.88	1.286 (0.007)
	ϕ2	600	0.175 (0.226)	3.484 (6.332)	0.84	1.258 (0.015)
		300	0.375 (0.458)	6.330 (5.365)	0.78	1.212 (0.029)
5	ϕ1	600	0.037 (0.053)	0.943 (0.898)	0.92	1.144 (0.003)
		300	0.074 (0.103)	1.784 (2.261)	0.89	1.128 (0.008)
	ϕ2	600	0.075 (0.112)	1.593 (0.968)	0.89	1.129 (0.007)
		300	0.168 (0.216)	2.842 (2.624)	0.84	1.105 (0.014)
6	ϕ1	600	0.024 (0.033)	0.779 (0.597)	0.93	1.459 (0.002)
		300	0.055 (0.086)	1.469 (2.903)	0.90	1.448 (0.005)
	ϕ2	600	0.083 (0.110)	1.778 (1.296)	0.88	1.438 (0.008)
		300	0.173 (0.221)	3.389 (2.688)	0.83	1.410 (0.016)

Note that MIMSE values (se) are ×10⁻⁴.

With respect to treatment selection accuracy as measured by PCD, we observe that larger sample sizes, fewer spurious variables, and a richer working model for ϕ result in higher accuracy in treatment selection in the independent test sets. Furthermore, the results show that our approach can provide treatment selection strategies that can come close to achieving the mean value of the response in the population under the optimal treatment.

In Web Appendix B, we give a brief discussion concerning inference for the difference in the expected values of the response under competing regimes. We also outline and comment on a simple bootstrap procedure for constructing confidence intervals for this difference. In Web Appendix C we show the results of applying this bootstrap procedure for constructing confidence intervals on the simulated data generated under Scenarios 1 – 3.

4. Application to MDD Treatment Data

To illustrate our proposed approach for developing a treatment decision rule using available baseline scalar and functional covariates, we consider data from a study that investigated the use of two treatments for MDD. In addition to standard clinical measures (e.g., age, gender, Hamilton Depression Rating Scale (HAM-D) score, etc.) the study also collected EEG measurements under a controlled resting condition in which subjects had their eyes open or closed. After these baseline data were collected, the participant was randomized to either an antidepressant (a selective serotonin reuptake inhibitor (SSRI)), or placebo. The participant was monitored via assessments at 1, 2, 3, 4, 6, and 8 weeks after initiation of treatment.

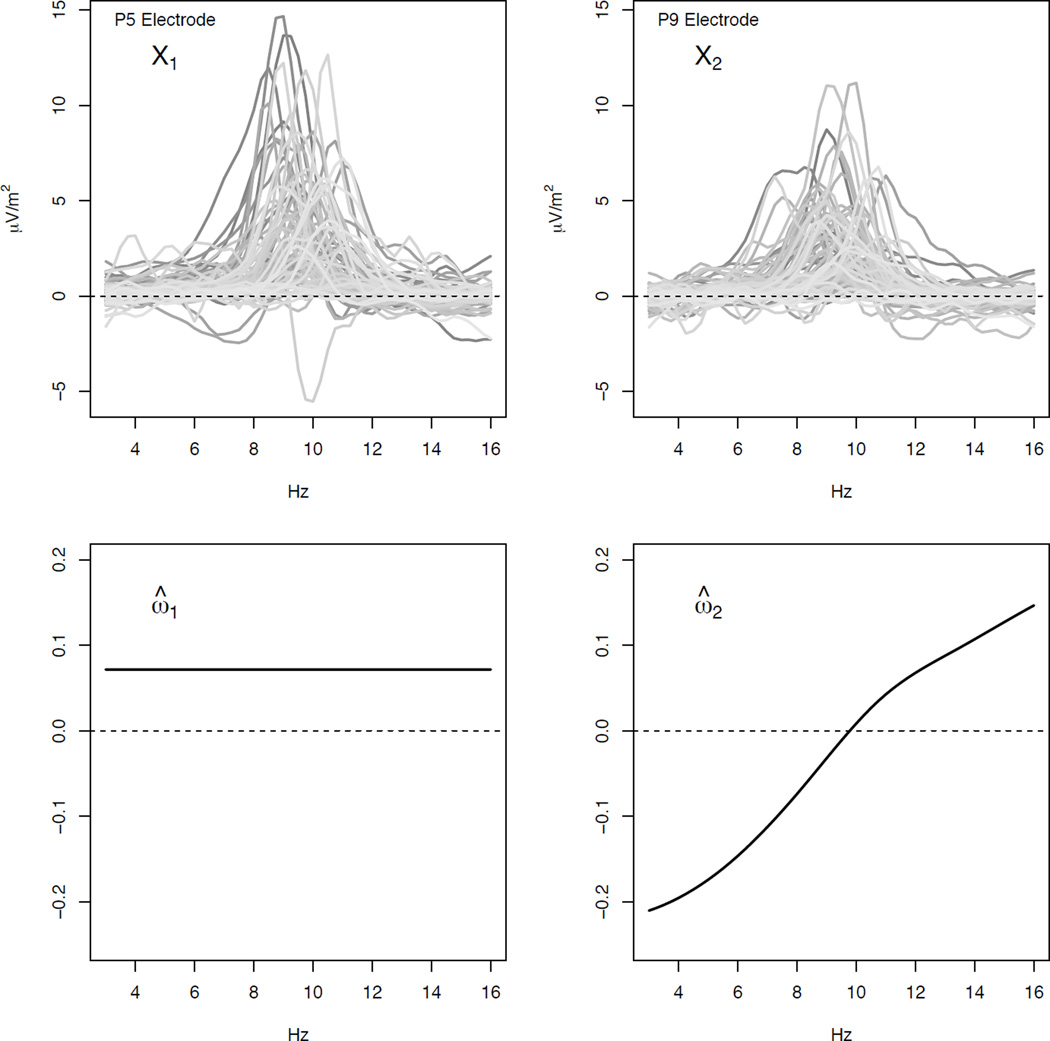
There are 92 subjects in the study. We consider a restricted set of baseline scalar covariates consisting of gender, age, and baseline HAM-D score. We also consider two baseline functional covariates derived from resting EEG using a 72-electrode montage. More specifically, these two functional covariates correspond to the curves giving the difference between current source density (CSD) amplitude spectrum values (μV/m²) when the participant’s eyes are closed and when they are open (closed - open) over a frequency range of 3 to 16 Hz for the P5 and P9 electrodes. This frequency range roughly corresponds to what are known as the theta and alpha frequency bands and these two electrodes are located in the posterior region of the 72-electrode montage. Prior studies have suggested that posterior theta and alpha rhythm of the EEG may be useful in differentiating patients who do or do not respond to SSRIs or other treatments for MDD (Bruder et al., 2008; Tenke et al., 2011). A detailed discussion of CSD measures in EEG is provided in Tenke et al. (2011). The top left and right panels of Figure 2 show the CSD difference curves corresponding to the P5 (X₁) and P9 (X₂) electrodes for the 92 subjects in our data set.

Figure 2.

Top Panels: CSD differences (eyes closed - eyes open) from the P5 channel (left) and P9 channel (right). Bottom Panels: Estimated contrast coefficient functions corresponding to the P5 channel (left) and P9 channel (right)

Of the 92 subjects that we use to develop a treatment decision rule, 48% were randomized to SSRI, 65% are female, the mean age is 39.05, and the mean baseline HAM-D score is 18.34. For the response, we consider HAM-D score at end of the treatment period. Thus lower values of the response variable are desirable. Three of the 92 subjects were missing their HAM-D score at week 8 so we chose to use their score at week 6 for the response.

Let Z = (Z₁, Z₂, Z₃)^⊤ be the vector of baseline scalar covariates where Z₁ = 1 if the patient is female and 0 otherwise, Z₂ = age, and Z₃ = HAM-D score at baseline. These scalar covariates are centered and scaled by their respective sample means and standard deviations before fitting the model. Furthermore, let X = {X₁, X₂} where X₁ and X₂ are the CSD difference curves corresponding to the P5 and P9 channels respectively. To estimate the decision rule, we assumed equal probability of receiving the SSRI or placebo and used a working baseline function given by $\varphi (\mathit{Z},\mathit{X})={\tilde{\mathit{Z}}}^{\top }\gamma +{\sum }_{\ell =1}^2\int X_{\ell }(s){\alpha }_{\ell }(s)ds$. We used 10 functional principal components to represent each of the functional covariates and a B-spline basis with 8 basis functions to represent each of the coefficient functions.

The estimated treatment decision rule is given by

$$ĝ(\mathit{Z},\mathit{X})=I\{-0.86+2.14Z_1+1.53Z_2+0.88Z_3+\int {\hat{\omega }}_1(s)X_1(s)ds+\int {\hat{\omega }}_2(s)X_2(s)ds>0\},$$

where ω̂₁ and ω̂₂ are shown in the bottom panels of Figure 2. If ĝ(Z, X) = 1 then the SSRI is selected, otherwise placebo is selected. Although complex, the estimated decision rule may provide some insight into how individual patient characteristics can be used to select treatment. First consider the scalar covariates. Adjusting for all other covariates, being female, being older than the average age in the sample, and having baseline HAM-D that is higher than the average in the sample all increase the value of the contrast and so might suggest the use of the SSRI over placebo. Next consider the functional covariates and their corresponding contrast coefficient estimates shown in Figure 2. Based on ĝ, adjusting for all other covariates, large positive CSD differences across the theta and alpha frequency bands corresponding to the P5 electrode suggest the use of the SSRI over placebo. The estimated contrast coefficient function corresponding to the P9 electrode shows that large positive CSD differences in the theta band, especially at lower frequencies, suggest the use of placebo over the SSRI and large positive CSD differences in the alpha band, especially at higher frequencies, suggest the use of the SSRI over placebo.

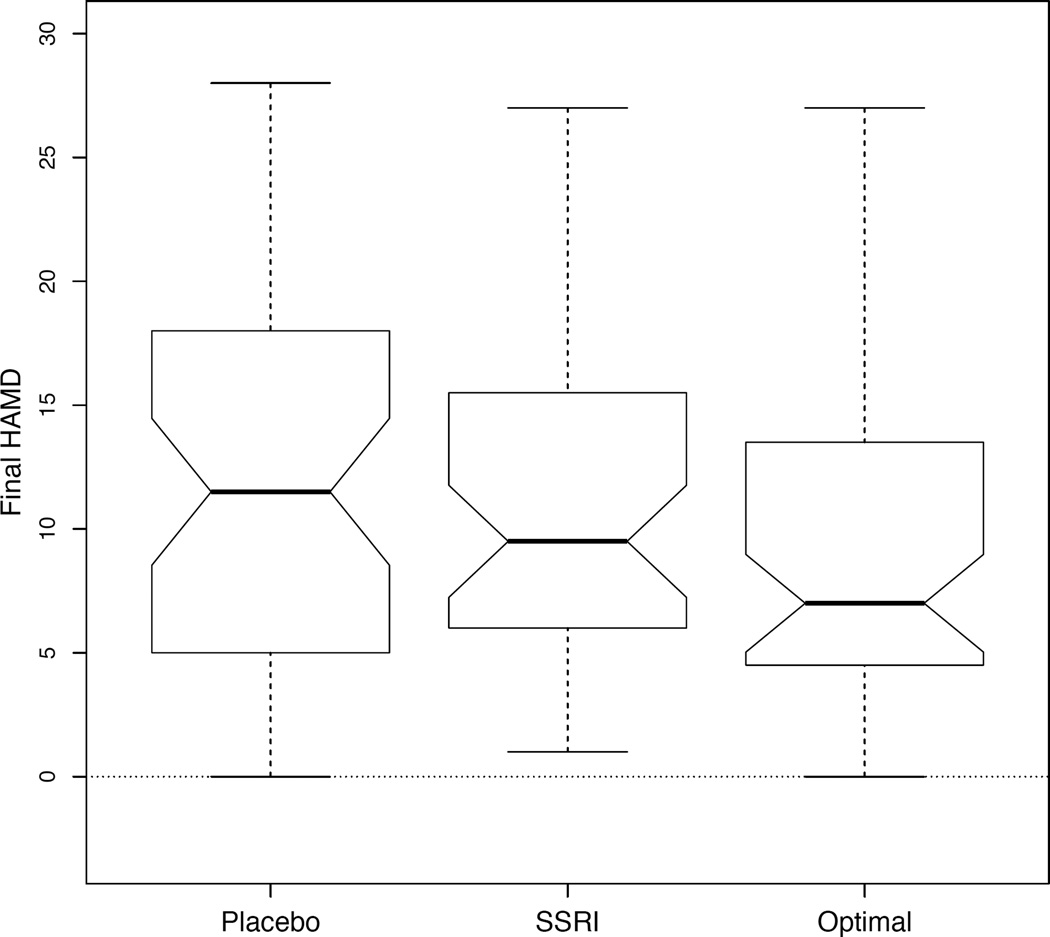
To assess treatment selection among the patients used to develop the decision rule, we compared the average value of the response among the following subgroups: (1) those who received placebo, (2) those who received the SSRI, and (3) those who received the treatment that would have been assigned if ĝ were used to assign treatment. There were 52 patients whose actual treatment assignment matched what would have been assigned based on ĝ (22 on placebo, 30 on the SSRI). Figure 3 shows the distributions of the HAM-D score at the end of treatment for each of these three subgroups. The mean HAM-D scores at the end of treatment are 11.42 for those on placebo, 10.93 for those on the SSRI, and 9.38 for those who received their estimated optimal treatment. We used the bootstrap procedure discussed in Web Appendix B (see note on issues related to using a bootstrap procedure) to construct 95% confidence intervals for the mean improvements in HAM-D score at the end of treatment comparing our treatment assignment model (denoted by g) to either (1) assigning the SSRI to all patients (denoted by 1) or (2) assigning placebo to all patients (denoted by 0). The 95% confidence interval for E{Y*(g)} − E{Y*(1)} is (−4.07, −0.06) and for E{Y*(g)}−E{Y*(0)} is (−4.65, −0.17). Both intervals suggest that the treatment regime based on the baseline scalar and functional predictors is preferable, perhaps only slightly, to assigning everyone either SSRI or placebo as it appears to lead to lower HAM-D score at the end of the treatment period.

Figure 3.

Boxplots comparing HAM-D scores at end of treatment for those on placebo, SSRI, or for those whose treatment matched the optimal treatment according to ĝ.

5. Discussion

We have proposed a method for constructing a treatment decision rule based on scalar and functional baseline covariates that casts estimation as a loss-minimizing procedure in the framework of A-learning. In the case of all scalar baseline covariates, A-learning has been shown to provide protection against mis-specification of part of the response model provided that the contrast is correctly specified. Our numerical investigations provide evidence that this property carries over to the case where the baseline covariates consist of both scalars and functions. Furthermore, it has been argued that A-learning is appealing because it may be reasonable to expect that there is a complex relationship between the baseline covariates and the response, but that the optimal treatment rule should depend on those baseline covariates in a simple manner (Schulte et al., 2014). Although the part of the model corresponding to the response among those on the “reference treatment” may be mis-specified, we recommend using a richer working model as we have evidence that a richer model leads to better estimation and treatment selection.

Regarding our application to the MDD data, one reason why the treatment assignment model that we consider did not lead to “substantially” better response may be that we are not considering baseline covariates that are most prescriptive of treatment. In practice, there may be relatively little clinical guidance on which baseline covariates are prescriptive of a particular treatment and so it may be desirable to incorporate a variable selection procedure into our approach that can identify such variables. Furthermore, our numerical investigations demonstrated that the inclusion of spurious variables in the response model can lead to poorer estimates of the contrast parameters and poorer performance with respect to treatment selection. Development of approaches that can both estimate treatment decision rules and select important prescriptive scalar and functional baseline covariates is crucial and could lead to better outcomes for patients suffering from MDD.