Adaptive sampling in two-phase designs: a biomarker study for progression in arthritis

Abstract

Response-dependent two-phase designs are used increasingly often in epidemiological studies to ensure sampling strategies offer good statistical efficiency while working within resource constraints. Optimal response-dependent two-phase designs are difficult to implement, however, as they require specification of unknown parameters. We propose adaptive two-phase designs that exploit information from an internal pilot study to approximate the optimal sampling scheme for an analysis based on mean score estimating equations. The frequency properties of estimators arising from this design are assessed through simulation, and they are shown to be similar to those from optimal designs. The design procedure is then illustrated through application to a motivating biomarker study in an ongoing rheumatology research program. Copyright © 2015 © 2015 The Authors. Statistics in Medicine Published by John Wiley & Sons Ltd.

1 Introduction

1.1 Two-phase designs with response-dependent sampling

Epidemiological studies with multiphase sampling designs ¹ yield efficient estimators of exposure effects when one or more of the exposure variables are expensive or difficult to measure ^2–4. Key early papers in examining two-phase designs for logistic regression include those of Breslow and Cain ⁵ and Scott and Wild ⁶. The considerable appeal of such designs has led to their use in many areas of health research including dementia ⁷, myocardial infarction ⁸, and nephroblastoma ⁹. Two-phase designs are perhaps the most widely employed multiphase design. In the first phase of sampling (phase-I), characteristics that are relatively inexpensive to measure are recorded for all individuals in a large sample; these characteristics may include the response of interest (e.g., disease status) as well as auxiliary covariates. This information is then used to inform the sampling scheme for a second phase (phase-II) in which a subsample of individuals from the phase-I sample is selected for measurement of the expensive exposure variable. Efficiency gains over use of simple random sampling at phase-II are realized when phase-I data are used effectively to inform the phase-II sampling design ^10,11 and partial information available from phase-I is exploited in analyses.

Reilly and Pepe ¹² develop mean score estimating equations for settings with incomplete covariate data which can be easily implemented in two-phase studies if phase-I data are discrete. This approach exploits information from individuals selected at both phases of sampling to achieve greater efficiency than is possible based only on ‘complete’ data (i.e., data collected only from the subsample selected at phase-II). In terms of design, the mean score is particularly attractive because closed-form expressions are available for the phase-II sampling probabilities which minimize the asymptotic variance of the resulting mean score estimator ^10,12. General use of these asymptotically-optimal phase-II mean score designs has been advocated because of the ease with which they can be implemented ³ and because these designs have been shown to be highly efficient in a variety of settings, even when analyses are not based on the mean score approach ^13,14. Implementation of asymptotically-optimal designs, however, requires specification of underlying population characteristics including population variances and values of the parameter(s) of interest. Often, these necessary design parameters are estimated using data from an external pilot study ^3,10,15, but external pilot data are also expensive to obtain, and the extra cost may not be justified or recovered by the subsequent efficiency gains.

We consider a multiphase sampling design in which each sampling phase uses internal pilot data collected previously for estimating the asymptotically-optimal sampling procedure for the next phase of sampling. We implement and study a fully adaptive phase-II sampling design in which the asymptotically-optimal design is re-estimated between the selection of every individual in phase-II, and we implement a more practical adaptive design in which the phase-II sample is divided into an internal pilot subsample (a phase-IIa sample), which exploits the phase-I data, and an approximately optimal subsample (a phase-IIb sample), which exploits information gathered at both phase-I and phase-IIa. By using such adaptive procedures, an asymptotically-optimal sampling design can be well approximated without the need for external pilot data. The use of internal pilot data to modify study design was advocated by Wittes and Brittain ¹⁶. Lohr ¹⁷ used a similar approach, called triple sampling, in estimation of a multivariate mean. Fedorov et al. ¹⁸ consider related adaptive designs in the design of dose-finding trials. Pepe et al. ¹⁵ acknowledged the possibility of such an adaptive approach to approximate optimal mean score designs and stated that this approach needs further exploration. This manuscript addresses this need.

This work is motivated by the need to derive a sampling scheme for a biomarker study involving a cohort of patients with psoriatic arthritis (PsA). We describe the particular details of this problem in the next subsection. The remainder of this article is organized as follows. In Section 2, we define notation and give a derivation of the mean score estimating equations and the limiting distribution of the resulting estimator. The adaptive two-phase design is then described in detail in Section 3. The results of empirical studies are discussed in Section 4. Concluding remarks are made in Section 5.

1.2 A biomarker study in psoriatic arthritis

Psoriatic arthritis is an inflammatory, potentially debilitating, form of arthritis associated with psoriatic skin involvement ¹⁹. The course of this disease is highly variable; many patients do not experience any joint destruction, while as many as 20% suffer extensive joint destruction and consequently experience significantly poorer quality of life and decreased functional ability after developing a more serious form of the condition called arthritis mutilans ²⁰. Mild cases of PsA are often successfully treated with nonsteroidal anti-inflammatory drugs, but more severe cases require third-line therapies involving disease-modifying antirheumatic drugs and biologic agents ²¹. The long-term use of these stronger therapies incurs considerable cost to the healthcare system and may be associated with increased risk of liver toxicity ²². It is therefore important to determine in which patients early and aggressive intervention is warranted to alter the disease course and maintain quality of life and functional ability. To this end, there is great interest in identifying biomarkers that are associated with rapid disease progression and disability ^21,22.

Researchers at the University of Toronto PsA Clinic maintain a registry of over 1000 patients with PsA ²⁰. Disease activity and progression in this registry cohort are tracked through annual clinic visits and biannual radiographic examinations. In addition, blood and urine samples from these individuals have been stored in a biobank. Samples from this biobank can be drawn for measurement of potentially important biomarkers. There is particular interest in examining the effect of the matrix metalloproteinase 3 (MMP-3) biomarker, which has been shown to be both associated with the presence of PsA in patients with psoriasis and correlated with disease activity in patients with other forms of arthritis ¹⁹.

Processing and testing of the serum samples are expensive and cannot feasibly be performed for all patients in the cohort. We therefore require design strategies so that a subset of patients can be selected for measurement of MMP-3 to provide optimal information regarding the association between levels of the expensive biomarker MMP-3 and disease progression. Because the erythrocyte sedimentation rate (ESR), a generic marker of inflammation, is commonly used for prognostic inferences, the goal is to assess the relationship between MMP-3 levels and progression while controlling for the ESR level. Pilot data from the University of Toronto Psoriatic Arthritis Clinic are used to frame the simulation studies reported in Section 4.

2 Response-dependent sampling with the mean score method

2.1 Notation and model assumptions

Let Y_i denote a discrete response, which could be binary, categorical, or multivariate in which case Y_i=(Y_i1,…,Y_iK)′ is a K × 1 vector for individual i, i = 1,2…. We let X_i denote an exposure variable of primary interest that is difficult or expensive to observe, and let V_i denote a discrete, inexpensive auxiliary covariate. Suppose that interest lies in estimation of the p × 1 parameter β indexing the conditional, possibly joint, probability mass function for Y_i given (X_i,V_i) denoted

1

The conditional distribution of X_i given V_i, denoted g(X_i|V_i;α), is indexed by a q × 1 parameter α, and we suppose that the marginal probability mass function of V is indexed by an r × 1 parameter γ. The full vector of random variables is therefore governed by the joint model f(Y,X,V;β,α,γ) = f(Y|X,V;β)g(X|V;α)h(V;γ), where α and γ are nuisance parameters that are routinely eliminated by conditioning on (X,V) when data are complete.

In a two-phase study, {(Y_i,V_i),i = 1,2,…,N} are observed for N individuals selected in a phase-I sample, but X_i is observed only for the n individuals selected for inclusion in the phase-II subsample, where n < N. We let R_i indicate selection of individual i into the phase-II sample so that X_i is known only for those n individuals for whom R_i=1. The response and auxiliary covariate are discrete in the present setting, which means that the phase-I sample can be subdivided into strata defined by (Y,V); we let 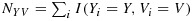denote the size of the corresponding strata, where the indicator function 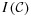is 1 if condition 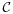is true and is 0 otherwise. We let 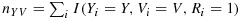represent the number of individuals randomly subsampled from the phase-I strata, and we suppose that these phase-II stratum sample sizes can be specified by the investigator; by design, a simple random sample of size n_YV will be selected for the measurement of X from the available N_YV individuals in stratum (Y,V). The resulting data will be missing at random ²³ because X⊥R|Y,V (i.e., missingness is conditionally independent of the potentially missing covariate given the phase-I data). We wish to employ optimal phase-II sampling designs that allocate resources to select individuals such that the asymptotic variance is minimized for the estimator of interest; ultimately, we wish to determine the optimal choices of n_YV for selecting the 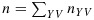individuals for whom the expensive covariate X will be observed.

2.2 The mean score method

Upon selection of the phase-II sample, X is unobserved for N − n individuals, so estimation of β must occur jointly with estimation of the nuisance parameter α in likelihood analysis. Estimation can be carried out by maximizing the observed data likelihood directly or by implementing an expectation–maximization algorithm ²⁴ in which the equations

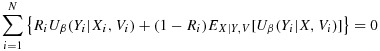2

and

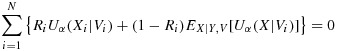are iteratively solved, where U_β(Y_i|X_i,V_i) = ∂ logf(Y_i|X_i,V_i;β)/∂β and U_α(X_i|V_i) = ∂ logg(X_i|V_i;α)/∂α ^23,25. The resulting maximum likelihood estimator for β will be consistent and fully efficient if all model assumptions are valid. It can be challenging to specify the nuisance probability model for X|V, and it is undesirable for inferences about β to be sensitive to misspecification of this model ²⁶.

To address this, Reilly and Pepe ¹² propose a pseudolikelihood method that leads to a mean score-estimating equation for β obtained through a noniterative, empirical approximation to the expectation in 2. When Y and V are discrete and the data are missing at random, the conditional expectation of the pseudoscore is estimated as

and the mean score estimating equations reduce to

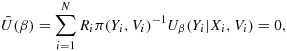where π(Y,V) = n_YV/N_YV ^12,25. The mean score method, therefore, can be viewed as a Horvitz–Thompson-type inverse probability weighted estimating equation for which the selection probabilities are estimated empirically ⁸.

Under mild regularity conditions ²⁷, a consistent estimator 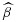is obtained as the solution to the mean score equation 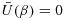. Moreover,

6

where ,

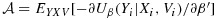and P(Y,V) is the joint probability mass function for (Y,V); see the Supporting Information for details. Reilly and Pepe ¹² show that when N and n are fixed, the form of this asymptotic variance can be exploited to give closed-form solutions for the optimal phase-II sampling design that selects individuals in order to minimize the asymptotic variance of an estimator of interest. Reilly and Pepe ¹² considered fixing the expected phase-II sample size through the constraint

8

If we wish to minimize the [k,k] entry of the covariance matrix defined in 6 corresponding to the estimator of a parameter of interest with this constraint, then the optimal stratum-specific sample sizes are

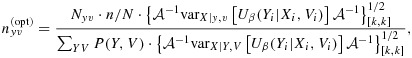where the [k,k] entry of a matrix 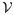is denoted by 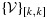. Here, we focus on minimizing the asymptotic variance for the estimator of a particular parameter; however, researchers are free to define optimality criteria in a variety of ways, and designs can naturally be modified to accommodate optimality criteria based on linear functions of the elements of the asymptotic variance matrix (e.g., analogues to A-optimality and C-optimality ²⁸ could be considered as described by McIsaac and Cook ¹³).

An obvious challenge in implementing an optimal design is that computation of these optimal stratum-specific sample sizes hinges on specification of the matrix 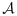, var_X|Y,V[U_β(Y_i|X_i,V_i)], and the joint probability P(Y,V) ¹². McIsaac and Cook ¹³ also noted that the expected sample size constraint of Reilly and Pepe ¹² may not be appropriate when the sizes of the phase-I strata are known. In the next section, we derive an adaptive procedure that uses a more suitable constraint and that does not require external information to specify the approximately optimal selection probabilities.

3 Adaptive response-dependent multiphase sampling designs

The proposed adaptive sampling strategy involves partitioning the phase-II sampling into a series of distinct subphases. Individuals in the first subphase of phase-II data collection cannot be selected optimally because at this point there are insufficient data to estimate the components necessary for approximating the optimal mean score design (i.e., 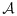 , var_X|Y,V[U_β(Y_i|X_i,V_i)], and P(Y,V) cannot all be estimated using only phase-I data). Subsequent subphases, however, can make use of the accumulating data to estimate the necessary design components, and therefore, one can approximate the asymptotically-optimal design ^18,29,30.

As an extreme implementation of the proposed approach, we consider a fully adaptive sampling strategy in which, following a small initial sample, selection probabilities are updated after each individual is sampled in phase-II. This fully adaptive design therefore features almost as many sampling subphases as there are individuals selected in phase-II. We also consider a two-stage adaptive sampling strategy that uses only two subphases of sampling individuals for measurement of the expensive covariates; we refer to these as phase-IIa in which n^(a) individuals are selected for measurement of X without information about the optimal design components, and phase-IIb in which we sample the remaining n^(b) phase-II individuals by exploiting the phase-I and phase-IIa data to approximate the asymptotically-optimal design.

In what follows, we describe how the two-stage adaptive sampling procedure enables one to approximate asymptotically-optimal sampling at the second subphase of phase-II (i.e., phase-IIb); this process can be generalized to a sampling design with an arbitrary number of subphases. The impact on efficiency of the number of sampling subphases and the relative sizes of each sampling subphase is explored through simulations in the next section, where we also examine the impact of using empirical estimators for 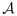, var_X|Y,V[U_β(Y_i|X_i,V_i)], and P(Y,V).

The sampling plan involves deciding how to distribute the fixed phase-II sample size of n = n^(a)+n^(b) individuals among the strata defined by phase-I data while adhering to the phase-II sample size constraint

10

where 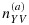represents the number of individuals selected from stratum (Y,V) at phase-IIa and 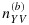is defined analogously for phase-IIb. We assume that the stratum sizes of the internal pilot study, 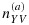, are fixed, and we select the remaining individuals using the optimal design, which minimizes the asymptotic variance of the estimator of interest (the [k,k] entry of the asymptotic covariance matrix in 6). Assuming that the necessary optimal design components are estimated as 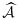, , 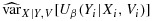and 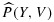using data collected at phase-I and phase-IIa, we wish to find the 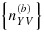that are stationary points of the Lagrangian

The optimal 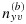is the solution to

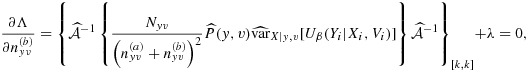and the optimal stratum-specific phase-IIb sampling sizes are therefore best selected as

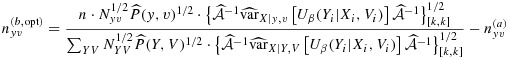13

under the constraints 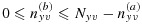. If 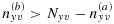for some (y,v), then one can set 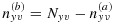and solve for the other phase-IIb sample sizes using an updated version of 13 ¹². Here, we need not worry about the degenerate case 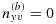but must simply ensure 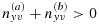. Note that 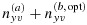is slightly different than 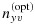of Reilly and Pepe ¹² owing to the different phase-II sample size constraints we adopt (i.e., 10 as opposed to 8), although the two will align when P(Y,V) is estimated empirically as .

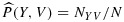4 Empirical properties of adaptive two-phase mean score designs

4.1 Design of simulation studies

In this section, we examine empirically the stratum-specific sampling probabilities and the efficiency of adaptive mean score designs in the context of the PsA biomarker study. In each simulation, we implement a nonadaptive sampling design based on proportional stratified sampling (i.e., where n_YV∝N_YV), a nonadaptive sampling designs based on balanced stratified sampling (i.e., where all n_YV are equal), a fully adaptive sampling design, two-stage adaptive designs with varying choices of n^(b), and a local asymptotically-optimal design based on the true (in practice, unknown) parameters. The latter is considered as a benchmark to assess how close to optimal the adaptive designs can behave. We also consider estimation of the design components 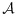, var_X|Y,V[U_β(Y_i|X_i,V_i)], and P(Y,V) in two ways. The first is by assuming parametric forms of the component models and finding interim estimates of necessary parameter values; 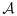, for example, would be estimated parametrically as 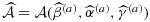where parameters are estimated based on the currently available (phase-I and phase-IIa) data. The second is through empirical estimation; for example, using

where 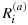indicates that individual i was selected in phase-IIa and .

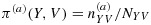In our simulation studies, we assume the correct parametric form when estimating design components; it would be impossible to guarantee that an assumed parametric form is correct in practice, but other studies have demonstrated that the efficiency of optimal mean score designs can be fairly robust to misspecification of such auxiliary models ^13,31. In addition, we note that misspecification of these auxiliary models at the design stage will not affect the consistency of the robust mean score estimation procedure. As suggested by Pepe et al. ¹⁵, we stabilized the estimation of the design components by adding two artificial observations to each phase-I stratum.

We consider here results from simulation studies that focus on Y and V as univariate binary variables but consider separately binary and continuous versions of the covariate X. Again, for the two-stage adaptive sampling, we consider phase-II selection in two steps. First, we select n^(a) individuals using proportional or balanced sampling. Second, we select the remaining n^(b)=n − n^(a) individuals according to the approximate optimal mean score design found by using both the phase-I and phase-IIa data to estimate the necessary design components parametrically or empirically. The fully adaptive sampling is similar, but it uses a small balanced sample at phase-IIa to allow for an initial estimate of the design components, and then individuals are selected one at a time with estimates of the design components being updated after the selection of each individual.

For the two-stage adaptive sampling, we consider 10 possible choices for the proportion of the phase-II sample selected at phase-IIb: we allow n^(b)/n to range from 0% to 90% in 10% increments. Note that when n^(b)/n = 0%, n^(b)=0, which represents a scenario where the entire phase-II sample is chosen through either proportional or balanced sampling (i.e., the design is nonadaptive). We frame the design in the context of the motivating two-phase biomarker study in PsA. Specifically, this study aims to examine optimal two-phase designs for selecting patients for measurement of the biomarker MMP-3 in the University of Toronto Psoriatic Arthritis Clinic with a view to examining the relationship between baseline MMP-3 levels and disease progression. We let Y denote a binary response indicating the fact that the disease has progressed over the period of follow-up, let V denote an inexpensive binary covariate indicating an elevated (abnormal) ESR measurement at the baseline assessment, and let X denote the baseline MMP-3 levels, the expensive covariate of interest.

For the simulation study, 2000 phase-I samples of size N = 800 were generated. For each individual, the response Y had conditional mean

15

and the binary covariates satisfied

and

17

where expit(Z)= exp(Z)/(1+ exp(Z)). The parameter values (β₀,β_x,β_v) = (−1.95,1.00,0.90), (α₀,α_v) = (1.05,−0.41), and γ₀=−0.04 were obtained from fitting models to a small independent historical sample of the PsA patients where MMP-3 levels were dichotomized using a clinically relevant cut point. We also considered the case in which X is a continuous variable representing the scenario in which MMP-3 levels were not dichotomized. Here, Y and V were still Bernoulli variables generated according to 15 and 17; however, we supposed X|V arose from a gamma distribution with shape α₀ and scale α₁+α_vV, as in

Because Y and V were discrete, we could still define strata as before at phase-I. The parameter values used in generating these data were (β₀,β_x,β_v) = (−2.18,0.03,.84), (α₀,α₁,α_v) = (1.40,10,5), and γ₀=−0.04. where values were chosen to reflect the empirical distribution of MMP-3 measurements given ESR status in the historical PsA data.

Optimal and adaptive designs were employed to minimize the asymptotic variance of the estimator of β_x, which was taken to be of special interest. Each design was executed for each of the 2000 simulated datasets, with n = 200 subjects sampled in phase-II. One way of contrasting the local asymptotically-optimal design and the adaptive designs is in terms of the proportion of individuals selected for measurement of X from each stratum, (n_YV−nYVopt)/N_YV. These are displayed in Figures 1 and 3 for the case where X is binary and in Figures 2 and 4 for settings involving a continuous X. The local asymptotically-optimal design here utilized the true parameters that generate the data and is therefore not practically feasible, while the adaptive approaches attempted to approximate this asymptotically-optimal design by estimating necessary components using phase-I and phase-IIa data. Figures 1 and 2 display the differences in sampling proportions between the asymptotically-optimal design and the adaptive designs that resulted from both parametrically and empirically estimating , var_X|Y,V[U_β(Y_i|X_i,V_i)], and P(Y,V) when using proportional stratified sampling at phase-IIa. The corresponding figures for the designs employing balanced sampling in phase-IIa are presented in Figures 3 and 4.

Figure 1.

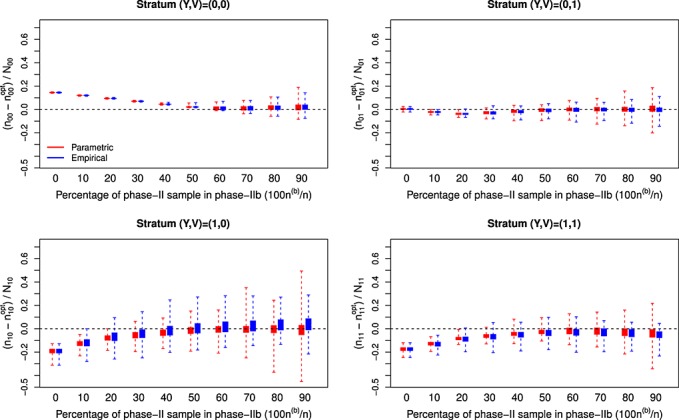
Empirical differences in sampling fractions between the asymptotically-optimal design and the two-stage adaptive designs employing proportional stratified sampling in phase-IIa according to the percentage of the phase-II sample that is selected at phase-IIb (n^(b)/n) for a binary expensive covariate; N = 800; n = 200; (β₀,β_x,β_v) = (−1.95,1.00,0.90), (α₀,α_v) = (1.05,−0.41), and γ₀=−0.04 ; n_YV represents the number of individuals selected for the measurement of X from the available N_YV individuals in stratum (Y,V) in the two-stage adaptive design, while represents the corresponding sample size for the asymptotically-optimal design. This two-stage adaptive design was derived for selecting individuals for measurement of a binary X and relied on either parametric or empirical estimation of design components from data collected in phase-I and phase-IIa.

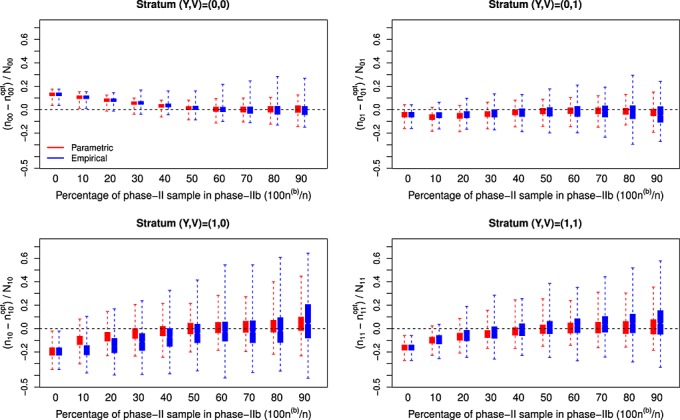
Figure 3.

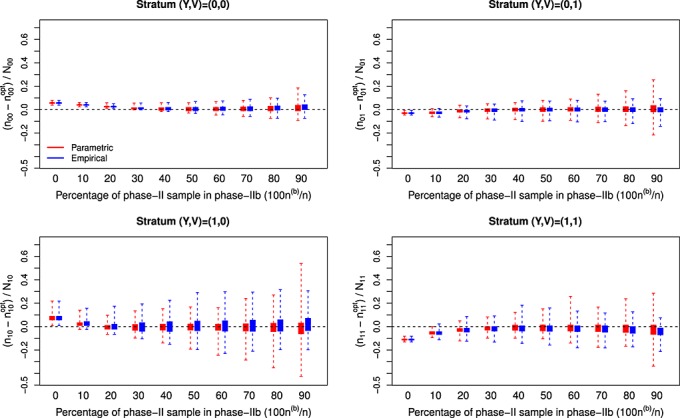
Empirical differences in sampling fractions between the asymptotically-optimal design and the two-stage adaptive designs employing balanced sampling in phase-IIa according to the percentage of the phase-II sample that is selected at phase-IIb (n^(b)/n) for a binary expensive covariate; N = 800; n = 200; (β₀,β_x,β_v) = (−1.95,1.00,0.90), (α₀,α_v) = (1.05,−0.41), and γ₀=−0.04 ; n_YV represents the number of individuals selected for the measurement of X from the available N_YV individuals in stratum (Y,V) in the two-stage adaptive design, while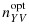 represents the corresponding sample size for the asymptotically-optimal design. This two-stage adaptive design was derived for selecting individuals for measurement of a binary X and relied on either parametric or empirical estimation of design components from data collected in phase-I and phase-IIa.

Figure 2.

Empirical differences in sampling fractions between the asymptotically-optimal design and the two-stage adaptive designs employing proportional stratified sampling in phase-IIa according to the percentage of the phase-II sample that is selected at phase-IIb (n^(b)/n) for a continuous expensive covariate; N = 800; n = 200; (β₀,β_x,β_v) = (−2.18,0.03,.84), (α₀,α₁,α_v) = (1.40,10,5), and γ₀=−0.04; n_YV represents the number of individuals selected for the measurement of X from the available N_YV individuals in stratum (Y,V) in the two-stage adaptive design, while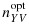 represents the corresponding sample size for the asymptotically-optimal design. This two-stage adaptive design was derived for selecting individuals for measurement of a continuous X and relied on either parametric or empirical estimation of design components from data collected in phase-I and phase-IIa.

Figure 4.

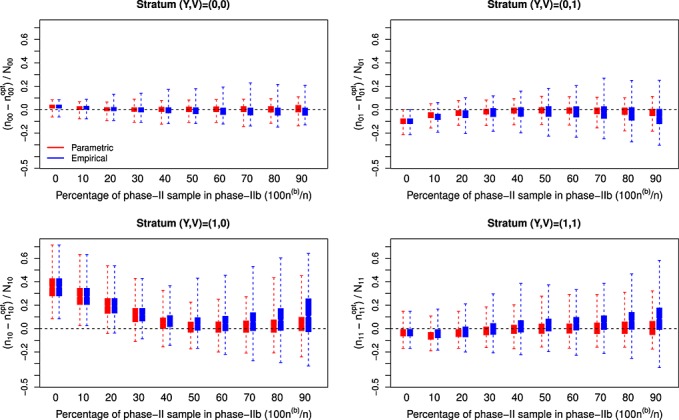
Empirical differences in sampling fractions between the asymptotically-optimal design and the two-stage adaptive designs employing balanced sampling in phase-IIa according to the percentage of the phase-II sample that is selected at phase-IIb (n^(b)/n) for a continuous expensive covariate; N = 800; n = 200; (β₀,β_x,β_v) = (−2.18,0.03,.84), (α₀,α₁,α_v) = (1.40,10,5), and γ₀=−0.04; n_YV represents the number of individuals selected for the measurement of X from the available N_YV individuals in stratum (Y,V) in the two-stage adaptive design, while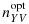 represents the corresponding sample size for the asymptotically-optimal design. This two-stage adaptive design was derived for selecting individuals for measurement of a continuous X and relied on either parametric or empirical estimation of design components from data collected in phase-I and phase-IIa.

The empirical relative efficiencies and empirical coverage probabilities of the estimators resulting from the different designs are presented in Table 1. The empirical relative efficiency (ERE) of design A was calculated as evar₀/evar_A·100%, where evar_A is the empirical variance of the estimator for β_x arising from design A and evar₀ is the corresponding empirical variance under the asymptotically-optimal design, which requires specification of the unknown parameter values. This definition is analogous with that of Fedorov et al. ¹⁸ who examined efficiency in the context of optimal design for dose-finding experiments. As an additional measure of the variation of estimators over the 2000 simulations, we also present in Table 1 the empirical relative interquartile range (ERI) calculated as IQR₀/IQR_A·100%, where IQR_A is the observed interquartile range among the estimates for β_x arising from design A and IQR₀ is defined analogously for the asymptotically-optimal design. Values of ERE or ERI less than 100% reflect a loss of precision relative to the optimal design, and values greater than 100% indicate greater local precision than realized with the asymptotically-optimal design using the true parameter values. Empirical coverage probabilities show the percentage of the simulations in which the true β_x is contained in 95% confidence intervals, which are constructed using sample estimates of the asymptotic variance in 6 upon completion of phase-II sampling.

Empirical relative efficiencies (ERE) and empirical relative interquartile ranges (ERI) compared with the asymptotically-optimal design based on true (unknown) parameters and empirical coverage probabilities (ECP) of estimators for β_x based on 2000 simulated datasets with N = 800 and n = 200.

	Binary X						Continuous X
	Parametric			Empirical			Parametric			Empirical
100n(b)/n	ERE	ERI	ECP	ERE	ERI	ECP	ERE	ERI	ECP	ERE	ERI	ECP
Two-stage adaptive – proportional sampling in phase-IIa
0*	76.6	88.7	95.5	76.6	88.7	95.5	88.9	94.4	95.2	88.9	94.4	95.2
10	85.0	93.4	95.3	84.3	90.2	95.2	94.7	97.7	94.8	89.4	97.9	94.8
20	86.3	89.9	94.7	84.6	90.9	94.8	94.0	96.9	94.7	87.8	92.2	94.0
30	94.0	97.8	95.2	89.3	97.9	93.8	102.6	99.8	95.2	93.2	97.1	94.6
40	96.3	96.3	95.0	103.1	100.8	95.4	100.7	104.3	94.8	86.0	91.1	93.2
50	98.2	95.0	94.8	92.6	96.3	94.2	103.2	102.4	95.1	88.5	94.7	93.3
60	103.1	100.0	95.2	95.2	96.5	94.8	105.0	102.0	95.5	88.2	97.0	93.7
70	97.2	98.2	95.0	95.4	98.8	94.4	103.0	103.3	94.6	93.9	96.9	94.8
80	100.7	103.1	95.1	100.8	101.3	95.0	107.9	105.2	95.6	85.6	96.6	94.5
90	98.6	102.2	95.4	97.7	97.5	94.5	103.7	103.8	95.0	82.8	94.0	94.7
Two-stage adaptive – balanced sampling in phase-IIa
0*	95.2	99.6	95.2	95.2	99.6	95.2	90.6	90.6	95.0	90.6	90.6	95.0
10	101.6	102.3	95.3	102.9	102.5	95.5	98.3	98.6	94.6	95.2	99.2	95.0
20	96.8	101.5	93.8	98.4	98.9	95.0	102.0	99.4	94.7	95.9	99.8	94.6
30	105.2	103.7	95.3	99.9	100.7	95.0	107.5	103.1	95.9	88.2	92.2	93.8
40	100.1	103.2	95.0	102.5	98.4	94.9	109.7	105.4	95.5	93.9	95.3	94.0
50	103.8	99.3	95.3	100.0	100.1	94.8	101.0	101.8	95.0	96.7	95.5	95.5
60	99.8	97.6	95.0	98.9	96.4	95.2	100.8	98.3	94.8	86.5	90.8	94.2
70	103.7	98.9	95.5	96.6	98.5	94.3	103.2	103.6	95.0	85.0	90.7	93.8
80	100.2	101.1	94.7	97.7	98.0	94.7	103.9	104.0	95.2	86.6	91.5	94.8
90	95.8	98.5	95.2	96.0	96.2	94.8	102.3	100.6	95.2	84.0	95.9	94.8
Fully adaptive
	102.4	107.0	95.3	99.0	96.7	94.5	102.4	101.9	95.3	86.8	89.1	94.3

The parameters were set to (β₀,β_x,β_v) = (−1.95,1.00,0.90), (α₀,α_v) = (1.05,−0.41), and γ₀=−0.04 for the case with binary X and to (β₀,β_x,β_v) = (−2.18,0.03,.84), (α₀,α₁,α_v) = (1.40,10,5), and γ₀=−0.04 for the setting with continuous X. Two-stage adaptive designs select n − n^(b) individuals using proportional or balanced sampling and use these individuals to estimate the design components either through parametric estimation (parametric) or through empirical estimation (empirical) to approximate optimal selection of the remaining n^(b) individuals. Nonadaptive designs are a special case of the two-stage sampling where all individuals are selected in phase-IIa. Fully adaptive designs involved selecting an initial balanced sample of size 40 (corresponding to 20% of n) and then selecting the remaining individuals one at a time while updating estimates of the design component after each individual is selected.

^**The nonadaptive design does not require estimation of the design components, so there is no distinction between design components being estimated ‘empirically’ or ‘parametrically’.

4.2 Empirical findings from simulation studies

The adaptive designs (i.e., those that selected some individuals in phase-IIb) resulted in sampling fractions that were much closer to the optimal designs on average than were the nonadaptive sampling designs (Figures 1234). However, the adaptive designs generally displayed greater variability in the sampling rates between simulations. As the fraction of individuals selected in phase-IIb increased two things occurred: (i) the average two-stage adaptive designs became closer to the asymptotically-optimal design, and (ii) the between-simulation variability in the two-stage adaptive designs increased. Selecting more individuals at phase-IIa allows for greater precision in estimating design components and, therefore, more stable designs. With more individuals selected at phase-IIa, however, fewer individuals can be selected according to the approximately optimal design at phase-IIb. This demonstrates a trade-off between precision and accuracy in the two-stage adaptive design when determining the fraction of individuals to select at each subphase of the phase-II sampling. The best properties of the adaptive sampling design (in terms of designs that are centered near the asymptotically-optimal design and have small between-simulation variability) resulted from balancing the number of phase-II individuals selected in the internal pilot study (phase-IIa) and the number of individuals that were selected according to the approximately optimal design (phase-IIb).

In the setting where X was binary, there was little difference between the adaptive approaches that resulted from estimating design components parametrically and those arising from estimating design components empirically either in terms of the designs themselves (Figures 1 and 3) or in terms of observed efficiency (Table1). However, in the setting with a continuous expensive covariate X, the greater efficiency of the parametric estimation of the design components translated into much less variability in the two-stage adaptive design (Figures 2 and 4) and, in turn, much greater efficiency in the estimator of interest (Table 1). In fact, when considering a continuous expensive covariate, the adaptive designs based on empirical estimation of design components offered no consistent efficiency gains over the nonadaptive sampling design; this was true for both two-stage adaptive and fully adaptive sampling designs based on empirical estimates of design components, and this result held both in terms of direct measures of ERE and in terms of the relative size of interquartile ranges (ERI), which is an alternate measure of the spread of resulting estimates that gives less weight to outliers. The adaptive designs (both two-stage and fully adaptive) based on parametric estimation of design components, on the other hand, consistently performed significantly better than the nonadaptive designs in terms of the efficiency achieved for the estimator of interest. In terms of the relative size of interquartile range, the parametric adaptive designs generally offered improvements over the nonadaptive designs; however, the nonadaptive balanced sampling design was very close to the asymptotically-optimal design for binary X and was not consistently improved by the adaptive procedures. The efficiency of the adaptive designs was often quite similar to the efficiency achieved by the local asymptotically-optimal sampling design, which of course cannot be implemented in practice. In fact, the adaptive designs often exceeded the asymptotically-optimal designs in terms of efficiency; we note that this apparently contradictory result is possible here because the benchmark designs, while obviously very efficient in these finite-sample settings, are only truly optimal as sample sizes tend to infinity.

In all cases, the empirical coverage probabilities were compatible with the nominal 95% level, which indicates that the estimated asymptotic standard errors for the adaptive design closely tracked the empirical standard errors. Therefore, the regular variance estimators worked well for these adaptive designs, which achieved efficiency that was very similar to that of the asymptotically-optimal design.

The nonadaptive balanced design was more efficient than the nonadaptive proportional stratified sampling design, but the nonadaptive designs were generally not as efficient as their adaptive counterparts. The fully adaptive designs based on parametric estimation of the design components generally led to the most precise estimates of effects. However, the two-stage adaptive designs are easier to implement in practice and were also very efficient when based on parametric estimation of design components. These two-stage adaptive designs were particularly effective when balancing the number of individuals selected in each of the two subphases of sampling and when using balanced sampling design for the internal pilot study. Although not presented here, these adaptive designs also generally resulted in an increase in efficiency for estimation of β₀ over nonadaptive designs; there was little impact on the efficiency for estimation of β_v.

5 Concluding remarks

We presented an adaptive approach to selecting individuals for measurement of an expensive covariate in a two-phase sampling design. This extension to Reilly and Pepe’s ¹² optimal mean score sampling design allows for explicit specification of near-optimal designs without a priori knowledge of the parameters and without the necessity for costly external pilot studies. These adaptive procedures are particularly important for elaborate response models where many parameters must be specified in order to derive the optimal design. The efficiencies of estimators under adaptive sampling based on parametric estimation of design components were generally very similar to those found under the theoretical optimal design, which cannot be implemented in practice. Previous studies have shown that the optimal mean score design that is being emulated by this adaptive procedure has desirable properties even when analyses are to be conducted using other methods ^3,13. Additionally, there was no evidence of bias among the adaptive sampling designs, and the empirical coverage probabilities were all compatible with the nominal levels.

Balanced sampling designs, as advocated by Breslow and colleagues ^5,9, were more efficient than proportional stratified sampling, but these nonadaptive designs could not achieve the same efficiency as the adaptive approaches. The fully adaptive designs could be very efficient but would be difficult to implement in practice. The two-stage adaptive procedure may be the most useful approach as it often offered near-optimal efficiency and would be relatively easy to implement in practice as it does not require re-estimation of the design components following the selection and response ascertainment of each individual. These findings of good efficiency and practical appeal in using a small number of phases as opposed to a fully adaptive sampling design are similar to the results seen in the setting of optimal dose-finding designs ¹⁸ and are analogous to the appeal of group sequential monitoring over sequential monitoring in clinical trials ³².

Other simulation studies showed very similar results and so have not been presented in depth here. Simulations involving clustered response vectors (based on ¹⁴) similarly showed that the adaptive design achieved levels of efficiency on par with the true optimal design; in those simulations, however, the nonadaptive balanced design was not nearly as efficient, so the benefit of the adaptive design was even more obvious.

One important finding here is that these two-stage adaptive designs should be based on parametric assumptions about necessary design components, rather than less precise empirical estimation. Focusing on parametric estimation at the design stage is reasonable as our goal is to employ the estimator from the most efficient design possible. This is especially true given that model misspecification at the design stage will not affect the consistency of the robust mean score estimation procedure. Additionally, the efficiency resulting from asymptotically-optimal mean score designs has been shown to be quite robust to model misspecification at the design stage ¹³.

There is also a trade-off between the potential efficiency of a large phase-IIb sample and the decreased precision of estimates of the design parameter values when phase-IIa is small in two-stage adaptive sampling. The two-stage adaptive designs that collected nearly equal numbers of individuals at phase-IIa and at phase-IIb were generally quite effective at generating near-optimal sampling fractions that were very efficient in finite samples.

We have focused here on the setting of a two-phase design in which phase-I data are available and one wishes to optimally select a fixed number of individuals for measurement of an expensive covariate during the second phase; this is precisely the setting of the motivating biomarker study. The simulations used were based on parameters derived from analyses based on a pilot study consisting of complete data from 20 arthritis patients with (Y,V) = (0,0), 7 patients with (Y,V) = (0,1), 17 patients with (Y,V) = (1,0), and 9 patients with (Y,V) = (1,1). If these data are taken as an internal pilot subsample (i.e., as a phase-IIa sample) in this setting where N₀₀/N = 0.39,N₀₁/N = 0.12,N₁₀/N = 0.28, and N₁₁/N = 0.21, then the two-stage adaptive sampling strategy would recommend the phase-IIb design 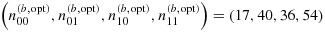in order to select the allotted 200 individuals for efficient estimation of β_x when MMP-3 measurements are to be dichotomized; if MMP-3 is to be considered continuously, then the optimal phase-IIb design is 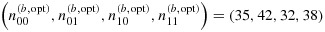for selection of the remaining 147 patients. Note that in order to achieve a balanced or proportional stratified sampling design, we would use 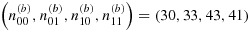and 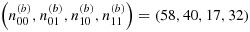, respectively, regardless of whether MMP-3 is to be dichotomized. The efficiency gained through this two-stage adaptive sampling strategy will depend on the accuracy of the parameters estimated at phase-IIa.

More generally, we recommend that the phase-II sampling be carried out adaptively in two stages as follows:

1. With a fixed number of individuals to be sampled in phase-II, half of them should be sampled using balanced stratified sampling with strata defined based on the phase-I data.

2. The remaining individuals to be sampled in phase-II should be chosen to satisfy the approximately optimal stratum-specific sampling sizes derived using 13 with available data being used in parametric estimation of necessary design components.

This approach would not be much more complex to implement than the nonadaptive two-phase designs in the motivating biomarker study, but it would lead to efficiency gains in the range of 5–20% when estimating the parameter of interest.

In settings different from the one we considered, it could be that the phase-I or phase-II sample sizes are not fixed in advance; further study of such settings is required to determine the best strategies for the use of adaptive two-phase designs.