The Flat-Bottom Strategy for Improved Accuracy in Protein Sidechain Placements

Abstract

We present a new strategy for protein sidechain placement that uses flat bottom potentials for rotamer scoring. The extent of the flat bottom depends on the coarseness of the rotamer library and is optimized for libraries ranging from diversities of 0.2 Å to 5.0 Å. The parameters reported here were optimized for forcefields using Lennard-Jones 12-6 van der Waals potential with DREIDING parameters but are expected to be similar for AMBER, CHARMM, and other forcefields. This Side-Chain Rotamer Excitation Analysis Method is implemented in the SCREAM software package (available in supplementary material). Similar scoring function strategies should be useful for ligand docking, virtual ligand screening, and protein folding applications.

1. Introduction

In developing general predictive approaches for structures of membrane proteins^1–3 (Membstruk), we found that current available sidechain placement methods, e.g. SCWRL, did not provide sufficiently accurate results to determine the helix-helix relative orientations within the membrane. Consequently, we developed the SCREAM approach reported here, which we have found to lead to dramatically improved protein structures. In this paper, we validate SCREAM against standard libraries of crystal structures. In a subsequent paper, we will report the accuracy of SCREAM in predicting stable membrane structures (where unfortunately there are very few accurate x-ray structures).

Sidechain placement methods play a major role in recent applications in the field of computational molecular biology; from protein design^4–6, flexible ligand docking⁷, loop-building⁸, to prediction of protein structures⁹. Much attention has been paid to this important problem, which is difficult because it is in a category of problems known as NP-hard¹⁰, for which no efficient algorithm is known to exist. Since the groundbreaking work by Ponder and Richards¹¹, many approaches have been developed, including mean-field approximation^12,13, Monte Carlo algorithms^14,15, and Dead-End Elimination (DEE)^16–19. In practice, however, studies have also concluded that the combinatorial issue may not be as severe as originally thought^20,21. Compared to the placement methods and rotamer libraries, scoring functions have not been studied as extensively^22–24. The focus of this paper is on the scoring function.

The scoring function is based on the all-atom forcefield DREIDING²⁵ which includes an explicit hydrogen bond term. The use of a rotamer library is widely used in sidechain prediction methods, and many authors have introduced quality rotamer libraries^21,26,27 since the Ponder library. To account for the discreteness of rotamer libraries, several approaches have been introduced, such as reducing van der Waals radii^28,29, capping of repulsion energy³⁰, rotamer minimization^14,31 and the use of subrotamer ensembles for each dominant rotamer³². We introduce a flat-bottom region for the van der Waals (VDW) 12-6 potential and the DREIDING hydrogen bond term (12-10 with a cosine angle term). The width of the flat-bottom depends on the specific atom of each sidechain, as well as the coarseness of the underlying rotamer library used.

We show in this study that accuracy can be improved substantially by introducing the flat-bottom potential, and in a systematic way. In addition to showing that placement accuracy is dependent upon the number of rotamers used in a library, we find that it is possible for suitably chosen energy functions to compensate the use of coarser rotamer libraries. We demonstrate a high overall accuracy in sidechain placement, and make comparison to the popular sidechain placement program SCWRL³³.

2. Materials and Methods

2.1 Preparation of Rotamer Libraries

Rotamer libraries of various diversities are derived from the complete coordinate rotamer library of Xiang²¹. We added hydrogens to the rotamers, and considered both δ and ε versions in the case for histidines. CHARMM charges are used throughout³⁴. Since the Xiang library was based on crystal structure data, we minimized each of the conformations so that the internal energies will be consistent with subsequent energy evaluations of the proteins. To do this we placed each sidechain on a template backbone (Ala-X-Ala in the extended conformation) and did 10 steps conjugate gradient minimization using the DREIDING forcefield.

We generated rotamer libraries of varying coarseness by a clustering procedure, using the heavy atom RMSD between minimized rotamers as the metric. Starting with the closest rotamers, we eliminated those within the specific threshold RMSD value choosing always the rotamer with the lowest minimized DREIDING energy. This threshold RMSD value is defined as the diversity of the resulting library. To ensure that rotamers can make proper hydrogen bonds, each sidechain conformation for serine, threonine, and tyrosine was repeated with each possible polar hydrogen position. Thus, for serine and threonine, the three sp³ position hydrogens were added to the hydroxyl oxygen, while for tyrosine, we add the out-of-place OH bonds 90 degrees from the phenyl ring in addition to two sp² positions in the plane. The final number of rotamers for libraries of different diversities is shown in Table 1.1.

Table 1.

[Table 1.1]
Diversity	Starting	0.2Ǻ	0.6Ǻ	1.0Ǻ	1.4Ǻ	1.8Ǻ	2.2Ǻ	3.0Ǻ	5.0Ǻ	All- Torsion
Rotamer Count	35828	14755	3195	1014	378	214	136	84	44	382

Table 1.1 δ and σ values for each atom on the Arginine side-chain, listed in order of distance away from the main chain. Nη1 and Nη2 are equivalent atoms; the average value is used in actual calculations. These numbers were obtained from the rotamer library of diversity 1.0Ǻ.
Dist. Deviation (Ǻ)	Mean (δ)	Corrected Error (σ)
Cβ	0.090	0.059
Cγ	0.245	0.153
Cδ	0.439	0.275
Nε	0.502	0.315
Cζ	0.588	0.369
Nη1, Nη2	0.858, 0.839	0.538, 0.526

Table 1.2. δ and σ values for each atom on the Lysine side-chain, listed in order of distance away from the main chain. These numbers were obtained from the rotamer library of diversity 1.0Ǻ.
Dist. Deviation (Ǻ)	Mean (δ)	Corrected Error (σ)
Cβ	0.089	0.056
Cγ	0.259	0.162
Cδ	0.406	0.254
Cε	0.596	0.373
Nζ	0.803	0.503

In addition, we constructed the “All-Torsion” rotamer library in which one rotamer for each major torsional angle (120 degrees for sp³ anchor atoms, 180 degrees for sp² anchor atoms) was included. The angles were obtained from the backbone independent rotamer library from Dunbrack³⁵ and built using the some procedure as described above.

All our rotamer libraries are backbone independent.

2.2 Preparation of Structures for Validation of SCREAM

We considered three sets of protein for validating and training SCREAM.

• Xiang: Xiang²¹ considered 33 proteins for testing their method for developing libraries of side chain conformations : 1aac, 1aho, 1b9o, 1c5e, 1c9o, 1cbn, 1cc7, 1cex, 1cku, 1ctj, 1cz9, 1czp, 1d4t, 1eca, 1igd, 1ixh, 1mfm, 1plc, 1qj4, 1ql0, 1qlw, 1qnj, 1qq4, 1qtn, 1qtw, 1qu9, 1rcf, 1vfy, 2pth, 3lzt, 5p21, 5pti and 7rsa. We have tested SCREAM for exactly these cases.

• Liang: Liang^22,36 considered 15 proteins for testing their method for scoring functions for choosing side chain conformations. Of these, the 10 were not in the Xiang set are denoted as the Liang set: 1bpi, 1isu, 1ptx, 1xnb, 256b, 2erl, 2hbg, 2ihl, 5rxn and 9rnt. The proteins that overlap with the Xiang set are not included.

• Other: In addition we included 10 proteins with resolution not worse than 1.8 Å from the SCWRL dataset: 1a8d, 1bfd, 1bgf, 1c3d, 1ctf, 1ctj, 1moq, 1rzl, 1svy and 1yge. Here we ignored structures with ligands or missing residues or which had a sequence identity of more than 50% with the Xiang or Liang sets. As will be described in later sections, this set is used only for deriving the σ-values and sidechain placement parameters.

For each of these 53 proteins, the raw atom coordinates were downloaded from the PDB database. Hydrogens were added using WHATIF³⁷ and ligands were typed using PRODRUG³⁸. Manual typing of ligands were carried out in cases where they cannot be typed by PRODRUG (~10 cases). Waters, solvents, and metals were kept when present.

These structures were then minimized (100 conjugate gradient steps) using the DREIDING forcefield. In all cases, the minimized structures differed by less than 0.3Ǻ total RMSD compared to the original crystal structures. All metals, prolines, cysteines in disulfide bonds and sidechains in coordination with metals were kept fixed throughout sidechain placement calculations.

2.3 Surface Area Calculations

Which residues were considered as buried or exposed was determined from the Solvent Accessible Surface Area (SASA), using a probe of radius 1.4 Å. The reference for fully exposed surface area for each sidechain type is a fully extended tri-peptide in the form of Ala-X-Ala. A sidechain with >20% SASA compared with the reference SASA was considered exposed. This percentage is smaller than the typical 50% level in the literature—around 25% for the Xiang set and 39% for the Liang set because we include solvent molecules as part of the structure.

2.4 Positioning of Sidechains

Placement of the rotamers on the backbone is decided by the coordinates of the C, C_α, N backbone atoms plus the C_β atom. To specify the position of the C_β atom we use the coordinates with respect to C, C_α, N based on the statistics gathered from the HBPLUS protein set (see above). This involves three parameters:

1. The angle of the Cα-C_β bond from the bisector of the C-Cα-N angle: 1.81 (from the HBPLUS protein set)

2. The angle of the Cα-C_β bond with the C-C_α-N plane: 51.1 (from the HBPLUS protein set); and

3. The Cα-C_β bond length: 1.55 Å (average value from the Other protein set).

Thus the C_β atom will generally have a different position from the crystal C_β position. As in common practice in the literature, we did not include this C_β deviation in the RMSD calculations.

2.5 Combinatorial Placement Algorithm

The SCREAM combinatorial placement algorithm consists of three stages: self energy calculation for rotamers, clash elimination, and further optimization of sidechains.

2.5.1 Stage 1: Rotamer Self Energy Calculation

The all atom forcefield DREIDING²⁵ was used to calculate the interactions between atoms, with a modification to be described in the scoring function section. The internal energy contributions E_internal (bond, angle and torsion terms and non-bonds that involve only the sidechain atoms) were pre-calculated and stored in the rotamer library. For each residue to be replaced, the interaction energy (E_sc-fixed) was calculated for each rotamer interacting with just the protein backbone and fixed residues (all fixed atoms). The sum of these two terms is the empty lattice energy (E_EL) of a rotamer in the absence of all other sidechains to be replaced

$$E_{EL}=E_{\mathit{\text{internal}}}+E_{sc-\mathit{\text{fixed}}}$$

We use the term ground state to refer to the rotamer with the lowest E_EL energy. All other rotamer states are termed excited states. Excited states with an energy 50 kcal/mol above the ground state were discarded from the rotamer list for the remaining calculations.

2.5.2 Stage 2: Clash Elimination

Eisenmenger et al.²⁰ showed that the sidechain-backbone interaction accounts for the geometries of 74% of all core sidechains and 53% of all sidechains. Thus, the ground state of each sidechain was taken as the starting structure. Of course, this structure might have severe VDW clashes between sidechains since no interaction between sidechains has been included. Elimination of these clashes was done as follows. A list of clashes of all ground state pairs, above a default threshold of 25kcal/mol was sorted by their clashing energies. The pair (A, B) with the worst clash was then subjected to rotamer optimization by considering all pairs of rotamers, and selecting the lowest energy to form a super-rotamer with a new energy:

$$E_{\mathit{\text{tot}}}(A,B)=E_{\mathit{\text{self}}}(A)+E_{\mathit{\text{self}}}(B)+E_{\mathit{\text{Int}}․}(A,B)\equiv E_{\mathit{\text{self}}}(AB)$$

where E_Int indicates the interaction energy between rotamer A and rotamer B, which was the only energy calculation done at this step since the E_EL terms were calculated in Stage 1. The ground state for this super rotamer now replaced the rotamer pair in the original structure. Since large sidechains such as ARG and LYS may have as many as Y rotamers for the 1.0A library, we limited the number of pairs to be calculated explicitly to 1,000, which we selected based upon the sum of the empty lattice energies. Of these interaction pairs we kept the ones with interaction energies below Z.

After resolving a clash, we considered the lowest X rotamer pairs from the above calculation as a super residue. Thus, subsequent clash resolution, say between residue C and residue A, will consider interactions of all sidechains of C with the X (A,B) rotamer pairs. Now the spectrum of interaction energies treats (A,B) as a super rotamer so that the (C, (A,B)) energy spectrum is treated the same as for a simple rotamer pair with the spectrum:

$$E_{\mathit{\text{tot}}}(A,B,C)=E_{\mathit{\text{self}}}(A)+E_{\mathit{\text{self}}}(B)+E_{\mathit{\text{self}}}(C)+E_{\mathit{\text{Int}}}(A,B)+E_{\mathit{\text{Int}}}(A,C)+E_{\mathit{\text{Int}}}(B,C)=E_{\mathit{\text{self}}}(AB)+E_{\mathit{\text{self}}}(C)+E_{\mathit{\text{Int}}}(A,C)+E_{\mathit{\text{Int}}}(B,C)\equiv E_{\mathit{\text{self}}}(AB)+E_{\mathit{\text{self}}}(C)+E_{\mathit{\text{Int}}}(AB,C)$$

This process continued by generating a new list of clashing residue pairs including the new (A,B,C), resolving the next worst clash as above. The procedure was repeated until no further clashes were identified between two rotamers or super-rotamers.

2.5.3 Stage 3: Final Doublet Optimization

It is possible for some clashes to remain after Stage 2, since the number of rotamers pair evaluations is capped (at 1,000) and also the numbers of rotamers in a super-rotamer (20). To solve this problem, the structure from end of stage 2 was further optimized. Sidechain pairs (termed doublets) were now ordered in decreasing energies in the presence of all other sidechains, and one iteration round of local optimization on those residue pairs was performed in that order. Any residue that had already been examined in this stage as part of a doublet was eliminated from further doublet examination. Always, the doublet with the lowest overall energy was kept.

2.5.4 Stage 4: Final Singlet Optimizations

The structure would undergo one final round of optimization, where all residues were examined one at a time, again in order of decreasing energies for the rotamer currently placed in the structure. Again, the rotamer with the best overall energy was retained for the final structure. More iterations rounds on the final result improved the overall RMSD (unpublished results), but we did not pursue this path³⁹ for the purposes of this paper.

We illustrate the effects of the doublet and singlet optimization stages by giving a specific example—1aac, using the 1.0Ǻ rotamer library and optimal parameters (to be described in a later section). After the clash elimination stage, the RMSD between the predicted structure and the crystal structure was 0.733Ǻ. The pair clashes remaining in this case included the pairs F57 and L67, V37 and F82, and V43 and W45. Doublets optimization brought the RMSD down to 0.703Ǻ. The final singlet optimization stage brought the RMSD value further down to 0.622Ǻ.

For this case, doublet optimization took 3 seconds, while singlet optimization took 13 seconds. For comparison, clash elimination took 30 seconds to complete, while the rotamer self energy calculation took 8 seconds.

2.6 The Flat-Bottom Scoring Function

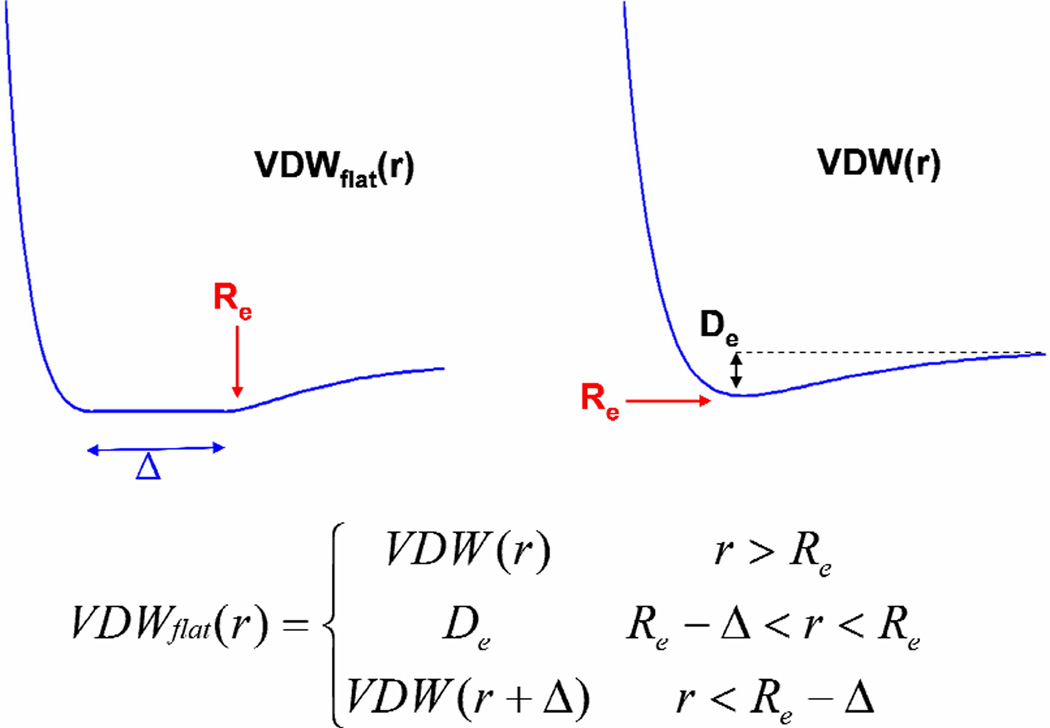
Since our library is discrete, the best position for a sidechain may lead to some contacts slightly too short. Since the VDW interactions becomes very repulsive very quickly for distances shorter than R_e, a distance too short by even 0.1A may cause a very repulsive VDW energy. This might lead to selecting an incorrect rotamer. In order to avoid this problem, we use a flat-bottom potential in which the attractive region is exactly the same down to R_e but the repulsive region is displaced by some amount Δ so that contacts that are slightly too short by Δ will not cause a false repulsive energy. The form of this potential is shown in Figure 1.

Figure 1.

The flat-bottom potential. The inner wall is shifted by an amount Δ.

We allow a different Δ for each atom of each residue of each diversity. The way this is done is by writing Δ as:

$$\mathrm{\Delta }=\mathrm{s}·\mathrm{\sigma }$$

Where s is a scaling factor and the σ values are compiled as follows.

2.6.1 Compilation of σ values

For each rotamer library we considered the 10 query protein structures in the HBPLUS set (see Materials and Methods). For each sidechain in each query structure, we picked the closest matching rotamer (in RMSD) from the library and record the distance deviation for each atom of the sidechain of that residue. Thus, the atoms at the tip of the longer sidechains such as arginine and lysine would have greater distance deviations than C_β atoms. The mean distance deviation (δ) for every atom of each amino-acid type over all 10 query proteins is then calculated. As an example, the δ values for arginine and lysine rotamers in the rotamer library of 1.0A diversity (rotamer libraries were described in Section 2.1) are listed in Table 1.1 and Table 1.2.

We assume that the error in positioning of any one atom of the sidechain will have a Gaussian distribution of the form:

$$f(r)\propto e^{-\frac{r^2}{2·{\sigma }^2}}$$

Where r is radial distance and σ represents the standard deviation. Thus,

$$\rho (r)\propto 4\pi r^{2}f(r)$$

is the probability of finding an atom at position r from the crystal position (which is weighted by a factor of 4πr² from the x, y and z distributions). The uncertainty δ in the Cartesian distance along the line between two atoms is related to σ by the form:

$$\delta =2·\sqrt{\frac{2·{\sigma }^2}{\pi }}$$

where δ is the value described above. This σ is listed for arginine and lysine in Table 1.1 and Table 1.2.

2.6.2 Scaling factor s

The Δ values for each sidechain atom type will depend on their σ values:

$$\mathrm{\Delta }=\mathrm{s}·\mathrm{\sigma }$$

The deviations for σ above provide a measure of relative uncertainties in the ability of a library to describe the correct position of the sidechain atoms. However, to obtain the absolute value of the flat-bottomness we allow an overall scaling factor for the flat-bottom portion of the potential for all atoms.

The value of s was optimized for the Xiang set of 33 proteins for libraries of diversities ranging from 0.2A to 5.0A as discussed in section 3.

2.6.3 Flat-bottom potential on Hydrogen bond terms

We use a flat-bottom for the VDW interactions and not for the Coulomb interactions because the VDW inner wall potential becomes repulsive very quickly with distance (e.g. 1/r¹²). Such scaling is not important for Coulomb since it scales as 1/r. Most forcefields use a modified VDW interaction between hydrogen bonded atoms. Current version of AMBER and CHARMM do this between donor hydrogen and the acceptor heavy atom, treating the interaction as a standard 12-6 Lennard-Jones with modified parameters. The flat-bottom for the other van der Waal interactions should apply equally well for these hydrogen bond terms. However, DREIDING uses an explicit 12-10 hydrogen bond term between the heavy atoms combined with a factor depending upon the linearity of the donor-hydrogen-acceptor triad:

$$E_{hb}=D_{hb}[5{(R_{hb}/R_{DA})}^{12}-6{(R_{hb}/R_{DA})}^{10}]{\text{cos}}^4({\theta }_{DHA})$$

where D_hb stands for the well-depth of the hydrogen bond potential, R_hb the equilibrium distance and θ_DHA is the angle between the hydrogen bond donor atom, hydrogen and the acceptor atom. We use a flat bottom potential for this DREIDING hydrogen bond term. However, we now allow both the inner and outer walls to shift by an amount Δ from the equilibrium point. The objective here is to also let the potential to capture the polar contacts that would otherwise be missed, both when a donor-acceptor pair is too close or too far away from each other.

2.6.4 Charges

We use the CHARMM³⁴ charges for the protein and water, since these are standard and well-tested values. For ligands and other solvents, we use QEq⁴⁰ charges, which provide values similar to those from quantum mechanics.

The Coulomb interaction between atoms 1 and 2 is written as:

$$E_{\mathit{\text{Coulomb}}}=\frac{c_0}{\epsilon }\frac{q_1{q}_2}{r_{12}}$$

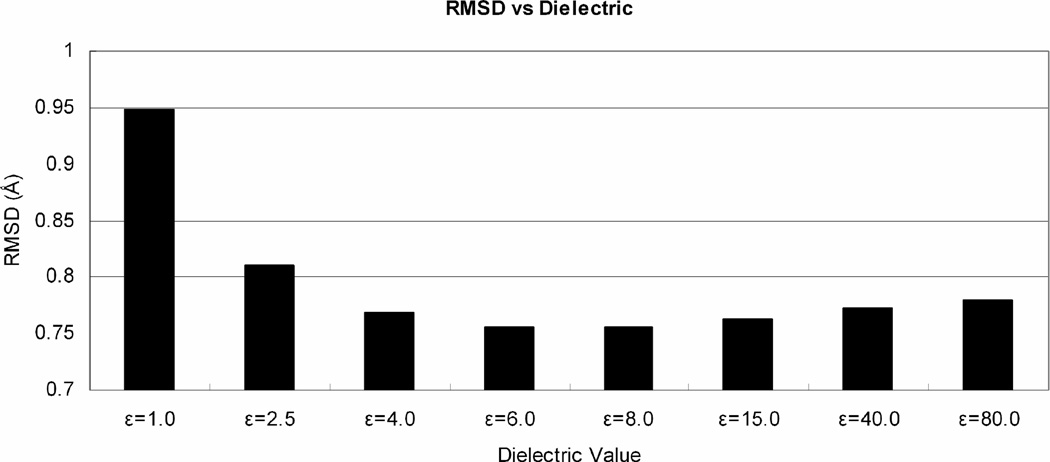
where q₁ and q₂ are charges in electron units, r₁₂ in Ǻ, ε the dielectric constant and c₀=332.0637 converts to energies in kcal/mol. After optimization on a Xiang set of proteins using the 1.0Ǻ diversity rotamer library and a scaling factor s=1.0, we chose the dielectric ε=6.0 (see Figure 2). Our calculation of electrostatics used a cubic spline cutoff beginning at 8 Å and ending at 10 Å.

Figure 2.

Effects on dielectric value on RMSD. The optimum value for the constant dielectric, ε=6.0 shown here, was obtained by fitting results for the Xiang set with a diversity of 1.0 Å and a scaling factor s of 1.0.

2.6.5 Total rotamer energies

The valence energies (bonds, angles, torsions and inversion) plus the internal HB, Coulomb and VDW energies of the rotamers were calculated beforehand and stored in the rotamer library. The final form of the scoring function is thus:

$$E_{\mathit{\text{Total}}}=\sum _i{E}_{EL}+\sum _{i<j}{E}_{\mathit{\text{Pair}}}$$

where E_EL is the sum over internal energies and the backbone interaction energies as described in Section 2.1 and

$$E_{\mathit{\text{pair}}}=E_{VDW}+E_{HB}+E_{\mathit{\text{Coulomb}}}$$

is the total non-bond energy between all pairs of atoms between a pair of residues.

For any particular atoms i and j, the total flat-bottom correction Δ_i,j for the VDW and HB terms is obtained from the individual Δ values of Δ_i and Δ_j using the relation:

$${\mathrm{\Delta }}_{i,j}=\sqrt{{\mathrm{\Delta }}_i^2+{\mathrm{\Delta }}_j^2}$$

This value corresponds to the standard deviation from the convolution of two normal distributions with standard deviations Δ_i and Δ_j.

3. Results and Discussion

3.1 Single Placement of Side-chains

To explore the effect on placement accuracy of using flat-bottom potentials, we increased the scaling factor s from 0.0 (no scaling) to 2.0 in 0.1 increments. To isolate the effects of the scaling, we placed sidechains one at a time onto the protein, in the presence of all other sidechains in their crystal positions. The values here represent the best possible results given an scoring function and a rotamer library²⁴. The Xiang set of proteins described in Materials and Methods are used here.

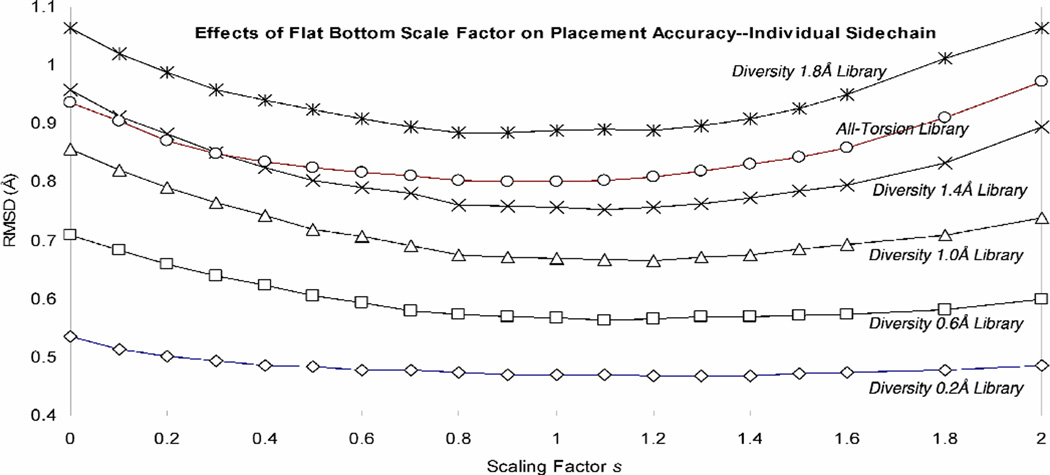
Figure 3 shows that the best scaling factor is s ~ 1 for all rotamer libraries. Note that s=1 for the 1.0A library leads to an accuracy of 0.665A which is much better than the accuracy of 0.71 Å obtained using s=0 (no scaling) for the much bigger 0.6A library.

Figure 3.

Single sidechain placement accuracy for various rotamer libraries at different s values. Shown are the libraries of 0.2 Å diversity (14755 rotamers), 0.6 Å diversity (3195 rotamers), 1.0 Å diversity (1014 rotamers), 1.4 Å diversity (378 rotamers), 1.8 Å diversity (218) and all-torsion (382 rotamers). The coarser the rotamer library is, the more pronounced the effect of s becomes.

Taking the all-torsion rotamer library as an example, the RMSD improves from 0.94 Å for s = 0 (no flat bottom) to 0.80 Å for s = 0.9. This library with 378 rotamers leads to an accuracy of 0.80 Å, which compares with the accuracy of 0.75 Å obtained using the 1.4 Å library, which has 382 rotamers.

We optimized the scaling factors for rotamer libraries of diversities ranging from just 5.0 Å (44 rotamers) to 0.2 Å (13,000 rotamers). Table 2.1 and Table 2.2 lists the optimum scaling factors and accuracies of these rotamer libraries, which lead to accuracies ranging from 0.47 Å (0.2 Å diversity) to 1.86 Å (5.0 Å diversity). We consider that the 1.0 Å library with an accuracy of 0.665 Å using 1014 total rotamers as a good compromise of efficiency and accuracy. These tables also list the results for the unscaled potential.

Table 2.

Table 2.1. Optimized s value for rotamer libraries of size ranging from 0.2Å to 5.0Å, plus the all torsion rotamer library. The s values for that gives the best RMSD value is listed.
Library	Number of Rotamers	Unmodified Potential (RMSD,Å)	Best s value	Best RMSD (Å)
0.2Å	14755	0.536	1.3	0.468
0.6Å	3195	0.710	1.1	0.564
1.0Å	1014	0.857	1.2	0.665
1.4Å	378	0.958	1.1	0.753
1.8Å	214	1.064	0.9	0.885
2.2Å	136	1.343	0.8	1.175
3.0Å	84	1.624	0.7	1.487
5.0Å	44	1.890	0.7	1.860
All Torsion	382	0.937	0.9	0.800

Table 2.2. Effect of s values on χ1/χ1+2 accuracy. Rotamer libraries of diversity ranging from 0.2Å to 5.0Å, plus the all torsion rotamer library are used. The best χ1+2 accuracy is used to determine the most effective scaling factor c. A χ angle is considered correct if within 40° of the corresponding χ angle in the crystal sidechain conformation.
Library	Number of Rotamers	χ1/χ1+2 accuracy from unmodified scoring function	Best scaling factor s	χ1/χ1+2 accuracy using best s value
0.2Å	14755	95.0% / 91.8%	1.3	96.3% / 93.4%
0.6Å	3195	92.6% / 87.7%	1.1	95.6% / 92.1%
1.0Å	1014	90.0% / 83.4%	1.2	95.3% / 90.4%
1.4Å	378	87.8% / 80.0%	1.2	94.7% / 88.9%
1.8Å	214	84.3% / 75.6%	1.2	91.5% / 83.8%
2.2Å	136	71.9% / 61.0%	0.8	79.1% / 68.0%
3.0Å	84	63.4% / 54.1%	0.7	68.4% / 58.9%
5.0Å	44	53.2% / 44.9%	0.7	54.9% / 45.8%
All Torsion	382	89.6% / 81.3%	1.1	93.3% / 86.8%

3.2 Effects of Buried vs. Exposed Residues

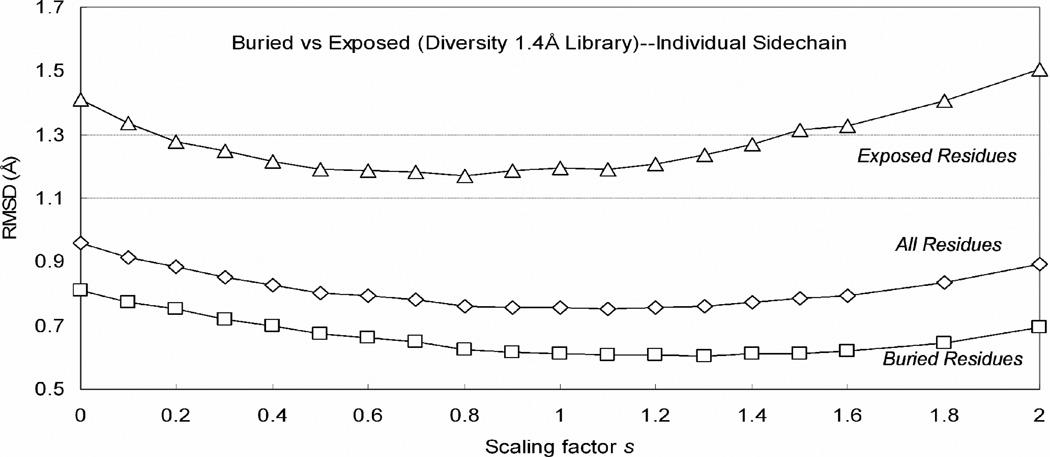
The percentage of exposed residues considered in section 3.1 is only 25% because crystallographic waters and solvents were included in the calculation. We consider this as the best test of the scoring function. However, in practical applications, such water and solvent molecules will not be present. This creates additional uncertainties for the surface residues whose positions should be affected by the solvent and water. Without such solvent molecules, the energy functions will tend to distort the sidechains to interact with other residues of the protein. Surface residues have more flexibility and it would be better to have smaller scaling factors for these sidechains. Thus, we optimized separate scaling factors for surface residues versus bulk. To do this, we calculated the SASA for the Xiang set and assigned all residues > 20% exposed as surface. The resulting optimized scaling factors are in Table 3.1. In Figure 4, we see that the accuracy for the 1.4 Å library increases from 0.809 (bulk) and 1.409 (surface) to 0.515 Å (bulk) and 1.107 Å (surface).

Table 3.1.

Accuracy comparison in single sidechain placements for buried and exposed residues for the Xiang test set.

Rotamer Library	Optimal Scaling Factor s for core residues	Optimal Scaling Factor s for surface residues	Core residue RMSD (Å) for optimal s	Surface residue RMSD (Å) for optimal s
0.2Å	1.4	0.6	0.309	0.939
0.6Å	1.2	0.8	0.414	1.010
1.0Å	1.2	0.9	0.515	1.107
1.4Å	1.3	0.8	0.605	1.171
1.8Å	1.2	0.7	0.742	1.227
2.2Å	0.8	0.6	1.105	1.371
3.0Å	0.7	0.6	1.439	1.625
5.0Å	0.7	0.7	1.835	1.935
All-Torsion	0.9	0.8	0.656	1.224

Figure 4.

The effects of varying the scaling factor s on placement accuracies for the exposed and core residues. Shown are results from the 1.4 Å diversity rotamer library results. Exposed residues account for approximately 25% of all residues.

The current SCREAM software does not distinguish between surface and bulk residues. In order to predict the surface residues prior to assigning the sidechains, we recommend using the alanized protein and rolling a ball of 2.9 Å instead of the standard 1.4 Å (supplementary material).

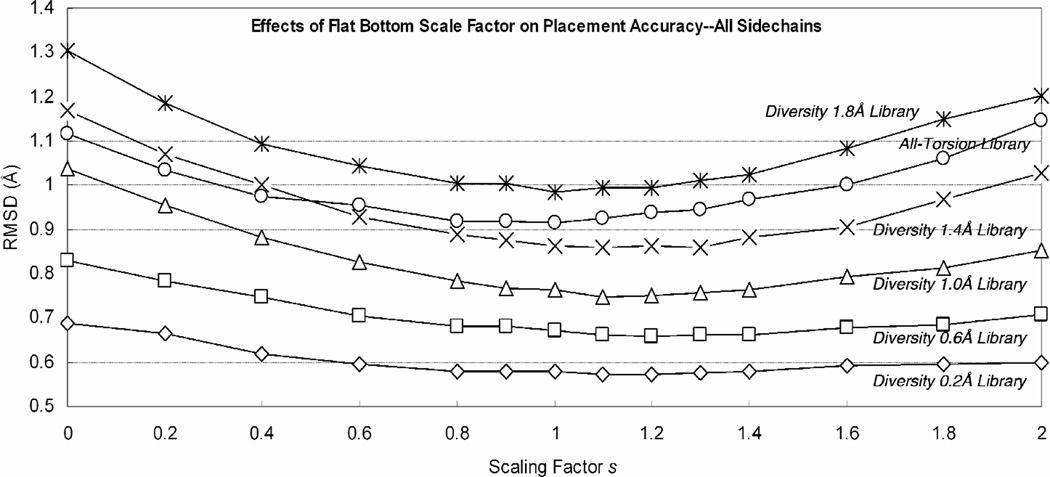
3.3 Placement of All Sidechains on Proteins, Comparison with SCWRL

The effectiveness of the flat-bottom potential in the single-placement setting extends to multiple sidechain placements. Based on the same Xiang test set of 33 proteins, we report the placement accuracy shown in Figure 5. The optimal s values were similar to the values from single placement tests. For example, the 1.0 Å library had an optimum scaling factor s=1.0 leading to an accuracy of 0.747Ǻ (compared to 0.665 Å for single placement). Overall, the accuracy discrepancy in multiple placement and single placement setting comes to a 0.09 Å RMSD. Using the χ1/χ2 criterion leads to similar conclusions, as seen in Table 4.2.

Figure 5.

Accuracy for simultaneously replacing all sidechains for various rotamer libraries at different s values. Shown are the libraries of 0.6 Å diversity (3195 rotamers), 1.0 Å diversity (1014 rotamers), 1.4 Å diversity (378 rotamers), 1.8 Å diversity (218) and all-torsion (382 rotamers).

Table 4.

Table 4.1. Optimized s value for rotamer libraries of size ranging from 0.2Å to 5.0Å, plus the all torsion rotamer library. The scaling factor s that gives the best RMSD value is included. For comparison, SCWRL gives a RMSD of 0.95Å for the same residues and proteins tested in this set.
Library	Number of Rotamers	Unmodified Potential (RMSD,Å)	Best Scale Factor s value	Best RMSD (Å)
0.2Å	14755	0.689	1.2	0.571
0.6Å	3195	0.830	1.2	0.657
1.0Å	1014	1.036	1.1	0.747
1.4Å	378	1.171	1.1	0.860
1.8Å	214	1.303	1.0	0.985
2.2Å	136	1.545	0.9	1.278
3.0Å	84	1.756	0.8	1.565
5.0Å	44	1.987	0.6	1.909
All Torsion	382	1.118	1.0	0.916
SCWRL	0.951Å

Table 4.2. Effect of s values on χ1/χ1+2 accuracy. Rotamer libraries of diversity ranging from 0.2Å to 5.0Å, plus the all torsion rotamer library are used. The best value for χ1+2 correctness is used to determine the most effective s value. A χ angle is considered correct if within 40° of the corresponding χ angle in the crystal sidechain conformation. The χ1/χ1+2 correctness for SCWRL is 86.4% / 79.7%.
Library	Number of Rotamers	χ1/χ1+2 accuracy from unmodified scoring function	Optimal s value	χ1/χ1+2 accuracy using optimal s
0.2Å	14755	91.4% / 86.6%	1.3	94.1% / 89.9%
0.6Å	3195	89.7% / 83.0%	1.1	93.8% / 88.5%
1.0Å	1014	84.5% / 75.6%	1.1	92.9% / 86.7%
1.4Å	378	81.7% / 71.4%	1.3	92.1% / 84.3%
1.8Å	214	77.4% / 67.3%	1.2	88.6% / 80.0%
2.2Å	136	66.8% / 55.0%	1.1	75.7% / 64.6%
3.0Å	84	60.6% / 50.5%	0.8	66.2% / 56.7%
5.0Å	44	52.1% / 43.9%	0.6	54.3% / 45.7%
All Torsion	382	85.0% / 73.4%	1.0	89.7% / 81.5%
SCWRL	86.4% / 79.7%

The overall improvement in RMSD of the optimal s values over the exact Lennard-Jones potential, however, is more dramatic than in the single placement tests. For instance, by introducing the optimal s value for the float-bottom potential, in the single sidechain placement case, the accuracy improved from 0.834 Å to 0.663 Å, an improvement of 0.17 Å; in the all-sidechain placement case, the improvements went from 1.024 Å to 0.755 Å, an improvement of 0.27 Å.

To compare our results with SCWRL, we applied SCWRL3.0 on the Xiang set of proteins. We found an accuracy of 0.85 Å for SCWRL. A direct comparison between SCREAM and SCWRL is difficult since SCWRL uses a backbone dependent rotamer library and a more sophisticated multiple sidechain placement algorithm. However, we note that the 1.8 Å SCREAM library, with just 214 rotamers, achieved an accuracy of 0.86 Å RMSD which is comparable to the 0.85 Å for SCWRL, which has a rotamer for each major torsion angle, coming to ~370 rotamers. Of course, SCWRL uses a backbone dependent rotamer library, so the specific torsion angles of those rotamers depend on the backbone φ-ψ angles.

3.4 Effects of Minimization on Structures from Different Scaling Factors

For efficiency in predicting the optimum combination of sidechain conformations, we use the discrete rotamers from the library with no minimization. Because of this, the closest rotamer in the library to the correct conformation may have short contacts. That is why we use the flat-bottom potential. Of course, after assigning the sidechains we need to optimize the structures in preparation for docking and other applications. To assess how well this optimization improves the accuracy we have minimized the sidechains for each structure for 100 steps (using DREIDING in vacuum) with the results in Table 5.1.

Table 5.1. Average energy values for the 33 proteins over varying s values. All energy values include valence and non-valence terms, and the units are presented in kcal/mol. The energies do not include interaction terms between atoms that are not involved in the sidechain placement calculations. Numbers in bold are the minimum values for each category.
s value	0.6Å Library		1.0Å Library		1.4Å Library		All-Torsion Library
	Starting Energy	Minimized Energy	Starting Energy	Minimized Energy	Starting Energy	Minimized Energy	Starting Energy	Minimized Energy
0	−1234.3	−3163.1	546.8	−2839.2	6957.0	−2544.8	1558154.0	−2317.1
0.2	−2237.0	−3225.5	530.7	−2969.3	2804.0	−2675.2	1260675.0	−2515.2
0.4	−2195.1	−3271.3	417.6	−3053.8	2610.3	−2790.4	34774.5	−2767.6
0.6	−2364.8	−3312.2	−624.4	−3102.8	3454.9	−2871.2	34628.7	−2826.2
0.8	−2227.6	−3328.1	−419.9	−3168.6	4970.1	−2929.7	41225.3	−2849.5
0.9	−2130.1	−3325.0	−166.4	−3165.1	10013.7	−2941.8	166369.5	−2836.7
1.0	−2041.5	−3331.6	143.2	−3166.3	132017.6	−2952.7	173157.0	−2854.6
1.1	−1952.9	−3341.3	1431.4	−3177.5	136424.5	−2945.5	53846.7	−2845.7
1.2	−1764.6	−3338.9	1885.2	−3171.0	146372.5	−2938.1	62057.7	−2794.9
1.3	−545.0	−3327.5	3278.3	−3161.9	161903.0	−2919.4	101904.8	−2783.0

Table 5.2. Average RMSD values (inÅ) for the Xiang set of 33 proteins, before and after minimization. Entries in bold correspond to those with the lowest DREIDING energies before and after minimization, see Table 5.1 for details.
Scaling Factor	0.6Å Library		1.0Å Library		1.4Å Library		All-Torsion Library
	Starting RMSD	Minimized RMSD	Starting RMSD	Minimized RMSD	Starting RMSD	Minimized RMSD	Starting RMSD	Minimized RMSD
0	0.830	0.737	1.036	0.930	1.171	1.061	1.112	1.003
0.2	0.784	0.694	0.954	0.848	1.071	0.962	1.035	0.916
0.4	0.746	0.658	0.884	0.773	1.003	0.887	0.975	0.848
0.6	0.706	0.615	0.827	0.718	0.930	0.814	0.954	0.823
0.8	0.681	0.591	0.784	0.668	0.888	0.767	0.920	0.787
0.9	0.682	0.591	0.766	0.651	0.877	0.752	0.917	0.786
1.0	0.672	0.581	0.764	0.647	0.863	0.736	0.916	0.780
1.1	0.662	0.569	0.747	0.625	0.860	0.729	0.923	0.786
1.2	0.657	0.562	0.752	0.629	0.861	0.727	0.937	0.799
1.3	0.662	0.568	0.758	0.632	0.860	0.724	0.946	0.803

We see that the initial configurations often have very high energies but after minimization these energies become fairly similar for different scaling factors with the same diversity. As expected, the best energies (in bold face) generally come from a scaling factor of 1.0 or 1.1. We note also that as the diversity of the library decreased, the energy of the final optimized configurations also decreased, indicating increased accuracy.

As expected, the RMSD also decreases as we minimize the structures. These results are shown in Table 5.2. For example, for the 1.0A library, accuracy improved from 0.747A to 0.625A.

3.5 Program Execution Performance

All tests have been run on Intel Xeon 2.33 GHz CPU single processors. The tradeoff in time vs. rotamer library size is detailed in Table 6. Obviously, the size of rotamer libraries affects the time spent on sidechain placement. Compared to SCWRL, the time required by SCREAM is relatively slow. However, SCWRL does not explicitly include hydrogen atoms, and use of united atom should reduce the computational time by SCREAM by a factor of about three³⁶.

Table 6.

Performance measure of SCREAM, with rotamer libraries of various diversities. The timing statistics were taken from the runs that gave the best energy values.

Library Diversity	Number of Rotamers	Time per protein	Χ1 (%)		χ1+2 (%)		RMSD (Å)
			Buried	All	Buried	All	Buried	All
0.2Å	14755	554 s	96.7	93.8	93.7	89.7	0.43	0.58
0.6Å	3195	291 s	96.1	93.5	91.6	88.0	0.53	0.67
1.0Å	1014	146 s	95.5	92.4	89.8	85.9	0.62	0.76
1.4Å	378	110 s	94.4	91.6	87.0	83.8	0.73	0.86
1.8Å	214	91 s	90.9	87.8	83.4	80.0	0.85	0.99
All-Torsion	382	147 s	92.4	89.7	85.2	81.5	0.78	0.92
SCWRL	n/a	3 s	90.3	86.4	84.4	79.7	0.79	0.95

It might appear that the increased accuracy of using SCREAM compared to SCWRL might not justify the increased expense. However, these test cases are all system for which exact structures are available. We have found in applications involving predictions of new structures that the SCREAM procedure works better than SCWRL, in particular for predicting GPCRs, as will be presented elsewhere⁴¹.

3.6 Tests on the Liang Set Using The Optimized Scaling Factor

In the previous sections, we optimized the scaling factors for the Xiang set and discussed the accuracy for the Xiang set. As to better indicate how well SCREAM works for new systems we tested the predictions for the Liang set using the scaling factors optimized for the Xiang set.

Rotamer libraries of practical use, including those of diversities 0.6 Å, 1.0 Å, 1.4 Å, 1.8 Å and the all-torsion rotamer library were used for this test. Results are shown in Table 7. For example, using the 1.4A library, we found an accuracy of 0.96Ǻ for all residues and 0.74Ǻ for the buried residues, which compares to 0.86Ǻ for all residues and 0.73Ǻ for the buried residues for the Xiang set. The reason for the decreased accuracy is that 40% of sidechains in the Liang set are solvent exposed compared to 25% for the Xiang set. The prediction of core residues is approximately at the same level of accuracy as reported in previous sections.

Table 7.

SCREAM predictions on the Liang test set using optimized scaling factor for rotamer libraries of various diversities. The percentage of buried residues in this test set is about 40%, greater than the 25% figure from the previous test set. We include crystal structure solvents in the predictions, and the increase in exposed residues is due to the fewer resolved solvents in those structures.

Library Diversity	Number of Rotamers	Run time per protein	χ1 (%)		χ1+2 (%)		RMSD (Å)
			Buried	All	Buried	All	Buried	All
0.6Å / s = 1.2	3195	78.9 s	96.4	90.8	92.6	84.3	0.52	0.80
1.0Å / s = 1.1	1014	41.0 s	93.6	89.1	87.1	80.7	0.69	0.93
1.4Å / s = 1.1	378	29.9 s	94.5	89.4	86.2	79.9	0.74	0.96
1.8Å / s = 1.0	214	27.6 s	90.3	85.2	83.5	77.0	0.84	1.05
All-Torsion / s = 1.0	382	32.5 s	93.4	87.6	87.3	79.4	0.77	0.99
SCWRL	n/a	2 s	90.5	83.7	84.3	75.5	0.82	1.10

3.7 Parameters for Other Lennard Jones Potentials

While the Lennard-Jones 12-6 potential is the most commonly used, it has been demonstrated that softer potentials improve placement accuracy⁴². Thus, we tested out Lennard-Jones potentials of the 7-6, 8-6, 9-6, 10-6 and 11-6 types on the 1.0Ǻ rotamer library for the Xiang protein set. As expected, the softer potentials performed better, but the results can be improved further by including a flat-bottom region in the potential. Results are shown in Table 8. The optimal value of the scaling factor s decreases with softer Lennard-Jones potentials, which was expected and was consistent with the flat-bottom potential approach. It is interesting to note that the 11-6 potential with optimized scaling factor s achieved the best overall RMSD value for this test, though the differences across the different Lennard-Jones potentials were small.

Table 8.

Effect of different Lennard-Jones potentials and their optimal scaling factor s. Tests were done on the Xiang protein set using the 1.0Ǻ rotamer library.

LJ Type	Unmodified Potential (RMSD, Ǻ)	Best Scale Factor s value	Best Scale Factor RMSD (Å)
7-6	0.831	0.4	0.767
8-6	0.845	0.6	0.752
9-6	0.855	0.7	0.752
10-6	0.911	0.8	0.749
11-6	0.963	1.0	0.741
12-6	1.036	1.1	0.747

3.8 Comparison with VDW Radii Scaling

We also test out using reduced VDW radii values on the 1.0Ǻ rotamer library for the Xiang protein set. The results are shown in Table 9. The improvement from using reduced VDW radii is not as pronounced as the improvement from using softer Lennard-Jones potential forms, described in the previous section.

Table 9.

Effects of VDW scaling. Tests were done on the Xiang protein set using the 1.0Ǻ rotamer library.

VDW Radii Scaling	RMSD (Ǻ)
75%	0.959
80%	0.884
85%	0.866
90%	0.896
95%	0.956
100%	1.036

3.9 Extension beyond the Natural Amino Acids

The σ values were calculated for the natural amino acids. To extend the flat-bottom potential approach for ligands and non-natural amino acids, a value for Δ or σ needs to be determined. These values clearly depend on how conformations were generated, but we recommend a simple scheme such as using Δ=0.4Ǻ for all atoms.

Conclusion

We show that sidechain placement using a flat bottom potential leads to excellent sidechain placement results with a simple combinatorial sidechain placement algorithm. We present a straightforward method for deriving these parameters and applied this to rotamer libraries with a wide range of diversities (0.2Ǻ to 5.0Ǻ). The potential is a simple modification of a Lennard-Jones potential, making it easy to incorporable into existing software.

A particularly important application for sidechain placement is in protein folding applications where one wants to find rapidly the best sidechain positions for each backbone configuration. A first application of SCREAM for such problems is the recent development of the MembSCREAM methodology for predicting three-dimensional structures for G-Protein Coupled Receptors⁴¹.