CCLasso: correlation inference for compositional data through Lasso

Abstract

Motivation: Direct analysis of microbial communities in the environment and human body has become more convenient and reliable owing to the advancements of high-throughput sequencing techniques for 16S rRNA gene profiling. Inferring the correlation relationship among members of microbial communities is of fundamental importance for genomic survey study. Traditional Pearson correlation analysis treating the observed data as absolute abundances of the microbes may lead to spurious results because the data only represent relative abundances. Special care and appropriate methods are required prior to correlation analysis for these compositional data.

Results: In this article, we first discuss the correlation definition of latent variables for compositional data. We then propose a novel method called CCLasso based on least squares with ${\ell }_1$ penalty to infer the correlation network for latent variables of compositional data from metagenomic data. An effective alternating direction algorithm from augmented Lagrangian method is used to solve the optimization problem. The simulation results show that CCLasso outperforms existing methods, e.g. SparCC, in edge recovery for compositional data. It also compares well with SparCC in estimating correlation network of microbe species from the Human Microbiome Project.

Availability and implementation: CCLasso is open source and freely available from https://github.com/huayingfang/CCLasso under GNU LGPL v3.

Contact: dengmh@pku.edu.cn

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Microbes play an important role in the environment and human life. Bacteria and archaea have been found in extreme conditions such as deep sea vents with high temperatures and rocks of boreholes beneath the Earth’s surface (Pikuta et al., 2007). The microorganisms affect environments where they exist, and vice versa. It is estimated that there are about 10 times microbe cells inhabiting our human body than human cells (Savage, 1977). Microbes affect the human life on our food, health and medicine (Gill et al., 2006). The way in which microbes affect the human health remains largely unknown. Analysis of the human microbiome may help us better understand our own genome.

The increasing quality and reducing cost of sequencing technologies provide great opportunity to analyze the microbe communities through sequencing. This represents a great improvement over traditional microbe studies which are hindered by several limiting factors. First, only a small proportion of microbes can be cultured under laboratory conditions. Second, only single microbe can be studied in laboratories but it is well known that most microbes need other microbes to survive. In contrast, sequencing technologies allow researchers to collect information from the whole genomes of all microbes in a community directly from their natural environment, facilitating mixed genomic surveys (Handelsman et al., 1998).

When data are available across many communities, the dependencies among microbes, which can be measured by correlations, may provide important clues on the interactions among microbes. However, one unique feature of sequencing-based survey data is that they only provide relative abundances of different microbes in a community because the sequencing results are a function of sequencing depth and the biological sample size (Ni et al., 2013). Therefore, metagenomic data collected from mixed genomic survey studies belong to the so-called class of compositional data in statistics. It was pointed out by Pearson (1897) more than one century ago that correlation analysis method designed for absolute values could lead to spurious correlations for compositional data. Great attention and specialized methods are needed to appropriately analyze and interpret compositional data. Filzmoser and Hron (2009) proposed a procedure based on balances to measure correlations for compositional data, but the groups defined by the balances cannot always be clearly defined and separated from each other. Faust et al. (2012) proposed CCREPE based on permutation and bootstrap to infer the correlated significance but it’s difficult to explain the difference between the permutation and bootstrap samples. Friedman and Alm (2012) introduced correlation concepts of latent variables based on log-ratio transformation of compositional data and proposed an approximation method called SparCC to infer the correlation matrix under sparse assumption. But SparCC does not consider the influence of errors in compositional data which may reduce the estimation accuracy. In addition, there is no guarantee that the inferred covariance matrix from SparCC is positive definite and even the correlation coefficients may fall outside $[-1,1]$.

In this article, we propose a novel method based on least squares with ${\ell }_1$ penalty after log ratio transformation for raw compositional data to infer the correlations among microbes through a latent variable model, called Correlation inference for Compositional data through Lasso (CCLasso). Similar to SparCC, CCLasso explicitly considers the compositional nature of the metagenomic data in correlation analysis, and it has the additional benefit that the estimated correlation matrix of the latent variables for compositional data is positive definite. We also propose an efficient alternating direction algorithm of augmented Lagrangian method to solve the optimization problem involved in our method. The tuning parameter that balances the loss function and sparse assumption is chosen through cross validation.

The performance of CCLasso is compared with SparCC through simulation studies, using several correlation network structures and sample sizes. The simulation results show that CCLasso gives more accurate estimation for correlation matrix than SparCC as well as better edge recovery. When CCLasso and SparCC are applied to estimate the correlation networks of microbes from Human Microbiome Project (HMP), we find that CCLasso is comparable with SparCC in view of consistent accuracy and reproducibility. But for shuffled HMP datasets there are supposed to be no correlations for any species, SparCC always results some small correlations while CCLasso shrinks these small values into 0. We believe that CCLasso can be applied to study correlations of compositional data arising from metagenomic data in natural environment and human body, and it is also broadly applicable in many other contexts where there is interest to assess correlations of variables from compositional data.

2 Methods

2.1 Correlation of latent variables for compositional data

Suppose there are p microbe species and their absolute abundances are random vector $y=(y_1,\dots ,y_p)$ which cannot be directly observed in practice. Instead, only the compositional random vector $x=(x_1,\dots ,x_p)$,

$$x_i=\frac{y_i}{{\displaystyle \sum _{k=1}^p{y}_k}},$$ (1)

can be observed from biological experiments. The absolute abundances y are called latent variables since they cannot be directly observed. The additive log normal distribution (Aitchison and Shen, 1980) is a special case for Equation (1) when y is from a multivariate logarithm normal distribution. The relations among y are of more relevance than x’s in both practice and theory. The interactions among microbe species are described by y while there is a negative correlation trend for compositional vector x from the constant sum constraint even in the absence of any correlations among y,

$${\displaystyle \sum _{k=1}^p{x}_k}=1\Rightarrow {\displaystyle \sum _{k\ne i}\text{Cov}}(x_i,x_k)=-\text{Var}(x_i).$$

Let $w={\displaystyle \sum _{k=1}^p{y}_k}$ be the total absolute abundance for microbe species. Covariances between the latent absolute abundance y, which cannot be observed, and those of its compositional representation x, which are observed, can be related through the base equation (1),

$$\begin{array}{c}\text{Cov}(\ln x_i,\ln x_j)= \text{Cov}(\ln y_i,\ln y_j)-\text{Cov}(\ln y_i,\ln w)\\ \hspace{1em}-\text{Cov}(\ln w,\ln y_j)+\text{Var}(\ln w), \end{array}$$

since $\ln x_i=\ln y_i-\ln w$. Let ${\Sigma }_{\ln x}=\text{Var}(\ln x)$, ${\Sigma }_{\ln y}=\text{Var}(\ln y)$ and $a=\text{Cov}(\ln y,\ln w)-\text{Var}(\ln w)1_p/2$ where $1_p$ is a $p\times 1$ vector of $1\prime$s, then the matrix form of connection between ${\Sigma }_{\ln x}$ and ${\Sigma }_{\ln y}$ can be described as

$${\Sigma }_{\ln x}={\Sigma }_{\ln y}-a{1}^T-1a^T.$$ (2)

We can focus on the correlation among log transforms of y and we also call $\ln y$ latent variables. When x is from additive logistic normal, the independences among $\ln y$ are equivalent to y. Since there is information loss from y to x through normalization procedure (Equation 1), the problem of estimating ${\Sigma }_{\ln y}$ from the sample estimation of ${\Sigma }_{\ln x}$ is undefined without any assumptions. This can be easily seen from Equation (2) that there are $p(p+1)/2$ equations but $p(p+1)/2+p$ unknown parameters.

One way to get around this problem is to assume that ${\Sigma }_{\ln y}$ is sparse which means that the interaction network among microbe species has a small proportion of all possible edges present compared to the fully connected network. Sparse structure is a very common assumption for under-determinated problems such as linear regression models (Tibshirani, 1996), Gaussian graphical models (Yuan and Lin, 2007) and compressed sensing (Candes and Tao, 2005) where the number of unknown parameters is larger, sometimes much larger, than the number of data points. For compositional data, there may exist several sparse networks corresponding to the same ${\Sigma }_{\ln x}$ because y and its scaled form $C(y)y$ (C(y) is any arbitrary positive random variable which is a scaling factor) cannot be distinguished from the base equation (1) if both ${\Sigma }_{\ln y}$ and ${\Sigma }_{\ln (C(y)y)}$ are sparse. The sparse level of ${\Sigma }_{\ln y}$ is the key because there is at most one sparse network ${\Sigma }_{\ln y}$ whose edge density is no greater than $\frac{1}{2}-\frac{1}{p-1}$ corresponding to the same ${\Sigma }_{\ln x}$. And this sparse density condition cannot be relaxed (See Supplementary Material). There are very few statistical methods available to investigate the correlation among the latent variables $\ln y$ with the exception of some recently introduced methods, e.g. SparCC (Friedman and Alm, 2012).

To remove a in the right hand of Equation (2), we can choose a matrix $\text{F}$ with $\text{Rank}(\text{F})=p-1$ and $\text{F}{1}_p=0$ and multiple $\text{F}$ on both sides in Equation (2),

$$\text{F}{\Sigma }_{\ln x}{\text{F}}^T=\text{F}{\Sigma }_{\ln y}{\text{F}}^T-\text{F}a{1}_p^T{\text{F}}^T-\text{F}1a_p^T{\text{F}}^T=\text{F}{\Sigma }_{\ln y}{\text{F}}^T.$$ (3)

The left hand of Equation (3) is the variance of $\text{F}\ln x$ and the right corresponding $\text{F}\ln y$. And their relationship can be seen as

$$\text{F}\ln x=\text{F}(\ln y-1_p\ln w)=\text{F}\ln y.$$

The above relation can explain the two constraints for $\text{F}$. $\text{Rank}(\text{F})=p-1$ ensures that there is a $1-1$ correspondence between x and $\text{F}\ln x$ since there is the constant sum constraint for x. So there is no loss of information in statistical inference from $\text{F}\ln x$ instead of x. $\text{F}{1}_p=0$ helps to cancel the common denominator w after log transformation. There are many such transformation matrices satisfying the two constraints, e.g. $\text{F}=({\text{E}}_{p-1},-1_{p-1})$ is the linear transformation for additive log ratio where the reference variables is x_p and $\text{F}={\text{E}}_p-1_p{1}_p^T/p$ for the centered log ratio for compositional data where ${\text{E}}_p$ is a p × p identity matrix (Aitchison, 1982).

Let $\Sigma ={\Sigma }_{\ln y}={[{\sigma }_{ij}]}_{p\times p}$. The sample version S of ${\Sigma }_{\ln x}$ can be obtained after the fraction estimation from raw data such as metagenomic data through the Bayesian pseudo count method (Agresti and Hitchcock, 2005). From Equation (3) and the sample estimation S for ${\Sigma }_{\ln x}$, we can get the following estimation equation,

$$\text{F}\Sigma {\text{F}}^T=\text{F}S{\text{F}}^T.$$ (4)

Since $\text{Rank}(\text{F})=p-1$ and Σ is a p × p positive definite matrix, Σ cannot be directly estimated through Equation (3). The additional sparse assumption for Σ is reasonable in many application contexts, such as metagenomic data, since most of variable pairs are not expected to be correlated when the number of components is large. Therefore, we can impose some sparsity constraints to help model and infer Σ without other prior information.

2.2 SparCC and its limitations

Friedman and Alm (2012) proposed an iterative approximation approach called SparCC to solve the estimation equation (4) for a number of special forms of transformation matrix $\text{F}$. In short, SparCC first obtains a rough estimation for variance of latent variable $\ln y_i$ and the corresponding correlation matrix. Then it uses a threshold to remove the most correlated pair and repeatedly estimates the variances and correlations until some terminating conditions are met.

Under the above notation, SparCC’s algorithm can be summarized as follows. First, SparCC obtains an estimation for the diagonal of Σ from a rough approximation that

$${\displaystyle \sum _{j\ne i}{\sigma }_{ij}}=0, \forall i.$$ (5)

The rough approximation (Equation 5) supplies additional p equations for Equation (4). This assumption means that every component has no correlations with others on average. Let ${\text{F}}_1=(-1_{p-1},{\text{E}}_{p-1})$ and ${\Sigma }^{12}={({\Sigma }^{21})}^T=\text{Cov}(\ln y_1,\ln y_{-1}),\hspace{0.17em}{\Sigma }^{22}=\text{Var}(\ln y_{-1})$ where $\ln y_{-1}={(\ln y_2,\dots ,\ln y_p)}^T$, then Equation (4) can be written as follows,

$$\begin{array}{c}(-1_{p-1},{\text{E}}_{p-1})\Sigma {(-1_{p-1},{\text{E}}_{p-1})}^T={\text{F}}_{1}S{\text{F}}_1^T\\ \Rightarrow 1_{p-1}{\sigma }_{11}{1}_{p-1}^T-1_{p-1}{\Sigma }^{21}-{\Sigma }^{12}{1}_{p-1}^T+{\Sigma }^{22}={\text{F}}_{1}S{\text{F}}_1^T. \end{array}$$

Computing the trace for both sides of above equation, we have

$$(p-1){\sigma }_{11}+{\displaystyle \sum _{i=2}^p{\sigma }_{ii}}-2{\displaystyle \sum _{i=2}^p{\sigma }_{1i}}=\text{tr}({\text{F}}_{1}S{\text{F}}_1^T).$$

If ${\displaystyle \sum _{i=2}^p{\sigma }_{1i}}=0$, then $(p-1){\sigma }_{11}+{\displaystyle \sum _{i=2}^p{\sigma }_{ii}}=\text{tr}({\text{F}}_{1}S{\text{F}}_1^T).$ Let ${\text{F}}_i,i=2,\dots ,p$ be the additive log ratio transformation matrix where the x_i is the reference variable, for example, ${\text{F}}_p=(\text{E},-1_{p-1})$. Then similar to ${\text{F}}_1$, we have $(p-1){\sigma }_{ii}+{\displaystyle \sum _{j\ne i}{\sigma }_{jj}}=\text{tr}({\text{F}}_{i}S{\text{F}}_i^T)$ for $i=2,\dots ,p$ from the assumption (Equation 5). The corresponding solution is

$${\sigma }_{ii}=\frac{1}{p-2}(\text{tr}({\text{F}}_{i}S{\text{F}}_i^T)-\frac{1}{2(p-1)}{\displaystyle \sum _{i=1}^p\text{tr}}({\text{F}}_{i}S{\text{F}}_i^T)),$$ (6)

since ${\left({\text{E}}_p+\frac{1}{c}{1}_p{1}_p^T\right)}^{-1}=\left({\text{E}}_p-\frac{1}{c+p}{1}_p{1}_p^T\right)$. Then the basic coefficients can be obtained after substituting Equation (6) into Equation (4). In fact, the above procedure is just a way to solve Equation (4) and Equation (5). This is called basic SparCC in Friedman and Alm (2012). A potential problem for SparCC is that σ_ii in Equation (6) can be negative, and so a minimal value $V_{\text{min}}$ is required to replace negative σ_ii. Second, SparCC employs an iterative refinement scheme through excluding the strongest correlated pair if the corresponding magnitude exceeds a given threshold α. The σ_ii is updated through removing the most significant correlation pair based on another assumption like Equation (5),

$${\displaystyle \sum _{j\notin C_i}{\sigma }_{ij}}=0,$$ (7)

where C_i denotes the set of indices of $\ln y_j$ identified to be strongly correlated with $\ln y_i$. Finally, SparCC repeats the former two steps to update the variance σ_ii and the correlation matrix of $\ln y$ through the threshold α for a given iteration time or until no new strongly correlated pair is identified or only three components left. And SparCC selects a correlation threshold to give an interaction network.

As far as we are aware, SparCC is the first method to infer the correlations among latent variables $\ln y$ for compositional data. Its second step is an effective method to remove the strong assumption (Equation 5) in the first approximation step and Equation (7) is approximately right after removing the strongest pairs. Although it represents a significant advance in analyzing compositional data, SparCC has some limitations in the approximations. First, SparCC directly solves Equation (4) with a series of approximate assumptions, and the accuracy of Equation (4) is influenced by the errors resulting from these approximations. Second, there is no consideration for the overall property of the estimated correlation matrix. SparCC cannot guarantee the inferred correlation matrix to be positive definite and even the estimated correlations may fall out of $[-1,1]$.

2.3 CCLasso

We first note that the vectorization version of Equation (3) together with sample variance S is $\epsilon =(\text{F}\otimes \text{F})\text{vec}(\Sigma -S)$, where ε satisfies $\text{E}(\epsilon )=0$ and $\text{Var}(\epsilon )=(\text{F}\otimes \text{F})\text{Var}(\text{vec}(S))({\text{F}}^T\otimes {\text{F}}^T)$. Let $V_S=\text{Var}(\text{vec}(S))$, then an inverse variance weighted loss function can be given as follows,

$$\begin{array}{c}{\text{LOSS}}_1(\Sigma )=\frac{1}{2}{(\text{vec}(\Sigma -S))}^T({\text{F}}^T\otimes {\text{F}}^T){((\text{F}\otimes \text{F})V_S({\text{F}}^T\otimes {\text{F}}^T))}^{-1}\\ \hspace{1em}(\text{F}\otimes \text{F})(\text{vec}(\Sigma -S)), \end{array}$$ (8)

where the inverse symbol $M^{-1}$ is the Moore-Penrose pseudo inverse of M (Penrose and Todd, 1955). The solution to minimize ${\text{LOSS}}_1(\Sigma )$ in Equation (8) satisfies the estimation equation (4). One important property of the loss function (Equation 8) is that it is invariant for any choice of the linear transformation matrix $\text{F}$. This property results from the fact that the information for Σ in the original data is kept after log ratio transformation.

The loss function ${\text{LOSS}}_1(\Sigma )$ in Equation (8) is too complex to be handle for the high-dimensional covariance matrix V_S ($p^2\times p^2$). Inspired by Zhang and Zou (2012) for variance approximation of sample variance, we can use the following loss function to substitute Equation (8),

$${\text{LOSS}}_1\prime (\Sigma )=\frac{1}{2}\text{tr}((\text{F}(\Sigma -S){\text{F}}^T){(\text{F}S{\text{F}}^T)}^{-1}(\text{F}(\Sigma -S){\text{F}}^T)).$$ (9)

The transformation matrix $\text{F}$ in Equation (9) should be chosen reasonably. Considering the symmetry of components, let ${\text{F}}_0={\text{E}}_p-\frac{1}{p}{1}_p{1}_p^T$ be the transformation matrix of centered log ratio with symmetric projection property ${\text{F}}_0^2={\text{F}}_0, {\text{F}}_0^T={\text{F}}_0$. It is suggested that treating the weighting covariance matrix in loss functions as diagonal performs well in some high-dimensional problems (Chen et al., 2013). Let $V={(\text{diag}({\text{F}}_{0}S{\text{F}}_0^T))}^{-1}$. We may consider another substitute for loss function,

$$\begin{array}{c}\text{LOSS}(\Sigma )=\frac{1}{2}\text{tr}(({\text{F}}_0(\Sigma -S){\text{F}}_0^T)V({\text{F}}_0(\Sigma -S){\text{F}}_0^T))\\ =\frac{1}{2}||{\text{F}}_0(\Sigma -S){\text{F}}_0|{|}_V^2. \end{array}$$ (10)

The diagonal matrix V can be seen as a standardization matrix for ${\text{F}}_0(\Sigma -S){\text{F}}_0$. The key idea of our method is that we use the loss function (Equation 10) because of its simplicity.

A reasonable approach to incorporating the sparse assumption for Σ is to minimize loss function plus a suitable penalty. An ideal penalty function is the number of non-zero elements in ${\Sigma }^{-}$ which is the off diagonal of Σ. But it is computationally intractable where the optimization involving $||{\Sigma }^{-}|{|}_0$ is a combinatorial optimization problem with an exponential complexity. A commonly used approach is to replace ${\ell }_0$-norm by ${\ell }_1$-norm (Tibshirani, 1996; Yuan and Lin, 2007). We consider the following objective function combining loss function and ${\ell }_1$ penalty,

$$f(\Sigma )=\text{LOSS}(\Sigma )+\text{PEN}(\Sigma )=\frac{1}{2}||{\text{F}}_0(\Sigma -S){\text{F}}_0|{|}_V^2+{\lambda }_n||{\Sigma }^{-}|{|}_1,$$ (11)

where $\text{PEN}(\Sigma )={\lambda }_n||{\Sigma }^{-}|{|}_1$. The tuning parameter ${\lambda }_n\ge 0$ in Equation (11) is used to balance the fit of model (3) and the sparsity assumption of Σ. CCLasso aims to find a positive definite matrix $\widehat{\Sigma }$ so that

$$\widehat{\Sigma }=\underset{\Sigma \succ 0}{\arg \min }f(\Sigma )=\underset{\Sigma \succ 0}{\arg \min }\frac{1}{2}||{\text{F}}_0(\Sigma -S){\text{F}}_0|{|}_V^2+{\lambda }_n||{\Sigma }^{-}|{|}_1,$$ (12)

where $\Sigma \succ 0$ means Σ should be positive definite. The corresponding correlation matrix estimation can be derived from standardizing the diagonal elements of $\widehat{\Sigma }$. The optimization problem involved in Equation (12) is convex since both the objective function $f(\Sigma )$ and the constraint region $\{\Sigma |\Sigma \succ 0\}$ are convex. So the local minimization of Equation (12) is global.

Compared with SparCC, CCLasso explicitly considers the error terms behind the estimation equation (4) through the loss function (Equation 10). The sparse assumption is directly handled through an additional ${\ell }_1$-type penalty function in contrast to the additional assumption (Equation 7) for SparCC. The estimated correlation matrix from Equation (12) is positive definite and its elements are located in $[-1,1]$ from the positive definite restriction.

2.4 Optimization algorithm and choice of λ_n

We develop an efficient algorithm based on the alternating direction method to solve the constrained optimization problem in CCLasso (Zhang and Zou, 2012). A relaxed version for Equation (12) can be obtained after removing the positive definite constraint,

$$\tilde{\Sigma }=\underset{\Sigma ={\Sigma }^T}{\arg \min }\frac{1}{2}||{\text{F}}_0(\Sigma -S){\text{F}}_0|{|}_V^2+{\lambda }_n||{\Sigma }^{-}|{|}_1.$$ (13)

If the solution $\tilde{\Sigma }$ in Equation (13) is positive definite, $\widehat{\Sigma }=\tilde{\Sigma }$. Otherwise the nearest positive definite matrix to $\tilde{\Sigma }$ is used as $\widehat{\Sigma }$.

To derive an alternating direction method for Equation (13), we introduce a new matrix ${\Sigma }_1$ and rewrite Equation (13) as follows,

$$(\tilde{\Sigma },{\tilde{\Sigma }}_1)=\underset{\Sigma ={\Sigma }^T,{\Sigma }_1=\Sigma }{\arg \min }\frac{1}{2}||{\text{F}}_0(\Sigma -S){\text{F}}_0|{|}_V^2+{\lambda }_n||{\Sigma }_1^{-}|{|}_1.$$

We consider the augmented Lagrangian function

$$\begin{array}{c}L(\Sigma ,{\Sigma }_1,\Lambda )=\frac{1}{2}||{\text{F}}_0(\Sigma -S){\text{F}}_0|{|}_V^2+{\lambda }_n||{\Sigma }_1^{-}|{|}_1\\ \hspace{1em}+\text{tr}(\Lambda (\Sigma -{\Sigma }_1))+(\rho /2)||\Sigma -{\Sigma }_1|{|}_F^2, \end{array}$$

where $||·|{|}_F$ is the matrix Frobenius norm. Let $({\Sigma }^k,{\Sigma }_1^k,{\Lambda }^k)$ be the solution at step k, we update $(\Sigma ,{\Sigma }_1,\Lambda )$ according to

$${\Sigma }^{k+1}=\underset{\Sigma ={\Sigma }^T}{\arg \min }L(\Sigma ,{\Sigma }_1^k,{\Lambda }^k),$$ (14)

$${\Sigma }_1^{k+1}=\underset{{}_{{\Sigma }_1}}{\arg \min }L({\Sigma }^{k+1},{\Sigma }_1,{\Lambda }^k),$$ (15)

and ${\Lambda }^{k+1}={\Lambda }^k+\rho ({\Sigma }^{k+1}-{\Sigma }_1^{k+1})$. Let ${\Sigma }^{k+1}=S+{\Delta }^{k+1}$ for (14), we can write

$${\Delta }^{k+1}=\underset{\Delta ={\Delta }^T}{\arg \min }\frac{1}{2}||{\text{F}}_0\Delta {\text{F}}_0|{|}_V^2+(\rho /2)||\Delta |{|}_F^2+\text{tr}(\Delta ({\Lambda }^k+\rho (S-{\Sigma }_1^k))).$$

The above objective function on the right is quadratic for Δ and ${\Delta }^{k+1}$ is the solution of the following equation,

$$\frac{1}{2}({\text{F}}_{0}V{\text{F}}_0\Delta {\text{F}}_0+{\text{F}}_0\Delta {\text{F}}_{0}V{\text{F}}_0)+\rho \Delta =-({\Lambda }^k+\rho (S-{\Sigma }_1^k)).$$

Let $F_0=U{D}_0{U}^T,\hspace{0.17em}{(U^{T}VU)}_{11}/2\rho +{\text{E}}_{p-1}/2=U_{0}D{U}_0^T$ (the subscript ₁₁ means removing the last row and column) be the eigenvalue decomposition for the corresponding matrix and $M=-U^T({\Lambda }^k+\rho (S-{\Sigma }_1^k))U/\rho$, then the solution for the above equation is

$${\Delta }^{k+1}=U\left(\begin{array}{cc}{U}_0\{(U_0^T{M}_{11}{U}_0)·C\}{U}_0^T& M_{12}\\ M_{21}& M_{22}\end{array}\right)U^T,$$ (16)

where $°$ is the Hadamard product of matrices and $C_{ij}=\frac{1}{D_{ii}+D_{jj}}$.

To update ${\Sigma }_1^{k+1}$, we define an operator $G(A,\lambda )$ as follows,

$$G{(A,\lambda )}_{ij}=\{\begin{array}{cc}{A}_{ij}& i=j,\\ A_{ij}-\lambda & i\ne j, A_{ij}>\lambda ,\\ A_{ij}+\lambda & i\ne j, A_{ij}<-\lambda ,\\ 0,& i\ne j, -\lambda \le A_{ij}\le \lambda .\end{array}$$

From Equation (15), we write

$${\Sigma }_1^{k+1}=\underset{{\Sigma }_1}{\arg \min }(\rho /2)||{\Sigma }_1|{|}_F^2-\text{tr}({\Sigma }_1({\Lambda }^k+\rho {\Sigma }^{k+1})),$$

then the solution of the above problem is ${\Sigma }_1^{k+1}=G\left(\frac{{\Lambda }^k}{\rho }+{\Sigma }^{k+1},\frac{{\lambda }_n}{\rho }\right).$ The following algorithm summarizes the details to carry out the above alternating direction method to solve the optimization problem (Equation 12) for CCLasso.

1. Initialization: k = 0, ${\Lambda }^0$, ${\Sigma }_1^0={\text{E}}_p$.

2. Repeat (a)-(d) until ${\Sigma }^k$ and ${\Sigma }_1^k$ converge:

   1. ${\Sigma }^{k+1}\leftarrow S+{\Delta }^{k+1}$ where ${\Delta }^{k+1}$ is given in Equation (16);
   2. ${\Sigma }_1^{k+1}\leftarrow G(\frac{{\Lambda }^k}{\rho }+{\Sigma }^{k+1},\frac{{\lambda }_n}{\rho })$;
   3. ${\Lambda }^{k+1}\leftarrow {\Lambda }^k+\rho ({\Sigma }^{k+1}-{\Sigma }_1^{k+1})$;
   4. $k\leftarrow k+1$.

3. Return the converged ${\Sigma }^k$ as the solution for $\tilde{\Sigma }$ defined in Equation (13).

The tuning parameter ${\lambda }_n\ge 0$ in Equation (11) has to be tuned since it controls the balance between fitness of model (Equation 3) and the sparsity assumption. A K-fold general cross validation of loss function (Equation 10) is used to choose λ_n in this article. First, all samples are divided into K disjoint subgroups as folds noted by I_k for $k=1,\dots ,K$. These folds will be used as the training set and testing set in turn. Second, for each $k=1,\dots ,K$, compute S_k and $S_{-k}$ corresponding to the sample estimation of $\text{Var}(\ln p)$ through I_k and $I_1,\dots ,I_{k-1},I_{k+1},\dots ,I_K$. The subscript –k means using all samples with the k-th fold left out. The weight matrix V for both training data and testing are based on all data. Thirdly, let $S=S_{-k}$ and compute the estimation ${\widehat{\Sigma }}_{-k}$ through Equation (12) for each $1\le k\le K$. Then compute the mean of K-fold cross validated errors for the tuning parameter λ_n,

$$\text{CV}({\lambda }_n)=\frac{1}{K}{\displaystyle \sum _{k=1}^K\frac{1}{2}}||{\text{F}}_0({\widehat{\Sigma }}_{-k}-S_k){\text{F}}_0|{|}_V^2.$$

Finally, we choose ${\lambda }_n^{*}=\arg {\min }_{{\lambda }_n}\text{CV}({\lambda }_n)$ as the final tuning parameter.

3 Results

3.1 Simulation studies

Though a goal of a genomic survey study is to infer the correlations among members of microbe communities from the abundance count matrix, the estimation accuracy of correlation matrix using either CCLasso or SparCC can be compared to assess their relative performance since they are both based on the same latent assumptions described in Equation (1). The essential difference between these two methods is the estimation procedure after obtaining the fraction estimation.

The compositional data are simulated from the additive logistic normal distribution with a given mean and covariance matrix,

$$\ln y\sim \text{N}(\mu ,\Sigma ), x_i=\frac{y_i}{{\displaystyle \sum _{k=1}^p{y}_k}}.$$

The variation parameter of μ controls the unbalance of components. Every element of μ is generated from a uniform distribution of $[-0.5,0.5]$. We focus on performance comparison between SparCC and CCLasso on sparse correlation matrix with varying levels of sparsity in our simulations. Five covariance structures are considered:

1. Random Model: Every pair of components is connected with a given probability 0.3 and the correlation strength is ±0.15 with equal probability 0.5.

2. Neighbor Model: Randomly select p points in the ${[0,1]}^2$ plane. Then connect the 10 nearest neighbors for each point with the correlation strength 0.5.

3. AR(4) Model: Connect pair (i, j) if $|i-j|\le 4$, and set the correlation strength as 0.4, 0.2, 0.2 or 0.1 as the distance is 1, 2, 3 or 4, respectively.

4. Hub Model: Randomly select 3 points as hubs and the other p – 3 points as common points. Then connect each hub to others with a probability 0.7 while creating edges with probability 0.2 among the common points and all edge strength is set to be 0.2.

5. Block Model: Divide p points into 5 blocks equally. Connect each pair in the same block with probability 0.6 and correlation strength 0.4 while connecting points in different blocks with probability 0.2 and correlation strength 0.2.

To make the covariance matrix positive definite, the diagonal elements of Σ are set large enough and then normalized all as 1. The random model is a very common graph model in which every possible edge occurs independently with the same probability. Through setting the strength as ±0.15 with equal probability, the random model roughly satisfies assumptions Equations (5) and (7) of SparCC. The neighbor model is a 2-dimensional geography model in which edges exist among nearest neighbors. The $\text{AR}(4)$ model can be considered as a model where points are ordered linearly along a line where edges exist between those nodes whose distance is no more than 4, and the correlation decreases as the distance increases. The hub model describes a graph where some special nodes, called hubs, are connected to others with a higher probability than the connection probabilities among other nodes. The block model defines network clustering where edge probabilities are higher within groups than between groups. All models are sparse with different degrees of sparsity. The expect number of edges in the neighbor and $\text{AR}(4)$ model is proportional to p while p² for the random, hub and block model.

For all the models, we set p = 50 and consider different sample sizes n = 200, 300 and 500. For each model, and three combinations of (p, n), we repeat simulations 100 times. The tuning parameter λ_n is determined through 3-folds cross validation, and all data are used to estimate Σ and the correlation matrix. We reimplemented SparCC using R and the default tuning parameters $\alpha =0.1$, k_max = 10 and $V_{min}={10}^{-4}$ are used while the final correlation is truncated by –1 and 1 as the lower and upper limit. SparCC is robust for its tuning parameters since only the strongest pair is removed in each iteration (Supplementary Fig. S1).

To compare the performance between CCLasso and SparCC for each combination of model setting and sample size, we define the correlation inference accuracy by the mean absolute error $d_1(\widehat{\rho },\rho )=\frac{2}{p(p-1)}{\displaystyle \sum _{i<j}|}{\widehat{\rho }}_{ij}-{\rho }_{ij}|$ and the Frobenius norm distance $d_F(\widehat{\rho },\rho )=||\widehat{\rho }-\rho |{|}_F$ between the estimated correlation matrix $\widehat{\rho }$ and the true one ρ. The area under the receiver operation characteristics curve (AUC) is used to assess the performance of CCLasso and SparCC on recovering the non-zero entries in the sparse covariance matrix Σ to avoid the threshold parameter selection.

Table 1 summarizes the performance of CCLasso and SparCC for simulation studies in view of d₁ and d_F distances and AUC. As the sample size increases from 200 to 500, both d₁ and d_F decrease for both CCLasso and SparCC in each simulation setting. The estimation errors of CCLasso are smaller than SparCC. And the corresponding results suggest that CCLasso performs better than SparCC in simulations. This may be due to the fact that CCLasso considers random errors while SparCC does not. For edge recovery, CCLasso also performs better than SparCC except for the random graph model when sample size is 200 and 300. This can be explained by the fact that the random model roughly satisfies assumptions Equations (5) and (7) of SparCC. The accuracy and AUC are not vey consistent such as d₁ and d_F for CCLasso is smaller than SparCC but the AUC for SparCC is larger than CCLasso in the random model. This phenomenon’s reason is that the accuracy measures the continuous distance between the estimation and the true one while AUC shows the discrimination between the non-zeros and zeros.

Table 1.

Performance comparisons of CCLasso and SparCC based on simulation results

n	Method	d1	dF	$\text{AUC}$
Random Model
200	$\text{CCLasso}$	0.033(0.001)	2.954(0.049)	0.791(0.015)
	$\text{SparCC}$	0.057(0.001)	3.528(0.080)	0.823(0.014)
300	$\text{CCLasso}$	0.028(0.001)	2.409(0.057)	0.885(0.012)
	$\text{SparCC}$	0.047(0.001)	2.901(0.059)	0.891(0.011)
500	$\text{CCLasso}$	0.023(0.001)	1.994(0.053)	0.953(0.007)
	$\text{SparCC}$	0.038(0.001)	2.332(0.056)	0.951(0.006)
Neighbor Model
200	$\text{CCLasso}$	0.039(0.003)	3.355(0.206)	0.948(0.015)
	$\text{SparCC}$	0.076(0.001)	4.606(0.081)	0.888(0.014)
300	$\text{CCLasso}$	0.033(0.002)	2.675(0.151)	0.986(0.006)
	$\text{SparCC}$	0.070(0.001)	4.176(0.060)	0.931(0.009)
500	$\text{CCLasso}$	0.026(0.002)	2.064(0.121)	0.999(0.001)
	$\text{SparCC}$	0.065(0.001)	3.800(0.041)	0.967(0.006)
AR(4) Model
200	$\text{CCLasso}$	0.021(0.001)	2.444(0.134)	0.885(0.021)
	$\text{SparCC}$	0.061(0.001)	3.766(0.087)	0.858(0.019)
300	$\text{CCLasso}$	0.018(0.001)	1.994(0.133)	0.922(0.017)
	$\text{SparCC}$	0.052(0.001)	3.210(0.078)	0.890(0.017)
500	$\text{CCLasso}$	0.015(0.001)	1.549(0.087)	0.958(0.011)
	$\text{SparCC}$	0.044(0.001)	2.693(0.059)	0.918(0.011)
Hub Model
200	$\text{CCLasso}$	0.037(0.001)	3.453(0.037)	0.749(0.021)
	$\text{SparCC}$	0.067(0.001)	4.194(0.070)	0.690(0.014)
300	$\text{CCLasso}$	0.036(0.001)	3.133(0.047)	0.768(0.021)
	$\text{SparCC}$	0.059(0.001)	3.686(0.049)	0.735(0.012)
500	$\text{CCLasso}$	0.032(0.001)	2.918(0.048)	0.828(0.018)
	$\text{SparCC}$	0.051(0.001)	3.248(0.043)	0.788(0.010)
Block Model
200	$\text{CCLasso}$	0.039(0.001)	3.307(0.113)	0.782(0.014)
	$\text{SparCC}$	0.070(0.001)	4.268(0.072)	0.734(0.010)
300	$\text{CCLasso}$	0.035(0.001)	2.773(0.079)	0.854(0.014)
	$\text{SparCC}$	0.062(0.001)	3.788(0.052)	0.765(0.011)
500	$\text{CCLasso}$	0.029(0.001)	2.258(0.076)	0.924(0.011)
	$\text{SparCC}$	0.057(0.001)	3.374(0.038)	0.796(0.012)

d₁ and d_F are the two distances between the estimated correlation matrix and the true one defined in the text. AUC is the area under the receiver operation characteristics curve. The results are the averages over 100 simulation runs with standard deviations in brackets.

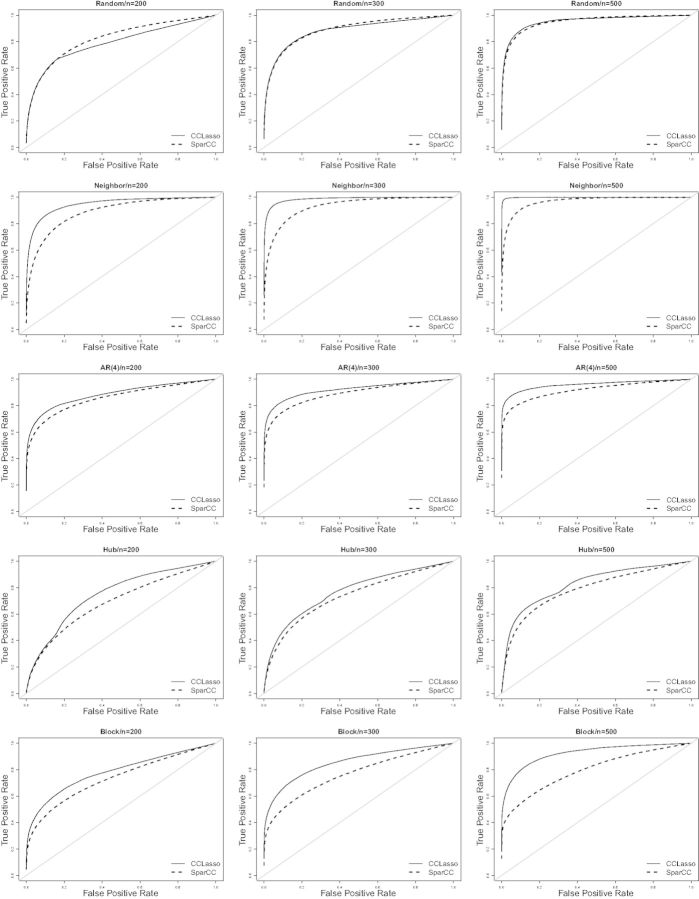
More detailed results for ROC are shown in Figure 1. As the sample size increases, the gap between CCLasso and SparCC increases. For the low false-positive rate such as 0.1, the true-positive rate for CCLasso is larger than SparCC except the random graph model. An interesting phenomenon is that both CCLasso and SparCC perform poorly for the hub model, but as sample size increases the estimation efficiency improves. One should use a much larger sample size for some special graphical structures such as the hub model and the block model than others for given precision. We also compare CCREPE with CCLasso through ROC and find the performance of CCREPE is similar to SparCC (Supplementary Fig. S2).

Fig. 1.

ROC curves of CCLasso and SparCC. The true-positive rate is averaged over 100 replications after fixing the false-positive rate and the gray line is baseline reference

3.2 HMP data

Because of close relationships between ourselves and the microbes in our body, the Human Microbiome Project Consortium (2012a,b) aims to investigate the fundamental roles of the microbes in human health and disease. The high-quality sequencing reads in 16S variable regions 3–5 (V35) of HMP healthy individuals are used to explore the correlation interactions among the microbes in 18 body sites and the corresponding operational taxonomic units (OTUs) are obtained from the HMPOC dataset, available at http://www.hmpdacc.org/HMMCP/. We consider Phase I production study (May1, 2010) and the first sample collected for multiple samples from the sample body site of the same individual. The data are further filtered by removing samples with less than 500 reads or more than 60% 0s are collected and by removing OTUs that are represented by less than 2 reads per sample on average or more than 60% 0s. The transformation from counts to compositional data cannot be directly normalized since both CCLasso and SparCC assume that the 0s in the OTU counts are not real 0 fractions. CCLasso adds all counts by the maximum rounding error 0.5 and then normalizes the counts to get compositional data. Friedman and Alm (2012) provided Bayesian framework to estimate the fractions from counts for SparCC. The final estimation for SparCC is the median of estimations in 20 replicated samples from the posterior distribution of fractions.

Since there is no prior information for true correlation network of taxon–taxon interaction in real data, we use consistent accuracy and reproducibility to compare the performance of CCLasso and SparCC. First, all data are used to construct a gold standard reference correlation matrix for CCLasso and SparCC. The estimated correlation matrix in this step is treated as “known” since all data are used. Second, we randomly select half samples to estimate the correlation matrix through CCLasso and SparCC. The consistent accuracy is measured by the Frobenius norm distance between the estimated correlation matrices of the first and second step. The consistent reproducibility is measured by the fraction of the same edges shared for these two steps in the first gold reference network which only the top 1/4 edges is used. This procedure is repeated 20 times for stable results.

The results are summarized in Table 2. CCLasso and SparCC have similar performance in terms of consistent accuracy and reproducibility. When the sample size is small, the reproducibility is low. Even for large sample size such as left Antecubital fossa, the reproducibility is only 0.64 for both CCLasso and SparCC. We can find consistent accuracy and reproducibility are not good criteria from the simulation data (Supplementary Table S1). Since there are several optimization procedures for the cross validation of CCLasso, SparCC is faster than CCLasso (Supplementary Table S2). The reproducibility is robust for the top edges’ choice (Supplementary Table S3). We also compare the inferred correlation network from CCLasso and SparCC using all samples for all body sites and find their results are very similar (Supplementary Fig. S3 and Table S4).

Table 2.

Consistent Frobenius accuracy and reproducibility for CCLasso and SparCC in different body sites from HMP data

Body	Sample	Frobenius Accuracy		Reproducibility
Site	Size	CCLasso	SparCC	CCLasso	SparCC
AntNar	152	2.28(0.17)	2.22(0.12)	0.70(0.05)	0.68(0.05)
AKerGin	193	1.71(0.13)	1.56(0.14)	0.75(0.04)	0.77(0.05)
BucMuc	196	2.47(0.17)	2.11(0.11)	0.71(0.03)	0.72(0.03)
HarPal	197	2.57(0.18)	2.24(0.13)	0.79(0.03)	0.80(0.03)
LAntFos	51	4.35(0.31)	6.57(0.51)	0.64(0.05)	0.64(0.04)
LRetCre	123	2.24(0.21)	2.30(0.15)	0.69(0.04)	0.66(0.04)
MidVag	45	2.69(0.48)	3.35(0.59)	0.64(0.08)	0.64(0.07)
PalTon	203	2.76(0.17)	2.31(0.17)	0.83(0.02)	0.83(0.02)
PosFor	22	3.34(0.68)	2.98(0.80)	0.67(0.14)	0.68(0.11)
RAntFos	54	3.31(0.37)	6.32(0.32)	0.54(0.03)	0.60(0.04)
RRetCre	85	2.64(0.17)	3.50(0.20)	0.63(0.04)	0.61(0.05)
Saliva	184	2.95(0.14)	2.75(0.13)	0.75(0.03)	0.77(0.03)
Stool	190	1.81(0.13)	2.10(0.16)	0.72(0.04)	0.71(0.03)
SubPla	205	2.89(0.23)	2.45(0.18)	0.82(0.02)	0.84(0.03)
SupPla	207	2.74(0.22)	2.31(0.12)	0.82(0.02)	0.85(0.02)
Throat	197	2.79(0.15)	2.48(0.14)	0.79(0.03)	0.80(0.02)
TonDor	207	2.52(0.22)	2.00(0.17)	0.83(0.02)	0.84(0.02)
VagInt	52	2.93(0.27)	2.94(0.21)	0.65(0.06)	0.63(0.05)

AntNar, anterior nares; AKerGin, attached keratinized gingiva; BucMuc, Buccal mucosa; HarPal, hard palate; LAntFos, left antecubital fossa; LRetCre, left retroauricular crease; MidVag, mid vagina; PalTon, palatine tonsils; PosFor, posterior fornix; RAntFos, right antecubital fossa; RRetCre, right retroauricular crease; SubPla, subgingival plaque; SupPla, supragingival plaque; TonDor, tongue dorsum; VagInt, vaginal introitus.

The results are the averages over 20 replication runs with standard deviations in brackets.

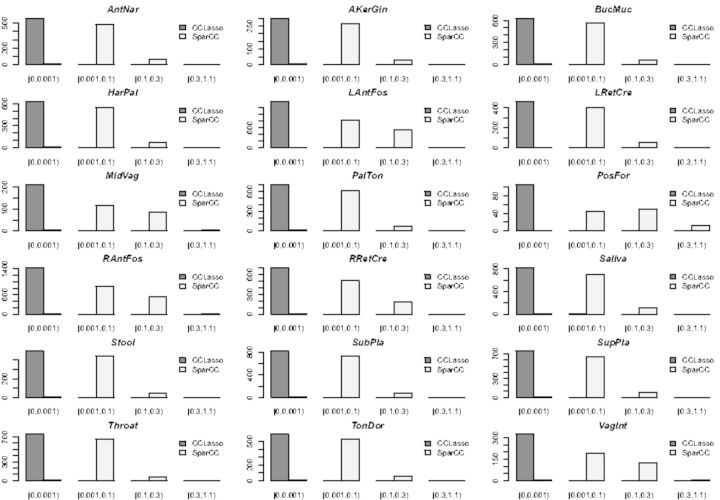
We also compare the performances between CCLasso and SparCC through shuffled HMP data. The individual counts are permuted for each OTUs, so it is supposed not to find any correlations among species. Figure 2 shows the histograms of estimated correlations through CCLasso and SparCC for the shuffled datasets. Almost none correlations are detected by CCLasso but there are always some small correlations inferred from SparCC. In this way, CCLasso outperform SparCC. We use CCLasso and SparCC for the other dataset and find SparCC detects too many strong meaningless edges (Supplementary Fig. S4).

Fig. 2.

Histogram of estimated correlations through CCLasso and SparCC for shuffled HMP datasets

4 Discussion

Although compositional data arise naturally in many practical problems, researchers are generally more interested in the latent variables that underlie these data. For example, in genomic survey studies, it is of great interest to infer the dependency among different bacteria from the observed relative abundance, instead of the absolute abundance, of the bacteria. Therefore, there is a need to infer the correlation matrix among the latent variables for the compositional data. In this article, we have proposed a novel method to infer the correlations among the latent variables for compositional data. We use the sparse assumption to help estimate the correlation matrix of latent variables through solving the constant sum constraint problem. The simulation results show that CCLasso has better performance than SparCC, the only available method in the literature that we are aware of that attempts to solve this problem from a latent variable viewpoint. For the HMP data, CCLasso has similar consistent accuracy and reproducibilities as SparCC. But from the shuffled HMP datasets, we find that SparCC always gives some nonzero estimations.

Though CCLasso performs better than SparCC in simulation studies, it has similar difficulties as SparCC such as reliable component fraction estimation and only linear relation explained. We adopt the simple pseudo count 0.5 to avoid 0 components for HMP datasets. There are other normalization methods that accounts for under sampling such as Paulson et al. (2013) introduced a methodology to assess differential abundance in sparse high-throughput microbial marker-gene survey data. Recently, Biswas et al. (2014) proposed a Poisson-multivariate normal hierarchical model to learn direct interactions removing confounding predictors’ effect from metagenomics sequencing experiments. The assumption of Biswas et al. (2014) is similar to CCLasso from the latent model view, but the essential difference between them is the compositional assumption. Future work will concentrate on improvement of the components estimation accounting for under sampling and exploring nonlinear relationships among microbes.

Funding

This work was supported by the National Natural Science Foundation of China (Nos. 31171262, 31428012, 31471246), and the National Key Basic Research Project of China (No. 2015CB910303). H.F.’s work was supported in part by a fellowship from Graduate School of Peking University. H.Z.’s work was supported in part by NIH GM59507.

Conflict of Interest: none declared.