Visualizing spatial population structure with estimated effective migration surfaces

Abstract

Genetic data often exhibit patterns broadly consistent with “isolation by distance” – a phenomenon where genetic similarity decays with geographic distance. In a heterogeneous habitat this may occur more quickly in some regions than others: for example, barriers to gene flow can accelerate differentiation between neighboring groups. We use the concept of “effective migration” to model the relationship between genetics and geography: in this paradigm, effective migration is low in regions where genetic similarity decays quickly. We present a method to visualize variation in effective migration across the habitat from geographically indexed genetic data. Our approach uses a population genetic model to relate effective migration rates to expected genetic dissimilarities. We illustrate its potential and limitations using simulations and data from elephant, human and A. thaliana populations. The resulting visualizations highlight important spatial features of population structure that are difficult to discern using existing methods for summarizing genetic variation.

Introduction

All natural populations exhibit “structure”: some individuals are more closely related than others. Population structure is shaped by many factors, but probably most influential are the barriers to gene flow that the population has experienced during its evolutionary history – barriers that may be due to extrinsic factors (such as topography or environment) or intrinsic factors (such as mate recognition, reproductive compatibility, or complex interactions in social species such as humans). Studying genetic structure can therefore yield insights into the demographic and evolutionary processes that have shaped the population ^{1, 2}, and help answer questions related to, for example, adaptation ³, speciation ⁴, hybridization ⁵, introgression ⁶ or recombination ^7. Understanding genetic structure may also be useful in contexts other than evolutionary genetics – for example, to identify genetically distinct groups that may require special conservation status ⁸, to detect the geographic origin of samples ^{9, 10} or to help correct for confounding in genome-wide association studies ^{11, 12}.

These questions have motivated the development of many statistical methods for analyzing population structure. Admixture-based clustering ^{13, 14} and principal components analysis (PCA) ^{15, 16} are most widely used. Both approaches summarize the major patterns of population structure in explicit and intuitive visual representations, which can help to generate and refine hypotheses about biological and evolutionary processes and to identify sample outliers or other unexpected patterns. Aside from this shared feature, admixture-based and PCA-based methods have distinct strengths and limitations. Clustering methods are particularly useful when the population is well represented by a small number of relatively distinct groups, possibly with recent admixture; they are less successful in characterizing continuous patterns of genetic variation. In comparison, PCA is arguably better adapted to continuous settings ¹⁵ and has proven helpful in diagnosing isolation by distance ¹⁷ as a feature of the data ¹⁸. However, PCA is heavily influenced by sampling biases, i.e., more data being collected preferentially from some regions than others ^{19, 20, 21}. And while PCA projections are often interpreted post hoc with geographic information in hand, PCA ignores the sampling locations even if they are known – information that can be particularly helpful if the data exhibit a degree of isolation by distance.

Motivated by this, we developed a novel tool for visualizing population structure in an important setting that is not ideally served by existing methods: the setting where individuals are sampled from known locations across the habitat (the samples are “geo-referenced”) and where the population structure is broadly, but perhaps not entirely, consistent with isolation by distance. We aim to produce visualizations that highlight deviations from exact isolation by distance, and thus identify corridors and barriers to gene flow, if they exist. Our method, EEMS, shares goals with several spatial approaches ^{22, 23, 24}, but is unique in explicitly representing genetic differentiation as a function of the migration rates in an underlying population genetic model. EEMS is conceptually related to early work on inferring migration rates from genetic data ²⁵, although the details – and particularly the use of “resistance distance” ²⁶ – are closer to recent work on landscape connectivity ²⁷. The Supplementary Note includes further discussion on how EEMS compares with related work.

Results

Outline of the EEMS method

Figure 1 provides a schematic overview of our approach. EEMS is based on the stepping stone model ²⁸, in which individuals migrate locally between subpopulations (demes) and migration rates can vary by location. To capture continuous population structure, we cover the habitat with a dense regular grid; each deme exchanges migrants only with its neighbors. Under the stepping stone model, expected genetic dissimilarities depend on the sample locations and the migration rates. The expected genetic dissimilarity between two individuals can be computed by integrating over all possible migration histories in their genetic ancestry and we approximate it using resistance distance, a distance metric from circuit theory that integrates all possible migration routes between two demes ²⁶. The estimation procedure adjusts the migration rates of all edges in the graph so that the genetic differences expected under the model closely match the genetic differences observed in the data; it also encourages nearby edges to have similar migration rates. The estimates are then interpolated across the habitat to produce an “estimated effective migration surface” – hence EEMS – which provides a visual summary of the observed genetic dissimilarities and how they relate to geographic location. For example, if genetic similarities tend to decay faster in some regions, those areas will have lower effective migration. If, on the other hand, the relationship between genetic similarity and geographic distance is the same throughout the habitat, the estimated surface will be relatively constant. We use the term “effective” because the model makes assumptions (most importantly, equilibrium in time) that may preclude interpreting effective migration as representing historical rates of gene flow. Nonetheless, we illustrate that the method provides an intuitive and informative way to visualize patterns of population structure in geo-referenced samples.

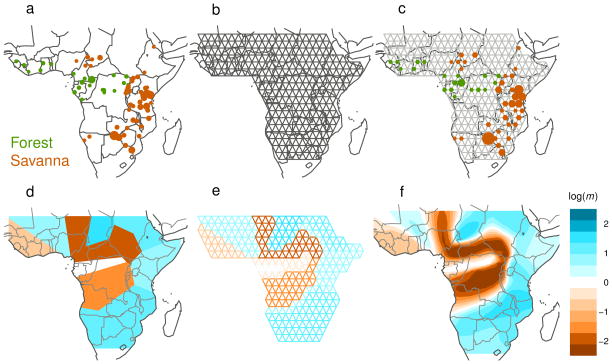
Figure 1.

A schematic overview of EEMS, using African elephant data for illustration. (a–c) Setting up the population grid: (a) Samples are collected at known locations across a two-dimensional habitat; green and orange colors represent two subspecies – forest and savanna elephants. (b) A dense triangular grid is chosen to span the habitat. (c) Each sample is assigned to the closest deme on the grid. (d–f) Estimated Effective Migration Surface (EEMS) analysis: (d) Migration rates vary according to a Voronoi tessellation which partitions the habitat into “cells” with constant migration rate; colors represent relative rates of migration, ranging from low (orange) to high (blue). (e) Each edge has the same migration rate as the cell it falls into. The cell locations and migration rates are adjusted, using Bayesian inference, so that the expected genetic dissimilarities under the EEMS model matches the observed genetic dissimilarities. (f) The EEMS is a color contour plot produced by averaging draws from the posterior distribution of the migration rates, interpolating between grid points. Here, and in all other figures, log(m) denotes the effective migration rate on the log₁₀ scale, relative to the overall migration rate across the habitat. (Thus log(m) = 1 corresponds to effective migration that is 10-fold faster than the average.) The main feature of the elephant EEMS is a “barrier” of low effective migration that separates the habitats of the two subspecies: forest elephants to the west, and savanna elephants to the north, south and east.

Simulations under the stepping stone model

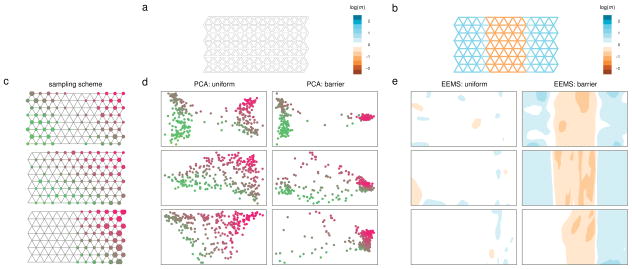
We illustrate the benefits and limitations of EEMS with several simulations. We used the program ms ²⁹ to simulate data under two migration scenarios: in the “uniform” scenario, which represents pure isolation by distance, migration rates do not vary throughout the habitat (Fig. 2a); in the “barrier” scenario a central region with lower migration rates separates the east and the west of the habitat (Fig. 2b). We applied both EEMS and PCA to data generated under these scenarios and under three different sampling schemes (Fig. 2c). The results illustrate two key points. First, whatever the sampling scheme, the migration scenario is easier to discern from the EEMS contour plots (Fig. 2e) than from the PCA projections (Fig. 2d). For the isolation by distance situation, the surfaces are approximately uniform under all three sampling schemes, and for the barrier simulation, the surfaces highlight the barrier as an area of lower effective migration. In contrast, the simple nature of the underlying structure is not obvious from the PCA projections in either setting, and indeed, the PCA results for the different scenarios do not differ in an easily identifiable, systematic way. Second, EEMS is less sensitive to the underlying sampling scheme than PCA. Indeed, the inferred surfaces are qualitatively unaffected by sampling scheme, except in the extreme case where there are no samples taken on one side of the migration barrier. This renders the migration rates on that side of the barrier inestimable from the data, so that estimates in that region are driven by the prior which assumes no heterogeneity in migration rates. In contrast, PCA is heavily influenced by irregular sampling ^{19, 20, 21}. For example, biased sampling and the presence of a barrier can both produce clusters in the PCA results (top row in Fig. 2d).

Figure 2.

Simulation comparing EEMS and PCA analysis. For each method, we show results for two migration scenarios, representing “uniform” migration and a “barrier” to migration, and three different sampling schemes. (a,b) The true underlying migration rates under the two scenarios; colors represent relative migration rates. (c) The three sampling schemes used; the size of the circle at each node is proportional to the number of individuals sampled at that location, and locations are color-coded to facilitate cross-referencing the EEMS and PCA results. (d) PCA results. (e) EEMS results. In contrast to PCA, EEMS is robust to the sampling scheme and shows clear qualitative differences between the estimated effective migration rates under the two scenarios, which reflect the underlying simulation truth.

Effective migration versus actual migration

Population genetics uses extensively the notion of “effective population size”, which can be informally defined as the size of an idealized (random-mating, constant-sized) population that would produce patterns of genetic variation similar to those observed empirically. The effective size of a population is typically quite different from its census size. Similarly, an effective migration surface represents rates that, within an idealized stepping stone model evolving under equilibrium in time, would produce genetic dissimilarities similar to those observed in the data. However, the effective migration rates can be different from the actual migration rates in the population.

To illustrate this idea we compare two migration scenarios that both produce an “effective barrier to migration”: in Figure 3a the barrier results from a lower population density in the central region, in Figure 3b the barrier results from a population split. In both cases the contour plot correctly reflects spatial structure: individuals on either side of the central region are less genetically similar than expected under pure isolation by distance. Indeed, in this case both effective migration surfaces accurately reflect average rates of historical gene flow. However, it should be clear that care is warranted in linking effective migration to inferences about the actual underlying migration process.

Figure 3.

Simulations illustrate that EEMS infers effective migration rates, rather than actual steady-state migration rates. (a) Individuals have uniform migration rates but the central area has lower population density (those demes have fewer individuals, which is represented by smaller circles in gray). Thus fewer migrants are exchanged per generation in the central area, producing an effective barrier to gene flow that is reflected in the EEMS. (b) A simple “population split” scenario: migration is initially uniform, but at some time in the past a complete barrier to migration arises in the central area (represented by dashed edges). Under this scenario the groups on either side of the central region diverge, which creates a barrier in the EEMS.

These results also emphasize that, because EEMS characterizes expected genetic differentiation, it cannot distinguish between different scenarios that produce similar expectations for the pairwise genetic dissimilarities; this is also true for PCA ²⁰. In some cases it may be possible to distinguish among such scenarios using other aspects of the data, but we do not pursue this here.

Effects of SNP ascertainment

The model underlying EEMS formally assumes that observed biallelic loci are a random sample of biallelic loci polymorphic in the sample and hence that the loci are “unascertained”. This assumption holds for complete sequence data but not for genotyped SNPs, which are biased towards higher minor allele frequencies and could also be biased towards higher levels of polymorphism in certain geographic locations. To assess robustness of EEMS to this assumption, we performed simulations in which SNPs were ascertained as polymorphic in a small panel preferentially sampled from one geographic area. Results show that EEMS is qualitatively robust to this bias (see Supplementary Note and Supplementary Fig. 1).

As described in Online Methods, EEMS also estimates the effective diversity rate within each deme – a parameter that reflects the expected genetic dissimilarity of two individuals sampled from that location. In contrast to effective migration, effective diversity is sensitive to geographically biased SNP ascertainment (Supplementary Fig. 1b). Intuitively, ascertaining common SNPs increases the average number of differences among all individuals, and so increases the observed diversity. Geographically biased ascertainment can therefore create apparent geographic differences in diversity where none exist. However, we expect the effect of ascertainment on how, qualitatively, genetic dissimilarity decays with distance – and hence its effect on the estimated migration surface – to be less pronounced, and our simulation results support this view.

Anisotropic migration

EEMS cannot infer directions of migration because the underlying model assumes that migration rates are symmetric. Nonetheless, EEMS is not entirely incapable of representing directional differences in migration (“anisotropic migration”). This is because, at any given deme, edges radiate in six directions and each edge has its own migration rate. To illustrate, we performed simulations where throughout the habitat migration occurs at a much higher rate in the NS direction than in the EW direction: the resulting surface reflects this by interspersing vertical “corridors” that facilitate NS migration with vertical “barriers” that inhibit EW migration (Supplementary Fig. 2).

Diagnosing deviations from an EEMS fit

Although EEMS assumes stationary symmetric migration in a closed regular triangular grid, it would be a mistake to interpret EEMS results as a validation of this population genetic model over others. Instead EEMS is an exploratory tool for visualizing patterns of genetic variation in geo-referenced data. As in Figure 3b, EEMS can provide useful summaries even if the data was not generated under equilibrium; however, not all patterns of genetic differentiation can be well represented by EEMS. To identify deviations from the fitted model, the pairwise genetic differences predicted by EEMS are plotted against the pairwise genetic differences observed in the data. If a few individuals or sampling locations produce strong deviations, it may be prudent to remove them, or to check that the results are robustness to their inclusion (see Supplementary Note and Supplementary Fig. 3 for a scenario with recent migration).

Supplementary Figure 3 illustrates these diagnostic plots in a situation where several individuals have recently migrated from one end of the habitat to the other (or perhaps their sampling location was wrongly labeled). The “migrants” are genetically distinct from other nearby individuals, which EEMS represents with a barrier around them (Supplementary Fig. 3a). However, as the diagnostic plot indicates (Supplementary Fig. 3b), EEMS cannot represent the fact that the “migrants” are genetically similar to some very distant individuals. In principle, this could be captured by a corridor of migration linking the migrants to their original location, but EEMS does not do this, presumably because inserting such a corridor would make the overall model fit worse. We supply further examples of these diagnostic plots for all our empirical examples (Supplementary Figures 10, 12 and 16).

Empirical results

Elephants in Sub-Saharan Africa

The African elephant (Loxodonta africana) has two recognized subspecies: the forest elephant (L. a. cyclotis) and the savanna (or bush) elephant (L. a. africana). Both subspecies are under threat, partly from poaching, and a large sample was collected and genotyped at 16 microsatellite loci to help assign contraband tusks to their location of origin and thus facilitate conservation efforts ⁹. We analyze a geo-referenced dataset that contains 211 forest and 913 savanna elephants ³⁰.

The African elephant provides a helpful illustration because the subspecies structure is clear and strongly correlated with geography: its primary feature is the low effective gene flow between forest and savanna elephants despite their geographic proximity. Correspondingly, the estimated effective migration surface is dominated by a strong barrier between their habitats (Fig. 4b). To a degree, EEMS captures its winding shape, though our method, based on Voronoi tessellations, is better adapted to visualize barriers with simpler structure. This is also an empirical example of an effective barrier to migration due to a non-equilibrium history of drift after divergence (as in Figure 3b).

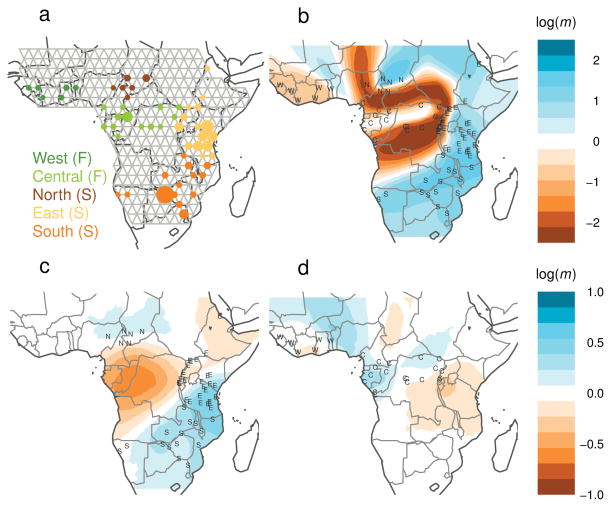
Figure 4.

EEMS analysis of African elephant data ³⁰. (a) African elephant samples are collected from two subspecies in five biogeographic regions: the forest elephant subspecies (in green) inhabits the west and central regions; the savanna elephant subspecies (in orange) inhabits the north, east and south regions. (b) Estimated effective migration rates for forest and savanna samples analyzed jointly. (c,d) Estimated effective migration rates for savanna and forest, respectively.

For the African elephant, one of the sixteen genotyped loci is extremely informative: the surface inferred from this locus alone is similar to that from all sixteen loci (Supplementary Fig. 5). However, the surface from the remaining fifteen loci is also qualitatively similar (Supplementary Fig. 6a); therefore the strongly differentiated locus is consistent with the others. (In principle, differences in effective migration among loci could provide a test for selection ³¹.)

Since strong differentiation between the two subspecies dominates EEMS, we also analyzed forest and savanna samples separately to assess subtler structure within each group. The presence of substructure has been detected previously ⁹ and the habitat can be divided into five broad biogeographic regions (Fig. 4a): West and Central (forest); North, East and South (savanna). The savanna surface (Fig. 4c) shows a “corridor” of higher effective migration connecting the South and East regions, and a barrier separating them from the North. The barrier coincides with forest habitat, which forms a known barrier to migration for savanna elephants; the corridor is consistent with previous observations, from mitochondrial data, that South and East elephants are more similar genetically than their geographic distance would suggest ³². The forest surface (Fig. 4d) also shows a corridor of higher effective migration, which connects the West and Central regions. The two subspecies-specific contour plots suggest that there is more deviation from uniform migration (stronger deviation from isolation by distance) in the savanna elephants. These patterns are harder to recognize in the corresponding PCA plots (Supplementary Fig. 7) or admixture-based analyses (Supplementary Figures 8 and 9).

In addition to effective migration, our method also estimates the effective diversity within each deme; these parameters reflect the expected genetic dissimilarities of two individuals from the same location. For the African elephant, the inferred effective diversities are higher in forest regions than in savanna regions (Supplementary Fig. 6b). This represents, in a direct visual way, the observation that forest elephants have higher heterozygosity than savanna elephants ³³.

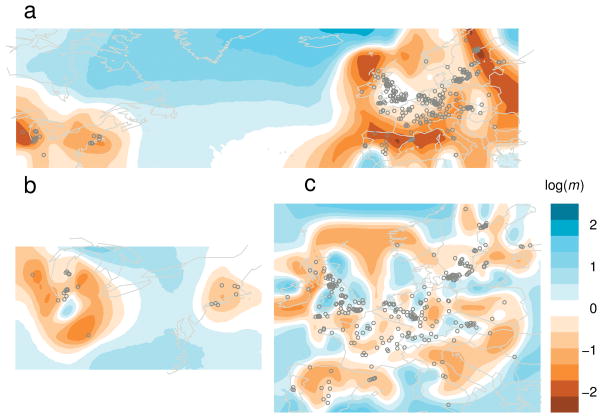
Humans in Europe and Sub-Saharan Africa

We analyze two large-scale genome-wide datasets to visualize the genetic structure of human populations on two continents: a collection of 1,201 individuals from 13 Western European countries ^{18, 34} and a collection of 314 individuals from 21 Sub-Saharan African ethnic groups ^{35, 36, 37}.

The two leading PCs are correlated with geographic location in both datasets ^{18, 37, 38}. This suggests that genetic similarity tends to decay with geographic distance (Supplementary Fig. 11) and thus the data are broadly consistent with isolation by distance. On the other hand, EEMS highlights patterns that deviate from exact isolation by distance (Fig. 5).

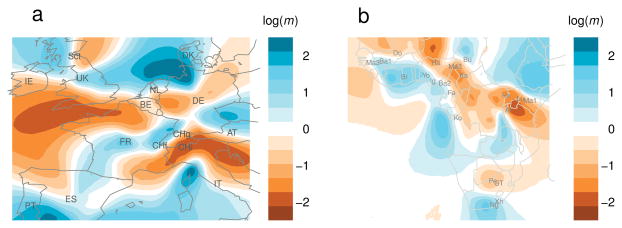
Figure 5.

EEMS analysis of human population structure in Western Europe and in Sub-Saharan Africa. (a) Effective migration rates in Western Europe, estimated using geo-referenced data from the POPRES project ³⁴. (b) Effective migration rates in Sub-Saharan Africa, estimated using geo-referenced data from two previously published studies ^{35, 36}.

In Europe (Fig. 5a), the areas of highest effective migration span the North Sea and the Mediterranean, likely due to historic contacts between peoples bordering these bodies of water; other areas of high migration span central France and Austria. Some regions of low effective migration align with topographic barriers: the Alps and the Atlantic; an area of low migration also spans Germany. Visually there are two east-to-west barriers and so the effective migration surface supports the idea that population structure in Europe is characterized by a north/south cline ³⁹. Thus, while the PCA plot may suggest a simple relationship between genetics and geography ¹⁸, EEMS highlights more complex spatial patterns of differentiation. In POPRES, the geographic information is imprecise because locations were assigned based on nationality. The EEMS results are largely robust to this location uncertainty, which we assessed by adding random jitter to the assigned locations (Supplementary Fig. 13).

In Africa (Fig. 5b), EEMS highlights a corridor of higher effective migration along the Atlantic coast, relative to lower effective migration inland. This indicates that – at a given distance apart – the coastal populations are more genetically similar than the inland populations. The U-shaped tail of this corridor suggests higher than expected genetic similarity between some ethnic groups in the west and in the east. Non-genetic information about the subpopulations can help clarify this pattern: the Fang (Fa) and the Kongo (Ko) in the west, and the Luhya (Lu) in the east speak Bantu languages, so we hypothesize that the link is partly due to shared ancestry between Bantu speaking groups (Supplementary Fig. 15). In an EEMS analysis after excluding the Luhya, the definition of the corridor connecting the east with the west is greatly decreased (Supplementary Fig. 14), which supports our hypothesis.

EEMS attempts to explain observed genetic dissimilarities using (an approximation to) the stepping stone model. Some datasets may contain features that are not captured by this model such as recent long-distance migrants. To check the model fit we compare the fitted and observed genetic dissimilarities. For both human datasets, those values agree well (Supplementary Figures 12 and 16) and they agree better under the estimated migration patterns than under a constant migration model: the proportion of variance explained increases from 14.2% to 97.8% for the European data and from 16.4% to 91.4% for the African data. Therefore non-stationary effective migration provides a better explanation for the observed spatial differentiation than simple isolation by distance.

A. thaliana in Europe and North America

Arabidopsis thaliana is a small flowering plant with natural range in Europe, Asia and North Africa, which is now also found in North America. Although A. thaliana is a selfing plant with low gene flow, its genetic variation has significant spatial structure ^{40, 41}. In Europe A. thaliana exhibits patterns consistent with isolation by distance, with an east/west gradient that has been interpreted as evidence for post-glaciation colonization ^40. In North America there is less spatial structure, likely due to recent human introduction from Europe ⁴⁰. We analyze A. thaliana data from the Regional Mapping (RegMap) project ⁴², which includes 979 accessions from Europe and 180 accessions from North America.

In a combined analysis of the North American and European data (Fig. 6a), EEMS infers a corridor of high effective migration across the Atlantic Ocean, relative to lower effective migration within each continental group; this highlights the strong genetic similarity between the European and North American samples. EEMS assumes that migration is symmetric and so it cannot infer a direction for gene flow, but the effective migration surface is consistent with the hypothesis that recent migration introduced A. thaliana from Europe to North America ⁴³.

Figure 6.

EEMS analysis of Arabidopsis thaliana data from the RegMap project ⁴²: (a) Estimated effective migration rates in North America, Europe and across the Atlantic Ocean; (b) Estimated effective migration rates in North America; (c) Estimated effective migration rates in Europe.

In North America EEMS infers an area of high migration connecting the two sampled regions, Lake Michigan and the Atlantic coast (Fig. 6b). This indicates that accessions from these regions are distant geographically but similar genetically, probably due to human-assisted long-range “migration” rather than natural dispersal. This is consistent with the observation that there is extensive haplotype sharing not only within but also between sampling locations ⁴⁰.

In Europe the effective migration surface highlights several regions (Fig. 6c). For example, in the British Isles, a region of lower migration separates the northern British Isles from the rest of Britain, which in turn is also separated from France. There is substructure within both France and Germany as well. In France, accessions in the north and the south are separated by a region of lower effective migration through central France. In Central Europe, areas of higher effective migration link northern Germany with South Sweden and Norway, and southern Germany with Austria, Switzerland and the Czech Republic. In contrast, effective migration is substantially lower in Southern Europe. PCA produces patterns consistent with the EEMS results about A. thaliana in France and Central Europe, which we confirm by zooming on these regions and coloring the samples according to latitude and longitude rather than country of origin (Supplementary Fig. 17).

Discussion

EEMS (Estimated Effective Migration Surfaces) is a new method for analyzing population structure from geo-referenced genetic samples. EEMS produces an intuitive visual representation of spatial patterns in genetic variation and highlights regions of higher-than-average and lower-than-average historic gene flow. EEMS is specifically applicable when the data conforms roughly to “isolation by distance”, i.e., in settings where genetic similarity tends to decay with geographic distance, but where this decay with distance may occur more quickly in some regions than in others.

EEMS uses the concept of “isolation by resistance”, which aims to characterize how genetic differentiation accumulates in non-homogeneous landscapes ²⁶, by integrating over all possible migration paths between two points. This provides an efficient approximation to the structured coalescent and, in some cases, better prediction of genetic differentiation than uniform isolation by distance ⁴⁴.

In previous work, isolation by resistance is often used to build up a connectivity map from known landscape features ^{26, 44}. The concept has also been incorporated into an inference procedure to test whether genetic distances are impacted by specific observed features such as altitude or river barriers ²⁷. In contrast, EEMS estimates effective migration from genetic data without the need to observe environmental variables, and thus provides an exploratory tool for spatial population structure. The hypothesis-driven and exploratory approaches are complementary and both can be useful in many applications.

Although EEMS is designed to visualize continuous population structure in space, it is built on a dense regular grid of discrete demes, with migration between neighboring demes. Since the demes do not correspond to predefined subgroups, the size and registration of the grid are arbitrary. The choice of grid may be influenced by factors such as sampling density (in a sufficiently dense grid different sampling locations would correspond to different demes) and computational tractability (computation scales cubically with the number of demes). In practice, we have found that results are qualitatively robust across a range of grids (Supplementary Fig. 4), but details can change and we suggest averaging the estimates over several different grids. In principle, it would be attractive to dispense with the grid altogether and use models of continuous migration; however, such models present theoretical and mathematical challenges ⁴⁵ and at present we do not know how to achieve this.

EEMS requires that each sample has a specified geographic origin, but in some cases this information may be known imprecisely (as in the analysis of human genetic variation in Europe for example). To better deal with imprecision in geographic origin, the uncertainty could be incorporated into the model: the actual location of each individual will be treated as an unobserved latent variable, given a prior distribution and integrated out in the MCMC estimation scheme ¹⁴. This approach might also improve robustness to errors such as sample switches, by identifying individuals whose genetic origin differs appreciably from their physical sampling location. A similar extension could help with “spatial localization” (the problem of inferring the origin of individuals with unknown location) in non-stationary isolation by distance settings ^{9, 10}.

Like PCA, EEMS works with a dissimilarity matrix that summarizes pairwise dissimilarities by averaging across markers. Once this matrix is computed, the complexity per MCMC iteration does not depend on the number of SNPs and so EEMS is computationally tractable for large datasets. Moreover, like PCA, this features means that EEMS could be applied to visualize any dissimilarity matrix computed from geo-referenced data. For example, it could be used to visualize dissimilarity matrices computed from non-genetic features such as language. EEMS will be most useful when similarity tends to decay with geographic distance, but this is easily assessed.

Summarizing genetic data by a pairwise dissimilarity matrix does, however, result in some loss of information; for example, in a genetic context, it limits what demographic scenarios that EEMS can distinguish ²⁰. In this regard, it may be helpful to visualize dissimilarity matrices that emphasize different aspects of the data, perhaps different historical timescales. For example, ChromoPainter ⁴⁶ produces a measure of genetic similarity that tends to emphasize the most recent coalescent events between samples (rather than their average coalescence times). Distance matrices based on rare SNPs could also reveal more recent dispersal history ⁴⁷.

Online methods

EEMS uses a population genetic model that involves migration on an undirected graph G = (V,E) with vertices (demes) V connected by edges E. The graph G is a regular triangular grid, which is fixed and embedded in a two-dimensional plane, so that each deme has a known location and only neighboring demes are directly connected (Figure 1b). The density of the grid is pre-specified by the user and depends on both computational considerations – computational complexity scales cubically with the number of vertices – and the resolution of the available spatial data.

The EEMS model has migration parameters m and diversity parameters q, where m = {m_e: e ∈E} specifies an effective migration rate on every edge and q = {q_v: v ∈V} specifies an effective diversity rate for every deme. Intuitively, the migration rates m characterize the genetic dissimilarities between distinct demes, while the diversity rates q characterize the genetic dissimilarities between distinct individuals from the same deme. The EEMS model is a special case of the general stepping stone model ²⁸, which allows directed migration as well as migration between demes that are not located close in space.

We use Bayesian inference to estimate the EEMS parameters m and q. Its key components are the likelihood, which measures how well the parameters explain the observed data, and the prior, which captures the expectation that m and q have some spatial structure (in particular, the idea that nearby edges will tend to have similar migration rates).

The likelihood

We first specify the likelihood for SNP data (on n individuals at p SNPs) and then extend it to microsatellites. The initial step is to summarize the observed genetic data by the matrix of average genetic differences, D, between every pair of sampled individuals. (The matrix D is defined precisely below.) This approach – using the matrix of pairwise dissimilarities as a sufficient statistic for the population parameters – assumes that D contains most of the information about m and q. This may not be completely true but the idea of performing inference using pairwise genetic (dis)similarities has a long history in both population genetics and phylogenetics ^{48, 49, 50} and many existing methods make a similar assumption. For example, PCA ¹⁵ and TreeMix ⁵¹ both work with the genetic covariance matrix.

Let D_ij denote the observed genetic dissimilarity between individuals i and j. The expected value of D_ij is determined, up to a constant of proportionality that reflects the mutation rate, by how closely related i and j are, or more precisely, by their expected coalescence time. This expected value in turn depends on the sampling locations δ(i),δ(j) and the population parameters m,q: individuals sampled from demes that are connected by many short paths containing edges with high migration rates tend to be more closely related, and hence more similar genetically, than individuals sampled from demes connected only by paths that are long and/or contain edges with low migration rates. The expected coalescence times can be computed, at some computational expense, by solving a large set of simultaneous equations. Alternatively, they can be approximated – at lower, but still nontrivial, computational cost – using the concept of “resistance distance” ²⁶. We implemented both metrics and found them to produce qualitatively similar effective migration surfaces, and so here we present results obtained using resistance distances.

Letting σ² denote the constant of proportionality mentioned above, we can write

$$E\{D\mid m,q,{\sigma }^2\}={\sigma }^2\mathrm{\Delta }(m,q),$$ (1)

where Δ(m,q) is the matrix of expected dissimilarities that can be computed for any m and q. Our modeling approach assigns high likelihood to values for m,q,σ² such that σ²Δ(m,q) ≈ D, while taking some account of dependencies among elements of D and of linkage disequilibrium among markers.

To make our specification precise we introduce some notation: Z_il is the genotype of individual i at locus l, coded as 0, 1 or 2 copies of the minor allele; Z is the n×p matrix of genotypes. D_ij = (1/p)Σ_l(Z_il − Z_jl)² is the average squared difference between i and j based on p markers; D is the n×n matrix of observed genetic dissimilarities. L is the (n−1)×n matrix such that L_i = e_i − e_i+1 where L_i is the i-th row of L and e_i is a row vector with 1 in the i-th component and 0s elsewhere. And W is the (n−1)×(n−1) matrix −LDL′. It can be shown that W = 2(LZ)(LZ)′; if the n individuals are linearly independent, which requires p≥n, this characterization implies that W is positive definite ²⁷.

The matrix L forms a basis for the space of contrasts on n items. (For example, e_i − e_i+1 is a contrast between the i-th and (i+1)-st items.) Since L is a basis, W is a one-to-one mapping of D and we can specify a model for D by specifying a model for W ⁵². The advantage of specifying a model for W, rather than D, is that, since it is positive definite, W can be modeled by the Wishart distribution, which is parametrized by the expectation, E{W}, and a scalar parameter k (the degrees of freedom). Using equation (1), the expectation is given by

$$\mathrm{E}\{W\mid m,q,{\sigma }^2\}=-L\mathrm{E}\{D\mid m,q,{\sigma }^2\}{L}^{\prime }=-{\sigma }^{2}L\mathrm{\Delta }(m,q)L^{\prime }.$$ (2)

We treat the degrees of freedom k as an additional free parameter.

Putting this together yields a closed form for the density f of the statistic W and thus for the likelihood l of the parameters k,m,q,σ² since l(k,m,q,σ²) = f(W|k,m,q,σ²). Specifically,

$$W\mid k,m,q,{\sigma }^2~{\mathrm{W}}_{n-1}\left(k,-\frac{{\sigma }^2}{k}L\mathrm{\Delta }(m,q)L^{\prime }\right).$$ (3)

We make the following observations:

1. Although we defined Z_il as the number of copies of the minor allele, the differences (Z_il − Z_jl)² do not depend on the allele labeling and neither does the likelihood.

2. If the genotypes Z were independent across loci and normally distributed, then standard Gaussian theory would imply that W has a Wishart distribution, with the degrees of freedom k equal to the number of SNPs p. However, genotypes are neither normal nor independent, and rather than fix k=p, we estimate the degrees of freedom k, under the assumption n≤k≤p. The smaller k is, the higher the variance of W about its expectation; E{W} does not depend on k in our parametrization. By allowing k<p we can, to some extent, account for sources of model mis-specification such as linkage disequilibrium.

3. In defining W = −LDL′ we introduced a specific matrix L. However, other choices for L would yield equivalent likelihoods as long as the n−1 rows of L form a basis for the contrasts of n elements. (A contrast is a linear combination whose coefficients add to 0.) This property ensures that W is a one-toone mapping of D and that we would get exactly the same likelihood with any basis L, up to a constant of proportionality that does not depend on the parameters ⁵².

Application to microsatellites

At a microsatellite locus, an allele is typically coded as the number of repeats of a specific motif. To apply our method to microsatellites we define the genotype Z_il to be the average of the two alleles that individual i carries at locus l. This approach could likely be improved upon, but it suffices for our analysis of the African elephant data.

We then define D^(l) as the matrix of pairwise differences D_ij^(l) = (Z_il − Z_jl)² at locus l and W^(l) = −LD^(l)L′ as the corresponding transformation in terms of the basis L. Since different microsatellites have different mutation rates, we introduce locus-specific scale parameters ${\sigma }_l^2$: l = 1,…,p. For locus l equation (1) becomes

$$\mathrm{E}\{D^{(l)}\mid m,q,{\sigma }_l^2\}={\sigma }_l^2\mathrm{\Delta }(m,q).$$ (4)

Each matrix W^(l) has rank one and we define the likelihood by assuming that W^(l) has a (singular) Wishart distribution with one degree of freedom:

$$W^{(l)}\mid m,q,{\sigma }_l^2~{\mathrm{W}}_{n-1}\left(1,-{\sigma }_l^{2}L\mathrm{\Delta }(m,q)L^{\prime }\right),$$ (5)

and that the p microsatellite loci are independent. (Thus the degrees of freedom are effectively fixed to k=p.)

The dissimilarity matrix

In population genetics, the expected genetic dissimilarity between two samples is a function of their expected coalescence time. Indeed, for haploid samples at biallelic loci, as the mutation rate tends to 0, it can be shown that (see Supplementary Note)

$$\mathrm{E}\{D_{ij}\mid m,q\}\propto T_{\delta (i)\delta (j)}(m,q),$$ (6)

where δ(i) denotes the deme from which sample i is drawn and T_αβ(m,q) is the expected coalescence time of two independent haploid samples taken from demes α and β. Thus in equation (1) we have

$${\mathrm{\Delta }}_{ij}(m,q)=T_{\delta (i)\delta (j)}(m,q).$$ (7)

Similarly, for diploid samples, we have (see Supplementary Note)

$${\mathrm{\Delta }}_{ij}(m,q)=4T_{\delta (i)\delta (j)}(m,q)-T_{\delta (i)\delta (i)}(m,q)-T_{\delta (j)\delta (j)}(m,q).$$ (8)

For any particular value of the parameters m and q, the matrix T(m,q) – and hence Δ(m,q) – can be computed by solving a system of linear equations ^{53, 54}.

However, computing the matrix of expected coalescence times T is expensive: it requires solving a linear system with d(d+1)/2 unknowns to find all pairwise expected coalescence times in a graph with d demes; this has complexity O((d²)³). To reduce the computational cost, for all results presented here, we approximate coalescence time using the concept of “effective resistance” – a distance metric for weighted undirected graphs ⁵⁵. Computing the matrix of effective resistances R is less intensive because we can obtain all pairwise resistance distances by inverting a d×d matrix ⁵⁶; this has complexity O(d³). (Efficiency can be improved further by computing the subset of resistance distances between sampled demes only; see Supplementary Note.)

To approximate coalescence times using effective resistances, let R_αβ(m) denote the resistance distance between demes α and β in the graph G. (Note that R_αβ is not a function of only the local migration rate m_αβ, but is determined by the global migration pattern m.) The effective resistances R are approximately related to the expected coalescence times T through ²⁶:

$$R_{\alpha \beta }/4\approx T_{\alpha \beta }~(T_{\alpha \alpha }+T_{\beta \beta })/2.$$ (9)

This approximation is exact for isotropic migration (i.e., if the demes are equivalent with respect to the rate and pattern of migration), and for more general migration models the approximation gets better as the migration rates increase ²⁶. Using equation (9) we approximate the expected coalescence time between two haploid samples from demes α and β as

$$T_{\alpha \beta }=T_{\alpha \beta }-(T_{\alpha \alpha }+T_{\beta \beta })/2+(T_{\alpha \alpha }+T_{\beta \beta })/2\approx R_{\alpha \beta }/4+(q_{\alpha }+q_{\beta })/2.$$ (10)

That is, for each pair of demes α and β we split the expected coalescence time T_αβ into a between-demes component, which is approximated by the (scaled) effective resistance R_αβ, and a within-demes component (q_α+q_β)/2, which is determined by the diversity rates q. The effective resistances R = (R_αβ) depend on m; the vector q is treated as a free parameter. We then obtain Δ(m,q) by substituting T(m,q) with its approximation according to equation (10).

The prior

Voronoi prior on migration rates

Our prior for the migration rates m captures the idea that nearby edges will tend to have similar rates, while it also allows the rates to vary among edges. We parametrize the prior on m using a Voronoi tessellation of the two-dimensional habitat H, which partitions H into C convex polygons (cells) as follows. First select C distinct points (seeds) s₁,…,s_C within H. Then define cell c to be the set of points in H that are closer to seed s_c than to any other seed. Given a Voronoi tessellation of H, we associate with each cell c a migration rate m_c. We use these to induce a migration rate on each edge in the graph G, with the migration rate of the edge joining demes α and β given by

$$m_{\alpha \beta }=(m_{c_{\alpha }}+m_{c_{\beta }})/2,$$ (11)

where c_α is the cell containing deme α. Migration rates should be positive and therefore we parametrize the m_c values on the log₁₀ scale. Further, to capture the idea that the migration rates of different cells may be similar to one another we parametrize them as deviations from an overall mean rate μ:

$${log}_{10}(m_c)=\mu +e_c,$$ (12)

where the “effect” of cell c, denoted by e_c, determines whether the local dispersal in cell c is faster or slower than the average.

In this formulation, migration rates on every edge in the graph are determined by the parameters (C,s₁,…,s_C,e₁,…,e_C,μ). To complete the Bayesian specification we place priors on the model parameters. For the number of Voronoi cells, C|r,u ~ Neg-Bi(r,u) is the zero-truncated negative binomial distribution with shape (number of failures) r and probability of success u. The zero-truncated negative binomial has support {1,2,3,…}; we truncate the support at zero because the Voronoi tessellation should have at least one cell. For all analyses described here, we used r = 10 and u = 2/3, which results in a diffuse prior on C, with prior mean 20 and prior variance 60.

For the cell locations, s₁,…,s_C|C ~ U(H) is the uniform distribution with support the habitat H. For the cell effects, e₁,…,e_C|C,ω² ~ N_[−2,+2](0,ω²) is the truncated normal distribution with mean 0, variance ω² and support [−2,+2]. For the overall migration rate, μ ~ U(−2.477,+2.477) and for the variance between cells, ω² ~ Inv-G(c_ω/2, d_ω/2) is the inverse gamma distribution with shape c_ω/2 and scale d_ω/2. In all results presented here we used c_ω = 0.001, d_ω = 1, which results in a diffuse prior distribution.

The lower and upper bounds on the mean log migration rate μ are chosen so that on the original scale the mean migration rate varies in the range [1/300,300]. The bounds are somewhat arbitrary, and chosen to reflect values that might be considered “very small” (approaching the limit of discrete demes evolving independently) and “very large” (approaching a panmictic population). The cell effects e₁,…,e_C are constrained to lie in the range [−2,+2], so that the migration rate of a cell can vary within a factor of 100 from the mean migration rate.

Other priors

If there are more genotyped markers than sampled individuals, we can estimate the degrees of freedom k. The prior on k is uniform on the log₁₀ scale, to reflect our uncertainty about the order of magnitude of this parameter: π(k) ∝ 1/k. The prior is proper because k is bounded: n≤k≤p where n is the number of samples and p is the number of SNPs.

For the Wishart scale parameter, σ² ~ Inv-G(c_σ/2, d_σ/2). In all results presented here we used c_σ = 0.001, d_σ = 1, which results in a diffuse prior distribution.

General comments on prior selection

For all priors, we attempted to select hyperparameters that are suitable for “general application”. Where we use cut-offs, they were chosen generously to allow a wide range of values. For example, the bounds on the migration parameters e₁,…,e_C allow them to vary by a factor of 10,000 and we do not envisage many situations would require a wider range. Our choice for the hyperparameters c,d on the scale parameters σ²,ω² corresponds to a very diffuse prior distribution for both scales, which essentially allows them to take any value dictated by the data. We emphasize that we used exactly the same parameter settings for all examples shown. The variety of estimated effective surfaces suggests that our priors are sufficiently flexible to be appropriate in a wide range of problems.

Markov Chain Monte Carlo estimation

EEMS uses Markov Chain Monte Carlo (MCMC) to estimate the migration and diversity parameters, by sampling from their posterior distribution given the observed genetic dissimilarities. The two Voronoi tessellations (one describes the spatial structure in the migration rates m, the other in the diversity rates q) are independent of each other and are updated with a birth/death move because the number of Voronoi cells is unknown. (The proposal either adds a new cell, or - if there are at least two cells - removes an existing one.) The location and rate parameters of a randomly chosen cell are updated with a random-walk Metropolis-Hastings step. (Each cell in the migration Voronoi has an effective migration rate; each cell in the diversity Voronoi has an effective diversity rate.) The Supplementary Note provides further details on computational methods.

Computational time

The computational cost of EEMS is cubic in the size of the population grid and the current implementation does not scale well beyond 1,000 demes. We typically run the MCMC sampler for at least 8 million iterations, which takes about 15 hours of actual CPU time for a grid with 500 demes. For assessing convergence, it is important to simulate several realizations of the Markov chain, i.e., start EEMS several times with a different random seed. The software allows restarting the MCMC sampler if the diagnostic posterior trace plot indicates the chain has not converged in the specified number of iterations. For the analyses presented here, we used grids that range from 120 to 520 demes and we averaged results across at least 8 independent realizations.

Color scheme

Since the primary output of EEMS is a visual summary of spatial patterns, we have paid attention to the details of this display. We selected a color scheme that is colorblind friendly ⁵⁷ and that “balances” high versus low migration. (For example, the colors attempt to give similar visual prominence to regions with effective migration that is 10 times higher and 10 times lower than the average.) We chose the scale so that small differences in effective migration rates – say, less than a factor of two – tend not to be emphasized. These choices might be improved upon with further experimentation, and indeed, some color schemes or scales may work better for some datasets than others. However, we caution against using a scale that is too narrow, which risks over-emphasizing trivial differences in estimated effective migration surfaces.

Empirical datasets

We illustrated EEMS with four diverse empirical examples: an African elephant dataset with strong differentiation between two geographically divided subspecies; two human datasets with individuals sampled across Europe and Sub-Saharan Africa where genetic differentiation varies (somewhat) continuously with latitude and longitude; and an A. thaliana dataset with genetic variation characterized by strong genetic similarity between Europe, where the plant is native, and North America, which it colonized in the last three hundred years. Details about each dataset and how it can be accessed are provided in the Supplementary Note.