Reaction time in ankle movements: a diffusion model analysis

Abstract

Reaction time (RT) is one of the most commonly used measures of neurological function and dysfunction. Despite the extensive studies on it, no study has ever examined the RT in the ankle. Twenty-two subjects were recruited to perform simple, 2- and 4-choice RT tasks by visually guiding a cursor inside a rectangular target with their ankle. RT did not change with spatial accuracy constraints imposed by different target widths in the direction of the movement. RT increased as a linear function of potential target stimuli, as would be predicted by Hick–Hyman law. Although the slopes of the regressions were similar, the intercept in dorsal–plantar (DP) direction was significantly smaller than the intercept in inversion–eversion (IE) direction. To explain this difference, we used a hierarchical Bayesian estimation of the Ratcliff's (Psychol Rev 85:59, 1978) diffusion model parameters and divided processing time into cognitive components. The model gave a good account of RTs, their distribution and accuracy values, and hence provided a testimony that the non-decision processing time (overlap of posterior distributions between DP and IE < 0.045), the boundary separation (overlap of the posterior distributions < 0.1) and the evidence accumulation rate (overlap of the posterior distributions < 0.01) components of the RT accounted for the intercept difference between DP and IE. The model also proposed that there was no systematic change in non-decision processing time or drift rate when spatial accuracy constraints were altered. The results were in agreement with the memory drum hypothesis and could be further justified neurophysiologically by the larger innervation of the muscles controlling DP movements. This study might contribute to assessing deficits in sensorimotor control of the ankle and enlighten a possible target for correction in the framework of our on-going effort to develop robotic therapeutic interventions to the ankle of children with cerebral palsy.

Introduction

The connection between reaction time (RT) measurements and the undergoing neurophysiological processes has been known since 1868 (Donders 1969) and formulated to a robust model by Hick and Hyman (Hick 1952; Hyman 1953). According to the Hick–Hyman law, there is a positive linear relationship between the response latency, T, and the stimulus information. Using the measure of information entropy (Shannon and Weaver 1949), the average T can be approximated by

$$T=a+b\sum _i^n{p}_i{\log }_2\left(\frac{1}{p_i}+1\right),$$

where p_i refers to the probability of the ith stimulus–response (S–R) alternative, n is the number of S–R alternatives and a, b are empirically determined constants. For n = 0, there is one S–R and subjects execute a simple RT experiment; for n ≥ 1, there are n S–R alternatives and subjects execute a choice RT experiment. Simple RT in healthy subjects averages 220 ms (Laming 1968) and a typical average choice RT increases by 100 ms per doubling of the S–R alternatives (Boff et al. 1994). As the time for motor preparation and response is the same across simple and choice RT experiments (Miller and Low 2001), the differences in RT are attributed to processing time.

RT is a well-studied behavioral indicator of neurological integrity. Significant delays in RT measures have been found in basal ganglia disorders, such as Parkinson's disease (PD) (Evarts et al. 1981; Goodrich et al. 1989; Brown et al. 1993) and Huntington's disease (Jahanshahi et al. 1993), and are commonly related to a deficit in motor planning (Marsden 1982; Rogers and Chan 1988). RT deficits have also been used to assess the level of cognitive diseases, such as Alzheimer's disease (Gorus et al. 2008; Martelli et al. 2012) and mild cognitive impairment (Fernaeus et al. 2013) in adults as well as cerebral palsy (CP) (Horgan 1980; Chang et al. 2005), autism (Schmitz et al. 2007), attention deficit hyperactivity disorder (Zahn et al. 1991; Leth-Steensen et al. 2000) and dyslexia (King et al. 2008) in children. A recent shift of interest from RT slowing to intra-individual RT variability over the trials of a given task has also linked RT to structural and functional brain characteristics, such as white matter degradation (Fjell et al. 2011; Tamnes et al. 2012), disconnectivity in associate pathways (Moy et al. 2011), impaired top-down executive and attentional control processes (Anstey et al. 2007), cognitive disorder, neurotransmitter dysfunction, fatigue, and stress (MacDonald et al. 2009). Interestingly, impaired RTs appear responsive to intervention. RT has been used to quantify restoration of motor functions according to given cognitive contexts in PD patients treated with deep brain stimulation (Mirabella et al. 2013). In addition, exercise and practice improve simple and choice RT in both young and older adults (Rikli and Edwards 1991; Light et al. 1996; Baird et al. 2007; Bisson et al. 2007). RT has been studied extensively in the past but never before in the ankle.

We became interested in the ankle because of its crucial role in human walking (Roy et al. 2009), the fact that lower-extremity movements, being older phylogenetically, are not necessarily controlled in the same fashion as the upper extremity movements and the potential of ankle RT to be used as an assessment tool in sensorimotor therapy of the lower limbs. Twenty years after the early studies for neurorehabilitation with the MIT-Manus (Krebs et al. 1998), we are focusing our research on what constitutes an ideal therapy intervention and on how to tailor therapy to a particular patient's needs (Krebs and Hogan 2012), including children with CP (Fasoli et al. 2012). We had introduced and tested extensively the concept of an adaptive assist-as-needed controller for upper extremities (Krebs et al. 2003). We are now extending the concept of performance-based progressive robotic therapy to meet the needs and special characteristics of the lower extremities in children with CP (Michmizos and Krebs 2012a, 2014a). Briefly, our algorithm identifies the ability of the youngster to move and point with the ankle in visually-guided, visually-evoked games (Michmizos and Krebs 2012b), and then independently adjusts the speed of the gameplay and the size of the target (Michmizos and Krebs 2012a). Our developed games, inspired by the motor learning principles, have embedded into their design ankle movements for simple and choice RT up to 4 S–R (2 bits) (see Figs. 2–5, Michmizos and Krebs 2012b). RT shows a great potential to be integrated into our adaptive assist-as-needed robotic therapy delivered to both the upper and lower limbs of CP children (Krebs et al. 2003, 2011). Establishing a speed-accuracy tradeoff in human ankle movement could be coupled with the metrics anticipated to quantify separately the ability to move fast and accurately. This would allow us to (a) assess the level of motor-related impairment in CP, and (b) provide targeted therapy driven by one's inability to move quickly or accurately.

Fig. 2.

Subject performing the experiment. Irrelevant background has been removed

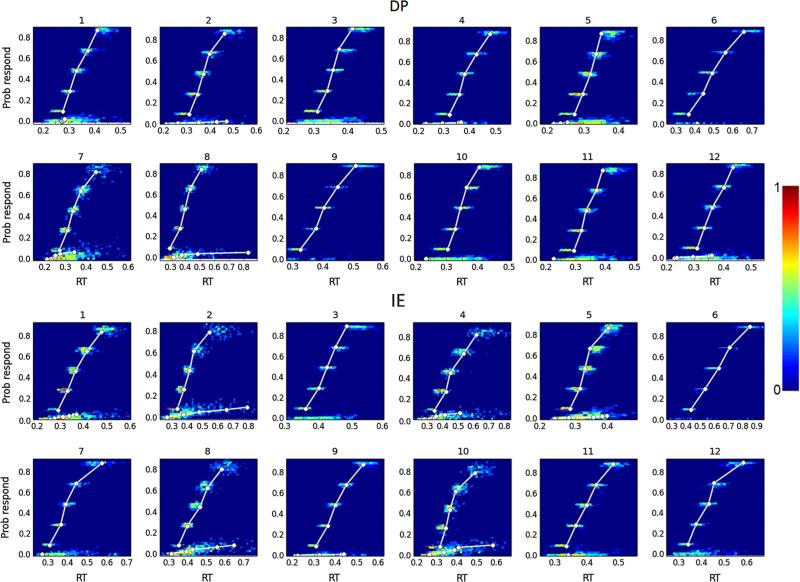
Fig. 5.

Posterior predictive quintiles for the best-fit {a, v, T_er} model to the data from Experiment 1. The fits to the RT for DP (upper part) and IE (lower part) ankle movements are shown for the 12 subjects. Predicted quintile locations are shown as probability densities. The white lines connect the empirically estimated quintiles (white circles)

The ankle is composed of a series of joints that are highly integrated, the most important of which are the talocrural joint (upper ankle joint), which articulates along a single axis and permits raising or lowering the foot (dorsal–plantar flexion—DP) and the subtalar joint (lower ankle joint), which permits inversion and eversion (IE), the turning of the ankle and foot toward and away from the midline, respectively (Moore et al. 2010). Herein, we describe a combination of experimental data analysis with diffusion modeling of ankle RT, which revealed interesting similarities and important differences on controlling the different ankle joints. Specifically, the goals of the present study were four. The first was to test whether Hick–Hyman law applied to ankle movements. The second goal was to determine whether the slope and intercept of the Hick-Hyman law changed systematically between DP and IE. The third goal was to determine whether RT changed with spatial accuracy constraints, i.e., visually-guided ankle movements toward targets with different widths. This question is important as behavioral studies in the upper limbs suggest that spatially precise movements restrict control to the contralateral hemisphere in unilateral and bilateral movements (Garry and Franks 2000, 2002). These findings are reinforced by neural studies indicating that there are cortical cells responsible for controlling movement precision and that the involvement of these cells is based on a selective mechanism dependent on task requirements (Schieppati et al. 1996). The fourth goal was to explain any systematic relationship found in RT between DP and IE movements by fitting a structure model to the experimental data and using it to inform possible neurophysiological explanations.

The diffusion model

The diffusion model (Ratcliff 1978) is a sequential sampling model of the cognitive processes involved in simple (single stage) and fast (average RT < 1.5 s) 2-choice decisions. For a thorough review see (Ratcliff and McKoon 2008) and for the mathematical details of the model, see (Ratcliff and Tuerlinckx 2002). Briefly, each choice is represented as an upper and lower boundary. A drift-process accumulates evidence over time until it reaches one of the two boundaries and starts the corresponding response (Fig. 1). The speed with which the accumulation process approaches one of the two boundaries is called drift-rate, v. Because there is noise in the drift process, the time of the boundary crossing and the selected response will vary between trials. The distance between the two boundaries (i.e., threshold a) influences how much evidence must be accumulated until a response is executed. The model divides the decision process into three primary processing components: the non-decision time that typically includes stimulus encoding, memory access (in memory tasks), retrieval cue assembly and response execution (T_er); the criteria used to make a decision (0 and a, starting at z); the quality of information extracted from stimuli (the drift rate, v); and estimates of the trial-to-trial variability in these components. The variability parameters model participants’ inability to set parameters at identical values from trial to trial: s_t is the range in T_er, s_z is the range of the starting point, and η is the standard deviation in the mean drift rate. These model components produce traditional measures of processing speed, as well as predictions for accuracy and RT distributions for correct and error responses.

Fig. 1.

A typical illustration of the diffusion model. Two simulated paths with drift rate v, boundary separation a, and starting point z; η is the SD in drift rate across trials, s_z is the range of the distribution of starting point (z) across trials and s_t is the range of the distribution of non-decision times across trials. The duration of T_er determines the non-decision component of the RT and includes the time needed for stimulus encoding, response execution, etc. The decision process starts at z and terminates when one of the two boundaries is reached. The sample paths represent moment-by-moment fluctuations in the evidence favoring two possible responses, which is due to noise in the decision process

The Ratcliff diffusion model (RDM) has been successfully used to interpret RT results in both normal and impaired populations of children, adults and the elderly as well as across various modalities including typical computer screen tests, MRI scans and neuroelectrophysiological recordings (Ratcliff 1978; Ratcliff and McKoon 1981; Ratcliff et al. 2004b, 2012; Ditterich 2006; Jepma et al. 2009; White et al. 2010a, b; Mulder et al. 2012; Naples et al. 2012; Merkt et al. 2013). The RDM main parameters, T_er, a, and v, can be related to neurophysiological features affording some insights into the underlying cognitive processes (Voss et al. 2004; Gold and Shadlen 2007). Specifically, T_er characterizes the time to prepare and encode processes preceding the decisional phase plus the time of the actual motor processes. The response boundary, a, is a measure of response caution and can be controlled by the decision-maker; as the distance between decision boundaries gets larger, it takes longer for the decision process to reach a threshold, which decreases the probability of an erroneous response. The drift rate, v, is a measure of the amount of information accumulation (stimulus evidence) per time unit. It depends on the quality of the stimulus and the perceptual system; a larger drift rate means more information can be gathered in a shorter period. Here we applied the RDM to the ankle data to see whether the diffusion model could adequately fit RT measured in the ankle and to find evidence of the neurophysiological processes that could account for the observed discrepancy between DP and IE RT values.

Methods

Subjects

Twenty-two healthy young adults were recruited for this study. Subjects were predominantly Caucasians and were post-doctoral, graduate or undergraduate students at the Massachusetts Institute of Technology (three females). All subjects had normal or corrected-to-normal vision and were right-foot dominant according to their preferential use of the foot during daily activities, such as kicking a ball. Participants had no reported history of traumas or neuropathies to the lower limbs. All subjects were naive to the task upon enrollment and gave written informed consent according to the procedure approved by the Massachusetts Institute of Technology Committee on the Use of Humans as Experimental Subjects. Participants were randomly chosen to populate two experimental groups with 12 and 10 subjects. Average biometric data for Group 1 (Group 2) were 26 ± 4 (25 ± 4) years of age, 1.75 ± 0.07 (1.78 ± 0.09) m in height, 70 ± 10 (74 ± 13) kg in mass (mean ± SD).

Experimental apparatus

The RT was measured for DP and IE ankle pointing movements using a highly back-drivable, wearable Anklebot robot (Interactive Motion Technologies, Watertown, MA). The robot allows the maximum range of motion required for the typical gait of healthy or pathological subjects (Perry 1992; Roy et al. 2009). Subjects wore a modified shoe and a knee brace, to which the robot was connected. Subjects were seated and the knee brace was securely fastened to the chair to fully support the weight of the robot and to ensure that measurements were made in a repeatable posture. The chair was placed 1.5 m away from a 60-inch 1080p (Full HD), 120 Hz, 1,024 × 768 Liquid Crystal TV (Sharp LC60L, Sharp Electronics Corporation) which was positioned at eye level (Fig. 2). For this study, the robot acted as a passive device and recorded simultaneously the DP and IE positions. Ankle position kinematics, with respect to the zero-angle (neutral position, defined below), were recorded at 200 Hz sampling frequency (Roy et al. 2009) and were converted to screen pixels for visualization purposes. Visual feedback was given online to the subjects as a moving circular cursor (d = 23 pixels). A DP (IE) movement of the ankle moved the cursor vertically (horizontally); hence the cursor moved in a 2D coordinate system with the origin corresponding to the ankle's neutral position, defined as the sole being at a right angle to the tibia. Visualization software was written in TCL/TK and run on a PC equipped with Linux Ubuntu operating system.

Stimuli

The main manipulation in both experiments was direction of movement. Stimuli were black rectangles displayed against a white background on the monitor. The coordinates of the target centers were (0, ±s) and (±s, 0) in the coordinate system defined above, for DP and IE directions, respectively. Parameter s remained fixed across targets and corresponded to 0.2 rad (12°) in ankle rotation for both directions, within a comfortable range of motion for the ankle. Targets disappeared only when the cursor representing the ankle pointing movement landed inside the rectangle. The interstimulus interval between target presentations ranged between 800 and 1,200 ms. An outbound target—a target away from the origin—was followed by an inbound target—a target centered in the origin—and vice versa. Outbound targets were equiprobable. In addition, we experimented on the possible effect of stimulus difficulty to RT. The target width, in the direction of the movement, was equiprobably selected between 0.03 (45 pixels) and 0.08 rad (120 pixels), with a step increment of 0.01 rad (15 pixels); rads correspond to ankle rotation.

Experimental protocols

We employed two distinct experimental protocols. Subjects were instructed to point with their ankle “as fast and accurately as possible.” In Experiment 1 (Group 1), there were two blocks, one in DP and the other in IE directions, each having 180 pointing movements toward targets constrained to 1D (90 outbound, 2-choice tasks and 90 inbound, simple choice tasks, per block). The presentation order of the blocks was counterbalanced across participants. Experiment 2 (Group 2) had a single block requiring 360 pointing movements (180 outbound, 4-choice tasks and 180 inbound, simple choice tasks). In both experiments, for each of the six different target widths, 30 targets (15 inbound and 15 outbound) were presented in a random fashion. The overall short duration of the Experiments minimized chances of fatigue (total duration for protocol 12 min). Participants in Group 1 were allowed to take a short rest break (1 min) between the two blocks; Group 2 had no breaks. For each subject, we collected 90 RTs per direction which were smaller than a typical RT task that usually includes 400–800 decisions; yet, we deemed that necessary to minimize muscle fatigue and its effect on the measured RT (Morris 1977; Hanson and Lofthus 1978; Yeung et al. 1999; Moore et al. 2002) and to make a reasonable compromise between high reliability and between-group comparison (Salthouse and Hedden 2002).

Kinematic analysis

We measured the temporal distance between the onset of a stimulus and the start of the ankle movement as defined by a velocity threshold of 5 % of the peak speed (Buchanan et al. 2003, 2006). We also excluded non-discrete movements, i.e., those in which the ankle velocity at the onset of the target was larger than 0.001 rad/s. For each movement, we estimated the angle of the instantaneous velocity vector [approximated by the ankle velocity in the first 15 ms (three samples) of the movement], $a_v={\tan }^{-1}\left(\frac{v_{\mathrm{DP}}}{v_{\mathrm{IE}}}\right)$, where v_DP (v_IE) was the velocity in the DP (IE) direction. Error choices were defined as initial ankle movements away from the target. They were followed by a prominent movement correction, either as a complete stop or an abrupt change in the initial trajectory, identifiable by |a_v| > π/4, assuming a_v = 0 as the optimal response.

Hierarchical Bayesian estimation of the RDM parameters

The parameters of interest in the present study corresponded to drift rate (v), boundary separation (a), and non-decision components (T_er). The other parameters were important during model fitting but did not apply to our main hypotheses. Furthermore, visual inspection showed that none of them varied meaningfully across directions or targets widths. To effectively address the low number of RT measurements per subject, we used the hierarchical drift diffusion model (HDDM; Wiecki et al. 2013) for fitting the RDM to the ankle RT. HDDM is a Python-based toolbox that uses hierarchical Bayesian estimation of the RDM parameters to allow simultaneous estimation of subject and group parameters, where individual subjects are assumed to be drawn from a group distribution. HDDM produces better estimates when less RT values are measured relative to non-hierarchical or non-Bayesian methods (Wiecki et al. 2013). It utilizes the likelihood function optimized for speed (Navarro and Fuss 2009) and has a built-in Bayesian hypothesis testing and several convergence and goodness-of-fit diagnostics that couple with Markov chain Monte Carlo (MCMC; Gamerman and Lopes 2006) simulations used to estimate the joint posterior distribution of the model parameters. Therefore, it provides straightforward measures of uncertainty in the estimated parameters, such as significance testing applied directly on the posterior distribution (Lindley 1965; Kruschke 2010).

HDDM (v.0.5.4) offers a variety of heuristic tests to assess convergence of group and individual subjects’ models. To decide on adequate burn-in samples and thinning, we relied on visual observation of the trace (no drifts or large jumps), its autocorrelation (lower than 0.05 in <40 samples) and the marginal posterior (it should be Gaussian). We further tackled convergence using the Gelman–Rubin test, which ensures that between-chain variance is indistinguishable to within-chain variance, the MC error (it should be <1 % of the posterior standard deviation) and the Geweke statistic, which ensures stability of first order statistics in the beginning and end of a posterior chain.

To compare the models with different numbers of parameters, we combined the deviance information criterion (DIC) and posterior predictive checks (PPC). As a hierarchical modeling generalization of the Akaike and Bayesian Information Criteria, DIC is a flexible goodness-of-fit measure used to assess the performance of competitive Bayesian models by penalizing for the number of parameters in a model (Spiegel-halter et al. 2002). It is defined as $\mathrm{DIC}=D\left(\widehat{\theta }\right)+2p_D$, where $p_D=\stackrel{‒}{D}-D\left(\widehat{\theta }\right)$ is the effective number of parameters, $\widehat{\theta }$ and $\stackrel{‒}{\theta }$ are, respectively, the maximum likelihood estimate and the expectation of θ, the unknown parameters of the model, and D(θ) = −2 log (p(y|θ)) + C, y are the data and p(y|θ) is the likelihood function. Despite its extended use, the DIC is known to be biased toward selecting the model with greater complexity. In addition, although models with smaller DIC should be generally preferred against models with larger DIC values, it is difficult to safely assess what would constitute an important difference in DIC. Therefore, to better support the goodness-of-fit for our models, we employed PPC on subject and group data (Gelman and Hill 2007 and references therein). Briefly, we generated replicates of the datasets using the posterior predictive distributions of the RDM parameters and compared these replicate datasets to our data. If the model adequately describes the data, the predictions based on the model parameters should closely approximate the observed data (Matzke et al. 2013). We assessed model adequacy using the mean squared error (MSE) as a discrepancy statistic. The best-fit model would result in more accurate and less variable estimates than estimations from other models. Therefore, we estimated the MSE for the accuracy as well as the 10th, 50th (mode) and 90th quantiles, for each subject.

We fit eight different models to allow for the exhaustive combination of a, v, and T_er parameters to vary between movement directions. As there was no design bias on the two dimensions, the starting point, z, was equidistant from the response boundaries (z = 0.5). The across-trial range in non-decision time, s_t, and the across-trial variability in starting point, s_z, were estimated for each subject separately. Due to high accuracy tasks, there were too few samples to allow convergence for the across-trial variability in drift rate, η. Therefore, we regarded η to be negligible. We ran 31,500 iterations per model. After discarding 1,500 draws for burn-in, we thinned the remaining output by 2 and stored a final posterior sample of size 15,000. The HDDM convergence diagnostics suggested that these numbers were enough to ensure MCMC convergence. Larger final posterior sample size did not alter considerably the DIC values and did not change the PPC model comparison results. Assuming that outliers came from a different process for which we made no assumptions about its generation, and hence followed a uniform distribution (Ratcliff and Tuerlinckx 2002; Wiecki et al. 2013), we used HDDM to estimate the probability of the contaminants in our data set; the estimated probability was 0.01. In our runs, we assumed the probability for RT outliers as 0.02 as this percentage gave consistently the smallest DIC values, across tested models.

We generated posterior predictive data sets and computed predicted discrepancy measures for all the draws in the final posterior sample. To infer on systematic differences of an RDM parameter across conditions, we did significance testing directly on the posterior probability density plots. Since the posterior of the group distributions was our belief in the parameter group values, we compared the posterior means of the group distributions, given their distribution width that defined a measure of confidence (credibility) in that parameter value. For a given parameter, the statistical significance of its change between movement directions was inferred by the proportion of the overlap in the posteriors of the two conditions (Wiecki et al. 2013).

Results

We present the data analyses in two parts: (a) traditional analysis of mean RTs, and (b) corresponding hierarchical Bayesian estimation of the Ratcliff diffusion model parameters.

Errors

Accuracy values were well above chance across subjects for both Groups. For Experiment 1, the average error rates (μ ± σ) were (3.0 ± 2.5) % for DP and (5.6 ± 4.7) % for IE; they were not found to be significantly different (two-tailed t test, t(11) = 2.7, p > 0.16). For Experiment 2, the average error rate was (1.7 ± 2.1) % for DP and (4.5 ± 2.8) % for IE; interestingly, these error percentages were found to be significantly different (two-tailed t test, t(9) = −2.1, p < 0.002). The first order statistics of the error rates were small enough (e.g., a 3–5 % error corresponded to 3–4 discrete movements toward a false direction) to exclude error RTs from the subsequent (traditional) analysis. This is important as Hick's law is predicated on small and approximately equal error rates across different response set sizes.

Effect of ankle movement direction on average reaction time

We examined RT and accuracy for correct “left” (“down”) and “right” (“up”) targets and found that, for both directions, they did not differ from each other systematically (two-tailed t test on each subject from both Experiments, p > 0.8). In addition, the probability of responding correctly to large targets was about the same as the probability of responding correctly to small ones. This allowed us to collapse “left” and “right” as well as “up” and “down” conditions for estimating average RTs and fitting the models.

Effect of stimulus spatial constraint on average reaction time

The end-movement accuracy constraint was not found to affect processing time as depicted by the mean RT for the tested range of the six different target widths. For each subject, we did a one-way between-targets ANOVA with target width as the independent variable and RT as the dependent variable. No significant effect of spatial constraints was found in any of the subjects from Experiment 1 (F < {1.22; 1.06}), (p > {0.32; 0.38}) and Experiment 2 (F < {1.51; 1.39}), (p > {0.26; 0.24}) for {DP; IE} movements, respectively. Taken together, these results allowed us to collapse the 6 target accuracy constraints to a single case in each experiment.

Hick–Hyman law application to ankle movements

Latency data from both Experiments were combined to produce Fig. 3. RTs for 0-bit did not differ significantly between the two groups (two-tailed t tests for DP and IE movements, p > 0.85); hence, 1-choice data from all 22 subjects were included to estimate the average RT for 0-bit. The median RT, averaged across subjects, is shown as a linear function of information bits for DP and IE movements (Fig. 3, top). The relationship also held for most of the quantiles in the empirical distributions of RT (Fig. 3, bottom); curves are vincentized in 20 bins across subjects (0-bits: Group 1 and Group 2, 1-bit: Group 1, 2-bits: Group 2). Although here we present the results for vincentized data, it seems important to note that Hick–Hyman law was found to be very consistent across all individual participants, except one (Subject 6) with an unusually large RT on both DP and IE (median = 550 ms). Hence, not only the number of S–R alternatives affected the average RT but the effect was different for the two ankle movement directions. That difference between DP and IE movements indicates that the same stimuli influence differently motor processes in the two joints of the ankle. We now seek to specify the nature of this influence and whether it is associated with one or more of the components of the decision process.

Fig. 3.

(up) Average RT for all subjects in Experiment 1 and Experiment 2, as a function of bits of information, for DP and IE ankle movements. Error bars correspond to standard errors; (bottom) cumulative distribution function (CDF) of the vincentized (20 bins) RT across subjects, for DP (left) and IE (right) ankle movement. 0 bits RTs have combined data from Experiment 1 to Experiment 2

Hierarchical Bayesian diffusion model analysis of ankle RT

We first removed short (<0.2 s) and long (>1 s) RTs [<2 % of responses, which is consistent with (Ratcliff and McKoon 2008)]. To assess which parameters were affected by ankle movement direction, we analyzed the impact on the pointing movement direction on the estimates of the a, v and T_er parameters under the assumption that the direction of the target (i.e., up vs. down and left vs. right) had no effect on the recorded RT.

Effect of spatial accuracy constraints of aimed ankle movements on drift rate and non-decision time

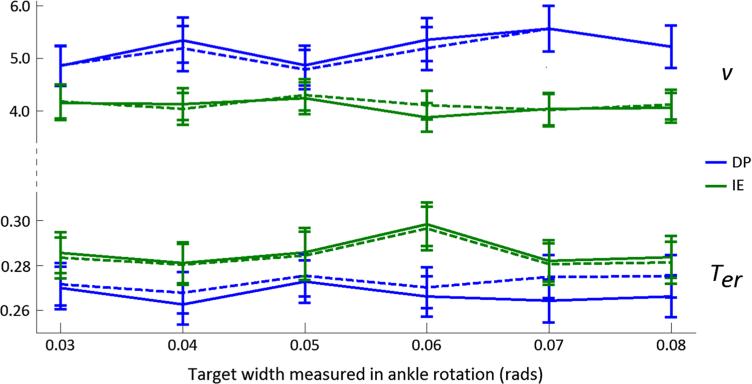
We modeled changes in performance across stimulus conditions (task difficulty) by allowing v and T_er to vary separately and in combination across the six different target widths. The drift rate, v, is typically assumed to change with stimulus (Ratcliff et al. 2004a, 2010; Jepma et al. 2009). We also allowed T_er to vary, to examine any differences in non-decision processes, such as motor planning. The three models captured adequately changes in RT distributions and accuracy values as the posterior predictive distribution for the 10th, 50th, and 90th quantiles and accuracy had MSE that were lower than 10⁻³, across subjects (comparable with Table 1 MSE values). Drift rates and non-response times for the six different target widths did not vary in a systematic way (Fig. 4). Hence, for the following analysis of the ankle movement direction, we assumed a common drift rate and non-response time across targets of different width.

Table 1.

DIC and PPC for the eight models in Experiment 1

Model constraints	DIC (pD)	Median MSE (×10–6)
		Accuracy		10th quantile		50th quantile		90th quantile
		DP	IE	DP	IE	DP	IE	DP	IE
{a, v, Ter}	–4,551 (58)	314	503	195	229	81	140	168	603
{a, v}	–4,508 (60)	574	530	130	280	85	197	189	868
{a, Ter}	–4,495 (45)	425	612	518	151	96	153	356	630
{v, Ter}	–4,533 (48)	541	560	158	304	112	188	213	672
{a}	–4,455 (48)	541	524	330	167	92	166	339	899
{v}	–4,479 (51)	562	560	90	734	95	291	208	857
{t}	–4,453 (47)	353	575	630	200	112	165	640	824
{none}	–4,241 (35)	425	598	517	2,964	306	2,819	556	5,065

PPC estimated the median MSE of the accuracy and the 10th, 50th and 90th quantiles, across subjects. The best (lowest) numbers are shown in bold

Fig. 4.

Effect of target width on group drift rate and non-response time, for DP and IE ankle movements, as simulated by {v} (solid lines, upper panel), {T_er} (solid lines, lower panel) and {v, T_er} (dotted lines, both panels) RD models, using the data from Experiment 1. Error bars correspond to the SD of the posterior distributions

Effect of ankle movement direction on sensorimotor processes

We estimated the DIC and the PPC for each of the eight candidate hierarchical Bayesian model fits to data from Experiment 1. Table 1 presents results for the group models.¹ Since we were mainly interested in group wide effects, we omit the detailed report of the subject parameters. The {a, v, T_er} model had consistently the best (smallest) DIC value as well as the smallest MSE for the accuracy, the 50th and 90th quantiles. Although other models had smaller MSE for the 10th quantile for DP or IE direction, none of these models were better than the {a, v, T_er} when MSE for DP and IE were considered together. Consequently, we regarded the {a, v, T_er} model as the best-fit model. Visual comparison between the subject-specific posterior predictive densities of the quintiles and the empirically estimated quintiles for DP and IE directions confirmed the adequate model fit (Fig. 5). The model captured individual variations in RT as a function of ankle movement direction for both correct and erroneous responses and also succeeded in accounting for accuracy (Table 1). In some subjects, the model was also successful with error RT, but it rarely addressed the shapes of error RT distributions, possibly due to their low number. Therefore, the parameter values are very likely to represent the behavior of the components of processing in the simulated experiment.

To examine systematic differences between the two ankle directions, we plotted their group posteriors on a single plot and estimated the overlap of the posteriors. Figure 6 shows the estimated distribution of the posteriors as a function of condition. Mean (SD) values of the group variability posteriors were s_t = 0.135 (0.010) and s_z = 0.561 (0.082). We computed the proportion of the posteriors in which a parameter of interest for one condition was greater than the other: Compared to DP, the posterior distributions of v and T_er were significantly different in IE (overlap of posterior probabilities <{0.01, 0.045}, respectively) whereas the posteriors of a had a clear (but not significant) trend of increasing in IE (overlap of posterior probabilities < 0.1). The between-conditions differences in the mean posteriors in v, and T_er were also significant across individual subjects; the mean posterior of a for IE increased significantly in 8 out of 12 subjects.

Fig. 6.

Posteriors of the boundary, a, (left), drift rate, v, (middle) and non-decision time, T_er, (right) for DP (blue) and IE (green) ankle RT for the best-fit {a, v, T_er} group model to the data from Experiment 1 (color figure online)

To check the robustness of our proposed best-fit model, we examined if results would change when we changed data. Under the general assumption that models are hardly ever true but some of them fit the data well and, hence, allow for useful inference, we used the data from Experiment 2 by collapsing the data across all DP and all IE outbound movements. Interestingly, we found the same trends in a, v and T_er as the mean (SD) of the posterior distributions changed from 1.093 (0.075) to 1.145 (0.061) (overlap of posterior probabilities < 0.24), from 5.874 (0.356) to 5.001 (0.296) (overlap of posterior probabilities < 0.006) and from 0.303 (0.005) to 0.321 (0.004) (overlap of posterior probabilities < 0.0004), respectively. Mean (SD) values of the group variability posteriors were s_t = 0.140 (0.007) and s_z = 0.685 (0.053).

Discussion

In this article, we explored perceptual decision making in a multiple-alternative experimental paradigm in which subjects used their ankle to respond to simple RT tasks and equiprobable on-screen presentation of targets. Our first goal was to test whether Hick–Hyman law holds on ankle RT measurements. The Hick–Hyman law was found to apply to the ankle as average RTs for both DP and IE movements increased linearly with up to 2 bits of information. Our second goal was to test whether the slope and intercept of the Hick–Hyman law changed systematically between DP and IE. While having very similar slopes, the two regression lines revealed a significant decrease of the average RT for DP compared to that for IE movements; the decrease was constant across the tested bits of information. Our third aim was to examine the differences, if any, imposed by the spatial constraints at the end of each movement. Based on our modeling analysis, we found no evidence of a significant change in the tested cognitive components of the RT. Our fourth aim was to apply the RDM to ankle data and test whether it could successfully simulate the 2-alternative forced choice tasks from Experiment 1. We examined a range of architectural features that the RDM could take and tried to determine which would best fit our data. Among the tested models, the {a, T_er, v} model consistently accounted for the data with the best (lowest) DIC value and the lowest MSE for the accuracy and posterior predictive quantiles. Model parameter estimates were then interpreted as meaningful components of cognitive processing to explain the intercept differences found in the regressions between DP and IE.

Our analyses were confined by constraints in experimental conditions. We manipulated the stimulus difficulty with target width to align with the speed-accuracy tradeoff being at the core of our adaptive rehabilitation approach (Michmizos and Krebs 2012a). Our analysis demonstrated that the target width did not have a substantial effect on the decision process as depicted by the rate of evidence accumulation and non-decision time. An important limitation of our study was that no tests were done for more than 2 bits. This might affect the generalization of our findings as the absence of a relationship between S–R alternatives and RT have been reported (Teichner and Krebs 1974; Longstreth et al. 1985) including ones that involve visual targets (Heywood and Churcher 1980; Kveraga et al. 2002). However, in most of these studies, the law starts to break from as low as 1 bit (Kveraga et al. 2002). Therefore, the [0, 2] bits range of testing seems to be adequate to support our hypothesis and, at the same time, be incorporated into our rehabilitation games (Michmizos and Krebs 2012b) since a maximum of four choices is empirically found to keep the gaming environment balanced between being simple and engaging. By lowering the trial numbers, we also compromised the accuracy of our model estimation. To ensure the accurate estimation of RDM parameter values, a common methodology is to use large trial numbers (N ≥ 400). Yet, such long testing of the ankle movement might induce fatigue and modify RT (Morris 1977; Hanson and Lofthus 1978; Dutilh et al. 2011). The N = 360 inbound and outbound repetitions (completed in 12= min) per subject were empirically chosen so that fatigue, either central or peripheral, could not affect outcomes. It is worth noticing that RDM has been applied successfully to experiments with as low as N = 72 trials per subject (Klauer et al. 2007) and that HDDM has been tested successfully for convergence with <100 trials per condition (Wiecki et al. 2013). Finally, although not completely justified, our modeling approach of Experiment 2 data confirmed a consistent change in the a, v and T_er parameters between the two ankle movements, at least for our two experimental paradigms. Nonetheless, to infer on the generalization of our conclusions beyond a 2-choice task, one should employ modeling approaches that are designed to simulate more than two S–R and their underlying decision processes (e.g., Leite and Ratcliff 2010; Van Maanen et al. 2012).

Possible neurophysiological explanations for RT differences between DP and IE movements

The RDM analysis suggested that multiple components of the decision process were responsible for the significant speed-up in RT for DP movements (Fig. 3). In our experiments, participants first encoded the visual stimulus, then used encoded information to make a decision, and finally moved their ankle toward the target using visual feedback. The shortening of the non-decision component, T_er, in DP direction (Fig. 6), indicated that stimulus encoding, response preparation and/or motor execution were speeded in that direction (Luce 1986). A previous application of the RDM revealed that increasing the number of alternatives imposes a “psychological” burden to the subjects that affects the preparation time to respond (Leite and Ratcliff 2010). Although this burden could have been present in our experiment when moving the ankle in the “easier” DP direction, compared to the “harder” IE direction, our subjects had an a priori knowledge of the subsequent ankle direction in Experiment-1. Therefore, our findings seem to be more consistent with the “memory drum” theory: more difficult (complex) responses require more stored information, and hence take longer (Henry and Rogers 1960; Klapp 2010). T_er decease in DP might also have a further neurophysiological explanation. Tibialis anterior (a main muscle for DP movement) normally has stronger or more direct cortical projections than the small muscles of the foot that control IE movements (Brouwer and Ashby 1992). The tight coupling between neurons in motor cortex and the spinal motor neurons, attributed to projections of the fast corticospinal pathway with monosynaptic projections to motoneurons, might have contributed to the decrease in motor execution time for DP movements, compared to IE. Additionally, in relation to a common interpretation of the boundary parameter, a, as a measure of cautiousness in stimulus processing (Ratcliff et al. 2001, 2004b; Ratcliff and Van Dongen 2009), we found that a was considerably smaller in DP (although no instruction emphasized speed) than in IE (although no instruction emphasized accuracy). Slow RT might represent a general tendency of being more careful and monitoring responses more thoroughly, a characteristic commonly found in the elderly (Botwinick 1966; Welford 1968). Comparing the RDM results from both experiments, we found that the difference in a between movement directions was less prominent in Experiment 2. In addition to the possible inadequacy of the RDM application on a 4-choice task, another explanation might exist. The interweaving of DP and IE ankle movements in Experiment-2 might have affected the two response strategies and, hence, their boundary separations. This is consistent with a recent study on the neural mechanisms of response caution modulation that revealed an area in arterior cingulate cortex that is involved in fast switching between response caution regimes (van Maanen et al. 2011).

One must take our results with the appropriate caveats as the RDM critical assumptions can be disputed. For example, studies have questioned the model's working hypothesis that information processing is comprised of a sequence of discrete non-overlapping stages (Spencer and Coles 1999). Nevertheless, all fitted models were capable of reproducing correct RT distributions well, although missing some of the error RT distributions, especially in high accuracy tasks (correct percentage >0.95). Fortuitously, the RDM parameters that were free across conditions varied consistently across the tested models. For example, the drift rate, v, was found to decrease significantly from DP to IE movements for the {v}, {a, v}, {v, T_er} and {a, v, T_er} models. Therefore, simulation results seem to be consistent with each other and with what is known about encoding and motor response sub-processes. Furthermore, there are several theoretic and experimental reasons to assume that the RDM gives an accurate reflection of how the decision process is implemented in the brain. First, the diffusion decision process is optimal in the sense that it gives the fastest responses for a fixed level of accuracy or the highest accuracy for a fixed RT (Wald 2004). Second, recent single-cell studies have begun to provide complementary evidence to the results of behavioral experiments and link RT distribution and accuracy data in the behavioral domain to the dynamics of neuronal activity during decision-making behavior (Ditterich 2006; Gold and Shadlen 2007), including event-related potential (Philiastides et al. 2006) and fMRI measures (Heekeren et al. 2004). Third, T_er and a are determined to a large degree by the position of the 0.1 quintile. Figure 5 shows that the 0.1 quintile is quite well located from the RDM, across subjects. The drift rate determines position along the x-axis of the quintile probability function, not its shape; again, this was well predicted by the model. Fourth, the value of T_er locates only the vertical positions of the quintile probability functions (Fig. 5); it does not influence their shape. Finally, in the analysis by Ratcliff et al. (2004b) of the correlations between model parameters and mean RT, T_er, is found to be correlated only with mean RT. Since the mean RT increases between DP and IE conditions, this is an additional indication that T_er should also increase.

Processing speed is “a fundamental property of the central nervous system” (Madden 2001), and RTs are measures of that speed. The evidence that the direction of stimulus and its probability of occurrence affect the speed of motor processes might have important implications for future studies on the pathophysiology of movement. Since our results show that the RDM could be extended to ankle RT, our model analysis could potentially be extended to a model of motor impairment in the lower limbs to assess, if not predict, the level of response to a therapeutic intervention. For example, studies have shown that practice decreases the intercept and the slope of the relationship between S–R alternatives and RT, indicating that not only do RTs decrease with practice but also that the effect of S–R alternatives decreases with practice (Teichner and Krebs 1974; Heywood and Churcher 1980; Longstreth et al. 1985). As an analogy to the “Brinley function” (Brinley 1965; Luna et al. 2004), we could seek a common metric for measuring relative differences in ankle movements across highly diverse tasks, such as the slope of the linear regression function in which normal subjects’ responses are plotted against impaired subjects’ responses for various ages. Interactions of RT with manipulations that influence motor processes (e.g., increased tonic muscle tension commonly found in CP) could also be interpreted jointly in an effort to quantify motor impairment. Since motor system disorders, such as the ones present in CP, often affect both upper and lower parts of the body, it would be important to evaluate the consistency (or lack of it) of our data analysis and simulation results when we apply our paradigm to hand or wrist movements. A detailed understanding of processing similarities and differences associated with disorders of the sensorimotor system across modalities, could evaluate the response to a therapeutic intervention and potentially lead to better assessment of neurological diseases that originate in the brain but affect the periphery.

Conclusion

This work revealed an interesting similarity and an important difference between DP and IE movements of the ankle joints. The similarity is that the RT measured in both ankle movements increased with the number of stimuli at an equal pace. The difference is that, for the same stimulus difficulty, RT differed significantly when the ankle movement was controlled by the subtalar rather than the talocrular joint. Our analysis using the hierarchical Bayesian diffusion model gave behavioral and neurophysiological insights on the processing components that seem to affect the RT differences measured in DP and IE ankle movements. In terms of ankle sensorimotor rehabilitation, these results suggest that it may be helpful to examine each ankle joint separately or at least to limit the number of potential stimuli displayed at any particular time.