PARMBSC1: A REFINED FORCE-FIELD FOR DNA SIMULATIONS

Abstract

We present parmbsc1, a new force-field for DNA atomistic simulation, which has been parameterized from high-level quantum mechanical data and tested for nearly 100 systems (~140 μs) covering most of the DNA structural space. Parmbsc1 provides high quality results in diverse systems, solving problems of previous force-fields. Parmbsc1 aims to be a reference force-field for the study of DNA in the next decade. Parameters and trajectories are available at http://mmb.irbbarcelona.org/ParmBSC1/.

Force-field development is tightly connected to the extension of simulation time scales. As molecular dynamics (MD) trajectories are extended, errors previously undetected in short simulations emerge, creating the need to improve the force-fields¹. For example, AMBER parm94-99 was the most used force-field in DNA simulations until multi-nanosecond simulations revealed severe artifacts^2,3, thus fueling the development of parmbsc0^2,4, which, in turn, started to show deviations from experimental data in the μsec regime (for example an underestimation of the twist, deviations in sugar puckering, biases in ε and ζ torsions, excessive terminal fraying^2,5, and severe problems in representing certain non-canonical DNAs^1,6). Various modifications have been proposed to address these problems, such as the OL-ones^5,6 designed to reproduce specific forms of DNA. While these and other tailor-made modifications are useful, there is an urgent need for a new general-purpose AMBER force-field for DNA simulations to complement recent advances in the CHARMM family of force-fields (Online Methods). The parmbsc1 force-field presented here is designed to solve these needs, and aims to become a widely-used general-purpose (see simulated systems in Supplementary Table 1) force-field for DNA simulations.

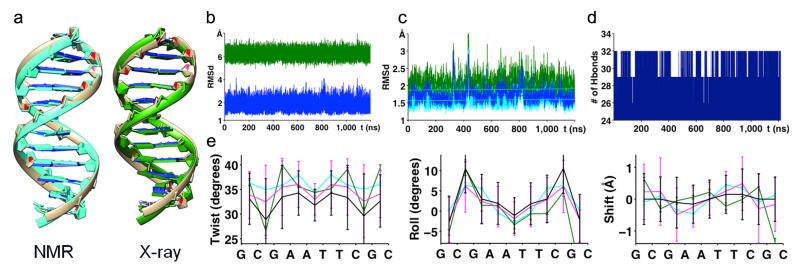
As described in the Online Methods, parmbsc1 showed a great ability to fit QM data, improving parmbsc0 results. The QM-derived parameters were first tested on the Drew-Dickerson dodecamer (DDD), the most studied DNA structure^2,7, typically used as benchmark in force-field developments. The trajectories sampled a stable B-type duplex that remained close to the experimental structures (Fig. 1 and Supplementary Table 2), preserving hydrogen bonds and helical characteristics, even at the terminal base pairs, where fraying artifacts are common using other force-fields^2,8 (see Online Methods, Supplementary Table 2 for a comparison of parmbsc1 with other force-fields, and the Supplementary Discussion on fraying based on experimental and theoretical results). The average sequence-dependent helical parameters (Fig. 1 and Supplementary Figs. 1 and 2), and BI/BII conformational preferences (Supplementary Table 2 and Supplementary Fig. 3) matched experimental values (for the comparisons with estimates obtained with other force-fields see Supplementary Notes). Furthermore, parmbsc1 reproduced residual dipolar couplings (Q-factor = 0.3) and NOEs (only two violations), giving success metrics similar to those obtained in the NMR-refined structures (Supplementary Table 3).

Figure 1. Analysis of the Drew-Dickerson dodecamer.

(a) Visual comparison of MD average structure (brown) and NMR structure (PDB id: 1NAJ) (light blue) and X-ray structure (PDB id: 1BNA) (green). (b) RMSd of 1.2 μs trajectory of DDD compared with BDNA (blue) and A-DNA (green) form (coming from Fiber). (c) RMSd compared to experimental structures (with (dark) and without (light) ending base-pairs): X-ray (green) and NMR (blue). Linear fits of all RMSd curves are plotted on top. (d) Evolution of total number of hydrogen bonds formed between base pairs in the whole duplex. (e) Helical rotational parameters (twist, roll, and tilt) comparison of average values per base-pair step (standard deviations are shown by error bars) coming from NMR (cyan), X-ray (dark green), 1 μs parmbsc0 trajectory⁷ (black) and 1.2 μs parmbsc1 trajectory (violet).

We evaluated the ability of parmbsc1 to represent sequence-dependent structural features from simulations on 28 B-DNA duplexes (Supplementary Table 4). The agreement between simulation and experiment was excellent (RMSd/base pair of 0.1 or 0.2 Å). Almost no artifacts arising from terminal fraying were present, and the average helical parameters (twist and roll from simulations: 33.9 ° and 2.5 ° respectively), matched values from the analysis of the PDB (33.6 ° and 2.9 °)⁹. Moreover, parmbsc1 was able to reproduce the unique properties of A-tracts¹⁰ (Supplementary Figs. 4–6), and capture sequence-dependent structural variability (Supplementary Fig. 7). We also studied longer duplexes (up to 56 bp) to ensure that a possible accumulation of small errors given by the force-field did not compromise the description of the DNA, finding excellent results (Supplementary Table 5). The expected spontaneous curvature was clearly visible in both static and dynamical descriptors, demonstrating that parmbsc1 trajectories were able to capture complex polymeric effects (Supplementary Table 5).

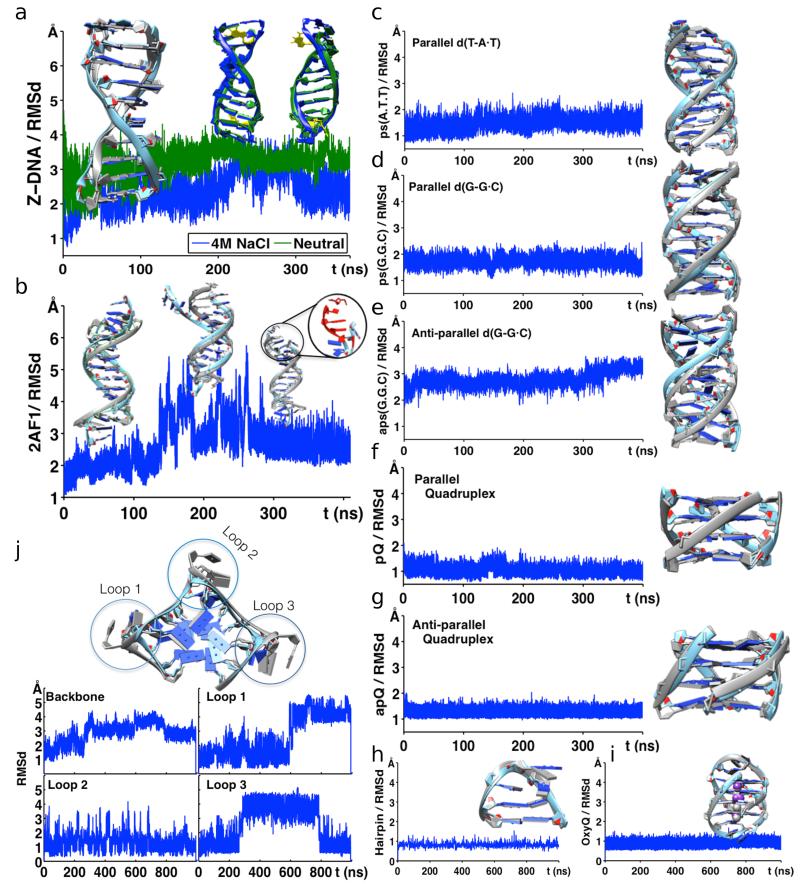
We also explored the ability of parmbsc1 to represent unusual DNAs, such as: a Holliday junction, a complex duplex-quadruplex structure which was fully preserved in μsec-long trajectories (Supplementary Figs. 8 and 9); or the Z-DNA, a levo duplex containing nucleotides in syn, for which parmbsc1 not only provided stable trajectories (Fig. 2a), but also reproduced the experimentally known salt dependence, confirming that the conformation is stable only at high (4 M) salt concentration¹¹. For Hoogsteen-DNA (H-DNA), simulations with parmbsc1 showed a stable duplex for more than 150 ns (Fig. 2b), and severe distortions in longer simulation periods (Supplementary Fig. 10), as expected from its metastable nature¹². Equivalent results were obtained for another metastable structure: the parallel poly-d(AT) DNA (Supplementary Fig. 11)¹³. Parmbsc1 simulations not only reproduced the known structure of parallel d(T-A·T) and d(G-G·C) triplexes (Figs. 2c,d), but also showed correctly that the equivalent antiparallel structures are unstable in normal conditions (Fig. 2e)¹⁴. Finally, parmbsc1 was able to reproduce experimental structures of both parallel and antiparallel DNA quadruplexes with RMSd < 2 Å (Figs. 2f,g).

Figure 2. Analysis of non-canonical DNA structures.

(a) Comparison of Z-DNA (PDB id: 1I0T) simulations in neutralized conditions (green) and in 4 M solution of Na⁺Cl⁻ (blue). Structural comparisons at given time points are shown above the RMSd curves. (b) Simulation of anti-parallel H-DNA (PDB id: 2AF1) showing deviation of the structure over time (highlighted in red). RMSd of (c) parallel d(T-A•T)₁₀, (d) parallel d(G-G•C)₁₀, and (e) antiparallel d(G-G•C)₁₀ triplexes. (f) Parallel (PDB id: 352D) and (g) anti-parallel (PDB id: 156D) quadruplex showing stable structures over time. (h) Structural stability of d(GCGAAGC) hairpin (PDB id: 1PQT) and (i) OxyQ quadruplex (PDB id: 1JRN) with ions, over time. (j) Human Telomeric Quadruplex (PDB id: 1KF1) with highlighted loops. RMSd of HTQ backbone, loop 1, loop 2 and loop 3 regions are shown below. In all panels, parmbsc1 (final, averaged or at a given trajectory point) structures (light blue; also green for Z-DNA) are overlapped over experimental structure (grey) for comparison. See Supplementary Table 1 for information on the PDB structures.

We explored also the ability of parmbsc1 to reproduce the complex conformation of hairpins and loops, exceptionally challenging structures for force-fields¹⁵. We performed μs simulations of the d(GCGAAGC) hairpin (PDB: 1PQT), the 4T-tetraloop in Oxytricha nova quadruplex d(G₄T₄G₄)₂ (OxyQ; PDB: 1JRN), and the junction loops in the human telomeric quadruplex (HTQ; PDB: 1KF1). Parmbsc1 provided excellent representations (RMSd around 1 Å) of the d(GCGAAGC) hairpin (Fig. 2h), and of the OxyQ quadruplex (Fig. 2i). For the very challenging HTQ structure, parmbsc1 maintained the stem structure 20 times longer than in previous simulations¹⁵, and recognized the large flexibility of the loops in the absence of the lattice-contacts (Supplementary Fig. 12), showing that, as predicted¹⁶, not only the crystal, but also other loop conformations were sampled (Fig. 2j).

As an additional critical test of the new force-field we predicted NMR observables from parmbsc1 trajectories (Online Methods). We obtained equivalent NOE violation statistics to those determined from NMR-derived ensembles (Supplementary Tables 6 and 7, and Supplementary Fig. 13). This agreement was maintained in de novo predictions, i.e. in those cases where NMR observables were collected in one of our laboratories after parmbsc1 development (Supplementary Table 8). Finally, it is worth noting that parmbsc1 trajectories reproduced the structure of DNA in crystal environments, giving a RMSd between the simulated and crystal structures of only 0.7 Å, and average twist differences below one degree, improving any previous calculations (Online Methods and Supplementary Figs. 14 and 15).

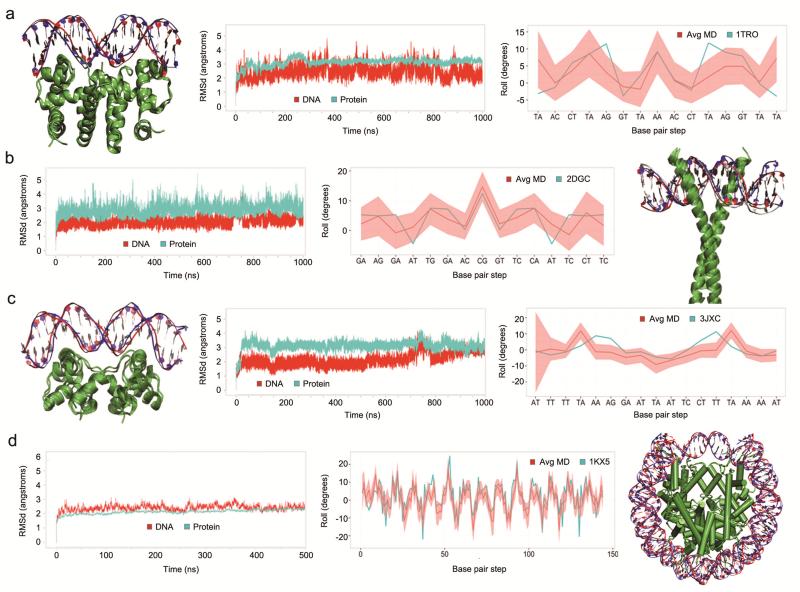
Our final structural test was to explore the ability of parmbsc1 to reproduce the conformation of DNA in complex with other molecules. We studied four diverse protein DNA complexes (PDB: 1TRO, 2DGC, 3JXC and 1KX5), and two prototypical drug DNA complexes. In all cases, we found excellent agreement (RMSd for DNA around 2–3 Å in protein-DNA complexes, and 1–2 Å in drug-DNA complexes) with experiments (Fig. 3 and Supplementary Figs. 16 and 17).

Figure 3. Analysis of DNA-protein complexes.

Structural details of microsecond trajectories of four complexes with PDB id: 1TRO (a), 2DGC (b), 3JXC (c) and 1KX5 (d) (500 ns trajectory). Each plot shows overlap of the MD starting (red) and final (blue) structures, time dependent mass-weighted root mean square deviation (RMSD in Å) of all DNA (red) and protein (cyan) heavy atoms, and comparison of the values of rotational helical parameter roll (in degrees) at each base pair step calculated from the X-ray crystal structure (cyan) and averaged along the MD simulation (red line with the standard deviation envelope in light red). For clarity, in the 1KX5 plot of the roll value, the base pair steps are defined by the number of the position along the DNA strand and not by the base pair step name.

A force-field should not only reproduce the structure of DNA, but also its mechanical properties¹. To evaluate the performance of parmbsc1 we firstly evaluated the μs-scale dynamics of the central 10 base pairs of the DDD. The agreement between parmbsc0 and parmbsc1 normal modes and entropy estimates (Online Methods and Supplementary Table 9) demonstrated that parmbsc1 does not “freeze” the DNA structure, a risk for a force-field reproducing well average properties. This was further confirmed by the ability of parmbsc1 to reproduce the DNA dielectric constant (8.0 ± 0.3 for DDD versus the experimental estimate of 8.5 ± 1.4; see Supplementary Fig. 18), and also the cooperative binding (around 0.7 kcal mol⁻¹) of Hoechst 33258 to DNA. We then computed the helical stiffness matrices for the ten unique base pair steps^17,18. Parmbsc1 values were intermediate between parmbsc0 and CHARMM27 stiffness parameters¹⁸, and substantially smaller than those suggested by Olson and coworkers¹⁷ (Supplementary Table 10 and Supplementary Fig. 19); the dependence of the stiffness parameters on sequence were similar for parmbsc1 and parmbsc0¹⁷.

The persistence length, the torsional, and the stretching modules were obtained from simulations of long (up to 56 bp) duplexes (Online Methods). Parmbsc1 predicted persistence lengths in the range of 40–57 nm (Supplementary Table 11), close to the generally accepted value of 50 nm. The computed static persistence length, stretch and twist torsion modules were around 500 nm, 1,100–1,500 pN, and 50–100 nm respectively, also in agreement with experimental values (Supplementary Table 11). Finally, we explored the ability of parmbsc1 to describe relaxed and stressed DNA minicircles. We performed three 100 ns simulations of a 106-bp minicircle with ten turns (106t10), which should have zero superhelical density (σ = 0) and therefore no denatured regions^19,20 (Supplementary Fig. 20). A kink was observed only in a single replica for one of the register angles, while in the remaining simulations the DNA remained intact (Supplementary Fig. 20). On the contrary, negatively supercoiled 100-bp (100t9; σ = −0.05) and 106-bp (106t9, σ = −0.10) minicircles formed distortions due to the superhelical stress, as previously reported experimentally using enzymes that digest single stranded DNA^19,20.

After demonstrating the ability of parmbsc1 to describe stable and metastable DNA structures and DNA flexibility, we finally studied conformational transitions. Parmbsc1 reproduced the spontaneous A to B transition in water, and the A form was found, as expected, to be stable in 200 ns control simulations in a 85 % ethanol and 15 % water mixture (Supplementary Fig. 21). Parmbsc1 also reproduced the unfolding of DNA d(GGCGGC)₂in a 4 Molar pyridine (Supplementary Fig. 21), and the effective folding of d(GCGAAGC) in water (Supplementary Fig. 22), suggesting the ability to capture long-scale conformational changes in DNA.

Based on the wide series of tests reported here we concluded that parmbsc1 provides good representations of the static and dynamic properties of DNA, and therefore anticipates that parmbsc1 will be a valuable reference force-field for atomistic DNA simulations under a diverse range of conditions.

ONLINE METHODS

Parameterization procedure

All backbone torsion angles, except the recently corrected α and γ⁴, were parameterized using representative model compounds (Supplementary Fig. 23), for which torsional profiles were obtained at the MP2/aug-cc-pVDZ level using B3LYP/6-31++G(d,p)-optimized geometries^21-23. Single-point calculations at crucial points of the conformational space were performed at the CCSD(T)/complete basis set (CBS) level^24-26. Solvent effects were introduced using our MST²⁸ method as implemented in Gaussian (http://www.gaussian.com). See Supplementary Notes for additional details on QM calculations.

Parameters were fitted using a flexible Monte-Carlo procedure⁴, which minimizes the error between QM reference profiles (in solution) and classical potentials of mean force calculations in aqueous solution obtained from umbrella sampling calculations²⁹. By default we used gas phase-fitted values as first guess, and always limited the torsional representation to a three Fourier expansion terms, while reinforcing in the fitting the weight of the points described at the highest level of theory and those geometrical regions that are specially populated in experimental structures. Around 5–10 acceptable solutions of the Monte Carlo refinement were tested on short MD simulations (around 50–100 ns) for one small duplex d(CGATCG)₂ rejecting those leading to distorted structures. The optimum parameter set, without additional refinement was extensively tested against experimental results. Additional details (and references) on the parameterization procedure are given in the Supplementary Notes. Note that the way in which the parameters were derived does not guarantee their validity for RNA simulations. The use of others, already validated, RNA force-fields are recommended.

As shown in the Online Methods Table 1, refined parmbsc1 parameters fit very well high-level QM data. The syn-anti equilibrium, which was non-optimal in parmbsc0, is now well reproduced (Supplementary Fig. 24). The fitting to sugar puckering profile was improved by increasing the East barrier, and by displacing the North and South minima to more realistic regions (Online Methods Table 1 and Supplementary Fig. 25). Additionally, parmbsc1 provides ε and ζ conformational map almost indistinguishable from the CCSD(T)/CBS results in solution (Supplementary Fig. 26), with errors in the estimates of relative BI/BII stability and transition barrier equal to 0.2 and 0.0 kcal mol⁻¹ respectively.

Online Methods Table 1.

Differences between QM and force-field estimates for the parameterized systems. Values refer to calculations performed in water.

Torsion	Adenosine	Guanosine	Cytosine	Thymidine
Glycosidic torsion (χ)
Geometries (°) a
Anti	14 / 40	9 / 40	2.5 / 1	2.5 / 1
Barrier	1.5 / 11	2.5 / 15	13 / 10	11 / 11
Syn	7 / 32	2.5 / 30	12 / 30	−12 / 30
Energies (kcal mol−1) b
Anti/Syn	0.0 / −0.3	−0.4 / −0.6	−1.1 / 1.3	−0.8 / 1.7
Barrier C	0.3 / −2.0	0.0 / −2.1	−0.6 / −0.7	−0.9 / −1.2
Profile	0.3 / 2.5	1.2 / 2.8	0.9 / 4.0	0.9 / 3.9
Phase angle (P)
Geometries (°) a
North	10 / 30	10 / 10	10 / 40	0 / 10
East	0 / 10	0 / 0	10 / 10	0 / 10
South	0 / 0	10 / 10	0 / 0	0 / 0
Energies (kcal mol−1) b
North/South	−0.1 / −1.5	0.0 / −1.0	−0.6 / −1.6	0.5 / −0.5
East Barrier	−0.2 / 0.4	−0.5 /0.7	−0.1 / 1.2	−0.8 / 0.0
Profile	0.4 / 0.6	0.5 / 0.4	0.4/ 0.7	0.2 / 0.5

^aErrors in the position of the minima and transition state when parmbsc1 (first number in the cell) or parmbsc0 (second number in the cell) values are compared with MP2 geometries.

^bErrors in the estimates of the relative stability and transition barrier when parmbs1 (first number in the cell) or parmbsc0 (second number in the cell) values are compared with single-point CCSD(T)/CBS results.

^CEnergy values refer to barrier at χ around 120 degrees, note that the large barrier located at χ around 0 is very well reproduced at the parmbsc1 level, but very poorly at the parmbsc0 one (Supplementary Fig. 24).

Validation MD simulations

We performed an extensive set of simulations of a wide variety of DNA systems (Supplementary Table 1) with a total simulation time of ~140 μs, which represents the most comprehensive analysis of DNA dynamics published to date. MD simulations were performed using AMBER (http://www.ambermd.org) or GROMACS³⁰ (for the impact of using one or the other simulation engine in the calculations see Online Methods and Supplementary Fig. 27). Unless otherwise stated, calculations were done using TIP3P³¹ solvated systems under NPT (P = 1 atm; T = 300 K) conditions. For discussion on the impact of ionic strength in the trajectories see Supplementary Notes and Supplementary Fig. 28. Simulations mimicking crystal environments were carried out as described elsewhere³² for d(CGATCGATCG)₂ (PDB: 1D23) using 2 μsec simulation with 12 unit cells (or 32 duplexes) in the simulation periodic box (Supplementary Fig. 14); for a total of 64 μsec of duplex simulation.

A variety of analysis was performed to characterize the mechanical properties of DNA based on MD simulations. These include pseudo-harmonic analysis as described elsewhere^33-35 (see Supplementary Notes for additional details). The calculation of polymer deformation parameters (persistence length, stretch and twist torsion modules) was done following different approaches to reduce errors associated to the use of a single method to move from atomistic simulations to macroscopic descriptors: i) extrapolation of base step translations and rotations^17,35, ii) analysis of the correlations in the conformations and fluctuations of the DNA at different lengths³⁶, and iii) an implementation of Olson’s hybrid approach, which requires additional Monte Carlo simulations using MD-derived stiffness matrices³⁷. Dielectric constants of DNA were computed using Pettit’s procedure^38,39.

The trajectories were analyzed using AMBER (http://www.ambermd.org), GROMACS³⁰, NAFlex³³, and Curves+ tools⁴⁰, as well as with in-house scripts.

Geometry annotation

We followed standard default geometrical definitions for defining the conformational regions of the different torsion angles and for annotating hydrogen bonds (Supplementary Notes). Reference A-DNA and B-DNA fiber conformations were taken from Arnott’s values⁴¹.

Availability of force-field parameters and porting to different MD codes

The refined parameters are incorporated in amber-format libraries accessible from http://mmb.irbbarcelona.org/ParmBSC1/. Porting to GROMACS format was done from amber topology files using external utilities (amb2gmx⁴² and acpype⁴³ tools accessible at https://simtk.org/home/mmtools and https://github.com/choderalab/mmtools). As shown for a test case in Supplementary Fig. 27, the use of GROMACS or AMBER (CPU or GPU versions of the code) does not introduce any significant change in the trajectories. Porting to NAMD (http://www.ks.uiuc.edu/Research/namd) is not required since direct reading of AMBER topology files is possible.

NMR analysis

We used MD ensembles to compute theoretical estimates of NMR observables using standard methodologies (Supplementary Notes). Such estimates were compared with those available in BioMagResBank⁴⁴. When NMR data was determined de novo, the spectra were collected using default strategies summarized in Supplementary Notes.

Comparison with previous force-fields

It is out of the scope of this work to compare the performance of parmbsc1 with respect to other force-fields for all possible families of DNA. However we performed some tests for DDD, the most known B-DNA duplex, using in addition to parmbsc1, the default parmbsc0^4,45,46, parmbsc0-OL1⁵ (ε and ζ corrections), parmbsc0-OL4⁶ (χ corrections), parmbsc0-OL1+OL4^5,6, Charmm36⁴⁷ and a modified parmbsc0 developed by mixing corrected χ values and scaled-down van der Waals interactions⁴⁸. In all cases simulations were extended for at least 1 μs under identical simulation conditions. As shown in Supplementary Table 2 parmbsc1 provided clearly the best description of the duplex, while some of the existing force-field showed non negligible artifacts (a more detailed discussion is provided in Supplementary Discussion and Supplementary Figs. 29-31).

The effect of ionic strength and the nature of counterion

To evaluate potential differences in simulations arising from the ionic strength we performed additionally 2 μs simulations of DDD with extra salt: Na⁺Cl⁻ 150 mM, and 500 mM. These additional calculations were performed using the same conditions outlined previously, showing results that are quite independent on the exact choice (in the 0–500 mM range) of the added extra salt (Supplementary Notes and Supplementary Fig. 31).

A more detailed description of the methods used for parameterization, trajectory collection and analysis, with additional references are included in Supplementary Notes.

Data Management

Trajectories and the analysis performed were placed in a novel dual database framework for nucleic acid simulations using Apache’s Cassandra to manage trajectory data, and MongoDB to manage trajectory metadata and analysis. Results are available at http://mmb.irbbarcelona.org/ParmBSC1/. Details on the Barcelona’s nucleic acids database will be presented elsewhere.