Addressing Item-Level Missing Data: A Comparison of Proration and Full Information Maximum Likelihood Estimation

Abstract

Often when participants have missing scores on one or more of the items comprising a scale, researchers compute prorated scale scores by averaging the available items. Methodologists have cautioned that proration may make strict assumptions about the mean and covariance structures of the items comprising the scale (Schafer & Graham, 2002; Graham, 2009; Enders, 2010). We investigated proration empirically and found that it resulted in bias even under a missing completely at random (MCAR) mechanism. To encourage researchers to forgo proration, we describe an FIML approach to item-level missing data handling that mitigates the loss in power due to missing scale scores and utilizes the available item-level data without altering the substantive analysis. Specifically, we propose treating the scale score as missing whenever one or more of the items are missing and incorporating items as auxiliary variables. Our simulations suggest that item-level missing data handling drastically increases power relative to scale-level missing data handling. These results have important practical implications, especially when recruiting more participants is prohibitively difficult or expensive. Finally, we illustrate the proposed method with data from an online chronic pain management program.

Researchers frequently collect item-level data using questionnaires and compute scale scores by summing or averaging the items that measure a single construct. For example, clinical psychologists use the Beck Depression Inventory (BDI-II) to measure symptoms of depression, personality psychologists use the NEO Personality Inventory (NEO-PI-3) to measure the Big Five personality traits, educational researchers use the Child Behavior Checklist (CBCL) to measure behavioral problems in children, and health psychologists use the Brief Pain Inventory (BPI) to measure pain severity and interference. As with almost all research involving quantitative methods, missing data on the items comprising these scales are inevitable. Participants may inadvertently skip items, refuse to answer sensitive items, or skip items that do not apply to them. Item-level missing data can also result from a planned missing data design (Graham, Taylor, Olchowski, & Cumsille, 2006). Despite the widespread use of questionnaire data, very little research focuses on item-level missing data handling.

Often when participants have missing scores on one or more of the items comprising a scale, researchers compute prorated scale scores by averaging the available items (e.g., if a participant answers eight out of ten items, the prorated scale score is the average of the eight responses). Averaging the available items is equivalent to imputing each participant’s missing scores with the mean of his or her observed scores, which is why it is sometimes referred to as person mean imputation. Averaging the available items does not have a well-recognized name (Schafer & Graham, 2002), but we have commonly seen it referred to as “proration” or as computing a “prorated scale score” in the applied literature. Thus, we adopt the name “proration” throughout the rest of this paper. An informal search of PsycARTICLES for the keyword “prorated” revealed that researchers regularly employ this procedure, with applications ranging from adolescent sleep (Byars & Simon, 2014), eating disorder risk (Culbert, Breedlove, Sisk, Burt, & Klump, 2013; Culbert et al., 2015), anxiety and depression (Forand & DeRubeis, 2013, 2014; Hazel, Oppenheimer, Technow, Young, & Hankin, 2014; Howe, Hornberger, Weihs, Moreno, & Neiderhiser, 2012), personality disorders (Krabbendam, Colins, Doreleijers, van der Molen, Beekman, & Vermeiren, 2015), posttraumatic stress (Neugebauer et al., 2014), violence risk (Olver, Nicholaichuk, Kingston, & Wong, 2014; Rice, Harris, & Lang, 2013), sex offender risk (Smid, Kamphuis, Wever, & Van Beek, 2014), and social climate (Tonkin, Howells, Ferguson, Clark, Newberry, & Schalast, 2012), to name a few. Researchers were quite inconsistent in their application of proration; the procedure was routinely applied with 20% of the item responses missing, with some studies reporting much higher thresholds (e.g., 50%). Interestingly, when the number of incomplete items exceeded the stated threshold, researchers tended to treat the entire record as missing (deletion). Collectively, these references suggest that researchers routinely encounter item-level missing data, and they often apply proration to deal with the problem.

Methodologists have raised several important concerns about proration. Schafer and Graham (2002) stated that “averaging the available items is difficult to justify theoretically either from a sampling or likelihood perspective” (p. 158). Proration redefines a scale such that it is no longer the sum or average of the k items comprising the scale; the definition of the scale now varies across participants and depends on the missing data patterns and rates in the sample. Schafer and Graham (2002) further warned that proration may produce bias even under a missing completely at random (MCAR) mechanism. Consistent with this statement, previous research has suggested that proration inflates estimates of internal consistency reliability under an MCAR mechanism and under a missing at random (MAR) mechanism (Downey & King, 1998; McDonald, Thurston, & Nelson, 2000; Huisman, 2000; Sijtsma & van der Ark, 2003; Enders, 2003). However, very little research examines proration for other analyses.

Graham (2009) speculated that proration may be reasonable when (1) a relatively high proportion of the items (and never fewer than half) are used to form the scale score, (2) the item-total correlations are similar, and (3) the internal consistency reliability of the scale is high. By contrast, methodologists have speculated that the procedure may be prone to bias when either the means of the items comprising a scale vary (Enders, 2010) or the inter-item correlations vary (Graham, 2009; Graham, 2012). Recall that proration is equivalent to imputing each participant’s missing scores with the mean of his or her observed scores. For these imputations to be valid, the incomplete items must have the same properties as the complete donor items. For example, if the means of the complete donor items are lower than the means of the incomplete items, the resulting imputations will be too low, thus biasing the scale scores. Lee, Bartholow, McCarthy, Pederson, and Sher (2014) demonstrated this issue for the Self-Rating of the Effects of Alcohol Scale (SRE), a 12-item scale that asks participants how many drinks they need to consume before experiencing certain effects (e.g., stumbling or lacking coordination while walking, unintentionally passing out or falling asleep). Item-level missing data arise when participants have never experienced one or more of these effects from alcohol consumption, and items with higher means have higher missing data rates. Lee et al. (2014) found that proration resulted in negatively biased scale scores on the SRE because the complete items (which were used to compute the prorated scale scores) had lower means than the missing items. Aside from Lee et al’s (2014) study, we are not aware of published studies that have systematically examined the impact of heterogeneous means and inter-item correlations on proration. We present simulation studies that examine this issue later in the paper.

Given the untenable assumptions of proration, researchers may wonder how to proceed when faced with item-level missing data. Methodologists currently recommend analyses that assume a more plausible missing at random (MAR) mechanism whereby the probability of missing data on a variable Y is unrelated to the would-be values of Y itself after controlling for other variables in the analysis. MAR-based analyses provide consistent parameter estimates under an MCAR or MAR mechanism and increase power relative to MCAR-based analyses such as listwise and pairwise deletion. Relying on MAR-based analyses is also preferable because methodologists have extensively researched when MAR-based analyses do and do not work. Multiple imputation and full information maximum likelihood (FIML) estimation are the predominant MAR-based analyses. Multiple imputation consists of three phases: the imputation phase, the analysis phase, and the pooling phase. First we create multiple (preferably 20 or more; Graham, Olchowski, & Gilreath, 2007) copies of the data set by drawing imputed scores from a distribution of plausible scores. When using a linear imputation model, these imputed scores can be viewed as the sum of a predicted score and a residual. We then analyze the imputed data sets as though they were complete data sets. Finally, we pool the parameter estimates and standard errors across the imputed data sets, which yields a single set of results. The FIML estimator investigated in this paper uses an iterative optimization algorithm to identify the set of parameter values that maximize the probability of the observed data. Rubin (1976) showed that, under an MAR mechanism, FIML estimation based on the available data yields appropriate likelihood-based inference. Unlike deletion methods, FIML does not exclude cases with missing scores. Including incomplete cases’ observed scores improves accuracy because associations between the incomplete variables and other (complete or incomplete) variables inform the estimation procedure about which values of the parameters are most likely.

With multiple imputation, we can address item-level missing data for a scale-level analysis without difficulty. Methodologists have proposed using item-level imputation, or imputing the items prior to computing the scale scores (Schafer & Graham, 2002; van Buuren, 2010; Enders, 2010). Including all of the items in the imputation phase maximizes the information used to create the imputations. Gottschall, West, and Enders (2012) compared efficiency differences between item-level imputation (i.e., impute-then-average or impute-then-sum) and scale-level imputation, or computing scale scores prior to the imputation phase and then imputing the incomplete scale scores for participants with missing scores on one or more of the items comprising the scale (i.e., average-then-impute or sum-then-impute). Gottschall et al. (2012) concluded that item-level imputation drastically increases power relative to scale-level imputation. Item-level imputation uses other observed items to predict the missing items whereas scale-level imputation uses other observed variables or scale scores to predict the missing scale scores. Because within-scale item correlations tend to be much stronger than between-scale correlations, scale-level imputation excludes the strongest predictors of the incomplete scale scores. Consequently, scale-level imputation reduces precision (i.e., increases standard errors, thus decreasing power) relative to item-level imputation. For measures of association in Gottschall et al.’s (2012) simulation study, scale-level imputation required a 75% increase in sample size to achieve the same precision (and thus power) as item-level imputation. The practical significance of these results is obvious, especially when recruiting more participants is prohibitively difficult or expensive.

Deciding how to address item-level missing data is much more ambiguous when using FIML. Assuming that researchers do not alter the analysis to accommodate the missing data, current implementations of FIML encourage researchers to perform scale-level missing data handling. For example, suppose we are interested in a bivariate regression between two scale scores. To estimate this regression model with FIML, we would treat a scale score as missing whenever one or more items comprising the scale are missing. The incomplete scale scores would then be used as input, and the FIML estimator would identify the set of parameter values that maximize the probability of the observed data. Based on the results from Gottschall et al. (2012), we would expect a drastic reduction in power because the analysis ignores the observed item responses for cases with missing scale scores. We could instead estimate a structural equation model that recasts the two scale scores as latent variables with the items as indicators. However, we find this strategy unsatisfactory because we believe that, when possible, researchers should apply the same analytic procedures that they would have used, had the data been complete.

Savalei and Rhemtulla (2014) proposed using a two-stage approach to address item-level missing data. The two-stage approach applies the following sequence of steps: (1) use FIML to estimate the item-level covariance matrix and mean vector (Stage 1a), (2) transform the item-level matrices into a scale-level covariance matrix and mean vector (Stage 1b), and (3) use a structural equation modeling software package to estimate the desired analysis from the scale-level matrices (Stage 2). The two-stage approach is promising because it is the true FIML analog of item-level imputation. However, implementing the two-stage approach is currently difficult because standard error computations require complex matrix manipulations and custom computer programming. As such, we do not investigate this procedure, but instead focus on an auxiliary variable method that researchers can apply with existing structural equation modeling software packages (Eekhout et al., in press). One of the major goals of this paper is to describe an FIML approach to item-level missing data handling that mitigates the loss in power due to missing scale scores and utilizes the available item-level data without altering the substantive analysis. We provide a preliminary investigation of this approach, comparing it to proration, which appears to dominate applied research. Methodologists have cautioned that proration may make strict assumptions about the mean and covariance structures of the items comprising the scale (Schafer & Graham, 2002; Graham, 2009; Enders, 2010), but few studies have formally examined this conjecture (Lee et al., 2014). Thus, another major goal of this paper is to investigate the performance of proration under different mean and covariance structures.

The organization of this paper is as follows. First we describe a simulation study evaluating proration. We then briefly review auxiliary variables and outline an FIML model that incorporates item-level information via auxiliary variables. We present two simulation studies that examine its performance, and we demonstrate its application with data from an online chronic pain management program. Finally, we explain the practical significance of the results and provide recommendations for addressing item-level missing data.

Simulation Study 1

As noted previously, methodologists have speculated that proration may be reasonable with uniform item means and inter-item correlations but not otherwise (Schafer & Graham, 2002; Graham, 2009; Enders, 2010). We investigated this proposition empirically, examining the performance of proration under different mean and covariance structures and under different missing data mechanisms. Based on limited existing research (Schafer & Graham, 2002; Graham, 2009; Enders, 2010), we hypothesized that proration would result in non-negligible bias when either the item means or inter-item correlations vary. This bias should be independent of the missing data mechanism, and we anticipated subpar performance under both MCAR and MAR mechanisms. By contrast, we expected proration to provide accurate parameter estimates when the item means and inter-item correlations are uniform. The simulation study described below examines these issues.

Manipulated Factors and Population Models

We implemented a full factorial design with five between-subjects factors: uniformity of the mean and covariance structures, number of items per scale (8 or 16), sample size (200 or 500), item-level missing data rate (5%, 15%, 25%), and missing data mechanism (MCAR, MAR due to an variable external to the scales, and MAR due to complete items on the scales). These conditions produced 108 between-subject design cells.

For the population models, we used a two-factor confirmatory factor analysis model to generate correlated continuous variables. The two factors were correlated at r = .30. We set the factor variances to 1 and set the residual variances for the items to (1 − λ²) such that the items were standardized to the z-score metric. The factor means were set to zero. The population model also included a variable external to the X and Y scales that correlated with each factor at r = .50. As described in the next section, we categorized the items and used scale scores (computed as the mean of the items) for the analyses, which were performed in Mplus 7.

To vary the uniformity of the mean and covariance structures, we (1) set all of the item means to be equal and set all of the inter-item correlations to be equal, (2) set the item means to be equal but varied the inter-item correlations, and (3) varied the item means but set all of the inter-item correlations to be equal. With uniform item means and inter-item correlations, we set all of the measurement intercepts (i.e., item means) to zero and fixed all of the standardized factor loadings to λ = .75. When varying the inter-item correlations, we set the measurement intercepts to zero and fixed half of the standardized factor loadings to λ = .75 and the other half to λ = .50. This configuration of loadings produced inter-item correlations of .56, .38, and .25. Finally, when varying the item means, all standardized factor loadings were set to λ = .75, and we set half of the measurement intercepts to zero and the other half to 0.50. Because the items were standardized, this difference in measurement intercepts corresponds to a medium effect size (Cohen, 1988). Graham (2009) speculated that proration may be reasonable when internal consistency reliability of the scale is high. We chose to implement a population model that produced scale scores with high internal consistency reliability (with eight items, the population reliability values were approximately .91 and .84 for the equal and unequal loading conditions, respectively) in order to demonstrate that proration can produce problematic parameter estimates, even under optimal conditions.

Data Generation

We used Mplus 7 to generate 1000 data sets with continuous variables for each of the 108 between-subjects design cells. Although we could have used continuous variables for the simulations, we used ordinal variables to more closely mimic Likert scale items that researchers would typically use when applying proration. We used the IML procedure in SAS 9.4 to categorize the underlying continuous variables (from Mplus 7) into seven-point discrete scales based on thresholds of z = −1.64485, −1.03643, −0.38532, 0.38532, 1.03643, and 1.64485. These thresholds produced symmetric ordinal distributions with category proportions of 5%, 10%, 20%, 30%, 20%, 10%, and 5%. We chose symmetric thresholds because doing so allowed us to more easily control mean differences via the measurement intercepts in the underlying continuous variable population model. The simulation scripts, raw results, and all other materials pertaining to the simulations are available upon request.

In all conditions, we imposed missing data on half of the items from each scale, deleting 5%, 15%, or 25% of the scores from each incomplete item. Although this choice was somewhat arbitrary, our informal review of published articles suggests that researchers do not apply proration when more than half of the items are missing. Thus, this missingness pattern likely represents an upper bound for the application of proration in practice. This design choice also aligns with Graham’s (2009) suggestion that proration may be reasonable when scale scores are based on at least half of the items. Considering the within-subject missing data rates, cases with at least one missing item had approximately 12%, 15%, and 19% of the items missing per scale, on average, when the proportion of missing scores on each incomplete item equaled 5%, 15%, and 25%, respectively. Our informal review of published articles suggests that researchers typically apply proration to individuals with 20% or fewer items missing (e.g., Hazel et al., 2014; Howe et al., 2012; Olver et al., 2014; Smid et al., 2014; Tonkin et al., 2012), although we found examples that employed higher cutoffs (Byars & Simon, 2014; Krabbendam et al., 2015; Rice et al., 2013). Thus, we believe that our item-level missing data rates produced missingness patterns that are fairly representative of published studies. When varying the item means or standardized factor loadings, we imposed missing data such that the complete items were not representative of the incomplete items. In the former case, items with a measurement intercept of zero were complete and items with a measurement intercept of 0.50 were incomplete (i.e., incomplete items had higher means, as in Lee et al., 2014). In the latter case, items with a standardized factor loading of λ = .50 were complete and items with a standardized factor loading of λ = .75 were incomplete (i.e., incomplete items had higher inter-item correlations).

As noted previously, we investigated three missing data mechanisms: an MCAR mechanism where missingness was unrelated to measured variables and to the values of X and Y, an MAR mechanism where missingness on half of the items was related to an external variable (henceforth abbreviated as an MAR-E mechanism), and an MAR mechanism where missingness on half of the items was related to a subset of complete items on the same scale (henceforth abbreviated as an MAR-I mechanism). For the MCAR mechanism, we generated a set of binary indicators for each case by sampling from a binomial distribution with success probabilities equal to the proportion of missing data (i.e., 5%, 15%, or 25%). We drew the indicators independently, such that each item from the incomplete subset could either be missing or complete, and we coded the target item as missing if its corresponding indicator equaled unity.

For the MAR mechanisms, the probability of missing data was positively related to scores on another variable (either an external variable or a complete item from the same scale). The deletion procedure for both MAR mechanisms worked as follows. Using a latent variable formulation for logistic regression (Agresti, 2012; Johnson & Albert, 1999), we derived the intercept and slope coefficients that produced an R² of approximately .40 between the cause of missingness (i.e., the external variable or the complete item) and the underlying latent missingness probabilities (we chose .40 to ensure a relatively strong selection mechanism). A custom Excel spreadsheet was developed for this purpose, which is available upon request. After determining the appropriate intercept and slope coefficients, we used a logistic regression equation to generate an N-row vector of missingness probabilities for each item. We then drew binary missing data indicators from a binomial distribution with a success rate equal to the missingness probability. We drew the indicators independently, such that each item in the incomplete subset could either be missing or complete, and we coded the target item as missing if its corresponding indicator equaled unity. In the condition where missingness was due to an external variable, all predicted probabilities for a given case were identical because all variables shared a common cause of missingness. However, the second MAR condition used multiple causes of missingness. Two complete items were used to generate item-level missing data for eight-item scales, and four complete items were used to generate item-level missing data for 16-item scales. In both cases, each complete item was responsible for missingness on two incomplete items.

Analysis and Outcomes

For the first simulation, we computed prorated scale scores for each data set by averaging the available items, and we subsequently used Mplus 7 to estimate seven parameters: the mean of X, the mean of Y, variances of X and Y, covariance between X and Y, correlation between X and Y, and regression coefficient. We examined standardized bias and mean square error (MSE) within each design cell. Bias refers to the difference between the average parameter estimate across the 1000 replications within a given design cell and the corresponding population parameter. Because the categorization procedure makes it difficult to derive the population values, we generated 1000 complete data sets within each design cell, and we used the average parameter estimates from these data sets as the population parameters. To compute standardized bias, we divided raw bias by the standard deviation of the complete-data parameter estimates (i.e., the empirical complete-data standard error) in each design cell. Standardized bias increases as sample size increases because parameters are more precisely estimated. However, this property of standardized bias is not concerning given that we investigated conditions with a sample size of 200. Collins, Schafer, and Kam (2001) suggested that standardized bias adversely affects efficiency, confidence interval coverage, and error rates when standardized bias exceeds 40% in either the positive or negative direction. Thus, we flagged standardized bias values greater than .40 in absolute value.

MSE is the average squared distance between the parameter estimates and the corresponding population parameter:

$$\mathit{\text{MSE}}=\frac{\sum {(\hat{\theta }-\theta )}^2}{1000}$$ (1)

where θ̂ is the parameter estimate, θ is the population parameter, and 1000 is the number of replications within a given design cell. MSE equals the squared bias plus the sampling variance of the parameter estimate, and thus captures the accuracy and precision of an estimator. In later simulation studies, we computed MSE ratios to compare two missing data handling methods. As we explain later, MSE ratios are practically useful because they express efficiency differences between two unbiased estimators on the sample size metric. Finally, we checked for outliers at the replication level for each outcome, but no replications were excluded due to extreme values.

Simulation Study 1 Results

We focus on standardized bias because we only examined one missing data handling method (proration) in this simulation study. Standardized bias values for conditions corresponding to a 25% item-level missing data rate are reported in Tables 1 to 3. (Values of absolute bias and relative bias for these conditions are reported in Tables A1 to A3 of the online appendix.) The influences of the other manipulated factors were relatively uniform across the three item-level missing data rates (5%, 15%, 25%).

Table 1.

Simulation Study 1, Standardized Bias from Proration – Uniform Item Means, Uniform Inter-Item Correlations

Parameter	Items Per Scale	Sample Size	MCAR Mechanism	MAR Mechanism Due to External Variable	MAR Mechanism Due to Complete Items on the Scale
Mean of X	8	200	−0.0037	−0.0074	0.1544
		500	0.0000	−0.0019	0.2495
	16	200	0.0076	0.0025	0.0851
		500	0.0021	0.0000	0.1319
Mean of Y	8	200	0.0026	0.0013	0.1662
		500	−0.0020	0.0000	0.2637
	16	200	0.0026	−0.0013	0.0832
		500	0.0000	−0.0021	0.1216
Variance of X	8	200	0.1603	0.1758	0.2848
		500	0.2663	0.2962	0.4769*
	16	200	0.0878	0.0987	0.1590
		500	0.1420	0.1599	0.2541
Variance of Y	8	200	0.1801	0.1964	0.3222
		500	0.2764	0.3111	0.5042*
	16	200	0.0787	0.0877	0.1458
		500	0.1302	0.1459	0.2303
Covariance	8	200	−0.0086	−0.0011	0.0321
		500	0.0069	0.0069	0.0674
	16	200	0.0023	0.0000	0.0197
		500	−0.0019	−0.0037	0.0315
Correlation	8	200	−0.0740	−0.0710	−0.0754
		500	−0.0933	−0.1053	−0.1053
	16	200	−0.0305	−0.0366	−0.0396
		500	−0.0560	−0.0633	−0.0608
Regression Coefficient	8	200	−0.0712	−0.0684	−0.0726
		500	−0.0907	−0.1023	−0.1000
	16	200	−0.0290	−0.0362	−0.0377
		500	−0.0514	−0.0607	−0.0584

Note. The table contains standardized bias values for conditions with a 25% item-level missing data rate. The item means and inter-item correlations were uniform.

Standardized bias values greater than or equal to .40 in absolute value are denoted by an asterisk (*).

Table 3.

Simulation Study 1, Standardized Bias from Proration – Varied Item Means, Uniform Inter-Item Correlations

Parameter	Items Per Scale	Sample Size	MCAR Mechanism	MAR Mechanism Due to External Variable	MAR Mechanism Due to Complete Items on the Scale
Mean of X	8	200	0.7012*	0.7728*	1.3568*
		500	1.1240*	1.2362*	2.1654*
	16	200	0.6906*	0.7664*	1.2285*
		500	1.1466*	1.2802*	2.0496*
Mean of Y	8	200	0.7387*	0.8150*	1.4230*
		500	1.1684*	1.2916*	2.2608*
	16	200	0.7166*	0.7914*	1.2754*
		500	1.1125*	1.2375*	1.9812*
Variance of X	8	200	0.1587	0.6583*	1.4043*
		500	0.2602	1.1069*	2.3601*
	16	200	0.0703	0.6150*	1.2319*
		500	0.1132	1.0062*	2.0031*
Variance of Y	8	200	0.1740	0.7312*	1.5637*
		500	0.2680	1.1369*	2.4294*
	16	200	0.0574	0.5861*	1.1870*
		500	0.0976	0.9467*	1.9038*
Covariance	8	200	−0.0186	0.6930*	0.3607
		500	−0.0124	1.1259*	0.5993*
	16	200	−0.0095	0.7182*	0.3650
		500	−0.0228	1.1464*	0.5798*
Correlation	8	200	−0.0817	0.4814*	−0.1322
		500	−0.1103	0.7818*	−0.1942
	16	200	−0.0366	0.5282*	−0.0687
		500	−0.0659	0.8415*	−0.1098
Regression Coefficient	8	200	−0.0790	0.4670*	−0.1279
		500	−0.1072	0.7622*	−0.1841
	16	200	−0.0364	0.5022*	−0.0684
		500	−0.0634	0.8075*	−0.1080

Note. The table contains standardized bias values for conditions with a 25% item-level missing data rate. The inter-item correlations were uniform but the item means varied.

Standardized bias values greater than or equal to .40 in absolute value are denoted by an asterisk (*).

Table 1 reports standardized bias values when the item means and inter-item correlations were uniform. Recall that this set of conditions should be optimal for proration because the observed items used to compute each case’s scale score are identical to the missing items. Although the standardized bias values noticeably depart from zero, very few design cells resulted in standardized bias values greater than .40 in absolute value. With an MCAR mechanism or MAR-E mechanism, none of the standardized bias values exceeded .40 in absolute value, though a number exceeded .10 in absolute value (i.e., 10% of the empirical complete-data standard error). However, standardized bias values were greater with an MAR-I mechanism.Table 2 reports standardized bias values when the item means were uniform but the inter-item correlations varied. Recall that the standardized factor loadings equaled λ = .50 for the complete items and λ = .75 for the incomplete items, such that the intercorrelations among the complete items differed from those among the incomplete items. The literature suggests that proration may be problematic under these conditions (Graham, 2009; Enders, 2010; Graham, 2012). Comparing Table 2 to Table 1, varying the inter-item correlations increased standardized bias. More design cells resulted in standardized bias values greater than .40 in absolute value (i.e., 40% of the empirical complete-data standard error). When the inter-item correlations varied, proration resulted in non-negligible bias even with an MCAR mechanism (range = 0 to 0.6121, or up to 61.21% of the empirical complete-data standard error). As shown in Table 2, standardized bias values were greater with an MAR-E mechanism than with an MCAR mechanism or MAR-I mechanism (range = 0.2169 to 0.8162, or 21.69% to 81.62% of the empirical complete-data standard error). As expected, standardized bias increased as sample size increased, likely because the parameters were more precisely estimated. However, we observed non-negligible values of standardized bias even with a sample size of 200.

Table 2.

Simulation Study 1, Standardized Bias from Proration – Uniform Item Means, Varied Inter-Item Correlations

Parameter	Items Per Scale	Sample Size	MCAR Mechanism	MAR Mechanism Due to External Variable	MAR Mechanism Due to Complete Items on the Scale
Mean of X	8	200	−0.0042	−0.2219	0.0997
		500	0.0022	−0.3423	0.1611
	16	200	0.0089	−0.2169	−0.0386
		500	0.0000	−0.3741	−0.0798
Mean of Y	8	200	0.0030	−0.2234	0.1065
		500	0.0000	−0.3497	0.1678
	16	200	0.0031	−0.2307	−0.0511
		500	0.0000	−0.3590	−0.0867
Variance of X	8	200	−0.1523	−0.2215	−0.0948
		500	−0.2611	−0.3748	−0.1634
	16	200	−0.3736	−0.4956*	−0.3998
		500	−0.6121*	−0.8162*	−0.6646*
Variance of Y	8	200	−0.1680	−0.2468	−0.1058
		500	−0.2609	−0.3741	−0.1533
	16	200	−0.3738	−0.4976*	−0.4041*
		500	−0.5919*	−0.7892*	−0.6499*
Covariance	8	200	−0.2211	−0.3424	−0.2140
		500	−0.3333	−0.5402*	−0.3264
	16	200	−0.2166	−0.3742	−0.2436
		500	−0.3544	−0.6000*	−0.3873
Correlation	8	200	−0.1894	−0.2996	−0.2012
		500	−0.2803	−0.4751*	−0.3064
	16	200	−0.0995	−0.2308	−0.1176
		500	−0.1655	−0.3693	−0.1799
Regression Coefficient	8	200	−0.1869	−0.2924	−0.1969
		500	−0.2755	−0.4630*	−0.2986
	16	200	−0.0967	−0.2222	−0.1140
		500	−0.1594	−0.3580	−0.1755

Note. The table contains standardized bias values for conditions with a 25% item-level missing data rate. The item means were uniform but the inter-item correlations varied.

Standardized bias values greater than or equal to .40 in absolute value are denoted by an asterisk (*).

Finally, Table 3 reports standardized bias values when the inter-item correlations were uniform across items but the item means varied. Comparing Table 3 to Table 1, varying the item means drastically increased standardized bias. All design cells resulted in standardized bias values greater than .40 in absolute value for the mean of X and mean of Y (range = 0.6906 to 2.2608, or 69.06% to 226.08% of the empirical complete-data standard error). Standardized bias values were greater with an MAR-E mechanism or MAR-I mechanism than with an MCAR mechanism. For the means and variances of X and Y, standardized bias values were greatest with an MAR-I mechanism. For measures of association (i.e., covariance, correlation, regression coefficient), standardized bias values were greatest with an MAR-E mechanism. As shown in Table 3, all of the design cells with an MAR-E mechanism resulted in standardized bias values greater than .40 in absolute value for all of the parameters (range = 0.4670 to 1.2916, or 46.70% to 129.16% of the empirical complete-data standard error).

In sum, our simulations show that the mean and covariance structures dictate the performance of proration more than the missing data mechanism and that proration can introduce substantial bias even under an MCAR mechanism. Given the bias resulting from proration, we do not consider this method for the remainder of this paper. Instead we focus on an FIML approach that uses auxiliary variables to preserve item-level information. We outline this method in the next section and then examine its performance with two simulation studies.

FIML Model with Items as Auxiliary Variables

Given that proration often resulted in non-negligible bias, we recommend forgoing proration and treating the scale score as missing whenever one or more items comprising the scale are missing. We can then address the missing scale scores using MAR-based approaches that have been extensively investigated in the past. As noted previously, we can use item-level imputation to mitigate the loss in power due to missing scale scores (Gottschall et al., 2012; Graham, 2012). In this paper, we describe an FIML model that incorporates items as auxiliary variables. This method is an FIML approximation to item-level imputation, but it is arguably easier for researchers to implement in practice.

When addressing missing data, methodologists recommend an inclusive analysis strategy that incorporates auxiliary variables into the analysis (Collins et al., 2001). Auxiliary variables would not appear in the complete-data analysis but are important for missing data handling because they correlate with the incomplete variable(s) and/or predict missingness. Previous research has demonstrated that strong correlations between auxiliary variables and the incomplete analysis variables can increase power—sometimes dramatically—by increasing precision (Collins et al., 2001; Graham, 2012). Items serve as useful auxiliary variables for increasing power because they tend to be highly correlated with the incomplete scale scores.

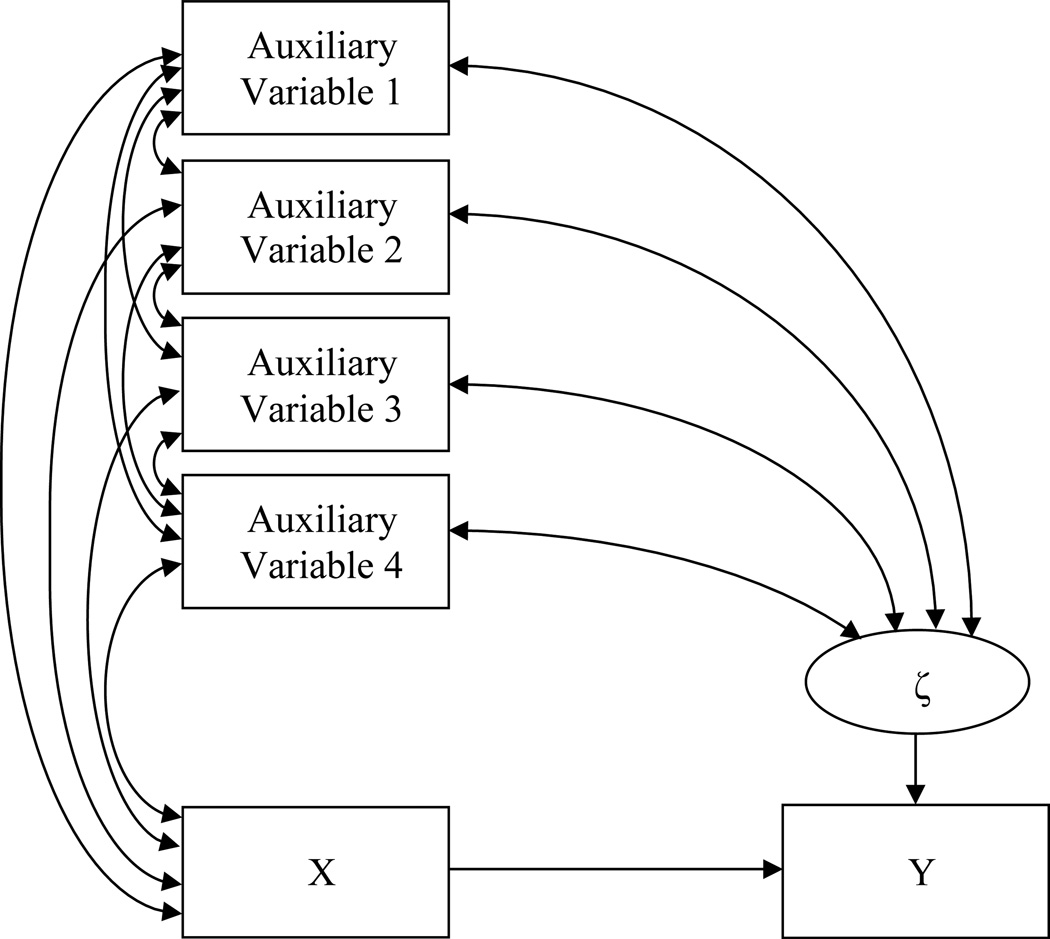
When using FIML, Graham (2003) proposed incorporating auxiliary variables using the saturated correlates model. For analyses with only manifest variables (e.g., scale scores), the saturated correlates model correlates an auxiliary variable with (1) other auxiliary variables, (2) exogenous variables, and (3) residuals of endogenous variables (Graham, 2003). Figure 1 shows a bivariate regression with four auxiliary variables; notice that the path diagram employs all three of Graham’s (2003) rules. Auxiliary variables do not change the interpretation of the parameter estimates, which is particularly important because the saturated correlates model allows researchers to implement an FIML analysis that honors the complete-data research goals.

Figure 1.

Path diagram of a bivariate regression with four auxiliary variables.

As described earlier, scale-level FIML treats the scale score as missing whenever one or more items comprising the scale are missing. The auxiliary variable approach to scale score analyses with FIML again treats the scale score as missing whenever one or more of the items are missing but incorporates a subset of the items as auxiliary variables. The auxiliary variable portion of the model serves to more precisely estimate the parameters, thus mitigating the loss in power due to the missing scale scores. Referring back to Figure 1, X and Y would be incomplete scale scores, and the auxiliary variables could be a collection of items from each scale. The model transmits the item-level information via the correlations among the auxiliary variables and the incomplete scale scores, thereby improving efficiency in a fashion that is analogous to item-level imputation. Again, using items as auxiliary variables does not alter the interpretation of the parameter estimates. Rather, the items simply improve the efficiency of the scale score parameters.

Although the model in Figure 1 uses relatively few auxiliary variables, the simulation results presented later in the paper suggest using a larger set of items as auxiliary variables, as doing so increases power. For a k-item scale, we can incorporate at most k – 1 items as auxiliary variables to avoid linear dependencies. For example, suppose that scale X consists of six items and scale Y consists of ten items. We could include up to five items from scale X and up to nine items from scale Y to address item-level missing data. We believe that choosing which item to omit depends on the missing data pattern. Transmitting information from an auxiliary variable to an incomplete analysis variable via correlations requires that missing scores on the analysis variable pair with observed scores on the auxiliary variable. As such, we recommend omitting the incomplete item that is most often concurrently missing with the other incomplete items because it will offer less information about the incomplete scale score. All else being equal, researchers could also choose to omit the item that is least central to the construct of interest. Finally, incorporating all but one item from each scale as auxiliary variables may still cause convergence issues. Consequently, it may be necessary to use fewer auxiliary variables to represent the item-level information. We discuss this issue later in the paper.

Simulation Study 2

In this simulation study, we compared the performance of scale-level FIML and FIML with items as auxiliary variables. We expected analyses using scale-level FIML to suffer from lower power when dealing with item-level missing data. However, we hypothesized that utilizing item-level information from the auxiliary portion of the model would mitigate the loss in power due to missing scale scores, much in the same way as item-level imputation. We first focused on FIML with all but one item from each scale as auxiliary variables because it incorporates as much item-level information into the analysis as possible. As such, we expected this method to provide the largest power gains relative to scale-level FIML.

We reused the data sets generated for the first simulation study, though we dropped conditions with an MCAR mechanism because theory and empirical research show that FIML performs well under an MCAR mechanism (which is not true of proration). For both missing data handling methods, we treated the scale score as missing whenever one or more of the items were missing. Recall that we imposed missing data on half of the items from each scale. For eight-item scales, the scale-level missing data rate equaled approximately 16%, 38%, and 55% when the item-level missing data rates equaled 5%, 15%, and 25%, respectively. For 16-item scales, the scale-level missing data rate equaled approximately 26%, 53%, and 69% when the item-level missing data rates equaled 5%, 15%, and 25%, respectively. As such, scales with more incomplete items (i.e., eight instead of four) had a higher proportion of cases with missing scale scores.

We used Graham’s (2003) saturated correlates model to incorporate auxiliary variables. When performing scale-level FIML, we included the variable external to the X and Y scales as an auxiliary variable. Including the (complete) external variable as an auxiliary variable forced all cases with missing X and Y scale scores into the analysis (cases with missing scores on both scales would otherwise be excluded). Doing so allowed us to compare power differences between the two methods because the analyses were based on the same sample size. When performing FIML with items as auxiliary variables, we included the external variable as an auxiliary variable along with the items. Although we would normally recommend omitting the item exhibiting the lowest coverage with the scale score, we arbitrarily excluded the first incomplete item from each scale, as they would possess roughly the same coverage rate as the other incomplete items.

Simulation Study 2 Results

FIML with items as auxiliary variables encountered convergence issues in conditions with 16 items per scale, sample size of 200, and 25% item-level missing data rate. Within these conditions, 78.70% of the replications successfully converged. These convergence issues are not surprising given the large number of parameters to estimate. In these conditions, 31 auxiliary variables (15 of the items from each scale plus the external variable) were correlated with (1) each other, (2) the predictor X, and (3) the residual of the outcome variable Y. Following Graham’s (2003) rules for the saturated correlates model resulted in over 500 correlations for just the auxiliary variable portion of the model. As such, the data did not contain enough information to support so many parameters. We explore some possible strategies for reducing the size of the auxiliary variable set later in this paper.

Standardized Bias

For each missing data mechanism and method, we computed the average standardized bias across all other conditions for each parameter. Analyses using scale-level FIML provided nearly unbiased parameters with an MAR-E mechanism. The average standardized bias ranged from −0.0209 to 0.0731 (i.e., up to 7.31% of the empirical complete-data standard error). Analyses using FIML with item-level auxiliary variables also provided unbiased estimates with an MAR-E mechanism. The average standardized bias ranged from −0.0170 to −0.0052 (i.e., up to 1.70% of the empirical complete-data standard error), which is negligible. Although both approaches were effectively unbiased, notice that incorporating item-level information resulted in somewhat more accurate parameter estimates. We would expect these bias differences to diminish at larger sample sizes given that FIML is a consistent estimator.

By contrast, scale-level FIML provided highly biased parameter estimates when missingness was a function of complete items. Almost all of the standardized bias values exceeded .40 in absolute value. Although the bias might seem counterintuitive, analyses using scale-level FIML followed an MNAR mechanism because the complete items that were responsible for missingness were not included in the analysis (i.e., the probability of missing data is related to the would-be value of the scale score because the analysis does not condition on the complete items that were responsible for missingness). Because the MAR assumption of FIML was violated, we would expect biased parameter estimates. By contrast, analyses using FIML with auxiliary variables followed an MAR mechanism because the complete items used to generate the item-level missing data were included in the analysis. Not surprisingly, the item-level auxiliary information eliminated nonresponse bias.

MSE Ratio

The MSE ratios described here are specific to conditions with an MAR-E mechanism. We did not compute or interpret the MSE ratios for conditions with an MAR-I mechanism given that scale-level FIML provided biased parameter estimates. Recall that MSE equals the squared bias plus the sampling variance of the parameter estimate. For two unbiased methods, the MSE ratios indicate differences in the sampling variances. Thus, a lower MSE corresponds to lower sampling variance and higher power. We computed MSE ratios by dividing the MSE from scale-level FIML by the MSE from FIML with items as auxiliary variables, such that values greater than 1 indicate that incorporating item-level information increased power (i.e., the sampling variance is higher for the model without item-level information).¹

To illustrate, MSE ratios for conditions with uniform item means and inter-item correlations and a sample size of 500 are reported in Table 4. We focus on these conditions because the MSE ratios were largely unaffected by sample size (200 or 500) and uniformity of the mean and covariance structures. Overall, the MSE ratios suggest that incorporating items as auxiliary variables drastically increases power relative to scale-level FIML. Notice that all of the MSE ratios are greater than 1. As seen in Table 4, the benefit of incorporating item-level information was greater with a higher item-level missing data rate. For example, for conditions with eight items per scale, the MSE ratio for the regression coefficient was 1.32 with a 5% item-level missing data rate, 2.00 with a 15% item-level missing data rate, and 3.00 with a 25% item-level missing data rate. As stated earlier, MSE ratios are useful because they express efficiency differences on the sample size metric. MSE ratios of 1.32, 2.00, and 3.00 indicate that the sample size for an analysis using scale-level FIML would need to be increased by 32%, 100%, and 200%, respectively, to yield the same sampling variance (and thus power) as FIML with items as auxiliary variables. These findings are consistent with those from Gottschall et al. (2012), which showed that item-level imputation drastically increases power relative to scale-level imputation. Finally, incorporating item-level information appears to result in greater power gains with more items per scale. However, this effect is difficult to interpret because the proportion of cases with missing scale scores was somewhat higher with 16 items per scale than with eight items per scale.

Table 4.

Simulation Study 2, MSE Ratios Comparing FIML with All But One Item from Each Scale as Auxiliary Variables to Scale-Level FIML

		MSE Ratio
Parameter	Item-Level Missing Data Rate	8 Items Per Scale	16 Items Per Scale
Mean of X	5%	1.1852	1.4545
	15%	1.7778	3.0909
	25%	2.7931	7.1304
Mean of Y	5%	1.2083	1.4583
	15%	1.9600	3.0417
	25%	3.4000	6.1200
Variance of X	5%	1.2727	1.5778
	15%	1.8246	2.7778
	25%	2.4590	4.7234
Variance of Y	5%	1.3774	1.6327
	15%	1.9636	2.7400
	25%	2.5345	4.4600
Covariance	5%	1.2857	1.7586
	15%	1.9189	3.0345
	25%	2.8684	5.3333
Correlation	5%	1.2778	1.7059
	15%	1.9474	3.0000
	25%	2.9500	5.1111
Regression Coefficient	5%	1.3158	1.7222
	15%	2.0000	3.0556
	25%	3.0000	5.1053

Note. The table contains MSE ratios for conditions with a sample size of 500. The item means and inter-item correlations were uniform. All of the MSE ratios are greater than 1, meaning that incorporating all but one item from each scale as auxiliary variables provided lower MSEs and thus higher power.

Simulation Study 3

Methodologists have explained that incorporating too many auxiliary variables via the saturated correlates model can lead to convergence issues (Enders, 2010; Graham, 2012), perhaps due to the structure of the saturated correlate model’s error covariance matrix (Savalei and Bentler, 2009). As noted previously, we observed up to a 30% failure rate in conditions with 16 items per scale, a sample size of 200, and a 25% item-level missing data rate. As such, the purpose of the third simulation study is to investigate strategies that preserve item-level information while reducing the size of the auxiliary variable set. One potential solution is to define an auxiliary variable set that includes incomplete items and a composite of the complete items (e.g., a parcel computed as the mean of the complete items). Another potential solution is to incorporate fewer items as auxiliary variables (e.g., half rather than all but one of the items from each scale). Our review of proration applications suggests that authors rarely describe exact patterns of item-level missingness, so we have no way of knowing which of these two alternatives is more applicable in practice. Thus, we examined both strategies in this simulation study. Because the goal of this simulation is to examine the efficiency achieved by reducing the complexity of the auxiliary variable model, we use item-level imputation as a gold standard against which to compare the FIML approaches.

As before, we reused the data sets generated for the first simulation study to investigate three between-subject factors—number of items per scale (8 or 16), sample size (200 or 500), and item-level missing data rate (15% or 25%)—for conditions with uniform item means and inter-item correlations and an MAR-E mechanism. We limit our attention to conditions with uniform item means and inter-item correlations because varying the item means and inter-item correlations had no impact on the FIML model with items as auxiliary variables. We compared the following methods: (1) FIML with all but one item from each scale as auxiliary variables (i.e., the strategy from Study 2 that suffered from convergence problems), (2) FIML with all but one of the incomplete items from each scale plus a parcel based on the average of the complete items as auxiliary variables, (3) FIML with only the complete items (i.e., 50% of the items from each scale) as auxiliary variables, and (4) item-level imputation. Item-level imputation was implemented via chained equations imputation in the BLImP software program (Keller & Enders, 2014). After examining convergence diagnostics, we generated ten imputed data sets from an MCMC algorithm with 1000 burn-in and 500 thinning iterations. We then used Mplus 7 to perform the scale-level analyses and to pool the resulting parameter estimates and standard errors. Although BLImP implements a latent variable imputation scheme that accommodates ordinal variables, we imputed the items as though they were continuous because this procedure is consistent with Gottschall et al. (2012) and because it is analogous to FIML’s treatment of the item-level auxiliary information. As before, we included the external variable as an auxiliary variable in all analyses to satisfy the MAR assumption of FIML.

Simulation Study 3 Results

The standardized bias values were negligible across all conditions, so we focus strictly on MSE ratios. We computed MSE ratios by dividing the MSE from item-level imputation by the MSE from each FIML approach. Recall that for two unbiased methods, the MSE ratios indicate differences in the sampling variances. In this simulation, values less that unity occur when item-level imputation is more efficient (e.g., a value of .95 means that the item-level imputation sampling variance is 95% as large as that of FIML), and values greater than unity result when FIML is more efficient. MSE ratios for conditions with a sample size of 500 are reported in Table 5. We focus on conditions with a sample size of 500 because the MSE ratios did not appreciably differ across the two sample sizes (200 and 500).

Table 5.

Simulation Study 3, MSE Ratios Comparing FIML Approaches to Item-Level Imputation

			MSE Ratio
Parameter	Items Per Scale	Item-Level Missing Data Rate	All But One Item from Each Scale as Auxiliary Variables	Incomplete Items and Composite of Complete Items as Auxiliary Variables	Half of the Items from Each Scale as Auxiliary Variables
Mean of X	8	15%	1.0000	1.0000	0.9643
		25%	0.9655	0.9655	0.8182
	16	15%	1.0000	1.0000	0.8800
		25%	0.9565	0.9565	0.6875
Mean of Y	8	15%	0.9600	0.9600	0.8889
		25%	1.0000	1.0000	0.7742
	16	15%	1.0000	1.0000	0.8571
		25%	0.9600	0.9600	0.6857
Variance of X	8	15%	0.9825	0.9825	0.9180
		25%	0.9672	0.9833	0.8116
	16	15%	1.0000	1.0000	0.8824
		25%	0.9787	0.9787	0.7541
Variance of Y	8	15%	1.0000	1.0000	0.8871
		25%	0.9655	0.9655	0.7746
	16	15%	1.0000	1.0000	0.8621
		25%	1.0200	1.0200	0.7500
Covariance	8	15%	0.9459	0.9459	0.8974
		25%	0.9737	0.9737	0.8333
	16	15%	1.0000	1.0000	0.8788
		25%	1.0000	1.0000	0.7895
Correlation	8	15%	0.9474	0.9474	0.9000
		25%	0.9500	0.9500	0.8182
	16	15%	1.0000	1.0000	0.8947
		25%	0.9444	1.0000	0.7391
Regression Coefficient	8	15%	0.9500	0.9500	0.9048
		25%	0.9524	0.9524	0.7917
	16	15%	1.0000	0.9474	0.8571
		25%	1.0000	1.0000	0.7917

Note. The table contains MSE ratios for conditions with a sample size of 500. We can interpret the MSE ratios by saying that the FIML approach is (MSE Ratio × 100)% as efficient as item-level imputation.

As might be expected, comparing item-level imputation to the FIML approach that used all but one item produced MSE ratios quite close to 1, indicating that these two methods provide virtually the same power; values ranged from 0.936 to 1.020, and the average MSE ratio across all design cells and parameters was 0.979. Averaging the complete items and using the resulting composites and incomplete items as auxiliary variables gave very similar results, with MSE ratios ranging from 0.944 to 1.020 and an average MSE ratio of 0.981. These results are not surprising given that the two FIML approaches essentially transmit the same item-level information, albeit with a different number of parameters (i.e., with complete data, the correlation between a scale score and a parcel is a function of the correlations between the scale score and items that form the parcel). As expected, the FIML analysis that used just the complete items (i.e., 50% of the items) resulted in lower power than the other methods under investigation. Specifically, MSE ratios ranged from 0.667 to 0.964 and the average MSE ratio was 0.831 (i.e., this FIML approach was 83% as efficient as item-level imputation, on average). These results show that there is clearly a benefit to using incomplete items as part of the auxiliary variable set. We return to these results later in the paper, where we provide some practical recommendations for researchers.

Analysis Example

To illustrate the use of items as auxiliary variables, we used a subset of data from an online chronic pain management program (Ruehlman, Karoly, & Enders, 2012). At pretest, the researchers collected a number of demographic variables (e.g., age, gender), psychological variables (e.g., depression), and a pain severity scale. Participants in the treatment group participated in the online chronic pain management program for several weeks, whereas participants in the waitlist control group received no treatment. At the end of the intervention period, researchers administered (along with other measures) a scale assessing pain interference with daily life. For the purposes of this illustration, we consider a regression model where pain interference is predicted by pretest measures and treatment group membership, as follows.

$$\text{interference}={\beta }_0+{\beta }_1(\text{age})+{\beta }_2(\text{female})+{\beta }_3(\text{severity})+{\beta }_4(\text{depression})+{\beta }_5(\text{txgroup})+\epsilon$$ (2)

Note that pain severity is measured by a three-item scale, and depression and pain interference are each measured by a six-item scale.

We started with a subset of 200 participants with complete data, and we used this group to illustrate the application of FIML to a planned missing data design. As seen in Table 6, the planned missing data design consisted of four test forms (missing data patterns), with 25% of the sample randomly assigned to each form. The design is similar to the standard three-form design described by Graham and colleagues (Graham, Hofer, & MacKinnon, 1996; Graham et al., 2006), except that we included a complete-data pattern to ensure that all bivariate associations among the scales were estimable. Importantly, the scale items are distributed across forms, such that each participant provides data for at least one scale item. We chose this configuration because the missing data literature does not provide a clear prescription for dealing with items in these designs; some sources recommend keeping items together (e.g., participants provide data on some questionnaires but not others), whereas other sources recommend distributing items across forms, as in Table 6 (Graham et al., 1996; Graham et al., 2006; Gottschall et al., 2012). It is important to note that incorporating item-level information via auxiliary variables is only possible when items from the same questionnaire appear on different test forms.

Table 6.

Planned Missing Data Design for the Analysis Example

Form	Variable Block
	X	A	B	C
	Age	S1	S2	S3
	Gender	D1, D2	D3, D4	D5, D6
	Treatment	PI1, PI2	PI3, PI4	PI5, PI6
1	Observed	Missing	Observed	Observed
2	Observed	Observed	Missing	Observed
3	Observed	Observed	Observed	Missing
4	Observed	Observed	Observed	Observed

Note. S = severity, D = depression, PI = pain interference. Each test form (missing data pattern) was comprised of 25% of the sample.

After generating the missingness patterns in Table 6, we used Mplus 7 to estimate the regression model using scale-level FIML and FIML with all but one item from each scale as auxiliary variables. In addition to the regression analyses, we estimated bivariate correlations among the three scale scores. The appendix gives the Mplus 7 input file for the FIML analysis with items as auxiliary variables. Table 7 gives the correlation coefficients and 95% confidence intervals based on 2000 bootstrap samples; although the analyses included all variables from the regression model, we restrict our attention to the correlations among the scales. As seen in the table, the point estimates differed slightly across the two methods, presumably due to efficiency differences. The most striking aspect of the table is the width of the 95% confidence intervals. The confidence intervals from FIML with items as auxiliary variables were much narrower than those from scale-level FIML; confidence intervals were between 33% and 48% narrower. Not surprisingly, this increase in precision would translate into a substantial increase in power.

Table 7.

Analysis Example Scale Score Correlations and 95% Confidence Limits

Correlation	Estimate	LCL	UCL	Width
	No Auxiliary Variables
Interference-Severity	0.57	0.34	0.74	0.40
Interference-Depression	0.24	−0.06	0.50	0.56
Severity-Depression	0.08	−0.24	0.35	0.59
	Items as Auxiliary Variables
Interference-Severity	0.59	0.43	0.69	0.27
Interference-Depression	0.19	0.03	0.32	0.29
Severity-Depression	0.10	−0.10	0.25	0.35

Turning to the regression model from Equation 2, Table 8 gives the regression coefficients and 95% confidence intervals based on 2000 bootstrap samples. The regression analyses produced a similar pattern of results. The FIML analysis with auxiliary variables had confidence intervals that were between 28% and 50% narrower than those from scale-level FIML. To compare these results to those from the simulation studies, we computed the ratio of squared standard errors (i.e., the ratio of sampling variance estimates), which is analogous to the MSE ratio reported in the simulation studies. For the treatment group regression coefficient, the ratio of squared standard errors equaled 2.57 when using items as auxiliary variables. This ratio suggests that scale-level FIML would require a sample size 2.57 times larger to achieve the same sampling variance as the FIML analysis with item-level auxiliary information. Overall, the analysis results in Tables 6 and 7 closely follow those from the simulation studies.

Table 8.

Analysis Example Regression Coefficients and 95% Confidence Limits

Coefficient	Estimate	LCL	UCL	Width
	No Auxiliary Variables
Intercept	−2.75	−6.23	0.18	6.41
Treatment Group	−0.28	−0.97	0.39	1.36
Female	−0.19	−0.98	0.60	1.58
Age	0.02	−0.02	0.06	0.08
Severity	0.89	0.50	1.31	0.81
Depression	0.36	−0.07	0.81	0.89
	Items as Auxiliary Variables
Intercept	−2.77	−4.89	−0.85	4.04
Treatment Group	−0.38	−0.81	0.03	0.83
Female	−0.16	−0.63	0.28	0.91
Age	0.01	−0.01	0.04	0.04
Severity	0.94	0.66	1.24	0.58
Depression	0.28	0.02	0.54	0.52

Discussion

Researchers routinely rely on proration to address item-level missing data. Understandably, researchers do not want to lose power or ignore potentially useful data from a partially-complete set of item responses. As such, researchers are reluctant to treat a scale score as missing whenever one or more of the items are missing. However, our simulations suggest that proration often results in bias. Consistent with suggestions from the literature, our results indicate that proration can produce accurate parameter estimates when the mechanism is MCAR and the item means and inter-item correlations are similar in value (Enders, 2010; Graham, 2009; Graham, 2012). However, consistent with Lee et al. (2014), proration is prone to substantial bias when either the correlations or the means differ. This feature of proration is problematic because questionnaire items are often designed to discriminate at different levels of the latent trait. For example, when measuring depression with the BDI-II, the item asking about suicidal ideation will naturally have a different mean than the item asking about feeling sad. We would also expect some pairs of items (e.g., the two items pertaining to fatigue and loss of energy on the BDI-II) to be more highly correlated than others (e.g., the fatigue item and the suicidal ideation item). Under these common conditions, proration can produce severe bias, even when the mechanism is MCAR.

Given its propensity for bias, we recommend forgoing proration in favor of an FIML analysis with item-level auxiliary information. Using item-level information for missing data handling is intuitively appealing because within-scale item correlations tend to be much stronger than between-scale correlations. Gottschall et al. (2012) reported rather drastic power gains from item-level imputation, and we observed very similar results from an FIML analysis that used items as auxiliary variables. Not only did the auxiliary variable method improve power, but it also eliminated bias that resulted when items were the cause of missingness.

In our simulations, the FIML analysis that used the largest possible auxiliary variable set (all but one item per scale) provided virtually the same efficiency as item-level imputation. By contrast, using only half of the items in the auxiliary variable model produced a noticeable drop in power, such that FIML was roughly 83% as efficient as the gold standard imputation procedure. As noted previously, the two-stage approach proposed by Savalei and Rhemtulla (2014) may prove to be an ideal option because it uses all of the available item-level data. However, until this procedure becomes available in software packages, our results suggest that researchers should strive to include as much item-level information as possible. One strategy that worked well in Study 3 is to average the complete items and use the resulting parcel in the FIML analysis (in addition to using the incomplete items). This procedure eliminated convergence problems while achieving the same efficiency as the all-but-one-item approach. It is difficult to give good rules of thumb because data-specific features likely dictate the number of items that can be included before estimation problems result. Nevertheless, the message from Study 3 is clear: more is better.

Although we chose conditions for the simulation studies that were representative of published research, the generalizability of all simulation studies is limited. First, we investigated three missing data mechanisms: MCAR, MAR due to a variable external to the scales, and MAR due to complete items on each scale. In practice, the causes of missingness are likely much more complex. Multiple variables may predict missingness, and the causes of missingness may vary across participants or across incomplete variables. Furthermore, the causes of missingness may not have been measured during data collection. Thus, the deletion procedures that we implemented may produce results that do not fully generalize to all scenarios. Second, as noted previously, the factor analysis model that we used as a population model produced scale scores with rather high internal consistency reliability. Although we anticipate that incorporating item-level information is beneficial in most cases, it may be less so when the inter-item correlations (and thus reliability) are lower. Future studies should investigate this issue. Third, the FIML approach assumes multivariate normality, but the items used as auxiliary variables in our simulations were not normally distributed; we chose categorization thresholds that produced symmetric distributions, but discrete variables are nonnormal by definition. Nevertheless, Rhemtulla, Brosseau-Liard, and Savalei (2012) suggested seven-category variables with symmetric thresholds may be treated as continuous. More severe violations of the multivariate normality assumption are common in practice (e.g., dichotomous items, items with highly skewed distributions). Future research should investigate the FIML approach with fewer response categories and different distribution shapes. Under these conditions, FIML may not perform as well as an imputation procedure that employs an appropriate model for the categorical variables (e.g., latent variable imputation; Keller & Enders, 2014).

In sum, our research suggests that proration results in bias even under an MCAR mechanism. In lieu of proration, we describe an FIML model that incorporates items as auxiliary variables. Consistent with Gottschall et al. (2012), we found that addressing missing data at the item level rather than the scale level drastically increases power. Our research further indicates that item-level missing data handling can protect against MAR violations that occur when items determine missingness. As such, we strongly recommend that researchers forgo proration and perform item-level missing data handling with MAR-based analyses.

Appendix

Mplus 7 Input File

To compute the scale scores used in the analysis model, add the items using the SUM function and then divide by the number of items. By using the SUM function, we only compute scale scores for cases with observed scores on all of the items. By contrast, the MEAN function computes the average regardless of item-level missing data, thus creating prorated scale scores. Below we show how to manually incorporate auxiliary variables, but this process can be automated using the AUXILIARY option with (m).

TITLE:

Regression Analysis with Items as Auxiliary Variables

DATA:

file = plannedmissing.dat;

VARIABLE:

names = txgrp female age

 sever1 sever2 sever3

 dep1 dep2 dep3 dep4 dep5 dep6

 interf1 interf2 interf3 interf4 interf5 interf6;

usevariables = txgrp female age

 sever2 sever3 dep2-dep6 interf2-interf6

 severity depress interf;

missing = all(−99);

DEFINE:

severity = sum(sever1-sever3) / 3;

depress = sum(dep1-dep6) / 6;

interf = sum(interf1-interf6) / 6;

ANALYSIS:

bootstrap = 2000;

MODEL:

interf on txgrp female age severity depress;

sever2 sever3 dep2-dep6 interf2-interf6 with

 txgrp female age interf severity depress

 sever2 sever3 dep2-dep6 interf2-interf6;

OUTPUT:

cinterval(bootstrap);