Abstract
Plasmodium falciparum is an obligate intracellular protozoan parasite that employs a highly sophisticated mechanism to access the protective environment of the host cells. Key to this mechanism is the formation of an electron dense ring at the parasite-host cell interface called the Moving Junction (MJ) through which the parasite invades. The MJ incorporates two key parasite components: the surface protein Apical Membrane Antigen 1 (AMA1) and its receptor, the Rhoptry Neck Protein (RON) complex, the latter one being targeted to the host cell membrane during invasion. Crystal structures of AMA1 have shown that a partially mobile loop, termed the DII loop, forms part of a deep groove in domain I and overlaps with the RON2 binding site. To investigate the mechanism by which the DII loop influences RON2 binding, we measured the kinetics of association and dissociation and binding equilibria of a PfRON2sp1 peptide with both PfAMA1 and an engineered form of PfAMA1 where the flexible region of the DII loop was replaced by a short Gly-Ser linker (ΔDII-PfAMA1). The reactions were tracked by fluorescence anisotropy as a function of temperature and concentration and globally fitted to acquire the rate constants and corresponding thermodynamic profiles. Our results indicate that both PfAMA1 constructs bound to the PfRON2sp1 peptide with the formation of one intermediate in a sequential reversible reaction: A↔B↔C. Consistent with Isothermal Titration Calorimetry measurements, final complex formation was enthalpically driven and slightly entropically unfavorable. Importantly, our experimental data shows that the DII loop lengthened the complex half-life time by 18-fold (900 s and 48 s at 25°C for Pf and ΔDII-Pf complex, respectively). The longer half-life of the Pf complex appeared to be driven by a slower dissociation process. These data highlight a new influential role for the DII loop in kinetically locking the functional binary complex to enable host cell invasion.
Introduction
Parasites in the phylum Apicomplexa include the etiological agents of malaria and toxoplasmosis. Malaria is a major health problem in much of the tropical and subtropical countries with an estimated 207 million cases in 2012 and 627,000 deaths, most of them children [1]. Amongst the 5 malaria species that affect humans, Plasmodium falciparum (Pf) is the most deadly form. Despite continuous efforts in vaccine development, prevention of malaria remains difficult and the spread of drug-resistant parasites highlights the critical need for new antimalarial strategies [2].
The invasion machinery is highly conserved in apicomplexan parasites and involves a structure called the moving junction (MJ) formed between the apex of the parasite and the host cell membrane [3]. The MJ anchors the parasite to the host cell membrane and allows its active internalization into a protective parasitophorous vacuole (PV). The MJ is initiated by injection of the Rhoptry Neck (RON) complex into the host cell, where RON2 spans the membrane and functions as a receptor for the Apical Membrane Antigen 1 (AMA1) protein located on the parasite surface [4–7]. It was recently reported that these proteins are essential for host cell invasion by P. falciparum and T. gondii [8, 9]. Plasmodium spp. encodes single copies of AMA (AMA1) and RON2 whose interaction is critical for invasion. Antibodies or peptides that prevent formation of the AMA1-RON2 complex also block invasion [10–17]. Therefore, disrupting the AMA1-RON2 complex offers new strategies for the development of anti-infectives.
Structural studies of ectodomains of AMA1 revealed a stacked three-domain architecture (DI, DII and DIII). Domains I and II are closely associated PAN domains that form a long and conserved hydrophobic trough partially occupied by a loop extending from domain II called DII loop [11, 12, 18, 19]. Analysis of AMA1 structures in apo and complex forms with antibodies or peptide inhibitors revealed that the DII loop is flexible and can adopt multiple conformations [11–13, 18–23]. In PfAMA1, the DII loop encompasses residues 346 to 395 (50 amino acids) that undergoes a substantial conformational change to reveal the binding site for PfRON2 [21]. Indeed, the crystal structure of P. falciparum AMA1 in complex with a 39-mer [2021–2059] PfRON2 peptide (sp) showed that the DII loop was disordered [23]. Notably, this small PfRON2sp synthetic peptide is able to compete in the nanomolar range with the native RON2 for AMA1 interaction in vivo [23].
The absence of polymorphisms in the DII loop suggests an important function for this substructure [24]. Recently, Parker et al. reported that the DII loop in T. gondii is able to regulate AMA1 selectivity for its cognate RON2 by competitive binding [25]. In this study, authors engineered a ΔDII-loop form of TgAMA1 where the DII loop (residues 333–369) was replaced by a short Gly-Ser linker. This truncated form of TgAMA1 preserved a similar affinity for TgRON2 [25]. In the present study, we investigated the kinetics and the thermodynamics of the interaction between PfRON2sp1 and both native and ΔDII-loop forms of PfAMA1. In contrast to T. gondii, the ΔDII-loop form of PfAMA1 exhibits a 2-fold weaker affinity for its PfRON2sp synthetic peptide. Our results provide the kinetic and thermodynamic rationale for a stabilizing role of the DII loop in P. falciparum AMA1-RON2 complex.
Materials and Methods
Peptides Synthesis (Table 1)
Table 1. PfRON2sp synthetic peptides.
Peptides were cyclized at the cysteine residues (bold). Unlabeled peptides were used for the complex dissociation experiments. F*: 5-carboxyfluorescein (5-FAM).
| Peptide name | Sequence |
|---|---|
| PfRON2sp1 (39 aa)[2021–2059] | DITQQAKDIGAGPVASCFTTRMSPPQQICLNSVVNTALS |
| F*PfRON2sp1 (39 aa)[2021–2059] | 5-FAM-DITQQAKDIGAGPVASCFTTRMSPPQQICLNSVVNTALS |
Unlabeled and fluorescein-labeled (F*) peptides corresponding to residues 2021–2059 of PfRON2sp1 were purchased from Kinexus (Vancouver, Canada) with a purity ≥ 95% and were disulfide cyclized. The labeled peptide is referred as F*PfRON2sp1.
PfAMA1 recombinant protein production
A codon-optimized gene encoding DI-DII of PfAMA1 3D7 [26] (residues 104–438; numbering based on the initiation methionine in the signal sequence, PF11_0344) was synthesized by GenScript and subcloned into a modified pAcGP67B vector (Pharmingen) for expression in insect cells using established protocols [22]. For the ΔDII-PfAMA1 construct, the segment KQYEQHLTDYEKIKEGFKNKNASMIKSAFLPTGAFKA (residues 351 to 387) within the PfAMA1 DI-DII construct was replaced with 7 Gly/Ser residues, and Ser/Thr residues in predicted N-linked glycosylation sites (NxS/T) were mutated to Ala. Proteins were purified by Ni-affinity chromatography, cleaved with thrombin to remove the hexa-histidine tag, further purified by size exclusion chromatography, and concentrated to between 4.5 and 20 mg/mL. Final yield of recombinant protein was between 3 and 20 mg per L of culture.
PfRON2D3 production
A sequence encoding a portion of PfRON2D3 (amino acids Asp2021 to Ser2059) was synthesized and subcloned into a modified pET32a vector (Novagen) incorporating N-terminal hexahistidine and thioredoxin (TRX) tags with a thrombin cleavage site. The fusion protein was produced in E. coli BL21 cells. For ITC experiments, thioredoxin fusion of PfRON2D3 was produced in E. coli BL21 cells and purified by nickel-affinity and SEC.
Isothermal Titration Calorimetry
Purified PfAMA1, ΔDII-PfAMA1, and PfRON2D3-TRX were dialyzed against ITC buffer (20 mM Hepes pH 7.5, 150 mM NaCl) at 4°C. All ITC experiments were carried out at 25°C on a MicroCal iTC200 instrument. The sample cell contained PfAMA1 or ΔDII-PfAMA1 (10 μM), and PfRON2D3-TRX (110 μM) was added in 17 injections of 2.2 μL each. For TRX-fused peptide, TRX was injected as a negative control and showed no detectable binding. Data were processed using Origin software (MicroCal) and the dissociation constants (Kd) were determined using a one binding site model.
Equilibrium Titrations and Kinetic Studies of PfAMA1-PfRON2sp1
All measurements were carried out in PBS buffer at pH of 7.4 with at least 0.1% BSA (Bovine Serum Albumin) on 96-well, black, flat microplates, made of a nonbinding surface (NBS) polystyrene nonionic hydrophilic surface (Cat No. 3993; Corning, Amsterdam, Netherlands).
Data acquisition was carried out on a Wallac 2103 HTS Microplate EnVision Reader, PerkinElmer (Wallac Oy) operated by Wallac EnVision Manager 1.12. The anisotropy (r) and total fluorescence (F) values were measured and stored in spreadsheets (S1 Text). The instrument was equipped with an: EnVision-2102 temperature control; Hamamatsu photomultiplier tube (R10130-10, serial No. AP7666); UV-Xenon fast tube lamp with spectral range 230–1100 nm; an optical module (481 FITC FP D505fp/D535, diameter 150 mm); 480 nm excitation filter (X480, 30 nm bandwidth, 70% T, 150 mm diameter); 535 nm S orientated emission filter (40 nm bandwidth, 80% T, 150 mm diameter); 535 nm P orientated emission filter (40 nm bandwidth, 80%T, 150 mm diameter). Titration scans were carried out by row-bi-directional, 10 flashes, 5–6 mm height, with a G factor of 1.04 and 750 PMT gain.
All experiments were carried out at 20°C, 25°C and 30°C with the temperature measured inside the wells with a thermocouple VWR traceable® (-200°C to 1370°C) with an error range of +/- 0.1°C. Long incubation times were allowed for uniformed temperature distribution of the plates for each of the 96 wells.
Binding titration experiments
Binding titration experiments were carried out with 10 nM of fluorescein labeled probe titrated with an increasing amount of protein (0 to 10 μM). Titration data was fitted by a nonlinear regression model embed in a simplex minimization routine solving the quadratic version of Eq 1 (S2 Text) where Kd is the dissociation constant, Y is the fraction saturation, P is the free protein, XT is the total labeled peptide (F*PfRON2sp1) and PT is the total protein [27]:
| (1) |
Association and dissociation kinetics
The association reactions were acquired with a final concentration of 10 nM of the labeled probe and 50, 100 and 200 nM of PfAMA1 and ΔDII-PfAMA1 proteins for concentration dependence experiments. The dissociation reactions were carried out with 10 nM of the preformed complex challenged with the unlabeled ligand (PfRON2sp1) at concentrations of 2500 nM and 5000 nM, for a 250× and 500× excess, respectively. A total of 48 association reactions and 12 dissociation reactions were collected at 20, 25 and 30°C, with data points collected at interval of 6 seconds for at least 10–15 minutes and stored in spreadsheets as a function of time. The kinetic traces were well described by double-exponential functions (S1 Table). Data sets were used in the global fitting step described below in order to propose the most probable reaction mechanism.
Global fitting procedure to calculate rate constants and reaction models
The association and dissociation kinetic data sets were fitted globally to extract rate constants (k) as a function of temperature according to the Arrhenius relationship (Eq 2) where Ea is the activation energy, A is the pre-exponential factor, T is the temperature in Kelvin degrees and R is the gas constant (1.987 cal K-1 mol-1).
| (2) |
We used the global fitting algorithm [27] to evaluate rate constants according to three reaction mechanisms: 1) A simple reversible reaction model (Eq 3) with two rate constants (k1, k2), a transition state (‡) and two activation energies (Ea1 and Ea2) for forward and reverse reactions.
| (3) |
2) A one-intermediate reversible reaction model (Eq 4) with two transition states (‡1 and ‡2), four rate constants (k1 to k4) and four activation energies (Ea1 to Ea4).
| (4) |
3) A unimolecular conversion between an inactive (A) and an active (A*) state of the protein (Eq 5).
| (5) |
The differential equations for the simplest model (Eq 3) is presented in the following matrix form (Eq 6) [28] which contains all species involved in the reaction such as unlabeled proteins (A), labeled peptide (B, F*PfRON2sp1) and complex (C, e.g. PfAMA1-F*PfRON2sp1). The kinetic response function (Eq 7) includes the specie concentrations calculated with the matrix, the quantum yield (QY) and anisotropy values (r) of the fluorescent species [29]. The resulted rate constants let us calculate the Kd (Eq 8).
| (6) |
| (7) |
| (8) |
The differential equations for the second model with one intermediate (Eq 4) is shown in Eq 9 in which C is the fluorescent intermediate and D the final complex. The kinetic response function and the Kd calculation are shown in Eq 10 and Eq 11, respectively.
| (9) |
| (10) |
| (11) |
The differential equations for the third model representing a conversion between an inactive (A) to an active state (A*) of the protein (Eq 5) is shown in Eq 12 in which B is the labeled peptide and C is the final complex. The kinetic response function and the Kd calculation are shown in Eq 13 and Eq 14, respectively.
| (12) |
| (13) |
| (14) |
Model evaluation
The global fitting procedure optimizes rate constants and activation energies by reducing the Residual Sum of Squared (RSS) between observed and calculated data points from association and dissociation experiments as well as Kd values at each temperature and concentration. In order to evaluate each model, we also calculated the Akaike selection criterion value (AIC) (Eq 15) [30, 31]. The AIC formula considers the number of estimated parameters k’ (e.g. rate constants and activation energies), the global Residual Sum of Squared (RSS) and the number (N) of observations (S3 Text). The term k’ adds a penalty to avoid an overfitting when the number of parameters increases. The lowest AIC value indicates the most probable model to describe the observed data.
| (15) |
Thermodynamics of the transition states (‡)
ΔH‡ ΔS‡ and ΔG‡ can be acquired by applying Eq 16 and the Eyring equation (Eq 17) [32] where k is the rate constant, kB is the Boltzmann’s constant (3.3 x 10−24 cal K-1) and h is the Planck’s constant (1.58 x 10−34 cal s).
| (16) |
| (17) |
Overall thermodynamic parameters
Overall thermodynamic parameters were calculated by two approaches: 1) by the summation of the transition-state parameters which were obtained by the global fitting of the kinetic data (Eq 16 and Eq 17). For example, the enthalpy cycle ΔΔH° was calculated by using enthalpies of activation (Eq 18). A similar summation can be carried out for the entropy ΔΔS° and for the free energy ΔΔG°.
| (18) |
2) by Isothermal Titration Calorimetry (ITC) experiments.
Results
The DII loop promotes a higher affinity interaction between PfAMA1 and PfRON2sp1 peptide
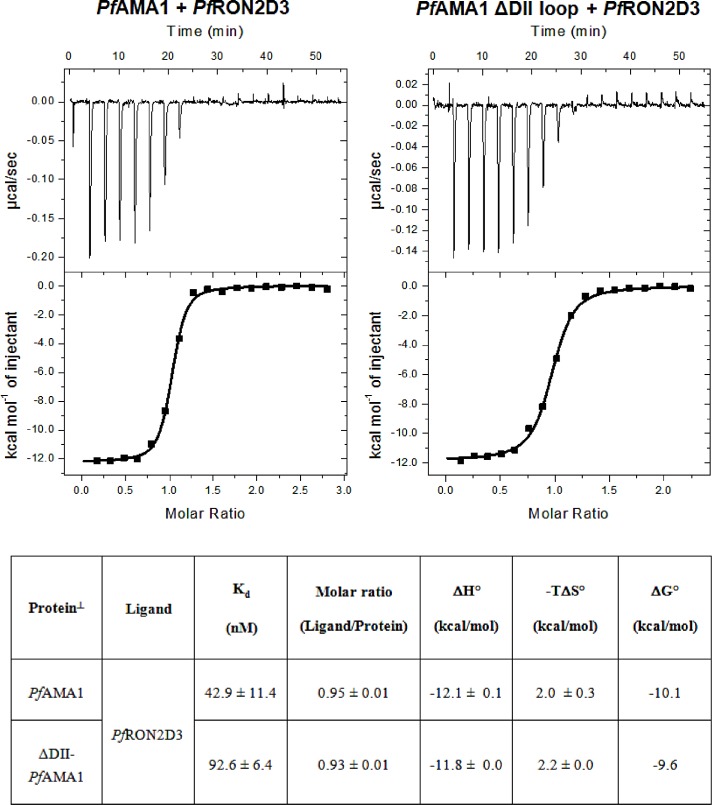
A ΔDII-PfAMA1 recombinant protein was constructed by replacing the segment KQYEQHLTDYEKIKEGFKNKNASMIKSAFLPTGAFKA (residues 351 to 387) within the PfAMA1 DI-DII construct with 7 Gly/Ser residues. Then, the equilibrium binding studies of PfAMA1 and ΔDII-PfAMA1 complexes were investigated by the change of fluorescence anisotropy upon binding (Fig 1) and by Isothermal Titration Calorimetry (ITC) (Fig 2). The anisotropy binding titrations were acquired with an increasing amount of unlabeled protein added to a constant amount of labeled peptide at 20°C, 25°C and 30°C. PfAMA1 bound to PfRON2sp1 peptide with an affinity of 42 nM, consistent with previously published SPR measurement (Table 2) [23]. These results correlated well with the data obtained from ITC experiments for PfRON2sp1 binding to PfAMA1 and ΔDII-PfAMA1 at 25°C (Fig 2 and Table 2). The truncated form ΔDII-PfAMA1 showed a 2-fold weaker affinity to the same PfRON2sp1 (92 nM). These results suggested an intriguing mechanism whereby the PfAMA1 DII loop enables a tighter interaction with PfRON2sp1.
Fig 1. Titration experiments: A) PfAMA1-F*PfRON2sp1, B) ΔDII-PfAMA1-F*PfRON2sp1 at 20°C (blue), 25°C (yellow) and 30°C (red) titrated with an increasing amount of protein and 10 nM of labeled peptide.
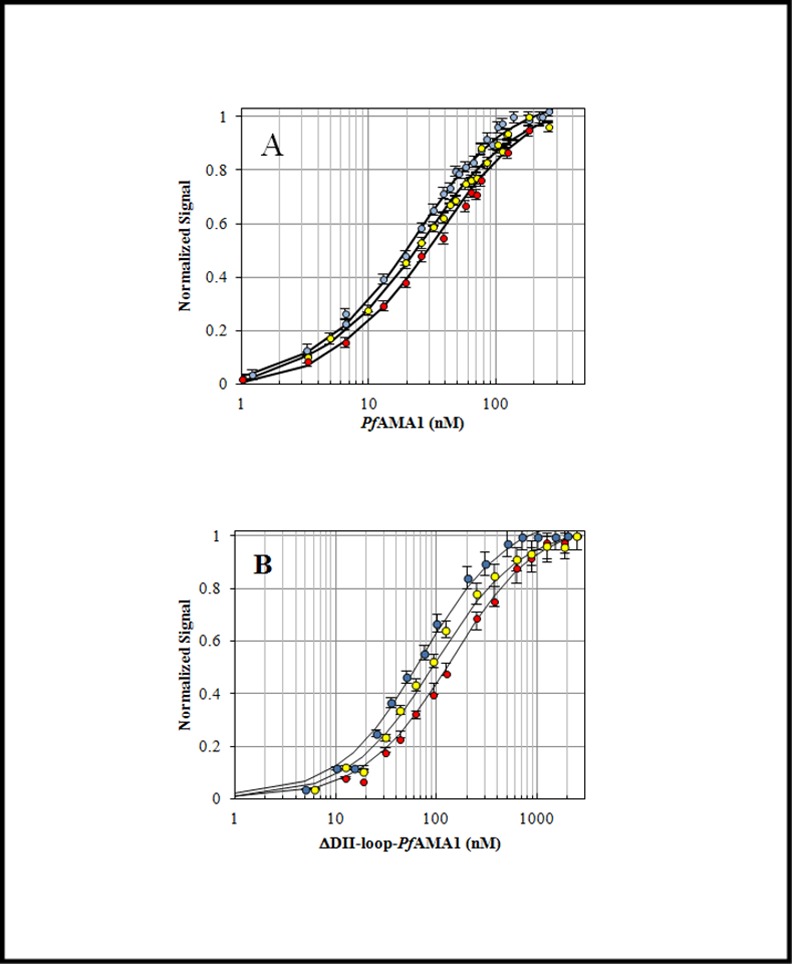
Solid lines represent the best fit (method in S2 Text). Error bars represent one standard deviation in the fluorescence-based experiments.
Fig 2. Isothermal Titration Calorimetry at 25°C.
A constant amount of protein (10 μM) was titrated with an increasing amount of PfRON2D3-TRX. Tabulated results represent the average of two experiments with standard deviation.
Table 2. Comparison of equilibrium dissociation constants (Kd) of complexes.
| Complex | Anisotropy Titration¶ Kd (nM) | Complex | ITC¶Kd (nM) | SPRKd (nM) | ||
|---|---|---|---|---|---|---|
| 20°C | 25°C | 30°C | 25°C | Room temp | ||
| PfAMA1-F*PfRON2sp1 | 31.0 ± 2 | 43 ± 3 | 61.0 ± 5 | PfAMA1-PfRON2D3 | 42.9 ± 11.4 | 20.3 ±6.3[23] |
| ΔDII-PfAMA1-F*PfRON2sp1 | 60 ± 5 | 94.0 ± 5 | 125 ± 10 | ΔDII-PfAMA1-PfRON2D3 | 92.6 ± 6.4 | ND |
¶Anisotropy titrations were carried out with an increasing amount of protein added to a constant amount of labeled probe (10 nM). In contrast, Isothermal Titration Calorimetry (ITC) experiments were carried out with a constant amount of protein and an increasing amount of peptide. ND: not determined.
The DII loop affects the binding kinetics
To probe the underlying mechanism by which the DII loop contributes to RON2 binding, we measured the association kinetics of both PfAMA1 and ΔDII-PfAMA1 with the peptide and dissociation for both Pf and ΔDII-Pf complex when challenged with unlabeled PfRON2sp1 peptide. In all cases, these association and dissociation experiments showed a biphasic behavior with a fast and a slow phase (Fig 3) suggesting an elaborate reaction mechanism (Eq 4 or Eq 5) instead of a simple and reversible mechanism (Eq 3).
Fig 3. Temperature dependence of association and dissociation kinetics: PfAMA1-F*PfRON2sp1 (A, B) and ΔDII-PfAMA1-F*PfRON2sp1 (C, D) at 20°C (blue), 25°C (yellow) and 30°C (red).
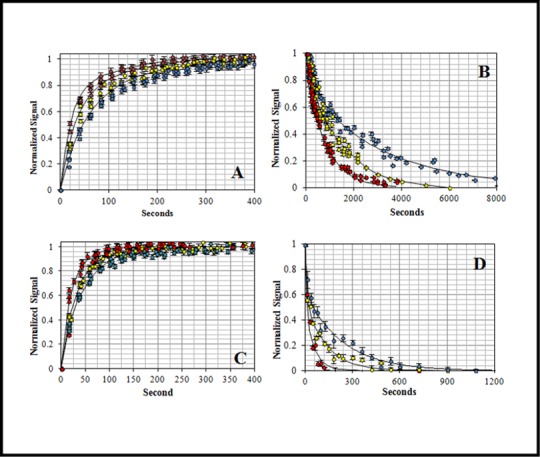
The association (A and C) and dissociation (B and D) reaction rates increased as temperature increases accordingly to positive activation energies. Complex dissociation curves were acquired by challenging a preformed complex (10 nM) with unlabeled PfRON2sp1 (500x excess). The solid black lines are the globally fitted data according to the one-intermediate model (Eq 4). Error bars represent one standard deviation in the fluorescence-based experiments.
The association reactions were collected at 20°C, 25°C and 30°C (Fig 3A and 3C) to acquire the forward association rate constants (kon) as a function of temperature. In all cases, the reaction signal increased as the reaction progressed and the complex was formed. The kinetic traces were initially analyzed using a double-exponential function (S1 Table). The association reactions showed a proportional increase in the rate when PfAMA1 and ΔDII-PfAMA1 concentrations increased from 50 nM to 200 nM for a ratio of 5×, 10× and 20× with respect to the F*PfRON2sp1 concentration (Fig 4A and 4B). These data are consistent with a bimolecular reaction where the rate constants depend on the concentration of both protein and peptide reactants. Importantly, the observed homogeneity and linearity of the plots indicated that aggregation effects can be excluded under these reaction conditions.
Fig 4. Concentration dependence of the association and dissociation kinetics: Association: A) PfAMA1 at 50 nM (blue), 100 nM (gold) and 200 nM (green) reacting with F*PfRON2sp1 (10 nM). B) ΔDII-PfAMA1 at 50 nM (blue), 100 nM (gold) and 200 nM (green) reacting with F*PfRON2sp1 (10 nM). The reaction speed increased proportionally to protein concentration. The curves showed a biphasic behavior suggesting the presence of a two-step reaction mechanism. Dissociation: C) PfAMA1-F*PfRON2sp1 at three temperatures (20°C, 25°C and 30°C) and D) ΔDII-PfAMA1-F*PfRON2sp1 at 20°C challenged with unlabeled PfRON2sp1 at 2500 nM (250x excess, gold, solid line) and 5000 nM (500x excess, green, dashed line).
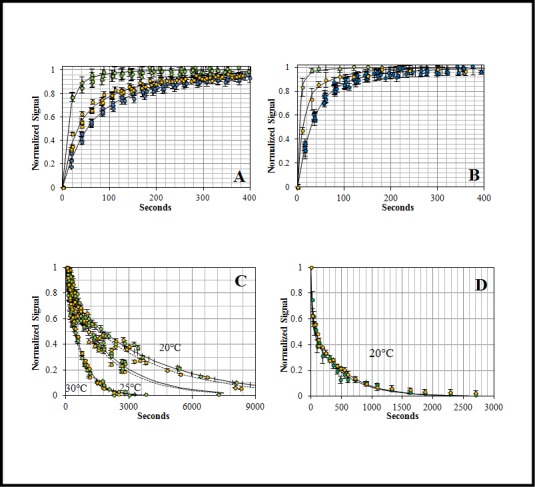
Both complex dissociations showed no concentration dependence. The concentration independence indicated the existence of a unimolecular process where the unlabeled peptide waits for the spontaneous leaving of the labeled peptide (F*PfRON2sp1) from the binding site. Error bars represent one standard deviation in the fluorescence-based experiments.
The dissociation experiments of the preformed complexes were carried out at the same temperatures (20, 25 and 30°C) using the unlabeled PfRON2sp1 peptide as the competing ligand in order to track the dissociation rate constants (koff) (Fig 3B and 3D). As the labeled peptide was replaced in the complex, the signal decreased as a function of time. For both complexes, the koff increased with increasing temperature. Interestingly, despite increasing the amount of unlabeled peptide (250× and 500×), the speed of the reaction remained unchanged for Pf and ΔDII-Pf complexes (Fig 4C and 4D). The concentration-independence of the dissociation suggested a unimolecular mechanism of dissociation, independent of colliding, in which the labeled-bound peptide must first leave the binding site before accommodating the unlabeled peptide.
Determination of the most probable reaction mechanism that describes the kinetics
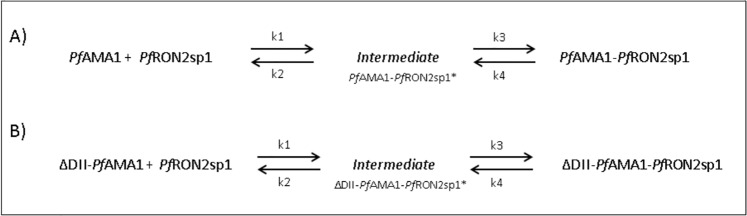
The strong biphasic association and dissociation curves of the complexes are indicative of an elaborate reaction mechanism (Fig 3 and S1 Table). Nevertheless, we evaluated three different models: 1) a simple reversible model (Eq 3), 2) a one-intermediate model (Eq 4) and 3) a model that involves activation (conformational conversion) of the protein (Eq 5). The differential equations of these models were embedded in a simple minimization algorithm previously described [27] to obtain the rate constants simultaneously as a function of temperature and concentration. When comparing models, the Akaike selection criterion (AIC) value was in favor of the one-intermediate model (Table 3, S3 Text, S2 Fig and S3 Fig and Fig 5) for both PfAMA1 and ΔDII-PfAMA1 reactions (Table 4, Figs 3 and 4 (solid lines)). The selection of the one-intermediate model was also supported by the excellent agreement with experimental complex half-life, which is defined as the time required for 50% of the complex decay (Table 5).
Table 3. Model Evaluation.
The most probable model has the lowest AIC value. The AIC criteria considers the goodness of the fit and places a penalty when the number of fitting parameters (k’) is increased (Eq 15). For F*PfRON2sp1 reacting with PfAMA1 and ΔDII-PfAMA1 proteins, the lowest value in both cases was achieved with the one-intermediate model.
| Reaction | Model | k’ | N*ln(RSS/N) | AIC |
|---|---|---|---|---|
| PfAMA1 + F*PfRON2sp1 | one-intermediate | 8 | -7.9 | 8.1 |
| PfAMA1 + F*PfRON2sp1 | simple | 4 | 14.1 | 22.1 |
| PfAMA1 + F*PfRON2sp1 | interconversion | 8 | 18.3 | 34.3 |
| ΔDII-PfAMA1 + F*PfRON2sp1 | one-intermediate | 8 | -14.6 | 1.4 |
| ΔDII-PfAMA1 + F*PfRON2sp1 | simple | 4 | 7.5 | 15.5 |
| ΔDII-PfAMA1 + F*PfRON2sp1 | interconversion | 8 | -5.4 | 10.6 |
Fig 5. Two-step reaction mechanism with one-intermediate state (I) of PfRON2sp1 peptide binding to A) PfAMA1 and B) ΔDII-PfAMA1.
Table 4. Calculated rate constants for Pf complexes for a one-intermediate model.
| PfAMA1-PfRON2sp1 | 20°C | 25°C | 30°C |
| k1 (M-1s-1) | 73500 (± 9460) | 114600 (± 12600) | 176000 (± 21000) |
| k2 (s-1) | 0.00478 (± 0.001) | 0.00759 (± 0.001) | 0.0119 (± 0.002) |
| k3 (s-1) | 0.00041 (± 0.0001) | 0.00053 (± 0.0002) | 0.00069 (± 0.0002) |
| k4 (s-1) | 0.0004 (± 0.0001) | 0.00072 (± 0.0002) | 0.00127(± 0.0004) |
| k1/k2 (× 106 M-1) | 15.4 (± 2.9) | 15.1 (± 2.8) | 14.8 (± 2.8) |
| k3/k4 | 1.0 (± 0.3) | 0.7 (± 0.2) | 0.5 (± 0.15) |
| Ka (μM) | 30.9 (± 8) | 26.2 (± 7) | 22.9 (± 6) |
| Kd (nM) | 32.3 (± 8) | 38.2 (± 10) | 43.8 (± 11) |
| ΔDII-PfAMA1-PfRON2sp1 | 20°C | 25°C | 30°C |
| k1 (M-1s-1) | 78900 (± 6300) | 116000 (± 9700) | 168400 (± 15000) |
| k2 (s-1) | 0.00417 (± 0.001) | 0.0099 (± 0.001) | 0.0229 (± 0.003) |
| k3 (s-1) | 0.00459 (± 0.002) | 0.0074 (± 0.003) | 0.0117 (± 0.004) |
| k4 (s-1) | 0.0812 (± 0.03) | 0.1099 (± 0.04) | 0.1473 (± 0.06) |
| k1/k2 (× 106 M-1) | 18.93 (± 2.5) | 11.70 (± 1.6) | 7.35 (± 1.0) |
| k3/k4 | 0.056 (± 0.01) | 0.067 (± 0.02) | 0.080 (± 0.02) |
| Ka (μM) | 20.0 (± 6.0) | 12.5 (± 3.8) | 7.9 (± 2.4) |
| Kd (nM) | 50.0 (± 15) | 80.1 (± 24) | 126.0 (± 38) |
Table 5. Observed and calculated complex dissociation half-life.
| Complex half-life⊥ | 20°C | 25°C | 30°C | |
|---|---|---|---|---|
| PfAMA1-F*PfRON2sp1 | Kd (nM) | 31.0 ± 2 | 43 ± 3 | 61.0 ± 5 |
| PfAMA1-F*PfRON2sp1 | Experimental | 1641 s (27.4 min) | 900 s (15.0 min) | 554 s (9.2 min) |
| PfAMA1-F*PfRON2sp1 | Calculated | 1730 s (28.8 min) | 960 s (16.0 min) | 544 s (9.1 min) |
| ΔDII-PfAMA1-PfRON2sp1 | Kd (nM) | 60.0 ± 5 | 94.0 ± 5 | 125 ± 10 |
| ΔDII-PfAMA1-PfRON2sp1 | Experimental | 100 s (1.6 min) | 48 s (0.8 min) | 30 s (0.5 min) |
| ΔDII-PfAMA1-PfRON2sp1 | Calculated | 166 s (2.8 min) | 69.9 s (1.2 min) | 30 s (0.5 min) |
⊥ Observed complex half-life, t1/2 = ln2 /koff slower [39]
Calculation of the thermodynamic parameters
The calculated thermodynamic parameters (Eq 16 and Eq 17) were in very good agreement with those obtained by ITC (Fig 2 and Table 6). Here, the enthalpy of activation (ΔH°‡) was calculated using the globally fitted Arrhenius temperature-dependent rate constants (Eq 2 and Eq 16) and the Gibbs free energy of activation (ΔG°‡) was calculated using the Eyring’s equation (Eq 17) to further deduce the entropy of activation (ΔS°‡). Finally, the global thermodynamic parameters ΔΔG°, ΔΔH° and -TΔΔS° of the reactions were calculated by the summation of the transition state energy values (Fig 6 and Table 6) [32]. Formation of both the PfAMA1-PfRON2sp1 and ΔDII-PfAMA1-PfRON2sp1 complexes were enthalpically driven but slightly entropically unfavorable (Fig 6 and Table 6) consistent with ITC results (Fig 2). Nevertheless, ΔDII-PfAMA1 reaction with F*PfRON2sp1 differed both in enthalpy and entropy profiles as indicated their calculated values at transition and intermediate states in Fig 6 (slashed line) to those of PfAMA1 reacting with the same peptide (solid line). Indeed, the intermediate (I) for Pf complex was entropically driven with a value of -TΔΔS°(I) = -9.13 Kcal/mol with a small change in ΔΔH°(I) = -0.67 Kcal/mol, whereas the intermediate (I) for ΔDII-Pf complex was enthalpically driven with a value of ΔΔH°(I) = -16.7 Kcal/mol but with an unfavorable entropy value of -TΔΔS°(I) = +7.06 Kcal/mol (Fig 6). These calculations indicate that despite the absence of the DII loop, which resulted in differences in entropy and enthalpy energies of the intermediate state, the same final complex is obtained where PfRON2sp1 is anchored at both ends of the PfAMA1 binding groove [25].
Table 6. Summary of the thermodynamic parameters for the binding of PfRON2sp1 to PfAMA1 and ΔDII-PfAMA1.
Calculations were carried out at 25°C, 1 M standard state and 1 atm according to the Eyring equation that relates rate constants with transition state thermodynamics [32].
| Reaction | Free energy(Kcal/mol) | Enthalpy(Kcal/mol) | Entropy(cal/°Kmol) | -TΔSi°(Kcal/mol) |
|---|---|---|---|---|
| PfAMA1-PfRON2sp1 | ||||
| Reactants‡1 | 10.55 | 15.39 | 16.24 | -4.84 |
| Intermediate ‡1 | 20.34 | 16.06 | -14.37 | 4.29 |
| Intermediate ‡2 | 21.9 | 9.42 | -41.91 | 12.5 |
| Complex ‡2 | 21.74 | 20.39 | -4.53 | 1.35 |
| Overall ⊥ | ΔΔG° = -9.63 | ΔΔH° = -11.64 | ΔΔS° = -6.77 | -TΔΔS° = 2.02 |
| ITC | ΔG° = -10.1 | ΔH° = -12.1 ± 0.1 | ΔS° = -6.7 | -TΔS° = 2.0 ± 0.3 |
| ΔDII-PfAMA1-PfRON2sp1 | ||||
| Reactants‡1 | 10.54 | 13.40 | 9.57 | -2.85 |
| Intermediate ‡1 | 20.18 | 30.10 | 33.25 | -9.91 |
| Intermediate ‡2 | 20.36 | 16.61 | -12.59 | 3.75 |
| Complex ‡2 | 18.76 | 10.51 | -27.68 | 8.25 |
| Overall⊥ | ΔΔG° = -8.04 | ΔΔH° = -10.6 | ΔΔS° = -8.59 | -TΔΔS° = 2.56 |
| ITC | ΔG° = -9.6± 0.0 | ΔH° = -11.8 ± 0.0 | ΔS° = -6.7 | -TΔS° = 2.2 ± 0.0 |
⊥Overall reaction thermodynamics were obtained by summation of transition states (ΔΔG = ΣΔGForward-ΣΔGReverse). For example, ΔΔG° = ΔG(‡1,k1)—ΔG(‡1,k2) + ΔG(‡2,k3)—ΔG(‡2,k4).
Fig 6. Thermodynamics profiles at 25°C, 1 M standard rate and 1 atm, A) ΔΔH°, B) -TΔΔS° and C) ΔΔG°: PfAMA1-F*PfRON2sp1 (solid line) and ΔDII-PfAMA1-F*PfRON2sp1 (slashed line).

The free energies, enthalpies and entropies of the protein and peptide were set to zero.
Discussion
To dissect the role of the PfAMA1 DII loop in regulating RON2 binding, we engineered a construct of PfAMA1 with the 37 residues DII loop [351–387] replaced with a shortened Gly-Ser linker of 7 residues. Based on the structural data, the ΔDII-PfAMA1 construct is expected to mimic the displaced DII loop form of PfAMA1 to present a mature ligand binding groove. Despite a similar structural architecture, PfAMA1 has not been shown to present cross genera RON2 binding as has been observed for TgAMA1 proteins [33]. Recently, Parker and Boulanger [25] proposed that the Tg DII loop acts as a structural gatekeeper by a mechanism of competitive binding with RON2. This mechanism enables the selective filtering of ligands that would not promote the functional AMA1-RON2 binary complex required for successful invasion of host cells. This mechanism of competitive binding is even more effective if the DII loop binds to the hydrophobic groove with a high affinity. However, Pf and Tg AMA1 differ markedly in the length and the mobility of their DII loop. TgAMA1 DII loop is 13 amino acids shorter than PfAMA1 DII loop and structural studies showed a tighter binding of the Tg DII loop in the ligand binding groove than for PfAMA1 DII loop. The higher mobility of the PfAMA1 DII loop is also supported by the lack of electron density in several crystal structures (PDB ID 2Q8B [11] and 4R1A [19]), by conformational exchange in 19NMR studies [34] and in molecular dynamics simulations [19]. As a result, a fast interconversion between a bound and an unbound Pf form of the DII loop is presumable, but only the unbound form gives access to an open binding site to PfRON2sp1. The initial and final states for both Pf and ΔDII-Pf complexes are expected to be structurally similar [25] and both showed a similar thermodynamic profile for the free energy ΔΔG° (Fig 2). In addition, both PfAMA1 and ΔDII-PfAMA1 possess a conserved apical groove that is surrounded by six loops from domain I (loops Ia to If), but these are expected to undergo the same structural rearrangements upon PfRON2sp1 binding. Thus, the observed differences between the two complexes are likely to be imparted primarily by the DII loop.
To better understand the role of the Pf DII loop upon RON2 binding, we investigated the kinetics and the thermodynamics of the interaction between PfRON2sp1 and both native and ΔDII-loop forms of PfAMA1. Kinetic reactions and Kd titration measurements were tracked by fluorescence anisotropy. For this purpose, we used of the previously described peptide PfRON2sp1 (PfRON2 segment [2021–2059]) [23] attached to the fluorescein probe 5-FAM (Table 1). The affinity values (Kd) calculated from titrations (Fig 1) were in close agreement with those obtained by SPR studies [23] and ITC (Fig 2), yielding a Kd of 42 nM and 94 nM for PfAMA1 and ΔDII-PfAMA1, respectively (Table 2) and thus validating the reliability of the fluorescence anisotropy method. We next measured the kinetics of PfAMA1-PfRON2sp1 interaction to determine the rate constants kon and koff as a function of temperature (Fig 3) and concentration of PfAMA1 (Fig 4). As the Kd is the ratio of the koff and kon, determining these values may reveal the differences of the association and dissociation kinetics of PfAMA1 and ΔDII-PfAMA1 with PfRON2sp1. Indeed, the preliminary analyses of the kinetic traces showed that the binding to ΔDII-PfAMA1 was only marginally faster than to PfAMA1. However, the rate of dissociation of the peptide from ΔDII-PfAMA1 was considerably faster (Fig 3B and 3D and S1 Table), resulting in an overall weaker affinity whereas the DII loop in PfAMA1 apparently slowed the dissociation event. These dissociation experiments were carried out at high excess of unlabeled PfRON2sp1 (250× and 500×) against Pf and ΔDII-Pf complexes (Fig 4C and 4D) and were not affected by increasing unlabeled RON2 peptide consistent with a unimolecular mechanism. Thus, the labeled bound PfRON2sp1 must first spontaneously leave the binding site before accommodating the unlabeled PfRON2sp1.
To further investigate the detailed binding mechanism, we carried out a global fitting integrating association, dissociation and titration equilibrium data into a model representing the simplest most probable reaction mechanism. The strongly biphasic kinetics (a fast and a slow phase) of both Pf complexes indicated a stepwise binding mechanism. Assessment of three different mechanisms resulted in a meaningful AIC value that favored the one-intermediate model (Table 3 and Fig 5). Based on this model, we then evaluated the respective rate constants (Table 4), complex half-life (Table 5) as a function of temperature and the thermodynamic profile (Table 6) and compared them to experimental results. At 25°C, the solid lines in Fig 3 represented the best fit of the experimental data. It is noteworthy that similar biphasic curves have been also observed in SPR experiments [35]. The affinity values (Kd) calculated from the globally fitted rate constants (k1, k2, k3 and k4, Table 4) were in close agreement with those obtained by other experiments (Table 2) as were the experimental and calculated complex half-life values (Table 5). The complex half-life decreased markedly with increasing temperature for both complexes but showed a very short value of 30 seconds at 30°C (and even a predicted value of 10 s at 37°C) for ΔDII-Pf complex as compared to the 9 minutes for Pf complex (Table 5 and Fig 7B).
Fig 7. Temperature-dependence of A) the ratio of rate constants k1/k2. The presence of the DII loop made the first rate constant ratio less affected by temperature changes, as seen for PfAMA1-F*PfRON2sp1 (yellow) in contrast with the slope observed for ΔDII-PfAMA1-F*PfRON2sp1 (red). B) Temperature dependence of the complex half-life which is defined as the time required for 50% dissociation of the complex.
At higher temperatures, the half-life decreased markedly. Error bars represent one standard deviation in the fluorescence-based experiments.
In the proposed model, the k1/k2 ratio for PfAMA1, which is the first step of the reaction, was less affected by the temperature contrary to the modified ΔDII-PfAMA1 (Table 4 and Fig 7A). As the rate constant k1 increased with higher temperature, this indicated that the reverse rate constant k2 increased proportionally for PfAMA1 but increased even more for ΔDII-PfAMA1. As well, rate constants k3 and k4 were 1 to 2 orders of magnitude faster for ΔDII-PfAMA1 than for PfAMA1 indicating markedly different kinetics of the second step of the reaction mechanism and suggesting that the DII loop affected strongly the release kinetics of the second step (k4). Indeed, based on this model, the simulation of the molar fraction of species as a function of time showed that the final ΔDII-PfAMA1 complex is predicted to be only 6% in comparison with 42% for the PfAMA1 complex at 25°C (Fig 8). Interestingly, we also could observe that the intermediate species predominates but that the formation of the final complex is faster for the ΔDII-PfAMA1 form (less than 100 s).
Fig 8. Reaction simulation of PfAMA1 (solid lines) and ΔDII-PfAMA1 (slashed lines) at 5 μM reacting with 1 μM of PfRON2sp1 at 25°C.

PfRON2sp1 is colored in green, Intermediate is colored in red and final complex is colored in black. The lack of the DII loop is predicted to decrease markedly the molar fraction of the final complex (black slashed lines) as compared to the native one (solid black lines). It is also noteworthy that the maximum complex concentration for ΔDII-PfAMA1 is obtained in less than 100 seconds whereas it needs more 400 seconds for PfAMA1.
The calculated thermodynamic profile indicated that the intermediate state was entropically driven in the case of PfAMA1, likely favored by the displacement of the DII loop and consequently not observed for the ΔDII-PfAMA1 form. It also indicated that, in this first step, the DII loop eased the releasing of the bound peptide in PfAMA1 because enthalpy values of activation and were almost equivalent (~15.4 and 16.1 kcal/mol, respectively (Table 6)) whereas in ΔDII-PfAMA1, these values were very different and implied that the reverse movement (to the initial unbound state) was more costly (13.4 and 30.1 kcal/mol, respectively (Table 6)). Thus, during the first step, the DII loop may act as a gatekeeper that would displace a low affinity ligand, for example another apicomplexa RON2 peptide, by a mechanism of competitive binding whereas in the case of the binding of its cognate PfRON2, the DII loop kinetically locks the functional binary complex that results from the second step of the reaction.
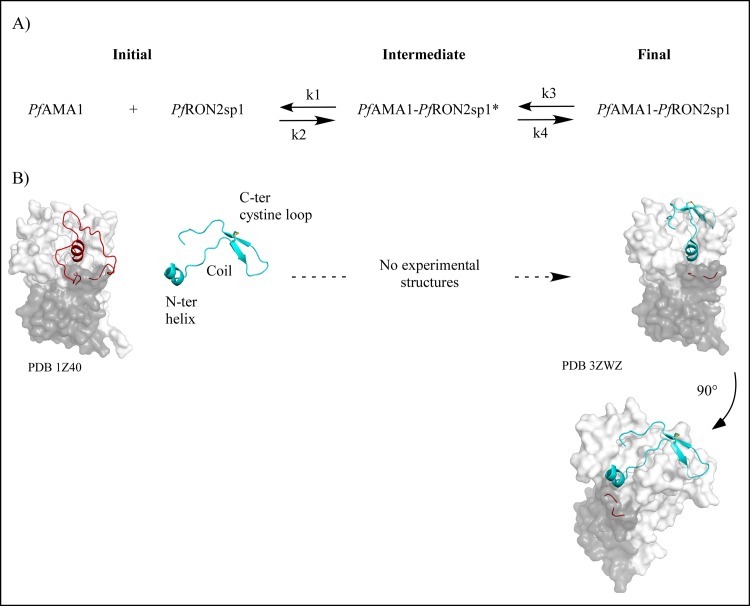
Different structural mechanisms could potentially describe the one-intermediate model with an initial encounter complex associated with rate constants k1 and k2 followed by the conversion of the intermediate complex into its final conformation (rate constants k3 and k4). Structural and Ala-scan results formerly suggested a stepwise binding mechanism where contact was initiated between the end of the AMA1 and the cystine loop followed by the binding of the helix part [21, 23]. In such a model, rate constants k3 and k4 would represent a conformational change of PfRON2sp1. Indeed, RON2 peptides are composed of three parts, a N-terminal helix, a coil and a disulfide-closed β-hairpin loop (also called cystine loop) (Fig 9) that possess some flexibility when compared to one another as suggested molecular dynamic studies (data not shown). However, it is important to point out that these kinetic experiments do not allow the indentification of the intermediate states. It must also be clarified that the present experimental data and models provide a rationale for an in vitro reductionist system far from physiological conditions and where PfRON2sp1 is a peptide extracted from the ectodomain of the 2189 residues membrane protein PfRON2 that may impact the flexibility of the extracellular domain in vivo. Further biophysical experiments will be required to follow the binding dynamics of PfAMA1 and PfRON2sp1 and to examine at the same time the kinetics of both the DII loop and the RON2 peptide (for example by using FRET experiments).
Fig 9. Known 3D Structures.
A) Two-step reaction mechanism with one intermediate of PfRON2sp1 peptide binding to PfAMA1. B) The apo structure of native PfAMA1 (PDB code 1Z40) is shown in surface representation (domain DI is colored in white and domain DII is colored in grey). The DII loop is in ribbon representation and colored in red. PfRON2sp1 is in ribbon representation and is colored in cyan and the disulfide bridge is colored in yellow. RON2 peptides are composed of three parts: a N-terminal helix, a coil and a disulfide-closed β-hairpin loop (also called cystine loop). In holo PfAMA1 (final complex), the displaced DII loop is not visible in the structure PDB code 3ZWZ. Co-structures showed that the N-terminal helix of PfRON2sp1 seated at one end of the AMA1 apical groove in place of the DII loop and extended through an ordered coil to the β-hairpin loop that bound the other end of the apical groove at the opposite of the DII loop [23].
Conclusion
In conclusion, we investigated the kinetics and the thermodynamics of the interaction of PfRON2sp1 with PfAMA1 and ΔDII-PfAMA1. The experimental data are consistent with an new influential role for the DII loop in kinetically locking the functional binary PfAMA1-PfRON2sp1 complex. Although the DII loop thermodynamically stabilizes the binding of PfRON2sp1 by a 2-fold larger affinity, we showed that the main effect is observed on the kinetics by restraining the release of the PfRON2 peptide and increasing the complex half-life by 18-fold with a value of 900 s (15 min) at 25°C for Pf complex in comparison with 48 s for ΔDII-Pf complex. Interestingly, the complex half-life of the PfAMA1-PfRON2sp1 complex is compatible with the time frame of erythrocyte invasion by Plasmodium falciparum merozoites [36–38]. Our data reveals a more comprehensive model of invasion in which the DII loop may be a key regulatory feature that determines the stability of the MJ.
Supporting Information
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
Abbreviations
- AMA1
Apical Membrane Antigen 1
- RON2
Rhoptry Neck Protein 2
- Pf complex
PfAMA1-F*PfRON2sp1
- ΔDII-Pf complex
ΔDII-PfAMA1-F*PfRON2sp1
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
This work was supported by the Centre National de la Recherche Scientifique (CNRS), the Agence Nationale de la Recherche (ANR-12-BSV3-0012-03), l’Institut National de la Santé et de la Recherche Médicale (INSERM) to DD and by the Canadian Institutes of Health Research (CIHR) grant MOP82915 to MJB. MJB also acknowledges the Canada Research Chair program for salary support. The authors thank CONACYT postdoctoral fellowships (130994, 162809) and Veracruz scholarship for RFD. RFD also acknowledges Infectiopôle Sud for salary support.
References
- 1.World Health Organization WMR. 2013. Available: http://www.who.int/malaria/publications/world_malaria_report/en/.
- 2.Bright AT, Winzeler EA. Epidemiology: resistance mapping in malaria. Nature. 2013;498(7455):446–7. Epub 2013/06/28. doi: 498446b [pii] 10.1038/498446b . [DOI] [PubMed] [Google Scholar]
- 3.Aikawa M, Miller LH, Johnson J, Rabbege J. Erythrocyte entry by malarial parasites. A moving junction between erythrocyte and parasite. J Cell Biol. 1978;77(1):72–82. Epub 1978/04/01. . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Besteiro S, Michelin A, Poncet J, Dubremetz JF, Lebrun M. Export of a Toxoplasma gondii rhoptry neck protein complex at the host cell membrane to form the moving junction during invasion. PLoS Pathog. 2009;5(2):e1000309 Epub 2009/02/28. 10.1371/journal.ppat.1000309 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Riglar DT, Richard D, Wilson DW, Boyle MJ, Dekiwadia C, Turnbull L, et al. Super-resolution dissection of coordinated events during malaria parasite invasion of the human erythrocyte. Cell Host Microbe. 2011;9(1):9–20. Epub 2011/01/18. doi: S1931-3128(10)00413-0 [pii] 10.1016/j.chom.2010.12.003 . [DOI] [PubMed] [Google Scholar]
- 6.Cao J, Kaneko O, Thongkukiatkul A, Tachibana M, Otsuki H, Gao Q, et al. Rhoptry neck protein RON2 forms a complex with microneme protein AMA1 in Plasmodium falciparum merozoites. Parasitol Int. 2009;58(1):29–35. Epub 2008/10/28. doi: S1383-5769(08)00111-6 [pii] 10.1016/j.parint.2008.09.005 . [DOI] [PubMed] [Google Scholar]
- 7.Besteiro S, Dubremetz JF, Lebrun M. The moving junction of apicomplexan parasites: a key structure for invasion. Cell Microbiol. 2011;13(6):797–805. Epub 2011/05/04. 10.1111/j.1462-5822.2011.01597.x . [DOI] [PubMed] [Google Scholar]
- 8.Yap A, Azevedo MF, Gilson PR, Weiss GE, O'Neill MT, Wilson DW, et al. Conditional expression of apical membrane antigen 1 in Plasmodium falciparum shows it is required for erythrocyte invasion by merozoites. Cell Microbiol. 2014;16(5):642–56. Epub 2014/02/28. 10.1111/cmi.12287 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lamarque MH, Roques M, Kong-Hap M, Tonkin ML, Rugarabamu G, Marq JB, et al. Plasticity and redundancy among AMA-RON pairs ensure host cell entry of Toxoplasma parasites. Nat Commun. 2014;5:4098. Epub 2014/06/18. doi: ncomms5098 [pii] 10.1038/ncomms5098 . [DOI] [PubMed] [Google Scholar]
- 10.Harris KS, Casey JL, Coley AM, Karas JA, Sabo JK, Tan YY, et al. Rapid optimization of a peptide inhibitor of malaria parasite invasion by comprehensive N-methyl scanning. J Biol Chem. 2009;284(14):9361–71. Epub 2009/01/24. doi: M808762200 [pii] 10.1074/jbc.M808762200 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Coley AM, Gupta A, Murphy VJ, Bai T, Kim H, Foley M, et al. Structure of the malaria antigen AMA1 in complex with a growth-inhibitory antibody. PLoS Pathog. 2007;3(9):1308–19. Epub 2007/10/03. doi: 07-PLPA-RA-0298 [pii] 10.1371/journal.ppat.0030138 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Henderson KA, Streltsov VA, Coley AM, Dolezal O, Hudson PJ, Batchelor AH, et al. Structure of an IgNAR-AMA1 complex: targeting a conserved hydrophobic cleft broadens malarial strain recognition. Structure. 2007;15(11):1452–66. Epub 2007/11/14. doi: S0969-2126(07)00336-X [pii] 10.1016/j.str.2007.09.011 . [DOI] [PubMed] [Google Scholar]
- 13.Vulliez-Le Normand B, Faber BW, Saul FA, van der Eijk M, Thomas AW, Singh B, et al. Crystal Structure of Plasmodium knowlesi Apical Membrane Antigen 1 and Its Complex with an Invasion-Inhibitory Monoclonal Antibody. PLoS One. 2015;10(4):e0123567 Epub 2015/04/18. 10.1371/journal.pone.0123567 PONE-D-14-56188 [pii]. . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dutta S, Dlugosz LS, Drew DR, Ge X, Ababacar D, Rovira YI, et al. Overcoming antigenic diversity by enhancing the immunogenicity of conserved epitopes on the malaria vaccine candidate apical membrane antigen-1. PLoS Pathog. 2013;9(12):e1003840 Epub 2014/01/05. 10.1371/journal.ppat.1003840 PPATHOGENS-D-13-00544 [pii]. . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lamarque M, Besteiro S, Papoin J, Roques M, Vulliez-Le Normand B, Morlon-Guyot J, et al. The RON2-AMA1 interaction is a critical step in moving junction-dependent invasion by apicomplexan parasites. PLoS Pathog. 2011;7(2):e1001276 Epub 2011/02/25. 10.1371/journal.ppat.1001276 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Srinivasan P, Yasgar A, Luci DK, Beatty WL, Hu X, Andersen J, et al. Disrupting malaria parasite AMA1-RON2 interaction with a small molecule prevents erythrocyte invasion. Nat Commun. 2013;4:2261. Epub 2013/08/03. doi: ncomms3261 [pii] 10.1038/ncomms3261 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Collins CR, Withers-Martinez C, Hackett F, Blackman MJ. An inhibitory antibody blocks interactions between components of the malarial invasion machinery. PLoS Pathog. 2009;5(1):e1000273 Epub 2009/01/24. 10.1371/journal.ppat.1000273 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bai T, Becker M, Gupta A, Strike P, Murphy VJ, Anders RF, et al. Structure of AMA1 from Plasmodium falciparum reveals a clustering of polymorphisms that surround a conserved hydrophobic pocket. Proc Natl Acad Sci U S A. 2005;102(36):12736–41. Epub 2005/09/01. doi: 0501808102 [pii] 10.1073/pnas.0501808102 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lim SS, Yang W, Krishnarjuna B, Kannan Sivaraman K, Chandrashekaran IR, Kass I, et al. Structure and Dynamics of Apical Membrane Antigen 1 from Plasmodium falciparum FVO. Biochemistry. 2014;53(46):7310–20. Epub 2014/11/02. 10.1021/bi5012089 . [DOI] [PubMed] [Google Scholar]
- 20.Pizarro JC, Vulliez-Le Normand B, Chesne-Seck ML, Collins CR, Withers-Martinez C, Hackett F, et al. Crystal structure of the malaria vaccine candidate apical membrane antigen 1. Science. 2005;308(5720):408–11. Epub 2005/02/26. doi: 1107449 [pii] 10.1126/science.1107449 . [DOI] [PubMed] [Google Scholar]
- 21.Tonkin ML, Roques M, Lamarque MH, Pugniere M, Douguet D, Crawford J, et al. Host cell invasion by apicomplexan parasites: insights from the co-structure of AMA1 with a RON2 peptide. Science. 2011;333(6041):463–7. Epub 2011/07/23. doi: 333/6041/463 [pii] 10.1126/science.1204988 . [DOI] [PubMed] [Google Scholar]
- 22.Crawford J, Tonkin ML, Grujic O, Boulanger MJ. Structural characterization of apical membrane antigen 1 (AMA1) from Toxoplasma gondii. J Biol Chem. 2010;285(20):15644–52. Epub 2010/03/23. doi: M109.092619 [pii] 10.1074/jbc.M109.092619 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Vulliez-Le Normand B, Tonkin ML, Lamarque MH, Langer S, Hoos S, Roques M, et al. Structural and functional insights into the malaria parasite moving junction complex. PLoS Pathog. 2012;8(6):e1002755 Epub 2012/06/28. 10.1371/journal.ppat.1002755 PPATHOGENS-D-11-02790 [pii]. . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chesne-Seck ML, Pizarro JC, Vulliez-Le Normand B, Collins CR, Blackman MJ, Faber BW, et al. Structural comparison of apical membrane antigen 1 orthologues and paralogues in apicomplexan parasites. Mol Biochem Parasitol. 2005;144(1):55–67. Epub 2005/09/13. doi: S0166-6851(05)00223-9 [pii] 10.1016/j.molbiopara.2005.07.007 . [DOI] [PubMed] [Google Scholar]
- 25.Parker ML, Boulanger MJ. An Extended Surface Loop on Toxoplasma gondii Apical Membrane Antigen 1 (AMA1) Governs Ligand Binding Selectivity. PLoS One. 2015;10(5):e0126206 Epub 2015/05/09. 10.1371/journal.pone.0126206 PONE-D-15-10388 [pii]. . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gupta A, Bai T, Murphy V, Strike P, Anders RF, Batchelor AH. Refolding, purification, and crystallization of apical membrane antigen 1 from Plasmodium falciparum. Protein Expression and Purification. 2005;41(1):186–98. Epub 2005/04/02. doi: S1046-5928(05)00007-0 [pii] 10.1016/j.pep.2005.01.005 . [DOI] [PubMed] [Google Scholar]
- 27.Delgadillo RF. Acceptor detected fluorescence resonance energy transfer for measurement up to 250 A and biophysical studies on core TATA binding protein-DNA complex ETD collection for University of Nebraska—Lincoln Paper AAI3388957 359, http://digitalcommonsunledu/dissertations/AAI3388957 2009.
- 28.Moore JW, Pearson RG. Kinetics and Mechanism. 3rd ed. New York: John Wiley & Sons; 1981. [Google Scholar]
- 29.Otto MR, Lillo MP, Beechem JM. Resolution of multiphasic reactions by the combination of fluorescence total-intensity and anisotropy stopped-flow kinetic experiments. Biophys J. 1994;67(6):2511–21. . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Akaike H. A new look at the statistical model identification. Ann Inst Stat Math. 1973;22:203–17. [Google Scholar]
- 31.Burnham KP, Anderson DR. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. 2nd ed. ed: Springer-Verlag; 2002. [Google Scholar]
- 32.Eyring H. The Activated Complex in Chemical Reactions J Chem Phys 1935;3 (2): 107–15. [Google Scholar]
- 33.Tonkin ML, Crawford J, Lebrun ML, Boulanger MJ. Babesia divergens and Neospora caninum apical membrane antigen 1 structures reveal selectivity and plasticity in apicomplexan parasite host cell invasion. Protein Sci. 2013;22(1):114–27. Epub 2012/11/22. 10.1002/pro.2193 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ge X, MacRaild CA, Devine SM, Debono CO, Wang G, Scammells PJ, et al. Ligand-induced conformational change of Plasmodium falciparum AMA1 detected using 19F NMR. J Med Chem. 2014;57(15):6419–27. Epub 2014/07/30. 10.1021/jm500390g . [DOI] [PubMed] [Google Scholar]
- 35.Seidel SA, Dijkman PM, Lea WA, van den Bogaart G, Jerabek-Willemsen M, Lazic A, et al. Microscale thermophoresis quantifies biomolecular interactions under previously challenging conditions. Methods. 2013;59(3):301–15. Epub 2012/12/29. doi: S1046-2023(12)00306-4 [pii] 10.1016/j.ymeth.2012.12.005 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gilson PR, Crabb BS. Morphology and kinetics of the three distinct phases of red blood cell invasion by Plasmodium falciparum merozoites. Int J Parasitol. 2009;39(1):91–6. Epub 2008/10/28. doi: S0020-7519(08)00378-0 [pii] 10.1016/j.ijpara.2008.09.007 . [DOI] [PubMed] [Google Scholar]
- 37.O'Donnell RA, Blackman MJ. The role of malaria merozoite proteases in red blood cell invasion. Curr Opin Microbiol. 2005;8(4):422–7. Epub 2005/07/16. doi: S1369-5274(05)00091-3 [pii] 10.1016/j.mib.2005.06.018 . [DOI] [PubMed] [Google Scholar]
- 38.Boyle MJ, Wilson DW, Richards JS, Riglar DT, Tetteh KK, Conway DJ, et al. Isolation of viable Plasmodium falciparum merozoites to define erythrocyte invasion events and advance vaccine and drug development. Proc Natl Acad Sci U S A. 107(32):14378–83. Epub 2010/07/28. doi: 1009198107 [pii] 10.1073/pnas.1009198107 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Dahl G, Akerud T. Pharmacokinetics and the drug-target residence time concept. Drug Discov Today. 2013;18(15–16):697–707. Epub 2013/03/19. doi: S1359-6446(13)00068-8 [pii] 10.1016/j.drudis.2013.02.010 . [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.