Weakly Deleterious Mutations and Low Rates of Recombination Limit the Impact of Natural Selection on Bacterial Genomes

ABSTRACT

Free-living bacteria are usually thought to have large effective population sizes, and so tiny selective differences can drive their evolution. However, because recombination is infrequent, “background selection” against slightly deleterious alleles should reduce the effective population size (N_e) by orders of magnitude. For example, for a well-mixed population with 10¹² individuals and a typical level of homologous recombination (r/m = 3, i.e., nucleotide changes due to recombination [r] occur at 3 times the mutation rate [m]), we predict that N_e is <10⁷. An argument for high N_e values for bacteria has been the high genetic diversity within many bacterial “species,” but this diversity may be due to population structure: diversity across subpopulations can be far higher than diversity within a subpopulation, which makes it difficult to estimate N_e correctly. Given an estimate of N_e, standard population genetics models imply that selection should be sufficient to drive evolution if N_e × s is >1, where s is the selection coefficient. We found that this remains approximately correct if background selection is occurring or when population structure is present. Overall, we predict that even for free-living bacteria with enormous populations, natural selection is only a significant force if s is above 10⁻⁷ or so.

IMPORTANCE

Because bacteria form huge populations with trillions of individuals, the simplest theoretical prediction is that the better allele at a site would predominate even if its advantage was just 10⁻⁹ per generation. In other words, virtually every nucleotide would be at the local optimum in most individuals. A more sophisticated theory considers that bacterial genomes have millions of sites each and selection events on these many sites could interfere with each other, so that only larger effects would be important. However, bacteria can exchange genetic material, and in principle, this exchange could eliminate the interference between the evolution of the sites. We used simulations to confirm that during multisite evolution with realistic levels of recombination, only larger effects are important. We propose that advantages of less than 10⁻⁷ are effectively neutral.

INTRODUCTION

Although free-living bacteria often exist in huge populations, the key parameter to describe how important selection is during bacterial evolution is the effective population size (N_e). Bacterial effective population sizes have been estimated to be 10⁷ to 10⁸ (1) or even 10⁹ to 10¹³ (2). Because the frequency of a deleterious allele declines exponentially with 2 × N_e × |s|, where s is the selection coefficient, the higher estimates of N_e imply that alleles that increase fitness by 10⁻⁸ should dominate the population. In other words, they imply that bacterial genomes should be highly optimized by natural selection.

We argue that such high estimates of N_e are theoretically problematic because of population structure and are theoretically implausible because of the low rates of recombination of bacterial evolution. The high estimates of N_e are based on the nucleotide diversity, π (the fraction of nucleotides that differ between individuals), the per-base mutation rate, μ, and the prediction that π = 2 × N_e × μ in a haploid population that is evolving neutrally. For free-living bacteria cultivated in the laboratory, μ = 2 × 10⁻¹⁰ to 2 × 10⁻⁹ mutations per nucleotide per generation (1, 3). In nature, the mutation rate might be elevated due to stationary phase or stressful conditions (4–6), or because “mutator” strains are selected for during adaptation to a new environment (7). If the mutation rate is higher than expected, then N_e will be overestimated.

A deeper problem with estimating N_e this way lies in the concept of a bacterial species (8). The equation π = 2 × N_e × μ applies to a well-mixed population, but many estimates are based on the diversity within a bacterial “species” (1). However, in bacteria, there is no clear species boundary, so we feel that it is better to view bacteria as structured populations, with recombination occurring at high rates between closely related lineages and at much lower rates between distantly related lineages, as the rate of homologous recombination decays rapidly with increasing nucleotide divergence (9). Alternatively, in the ecotype model, different subpopulations are adapted to different niches (10), which can reduce contact between and hence recombination between the subpopulations. For example, homologous recombination occurs between two closely related populations of Vibrio cyclitrophicus at about half the rate that it occurs within each population (11). Similarly, homologous recombination occurs within clades of commensal or pathogenic Escherichia coli at roughly 4-fold-higher rates than between these clades (12), and homologous recombination between human and environmental strains of E. coli seems to be rare (13). At the other extreme, homologous recombination can occur between bacteria from different species (9). Although this usually occurs at low rates, some strains of Campylobacter coli have 10 to 23% DNA that introgressed from Campylobacter jejuni by homologous recombination, even though the two species of Campylobacter are around 15% different at the nucleotide level (14).

When an allele is transferred between subpopulations by recombination, it can be viewed as migration of the allele (not the organism) between subpopulations. In a subdivided population, to determine the strength of natural selection, N_e should be estimated from the diversity within a population rather than across populations (15). Another way of thinking about this is that bacteria undergo recombination with distant lineages at low rates, which will increase the diversity (π) and hence the estimated effective population size (N_e).

Although N_e should be estimated from the nucleotide diversity within a population, we are only aware of a few genome-wide estimates of the genetic diversity within a population of free-living bacteria. First, for two recently separated populations of Vibrio cyclitrophicus that are adapted to different sizes of food particles, π is ≈0.006 for the main chromosome within either population (11). From the equation N_e = π/(2 × μ) and using the highest bacterial mutation rate (excluding endosymbionts and small genomes) of 2 × 10⁻⁹ (1), we estimate N_e to be ≈3 × 10⁶ within each population. This may be an underestimate of N_e, because all positions in the genome were included in the estimate of diversity, and the majority of them are nonsynonymous positions within protein-coding genes, which are generally under selection (16). Correcting for this might double the effective population size, and using the mutation rate of E. coli would increase it 10-fold, leading to an estimate for N_e of ≈6 × 10⁷. Second, a large subgroup of Vibrio parahaemolyticus has high rates of recombination, which seems to eliminate any subpopulation structure (17). The synonymous diversity within this group was 0.026, which implies an N_e of ≤7 × 10⁷ if we use E. coli’s mutation rate as a lower bound. Third, Kashtan and colleagues (2) identified subgroups of the ocean cyanobacterium Prochlorococcus that are found in the same part of the ocean and which share almost all of their genes, which those authors termed “backbone subpopulations.” The cells within a subpopulation differed at about 1.2% of sites on average (2). The mutation rate of Prochlorococcus is probably between 5 × 10⁻⁹ (given the accumulation of 16 single-nucleotide changes over 1,500 generations of culturing [18]) and 2 × 10⁻¹⁰ (as with E. coli, which has similar rates of spontaneous antibiotic resistance [19]). This implies that N_e is 5 × 10⁶ to 10⁸, or severalfold higher if most sites are under selection. Using the same data, Kashtan and colleagues instead estimated an effective population size of above 10⁹, and given that the upper surface of the ocean is well-mixed, they argued that the effective population size should be close to the actual population size, which is around 10¹³ or higher. Their estimate of N_e is far higher than ours because they assumed that most sites (even 4-fold degenerate coding sites) are not neutral and that any neutral sites would vary across their sample. However, they only examined 90 cells, so this assumption seems to us to be very optimistic. This discrepancy also illustrates another issue with estimating N_e, which is that if synonymous changes are under selection (with N_e × |s| > 1), then it is difficult to identify the neutral sites that would ideally be used to estimate N_e. In most bacteria, the GC content at 4-fold degenerate sites seems to be biased upwards relative to the mutational equilibrium or relative to the GC content of noncoding sites (20–22), which implies that selection based on codon usage or biased gene conversion (23) affects the synonymous sites; either way, N_e will be underestimated.

A theoretical problem with very large effective population sizes arises from the low rate of recombination in bacteria, which implies that alleles across the entire genome are linked together for many generations. When many linked sites are under selection against weakly deleterious mutations, this “background selection” can reduce the effective population size by orders of magnitude (24, 25). Background selection also reduces the importance of natural selection at other sites (25, 26). From sequencing of related bacteria, one can estimate the rate at which nucleotide changes occur by homologous recombination relative to the rate at which they occur by mutation (r/m). (The rate r is different from the rate of recombination events, because an event involving closely related strains might not lead to any changes while an event involving distantly related strains might lead to multiple nucleotide changes.) A survey of multilocus sequence typing data found a range of r/m values from 0.1 to 63 for free-living bacteria, with a median value of about 2 (27). But it is not known how these low rates of recombination would affect background selection.

To study how population structure and background selection affect N_e and the scope of natural selection, we built population genetics models and conducted population genetics simulations. First, we investigated how models of background selection (24, 28) might apply to bacteria. To confirm their predictions that N_e ≪ N, we simulated the clonal evolution of a population with 10⁶ weakly selected sites and up to 10⁹ individuals. This is a small population size for bacteria, and our simulations used a high mutation rate to make up for it; nevertheless, the number of individuals in our simulations is orders of magnitude higher than in previous simulations of background selection (24–26). We show that N_e (as estimated from neutral diversity) is orders of magnitude lower than N and that N_e grows slowly with N. We also show that the importance of selection in these simulations is roughly in accord with N_e, albeit slightly weaker. Finally, we show that with realistic rates of recombination (we simulated r/m values up to 27), background selection remains a major force, as N_e only increases by 5-fold.

Also, as mentioned above, from the standpoint of the allele being transferred, recombination between populations can be viewed as the allele migrating between different subpopulations. Population genetics theory suggests that to predict the effectiveness of selection in a structured population, N_e should be estimated from the diversity within a population (15), but we did not find an empirical demonstration of this in the literature. Our simulations show that selection acts roughly as expected, given the correct (within-subpopulation) estimates of N_e, so that the migration of alleles between subpopulations leads to stronger selection. We predict that moderate rates of recombination (r/m = 2) could lead to a large increase in N_e by this mechanism.

Our results suggest that estimates of bacterial N_e values based on the diversity within a species (as opposed to a population) are far too high, that the N_e of free-living bacteria should be relatively low because of background selection, and that in these scenarios, the strength of natural selection is consistent with N_e as estimated based on within-subpopulation diversity.

RESULTS

Background selection should drastically reduce the effective population size of bacteria.

We began with theoretical models of the effect of background selection, or the linkage between many alleles (24, 28). If there are many weakly selected sites, as we propose, then this is also referred to as Hill-Robertson interference, or interference selection. For example, consider the genomes of Prochlorococcus sp., which are typically around 1.5 to 2 Mb. Suppose that many sites in the genome, such as 4-fold degenerate synonymous sites, are weakly selected. Bulmer (29) estimated theoretically that the selective cost of a slow codon in a protein that accounts for a fraction (P) of the cell’s protein would be between 0.001 × P and 0.01 × P. An expressed gene can account for anywhere from 5 × 10⁻⁶ to 0.01 of cellular protein (30; M. N. Price et al., submitted for publication), which implies an s value of 5 × 10⁻⁹ to 10⁻⁴. There will be at least hundreds of thousands of these weakly selected sites—let us assume 1 million. Since recombination seems to occur at low rates, let us ignore it for now. If the mutation rate is (conservatively) 2 × 10⁻¹⁰, then there would be a total of U = 2 × 10⁻⁴ slightly deleterious mutations per generation. Suppose that the typical s value is 10⁻⁶. Since N_e × s is >1, these mutations will persist for roughly 1/s generations, and the average individual will have U/s = 200 deleterious mutations. These will reduce its fitness by a total of U = 0.0002. Since N × s ≫ 1, descendants of those individuals with unusually few deleterious mutations should eventually dominate the population. The number of mutations per individual is expected to be Poisson distributed (31), so the expected number of individuals with absolutely no deleterious mutations is N × exp(−U/s). If the total population size is 10¹³, then it is extremely unlikely that there are any individuals that have no deleterious mutations. (The expected number of such individuals is 10⁻⁷⁴.) As long as U/s is >30, it is likely that all individuals have some deleterious mutations. If mutations are irreversible, then the fact that it is nearly certain that all individuals have at least one deleterious mutation means that deleterious mutations will continuously accumulate; this is known as Muller’s ratchet. However, even when mutations are reversible, a similar dynamic leads to a strong reduction in the effective population size (25). Intuitively, only individuals that carry the fewest deleterious alleles are likely to have any descendants in the long run, and these individuals will be a small fraction of the population.

In contrast, in the above scenario, if the associated sites were more strongly selected (s = 10⁻⁴), then 14% of individuals would have no mutations, and N_e would be reduced by roughly 7-fold. This illustrates how linkage with many weakly selected sites has a much larger effect on N_e than linkage with many strongly selected sites. For this reason, we focused on the “interference selection” regime (24) of selection against many weakly selected sites. For situations like our Prochlorococcus scenario, with many sites and very weak selection, two published models allow us to estimate the reduction in effective population size. These models assume that mutations are irreversible, which is not realistic, but we show below that they still give reasonable estimates for the effective population size.

First, Gordo and colleagues (28) provided a set of equations for estimating the coalescence time, and hence the effective population size. For N = 10¹³, U = 2 × 10⁻⁴, and s = 10⁻⁶, these equations imply that N_e = 8.6 × 10⁵. This drastic reduction in N_e is fairly robust to changes to the parameters: varying the strength of selection by 10-fold in either direction alters N_e by less than 3-fold (to 4.4 × 10⁵ or 2.3 × 10⁶). Increasing the mutation rate by 10-fold, which might be more realistic, reduces N_e by less than 3-fold (to 2.4 × 10⁵). Changing the total population from 10¹³ to either 10⁶ or 10⁹ changes N_e by less than 2-fold (N_e = 6.5 × 10⁵ to 4.5 × 10⁵). Reducing the number of nearly neutral sites from 1 million to 300,000 increases N_e by about 2-fold (to 1.8 × 10⁶). Thus, the coalescent approach predicts that background selection will reduce the effective population size of Prochlorococcus to around 10⁶.

Second, Good and colleagues (24) described an approach for modeling background selection based on two key parameters: either the number of individuals with no deleterious mutations (when this is sizable), or N × σ, where σ is the standard deviation of fitness in the population. Under a very large population approximation, and using the same parameters described above, their model predicts N_e is ≈1.7 × 10⁶, or about 2-fold higher than with the coalescent approach. They also used simulations to measure the effects on population diversity for a range of these key parameters, and they described a “coarse-grained” approach to convert from parameters of interest to the relevant simulation. Hence, their coarse-grained approach allows them to estimate the reduction in diversity for arbitrary parameters. These coarse-grained estimates are more accurate than the very large population approximation, but unfortunately, our above scenario is too large to convert to their simulation results. For a more moderate population size of N = 10⁹, U = 2 × 10⁻⁴, and s = 10⁻⁶, their coarse-grained estimate for N_e is 1.1 × 10⁵, which is again about 2-fold higher than what the coalescence equations predict for this scenario (N_e of 6.5 × 10⁵).

Overall, the existing theories suggest that, due to background selection, the effective population sizes of clonal bacterial populations will be orders of magnitude less than their actual size, with an N_e of <10⁷ even if N = 10¹³. This suggests that subtly deleterious alleles (i.e., s = −10⁻⁷) might not be removed by natural selection.

Background selection reduces the effectiveness of selection even more than it reduces neutral diversity.

Given that bacteria experience huge reductions in population diversity due to background selection, does N_e, as estimated from the nucleotide diversity at neutral sites, still allow us to estimate the strength of selection? Similarly, does background selection reduce N_e to the point that the frequency of deleterious alleles at the background sites is consistent with the standard expectation given N_e × s? Kaiser and Charlesworth (25) simulated selection, reversible mutation, and drift with a haploid population of 1,000 individuals and up to 1.3 million sites, which included a mixture of selected (nonsynonymous) sites (typical N × s product of 10) and neutral (synonymous) sites. They found that in the absence of recombination, as the number of linked sites grew, the strength of selection was reduced as N_e was reduced. (They studied the diversity at nonsynonymous sites, rather than the prevalence of preferred alleles, but this should yield equivalent information.) They also found a similar pattern with simulations that included a significant rate of gene conversion, which is analogous to recombination in bacteria. However, their parameters led to at most a 100-fold reduction in population diversity, while we are proposing a much larger reduction.

Charlesworth (31) reviewed several other studies and reported that the reduction in diversity is in accord with the weakening of selection when the allele of interest is more weakly selected than the background selection. However, we expect that background selection would operate on the weakest set of deleterious alleles, as the stronger mutations would be removed by selection more quickly. Also, these additional studies did not consider the interference selection regimen, in which all individuals contain deleterious mutations [N × exp(−U/s) ≪ 1].

To confirm the results (25) for parameter ranges that are relevant to bacteria, we simulated background selection with reversible mutations. We considered a large number of sites, each with two states, that shared a single coefficient of selection. Many of our simulations also incorporated another two-state “focal” site which was either neutral, so that we could estimate neutral diversity and N_e, or had another selection coefficient, so that we could observe the effect on selection. All sites had the same mutation rate in both directions. These simulations did not include any recombination.

To choose our parameters, we considered a large population, as expected for Prochlorococcus. Realistic parameters might be N = 10¹³, background s = 10⁻⁶, μ = 2 × 10⁻¹⁰, and 10⁶ selected sites (U = 2 × 10⁻⁴). As this is not feasible to simulate, we scaled these parameters by 10³ to give N = 10¹⁰, s = 10⁻³, and μ = 2 × 10⁻⁷. This corresponds to speeding up mutation, selection, and genetic drift by the same amount, and according to the theory of Good and colleagues (24), this will leave N_e/N unchanged. These parameters are still challenging to simulate, but scaling them further is problematic because there is already close to one mutation per individual per generation (U = 0.2). Instead, we studied a population that is 10- to 1,000-fold smaller (N = 10⁷ to 10⁹). Reducing N from 10¹⁰ to 10⁷ is expected to reduce N_e by just 19% or 26% (using the models of reference 28 or reference 24, respectively).

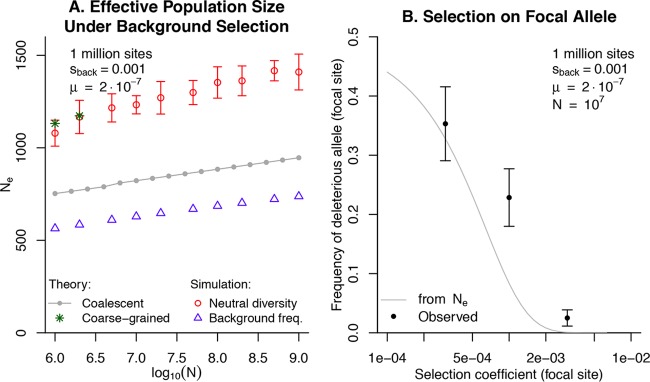
As shown in Fig. 1A, the simulations confirmed that background selection leads to an orders-of-magnitude reduction in effective population size. For example, with N = 10⁷, the diversity at a neutral site implies that N_e = 1,199 ± 54 (95% confidence interval). Deleterious alleles at the background sites were more common than expected given the neutral diversity (22.1%, with negligible variation between simulations, instead of 7.5% to 9.2%). If the frequency at deleterious alleles (f_del) is used to estimate N_e, then this corresponds to a 2-fold underestimation of N_e. [The estimate of N_e is from the equation f_del/(1 −f_del) ≈ exp(−2 × N_e × |s|); see reference 29.] Both of the theoretical predictions were within this 2-fold range.

FIG 1 .

Simulations of background selection without recombination. (A) Estimates of effective population size (N_e), as a function of actual population size (N). Note the log on the x axis. N_e was predicted theoretically by using the coalescent (28) or coarse-grained transformation to match smaller simulations (24). The coarse-grained approach was only possible for up to 2 × 10⁶ individuals. N_e was also estimated from simulations with 10⁶ to 10⁹ individuals, based on either the average diversity at a neutral site, π, or the frequency of deleterious background alleles, f_del. (B) The effectiveness of selection on a focal allele in the presence of background selection. The x axis shows the selection coefficient of the focal allele (note the log scale), and the y axis shows the average frequency of the deleterious allele at that site. The curve shows the theoretical expectation given N_e (as estimated using diversity at a neutral site). In both panels, the vertical bars show 95% confidence intervals.

We also wondered if the frequency of alleles at a site with a different selection coefficient (stronger or weaker than the background selection) would be consistent with N_e. We considered a site with selection ranging from s = 0.0003 to s = 0.003 (along with the 1 million background sites that had s values of 0.001). As shown in Fig. 1B, we found that deleterious alleles at the focal site were more common than expected, as if N_e were roughly 2-fold lower than implied by neutral diversity. This was similar to the effect at background sites, discussed above. These deviations from simple N_e thinking are not surprising, given that background selection alters the shape of the coalescent (32).

Overall, we concluded that background selection yields dramatic reductions in the effective population size, as indicated by diversity at neutral sites, and that the effectiveness of selection is a bit lower than expected given the diversity at neutral sites.

Homologous recombination is far less effective than sexual recombination in overcoming background selection.

So far, we have ignored recombination, but bacterial genomes recombine at significant rates, with r/m values of 0.1 to 63 for free-living bacteria (27). The impact of sexual recombination on background selection has been modeled (24, 26), but it is not clear if these findings apply to homologous recombination. So, we investigated the effects of various rates of recombination.

We first studied a system that was small enough for exact simulations, with 5,000 individuals and 1,000 weakly selected sites. To obtain a strong reduction in N_e due to background selection with no recombination, we chose s = 0.02 and U = 0.4, so the coalescent approach predicts that the N_e is 99, or about 50-fold smaller than the number of individuals. We considered recombination events that moved 1, 10, or 50 sites, and in each generation, up to 40% of individuals experienced a recombination event (R = 0.4). We measured the frequency of deleterious alleles (f_del) and also the average diversity at an additional neutral site (π_neutral), and we estimated N_e from each of these. As shown in Table 1, recombining a single nucleotide had little impact on either estimate of N_e, even though the number of population-wide events per nucleotide per generation was as high as 0.4 × 5,000/1,000, or 2. In contrast, for sexual recombination, a population-wide rate of 0.25 events per nucleotide has been proposed to be sufficient to eliminate background selection (26). Larger recombination events did yield increases in N_e, whether estimated from the frequency of deleterious alleles or from the average diversity at a neutral site (Table 1). With R = 0.4 and 50 sites being moved, the frequency of deleterious alleles (0.021) was very close to the infinite population limit of roughly μ/s = 0.02, so that we could not estimate N_e exactly. In the other simulations, estimates of N_e from neutral diversity were consistently higher than estimates of N_e from deleterious allele frequencies, as we saw previously for the large simulations with no recombination. With recombination, the ratio of the two estimates ranged from 1.8 to 1.4. We also imitated sexual recombination by moving half of the sites (500) in each event, and with R = 0.1, the frequency of deleterious alleles was near the μ/s limit (f_del = 0.014).

TABLE 1 .

Exact simulations of background selection with recombination^a

Rateb	No. of sitesc	fdel	πneutral	πback	Ne(f)	Ne(π)	Fast fdeld
0	0	0.108	0.071	0.049	52.8	88.5	0.114
0.1	1	0.106	0.073	0.049	53.4	90.9	0.114
0.1	10	0.087	0.075	0.049	58.7	93.1	0.095
0.1	50	0.041	0.088	0.046	79.1	109.9	0.035
0.4	1	0.100	0.079	0.049	54.9	99.1	0.115
0.4	10	0.047	0.083	0.047	75.1	103.4	0.052
0.4	50	0.021	0.132	0.039	>90	165.4	0.017

^aOur simulations were based on 5,000 individuals, 1,000 sites, s = 0.02, and U = 0.4.

^bRecombination events per individual per generation.

^cNumber of sites moved by each recombination event.

^dThe average frequency of deleterious alleles in fast approximate simulations.

Overall, we confirmed that homologous recombination can counteract background selection, but because far fewer sites are transferred, it has far less impact than sexual recombination. The impact of recombination on either the frequency of deleterious alleles or the diversity at neutral sites was consistent, in the sense that both imply similar increases in N_e.

A fast approximation for simulating homologous recombination.

To study the impact of homologous recombination in a more realistic setting, we needed to incorporate recombination into our fast simulations. These simulations do not record the state of each allele or each individual, but only the number of individuals with a given number of deleterious alleles. In this framework, we modeled a recombination event as altering the number of deleterious alleles in the recipient, and we estimated the mean and variance of this change. If the recipient has b deleterious alleles and replaces r_sites of them with alleles from a random individual, then the average change to b will be (b_avg − b) × (r_sites/n_sites), where b_avg is the number of deleterious alleles in the average individual and n_sites is the total number of background-selected sites. To estimate the variance of the change to b due to recombination, we assumed that the diversity at background-selected sites (π_back) is approximately uniform across the genome (33) and across pairs of individuals. In this case, the variance (V_r) will be equal to r_sites × π_back.

To test this approximation, we used the observed diversity at background sites in the small detailed simulations to estimate V_r and then ran fast simulations with the same parameters. As shown in Table 1, the fast simulations gave approximately the correct frequency of deleterious alleles, f_del, with a relative error of less than 25%. (Even in the no-recombination case, the results did not match exactly; this might be because the fast simulations do not allow multiple mutations in one individual in one generation, or because the number of individuals in the fast simulations fluctuated slightly because we simulated genetic drift via binomial sampling of the number of individuals of each genotype.)

Although this approximation works reasonably well, to use it for new parameters, we need to estimate the diversity at background sites. Note that π_back is <π_neutral, as even weak selection should reduce diversity below that of neutral sites. Also note that π_back is ≤2 × f_del × (1 − f_del), as the two terms are (on average) equal for unrelated individuals. Thus, our estimate is that π_back is the minimum of these two constraints. As this estimate may be high, our fast simulations may overstate the impact of recombination.

Bacterial rates of recombination are insufficient to overcome background selection.

We applied our fast approximation to large populations (N = 10⁶ to 10⁹) with the same parameter settings as for the experiment shown in Fig. 1. To constrain the impact of recombination, we assumed that diversity at neutral sites is at most 0.03. We assumed that each recombination event affects 300 weakly selected sites (V_r ≤ 9), which corresponds roughly to a recombination event of 1 kb and 30% of sites being weakly selected. We considered a range of recombination rates from 0.001 to 0.9 events per individual per generation. (Since the other parameters were chosen to be 1,000 times faster than those of an actual bacterium, this corresponds to 10⁻⁶ to 0.0009 recombination events per actual bacterium per generation.) To convert the recombination rates to r/m, we assumed that 20% of sites are effectively neutral and that most of the diversity is at the neutral sites, so that the typical recombination event causes 1,000 × 20% × 0.03 = 6 changes. This implies that our highest recombination rate (R = 0.9) corresponds to an r/m of (6 × 0.9)/U = 27. If there is significant diversity at background sites, then r/m will be somewhat higher than indicated, so for a given r/m, the impact of recombination will be overstated.

We found that realistic rates of recombination led to significant reductions in the frequency of deleterious alleles (Fig. 2). However, even for the highest rates we considered, the frequency was well above the infinite population limit. The lowest frequency of deleterious alleles that we observed was 0.00055, for N = 10⁹ and r/m ≈ 27; this frequency corresponds to an N_e of ≈3,800, or a roughly 5-fold increase in N_e over no recombination (N_e ≈ 730). At high or very low rates of recombination, varying the number of individuals (N) between 10⁶ and 10⁹ had little effect, but the impact of modest rates of recombination (R = 0.01 or r/m ≈ 0.3) depended on N. At high rates, tripling the rate of recombination reduced the frequency of deleterious alleles by around 2-fold and increased the implied N_e by 10 to 20%.

FIG 2 .

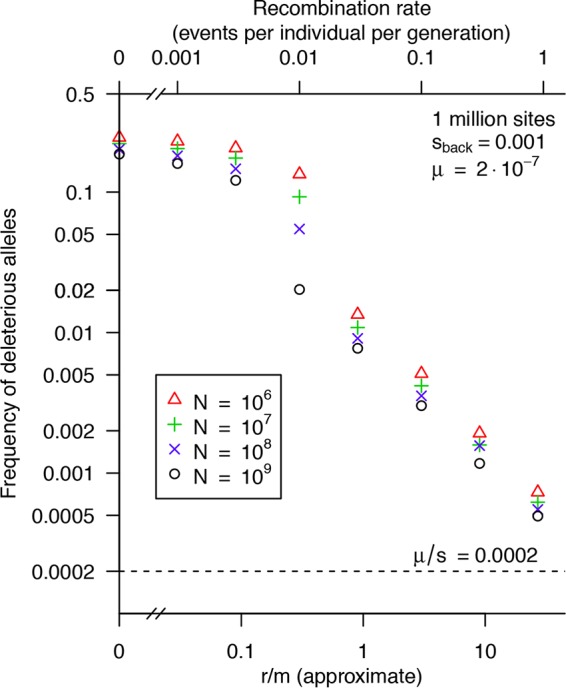
Realistic rates of homologous recombination do not eliminate background selection. Using fast approximate simulations of background selection with recombination and up to 10⁹ individuals, the graph shows how the average frequency of deleterious alleles (y axis) varies with the rate of recombination (x axis). Note the log scales on the axes. The dotted line shows the expected frequency (μ/s) for an infinite population.

We also considered that at low rates, bacteria might exchange larger parts of their genomes (34), as opposed to the roughly 1-kb recombination events discussed so far. So we performed simulations with recombination events that were 10- or 100-fold more frequent: 3,000 or 30,000 background sites exchanged, or roughly a 10- or 100-kb total. We reduced the rate of these events by 10- or 100-fold to keep r/m the same. For N = 10⁷ and r/m ≈ 0.9, we found that larger events reduced the frequency of deleterious alleles from 0.011 to 0.0047 or 0.0014. In other words, increasing the size of recombination events by 100-fold reduced f_del by roughly 6-fold and increased the apparent N_e from roughly 2,200 to roughly 3,300. This is still just 5-fold higher than with no recombination (N_e ≈ 630 for N = 10⁷).

Overall, the simulated frequencies of deleterious alleles imply that for moderate rates of recombination (r/m, ≤9), recombination might increase N_e by severalfold. The increase might be a bit larger if recombination events cover many kilobases or recombination rates are high (r/m ≈27). Because our estimates of π_back and r/m are conservative, these simulations may overstate the impact of recombination. Although we did not include a neutral site in these simulations, and therefore we cannot estimate π_neutral, smaller detailed simulations suggested that the impact on neutral diversity would be similar (Table 1).

Recombination between subpopulations can increase the strength of natural selection.

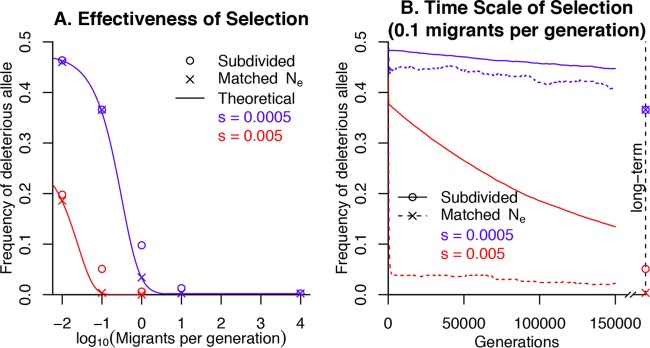
So far, we have considered background selection and recombination within a single population, but recombination often occurs between related bacteria from different subpopulations. In this case, a recombination event can be viewed as the migration of an allele between subpopulations. The theory of structured populations predicts that the strength of selection in a structured population can be estimated from the neutral diversity in a subpopulation, including diversity that was acquired from other subpopulations by migration (15). To verify this, we simulated selection against a weakly deleterious allele in a subdivided population with 100 subpopulations of 100 individuals each and a range of migration rates. The site had two alleles with equal mutation rates. We considered s = −5 × 10⁻⁴ or s = −0.005, which corresponds to N_total × s = −5 or −50. As shown in Fig. 3A, the average frequency of a deleterious allele increases as the migration rate decreases. This might seem to contradict the fact that the odds of a new mutation’s fixation, and the dependence of the fixation probability on the selection coefficient, is independent of population structure if migration is “conservative” and does not alter the size of each subpopulation, as in our simulations (35). The frequency of the deleterious allele is higher than implied by its (low) fixation rate, because in a subdivided population with very low migration rates, it takes a long time to purge the deleterious allele (36).

FIG 3 .

Selection in a subdivided population. We simulated the evolution of a weakly selected site with two alleles and equal mutation rates both ways (μ = 10⁻⁶) in a population of 10,000 haploid individuals divided into 100 subpopulations. (A) Under weak selection (s = 5 × 10⁻⁴ or s = 0.005), the average long-term frequency of the deleterious allele decreases as the migration rate rises. For comparison, we show simulations without population structure and with matching N_e (estimated from the subpopulation diversity). We also show theoretical predictions for the long-term frequency of the deleterious allele (given N_e). (B) The time scale of selection when there are 0.1 migrants per generation (N_e = 569). The x axis shows the number of generations, and the y axis shows the average frequency of the weakly deleterious allele. The right edge shows the long-term average frequency, as in panel A. At the beginning of each of 500 simulations, the deleterious allele had a frequency of 0.5: the early drop in allele frequencies is so rapid that it is barely visible in this plot.

To test if the strength of selection was consistent with the usual population genetics models, we compared the frequency of the deleterious allele with population structure to the frequency without population structure and with the population size set to a theoretical estimate of N_e based on within-subpopulation diversity. (In Materials and Methods, we explain how we used the diffusion approximation [35] to model the within- and between-subpopulation diversity rates for a site with two alleles and reversible mutations; the model is validated in Fig. S1 in the supplemental material.) We found that the weakening of selection due to population structure is mirrored by the reduction in N_e, although at intermediate migration rates, deleterious alleles were a bit more frequent than expected (Fig. 3A). The biggest discrepancy was that with 1 migrant per generation and s = 0.0005, the frequency of the deleterious allele was 0.098, but in simulations with N = 3,356 and no population structure, the frequency of the deleterious allele was just 0.034. This corresponds to a reduction of N_e × |s| from 1.7 to 1.1.

If diversity that arose from other subpopulations were ignored when estimating N_e (with the goal that N_e = N_sub), then this would understate the efficacy of selection, because even with less than one migrant per generation, gene flow reduces the frequency of deleterious alleles. For example, for a deleterious allele with s = −0.005, just 0.01 migrants per generation should in theory reduce the average frequency from 27% to 19%; in our simulations, the frequency dropped from 28% to 20%. On the other hand, if the efficacy of selection is estimated from diversity across a structured population [i.e., critical s ≈ 1/(2 × N_e) ≈ μ/π], then it will be dramatically overestimated. For example, with 0.1 migrant per generation, the within-subpopulation estimate of N_e is 574, which accurately predicts that a weakly deleterious allele with s = −0.0005 will have a frequency of about 0.36. However, the across-subpopulation estimate of N_e is 236,000, which would imply a very low frequency for this allele.

Subpopulation structure causes alleles to fix much more slowly (36), and not surprisingly, we found that subpopulation structure causes the deleterious allele frequency to reach equilibrium more slowly. With reversible mutations and moderately weak selection against an allele that is initially at a frequency of 0.5, we found that the change in the allele frequency was biphasic, with an initial drop that took N_e generations followed by a much slower decay (Fig. 3B). In simulations with population structure, the initial drop can be much smaller than in simulations that lack population structure and have the same N_e (Fig. 3B). This confirms that subpopulation structure causes allele frequencies to change more slowly than expected given the within-subpopulation diversity.

How do the migration rates in our simulations relate to estimates of r/m in bacteria? For example, suppose that r/m = 2 (the median ratio from reference 27), μ = 2 × 10⁻¹⁰, and π = 0.01. The rate of nucleotide changes due to recombination is (r/m) × μ and the rate at which a nucleotide is moved between individuals is (r/m) × μ/π = 4 × 10⁻⁸ per site per generation. With 100 subpopulations and an effective 10⁶ individuals within each subpopulation, in the absence of migration, the within-subpopulation diversity would be 2 × N × μ = 0.0004. With a migration rate of 4 × 10⁻⁸, our model predicts that within-subpopulation diversity will increase to 0.0195, which corresponds to increasing N_e by 49-fold. Across-population diversity would be 0.26. However, as discussed in the introduction, recombination occurs at severalfold-lower rates between subpopulations than within them, and so we used a “migration” rate of 10⁻⁸ instead. Then, the within-subpopulation diversity was 0.0082 and across-population diversity was 0.401 (near the maximum of 0.5). The near-saturation of across-population diversity might indicate that this migration rate is too low, but N_e still increased to 21-fold higher than the subpopulation size. Overall, by modeling recombination at one site as migration, we predict a high level of differentiation between subpopulations, but recombination still leads to significant increases in within-subpopulation diversity and hence in the scope of natural selection.

DISCUSSION

Just how small is the effective population size?

Our theoretical analysis of background selection implies that for a single subpopulation of free-living bacteria, N_e should be relatively small. For low rates of recombination, our models give N_e values of ≈10⁶, and our simulations imply that typical rates of recombination (r/m = 3, which is close to the median value [27]) would increase N_e by around 3-fold, to 3 × 10⁶. However, the estimates of N_e from subpopulations of V. cyclitrophicus or Prochlorococcus seem to be higher, perhaps around 10⁷. V. cyclitrophicus undergoes recombination at unusually high rates (r/m, >50 [11]), which could explain why it has a higher effective population size. But for Prochlorococcus, recombination is reported to be rare (r/m = 0.1 [2]), which should constrain N_e to be low because of background selection. This discrepancy might indicate that mutation rates are higher than we expect, that recombination has a larger impact in huge populations, that larger recombination events are occurring, or that the subpopulations are not defined narrowly enough and the individuals within each subpopulation are not truly competing with each other. A related issue is that nucleotide diversity (π) varies across the genome (2, 11). Because highly expressed genes in bacterial genomes tend to cluster together (37), the variation in diversity could reflect stronger selection on synonymous codons in highly expressed genes, so that they have fewer effectively neutral sites. Or, the variability of π could indicate selection for recombinant genotypes or frequency-dependent or niche-specific selection on some parts of the genome (2, 11), which was not considered in our models. As more genome sequences of closely related bacterial strains become available, it should become possible to address these questions.

Other mechanisms that reduce the effective population size.

Although we have so far considered the reduction in diversity and in N_e to be due to selection against deleterious mutations, adaptive evolution with little recombination could lead to similar reductions in diversity. Intuitively, genetic “draft” can push deleterious alleles to high frequencies if they are linked with more-beneficial adaptive alleles; if these beneficial alleles arise rarely, then this proceeds independently of stochastic variation in the number of descendants and hence regardless of population size (38). In fact, the modest level of diversity in bacterial species is sometimes seen as evidence of selective sweeps, because otherwise the estimates of N_e seem “absurdly low” (39). However, since background selection can also lead to low N_e, which is it?

We feel that it is difficult to reconcile the adaptive models with π/μ of ≈10⁷, as in subpopulations of Vibrio or Prochlorococcus, unless selective sweeps are very slow or very infrequent, or recombination is unusually common. For example, Gillespie (38) suggested that for a clonal population, π/μ ≈ 2 × t, where t is the number of generations between adaptive mutations that successfully fix. If the generation time is once per day, then a π/μ value of 10⁷ corresponds to an adaptive sweep occurring once every 14,000 years, which seems slow. (For comparison, it is estimated that a European population of Drosophila melanogaster [fruit flies] has accumulated about 60 beneficial mutations during the last 15,800 years [40].) Another possibility is that many simultaneous sweeps could occur in parallel—for example, many individuals could independently acquire a mutation that is advantageous after a change in conditions. Our intuition is that the number of simultaneous sweeps would need to be very high to maintain diversity, but as far as we know, this possibility has not been tested rigorously.

A related scenario is proposed for a “quasisexual” population of Synechococcus sp. growing in a microbial mat in a hot spring (41). The abundance of rare haplotypes was proposed to indicate positive selection on linked loci; before fixation, recombination would transfer the beneficial alleles to other lineages, so that the haplotypes would never reach high abundance and the sweep would not eliminate diversity. This population has a relatively high recombination rate, with an estimated population-scaled rate of events of ρ = 0.01 to 0.1. If we ignore selection and we assume that each recombination event moves δ = 1,000 nucleotides, then from ρ ≡ 2 × N_e × R, and π ≈ 2 × N_e × μ, we obtain r/m ≈ ρ × δ. So for Synechococcus, we estimate r/m = 10 to 100. We doubt that frequent partial sweeps could occur at more typical rates of recombination.

However, if selective sweeps do occur frequently, then natural selection might be even less effective than in our background selection models. During adaptive evolution with alleles of benefit s, alleles with (absolute) selection coefficients of less than s/10 or so might be effectively neutral (42). For example, if strongly beneficial combinations of alleles often arise and have an s of 10⁻⁵, then they would eliminate selection on subtle effects with an s value of 10⁻⁶, which are usually assumed to be important for bacterial evolution.

Another mechanism reduces the effective population size of many bacteria, but probably not freely living bacteria: patchy habitats. For example, for a commensal bacterium that lives in the gut of an animal, the effective population size might depend on the number of colonized hosts rather than the number of individual bacteria. This mechanism should not apply to planktonic bacteria, such as Prochlorococcus. In principle, this mechanism could apply to bacteria that grow on food particles, such as Vibrio, but since the particles are small and very numerous, patchiness cannot explain small effective population sizes such as N_e of ≈10⁷.

Conclusions.

In bacteria, background selection should reduce the effective population size to be orders of magnitude smaller than the actual population size, even if the population is well-mixed and even if the recombination rate is relatively high (r/m ≈27). Thus, background selection leads to a dramatic weakening of natural selection. On the other hand, the impact of recombination on the evolution of individual sites, due to sharing alleles across subpopulations, can increase within-subpopulation diversity, N_e, and the importance of natural selection. In either case, the diversity at neutral sites gives an approximate indication of how small of a selective effect is likely to be important. Because N_e under background selection is only slightly increased by large increases in the population size, we expect the effect of background selection to predominate. So, we propose that in bacteria, alleles that alter fitness by less than 10⁻⁷ or so are effectively neutral.

MATERIALS AND METHODS

Theoretical predictions of background selection.

We implemented the “coalescent simulation” equations (28) for estimating N_e by using R software. These equations are based on the frequency of having a given number of deleterious sites in a deterministic infinite-sized population. We computed these frequencies in log-space to avoid underflow. To reduce the running time and memory requirements, which scale as the square of the number of sites, we ignored the possibility of high numbers of deleterious sites if they occurred at frequencies of less than 10⁻²⁰. [Our code also truncates the number of deleterious sites to be at most 10 × (1 + U/s), but this is less stringent and does not affect the results.] As recommended by ref. 28, we used the correction of Gessler (43) to account for the absence of individuals with no deleterious mutations. Our code is available in the GordoNe() function.

To estimate N_e using the large N × σ limit, where σ is the standard deviation of fitness within the population, we used equations ST2.20 and ST2.22 from the supplementary material of reference 24. These led to the following equations: σ ≈ [2 U² × s⁴ × log(N³ × U × s²)]^1/6 and N_e ≈ [24 × log(Nσ)]^1/2/σ, which illustrates that N_e grows even more slowly than log(N). However, our simulations are still too small to reach this limit. For example, for N = 10⁷, U = 0.2, and s = 10⁻⁴, the large-limit equations predict N_e = 6,310 and σ = 0.0025, but simulations give values of N_e = 1,199 and σ = 0.0011.

As another way to predict the ratio of N_e/N due to background selection, we used the code provided in reference 24, which performs “coarse-grained” rescaling and interpolation between (precomputed) simulations.

Detailed simulations of background selection and recombination.

For a population of 5,000 individuals and 1,000 sites, we performed detailed simulations. Every site had two states, and we assumed the same selection coefficient (s) for all (S) background sites. We also included a single neutral site. At every generation, we mutated each site with probability μ. We selected a random fraction of individuals to undergo recombination events; each event moved the same number of sites from a random individual to that recipient. (These sites were adjacent background sites on a circular genome; the neutral site did not recombine.) Then, we sampled N individuals for the next generation according to their fitness. Our code is available in the backselAll2() function.

Fast simulations of background selection.

For simulations with larger populations, we counted the number of individuals with each genotype rather than representing the genotype of each of N individuals. At each generation, we performed deterministic mutation and selection to alter the frequency of each genotype, and we randomly generated the number of individuals for each genotype in the next generation according to a binomial distribution. The running time of this algorithm is proportional to the number of genotypes times the number of generations, so it does not depend directly on N. These simulations included S background-selected sites and one “focal” site, with two alleles at each site.

To reduce the number of genotypes that we considered, we limited the number of deleterious mutations for each individual (b) to a range, b_min to b_max. There are 2 × (b_max − b_min + 1) possible genotypes, with the factor of 2 arising from the two choices for the focal site. For each genotype, deleterious background mutations are gained at the rate (S − b) × μ and lost at a rate of b × μ. The focal allele mutates at rate μ. The fitness of each genotype was (1 − s)^b × (1 − s_f), where s_f was either the selective effect of the focal site or 0. Our code is available in the backsel2() function.

To identify the correct b_start value, we ran shorter test simulations with various values of b_start and checked if the population’s mean b was stable over time. For the range of b values, we usually used b_start ± 6 × V^1/2, where V is the maximum of U/s or b_start. For example, for simulations with N = 10⁷ and s_f = 0, b_start = 221,500, b_min = 218,676, and b_max = 224,324. We verified that the mean b in the population was never close to either boundary.

At the start of each simulation, every individual had b_start deleterious background mutations, and the frequency of each allele at the focal site was 0.5. When estimating the diversity or the strength of selection, we gave the simulation 10⁷ generations to equilibrate and then measured the focal allele over the next 2 × 10⁷ generations.

We also implemented a simpler model with no focal site [the backsel1() function], which was used for testing.

Fast simulations of background selection with recombination.

To add recombination to our fast simulations, we modeled recombination as a deterministic process: given a recombination rate, that fraction of individuals experience a change to their number of deleterious alleles b. The mean and variance of the change to b is given in the Results, and we use an approximately normal (but discrete) distribution to obtain the probability of a change from b to b’ for each pair of genotypes. To save time, we only allow changes to b of up to 5 times the expected standard deviation of the change. Also, the probability of a change from b to b’ depends on the average number of deleterious alleles, which changes slowly during a simulation. To save time, these probabilities are only updated once every 50 generations. Simulations with recombination were run for 200,000 to 400,000 generations and we searched for starting values of b that allowed convergence during this time. These simulations did not include a focal allele. Our code is available in the backselR() function.

Diffusion approximation for the neutral diversity in structured populations with reversible mutations.

We modified the diffusion approximation described in reference 35 for reversible mutations. We assumed n subpopulations of size N_sub each, with a total of N_sub × n individuals. We assumed that each allele migrates with frequency m to a randomly selected other subpopulation. Uniform mixing with no subpopulations corresponded to m = 1 − 1/n. At each generation, we performed mutation, coalescence (within a subpopulation only), and migration. Let J_w describe the odds that two alleles within the same subpopulation were identical. Let J_b describe the odds that two alleles from different subpopulations were identical. Intuitively, mutation creates diversity, so it reduces J_w and J_b; coalescence increases the chance that two individuals in a subpopulation are identical (increases J_w); and migration mixes the subpopulations together and causes J_w and J_b to become more similar. In the mutation step, let g = m² + (1 − m)² be the probability that mutation does not alter whether the two alleles are identical (i.e., either neither one changes or both change). Then, J_w → J_w × g + (1 −J_w) × (1 − g) and J_b → J_b × g + (1 − J_b) × (1 − g). In the coalescent step, J_w → 1/N_sub + (1 − 1/N_sub) × J_w, because there is 1/N_sub chance that the two parents are identical within a subpopulation; there is no change to J_b. In the migration step, let a = m²/(n − 1) + (1 − m)² be the odds that the pair was in the same subpopulation in the previous generation, given that they are in the same subpopulation now. Let b = [1 − (1 − m)² − m²/(n − 1)]/(n − 1) be the odds that the pair was in the same subpopulation in the previous generation, given that they were in different subpopulations now. Then, (J_w, J_b) → [a × J_w + (1 − a) × J_b, b × J_w + (1 − b) × J_b]. Given these three steps, which were performed at each generation, we solved for the fixed point by using matrix algebra. The within-population diversity is given by the equation π = 1 − J_w. The total diversity (ignoring the population structure) is given by 1 − J_w/n − (1 − 1/n) × J_b.

Simulations of structured populations.

At each generation, we updated allele frequencies deterministically to reflect selection, mutation, and migration, and then we used the binomial distribution [rbinom() in R] to select the actual number of representatives of the allele within each subpopulation in the next generation. Thus, the number of individuals per subpopulation will fluctuate stochastically around the target. [See the site1_sim() function.] We performed 500 independent simulations for each migration rate and for each selection coefficient. We verified the correctness of our simulations by comparison to the diffusion approximation in the absence of selection (see Fig. S1 in the supplemental material) and by reproducing Fig. 3 of reference 36, which involves selection and population subdivision but no mutation. Simulations started with an allele frequency of 0.5 in each subpopulation and ran for 10⁷ generations. Samples after 5 × 10⁶ generations were used to estimate the long-term diversity or the long-term frequency of deleterious alleles. For “matched” simulations with no migration or subpopulations [see the site1_simple() function], we used the same numbers of simulations and generations. Also, these simulations started at a random allele frequency, not at 0.5, but this should not affect the result.

The code that we used for this work, as well as R images of the simulation results, are available at http://genomics.lbl.gov/supplemental/backsel.

SUPPLEMENTAL MATERIAL

Figure S1 

Diversity in a subdivided population. Download