Monolithically Integrated μLEDs on Silicon Neural Probes for High-Resolution Optogenetic Studies in Behaving Animals

SUMMARY

We report a scalable method to monolithically integrate microscopic light emitting diodes (μLEDs) and recording sites onto silicon neural probes for optogenetic applications in neuroscience. Each μLED and recording site has dimensions similar to a pyramidal neuron soma, providing confined emission and electrophysiological recording of action potentials and local field activity. We fabricated and implanted the four-shank probes, each integrated with 12 μLEDs and 32 recording sites, into the CA1 pyramidal layer of anesthetized and freely moving mice. Spikes were robustly induced by 60 nW light power, and fast population oscillations were induced at the microwatt range. To demonstrate the spatiotemporal precision of parallel stimulation and recording, we achieved independent control of distinct cells ~50 μm apart and of differential somatodendritic compartments of single neurons. The scalability and spatiotemporal resolution of this monolithic optogenetic tool provides versatility and precision for cellular-level circuit analysis in deep structures of intact, freely moving animals.

INTRODUCTION

During the past few decades, electrical stimulation of the brain has brought tremendous insight on its functions (Tehovnik, 1996). To further advance neuroscience and study how large families of neurons interact with each other in complex networks, selective activation and silencing of single neurons of specific types is required. Currently, neither specific activation nor silencing of neurons can be achieved effectively by electrical stimulation (Butovas and Schwarz, 2003).

Recently, optogenetics has revolutionized neural circuit analysis by introducing photosensitive proteins (opsins) into specific cell types, so that these cells can respond to an optical stimulus with well-defined action potential patterns (Boyden et al., 2005; Deisseroth, 2011; Nagel et al., 2003). Using appropriate wavelengths to target a particular opsin, cell-type specificity can be achieved with well-controlled temporal resolution. For example, channelrhodopsin-2 (ChR2) and halorhodopsin can be co-expressed in the same cells, allowing depolarization and hyperpolarization of the target neurons using blue (~473 nm) or yellow (~590 nm) light, respectively (Gradinaru et al., 2010; Han and Boyden, 2007). In principle, this type of combinatorial cell-specific targeting allows sophisticated manipulations of neural activity. Assuming that single neurons can be addressed selectively, one could test spike timing during specific neural computations and behaviors at the temporal resolution of a few milliseconds in the intact brain.

Despite the rapid advancement of optogenetics in recent years, supporting technology to reliably deliver light to and record electrical signals from deep brain structures in freely moving animals is not readily available. Early work involving in vivo optogenetics relied on manual assembly of commercially available recording components such as metal electrodes (Anikeeva et al., 2012; Gradinaru et al., 2007) or passive high-density probes (Stark et al., 2012) with optical fibers, which are bulky and may suffer from misalignment errors. Moreover, the spatial resolution of fiber-based optogenetic devices is limited by the bulk of the implanted fibers. More recently, an engineering effort has evolved toward micro electro mechanical systems (MEMS) technologies for miniaturization, high-density integration, and patterning at the lithographic resolution. Planar probe architecture is an ideal platform for the integration of optics, because of the versatility of surface micromachining processes to form multiple layers of high-density active components. As the first step toward confining light output, our previous work has demonstrated a neural probe with integrated optical waveguide to couple light from an external optical fiber to a microscopic stimulation site (Wu et al., 2013). However, this approach is difficult to scale, due to the tethering optical fibers that can restrict animal movements and may cause mechanical damage to the implanted probe during behavioral experiments. To avoid using bulky fibers, another group has demonstrated the feasibility of coupling a bare laser diode chip (emission centered at 650 nm) to an integrated waveguide (Schwaerzle et al., 2013). Semiconductor diodes require only thin, flexible cables to power, which can alleviate constraints on behaving animals. While LEDs are available at much lower cost and in various wavelengths as compared to laser diodes, the coupling efficiency between an integrated waveguide to the Lambertian emission profile of LEDs is severely limited by the principle of etendue (Wilm, 2008).

This work describes an innovative solution to enhance both spatial resolution and scalability of optogenetic stimulation and recording probes. Instead of coupling extracranial light sources to waveguides, the light sources can be miniaturized and directly integrated at the stimulation sites. InGaN LEDs are potentially attractive for optogenetic applications because their emission wavelength can be tuned across the visible spectrum to target a range of opsins (Zhang et al., 2003). However, GaN-based materials have very limited substrate choices and are conventionally fabricated on either sapphire or SiC wafers for minimal dislocation density (Kukushkin et al., 2008). Indeed, microscopic LEDs (μLEDs) fabricated on a sapphire wafer were predicted to produce sufficient optical power to activate ChR2 without overheating the surrounding tissue (McAlinden et al., 2013) and demonstrated in vivo activation of cortical neurons in anesthetized mice (McAlinden et al., 2015). However, light scattering from the transparent sapphire substrate and having the recording sites on a separate silicon probe can limit the spatial resolution of the stimulation and recording. In addition, sapphire wafers cannot be micromachined accurately to form needle-like probe structures for minimal insertion damage. In principle, this limitation may be circumvented by transferring microfabricated LEDs from the sapphire wafer to another polymer substrate using the laser lift-off technique, which can provide injectable μLEDs (Jeong et al., 2015; Kim et al., 2013). Although the flexibility from the polymer substrate can alleviate micro-motion-induced tissue damage, the overall size of the injected components is several hundreds of microns in width (affecting large neuronal groups or entire regions) and is difficult to mount onto micro-drives for post-implantation fine-tuning of the insertion depth. In this work, we strive to push the limits of scaling, both in terms of the number of optical stimulation sites and component (μLED) size, with the goal of increasing the spatial resolution. In contrast to previous efforts (Kim et al., 2013; McAlinden et al., 2013), we monolithically integrated the μLEDs and recording electrodes on silicon probe shanks, with all dimensions defined with a resolution of < 1 μm. Unlike flexible probes, the rigid shanks and their integrated components remain intact after implantation to provide precise geometry of stimulation and recording sites for circuit mapping; the entire device is mounted on a movable micro-drive, enabling depth optimization. We demonstrate that these “μLED probes” enable control of spiking of single neurons and induce field oscillations of neuronal activity in the intact brain of freely moving mice with unprecedented resolution, so that optical stimulation of a very specific neural circuit is no longer limited by the light delivery methodology, but rather is bottlenecked by the expression specificity of current opsin technologies.

RESULTS

Design: Scalable and High-Precision Optogenetic Probe

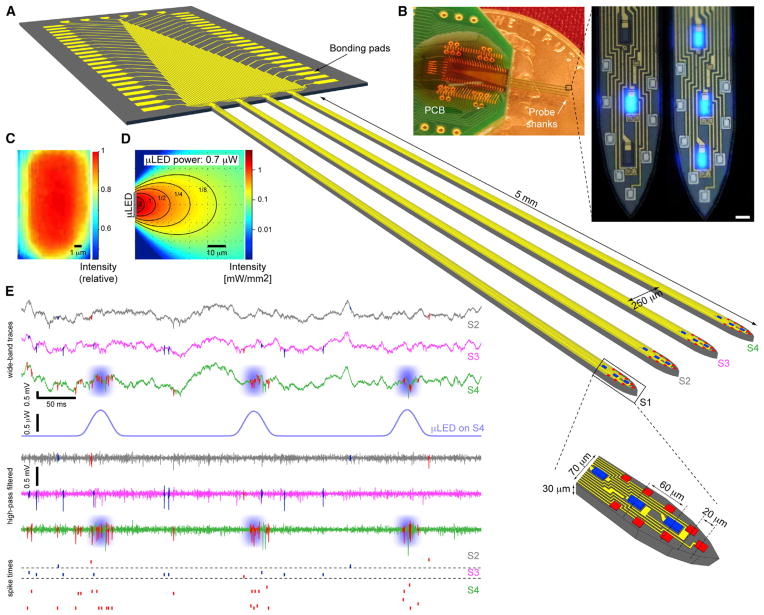
We have developed a multi-shank optogenetic neural probe that can provide spatially confined optical stimulation of simultaneously monitored neurons in behaving animals. A four-shank probe has a total of 12 μLEDs and 32 recording electrodes, all monolithically integrated on the probe tips to cover a 200 μm vertical span (Figure 1A). The electrodes have a vertical pitch of 20 μm, arranged in a high-density cluster designed to identify single units from a highly populated brain structure such as the CA1 pyramidal layer. At the center of each octo-electrode cluster, a linear array of three μLEDs with a 60-μm pitch is integrated. Each μLED has an emission area of 150 μm² (10 μm × 15 μm), comparable to the cross-section of a soma of a typical pyramidal neuron. The μLED is less than 0.5 μm thick, which is at least an order of magnitude thinner than optical fibers or integrated waveguides for reduced insertion damage. The fabricated probe is shown in Figure 1B with either a single or multiple μLEDs driven simultaneously. The relative intensity from a μLED as projected into a CCD camera is mapped in Figure 1C. The light output follows a Lambertian profile and is attenuated when propagating through the brain ambient (Figure 1D). Depending on the μLED output power and the threshold of cell activation, the effective stimulation resolution can be confined to the range of several tens of microns or less (Figure 3D). Because the μLED interconnection traces were lithographically patterned to have 4-μm width and 2-μm spacing, we could integrate three light sources per shank in this first-generation device, while maintaining the same 70-μm shank width that could only carry a single waveguide in previous designs (Wu et al., 2013). The μLED interconnection width of 4 μm was designed conservatively to avoid electromigration and Joule heating-induced defects in cases where current injection of more than 10 mA is needed (less than 10 μA is required for photostimulation of nearby neurons, see below). Connections to external electronics were made using flexible, lightweight cables, which enable free animal movements. Figure 1E demonstrates the recording of multiple cells from the hippocampal CA1 pyramidal layer and the optically induced, localized spiking during illumination by a particular μLED. With 12 μLEDs distributed across four probe shanks (250 μm pitch), there are 4,096 (2¹²) possible combinations at any time that can be programmed to manipulate multi-neuronal spike timing across a neuronal network. This will allow versatile manipulation of neural circuits in deep structures of behaving animals at an unprecedented spatiotemporal resolution.

Figure 1. μLED Probe Drives Localized Spiking in Freely Moving Mice.

(A) 3D schematic of the μLED probe in brain tissue. Probe consists of four shanks, and each shank is integrated with eight Ti/Ir recording sites (11 μm × 13 μm) and three interspersed μLEDs (10 μm × 15 μm).

(B) Photograph of an implantation-ready probe on a penny and high-magnification images of the illuminated μLEDs (inset, scale bar, 15 μm).

(C) The intensity map of a μLED as captured by a CCD camera.

(D) Estimated spread of light in brain during μLED illumination.

(E) Snapshot of 600 ms of continuous recording from the CA1 pyramidal cell layer of a freely moving CaMKII::ChR2 mouse. Wide-band (0.3–10,000 Hz) and high-pass filtered (800 Hz) traces are shown for three sites, one from each shank (S2, S3, S4), during illumination (peak power, 700 nW) of the central μLED on shank 4 (S4). Raster plots at bottom show spike times of pyramidal cells (PYR, red) and interneurons (INT, blue). Note time-locked spiking of multiple PYR on the illuminated (S4) but not other shanks.

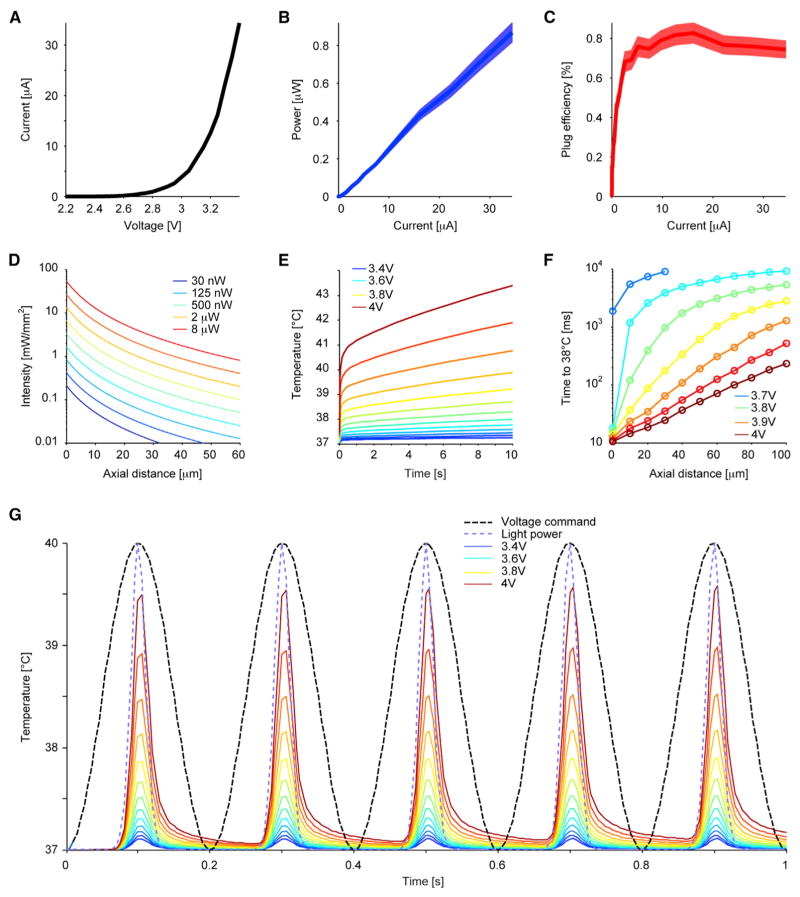
Figure 3. Characterization of the μLEDs.

(A) Current versus voltage.

(B and C) Optical power and plug efficiency versus current, respectively (mean and SEM, n = 5).

(D) Light intensity modeling in the brain along the main axis of the μLED (perpendicular to the probe surface) at a logarithmically spaced array of light power. At 4 μW (at which iHFOs are consistently generated, Figure 6), intensity falls below 1 mW mm⁻² by 37 μm from the μLED; at 40 nW (at which local spiking is consistently induced, Figure 4), intensity falls below 0.1 mW mm⁻² by 6 μm.

(E and F) Thermal modeling of μLED during continuous operation at various bias voltages: (E) μLED surface temperature rise over 10 s; (F) time required to elevate the brain temperature to 38°C at various distances away from the μLED surface.

(G) Thermal modeling of μLED using 5-Hz sinusoid voltage bias waveforms: the temperature rise follows the light power waveform (blue dash, normalized) rather than the voltage command (black dash, normalized), with minimal heat accumulation after five cycles. See also Figures S1 and S2.

Monolithic Integration of μLEDs on Silicon: Fabrication Process

In contrast to previous approaches using sapphire as the LED microfabrication substrate (Kim et al., 2013; McAlinden et al., 2013; Zhang et al., 2003), we have designed a process that can monolithically integrate InGaN μLEDs onto silicon substrate to achieve minimally invasive, needle-like shank structures using precise silicon micromachining techniques. Silicon also has approximately five times higher thermal conductivity than sapphire, allowing more effective dissipation of heat generated by the μLEDs (Mion et al., 2003). In addition, having an opaque silicon substrate confines light emission to the topside of the μLEDs, whereas the on-sapphire LEDs can emit light through the transparent probe shanks, leading to poor illumination resolution.

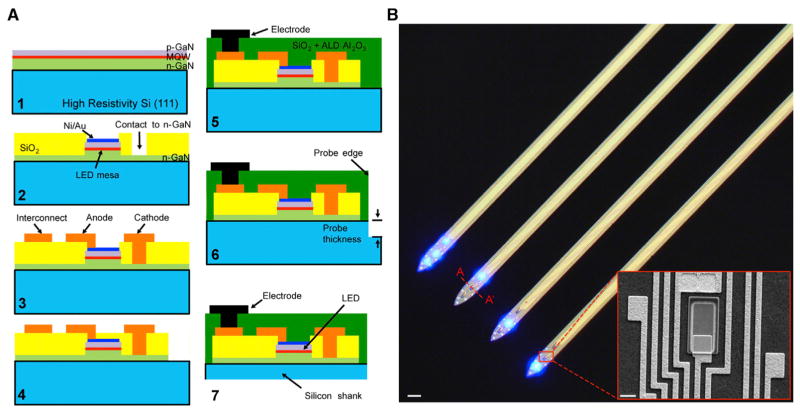
Fabrication steps are shown as schematics (Figure 2A) through the A-A′ cross-section (indicated in Figure 2B). Briefly, the process begins with a commercially available Si (111) wafer with quantum-well epitaxial layers grown to have a centered emission at 460 nm (Figure 2A1; NOVAGAN). The μLED mesa structures are defined by plasma etching. A Ni/Au (5/5 nm) layer spreads the injected current uniformly across the top surface of the μLED (Figure 2A2). The current spreading layer also forms an ohmic contact to the p-GaN layer with contact resistance of 10⁻⁵ Ω-cm and gives 75% transparency to blue light (460 nm). Deposition of a 500-nm-thick SiO₂ insulates the mesa sidewalls and n-GaN, with the contacts to the n-GaN layer opened by wet etching. A Ti/Al/Ti/Au (50/250/50/100 nm) layer is patterned to form parallel electrical interconnection lines to carry the signals from recording channels and to deliver power to the μLEDs (Figure 2A3). GaN is etched completely outside of the probe shanks to expose the underlying silicon (Figure 2A4). Next, Ti/Pt/Ir (10/50/50 nm) is sputtered and patterned to form the recording electrodes (11 μm × 13 μm; Figure 2A5). The electrode impedance is approximately 1 MΩ at 1 kHz. Finally, the silicon substrate is etched from the top (Figure 2A6) and the bottom (Figure 2A7) to release the 30-μm-thick probes from the wafer. The fabricated μLEDs can be controlled independently (Figure 2B and Movie S1). High-magnification SEM image of a μLED with the nearby interconnects and contacts (Figure 2B, inset) illustrates the high-precision alignment and integration density achieved by taking the monolithic approach.

Figure 2. μLED Fabrication.

(A) Fabrication process of the μLED probe shown across A-A′ (panel b): (1) epitaxial layers grown on a (111) silicon wafer; (2) formation of LED mesa and opening n-GaN contact; (3) patterning of Ti/Al/Ti/Au for interconnection lines; (4) plasma etching of field GaN; (5) deposition of oxide dual layer and patterning of recording electrodes; (6) frontside DRIE to define the probe shank dimensions; (7) backside thinning to release the probes from wafer.

(B) Microscope and SEM (inset) images of the released probe. Scale bars: 70 μm and 6 μm (inset).

See also Movie S1.

μLEDs Driven by μAmp Currents Provide Sufficient Light for ChR2 Activation without Excessive Heating

Electro-Optical Characterization of μLEDs

Compared with macro LEDs, the reduction of μLED size can help to distribute current evenly through the Ni/Au layer, leading to uniform light emission (Figure 1C). However, micro-features are potentially more sensitive to fabrication defects. In our design, multiple μLEDs biased under the same voltage show uniform emission, indicating consistent fabrication quality in terms of contact resistance, interconnect resistance, etc. (Figure 1B and Movie S1). Any variation would be observable as non-uniform illumination, since the optical power is an exponential function of the voltage across the μLED junction.

The detailed characterization of the μLEDs is summarized in Figure 3. Figure 3A shows the I/V curve of a representative μLED. The differential resistance increases as the μLED mesa area is reduced (Figure S1A). Figures 3B and 3C illustrate the operation consistency measured from five randomly selected μLEDs. As a reference, 0.15 μW light output corresponds to 1 mW mm⁻² intensity at the μLED surface (150 μm²). This intensity is sufficient to activate ChR2 (Stark et al., 2012) and can be achieved by applying less than 8 μA (Figure 3B). At high injection (~13 mA), the optical output saturates around 53 μW (353 mW mm⁻²), which offers the option to stimulate a larger cell population (Figure S1B). The measured peak plug efficiency is around 0.87% (Figure 3C). The attenuation of light intensity across the brain media is shown in Figure 3D, which further confines the stimulation toward a small group of neurons.

Thermal Modeling

The mechanism responsible for the generation of a neural action potential can be affected by temperature. Even during normal animal behavior, brain temperature change can be as much as 2°C–3°C between active and resting states, affecting the action potential waveform on the cellular and population scale in a complex manner (Andersen and Moser, 1995). We have developed a bio-heat transfer model using COMSOL Multiphysics (COMSOL Inc.) to simulate the temperature change during various μLED operation conditions. As there is no accepted threshold temperature for the safe operation of implantable neural devices (Elwassif et al., 2006), we loosely define the “threshold” as 1°C temperature rise in our analysis. To build a conservative model, we assumed that all electrical input power is converted into heat. In addition, we only analyzed the temperature increase caused by the most distal μLED (LED1 in Figure S2A). As illustrated in Figure S2B, the thermal energy generated at the μLED is most effectively dissipated through the thermally conductive silicon probe shank toward the proximal end. Therefore, LED1 generates the greatest temperature rise at any given input power, because the probe tip has the largest thermal resistance to the “heat sink.”

The induced temperature change is strongly dependent on the μLED input power waveform. With the initial temperature set to 37°C, Figure 3E shows the temperature rise at the surface of the μLED using the worst case: DC-bias at various input voltages. The result indicates that all operating conditions shown in Figures 3A–3C, which are below 3.4 V, are safe even when the μLED is driven continuously for 10 s. In addition to the thermal conduction through the silicon probe shank, the brain ambient also helps to dissipate heat via conduction and blood perfusion. Also, because of the large thermal capacitance of the brain, we expect the temperature rise of the brain to be slower than on the μLED surface. Figure 3F shows the time required to elevate the local brain temperature to 38°C for the higher-bias voltages (> 3.65 V), which increases exponentially as a function of the distance away from the μLED top surface. In vivo studies often use pulsed light output with duration under 100 ms. To achieve this light duration with minimal cross-talk onto the recording channels, we used low-frequency sinusoidal voltage waveforms in our in vivo experiments (Figure S3) to drive the μLEDs. Because the μLEDs emit light only above ~2.5 V, a 5-Hz voltage sinusoid (with a parametrically swept peak amplitude between 2.5 and 4 V; dashed black trace, Figure 3G) generates short light transients, which are essentially “rounded pulses” with a duration that varies linearly with the voltage command (44 ms with a 3 V peak; 74 ms with a 4 V peak, dashed blue trace, Figure 3G). Because of the small duty cycle (mean, 26%; range, 16%–37%), heat accumulation is minimal, with less than 0.1°C difference between the peak temperature of the first and the fifth cycle. Beyond 3.85 V input, the peak temperature can transiently reach 38°C; however, whether a few milliseconds of heating beyond 38°C has adverse effect on the adjacent neural network is unknown.

As an indirect assessment of the heating effect on neuronal activity, we compared the spike waveforms of CA1 pyramidal cells (PYR) during spontaneous activity and during same-shank illumination (Figure S4). At low bias voltages (≤3.1 V), waveforms during light were unmodified (p = 0.3, exact Binomial test; Figure S4A). Increasing light power caused increased distortion (rank correlation between voltage bias and waveform consistency, −0.2; p = 0.02, permutation test; Figures S4B–S4D). However, high-power illumination was occasionally accompanied by high-frequency (2 kHz) oscillations, limiting the interpretational power of these observations. A direct assessment of the heating effect was performed in control mice (without ChR2). No change on action potentials were detected (Figures S4E–S4G), demonstrating that thermal effects of brief μLED stimulation have negligible effects.

Spatial Control of Spiking with Sub-microwatt Power Light

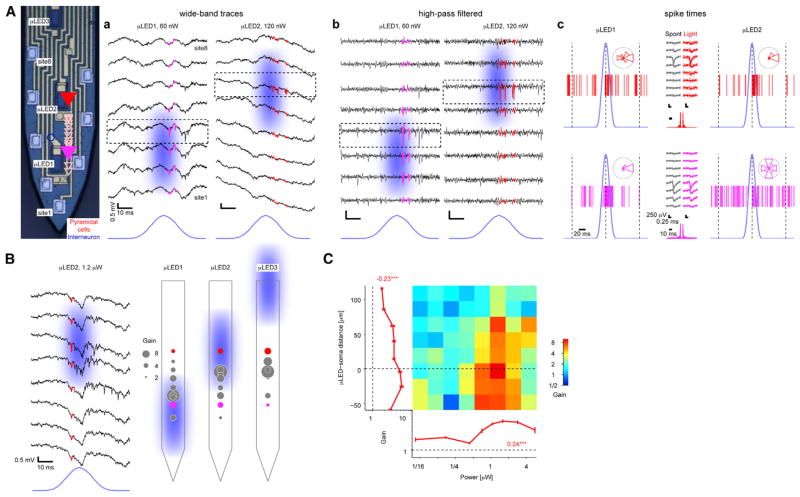
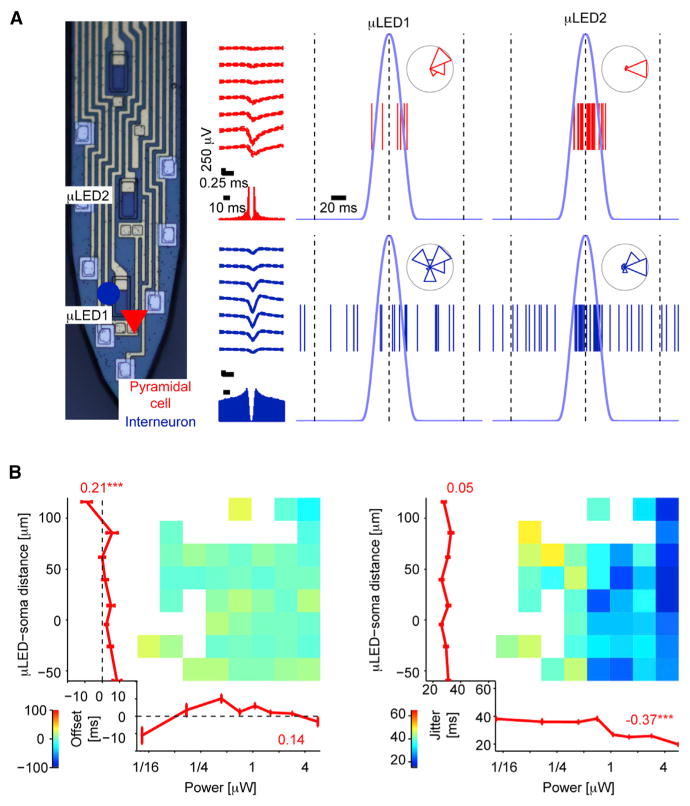
To test the in vivo performance of the μLED probes, we implanted them in the CA1 pyramidal cell layer (n = 6 mice). In CaMKII::ChR2 animals (n = 4; Figure 4) but not in control (wild-type, n = 2; Figure S3) animals, focal illumination via a single μLED induced spiking of nearby neurons in an intensity-dependent manner. Sub-microwatt (60–120 nW; “low power”) illumination induced time-locked spiking of one or more neurons in the immediate vicinity of the μLED (Figure 4A); assuming a neuron-μLED distance of 10 μm, this activation threshold translates to 0.1–0.2 mW mm⁻², values comparable to those observed using manually fabricated diode-probes (Stark et al., 2012, 2013). More cells were induced to spike upon “higher-power” illumination (0.8–1.2 μW; Figure 4B). Using “low-power” illumination from one of two μLEDs positioned 60 μm apart and thus straddling the CA1 pyramidal cell layer from above and below, distinct neurons could be controlled independently in the intact brain of freely moving mice (Figure 4A).

Figure 4. μLED Illumination Induces Local Spiking.

(A) Focal control of pyramidal cells (PYR) in distinct parts of the CA1 pyramidal cell layer (freely moving CaMKII::ChR2 mouse). a. Snapshots show wide-band traces from eight recording sites during brief illumination by two μLEDs. Pink/red traces depict spikes of two PYR responding to focal illumination. b. Same data, high-pass filtered (800 Hz) to emphasize spike timing and localization. c. Spike raster plots, showing all spikes that occurred during 90 periodic stimulation cycles at 330 nW. Insets show spikes binned according to time (light peak, phase zero; 100 ms offset, phase π). Note consistent spike waveforms during light and spontaneous (Spont) activity and time locking of pink (bottom) PYR to μLED1 and red PYR to μLED2.

(B) Spatial biasing of PYR spiking within CA1: (left) same recording sites as in (A) during light of ten times higher power, driving the red PYR and recruiting additional units; (right) illustration of spatial biasing by distinct same-shank μLEDs (peak power, 1.2 μW). Gain is defined as spiking rate during light divided by the baseline rate. Pink/red circles depict the same units shown in (A).

(C) Dependence of PYR (n = 38) gain on light power (abscissa) and μLED-soma distance, estimated by waveform amplitude distributions. Error bars, SEM; numbers, rank correlation coefficients; ***p < 0.005, permutation test. Gain is higher when light power is higher and when the μLED is very close or just below PYR somata.

See also Figures S3, S4, and S5.

To quantify the dependence of the magnitude of the induced spiking on μLED-neuron distance and light power, we estimated the location of the soma of each neuron according to the spike amplitude distribution (Figure 4Ac) and defined spiking “gain” as the spiking rate during light divided by the rate of the same neuron in the lack of illumination. Even during “high-power” illumination, when multiple neurons are typically driven, the effect on spiking was strongly dependent on the μLED position (Figure 4B). To distinguish between direct (light) and indirect (circuit) effects, we classified the recorded cells into PYR (directly activated in CaMKII::ChR2 mice due to the paucity of recurrent connections between PYR in CA1; Thomson and Radpour, 1991) and interneurons (INT; indirectly activated) using a Gaussian Mixture Model (Stark et al., 2013). Consistent with the examples (Figures 4A and 4B), the spiking gain of directly activated PYR depended on both light power (rank correlation: 0.24, p < 0.001, permutation test; 38 PYR yielding 690 cell/power/μLED combinations; Figure 4C) and μLED-soma distance (rank correlation: −0.27, p < 0.001; Figure S5B). A similar pattern was observed for indirectly driven interneurons (INT; rank correlation with light power: 0.32, p < 0.001; with μLED-soma distance: −0.19, p < 0.001; 11 INT, 235 cell/power/μLED combinations; Figure S5). Moreover, gain was consistently higher when the μLED was in stratum pyramidale or below the cell body (i.e., in stratum radiatum) than when the μLED was above (i.e., in stratum oriens; rank correlation: −0.23, p < 0.001; Figure 4C). Thus, the μLED probes enable independent control of distinct cell populations within the densely packed CA1 pyramidal cell layer.

Temporal and Multilayered Control

Neither the gain-intensity curve nor the gain-distance curve exhibited a step-function profile (Figure 4C). For the gain-intensity curve, this may be explained by some ChR2 activation even at very low power and subsequent gradual recruitment of ChR2 channels, and a similar explanation might account for distant somata. Yet the soma of a single neuron located close to the probe shank is expected to receive very different illumination by distinct neuron-size μLEDs, suggesting that the graded profile of the gain-distance curves (Figures 4C and S5) is due to activation of non-somatic ChR2. Consistent with this possibility, we occasionally observed more robust driving of spiking during stratum oriens (putatively basal dendritic; Figure 5A, μLED2) compared to direct somatic illumination (μLED1). A similar profile was observed for simultaneously recorded indirectly activated INT (Figure 5A).

Figure 5. Multilayered Control of Spiking.

(A) Spiking of a PYR (red triangle) and an inter-neuron (blue circle) recorded from the CA1 pyramidal cell layer of a freely moving CaMKII::ChR2 during illumination (4.2 μW, 30 cycles) within the layer (μLED1) and at more distant loci. Stratum oriens (μLED2) illumination induced more robust spiking than putative somatic illumination (μLED1).

(B) Dependence of spike timing on light power (abscissa) and μLED-soma distance. Left: PYR spiking offset (relative to time of peak light power) depends on μLED-soma distance. Numbers show circular-linear correlation coefficients; error bars, SEM; */***p < 0.05/0.005, permutation test; n = 38 PYR. Right: temporal jitter (SD of spike timing) consistently depends on light power but inconsistently on μLED-soma distance. Only distance-power bins in which the number of time-locked units exceeded chance (p < 0.05, Binomial test) are shown. Numbers, rank correlation coefficients. See also Figure S5.

To quantify the dependence of spike timing on μLED-neuron distance during periodically applied light, we assigned a “phase” for each spike: phase 0 corresponds to the time of peak light power, whereas phase π (or −π) corresponds to an offset of 100 ms from the peak. The mean of all spike phases defines the offset of spiking from time of peak light, and their standard deviation defines the temporal jitter in the induced spiking. Jitter consistently depended on light power (rank correlations: PYR: −0.37, p < 0.001; INT: −0.44, p < 0.001) but inconsistently on μLED-neuron distance (PYR: 0.05, p = 0.19; INT: −0.15, p = 0.03; Figure 5B; see also Figure S5). However, PYR jitter was always lower than the jitter of the indirectly activated INT, both overall (medians: PYR: 29 ms; INT: 46 ms; p < 0.001, Mann-Whitney U test) and for every distance bin (p < 0.01 for all eight bins). Spiking occurred consistently earlier for smaller μLED-neuron distances (PYR rank correlation: 0.21, p < 0.001; INT: 0.52, p < 0.001; Figures 5B and S5). Together, these observations indicate that multilayered control may be achieved using multiple μLEDs and emphasize the potential usefulness of confinement of opsin expression to restricted domains of neurons.

μLED Illumination Generates Synthetic Ripples

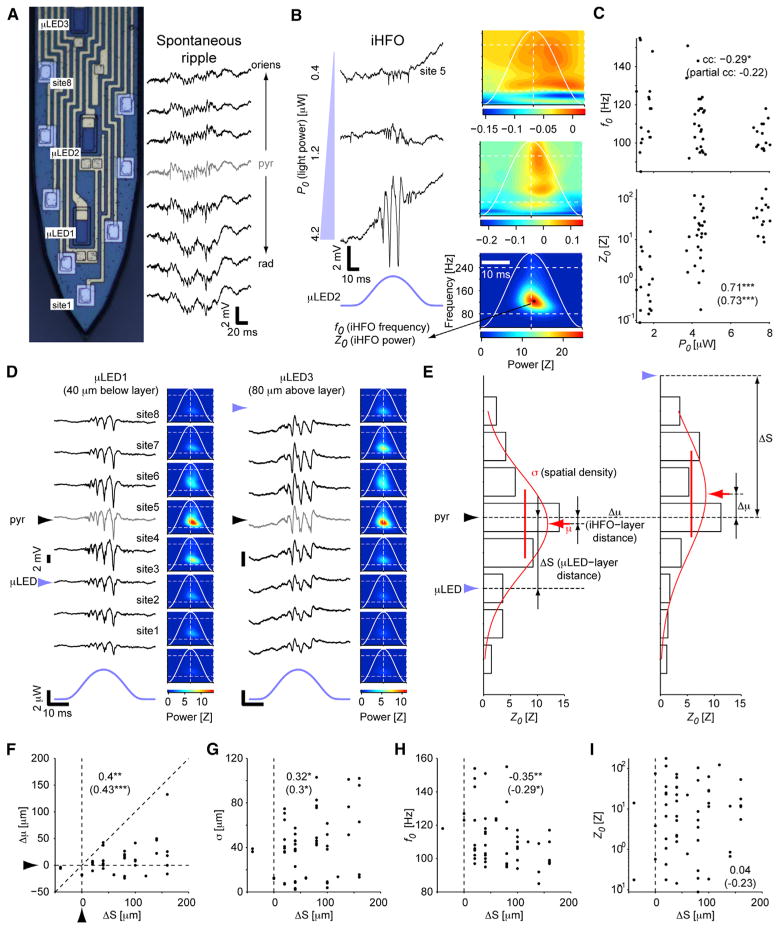
Upon recording from the CA1 pyramidal cell layer of freely moving mice, spontaneously occurring high-frequency “ripple” oscillations (Buzsáki et al., 1992) are readily observed. Since high-frequency oscillations (HFOs) can be induced synthetically by fiber illumination above the layer in intact rodents (Stark et al., 2014), we hypothesized that induced HFOs (iHFOs) could also be generated by more focal illumination. In contrast to single-cell activation, which could be driven non-somatically, the depth profile of the iHFOs may serve as a proxy to somatically confined opsin activation because of the synchronized somatic output of several cells, which can average out the effects of non-somatic opsin drive.

The center of the CA1 pyramidal cell layer was defined as the recording site with the peak ripple amplitude (Figure 6A). Intra-cortical illumination using a μLED close (≤20 μm) to the center of the layer generated iHFOs (frequency range, 85–155 Hz) with power increasing in an intensity-dependent manner (Figure 6B). While low-power illumination only induced spiking (Figures 1E, 4A, and 6B, top), illumination with higher power organized spiking into ripple-range oscillations of monotonically increasing amplitude (rank correlation between peak light power P₀ and peak oscillation power Z₀: 0.71; p < 0.001, permutation test; n = 56 recording sites; Figure 6C). These observations indicate that intra-layer illumination of pyramidal cells is sufficient to induce synthetic ripples.

Figure 6. Stimulation of Pyramidal Cell Dendrites Induces More Widespread and Slower Oscillations Than Somatic Stimulation.

(A) Snapshot of wide-band traces from eight recording sites of a shank implanted in CA1 of a freely moving mouse during a single CA1 ripple; gray trace indicates the estimated center of the CA1 pyramidal cell layer; pyr, stratum pyramidale; oriens, stratum oriens; rad, stratum radiatum.

(B) In CaMKII::ChR2 mice, focal illumination generates spiking and induced high-frequency oscillations (iHFOs) in an intensity-dependent manner. Example wideband traces at left, time-frequency decompositions at right (continuous wavelet transform; averages of 30 same-site stimuli).

(C) iHFO frequency and peak power depend on the applied light power. Data are from n = 56 sites in which iHFO amplitude exceeded chance and was time locked to light (p < 0.05, permutation test). Numbers: rank correlations; */**/***p < 0.05/0.01/0.005, permutation test. Numbers in parentheses: partial rank correlations (between the dependent variable and P₀, accounting for ΔS).

(D) Illumination below and above the layer (light power, 4.2 μW) generates distinct iHFO patterns. Left: example wide-band traces; right: averages.

(E) Method for determining the location of peak iHFO power (μ), spatial spread (σ), and iHFO and μLED location relative to CA1 pyramidal cell layer center (Δμ and ΔS).

(F–I) iHFO location (F), spatial density (G), and frequency (H), but not iHFO power (I) depend on μLED location relative to the layer. Data and conventions are the same as in (C) (here, partial rank correlations are between the dependent variable and ΔS, accounting for P₀). See also Figure S6.

Induced Ripple Properties Differ during Superficial and Deep Illumination

To determine the effect of input site (infra-layer, intra-layer, and supra-layer) on ripple frequency and spatial extent, we compared iHFOs recorded at the same sites by activating distinct same-shank μLEDs. When a μLED illuminated a region above the layer (closer to the “deep” sub-layers of CA1; Mizuseki et al., 2011), the locus of maximal iHFO power appeared to shift slightly above and iHFO frequency decreased, as compared with intra- or infra-layer illumination (“superficial” sub-layer; Figures 6D and S6). We quantified the influence of light source position relative to the layer center, ΔS, on the shift of the iHFO center relative to the same reference, Δμ (Figure 6E). Regardless of light power, the locus of maximal iHFO power depended on μLED position (rank correlation between Δμ and ΔS: 0.4; p = 0.005; since Δμ could depend on P₀, we also computed partial rank correlation between Δμ and ΔS, accounting for P₀: 0.43, p = 0.001; Figure 6F, left). These observations are consistent with the sublayer organization of the CA1 pyramidal layer (Mizuseki et al., 2011).

The spatial spread of the iHFOs was also influenced by μLED location: light sources above the layer induced a larger spread than intra-layer or infra-layer illumination (rank correlation between σ and ΔS: 0.32, p = 0.01; partial rank correlation between σ and ΔS, accounting for P₀: 0.3, p = 0.03; Figure 6G). Moreover, iHFO frequency depended on μLED location: intra-layer illumination induced higher-frequency oscillations than basal dendrite (stratum oriens) illumination (rank correlation between f₀ and ΔS: −0.35, p = 0.01; Figure 6H). In contrast, oscillation power was not consistently correlated with μLED location (rank correlation: 0.04, p = 0.78; Figure 6I). These observations are consistent with prior observations indicating that superficial and deep sublayers of the CA1 pyramidal layer express different biophysical properties (Mizuseki et al., 2011) and suggest that excitatory input at the stratum radiatum (arriving mainly from the CA3) can recruit a faster, more confined network than input to stratum oriens (from entorhinal cortex/amygdala; Nakashiba et al., 2009).

DISCUSSION

Understanding the operations of local circuits is a major goal in neuroscience, which requires both large-scale monitoring of neuronal activity and targeted perturbation of identified circuit elements (Buzsáki et al., 2015). The monolithically integrated μLED probes described in this work are expected to bridge the gap between the technological advances in semiconductors and advanced applications in systems neuroscience.

Novel Results

Taking advantage of the unprecedented spatial and temporal resolution of spike recording and control provided by the μLED probes, we have made two novel observations. First, we found that illumination of the cell bodies and apical dendrites in the stratum radiatum is more efficient in driving pyramidal cell spiking than stratum oriens illumination (Figure 4C). This may be due to a bias in opsin expression and/or to distinct biophysical properties of the large and thick apical (radiatum) and thin basal (oriens) dendrites of the ChR2-expressing pyramidal cells, the former being straight and the latter oblique (Pyapali et al., 1998).

Second, we found that focal illumination can generate synthetic CA1 ripples whose properties depend on the locus of the input, extending previous observations during fiber illumination (Stark et al., 2014). Infra-/intra-layer illumination induced ripples of the highest frequency, which were also most compact in the vertical dimension, while supra-layer (stratum oriens) illumination generated slower and more widespread oscillations (Figure 6). These observations indicate that despite the compactness of the CA1 pyramidal cell layer (~50 μm), multiple ripple generators can reside within the sublayers (Lee et al., 2014; Mizuseki et al., 2011).

Alternative Methods

By monolithically integrating μLEDs onto silicon probe shanks, we aimed to provide optical stimulation capability with high spatial resolution in addition to electrical recording at multiple locations. The μLEDs provide tunable illumination such that the tissue volume receiving sufficient power to activate ChR2 can match the tissue volume within the recording range of certain electrodes (Figures 1D and 3D). Such high spatial resolution control over spiking has been previously possible only by intra-cellular current injection or by two-photon microscopy combined with optogenetics (Packer et al., 2015; Rickgauer et al., 2014). Intracellular methods are not yet scalable in freely moving animals, while the all-optical approach is not applicable to deep structures in freely moving animals without the destruction of overlying brain tissue. Compared to these alternatives, the μLED probe approach is limited in that it only provides information about spiking (and not about intracellular calcium, Vm, or transmembrane currents) and should therefore be viewed as a complementary method.

Limitations and Potential Solutions

Despite recent advances introducing buffer layers between GaN and silicon, the interface defect density between GaN and silicon is still roughly ten times greater than that between GaN and sapphire. As a result, the internal quantum efficiency (IQE) of the μLED is limited: only approximately 33% of the injected carriers can produce photons (Zhu et al., 2011). These photons generated at the active region are emitted in all directions. Approximately 50% of the photons are emitted toward the substrate and are absorbed at the GaN/silicon interface. Of the remaining photons, only 8.8% can escape from total internal reflection (TIR) at the GaN/brain interface, which has a high index of refraction contrast (n_GaN = 2.45 and n_brain = 1.36). Additionally, the Ni/Au current spreading layer has 75% measured transparency to blue light. The photon extraction efficiency is therefore only 3.33%, which is similar to results from a previous report (Zhu et al., 2011). Therefore, the theoretical plug efficiency (P_out/P_in) for the μLED is limited to roughly 1.1% by IQE (33%) and extraction efficiency (3.33%) alone. Despite the seemingly low efficiency, it is shown that the μLEDs could operate at their steady state as well as transient, pulsed conditions to emit light at an intensity enough to activate ChR2 without heating the ambient tissue by more than 1°C. Heat dissipation in neuronal tissue is likely more effective than bench measurements, since local brain tissue is constantly perfused by fluid. Our experiments in control (opsin-free) mice explicitly demonstrate that a possible temperature effect does not induce or alter spiking activity.

A limitation of the current version of μLED probes is the low-frequency artifacts induced during periodic activation. These artifacts were also observed in opsin-free (wild-type) animals and were removed using offline adaptive filtering (Figure S3). As a result, they did not hinder the analysis of spiking or LFP effects (Figures 4, 5, and 6), but limited the range of stimulus waveforms that could be applied. A closer analysis of the interference waveform revealed that the coupled signal had two components. First, the sinusoid input voltage is coupled to nearby recording channels (see Figure S3A, waveform from Shank 1; and Figure S3Ca, waveform at near-threshold input). We attribute this effect to the μLED interconnects that are routed directly below the recording interconnects on the PCB. Direct voltage coupling between parallel interconnects on the probe shank is not likely because the μLED anode (positive) interconnects are always shielded by the μLED cathode (grounded) interconnects. A natural solution to this limitation is to use multiple metal layer PCBs with a shielded metal plane completely separating the recording channels and μLED channels. The second interference component is a rectified waveform that is coupled to all recording channels regardless of which μLED is driven. Because this effect only occurs when there is significant current flowing through the μLED (Figure S3C), we attribute this effect to capacitive coupling from the μLED n-GaN layer to the recording interconnects above: the μLED cathode will experience a finite voltage increase only when there is current. This hypothesis is also supported by the observation that the rectified signal is coupled to all recording channels (Figures S3A and S3C), as the n-GaN is a continuous layer underneath all recording channels (Figure 2A). One possible solution to minimize the coupling from n-GaN is to modify the fabrication process with the same strategy as the PCB design, by depositing additional metal layers between the recording and stimulation channels as a shield.

The final limitation to the current utility of the μLED probes relates to the available opsin technologies. Non-somatic opsin expression facilitated multilayered control (Figures 5 and 6), but also reduced the spatial resolution of spiking control, resulting in a graded gain-versus-distance profile (Figure 4D). Thus, the μLED probe can yield a better spatial resolution than it is currently possible with simple light activation of opsin-expressing neurons. The full advantage of our multi-site μLED probe technique will be achieved by confining opsin expression specifically to the axon initial segment, soma, or dendritic compartment. These spatially improved methods are within reach, and we expect that the μLED probes will enable true multiple single-neuron spatial control in the fully intact brain of freely moving animals in the near future.

Novel Applications

Far-reaching experiments will be possible by μLED probes. For instance, one could independently control superficial versus deep pyramidal cells in the CA1 pyramidal cell layer (Figure 6) and examine the behavioral context of ripples during which these distinct cells participate (Buzsáki et al., 1992; Girardeau et al., 2009) or their contribution to sequence generation (Foster and Wilson, 2006; Stark et al., 2015). Second, one could compare, in freely moving animals, the predictions of various models of phase precession generation (e.g., somatodendritic interference, dual oscillators, and network models; Harvey et al., 2009; O’Keefe and Recce, 1993) by controlling the input to distinct compartments of the same cell (Figure 5). These examples illustrate classes of experiments that were previously impossible to carry out: independent control of nearby neurons, and independent control of distinct inputs to a given neuron, both in deep structures of the intact brain of freely moving animals.

Future Directions

There are several possible extensions of the μLED probe approach, the most evident of which is its scalability. It is straightforward to produce probes with more shanks or sites and μLEDs per shank without changing μLED size or the ratio between the number of μLEDs and recording sites or overall probe geometry. To further increase the integration density of μLEDs and recording sites, the best strategies are to reduce the μLED mesa size (Figure S1A) and/or to decrease the recording interconnection width from 2 μm by at least an order of magnitude using electron-beam lithography techniques. Such modifications will enable increasing the μLED to recording site ratio, placing yet more recording sites within a given probe area, and produce probes with narrower shanks—while keeping light power sufficient for inducing spikes/iHFOs. Such multiple-site μLEDs probes will be especially useful in structures where cell bodies are present in the entire volume, such as neocortex or striatum. Second, variations in fabrication materials and processing steps may enable fabricating non-blue μLEDs and thus enable the control of multiple opsin types. Finally, modifications in probe packaging and combination with existing commercial devices may enable wireless control, on-probe digitization, and on-probe LED driving, among other options.

EXPERIMENTAL PROCEDURES

μLED Fabrication Process

We first etch the epitaxial layers to expose n-GaN, forming isolated μLED mesa structures. Then, a 500-nm-thick PECVD oxide is deposited to insulate the mesa sidewalls. Using the same photoresist mask, the oxide is wet etched to open contacts to p-GaN, and a semi-transparent Ni/Au (5/5 nm) layer is patterned by liftoff to form an ohmic contact to p-GaN. Later, a separate mask is used to open contacts to the n-GaN layer. The n-contacts have been defined close to the mesa to minimize series resistance through n-GaN while taking into consideration the alignment margins and routing of the interconnects. Next, a Ti/Al/Ti/Au (50/250/50/100 nm) layer is patterned to form the electrical interconnection lines for recording channels as well as for powering the μLEDs. The bottom Ti layer serves as the adhesion layer with a proper work function to form an ohmic contact with n-GaN. The line width and spacing are both 2 μm for the recording channels, while the line width for the LED power lines is 4 μm to reduce the resistance, which is roughly 125 Ω with the 5-mm-long metal interconnect.

Post-LED Fabrication Process

Post-LED fabrication begins with etching of the GaN layer in the field region (outside of the probe shank) completely to expose the GaN sidewalls and the underlying silicon substrate. Etching through the alternating stacks of GaN/AlN buffer layers shows distinctive colors, typically a mixture of red, green, and blue. This observation helps to time the etching process so that the gray silicon substrate would not be over etched to form a rough topology. Next, we deposit a double layer of dielectrics (30-nm-thick Al₂O₃ by atomic layer deposition (ALD) and 500 nm thick oxide by PECVD) to insulate the GaN layers. We etch the oxide bilayer to open contacts at the recording sites and pattern Ti/Pt/Ir (10/50/50 nm) over the contacts to form the recording electrodes. Finally, we use a double-sided DRIE process to release the probes from the wafer: from the front side, we etch a 30-μm-deep trench that defines the probe thickness and shape; later, we thin down the wafer from the backside using plasma until only 30-μm-thick silicon remains to release each probe from the wafer. By conservatively defining 30-μm-thick shanks, we are able to release the probes with a high yield by thinning the starting silicon substrate (500 μm thick) by 470 μm, which requires the etch non-uniformity to be less than 5%.

Thermal Modeling

We build a realistic 3D model in COMSOL Multiphysics from the actual single-shank layout used in the probe fabrication. Surrounding the probe shank is a cylinder block of brain tissue that extends 0.5 mm radially from the center of the probe shank. For silicon, the thermal conductivity, heat capacity, and density are 130 W m⁻¹ °C⁻¹, 700 J kg⁻¹ °C⁻¹, and 2,330 kg m⁻³, respectively. For the brain tissue, the thermal conductivity, heat capacity, and density are 0.45 W m⁻¹ °C⁻¹, 3,650 J kg⁻¹ °C⁻¹, and 1,040 kg m⁻³, respectively (Elwassif et al., 2006). The 1-μm-thick silicon dioxide insulator on the top side of the probe shank contributes negligibly toward heat capacity and is simply modeled as a “thin thermally resistive layer” with a thermal conductivity of 1.4 W m⁻¹ °C⁻¹. All GaN components are submicron in thickness and therefore are neglected in the thermal model. Heat transfer physics in the brain with consideration of the μLED heat source and dissipation due to blood perfusion is governed by Penne’s equation ρC_p(∂T/∂t) = ∇(k∇T) − ρ_bω_bC_b(T − T_b) + Q, where ρ is the brain density, C_p is the brain heat capacity, k is the brain thermal conductivity, ρ_b is the blood density (1057 kg m⁻³), ω_b is the volumetric blood perfusion rate per unit volume (0.012 ml s⁻¹ cm⁻³), C_b is the blood heat capacity (3600 J kg⁻¹ °C⁻¹), T_p is the body temperature (37°C), and Q is the μLED heat source (W m⁻³) (Elwassif et al., 2006). The initial temperature of the system is set at 37°C. We have assumed a conservative boundary condition where the outer boundaries of the system are thermally insulated without any fixed temperatures. In reality, heat dissipation such as air convection at the proximal end of the probe where it is outside of the brain can help to further reduce the temperature rise. The heat source, Q is defined as the product of the μLED voltage and current, so that 100% of input electrical power is assumed to have converted to thermal power. At any given voltage, the current is computed using the diode equation I = I_se^V/nV_t, where I_s and nV_t are 1.276 nA and 0.1989 V, respectively, and were derived from our measured data shown in Figure S1. We report the simulation results in terms of temperature rise versus input voltages because our in vivo experiments used a voltage source to drive the μLEDs.

Electrophysiological Procedures

Six male mice (26–33 gr, 2–4 months old) were used in this study: four CaMKII:: ChR2 (B6.Cg-Tg(Camk2a-cre)T29-1Stl female, Jackson Labs #005359; cross-bred with B6; 129S-Gt(ROSA)26Sor^{tm32(CAG-COP4}*^{H134R/EYFP)Hze}/J male, Jackson Labs #012569) and two wild-type (control; C57L/6J, Jackson Labs), as previously described (Stark et al., 2014). The first two CaMKII::ChR2 mice were used in an acute configuration under urethane anesthesia (1.5 g/kg; Stark et al., 2013) whereas the other mice underwent chronic implantation surgeries. In all animals, a craniotomy was made above the right hemisphere (PA −1.6 and ML 1.1 mm), and the μLED probe was lowered to an initial depth of 0.8 mm. Subsequent movements of the probe were made in 35–105 μm increments over 15 min (acute) or 12–24 hr (chronic) intervals until approaching the CA1 pyramidal cell layer, recognized by the appearance of multiple high-amplitude units and spontaneous ripple events. After the initial surgery, chronically implanted animals were kept one to a cage on a reversed light/dark cycle. All animal handling procedures were approved by the New York University Animal Care and Facilities committee.

The μLED probe was packaged with a PCB, to which two connectors were soldered, a 36 pin male (for recording 32 neuronal channels, a ground, and a reference; A79022-001, Omnetics) and an 18 pin male (for driving and grounding 12 μLEDs; A79006-001, Omnetics), and mounted on a movable micro-drive (full turn, 280 μm; accuracy, ~20 μm). Lightweight multi-strand Litz wires (36 AWG, Alpha Wire) were used to connect the μLEDs to the voltage source while permitting free animal movement. Before surgery, light power from the μLEDs was measured using a power meter (1936-C, Newport) versus voltage bias. During experiments, voltage bias was applied using a single channel of a waveform generator (50 MHz, 3390, Keithley) or a programmable DSP (25 kHz, RX8, Tucker-Davis Technologies), controlled by MATLAB (MathWorks). Extracellular activity was filtered (0.3–10,000 Hz), amplified (400×; RHA2132, Intan), digitized (14 bit, 20 kHz digitization; KJE-1001, AmpliPex), and continuously stored on disk; the applied voltage waveforms were recorded on 12 additional channels.

During experiments, neuronal activity was inspected for spontaneous spiking activity, and if encountered, a baseline period of at least 15 min was recorded followed by light stimulation. Photostimulation was performed at each μLED separately (interleaved); voltage commands had the waveform of 5 Hz sine waves, with the amplitude scaled between zero and V_max (V_max ranged between 2.5 V and 4 V at 0.1 V or 0.5 V increments). This translated to applied light with “rounded pulse” waveforms, with pulse duration ranging 33–74 ms (mean, 54 ms) and duty cycle ranging 16%–37% (mean, 26%); 15 pulses were applied over 3 s. Photostimulation was then followed by another period of baseline activity.

Data Analysis

For offline analysis, spike waveforms were extracted from the wide-band recorded signals. Waveforms were linearly detrended, projected onto a common basis obtained by principal component analysis of the data, and sorted automatically (Harris et al., 2000) followed by manual adjustment. Only well-isolated units (amplitude > 50 μV; L-ratio [Schmitzer-Torbert et al., 2005] < 0.05; ISI index [Fee et al., 1996] < 0.2) were used. Subsequently each unit was tagged as excitatory/inhibitory (based on peaks/troughs in the short-time [±5 ms] pairwise cross-correlation; p < 0.001, convolution test; Stark and Abeles, 2009) and/or classified as putative PYR or INT (based on a Gaussian-mixture model (Stark et al., 2013; p < 0.05). We recorded a total of 93 well-isolated cells from CA1 of four freely moving and two anesthetized mice (one session per animal). Of these, 62 were PYR and 31 were INT.

For the analysis of spike timing relative to the periodic voltage input (period, T = 200 ms; Figures 5 and S5), a phase was assigned to each spike: spikes occurring at the peak of the voltage bias (peak of light power, Figure 3) were assigned a phase of 0, and spikes occurring at the trough of the voltage bias (100 ms offset from the peak of the light power) were assigned a phase of π (or −π). We then computed, for each neuron, the circular resultant vector R of all spike phases; the length of R (circular variance) defines the temporal jitter J in the induced spiking ( $J=(T/2\pi )·\sqrt{-2log\mid R\mid }$), and its angle (mean phase) defines the offset of spiking from time of peak light ((T/2π)•∠R), both in ms.

During application of a voltage bias to μLEDs, time-locked artifacts were evident in the wide-band traces; these were observed even in saline (Figure S3A) and in wild-type animals (Figure S3C). At low voltages, sinusoidal (voltage-like) artifacts were typically localized to channels recorded on the same shank as the biased μLED (Figure S3) and became more widespread at higher bias, where superimposed rectified (current-like) artifacts dominated the low-frequency component of the extracellular signals (Figure S3C). Before spectral analyses (Figures 6 and S6), artifacts were removed by triggering, averaging, and subtracting, for each neuronal channel separately, resulting in “cleaned” traces.

For a given effect size, the power of any statistical test depends on the α level. To increase the sensitivity of detecting effects, results are reported based on a significance threshold α = 0.05, and all groups included enough samples to enable rejection of the null at that level. Resampling (one-sided permutation) tests were used for the testing the significance of rank correlations, and non-parametric testing was used in all other cases.

Highlights.

• Multiple μLEDs and recording sites were fabricated monolithically on silicon

• Spikes were robustly induced using ultra-low optical power (~60 nW)

• Neurons 50 μm apart were controlled independently in CA1 of freely moving mice

• Deep and superficial parts of CA pyramidal layer form distinct ripple generators