Dynamics of Mycobacteriophage-Mycobacterial Host Interaction: Evidence for Secondary Mechanisms for Host Lethality

Abstract

Mycobacteriophages infect mycobacteria, resulting in their death. Therefore, the possibility of using them as therapeutic agents against the deadly mycobacterial disease tuberculosis (TB) is of great interest. To obtain better insight into the dynamics of mycobacterial inactivation by mycobacteriophages, this study was initiated using mycobacteriophage D29 and Mycobacterium smegmatis as the phage-host system. Here, we implemented a goal-oriented iterative cycle of experiments on one hand and mathematical modeling combined with Monte Carlo simulations on the other. This integrative approach lends valuable insight into the detailed kinetics of bacterium-phage interactions. We measured time-dependent changes in host viability during the growth of phage D29 in M. smegmatis at different multiplicities of infection (MOI). The predictions emerging out of theoretical analyses were further examined using biochemical and cell biological assays. In a phage-host interaction system where multiple rounds of infection are allowed to take place, cell counts drop more rapidly than expected if cell lysis is considered the only mechanism for cell death. The phenomenon could be explained by considering a secondary factor for cell death in addition to lysis. Further investigations reveal that phage infection leads to the increased production of superoxide radicals, which appears to be the secondary factor. Therefore, mycobacteriophage D29 can function as an effective antimycobacterial agent, the killing potential of which may be amplified through secondary mechanisms.

INTRODUCTION

Bacteriophages have played an important role in the development of tools to study the molecular genetics of bacteria (1). Using model systems such as phage lambda as well as the T family phages of Escherichia coli, significant information has come to light regarding how bacteriophages have developed the ability to tinker with host metabolism in such a way that phage growth is assisted (2). Bacteriophage growth takes place in several steps. First, they attach to the cell surface. Their genetic material then is injected into their host (3, 4). DNA replication is initiated subsequently. The replicated DNA then is packaged and finally the cells lyse, resulting in the release of the newborn phages. The number of viable cells is reduced by the number of cells that undergo lysis. Thus, bacteriophages have the ability to reduce bacterial counts. The efficiency with which the bacterial loads are reduced will depend on the number of phage present, their adsorption efficiency, average time taken for a new phage to come out of the cell (latent period), and finally the growth rate of the host.

The ability of bacteriophages to act as bactericidal agents has prompted researchers to attempt the curing of bacterial diseases with their help. Prior to the antibiotic era, therapy for bacterial infections using bacteriophages was considered a viable option (5–9). There were reports that such approaches met with success, at least in some cases, where the wounds were external (10). However, with the demonstrated effectiveness of antibiotics, phage therapy lost its relevance. In recent times interest in phage therapy has resumed, particularly because antibiotic therapy has been found to be wanting in special circumstances, such as when resistance mechanisms develop due to genetic changes or phenotypic variations. Antibiotics also can be highly toxic; therefore, their scope becomes limited under certain circumstances (11, 12). Phages can be considered alternatives to antibiotics in different ways. They could be used directly to destroy the pathogen. Many of the phage-encoded products, such as lysins, are highly toxic (13) to bacteria; therefore, instead of using these phages directly, their products could be used (14–16). Finally, it is important to note that phages have the ability to inhibit the metabolism of their hosts (host inactivation) (17); hence, by understanding how they perform this act, it may be possible to develop new strategies that do not necessarily use the phage directly for intervention against bacterial diseases.

Tuberculosis (TB) is an age-old problem. The causative agent of TB, Mycobacterium tuberculosis, was discovered more than a century ago (18). Antibiotics against the bacterium are available (19). However, the disease refuses to die out. The major reason behind this is that the bacteria can transit into a dormant state and remain as a latent infection within the body. This latent form of the bacteria is not acted upon by most drugs, making it difficult to eradicate the disease (20–22). Phages for mycobacteria were reported more than 7 decades ago (23, 24). Some of the mycobacteriophages that have been studied extensively in mycobacterial research include the lytic phage TM4 (25, 26) and the lysogenic phage L5 (27, 28). Phage D29 is closely related to L5, although it is lytic in nature (29, 30). In recent times many more mycobacteriophages have been discovered, bringing the number of fully sequenced phages to 842 (31). Large numbers of novel genes have been identified, some of which have been biochemically characterized (32–34). However, a deep insight into how mycobacteriophages infect and grow on mycobacteria remains lacking. The objective of this study was to undertake a holistic analysis of the fate of both the phage and host in a situation where multiple infection cycles are allowed. Our special focus was to investigate the dynamics of bacterial killing by the phage. To answer the questions that arose in this study, a theoretical approach was considered in parallel with an experimental one. Bacterial and phage growth rates were calculated from experimental methods and used to develop delay differential equations (DDEs) which, when solved, gave significant theoretical insight into the rate of bacterial killing. Based on certain predictions made from the theoretical studies, further experiments were performed to explain the phenomenon. The study reveals that mycobacteriophage D29 can inactivate its host cells not only through lysis but also by a secondary mechanism in which the infected cells produce toxic amounts of superoxide.

MATERIALS AND METHODS

Bacteria, bacteriophage, and media.

Mycobacterium smegmatis mc²155 was used as the host strain for mycobacteriophage D29 infection. Phage D29 was obtained as a gift from Ruth McNerney (LSHTM Keppel Street, London, United Kingdom). A temperature-sensitive mutant of D29 (D29ts10), which grows at 32°C but not at 42°C, was raised in this laboratory. Mycobacterial cells were grown in Middlebrook 7H9 (Difco) medium in the presence of 0.2% glycerol and 0.25% bovine serum albumin (BSA) (HiMedia Laboratories, India) with 0.01% Tween 80. Phage amplification and infection were done in the same media except that Tween 80 was omitted. During phage infection, the medium was supplemented with 2 mM CaCl₂. For colony counting, MB7H9 hard agar plates were used. For plaque formation, the hard agar was overlaid with top agar with 2 mM CaCl₂.

Infection assay and phage growth.

Phage amplification was done through confluent lysis followed by suspension in SM buffer as described previously (32, 35). In the final step, the phage was purified by performing CsCl density gradient centrifugation. The purified phage was dialyzed using a dialysis buffer (50 mM Tris-Cl [pH 8.0], 10 mM NaCl, 10 mM MgCl₂). M. smegmatis cells were infected with mycobacteriophage D29 at a multiplicity of infection (MOI) of 1 or, as mentioned, in the presence of 2 mM CaCl₂. At different time points, aliquots were removed and centrifuged at 15,700 × g for 5 min. The pellet and supernatant fractions were separated. The numbers of PFU present in the pellet (infectious center) and the supernatant (free phage) were determined separately. The sum of the two values obtained at time zero, immediately after adding phage, was considered the input PFU. The effective MOI was determined by dividing the input PFU count by the total viable cell count, CFU, which was derived by plating the host cells on the same day.

Cell counting procedures.

For estimating the number of viable cells that were present per milliliter (CFU ml⁻¹) in a culture of M. smegmatis cells, either uninfected or infected by phage D29, the method of dilution plating on MB7H9 hard agar was used. Changes in the cell density were monitored by measuring optical density at 600 nm (OD₆₀₀) and also by performing fluorescence-activated cell sorting (FACS) using the FACSAria system (Becton Dickinson, NJ) (see the supplemental material). Cells were injected into the FACS machine at a flow rate of 10 μl min⁻¹, and sample recording was done for 15 s. The volume that was injected was calculated to be 2.4 μl. The number of dots that appear on a scatter plot (forward scatter [FSC] against side scatter [SSC]), corresponding to each injection, was recorded. Each dot represents a count (cell). Finally, cell density was expressed as counts per milliliter. That the dots represent cellular entities was verified by staining with either SYTO 13 (for all cells) or fluorescent diacetate (FDA) (for viable cells) (see Fig. S2 in the supplemental material).

Flow-cytometric monitoring of bacterial cell viability.

Live-dead staining was performed using a propidium iodide (PI)-FDA (Sigma) dual staining method. Mycobacterial cells (phage treated and untreated) were labeled with FDA and PI for cell viability assessment (36). One microliter of FDA stock solution (10 mg ml⁻¹ in acetone) and 1 μl of PI (5 mg ml⁻¹ stock) were added simultaneously to 200 μl of cell-phage suspension. The cells were incubated for 15 min at 37°C with the stain(s). They then were washed and resuspended in phosphate-buffered saline (PBS) buffer, pH 7.4, and analyzed using a FACSAria system (Becton Dickinson, NJ). The FDA fluorescence was measured through the FITC-Alexa Fluor 488 channel, and PI accumulation was determined using the PI channel. The photomultiplier tube (PMT) voltage was kept at 320 mV, and the FACS flow rate was 1 (10 μl min⁻¹). Ten thousand events were recorded for each sample. Dot plots were generated by plotting fluorescence in the respective channel against SSC. The data were analyzed by specific quadrant gating for each experiment and were the same for all assays. The analysis was done using FACS Diva software.

ROS generation assay.

Reactive oxygen species (ROS) generation in mycobacterial cells was monitored using the fluorescent dye dihydroethidium (DHE; Molecular Probes). Two hundred microliters of host-phage suspension was sampled, and 1 μl of the DHE stock (10 mM) was added to each sample and incubated at room temperature in the dark for 30 min. The cells were centrifuged at 15,700 × g for 5 min, and the resulting pellet was washed twice with 10 mM Tris-Cl buffer (pH 7.5), resuspended in 500 μl of the same buffer, and analyzed by FACS. DHE fluorescence was measured using the PI channel.

For the determination of ROS released (extracellular), nitroblue tetrazolium (NBT; SRL) reagent was used. To perform this assay, the cell suspension was centrifuged and the supernatant was taken. An equal volume of NBT (0.2% final concentration) was added to the supernatant and incubated for 30 min at 37°C in the dark. NBT oxidation by ROS was monitored at 560 nm in microtiter plates (Nunc, Thermo Scientific) using a microplate reader (BMG Labtech).

DDEs.

Using experimentally determined values of bacterial growth rate, phage adsorption rate, latent period length, and average burst size, it is possible to predict the number of bacteria that would survive phage attack after time t by using a set of delay differential equations (DDEs). These DDEs were solved using Flunkert-Schöll pydelay. Pydelay is based upon the Bogacki-Shampine method (BSM) (37). BSM is a third-order Runge-Kutta method with the first-same-as-last property.

Monte Carlo simulations.

We studied the interaction system by using Monte Carlo simulations, with cell division and phage infection both occurring randomly (38). A set of random samples was chosen from the population of phage and bacteria at the same ratio. For each bacterium in the population, a random number is generated from a uniform distribution. If it is less than the rate of division of bacteria, then the cell would divide. Phage infections were done in the same manner.

RESULTS

Kinetics of host cell depletion following phage addition.

In order to examine the effect of phage addition on susceptible cells, the OD₆₀₀ of a host cell culture infected at an MOI of 1 was measured in a time-dependent manner over a period of 3 h. Within this interval, and at this MOI, it is expected that at least 50% of the cells will be infected (see Fig. S1 in the supplemental material). Apart from optical density determination, a FACS-based experiment also was done to monitor changes in cell counts upon phage infection. Prior to applying these methods to monitor the effect of phage addition on cell density, preliminary experiments were done to examine their sensitivities. In the case of FACS, the cell density of serially diluted cells was determined by counting the number of dots that appear on a scatter plot (SSC versus FSC) following the injection of a fixed volume of sample, 2.4 μl. The number of dots that were registered by the FACS instrument in the injected volume of bacterial suspension was converted to counts per milliliter (see Table S1 in the supplemental material) by considering that each dot represents one cellular unit, irrespective of viability.

The counts per milliliter were found to vary linearly over a broad range of dilutions, from 1 (undiluted) to 10⁻³ (Fig. 1A). Thus, the linear relationship was found to be dynamic over this range of concentrations (at least three orders of magnitude). A similar experiment was performed by monitoring the OD₆₀₀, and a linear correlation between the OD₆₀₀ values and relative concentration was evident (Fig. 1B). Finally, a correlation was concluded to exist between the counts determined by FACS and the OD₆₀₀ values (Fig. 1C). The results obtained validate the use of the above-mentioned techniques for monitoring changes in relative cell densities.

FIG 1.

Determination of cell density using flow-cytometric and spectrophotometric methods. A culture of M. smegmatis cells grown overnight was serially diluted in MB7H9 medium, and the diluted samples were subjected to analysis. The number of cells (counts), irrespective of viability, present in a given volume of the sample (2.4 μl) was determined by flow cytometry using a FACS instrument. (A) The counts obtained (expressed as counts ml⁻¹) were plotted against relative concentration (conc.). (B) A similar approach was taken for investigating the correspondence between relative concentration and OD₆₀₀. (C) To determine the degree of correspondence between counts obtained by FACS and OD₆₀₀, the respective values were plotted against each other and subjected to linear regression analysis. The goodness of fit is indicated by the R² value. (D to F) Time-dependent changes in the OD₆₀₀ (D), counts ml⁻¹ (FACS analysis) (E), and viable counts (CFU) (F) following the addition of phage (MOI of 1). Error bars represent standard deviations from the means derived from three biological replicate experiments.

Standardized cell counting procedures were then used to monitor the variations in the number of countable cells following phage infection. The results indicate that the decrease in total cell numbers, as determined either by flow cytometry or spectrophotometry, was about 70% of the original value, which represents a difference of less than one order of magnitude (Fig. 1D and E; also see Fig. S2 in the supplemental material), whereas in the case of viable counts the decrease was about three orders of magnitude (Fig. 1F). Clearly there was a lack of correlation between the number of cells that were getting lysed and the number that were rendered nonviable.

Comparative effects of phage concentration on cell lysis and viability.

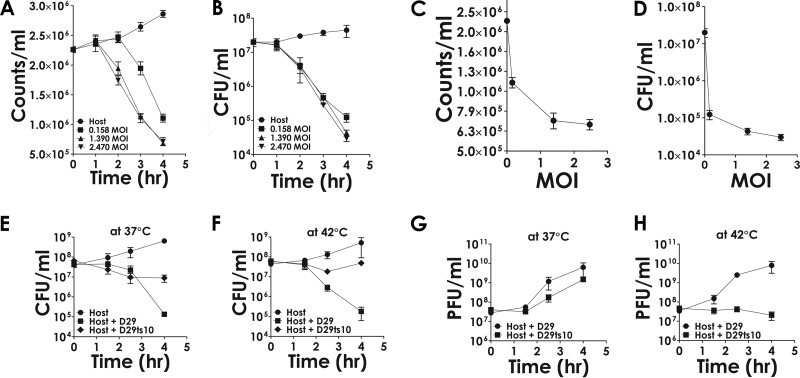
To uncover the reason behind the observed disparity between cell death and lysis, we tried to investigate how changes in phage concentration differentially affect the two phenomena. A fixed number of cells was infected with phage at various concentrations (MOIs). The effective MOI was determined by estimating the number of viable cells present (CFU) in the cell suspension prior to phage addition and the titer of the phage suspension used, which was determined in parallel. Cell lysis was monitored by FACS analysis, whereas cell death (viability) was monitored by CFU counting. The results (Fig. 2A and C) show that at the maximum effective MOI (2.47), the cell counts decreased about 5-fold, whereas at the same MOI, CFU counts decreased nearly 1,000-fold (Fig. 2B and D). This is consistent with previous observations. However, one can argue that the effects are nonspecific in nature. To eliminate such a possibility, related experiments were performed with a temperature-sensitive mutant (D29ts10) which does not grow at 42°C (Fig. 2H, compare squares to circles) but does so, although less efficiently than the wild type (D29), at 37°C (Fig. 2G). The results show that this mutant fails to kill the cells at 42°C (Fig. 2F, compare diamonds to squares). At 37°C (Fig. 2E), cell killing was observed, although to a lesser extent than that of the wild type. The results indicate that the cell death ensues only in the case of the wild type and not that of the mutant phage; hence, the phenomenon is specifically dependent on phage proliferation. Further evidence that the death of host cells is dependent on phage growth was obtained from experiments where phage titers and viable cell counts were monitored in parallel (see Fig. S3 in the supplemental material). It was observed that there was a time delay for the onset of death if the starting phage concentration was lower than that of the bacteria (MOI of 0.1). The time delay appears to be necessary for the phage titers to increase to a threshold value of 1 per host cell. The delay can be minimized by using a higher initial phage concentration (MOI of 1).

FIG 2.

Effect of phage on cell counts. (A and B) Phage was incubated with host bacteria at the indicated MOI, and the cell numbers were determined either by FACS analysis (A) or CFU determination (B) at the indicated time points. (C and D) The values corresponding to the 4-h (final) time point derived from panels A and B were plotted against the MOI to obtain a comparative idea about the rate at which cell counts decrease as the MOI is increased. (E and F) The comparative abilities of D29 and a mutant, ts10 (D29ts10), in bringing about host killing was examined at the permissive and nonpermissive temperatures of 37°C (E) and 42°C (F), respectively. (G and H) The corresponding growth patterns of the phage are shown. Each data point represents the mean values obtained from three biological replicates ± standard deviations.

Viability assays using fluorescent dyes.

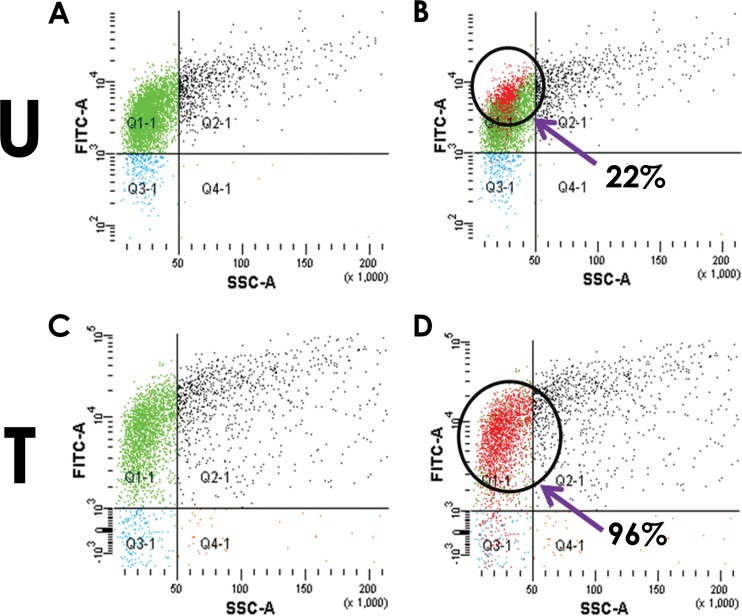
The results presented in the previous section indicate that a sizable fraction of the cells which have not lysed have been rendered nonviable. To explore the viability of the cells that have not undergone lysis, FDA-PI (live-dead) staining methods were applied. The experiment was carried out by infecting host cells at an MOI of 1 and incubating them for 4 h. The staining profiles of the cells either treated with phage for 4 h or left untreated were monitored. The fractions of the cell populations that were FDA positive were nearly the same (Fig. 3A and C, green dots) irrespective of whether the cells were untreated or phage treated. However, there was a distinct difference in the fraction of FDA-stained cells that accepted PI stain between untreated and treated cells (Fig. 3B and D). In the case of treated cells, nearly all (96%) of the FDA-positive cells also were positive for PI (Fig. 3D, red dots overlaid on green), whereas for untreated cells the corresponding value was only 22%. The results indicate that almost all of the cells that did not undergo lysis following 4-h treatments with phage stain heavily with PI and therefore are likely to be in a nonviable state, which is consistent with the drastic reduction in viable counts reported in the earlier sections.

FIG 3.

Live-dead staining of host cells treated with phage at an MOI of 1. Cells either untreated (U) or phage treated (T) were stained after 240 min (4 h) of phage addition. The FDA staining (A and C) and overlay of the PI staining (B and D) are shown. (B and D) The percentage of FDA-stained cells that also can be stained with PI (red dots overlaid on green) is indicated for untreated as well as treated cells.

Evidence for a secondary killing factor that acts in trans.

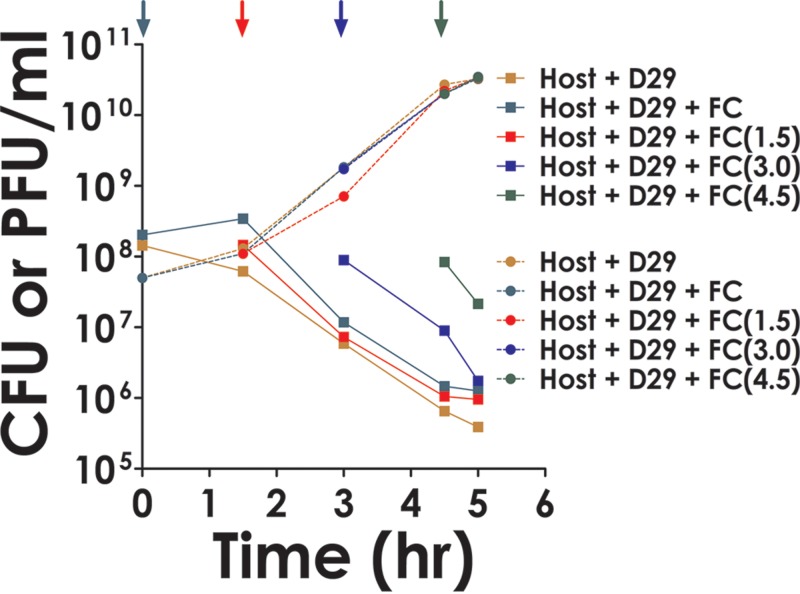
To determine how these cells were being rendered nonviable, theoretical modeling studies were done as described below (see Fig. 7). Such studies indicated that there must be a secondary factor involved in the process. The hypothesis put forward was that the host cells release certain products after phage infection which act extracellularly on other cells in trans and kill them. To test this possibility, cells not infected with phage, termed fresh cells (FC), were added to those that were infected, in the same proportion, either at time zero or at various time points subsequently (Fig. 4, colored arrows). The rate of decay of the combined cell population (initial and freshly added) then was examined. If the death of the freshly added cells required phage infection and lysis, then a delay period corresponding to at least the latent phase was expected. However, this was not observed. The results indicate that all cells, including the FCs (Fig. 4, traces corresponding to + FC lines), decayed at the same rate and that the secondary factor did not discriminate between the primary and secondary populations.

FIG 7.

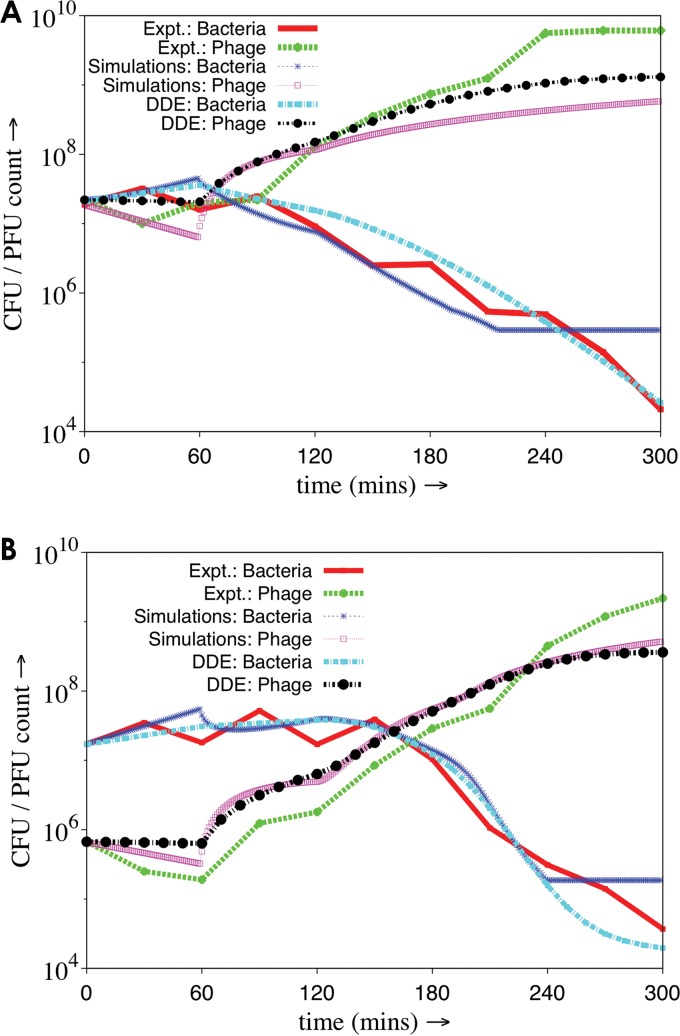
Comparison of the results of mathematical modeling and simulation analysis with those that were derived experimentally. All analyses were carried out either for high MOI (A) or low MOI (B), 1 and 0.1, respectively. The data points for the experimental traces (Expt. bacteria/phage) were derived from Fig. S3 in the supplemental material. Mathematical modeling was done as mentioned in Fig. S5 in the supplemental material. Simulations were performed as described in the text. Each trace has a specific color code and/or line pattern, as indicated in the figure.

FIG 4.

Indirect killing of host cells by phage. Cells (1.43 × 10⁸ CFU) were infected by phage (5 × 10⁷ PFU). Fresh cells (FC) (0.6 × 10⁸ CFU) were added either prior to the addition of phage (time zero) or at the indicated time points. The rate of host cell decay and phage growth following each addition then was determined and compared to those that were obtained for cases where no FC was added at any stage (host plus D29). Different color codes were used as indicated in the key. (CFU and PFU are indicated by squares and circles, respectively.)

Superoxide production following phage infection.

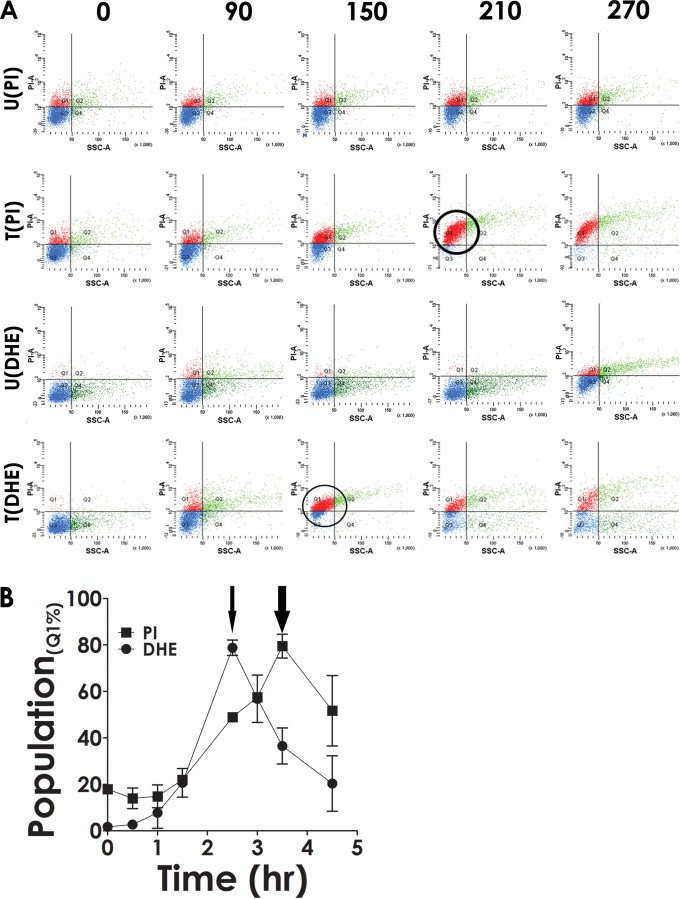
It is currently believed that bacterial cell death induced by external agents such as antibiotics is a complex process (39). The interaction between a lethal agent and a target leads to secondary events, such as the generation of ROS. In order to investigate whether there is any connection between cell death and ROS formation in the context of the present investigation, phage was added to host cells, followed by staining either by PI (for cell death) or DHE (for ROS) (40). The results indicate that there was a time-dependent increase in the population of PI-stained cells in the case of phage-treated cells [Fig. 5A, T(PI), red dots], whereas in the case of the control (untreated cells), no significant increase was observed [Fig. 5A, U(PI)]. This confirmed that following phage treatment, the cells were facing death. When another aliquot taken from the same phage-infected culture was stained with DHE, an increase in the fluorescent population was observed [Fig. 5A, T(DHE), red dots]. As before, the increased DHE staining was observed only in the case of the phage-infected cells, not in the uninfected ones [Fig. 5A, U(DHE)]. While performing these experiments, we observed that the maximum increase in DHE staining activity happened at an earlier time point than that for PI. To confirm this further, the PI and DHE staining experiments were repeated, this time in triplicate, and the average values obtained ± standard deviations were plotted against the time of infection. The results show that, indeed, DHE staining activity peaks prior to that of PI (Fig. 5B, thin arrow compared to thick arrow). The result suggests that ROS formation is the cause and cell death is the effect.

FIG 5.

Superoxide generation associated with phage growth. (A) Cell death and generation of superoxide were monitored at different stages of phage growth using PI and DHE as indicated. The cells were either treated with phage (T) or left untreated (U). The images are described as U(PI), T(PI), U(DHE), and T(DHE) depending on their treatment status. The numbers in boldface at the top indicate the time points, in minutes, at which monitoring was done. Thick (PI) and thin (DHE) circles highlight the presence of the maximum number of cells in the Q1 quadrant (highly stained population). (B) The experiment was repeated three times, and the mean population density ± standard deviation was plotted against time. Thick (PI) and thin (DHE) arrows point to the stage where maximum Q1 population density was achieved during the course of the experiment.

Effect of ROS antagonist on survival of phage-treated cells.

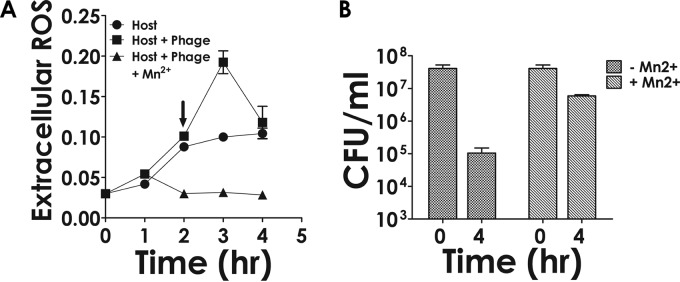
Mn²⁺ ions have the ability to scavenge ROS (41). Therefore, it was argued that if formation and release of superoxide radicals is the reason behind the death of cells, then by the addition of Mn²⁺, a superoxide radical scavenger (42), it should be possible to prevent cell death. To perform this experiment, phage was added to cells at an MOI of 1. After a period of 2 h, the time taken for adsorption to reach saturation and the latent phase to start, the infected cells were divided into two fractions. Mn²⁺ was added to one fraction at a final concentration of 5 mM, while the other fraction was left alone. Both fractions then were allowed to grow (Fig. 6A, squares). As a control, a culture which was not infected was monitored in parallel (Fig. 6A, circles). At regular intervals, the release of extracellular superoxide radicals was measured using the NBT assay (43). The results show that although in both uninfected and infected cases superoxide levels increased in a time-dependent manner, in the case of the latter (host plus phage), the increase was significantly greater than that of the former (host only). Moreover, as observed in the previous set of experiments, the activity was found to peak at an intermediate time point. Thus, the kinetics of extracellular ROS accumulation appears to be of the same pattern as that of its intracellular formation. When phage-infected cells were treated with the ROS blocker Mn²⁺, the superoxide level was found to decrease to a low level (Fig. 6A, triangles). The results indicate that phage-infected cells release more ROS than the uninfected ones; moreover, the released superoxide radicals can be neutralized by the addition of Mn²⁺. The effect of Mn²⁺ addition on the survival of host cells subjected to phage attack then was monitored. The results show that the viability of the cells improved significantly (Fig. 6B, CFU counts at 4 h). The observed increase in cell survivability in the presence of Mn²⁺ was not due to any inhibitory effect of Mn²⁺ on phage growth. This is evident from the observation (see Fig. S6 in the supplemental material) that the phage amplification was not affected significantly by the addition of Mn²⁺.

FIG 6.

Effect of Mn²⁺ on extracellular ROS generation and cell survival. (A) Time-dependent monitoring of ROS in the supernatant of phage-treated (host plus phage) or untreated cells (host) using NBT. In the case of the phage-treated cells, the experiment also was performed in the presence of Mn²⁺ (host plus phage plus Mn²⁺), which was added at the 2-h time point (arrow). (B) Survival of host cells following phage treatment performed either in the absence (−) or presence (+) of Mn²⁺ at the indicated time points. Each data point represents the mean ± standard deviation derived from three biological replicate experiments.

Mathematical modeling and Monte Carlo simulations are consistent with experimental results.

Mathematical modeling was performed at various stages of this study to obtain insight into the sequence of events that lead to cell death following phage infection. A series of delay differential equations (DDEs) was developed similar to those that have been used in previous studies to investigate phage-host relationships (see Fig. S5 in the supplemental material) (44–46). In these equations, S is the number of susceptible bacteria, P is the number of phage particles, I is the number of infected cells, r is the phage adsorption rate constant, q is the secondary killing factor, m is the fraction of infected cells getting lysed, α is the growth rate, τ is the latent period, and a is a DDE parameter. The fraction of cells that have adsorbed phage and the amount of lethal factor released thereof are denoted as rS and qmrS, respectively. The Heaviside step function is represented as Heavi. Thus, our proposed model is given by

$$dS/dt=\alpha S(t)-\mathrm{r}S(t)P(t)-qm\mathrm{r}S(t-\tau )\hspace{0.17em}P(t-\tau )S(t)\exp \left[\frac{-t}{(a\tau )}\right]\hspace{0.17em}\text{Heavi}(t-\tau )$$ 1

where αS(t) is cell growth, rS(t)P(t) is cell decay due to adsorption, and qmrS(t − τ) P(t − τ)S(t)exp[−t/(aτ)] Heavi(t − τ) is secondary cell decay due to the release of superoxide from lysed bacteria,

$$dI/dt=\mathrm{r}S(t)P(t)-m\mathrm{r}S(t-\tau )P(t-\tau )\hspace{0.17em}\text{Heavi}(t-\tau )$$ 2

where rS(t)P(t) is infected cells due to adsorption and mrS(t − τ)P(t − τ) Heavi(t − τ) is the fraction of cells lysed (infected cell population decay due to lysis), and

$$dP/dt=bm\mathrm{r}S\hspace{0.17em}(t-\tau )P(t-\tau )\hspace{0.17em}\text{Heavi}(t-\tau )-\mathrm{r}S(t)P(t)$$ 3

where b is burst size, mrS(t − τ)P(t − τ) Heavi(t − τ) is the fraction of cells lysed that result in new phages, and rS(t)P(t) is phage decay due to adsorption.

When we were developing these equations, it was necessary to incorporate two important concepts: (i) not all cells are lysed following infection, and (ii) lysed cells release certain secondary factors that cause cell death. Upon solving the DDEs it was possible to predict the cellular decay pattern following phage infection at two different MOIs, 1 and 0.1. The results show that the theoretical traces thus obtained matched the experimental results (Fig. 7).

A second approach used Monte Carlo simulation techniques to explain the results obtained. A set of samples were chosen randomly (38) from the population of phage and bacteria in the same ratio. For each bacterium in the population, a random number is generated from a uniform distribution. If it is less than the rate of division of bacteria, then the cell would divide. Phage infections happen in the same manner. In our simulations, cell division and phage infection both occur randomly. Initially, free phages are adsorbed on the bacterial cell surface. As in experiments, a growth rate of 0.02 cells min⁻¹ was considered for low and high MOI. The rate at which a phage particle infects an uninfected cell is exactly identical to the rate at which the phage number is witnessed to decrease uniformly in the first hour of experiments. For each infection event, the phage count and uninfected cell count is reduced by one. Phages adsorbed at the same rate throughout the simulation until the ratio of phage to uninfected bacteria exceeded one. After this, it would be hard for a phage particle to find an uninfected cell in its surrounding; hence, the chance of infection is much less and effectively can be ignored. An hour after the initiation of infections (or the latent period), bursting of infected cells begins due to phage growth and lysis. Ten percent of infected cells will burst after 60 min from when they were infected by free phages. For experiments performed at high MOI, 5% of infected cells will burst at each time point. For every infected cell which bursts, new phage particles will be released according to the experimentally determined burst size of 219 phage particles per infected cell. Along with that, we assume there is a release of certain unknown factors, like free radicals, into the environment (47, 48). Those free radicals could kill the uninfected cells present in the environment. Secondary killing is dependent on the instantaneous number of infected cells bursting and the average number of uninfected cells surrounding a newly infected cell at that moment in time. For experiments at both high and low MOI, 100 ensembles are taken into consideration. A detailed comparison of simulations, DDE, and experiments is shown in Fig. 7. The results indicate that in the case of DDE and simulation, the theoretical results and simulations agree with experiments and that the model assumed is, by and large, accurate.

DISCUSSION

Since phages have the ability to multiply and kill target bacteria, they have been termed self-replicating pharmaceuticals (49). In order to use bacteriophages as pharmaceuticals, however, it is necessary to obtain a quantitative and mechanistic insight into how they bring about the reduction in the bacterial population. To derive a quantitative relationship between phage growth and bacterial growth, it is necessary to take into account various factors, including the number of phages and bacteria present initially, the growth rate of the bacteria, the length of the latent phase of growth, burst size, and adsorption rate. The adsorption rate was determined on the basis of the assumption that as phages get adsorbed, their numbers in the supernatant decrease as described previously (50). The rate of decrease is expected to be proportional to the number of phages and bacterial cells present at any moment of time. Taking all these factors into consideration, an adsorption rate constant of 4.32E−11 cell⁻¹ phage⁻¹ min⁻¹ ml⁻¹ was used for theoretical analysis (see Fig. S4 in the supplemental material). The ratio of the phage to cell (MOI) will influence the number of bacteria that will be infected. Poisson's equation predicts that the number of infected bacteria will increase exponentially with the MOI. At an MOI of 1, nearly 60% of the cells get infected. The number of phages infecting the bacteria is expected to obey the Poisson distribution law, as was found to be the case in this study (see Fig. S1 in the supplemental material).

Bacteria on which phage has adsorbed ultimately are destined to be lysed after about 60 min of infection, which is the latent period. In a continuous infection model, phage adsorption will take place continuously, accompanied by lysis. Simple mathematical modeling predicts that within 100 min, the number of susceptible bacteria should go down by at least 100-fold at an MOI of 0.1. Such a hundredfold reduction in cell counts should result in substantial changes in optical density or cell counts using FACS, which was not observed. This indicated that only a fraction of the cells that were infected underwent lysis, whereas the rest did not. To explain this observation, a factor, m, was introduced which indicates that not all cells lyse following infection. The reason why only a fraction of the cells lyse is unclear. The inability of phage D29 to completely lyse host cells also was reported in a previous study, where it was shown that the optical density decreases to about 50% of the initial level (51). However, a mutant of D29 was found to induce a much higher level of lysis. It appears that the cell wall of mycobacteria is recalcitrant toward enzymatic hydrolysis, which is why the lysis following infection is so poor (51). What happens to the cells that do not lyse within the time span of 4 h is not clear. One possibility is that delayed lysis occurs, perhaps in a manner similar to that of T4 (52). On the other hand, the unlysed infected cells may die due to the phenomenon of host inactivation known to occur in lytic phages such as T4. The phenomenon also could resemble that observed in the case of Streptococcus thermophilus phages, which become replication defective after infecting the host (53). The host, S. thermophilus, benefits from the stalling of phage multiplication and lysis, as they get an opportunity to incorporate pieces of phage DNA into their CRISPR loci, resulting in phage resistance. As of now, a CRISPR system active against mycobacteriophage D29 is not known, although the possibility of identifying one in the future cannot be ruled out, since CRISPRs have been found in mycobacterial systems (54).

The observation that phage-mediated killing takes place through direct and indirect mechanisms is a new revelation. Apart from lysis due to infection, there appear to be other mechanisms that are involved in bacterial decay. This is evident from the observation that the decrease in the number of viable units far exceeds the number that have lysed. However, such decay occurs only after the latent period, as is evident from the observation that a minimum amount of time must elapse before cell lysis and/or death commences. Thus, we assume that certain factors are released into the solution after the lysis of infected cells along with the phage progeny. Therefore, we introduce a secondary killing factor that takes into account the amount of such factors released in the solution upon fractional lysis of infected cells after the latent period. These released factors interact with susceptible bacteria present in the solution and cause their decay. The factor, which apparently is an ROS, acts in trans, as is evident from the observation that freshly added uninfected cells become vulnerable immediately after they are mixed with the infected ones.

Thus, bacterial killing is an effect caused by two phenomena: infection, which results in the lysis of only a fraction of infected cells while rendering them nonviable, and secondary killing, which is the result of secondary factors released in the environment upon lysis. The interaction of secondary factors and susceptible bacteria is not linear but is instead a sharply decreasing function of time and changes with alterations in MOI. At a high MOI, the secondary factor interacts with a lesser number of susceptible bacteria present at that instant than during their interaction at low MOI. This is modeled by the factor a in the term for secondary decay in DDEs. It appears that as the MOI increases, the interaction of the secondary factor with the susceptible bacteria is hindered. Precisely how this happens is not clear. The presence of phage particles at higher densities could bind the secondary factor, nullifying its action. Alternatively, the cells may have developed the ability to resist oxidative damage by degrading the superoxide radicals (55).

The initial prediction that a secondary factor was involved came from mathematical modeling studies. The question therefore arises as to what the secondary factor could be. The results presented in this study reveal that a sizable fraction of the cells, almost 90%, stain with DHE following phage contact, indicating that superoxide generation is the secondary factor. The generation of superoxide peaks at a time point just prior to the onset of cell death, as determined by PI staining. The level of superoxide subsequently decreases, probably due to the action of dismutases. Precisely how superoxide radicals are generated remains to be investigated. In a recent study it was reported that contact between two different bacteria or between a bacterium and phage, or even a type VI secretion system (T6SS), can lead to the generation of superoxide radicals (56). Similarly, superoxide generation appears to be one of the mechanisms by which antibiotics having diverse modes of action induce cell killing (39). The demonstration that mycobacteriophages can kill their hosts through mechanisms other than lysis could lead us to new methods to combat TB. Methods to kill M. tuberculosis using mycobacteriophages already have been explored using the lytic mycobacteriophage TM4, which was introduced into a macrophage cell line harboring M. tuberculosis using M. smegmatis as a carrier, resulting in the reduction of pathogen counts (57, 58). Phage D29, the model system used in this study, has been found to be effective against Mycobacterium ulcerans in a murine footpad model (22). It is possible that some of the ameliorative effects of phage treatment observed in these studies are due to the enhanced release of superoxides, which, as mentioned above, can act in trans not only on the bacteria producing them but also on the bystanders. Therefore, the presence of phage-infected mycobacterial cells in the phagosome could result in enhanced killing. That superoxide release is the reason for cell killing following phage treatment is further substantiated by the observation that the addition of Mn²⁺ ions results in the quenching of superoxide release and a concomitant increase in host survival.

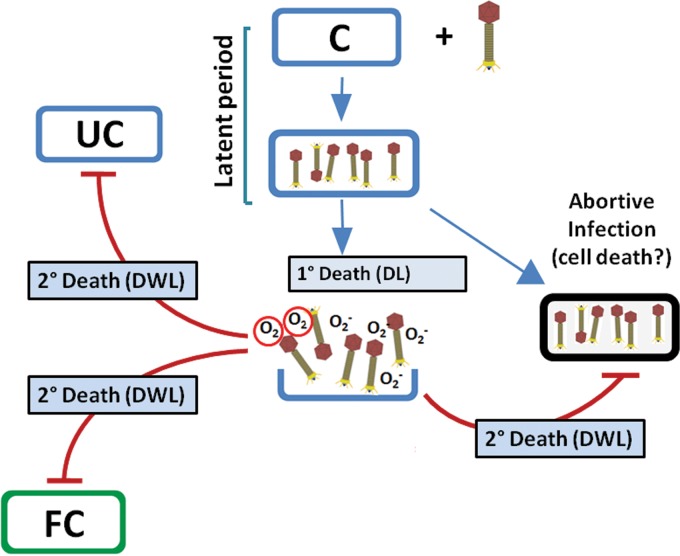
Based on the investigations performed in this study, the following model is proposed (Fig. 8). In this model, in the presence of phage a fraction of the cells are lysed, resulting in death by lysis (DL), whereas the remaining fraction that comes in contact with the phage undergoes cell death through secondary mechanisms, termed death without lysis (DWL). The phenomenon of DWL probably involves superoxide radicals. However, DWL also can happen due to other reasons, such as the induction of programmed cell death (PCD) through the mediation of toxin-antitoxin (TA) systems, as observed in the case of E. coli cells infected with phage P4 (59). The cycle of infection, phage release, and cell death through secondary mechanisms continues to be repeated, resulting in the lowering of viable counts by several orders of magnitude. Further investigations to deduce the pathway of generation of these reactive species need to be undertaken.

FIG 8.

Model to describe phage-induced killing of host cells. Following phage addition to the host cell (C) suspension, they are adsorbed (primary infection), giving rise to infectious center formation. A fraction of the infected bacteria lyse after the latent period, resulting in death due to lysis. This is the primary mechanism (1°) of cell death. Following lysis, progeny viruses are liberated along with superoxide radicals. These radicals act on uninfected (UC) as well as abortively infected cells and also fresh cells (FC) added externally after the initial phage-host interaction was established. A fraction of the cells infected with phage fail to undergo lysis (abortive infection). These cells also may become the target of superoxide radicals released from the cells that are getting lysed.

Funding Statement

S. Samaddar acknowledges the Council of Scientific and Industrial Research (CSIR, India) and R. K. Grewal, S. Sinha, and S. Ghosh thank the University Grant Commission (UGC, India) for their fellowships.