Statistical Significance of Clustering using Soft Thresholding

Abstract

Clustering methods have led to a number of important discoveries in bioinformatics and beyond. A major challenge in their use is determining which clusters represent important underlying structure, as opposed to spurious sampling artifacts. This challenge is especially serious, and very few methods are available, when the data are very high in dimension. Statistical Significance of Clustering (SigClust) is a recently developed cluster evaluation tool for high dimensional low sample size data. An important component of the SigClust approach is the very definition of a single cluster as a subset of data sampled from a multivariate Gaussian distribution. The implementation of SigClust requires the estimation of the eigenvalues of the covariance matrix for the null multivariate Gaussian distribution. We show that the original eigenvalue estimation can lead to a test that suffers from severe inflation of type-I error, in the important case where there are a few very large eigenvalues. This paper addresses this critical challenge using a novel likelihood based soft thresholding approach to estimate these eigenvalues, which leads to a much improved SigClust. Major improvements in SigClust performance are shown by both mathematical analysis, based on the new notion of Theoretical Cluster Index, and extensive simulation studies. Applications to some cancer genomic data further demonstrate the usefulness of these improvements.

1 Introduction

Clustering methods have been broadly applied in many fields including biomedical and genetic research. They aim to find data structure by identifying groups that are similar in some sense. Clustering is a common step in the exploratory analysis of data. Many clustering algorithms have been proposed in the literature (see Duda et al. (2000); Hastie et al. (2009) for comprehensive reviews). Clustering is an important example of unsupervised learning, in the sense that there are no class labels provided for the analysis. Clustering algorithms can give any desired number of clusters, which on some occasions have yielded important scientific discoveries, but can also easily be quite spurious. This motivates some natural cluster evaluation questions such as:

• how can the statistical significance of a clustering result be assessed?

• are clusters really there or are they mere artifacts of sampling fluctuations?

• how can the correct number of clusters for a given data set be estimated?

Several cluster evaluation methods have been developed. McShane et al. (2002) proposed a cluster hypothesis test for microarray data by assuming that important cluster structure in the data lies in the subspace of the first three principal components, where standard low dimensional methods can be used. Tibshirani and Walther (2005) proposed using resampling techniques to evaluate the prediction strength of different clusters. Suzuki and Shimodaira (2006) wrote an R package for assessing the significance of hierarchical clustering. Despite progress in this area, evaluating significance of clustering remains a serious challenge, especially in High Dimensional Low Sample Size (HDLSS) situations.

Numerous works on the application of Gaussian mixture models to cluster analysis have appeared in the literature. Overviews can be found in Mclachlan and Peel (2000); Fraley and Raftery (2002). Gaussian mixture models need estimation of the full parameters of each component, which can be quite challenging when tackling HDLSS problems. Recently, some regularization-based techniques have been applied to model-based clustering of high-dimensional data, see e.g. Pan and Shen (2007); Wang and Zhu (2008); Xie et al. (2008); McNicholas and Murphy (2010); Baek and McLachlan (2011). A more recent review in this area can be found in Bouveyron and Brunet-Saumard (2014).

Liu et al. (2008) proposed a Monte Carlo based method called Statistical Significance of Clustering (SigClust) which was specifically designed to assess the significance of clustering results for HDLSS data. An important contribution of that paper included a careful examination of the question of “what is a cluster?”. For this reason, with an eye firmly on the very challenging HDLSS case, their notion of cluster was taken to be “data generated from a single multivariate Gaussian distribution”. This Gaussian definition of “cluster” has been previously used by Sarle and Kuo (1993) and Mclachlan and Peel (2000) and Fraley and Raftery (2002). This was a specific choice, which made the HDLSS problem tractable, but entailed some important consequences. For example, none of the Cauchy, Uniform, nor even t distributions correspond to a single cluster in this sense. While this may seem to be a strong assumption, it has allowed sensible real data analysis in otherwise very challenging HDLSS situations, with a strong record of usefulness in bioinformatics applications, see e.g. Chandriani et al. (2009); Verhaak et al. (2010). From this perspective, SigClust formulates the problem as a hypothesis testing procedure with

• H₀: the data are from a single Gaussian distribution

• H₁: the data are not from a single Gaussian distribution.

As noted in Liu et al. (2008), this choice of null hypothesis is more sensible than say a difference between subgroups in terms of means, because clustering methods will split even a truely Gaussian population into (mean based) statistically significant subgroups. The test statistic used in SigClust is the 2-means cluster index which is defined as the ratio of the within cluster variation to the total variation. Because this statistic is location and rotation invariant, it is enough to work only with a Gaussian null distribution with mean 0 and diagonal covariance matrix Λ. The null distribution of the test statistic can be approximated empirically using a direct Monte Carlo simulation procedure. The significance of a clustering result can be assessed by computing an appropriate p-value. Recently, Maitra et al. (2012) proposed a non-parametric bootstrap approach for assessing significance in the clustering of multidimensional datasets. They defined a cluster to be a subset of data sampled from a spherically symmetric, compact and unimodal distribution and a non-parametric version of the bootstrap was used to sample the null distribution. It is important to note that their method has not been developed to handle HDLSS situations yet.

SigClust has given useful and reasonable answers in many high dimensional applications (Milano et al. (2008); Chandriani et al. (2009); Verhaak et al. (2010)). However, SigClust was based on some approximations and left room for improvement. In order to simulate the null distribution of the test statistic, SigClust uses invariance principles to reduce the problem to just estimating a diagonal null covariance matrix. This is the same task as finding the underlying eigenvalues of the covariance matrix. Therefore, a key step in SigClust is the effective estimation of these eigenvalues. Currently a factor analysis model is used to reduce the covariance matrix eigenvalue estimation problem to the problem of estimating a low rank component that models biological effects together with a common background noise level. However, the empirical studies in Section 3 show that when there are a few large eigenvalues this method can be dramatically improved.

Recently, many sparse methods have been introduced to improve the estimation of the high dimensional covariance matrix, see e.g. Meinshausen and Bühlmann (2006); Yuan and Lin (2007); Friedman et al. (2008); Rothman et al. (2008); Fan et al. (2009); Witten et al. (2009); Yuan (2010); Cai et al. (2011); Danaher et al. (2014), among many others. Let d denote the dimension of the feature space. Then, a critical difference between SigClust and these sparse approaches is that SigClust only needs estimates of the d eigenvalues instead of the d(d − 1)/2 parameters of the full covariance matrix. This is because, based on the rotation invariance of the test statistic, the null distribution of the test statistic used in SigClust is determined by the eigenvalues rather than the entire covariance matrix. Nevertheless, the sparse methods are somewhat related to the soft thresholding method proposed in this paper, in the sense that the latter also incorporates a type of L₁ penalty.

The contributions in this paper start by showing that, when the first eigenvalue is huge, the original SigClust (which in Section 2.2 is seen to be reasonably called hard thresholded) can be seriously anti-conservative. This behavior is studied using the novel notion of Theoretical Cluster Index. This also motivates an appropriate soft thresholding variation, which is seen to give vastly improved SigClust performance over a very wide range of settings, through both theoretical analysis and detailed simulations. The rest of the article is organized as follows. In Section 2, we first give a brief description of the SigClust procedure and the existing hard thresholding eigenvalue estimation approach. Then we use mathematical analysis, together with likelihood ideas to develop the new soft thresholding approach. To compare the performances of different methods, numerical studies are given in Section 3 for simulated and in Section 4 for real data examples. We provide some discussion in Section 5 and collect proofs of the likelihood derivation in the supplementary material.

2 Methodology

In this section, we first briefly review the SigClust method in Section 2.1. In Section 2.2, we provide an alternative likelihood based derivation, based on the hard thresholding ideas, for the estimation of the covariance matrix eigenvalues used in the original SigClust paper. Then we introduce a new soft thresholding approach, based on replacing the hard L₀ constraint, with a softer L₁ constraint, in Section 2.3. Insightful mathematical analysis, based on the new notion of Theoretical Cluster Index, which gives deep insights into the performance of these methods, and also suggests a reasonable tuning approach, is given in Section 2.4.

2.1 Review of the Original SigClust Method

SigClust is a clustering evaluation tool which can be used to assess the significance of a given clustering result by providing an appropriate p-value. Suppose that the original data set X, of dimension d × n, has d variables and n observations, i.e. X = [x₁, ⋯, x_n], where each x_i ∈ R^d. The null hypothesis of SigClust is that the data are from a single Gaussian distribution N(μ, Σ), where μ is a d-dimensional vector and Σ is a d × d covariance matrix. Given a clustering of the vectors in X, i.e. sets C₁ and C₂, where C₁ ∪ C₂ = {1, …, n} and C₁ and C₂ are disjoint, the strength of the clusters can be assessed using the two means cluster index (CI), which is the sum of the within class variation divided by the total variation. More precisely,

$$\mathrm{C}\mathrm{I}=\frac{{\sum }_{k=1}^2{\sum }_{i\in C_k}{\Vert {\mathbf{x}}_i-{\overline{\mathbf{x}}}^{(k)}\Vert }^2}{{\sum }_{i=1}^n{\Vert {\mathbf{x}}_i-\overline{\mathbf{x}}\Vert }^2},$$ (1)

where x̄^(k) represents the mean of the kth cluster for k = 1, 2 and x̄ represents the overall mean. CI can be based on either an input clustering, or can be calculated by a conventional k-means algorithm (MacQueen, 1967). SigClust uses CI as the test statistic which has the nice property of being both location and rotation invariant. This leads to a dramatic reduction in the number of parameters to be estimated. In particular, during simulation, the mean μ can be taken to be 0, because of the location invariance. In a parallel way, rotation invariance provides a major reduction in the parametrization of Σ to a diagonal matrix Λ = diag(λ₁, ⋯, λ_d), using the eigen-decomposition Σ = UΛU^T, where U is an orthogonal matrix (essentially a rotation matrix). A factor analysis model is used to estimate the d eigenvalues which are still a relatively large number of parameters compared with the sample size n for HDLSS data sets. Specifically, Λ is modeled as

$$\mathrm{\Lambda }={\mathrm{\Lambda }}_0+{\sigma }_N^{2}I,$$ (2)

where the diagonal matrix Λ₀ represents true underlying biology and is typically low-dimensional, and ${\sigma }_N^2$ represents the level of background noise. This model is identifiable because many of the diagonal elements of Λ₀ are zero. First σ_N is estimated as

$${\hat{\sigma }}_N=\frac{\mathrm{M}\mathrm{A}{\mathrm{D}}_{d\times n\text{data set}}}{\mathrm{M}\mathrm{A}{\mathrm{D}}_{N(0,1)}},$$ (3)

where MAD stands for the median absolute deviation from the median, and σ̂_N is rescaled by MAD_N(0,1) = 0.6745, the theoretical MAD of the N(0,1) distribution, to be on the correct scale. Then Λ is estimated to be

$${\hat{\lambda }}_j=\{\begin{array}{cc}{\tilde{\lambda }}_j\hfill & \hfill \text{if}{\tilde{\lambda }}_j\ge {\hat{\sigma }}_N^2\hfill \\ {\hat{\sigma }}_N^2\hfill & \hfill \text{if}{\tilde{\lambda }}_j<{\hat{\sigma }}_N^2,\hfill \end{array}$$ (4)

where (λ̃₁, ⋯, λ̃_d) are the eigenvalues of the sample covariance matrix.

The procedure for SigClust can be briefly summarized as follows:

• Step 1. Calculate the cluster index for the original data set based on the given two-cluster assignments. The cluster assignments can be obtained from previous knowledge about the data or from application of a clustering algorithm such as k-means.

• Step 2. Obtain estimates (λ̂₁, ⋯, λ̂_d) for the eigenvalues (λ₁, ⋯, λ_d) of Σ.

• Step 3. Simulate data N_sim times with each data set consisting of n i.i.d. observations from the null distribution (x₁, ⋯, x_d) with x_j drawn independently from the N(0,λ̂_j) distribution. Here N_sim is some large number.

• Step 4. Calculate the corresponding cluster index for each simulated data set from Step 3 to obtain an empirical distribution of the cluster index based on the null hypothesis.

• Step 5. Calculate a p-value (based on an empirical quantile) for the original data set and draw a conclusion based on a prespecified test level.

2.2 Likelihood Interpretation of the SigClust Method: Hard Thresholding

Now we first show that the solution (4) can also be obtained based on a more general likelihood consideration, which gives the SigClust method of Liu et al. (2008) a new interpretation. In factor models, the covariance matrix can be written as

$$\mathrm{\Sigma }={\mathrm{\Sigma }}_0+{\sigma }_N^{2}I$$ (5)

for some low rank positive semi-definite matrix Σ₀. Denote the precision matrix

$$C\equiv {\mathrm{\Sigma }}^{-1}\equiv {({\mathrm{\Sigma }}_0+{\sigma }_N^{2}I)}^{-1}=\frac{1}{{\sigma }_N^2}I-W_0$$ (6)

for some positive semi-definite matrix W₀ with rank(Σ₀)=rank(W₀).

To estimate Σ, we minimize the negative log-likelihood to yield the following semi-definite program

$${\text{argmin}}_C[-\text{log}|C|+\text{trace}(C\tilde{\mathrm{\Sigma }})],$$ (7)

$$\text{subject to}\hspace{1em}C=\frac{1}{{\sigma }_N^2}I-W_0,C,W_0⪰0,$$ (8)

where the sample covariance is denoted as Σ̃ = (1/n)(X − X̄)(X − X̄)^T and A ⪰ 0 means that A is positive semi-definite.

In factor models, we want to encourage a small number of factors which amounts to encouraging a small rank for Σ₀ or W₀. The direct approach to enforcing low rank Σ₀ or W₀ is to add an extra rank constraint:

$$\text{rank}(W_0)\le l,$$ (9)

where l is a pre-specified tuning parameter. Denote the eigen-decomposition W₀ = UDU^T and Σ̃ = ŨΛ̃Ũ^T, where D = diag(d₁, ⋯, d_d) and Λ̃ = diag(λ̃₁, ⋯, λ̃_d). Then $C=U(\frac{1}{{\sigma }_N^2}I-D)U^T$.

Theorem 1

For a fixed ${\sigma }_N^2$, the solution to (7),(8),(9) is given by U = Ũ and

$${\hat{d}}_k=\{\begin{array}{cc}\frac{1}{{\sigma }_N^2}-\frac{1}{{\tilde{\lambda }}_k}\hfill & \mathit{\text{if}}k\le l\mathit{\text{and}}{\tilde{\lambda }}_k>{\sigma }_N^2\hfill \\ 0\hfill & \mathit{\text{otherwise}}.\hfill \end{array}$$ (10)

Proof of this Theorem and other proofs are given in the supplementary material. By Theorem 1, we get the eigenvalues of the covariance matrix which are identical to (4) with suitable choices of l, i.e. greater than or equal to the number of eigenvalues which are bigger than ${\sigma }_N^2$ given by (4). We call this estimation the hard thresholding approach, so this name applies to the estimation used in Liu et al. (2008) as described in Section 2.1 above.

2.3 Soft Thresholding Approach

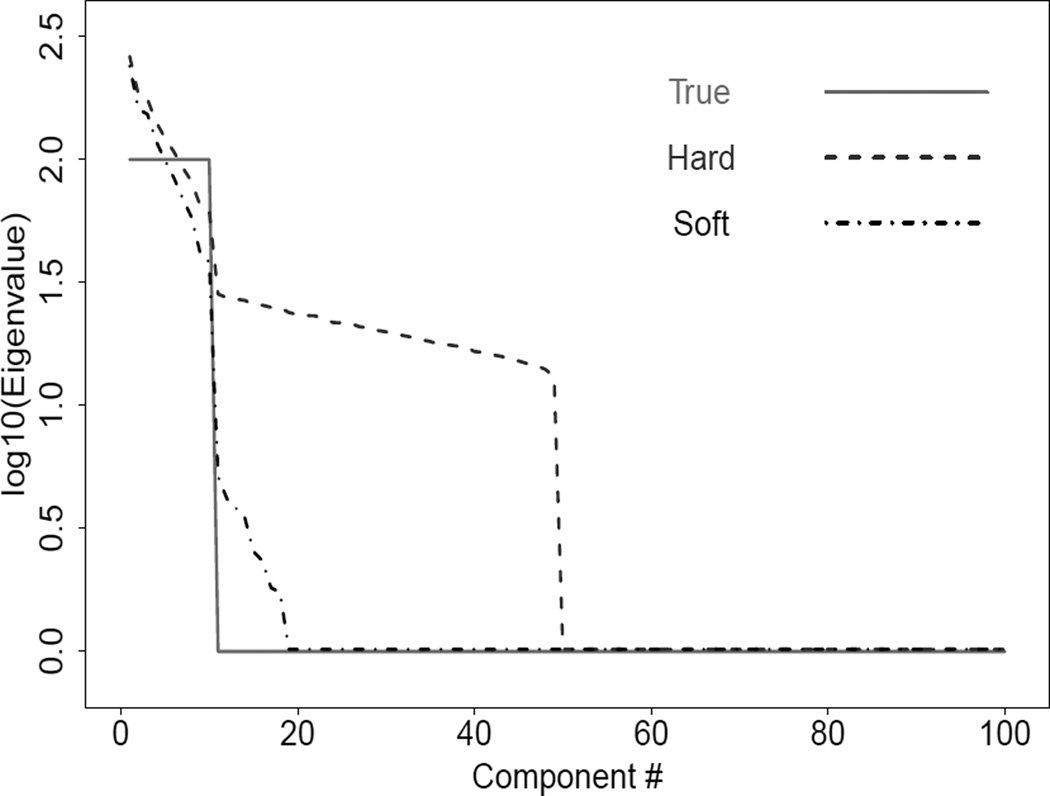
As mentioned in Liu et al. (2008), a challenge for the hard thresholding method is the effective estimation of the large eigenvalues in HDLSS settings. This is illustrated in Figure 1 using a simple HDLSS example with n = 50 and d = 1000. The data are generated from a multivariate normal distribution with covariance matrix Λ, where Λ is diagonal with elements $(\underset{w}{\underbrace{\upsilon ,\cdots ,\upsilon }},1,\cdots ,1)$. We consider υ = 100 and w = 10, which gives the true eigenvalue (solid) curve in Figure 1. In the HDLSS setting, it is well known that the sample estimators of the larger eigenvalues tend to grossly overestimate the corresponding true eigenvalues, because the total variation (both signal and noise) that is spread over the 1000 dimensional data set is concentrated in the first 50 non-zero eigenvectors. Note that for the first 50 entries the hard thresholding estimates (dashed curve) are the same as the sample eigenvalues. The rest of the sample eigenvalues are not shown, as they are 0, which cannot be plotted on this log scale. For entries 11–50, the estimated eigenvalues are far too high, because they have been raised by the concentration of the noise energy into these terms. This effect is precisely quantified in Baik and Silverstein (2006). This tendency for the hard thresholding to overestimate the true eigenvalues can create anticonservatism in SigClust, which will be mathematically analyzed in Section 2.4. In this section we propose a less aggressive thresholding scheme which can appropriately reduce the larger estimated eigenvalues to avoid this source of bias towards larger eigenvalues, called soft thresholding, shown as the dot-dashed curve in Figure 1.

Figure 1.

True and estimated covariance matrix eigenvalues based on the hard- and soft-thresholding methods for a simulated data set with d = 1000 and n = 50. This shows that some eigenvalues are highly over-estimated by the hard thresholding method. The soft thresholding method gives major improvement for this example.

Our approach is to replace the rank constraint (9) on W₀ by a smooth constraint. In particular, the L₀ constraint (9) becomes an L₁ constraint

$$\text{trace}(W_0)\le M$$ (11)

where the signal versus noise trade-off is controlled by a tuning parameter M ≥ 0. Denote λ_max(W₀) the largest eigenvalue of W₀, according to Theorem 1 of Fazel et al. (2001), trace(W₀) ≤ λ_max(W₀)rank(W₀). Therefore, the constraint above is a convex envelope to rank(W₀) (in the sense of being the biggest convex function below rank(W₀)) and therefore a convex relaxation of the constraint on rank(W₀). The tuning value M = 0 results in W₀ = 0, since W₀ ⪰ 0, so by (5) this gives a pure noise model with Σ = σ²I. As M increases, the non-noise component W₀ plays a stronger role in the estimation. The constraint (11) is a nuclear norm constraint, which has been well-studied in the convex optimization literature, see e.g. Fazel (2002).

Solution of the soft thresholding optimization problem, which is determined by (7), (8) and (11) is given in a closed form in Theorem 2 below.

Theorem 2

For a fixed ${\sigma }_N^2$, given M, the solution to the soft thresholding optimization problem:

$${\mathit{\text{argmin}}}_C[-\text{log}|C|+\mathit{\text{trace}}(C\tilde{\mathrm{\Sigma }})]$$

$$\mathit{\text{subject to}}\hspace{1em}C=\frac{1}{{\sigma }_N^2}I-W_0,C,W_0⪰0,\mathit{\text{trace}}(W_0)\le M$$

is given by U = Ũ as in Theorem 1 with soft thresholded estimated eigenvalues

$${\hat{\lambda }}_k=\{\begin{array}{cc}{\tilde{\lambda }}_k-\tau \hfill & \mathit{\text{if}}{\tilde{\lambda }}_k>\tau +{\sigma }_N^2\hfill \\ {\sigma }_N^2\hfill & \mathit{\text{if}}{\tilde{\lambda }}_k\le \tau +{\sigma }_N^2\hfill \end{array}={({\tilde{\lambda }}_k-\tau -{\sigma }_N^2)}_{+}+{\sigma }_N^2,$$ (12)

where τ is the solution of the equation

$$\sum _{k=1}^d{(\frac{1}{{\sigma }_N^2}-\frac{1}{{({\tilde{\lambda }}_k-\tau )}_{+}})}_{+}=M.$$ (13)

Note that the solution of this optimization problem (now using the constraint (13)) is essentially a constant downward shift of the estimated sample eigenvalues by the value τ, while still keeping them above ${\sigma }_N^2$. Because of this intuition and the relationship (13) between τ and M, it is useful to think of τ as a more insightful, but equivalent, version of the tuning parameter than M.

Figure 1 shows the improvements available in eigenvalue estimation, for that HDLSS example, from soft thresholding. The constant downward shift in estimated eigenvalues is hard to interpret because of the log scale used there. The consequences of this in terms of SigClust are demonstrated mathematically in Section 2.4 and through simulation in Table 1. A reasonable basis for choice of the tuning parameter τ will be derived from the concept of Theoretical Cluster Index (TCI), defined in Section 2.4.

Table 1.

Summary table of empirical SigClust p-value distribution over 100 replications based on four methods under different settings in Simulation 3.1. The mean and the numbers of p-values which are less than 0.05 (denoted as N5) and 0.1 (denoted as N10) are reported (d = 1000, n = 100).

		True			Sample			Hard			Soft
υ	w	Mean	N5	N10	Mean	N5	N10	Mean	N5	N10	Mean	N5	N10
1000	1	0.47	5	8	0.52	0	1	0.00	100	100	0.46	0	2
200	5	0.39	4	10	0.82	0	0	0.01	94	100	0.69	0	0
100	10	0.34	7	14	0.94	0	0	0.08	39	75	0.82	0	0
40	25	0.31	7	15	1.00	0	0	0.56	0	0	0.96	0	0
20	50	0.26	7	17	1.00	0	0	0.96	0	0	1.00	0	0
10	100	0.21	21	32	1.00	0	0	1.00	0	0	1.00	0	0
200	1	0.49	6	11	0.61	0	0	0.00	100	100	0.40	0	0
100	1	0.47	2	7	0.78	0	0	0.00	100	100	0.41	0	1
50	1	0.49	3	5	0.93	0	0	0.00	99	100	0.34	0	1
40	1	0.52	7	9	0.96	0	0	0.01	91	98	0.33	0	0
30	1	0.54	4	11	0.99	0	0	0.07	54	78	0.35	0	2
20	1	0.53	6	13	1.00	0	0	0.48	0	9	0.49	0	0
10	1	0.47	4	10	1.00	0	0	1.00	0	0	0.97	0	0
50	10	0.41	9	15	0.98	0	0	0.07	48	77	0.79	0	0
40	10	0.35	9	13	0.99	0	0	0.07	53	77	0.74	0	0
30	10	0.37	11	15	1.00	0	0	0.12	22	50	0.73	0	0
20	10	0.35	8	15	1.00	0	0	0.36	2	6	0.73	0	0
10	10	0.35	8	15	1.00	0	0	0.98	0	0	0.93	0	0
50	5	0.35	7	21	0.96	0	0	0.01	99	100	0.58	0	0
40	5	0.39	4	13	0.98	0	0	0.01	94	100	0.58	0	0
30	5	0.37	10	19	0.99	0	0	0.04	64	91	0.54	0	0
20	5	0.41	5	12	1.00	0	0	0.30	3	15	0.59	0	0
10	5	0.35	8	14	1.00	0	0	0.98	0	0	0.92	0	0
50	2	0.43	5	9	0.94	0	0	0.00	100	100	0.43	0	0
40	2	0.43	10	20	0.97	0	0	0.01	98	99	0.41	0	0
30	2	0.49	5	9	0.99	0	0	0.05	66	85	0.41	0	1
20	2	0.45	5	11	1.00	0	0	0.35	3	12	0.49	0	1
10	2	0.43	8	17	1.00	0	0	1.00	0	0	0.95	0	0
5	1	0.20	22	38	1.00	0	0	1.00	0	0	1.00	0	0
3	1	0.16	24	45	1.00	0	0	1.00	0	0	1.00	0	0
1	1	0.16	19	40	1.00	0	0	1.00	0	0	1.00	0	0

2.4 Theoretical Gaussian 2-means Cluster Index

Once the covariance matrix eigenvalues are estimated, we can proceed with the SigClust analysis. Toward that end, we need to determine the null distribution of the 2-means cluster index. In this section, we will derive a theoretical relationship between the cluster index and the eigenvalues which clarifies the performance of both hard and soft thresholding, and also leads to a useful choice of τ in the latter case.

As above, let x = (x₁, ⋯, x_d) be a d-dimensional random vector having a multivariate normal distribution of x ~ N(0,Σ) with mean 0 and covariance matrix Σ = UΛU^T. Denote ϕ(․) the multivariate normal probability density function with mean 0 and variance I. Define the theoretical total sum of squares as

$$\mathrm{T}\mathrm{S}\mathrm{S}=E{\Vert \mathbf{x}\Vert }^2=\int {\Vert \mathbf{x}\Vert }^2\varphi (\mathbf{x})d\mathbf{x}.$$ (14)

The theoretical within cluster sum of squares (WSS) is based on a theoretical analog of clusters, which is a partition of the entire feature space R^d into 𝒮₁ and 𝒮₂. Define μ₁ = ∫_x∈𝒮1 xϕ(x)dx/ ∫_x∈𝒮1 ϕ(x)dx and μ₂ = ∫_x∈𝒮2 xϕ(x)dx/ ∫_x∈𝒮2 ϕ(x)dx. Then we have

$$\mathrm{W}\mathrm{S}\mathrm{S}={\int }_{\mathbf{x}\in {𝒮}_1}{\Vert \mathbf{x}-{\mathit{\mu }}_1\Vert }^2\varphi (\mathbf{x})d\mathbf{x}+{\int }_{\mathbf{x}\in {𝒮}_2}{\Vert \mathbf{x}-{\mathit{\mu }}_2\Vert }^2\varphi (\mathbf{x})d\mathbf{x}.$$ (15)

These are combined to give TCI=WSS/TSS. The relationship between TCI and the covariance matrix eigenvalues is stated by the following theorem.

Theorem 3

For an optimal choice of 𝒮₁ and 𝒮₂, i.e. the split is chosen to minimize the total WSS over all possible splits (this is the theoretical analog of 2-means clustering), the Theoretical Cluster Index is

$$TCI=1-\frac{2}{\pi }\frac{{\lambda }_1}{{\sum }_{i=1}^d{\lambda }_i}.$$ (16)

Theorem 3 tells us that the optimal TCI is only determined by two quantities, the largest eigenvalue λ₁ and the total sum of eigenvalues ${\sum }_{i=1}^d{\lambda }_i$. In practice, different eigenvalue estimation methods give quite different estimates of these two quantities, which in turn leads to quite different SigClust performances.

For the sample covariance estimation method, the estimated λ₁ is typically larger (i.e. biased upwards) than the true value, in HDLSS situations. Since the sum of the sample eigenvalues is a consistent estimate of the total variation, i.e. the denominator of (16), it follows that the resulting estimate of TCI will generally be smaller (biased downwards) than the true TCI in that case, giving a larger p-value and thus a conservative result.

For the hard thresholding method, it follows from (16) that the sample and hard methods have the same numerator but the hard thresholding method gives a larger denominator. Thus the hard thresholding method has larger TCI, and consequently is always more powerful than the sample method. However, the hard thresholding method has large potential for creating type-I error. Consider potential biases in the estimation of λ₁ and ${\sum }_{i=1}^d{\lambda }_i$ defined as δ₁ and Δ respectively. Some algebra shows that the essential difference between the true TCI and the hard thresholding estimate is proportional to

$$E=\frac{{\lambda }_1+{\delta }_1}{{\sum }_{i=1}^d{\lambda }_i+\mathrm{\Delta }}-\frac{{\lambda }_1}{{\sum }_{i=1}^d{\lambda }_i}=\frac{{\sum }_{i=1}^d{\lambda }_i{\delta }_1-{\lambda }_1\mathrm{\Delta }}{{\sum }_{i=1}^d{\lambda }_i({\sum }_{i=1}^d{\lambda }_i+\mathrm{\Delta })}.$$ (17)

When

$${\delta }_1<\frac{{\lambda }_1\mathrm{\Delta }}{{\sum }_{i=1}^d{\lambda }_i},$$ (18)

i.e. when the first eigenvalue is large relative to the rest, the hard thresholding method will tend to be anti-conservative.

For the soft thresholding method, the large eigenvalues are subtracted by τ from the corresponding sample estimates. This will decrease both the numerator and denominator of (16) in contrast to the hard thresholding method. Our goal is to choose τ so that the type-I error can be controlled and at the same time the test is more powerful than the sample method. For this, a useful boundary is τ̃, which is energy conserving in the sense that the sum of the soft eigenvalues is the sum of the sample eigenvalues, i.e. τ̃ is the solution of the equation

$$\sum _{k=1}^d\{{({\tilde{\lambda }}_k-\tilde{\tau }-{\sigma }_N^2)}_{+}+{\sigma }_N^2\}=\sum _{k=1}^d{\tilde{\lambda }}_k.$$ (19)

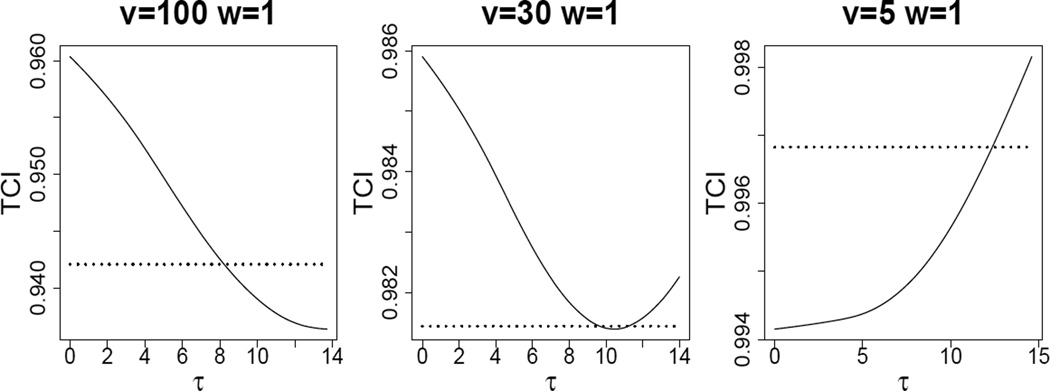
Another important endpoint of reasonable τ values, is τ = 0, which corresponds to hard thresholding (i.e. no reduction in eigenvalues). Note that the soft estimated version of the denominator of the fraction in (16) (i.e. the sum of the eigenvalues) is monotone decreasing in τ. At τ̃, this denominator is the same as the sample version. It follows that for τ between 0 and τ̃, soft thresholding gives bigger TCI than the sample covariance estimate, and thus a more powerful test. Figure 2 displays the relationship between TCI calculated from the eigenvalues estimated using the soft method and tuning parameter τ for three simulated data sets with d = 1000, n = 100, w = 1 and υ = 100, 30, 5 respectively. In Figure 2, the range of τ is [0, τ̃]. Depending on the context, SigClust can be anti-conservative at either end of the interval [0, τ̃]. This will happen at τ = 0, when the first eigenvalue is very large relative to the others (as shown in the left panel of Figure 2), and at τ = τ̃ when the first is only a little larger than the background noise (as happens in the right panel of Figure 2). The central panel of Figure 2 shows a compromise situation, where both endpoints can be anti-conservative, but there is a more reasonable choice in between. Because anti-conservatism can happen at either end of this interval, we recommend choosing the soft thresholded τ as conservative as possible, by taking τ^⋆ in [0, τ̃] to minimize TCI. The examples in Figure 2 show that, depending on the setting, τ^⋆ can be either 0 (hard thresholding, left), τ̃ (energy preserving, right) or something in between (central panel).

Figure 2.

Relationships between TCI and tuning parameter τ for three different settings (solid line). Dotted lines represent the TCI calculated from true eigenvalues. Shows situations where hard thresholding is anti-conservative (left panel), where energy preserving soft thresholding is anti-conservative (right panel), and where τ^⋆ is strictly between the two (central panel).

3 Simulation

In this section we investigate how the estimation of the covariance matrix eigenvalue affects the SigClust performance using extensive simulation studies. Four SigClust p-value computation methods are compared using the true covariance matrix as well as estimates from the sample, hard and soft thresholding approaches, which are referred to using those names.

We have performed simulations in both low and high dimensional situations. Here we focus on high dimensional results, because our main contribution is in HDLSS settings. Three types of examples are generated here including situations under both null and alternative hypotheses. The sample size is n = 100, dimension is d = 1000, and the number of data sets generated for each run is N_sim = 1000. Empirical quantiles, as discussed in Section 2.1, were used in each case. We evaluate different methods based on the criterion of whether or not they can maximize the power while controlling the type-I error. In Section 3.1, we consider examples of data under the null hypothesis, i.e., having only one cluster generated by a single Gaussian distribution. In each example we check the type-I error of each version of SigClust, for a wide variety of Gaussian null distributions, by studying how often it incorrectly rejects the null hypothesis H₀. In Sections 3.2 and 3.3, we explore the power of the different versions of SigClust, by considering data from a collection of mixtures of two Gaussian distributions with different signal sizes counting how often it correctly rejects the null hypothesis. We give combined discussion of the simulation results in Section 3.4.

3.1 Level of the Test

In order to evaluate the Type I error rates for different methods, data were generated under the null hypothesis, i.e. from a single multivariate Gaussian distribution with d = 1000 dimensional covariance matrix Λ which is diagonal with elements $(\underset{w}{\underbrace{\upsilon ,\cdots ,\upsilon }},1,\cdots ,1)$. We consider 31 combinations of υ and w with υ = 1, ⋯, 1000, and the corresponding w = 1, ⋯, 100, as shown in Table 1. The simulation procedure was repeated 100 times for each setting.

Table 1 summarizes the mean and the number of the p-values which are less than 0.05 (N5) and 0.1 (N10) based on different methods under the various parameter settings. Theoretically the p-value follows the uniform [0, 1] distribution since the data are generated from a single Gaussian distribution. As expected, the empirical distributions of p-values using the true method are relatively close to the uniform distribution. The sample method results in p-values whose means are always bigger than the expected ones. This is consistent with the theoretical results shown in Section 2.4. The N5 and N10 are almost all 0, so we conclude that the sample method is conservative in all of these settings. For settings of υ ≥ 30, i.e. for populations with a generally large first few eigenvalues (e.g. a strongly elongated distribution), with the exception of (υ, w) = (40, 25), results based on the hard thresholding method exhibits more small p-values than expected under the uniform distribution which implies that this approach is anti-conservative in that situation. On the other hand, the hard thresholding method tends to be quite conservative, for relatively small values of υ, e.g. for approximately more spherical Gaussian distributions. This also is a consequence of equation (17), because λ₁ = υ is small.

For the soft method, the results of Table 1 show conservative results in all settings. Like the sample method, the soft method effectively controls type-I error under the null hypothesis. But more importantly it can dramatically increase the power over the sample method under important alternative hypotheses as shown in the next section.

The means of the p-value populations give additional insights, and the results are mostly consistent with those from the quantiles. In particular, the means of the p-value from SigClust using the true eigenvalues are generally close to the desired value of 0.5, the means from the sample method tend to be larger, and the hard, soft fluctuate in a way that corresponds to their quantile behavior. An important point is that means from the soft method are generally substantially closer to 0.5 than is true for either the sample or the hard methods.

3.2 Power of Test for Signal in One Coordinate Direction

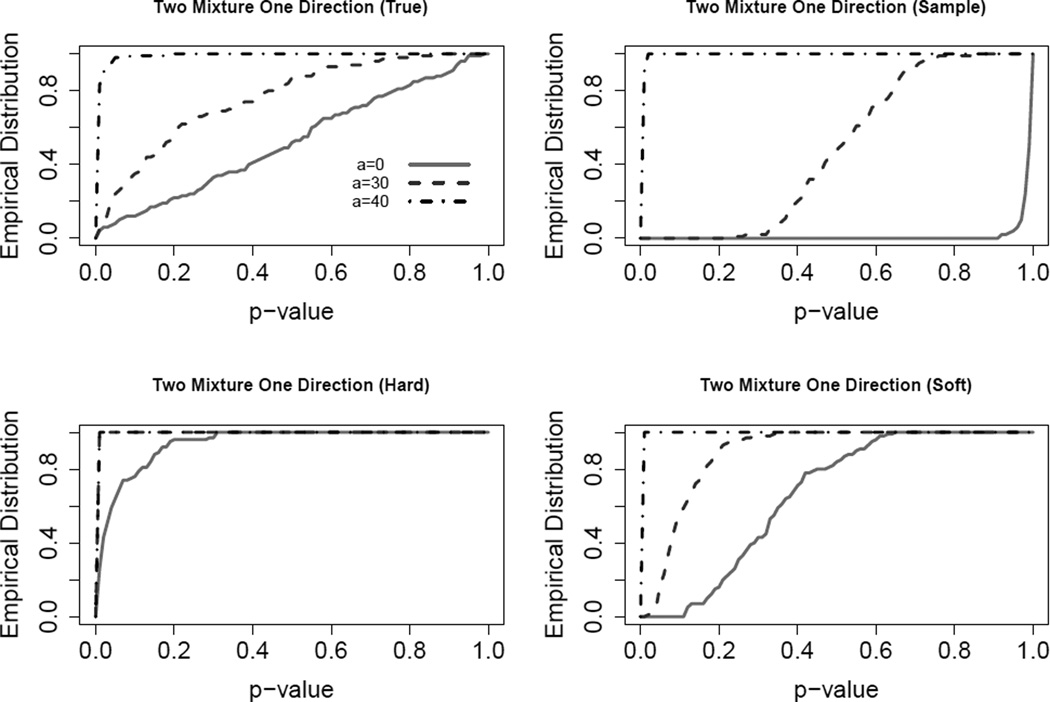
In this section, we compare the power properties of these various SigClust hypothesis tests. This is based on a mean mixture of two normal distributions, .5N(0, Λ)+.5N(μ, Λ), where μ = (a, 0, ⋯, 0) with a = 0, 30, 40 and as above $\mathrm{\Lambda }=\text{diag}(\underset{w}{\underbrace{\upsilon ,\cdots ,\upsilon }},1,\cdots ,1)$ a diagonal matrix. Here we focus on a similar setting as in the middle panel of Figure 2 with υ = 30 and w = 1. When a = 0, the distribution reduces to a single Gaussian distribution. The larger the a, the stronger the signal. The theoretical null distribution is N(0, Λ*), where Λ* = diag(λ₁ + 0.25a², λ₂, ⋯, λ_d). The empirical distributions of p-values based on 100 replications are shown in Figure 3. As expected, the true method (upper left) is very powerful under the alternative hypothesis and meanwhile can control the type-I error well under the null hypothesis (a = 0). The hard method (lower left) is grossly anti-conservative, since the solid curve bends far above the diagonal. The sample method (upper right) is too conservative, since the solid curve bends way below, and even for a = 30, is very low. The soft method (lower right) is close to the diagonal at a = 0, and is more powerful than the sample, in terms of bending upwards when there is signal in the data.

Figure 3.

Empirical distributions of SigClust p-values for Simulation 3.2. This shows sample is too conservative, hard is anti-conservative, while soft strikes a nice balance in overall performance.

3.3 Power of Test for Signal in All Coordinate Directions

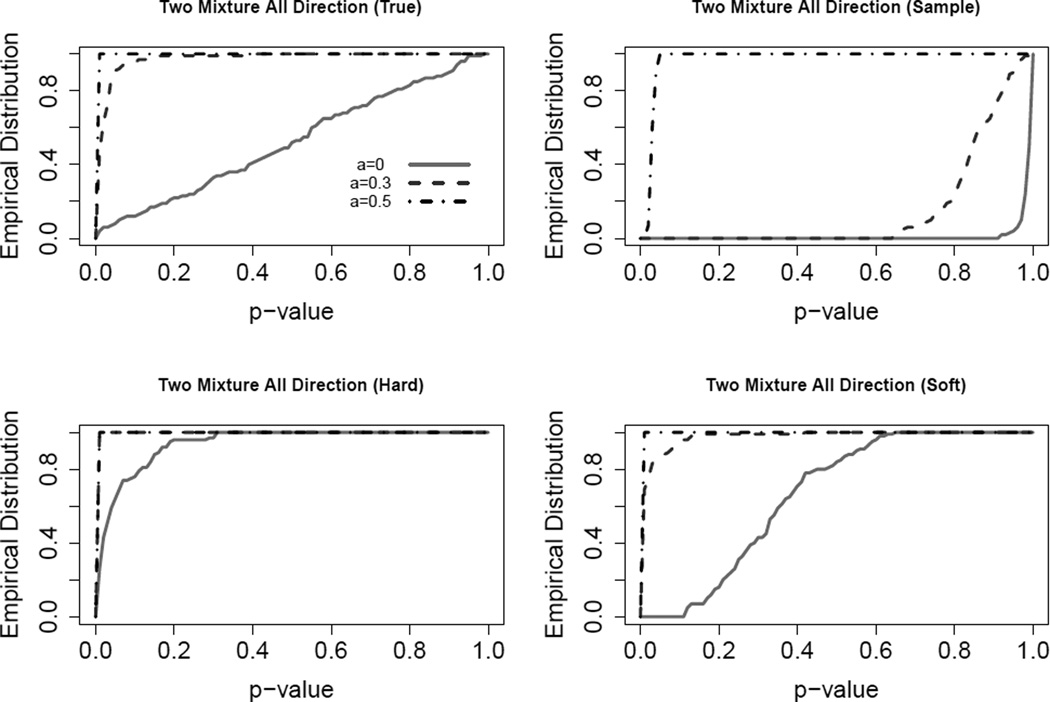
In the previous subsection, the signal is only in the first coordinate direction. Now we consider power using another example with the signal in all coordinate directions. Similarly, we generate data from a mixture of two Gaussian distributions, .5N(0, Λ) + .5N(μ, Λ), where μ = (a, a, ⋯, a) with a = 0, 0.3, 0.5 and $\mathrm{\Lambda }=\text{diag}(\underset{w}{\underbrace{\upsilon ,\cdots ,\upsilon }},1,\cdots ,1)$ with υ = 30 and w = 1 which is similar to the setting in the previous section. This signal is very small in each direction, but can be large when all directions are combined together. The empirical distributions of p-values calculated from the 100 simulated datasets based on different methods are displayed in Figure 4. For a = 0 the results are identical to the single cluster situation in Sections 3.1 and 3.2 with (υ, w) = (30, 1). The hard thresholding method always yields smaller p-values than expected and thus is strongly anti-conservative under the null hypothesis meaning it may not be trusted. In contrast, the soft method is conservative under the null but becomes powerful as the signal increases. When the signal is big enough, e.g. a = 0.5, all methods can identify the significant clusters. For small signal situations, e.g. a = 0.3, the soft method is much more powerful than the sample method.

Figure 4.

Empirical distributions of SigClust p-values for Simulation 3.3. The results indicate that hard is strongly anti-conservative, while sample is too conservative. Overall best is the soft method.

3.4 Simulation Summary

In summary, the sample method is strongly conservative and the hard thresholding method can be anti-conservative in certain situations. The soft thresholding method is in-between. Simulation results shown in Section 3.1 suggest that, under the null hypothesis, the performances of the hard thresholding method vary from strongly conservative to strongly anti-conservative depending on the situations which are mainly characterized by the quantity, υ. The soft method yields conservative results in all settings studied here. Simulation results from Sections 3.2 and 3.3 suggest that, under the alternative hypothesis, the hard thresholding method often has the largest power and the sample method has the smallest power. The soft method is appropriately in-between. If the signals are large enough, all methods can identify the significant clusters. However, in situations with relatively small signal, the sample method cannot distinguish the significant clusters. In practice, we recommend the soft method, i.e., small p-values from the soft method reliably indicate the existence of distinct clusters.

4 Real Data

In this section, we apply our methods to some real cancer data sets. As mentioned in Verhaak et al. (2010), GlioBlastoma Multiforme (GBM) is one of the most common forms of malignant brain cancer in adults. For the purposes of the current analysis, we considered a cohort of patients from The Cancer Genome Atlas Research Network (TCGA, 2010) with GBM cancer whose brain samples were assayed. Four clinically relevant subtypes were identified using integrated genomic analysis in Verhaak et al. (2010), they are Proneural, Neural, Classical, and Mesenchymal. As in Liu et al. (2008), we filter the genes using the ratio of the sample standard deviation and sample mean of each gene. After gene filtering, the data set contained 383 patients with 2727 genes. Among the 383 samples, there are 117 Mesenchymal samples, 69 Neural samples, 96 Proneural samples, and 101 Classical samples.

We applied SigClust to every possible pair-wise combination of subclasses and calculated the p-value based on the three different methods. Here the cluster-index is computed based on the given class label. Let MES stand for Mesenchymal samples and CL stand for Classical samples. Except the MES and CL pair, the p-values from all three methods were significant for each of the five other pairs which is consistent with the widely accepted fact that these are distinct clusters. For the MES and CL pair, the p-value was non-significant using the sample method (0.93) while it was significant both for hard (< 0.001) and soft (0.04) methods. This suggests that the sample was too conservative to find this important effect. Furthermore the hard method appears to give too strong a significance, consistent with its occasional theoretically predicted anti-conservatism.

The second real example we considered is a breast cancer data set (BRCA) also from The Cancer Genome Atlas Research Network which include four subtypes: LumA, LumB, Her2 and Basal and have been extensively studied by microarray and hierarchical clustering analysis (Fan et al., 2006). The sample size is 343 and the number of genes used in the analysis after filtering is 4000. Among 343 samples, there are 154 LumA, 81 LumB, 42 Her2 and 66 Basal.

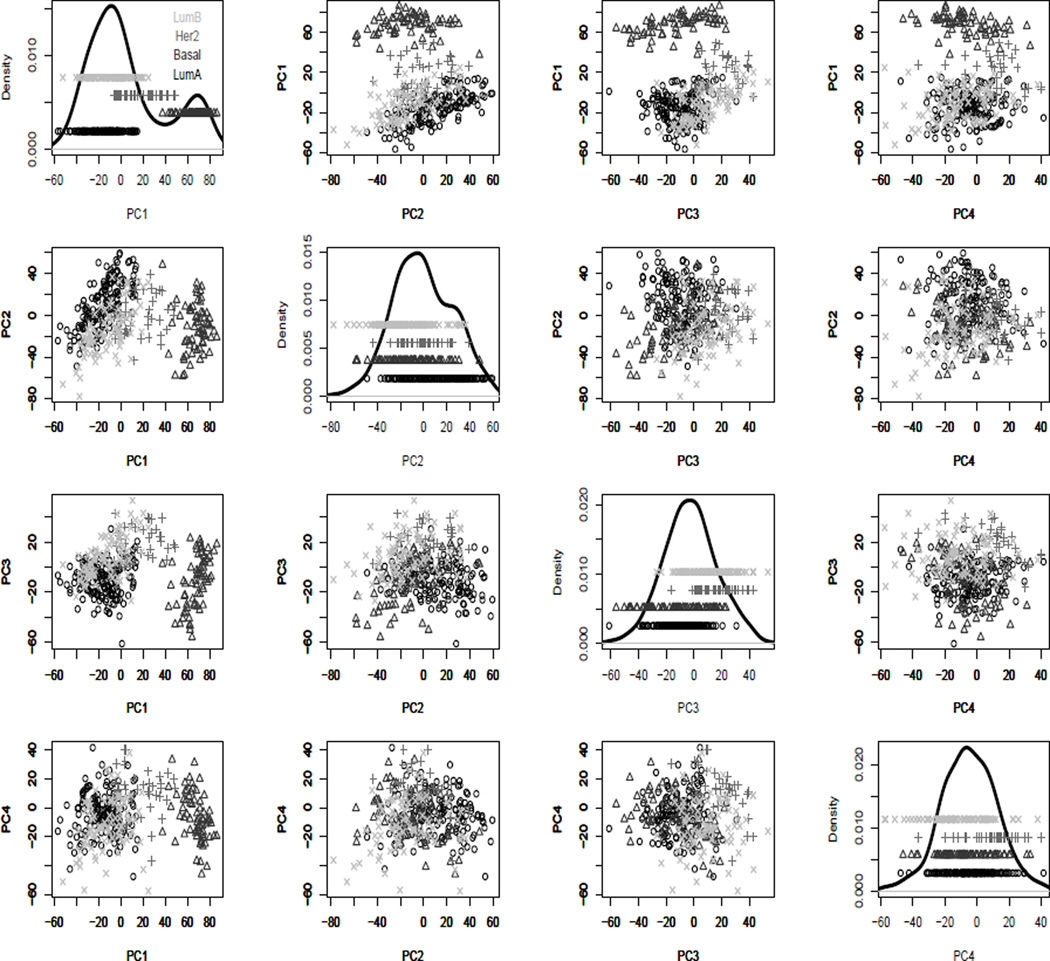
The results of applying SigClust to each pair of subclasses are shown in Table 2. For pairs including Basal, the p-values from all three methods are significant which implies that the Basal cluster is well separated from the rest. For the LumA and LumB pair, all methods report very high p-values, which suggests that they are actually one subtype. This is consistent with the findings of Parker et al. (2009), which suggest that these are essentially a stretched Gaussian distribution (thus not flagged by SigClust), with an important clinical division within that distribution. For the Her2 and LumB pair, all three methods give a non-significant p-value although not as big as for the LumA and LumB pair, so there is no strong evidence for them to be separated (although hard thresholding appears to be close to a spuriously significant result). For the Her2 and LumA pair, the hard method gives a very significant p-value, the soft method gives a nearly significant p-value, whereas the sample method fails to find the clusters. Thus the cluster difference for this pair is not as large as for the Her2 and LumB pair. Note that the p-values listed in Table 2 are consistent with the scatter plot in Figure 5 where the projections of the data points onto the first four principal component (PC) directions are displayed. Clearly, Basal is well separated from the remaining data. LumA and LumB are close together and LumB and Her2 are closer than LumA and Her2. These results are again consistent with our theoretical results that sample is often conservative, hard can occasionally be anti-conservative, and soft is an appropriate balance of these effects.

Table 2.

SigClust p-values for each pair of subtypes for the BRCA data. The known class labels are used to calculate the cluster index.

	Basal.LumA	Basal.LumB	Basal.Her2	LumA.LumB	Her2.LumB	Her2.LumA
Sample	< 0.001	< 0.001	0.015	1	0.99	0.77
Hard	< 0.001	< 0.001	< 0.001	0.89	0.051	< 0.001
Soft	< 0.001	< 0.001	< 0.001	1	0.95	0.059

Figure 5.

PCA projection scatter plot view of the BRCA data, showing 1D (diagonal) and 2D projections of the data onto PC directions. Groupings of colors and symbols indicate biological subtypes. Shows Basals are quite distinct from the others, and there is no strong evidence showing that LumA and LumB do not come from a single Gaussian distribution.

5 Discussion

In this paper, we developed a soft thresholding approach and examined its application to the SigClust method. We found that both the newly proposed soft thresholding and the hard thresholding proposed in the original SigClust paper can be derived under a likelihood based framework and usefully compared in terms of penalties in their respective regularizations (L₀ regularization for hard and L₁ for soft). Differences in performance were analyzed using the notion of Theoretical Cluster Index, which also indicated how the soft method should be tuned. Through extensive simulation, we compared the performance of the SigClust method based on different approaches in a wide variety of settings. As theoretically predicted, we found that the hard thresholding method would sometimes incorrectly reject the null while the sample and soft methods are always conservative. The soft approach was seen to have much better power properties than using the simple sample covariance estimation. We recommend that our newly proposed soft method be used in practice because it has been shown to control the type-I error as well as the sample method under the null hypothesis, while gaining much more power under the alternative hypothesis.

An important point is that our definition of clusters assumes a null Gaussian distribution. Thus SigClust may have limited use in categorical situations. However, in very high dimensional contexts, it may be possible to develop a limiting distribution theory by which most SigClust ideas still work. Another interesting open problem is finding a non-simulation calculation of the SigClust p-values.

This paper treats the case of 2 clusters, using a statistic based on k-means clustering. Interesting extensions include more than 2 clusters, and other clustering criteria, such as those underlying hierarchical clustering. The incorporation of alternate eigenvalue estimation methods is another interesting open problem.

In terms of software, the R package for the current version of SigClust can be freely downloaded on the CRAN website: http://CRAN.R-project.org/package=sigclust. Computation time depends on the number of simulated replications, and the size of the input data. In all cases here, we used N_sim = 1000 and a computer with RAM 16GB and processor 3.5GHz, and it took around 1 minute for each simulated data set described in Section 3 and 10 minutes for both the GBM data and the BRCA data described in Section 4.