Characterization of the domain orientations of E. coli 5’-nucleotidase by fitting an ensemble of conformers to DEER distance distributions

Summary

Escherichia coli 5’-nucleotidase is a two-domain enzyme exhibiting a unique 96° domain motion that is required for catalysis. Here we present an integrated structural biology study that combines DEER distance distributions with structural information from X-ray crystallography and computational biology to describe the population of presumably almost isoenergetic open and closed states in solution. Ensembles of models which represent the experimental distance distributions best are determined by a Monte Carlo search algorithm. As a result, predominantly open conformations are observed in the unliganded state indicating that the majority of enzyme molecules await substrate binding for the catalytic cycle. The addition of a substrate analog yields ensembles with an almost equal mixture of open and closed states. Thus, in the presence of substrate efficient catalysis is provided by the simultaneous appearance of open conformers (binding substrate or releasing product) and closed conformers (enabling the turnover of the substrate).

Introduction

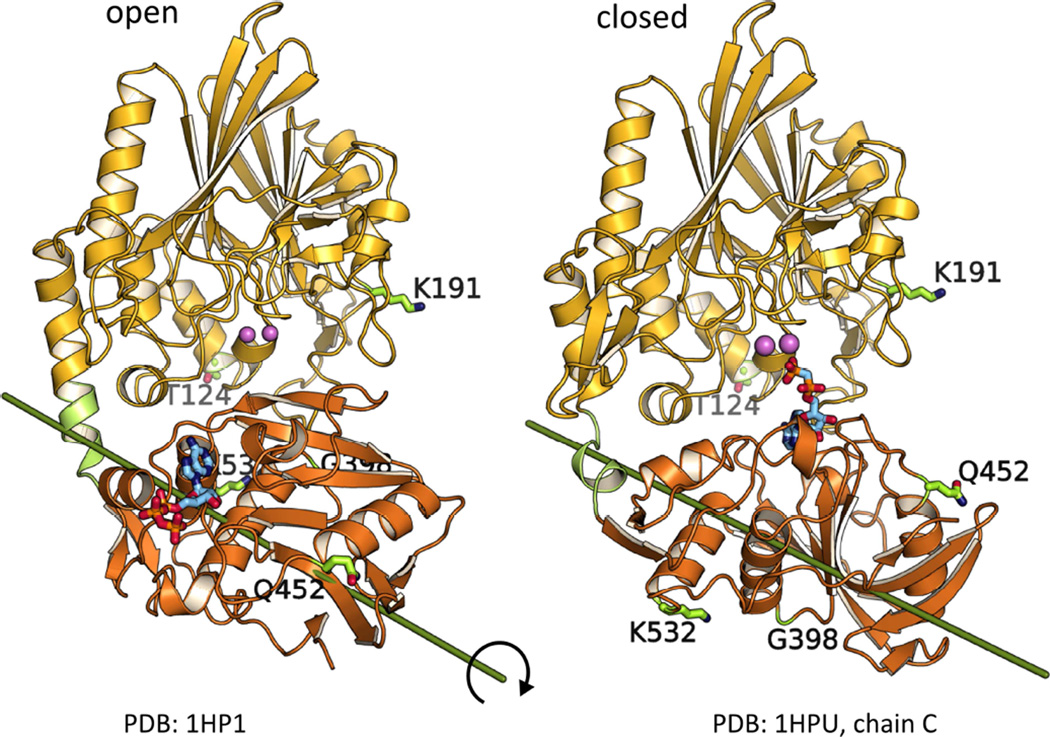
Escherichia coli 5’-nucleotidase (5NT) belongs to the superfamily of calcineurin metallophosphatases (Knöfel and Sträter, 1999). It is a two-domain enzyme with a dimetal center located in the N-terminal domain where various substrates including nucleotides, nucleotide sugars or dinucleotides are hydrolyzed (Glaser et al., 1967; Neu, 1967; Ruiz et al., 1989; Knöfel and Sträter, 1999, 2001b; Schultz-Heienbrok et al., 2005; Krug et al., 2013). Substrates bind to the C-terminal domain in the open state and a 96° rotation of this domain around its center enables hydrolysis via formation of the closed state (Figure 1). Substrate binding to and product release from the open state are necessary for catalysis since the active site is occluded from solvent in the closed state (Schultz-Heienbrok et al., 2005). Due to the extensive domain rearrangement of the unique ball-and-socket-type motion and due to the availability of several crystal structures in different packing arrangements, 5NT is an excellent model enzyme for studying structure-function-relationships of domain motions in catalysis.

Figure 1. EPR spin label positions in the open and closed crystal structures of 5NT.

The N-terminal domain (yellow) contains the dimetal center (pink), the C-terminal domain (orange) the substrate binding pocket. The rotation axis between the open and closed states is indicated. For EPR studies six double cysteine variants (with one cysteine in each domain) were prepared (see also Figure S1). The labeling sites are indicated by the original amino acid side chain (before the mutation) depicted as sticks.

By hydrolysis of extracellular nucleotides, the bacterial 5NT provides nucleosides and phosphate as nutrients to the cell (Zimmermann, 1992). Furthermore, microbial pathogens impair immune functions of the infected hosts by generation of anti-inflammatory adenosine (Antonioli et al., 2013). 5NT activity was shown to interfere with host-immune responses for a number of bacterial microorganisms (Thammavongsa et al., 2009; Fan et al., 2012; Firon et al., 2014; Liu et al., 2014). Moreover, 5NT is the bacterial homolog of ecto-5’-nucleotidase (also known as CD73), an enzyme which is part of the purinergic signaling cascade where extracellular nucleotides or their degradation products interact with P2X, P2Y and P1 receptors. CD73 activity is the dominant source of extracellular adenosine, a potent immunosuppressant. Notably, CD73 is overexpressed in several cancer cell lines (suppressing the immune response) and CD73 inhibitors are promising candidates for cancer immunotherapy (Zimmermann et al., 2012; Antonioli et al., 2013). Crystal structures show that CD73 undergoes a similar domain rearrangement as 5NT (Heuts et al., 2012; Knapp et al., 2012a; Knapp et al., 2012b). 5NT has been captured in a total of 16 conformers by X-ray crystallography comprising open, closed and intermediate states (Knöfel and Sträter, 1999, 2001b, 2001a; Schultz-Heienbrok et al., 2004, 2005). Here we set out to address the following questions via site-directed spin-labeling (SDSL) and EPR spectroscopy: 1) Are the crystallographic conformers sufficient to characterize the conformational equilibrium in solution or do we observe additional conformers?, 2) How is the equilibrium between open and closed states affected by ligand binding to the active site?, 3) How many distance distributions are required to characterize the spatial arrangement of the two domains and the equilibrium of different states?, 4) To what extent do the spin labels influence the equilibrium, which might involve almost isoenergetic states?

To answer these questions and define the conformational dynamics an integrated structural biology approach was used. Spin label sites to measure distances by double electron-electron resonance spectroscopy (DEER) were specifically selected to capture the domain motion postulated by the crystal structures. To quantitatively analyze the DEER distance distributions which report dynamic modes that modulate the distance between two labels (Mchaourab et al., 2011; Jeschke, 2012) we developed a Monte Carlo search algorithm that reproduces experimental distributions in terms of the underlying populations in a self-consistent manner by selecting conformers from a pool of structures. Different initial pools with increasing structural diversity (i.e. crystal structure conformers, models from molecular dynamics (MD) or from docking of the domains) were used to find the best fit to the distance distributions. Furthermore, implicit and explicit spin label representations were compared. Finally, by the introduction of a leave-one-out procedure, we developed a strategy to avoid over-fitting the structure ensembles to the experimental data and to demonstrate the predictive power of the ensembles.

Results

EPR reeals conformational changes upon addition of inhibitor

SDSL methods in combination with EPR distance measurements are widely used to characterize structure-function relationships of proteins (Hubbell et al., 2000; Columbus and Hubbell, 2002; Fanucci and Cafiso, 2006). Covering a distance range between 20 and 80 Å they constitute an ideal way to obtain information about the inter-domain orientation in modular proteins (Ward et al., 2009) or can be used to dock protein complexes on the basis of distance distributions (Edwards et al., 2014). To characterize the relative orientation and translation of 5NT’s two domains, i.e. two rigid bodies, six free parameters are required. In this study, five labeling sites (T124C, K191C, G398C, Q452C, K532C) were selected constituting a set of six residue pairs with preference for observing large changes in distances in orthogonal directions. Thus, the number of residue pairs is at a minimum to define the relative orientation of two completely independent rigid bodies. However, the use of docked models, of models along a simulated path between open and closed states, and finally of the crystallographically observed states significantly reduces the degrees of freedom of the system to be characterized. The resulting six double cysteine mutants T124C/G398C, T124C/Q452C, T124C/K532C, K191C/G398C, K191C/Q452C and K191C/K532C (Figure 1, Figure S1) showed a specific activity of 70 to 120% of that of wild-type 5NT. Labeling with MTSSL did not significantly alter these values. Thus, the modification and the labeling did not disturb catalysis.

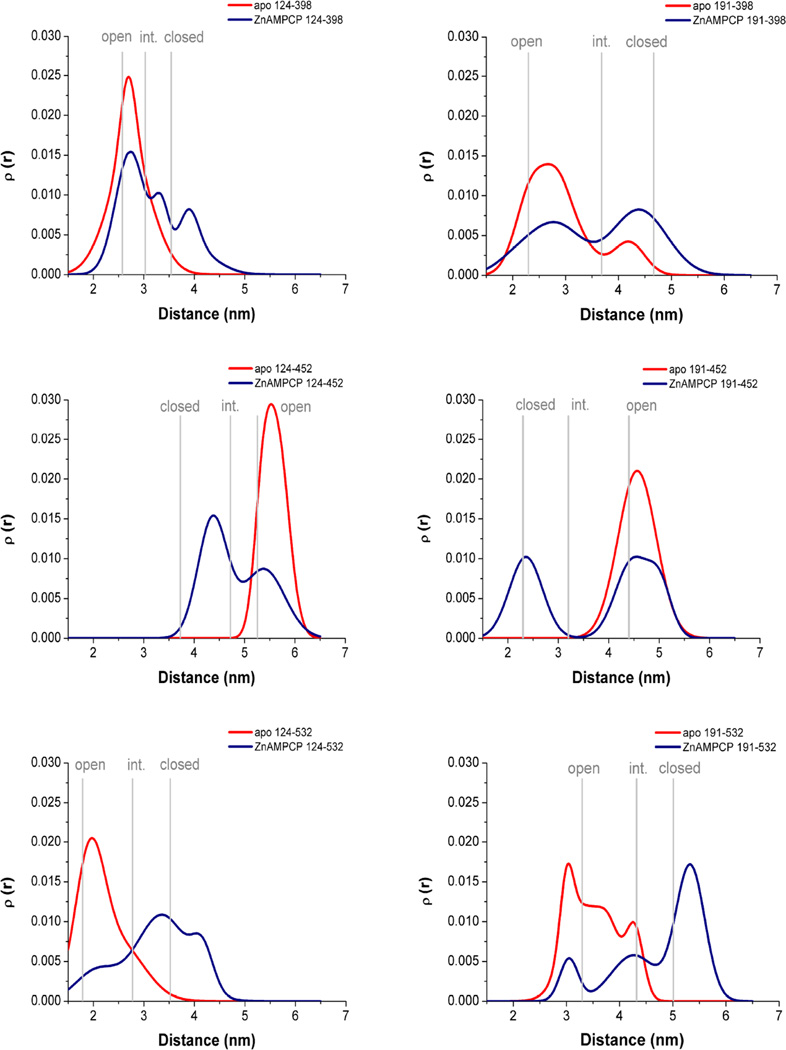
Crystal structures of 5NT in complex with the non-hydrolyzable ADP analog AMPCP show that the inhibitor binds between the two enzyme domains in a conformation that probably corresponds to the catalytically competent Michaelis complex (Knöfel and Sträter, 2001b). Thus, protein samples of inhibitor-free (apo) and inhibitor-bound states, i.e. after addition of saturating amounts of AMPCP and Zn²⁺ (ZnAMPCP), were investigated. Dipole-dipole couplings between the introduced methanethiosulfonate spin labels (MTSSL) were measured with DEER and the distance distributions (Figure 2, Figure S2) were derived utilizing Tikhonov regularization (Chiang et al., 2005). All mutants showed a shift of the distance distribution between the apo and the ZnAMPCP state indicating a conformational change upon addition of inhibitor. Depending on the positions of the spin labels the distances increased or decreased with the domain closure motion. Although the distance distributions differ in the number of observed maxima, the height of the peaks, and their broadness, all apo states sampled predominantly monomodal distributions with maxima indicative of the open conformations. In contrast, in the ZnAMPCP states, multimodal distance distributions were observed corresponding to a mixture of different states. Also, there was very little change in the continuous wave (CW)-EPR spectra (Figure S2) under the different conditions, supporting large-scale protein reorientation for the changes seen in the DEER experiments and minimal change in the local environment of the spin label upon domain closure.

Figure 2. DEER distance distributions of six MTSSL labeled 5NT mutants.

The apo (red) and the ZnAMPCP bound state (blue) are compared. Labeling positions are indicated. Gray bars mark the expected distances of the spin labels in the crystallographically open, intermediate and closed states (as estimated from theoretical distance distributions of all crystal structure conformers calculated with the rotamer library using the program MMM, see also Figure S3 (Polyhach et al., 2011)). For CW-EPR data and DEER traces compare Figure S2.

A comparison of the broadness and shape of the experimental distance distributions in the open enzyme with distributions simulated based on the rotamer library as implemented in MMM (Polyhach et al., 2011) showed that the experimental distributions mostly have less maxima or a less pronounced “fine structure” of narrow peaks (Figure S3). After averaging the simulated distance distributions of the seven open crystal forms, the shape of the resulting averaged distance distribution was more similar to the experimental observations. Previous work (Polyhach et al., 2011; Alexander et al., 2013) has shown that distance distributions obtained with the MMM rotamer library over-estimate the breadth of tight distributions. Therefore, the good match of the averaged distributions and the experimental data would suggest that the ∼10° of inter-domain flexibility within the open or closed states of 5NT (Knöfel and Sträter, 2001a) contributes to the overall width of the distributions.

Ensemble fitting to characterize conformational ensembles

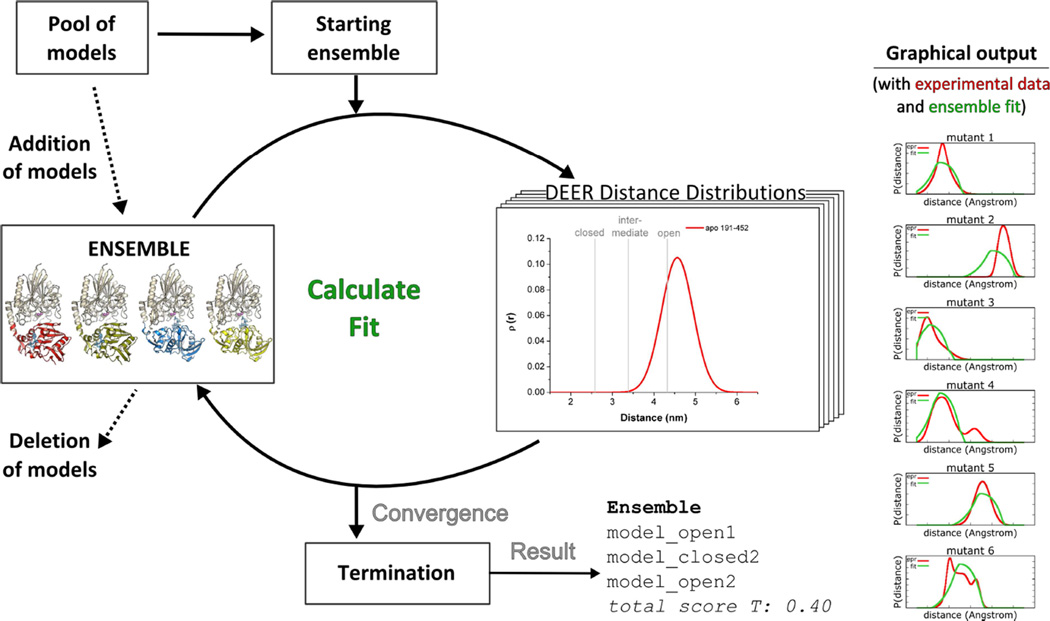
For a quantitative description of the conformational population in the apo and the ZnAMPCP states an ensemble fitting procedure was employed (Figure 3). A starting ensemble was randomly chosen from the pool of models. To improve the fit of the distance distributions further models were added, replaced or removed from the ensemble based on a Monte Carlo algorithm. The total score T served as a quality indicator for the fits. To account for the flexibility of the spin label, the probability function of the knowledge-based potential from the motion-on-a-cone model (Alexander et al., 2008; Hirst et al., 2011) and in a second approach full-atom representations derived from RosettaEPR (Alexander et al., 2013) were used. This allowed for a comparison of implicit vs. explicit spin label representations.

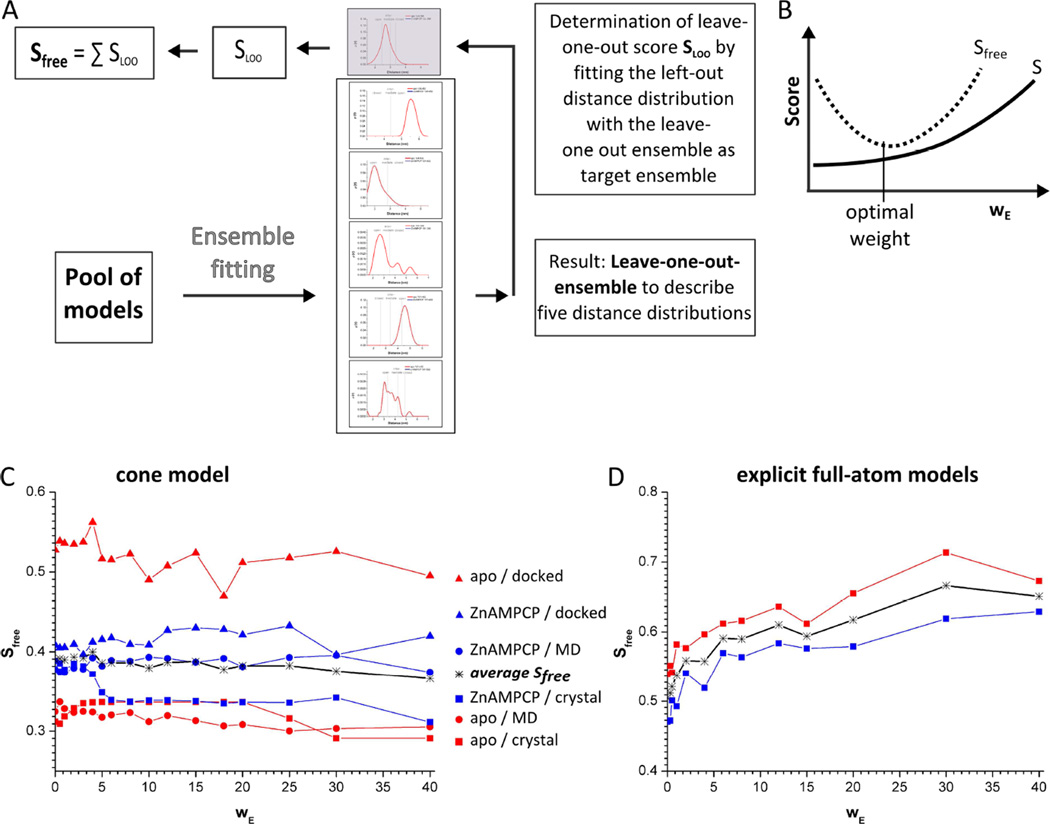
Figure 3. Scheme for ensemble fitting of 5NT distance distributions.

From a pool of models an initial starting ensemble is randomly selected by a Monte Carlo search algorithm to describe the experimental data. Then, during optimization models are added to and/or deleted from the ensemble until the termination criterion is fulfilled. As output an ensemble, a score and a graphical comparison of the experimental data and the fit by the ensemble are given. See experimental results Figure S4.

Generation and description of the models in the pool for fitting to the distance distributions

Crystal structure conformers

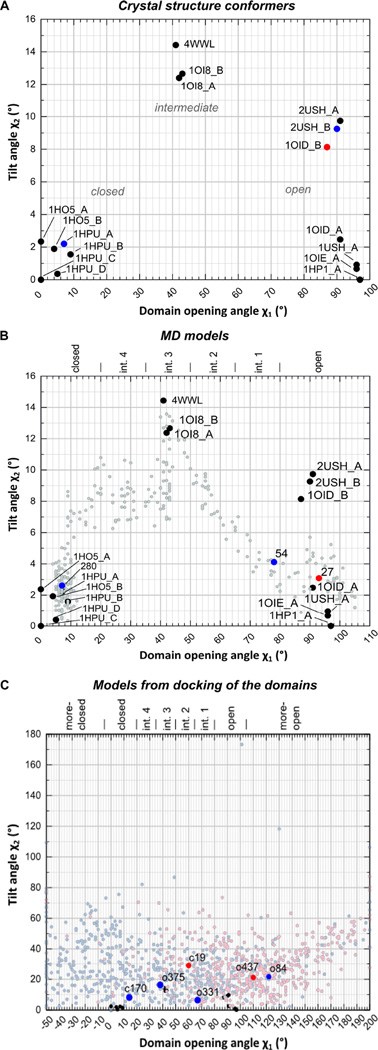
16 available crystallographic conformers were used for ensemble fitting. For a comprehensive description of the relationship between these conformers they are described relative to models from an artificial linear path (i.e. rotation around a single axis) between the most open and the most closed conformers. This is helpful as two conformers can have a similar rotation angle relative to the most closed conformer 1HPU_C, but are not necessarily the same. The aim of this “linear path analysis” is to describe differences between two conformers in more detail than by the calculation of rotation angles relative to only one reference conformer (Knöfel and Sträter, 2001a; Schultz-Heienbrok et al., 2004). For a given conformer, the angle χ₁ describes the inter-domain rotation angle of the most similar conformer on the linear rotation path between the open and closed states. χ₂ represents the tilt angle of the analyzed conformer to the most similar conformer on the linear path, i.e. the “deviation” of the conformer from the linear path (see Experimental procedure for further details).

The 2D–plot of the angles χ₁ and χ₂ shows that the crystallographically observed open and closed conformers each span a χ₁-range of about 10° on the linear path (Figure 4A). Furthermore, the open crystallographic conformers show a tilt angle χ₂ up to 10° whereas the closed conformations are more similar to each other with χ₂ ≤ 3°. The intermediate conformations with χ₁ ≈ 45° show the highest tilt from the linear path with χ₂ ≈ 14° which is a result from steric clashes (manuscript in preparation). The description of the conformational space of the crystal conformers is limited to a set of seven open, three intermediate and six closed conformations. To test if additional conformations improve the fit of the experimental data, further conformers were generated in silico, either by targeted MD simulation or by docking of the two domains.

Figure 4. χ₁,χ₂-plots of 5NT crystal structures, MD models and models from docking of the two domains.

χ₁ describes the domain opening angle on the 1HPU_C-1HP1-rotation. χ₂ is the tilt angle relative to the reference state. Crystal structure conformers are shown as filled circles (black) in all panels. Conformers which were found by ensemble fitting to describe the experimental DEER distance distribution with the cone model at w_E = 40 are indicated as red (apo) and blue points (ZnAMPCP) and by their model ID. In C) models from docking of the two domains were prepared with 1HPU_C (closed, light blue) and with 1HP1_A (open, light red). For definitions of the conformers in B) and C) see also Table S1, Table S2.

MD models

Figure 4B shows the χ₁,χ₂-plot of the models generated by a targeted MD simulation between the open and closed state to fill in the gaps between the crystal structures. The simulated domain rearrangement between the open and closed conformers takes a path via the crystallographically observed intermediate conformations (manuscript in preparation).

Docked models

To generate an even larger conformational diversity in the model pool, we built models with different domain orientations via a docking algorithm. About 22% of the models have a domain orientation similar to that of the crystal structures, i.e. with −5° ≤ χ₁ ≤ 105° and χ₂ ≤ 20°. The other models are according to their χ₁ values more closed or more open and/or their tilt angle from the linear path is considerably higher (χ₂ > 20°) than that of the crystal structures (Figure 4C). We found it necessary to prepare models starting from an open (1HP1_A) as well as a closed (1HPU_C) conformation as the resulting docked models cluster in distinct regions of the plot. This is likely caused by local structural differences predominantly located in the N-terminal domain of 5NT. In 1HP1_A residues 323 to 331 are not defined, in 1HPU_C they form a β-hairpin structure. Furthermore, residues of the 180s loop which is located at the domain interface undergo a conformational change between the two states (Knöfel and Sträter, 1999).

Validation of ensemble fitting and determination of the optimal ensemble size score

To evaluate the results of ensemble fitting with respect to the possibility of over-fitting, a free score S_free was introduced as a quality indicator (Figure 5A). S_free was determined by the leave-one-out approach and is the sum over six leave-one-out scores (S_LOO). Firstly, with S_free the optimal ensemble size N was evaluated. The total score T is defined by T = S + w_EE, with S being the comparison to the EPR distance distributions and E representing the ensemble size score which is given as N, the number of models in the ensemble, divided by P, the total number of models in the pool. The weighting term (w_E) serves as penalty score for N in the fitting procedure. A large number of models (i.e. allowed by a low w_E) may improve the fit to the observed distance distributions (decrease of S) but will at some point result in over-fitting (increasing S_free, Figure 5B). Indeed, for all fits with the cone model as well as with the full-atom spin label the number of models in the ensemble decreased strongly with increasing w_E (see Figure S5). However, the dependency of S and S_free on the ensemble size was found to be different for implicit (cone model) and explicit (full-atom) spin labels. For the cone model, the average of the fittings for the two data sets (apo and ZnAMPCP) with the three different pools of models showed only a small dependency of S and S_free on the ensemble size (Figure 5C, Figure S5). The best results were obtained with w_E = 40, the highest weighting term tested here. Further calculations with w_E > 40 were not employed as for the crystal structures and the MD models the ensemble size was generally already at a minimum (N=1 for the apo structure and N=2 for the AMPCP-liganded enzyme) at this penalty weight (see below). In the following, the ensembles were analyzed for the conditions that resulted in the lowest S_free values i.e. at w_E =40.

Figure 5. Determination of the optimal ensemble size by variation of the penalty factor w_E.

S_free describes the goodness of the fit to the distance distributions using a leave-one-out procedure. A) Scheme for determination of S_free. B) Expected dependency of the calculated S and S_free on the weight of the ensemble size ( w_E ). The minimum of S_free defines the optimal w_E. C) and D) Dependency of S_free on w_E for ensemble fitting with the cone model or explicit full-atom models. Each curve represents the average of the best 10% of the fits. The minimum of all curves, i.e. of the average S_free, is obtained at w_E = 40 for the cone model and w_E = 0 for the full-atom models (see also Figure S5).

Analysis of the ensemble fitting with the cone model

To describe the conformational population of 5NT in solution the six experimental distance distributions were fit based on the knowledge-based potential of the cone model (Table 1, Figure 4). Comparing the results shows that the fitting scores decreased (i.e. improve) with the inclusion of more diverse models, i.e. S(crystal structures) > S(MD models) > S(docked models), while S_free was increasing in this order (Table 1). Only for the apo data S_free(crystal structure) and S_free(MD models) were similar with S_free≈03. Thus, the inclusion of additional conformers as generated by the directed MD simulation did not improve the fits of the apo data significantly or resulted in over-fitting as in the case of the ZnAMPCP data and the docked models. From this we conclude that the crystal conformers are sufficient to describe the distance distributions based on the available data size of six distance distributions and the accuracy of the data.

Table 1.

Description of the conformational states of 5NT by ensemble fitting with different pools of models using the cone model.

Fit with crystal structures
Scores ± SD	Apo	open	int.	closed
S = 0.2911 ± 0.0000	all six	100%	0%	0%
SLOO = 0.0338 ± 0.0000	LOO 124/398	100%	0%	0%
SLOO = 0.1062 ± 0.0000	LOO 124/452	100%	0%	0%
SLOO = 0.0315 ± 0.0000	LOO 124/532	100%	0%	0%
SLOO = 0.0453 ± 0.0000	LOO 191/398	100%	0%	0%
SLOO = 0.0265 ± 0.0000	LOO 191/452	100%	0%	0%
SLOO = 0.0477 ± 0.0000	LOO 191/532	100%	0%	0%
Sfree = 0.2910 ± 0.0000	average ratio	100%	0%	0%
Scores ± SD	ZnAMPCP	open	int.	closed
S = 0.3110 ± 0.0000	all six	50%	0%	50%
SLOO = 0.0195 ± 0.0000	LOO 124/398	50%	0%	50%
SLOO = 0.0772 ± 0.0000	LOO 124/452	50%	0%	50%
SLOO = 0.0594 ± 0.0000	LOO 124/532	50%	0%	50%
SLOO = 0.0192 ± 0.0000	LOO 191/398	50%	0%	50%
SLOO = 0.0476 ± 0.0000	LOO 191/452	50%	0%	50%
SLOO = 0.0884 ± 0.0006	LOO 191/532	50%	0%	50%
Sfree = 0.3110 ± 0.0006	average ratio	50%	0%	50%

Fit with MD models		106≤χ1≤80°	80°<χ1≤65°	65°<χ1≤50°	50°<χ1≤35°	35°<χ1≤20°	20°<χ1≤0°
Scores ± SD	Apo	open	int. 1	int. 2	int. 3	int. 4	closed
S = 0.2689 ± 0.0000	all six	100%	0%	0%	0%	0%	0%
SLOO = 0.0250 ± 0.0000	LOO 124/398	100%	0%	0%	0%	0%	0%
SLOO = 0.1070 ± 0.0020	LOO 124/452	100%	0%	0%	0%	0%	0%
SLOO = 0.0268 ± 0.0000	LOO 124/532	100%	0%	0%	0%	0%	0%
SLOO = 0.0678 ± 0.0000	LOO 191/398	100%	0%	0%	0%	0%	0%
SLOO = 0.0229 ± 0.0000	LOO 191/452	100%	0%	0%	0%	0%	0%
SLOO = 0.0557 ± 0.0000	LOO 191/532	100%	0%	0%	0%	0%	0%
Sfree = 0.3052 ± 0.0020	average ratio	100% ± 0	0%	0%	0%	0%	0%
Scores ± SD	ZnAMPCP	open	int. 1	int. 2	int. 3	int. 4	closed
S = 0.2690 ± 0.0027	all six	0%	50%	0%	0%	0%	50%
SLOO = 0.0402 ± 0.0036	LOO 124/398	0%	50%	0%	0%	0%	50%
SLOO = 0.0583 ± 0.0082	LOO 124/452	0%	50%	0%	0%	0%	50%
SLOO = 0.0559 ± 0.0010	LOO 124/532	50%	0%	0%	0%	0%	50%
SLOO = 0.0445 ± 0.0024	LOO 191/398	0%	50%	0%	0%	0%	50%
SLOO = 0.0865 ± 0.0008	LOO 191/452	0%	50%	0%	0%	0%	50%
SLOO = 0.0888 ± 0.0048	LOO 191/532	50%	0%	0%	0%	0%	50%
Sfree = 0.3742 ± 0.0208	average ratio	14% ± 24%	36% ± 24%	0%	0%	0%	50% ± 0

Fit with docked mod.		χ1>105°	105≤χ1≤80°	80°<χ1≤65°	65°<χ1≤50°	50°<χ1≤35°	35°<χ1≤20°	20°<χ1≤−5°	−5°>χ1
Scores ± SD	Apo	more- open	open	int. 1	int. 2	int. 3	int. 4	Closed	more- closed
S = 0.2394 ± 0.0074	all six	50%	0%	0%	50%	0%	0%	0%	0%
SLOO = 0.0684 ± 0.0193	LOO 124/398	50%	0%	0%	50%	0%	0%	0%	0%
SLOO = 0.1017 ± 0.0345	LOO 124/452	50%	0%	0%	50%	0%	0%	0%	0%
SLOO = 0.0852 ± 0.0161	LOO 124/532	50%	0%	0%	50%	0%	0%	0%	0%
SLOO = 0.0995 ± 0.0000	LOO 191/398	100%	0%	0%	0%	0%	0%	0%	0%
SLOO = 0.1069 ± 0.0415	LOO 191/452	50%	0%	0%	50%	0%	0%	0%	0%
SLOO = 0.0335 ± 0.0092	LOO 191/532	50%	0%	0%	50%	0%	0%	0%	0%
Sfree = 0.4952 ± 0.1206	average ratio	57%±19%	0%	0%	43% ± 19%	0%	0%	0%	0%
Scores ± SD	ZnAMPCP	more- open	open	int. 1	int. 2	int. 3	int. 4	closed	more- closed
S = 0.2222 ± 0.0120	all six	25%	0%	25%	0%	25%	0%	25%	0%
SLOO = 0.0348 ± 0.0113	LOO 124/398	25%	0%	25%	0%	0%	25%	25%	0%
SLOO = 0.0841 ± 0.0170	LOO 124/452	25%	25%	0%	0%	0%	25%	25%	0%
SLOO = 0.0194 ± 0.0103	LOO 124/532	25%	25%	0%	0%	0%	25%	25%	0%
SLOO = 0.0776 ± 0.0180	LOO 191/398	0%	0%	25%	25%	25%	0%	25%	0%
SLOO = 0.1159 ± 0.0165	LOO 191/452	25%	0%	25%	0%	25%	25%	0%	0%
SLOO = 0.0880 ± 0.0244	LOO 191/532	0%	33%	0%	0%	33%	0%	0%	33%
Sfree = 0.4198 ± 0.0975	average ratio	18%±12%	12% ± 15%	14% ± 13%	4% ± 9%	15% ± 15%	14% ± 13%	18% ± 12%	5%±13%

S and S_LOO are given as average of the best 10% of the fits with their SD at w_E=40. S_free is the sum of the six S_LOO . For each pool of models the conformational population of the best fit is given (see also Table S3).

We also evaluated how well each of the 16 crystal structure conformers alone fits the experimental distance distributions (Table 2). This analysis clearly reveals that intermediate (with S>1.0) and closed conformations (with S ≈ 2) are, compared to the open conformations (with S ≈ 0.3), not appropriate to solely describe the apo data. 1OID_B exhibits the best fit (S = 0.29). This conformer was also selected in the ensemble fittings with w_E = 40 (Figure S4). The ensembles based on the MD model pool likewise consist of only one open conformer for the apo data. Thus, on the basis of the refinements against the crystal and MD conformers we conclude that the apo state comprises almost exclusively open conformations. Although intermediate conformers were observed for the docked models (∼43%) no conformation with a rotation angle χ₁ less than 50° is included in the final ensemble (Table 1). This indicates that the enzyme does not adopt the closed state to a measurable extent in the absence of substrate/inhibitor. Furthermore, as the standard deviation (SD) in the fits of the docked models are generally high and S_free indicates over-fitting, we do not consider the finding of non-open conformers as a definite indication of the existence of such states. The same is concluded for the finding of more-open conformers (χ₁ > 105°) in the final ensembles for the apo-and the ZnAMPCP data.

Table 2.

Individual fits of each of the 16 crystal structure conformers to the apo and ZnAMPCP bound states of 5NT.

crystal structure	conformation	Score apo	Score ZnAMPCP
1HP1_A	open	0.36	1.12
1USH_A	open	0.37	1.12
2USH_A	open	0.31	1.00
2USH_B	open	0.30	1.01
1OID_A	open	0.35	1.06
1OID_B	open	0.29	1.01
1OIE_A	open	0.38	1.11
1OI8_A	intermediate	1.25	0.51
1OI8_B	intermediate	1.26	0.52
4WWL_A	intermediate	1.29	0.52
1HPU_A	closed	1.97	0.90
1HPU_B	closed	1.93	0.86
1HPU_C	closed	2.02	0.96
1HPU_D	closed	1.97	0.91
1HO5_A	closed	2.03	0.97
1HO5_B	closed	1.98	0.92

Furthermore, in the fits with the crystal structures, the open model 1OID_B was found for the apo data and the open model 2USH_B for the ZnAMPCP data. However, we assume that this is no indication for different open states in the presence or absence of nucleotide as the models are exchangeable with no significantly worse S (not shown). Fitting of the apo data with the docked models at w_E = 40 yielded ensembles with at least 2 models (Figure S4). By increasing to w_E = 400 the ensemble size was reduced to one model to determine how similar the resulting docking models would be to the crystallographic open conformers if only a single conformer is available to fit the distance distributions. Out of 10 different solutions, the best fit is represented by a more-open conformation (χ₁ = 110°, χ₂ = 21.2°). But also an open conformer (χ₁ = 94°, χ₂ =2.9°) is among the best 10% of the fits which is very similar to the crystallographic open states. This finding corroborates the notion that the crystallographically observed open conformers are also present in solution. It also shows that this state can be modeled with very good accuracy based only on the docked models. We assume that the other more diverse solutions may be avoided by including more distance distributions or by a less flexible spin label. For the ZnAMPCP state, no single crystal conformer is sufficient to obtain a good fit to the experimental distance distributions (Table 2). The best score of S = 0.51 obtained for the intermediate conformer 1OI8_A is significantly worse than S = 0.31 for an ensemble of one open (2USH_B) and one closed structure (1HPU_A) after fitting with all available crystal structure conformers (Figure 4, Figure S4). Thus, the inclusion of at least two conformers in the ensemble is required for a reasonable characterization of the inhibitor-bound state. Indeed, all ensembles describing the ZnAMPCP-bound state are a mixture of different conformers. Based on the crystal conformers, a 1:1 equilibrium of open and closed conformations is observed with low SD. As the variability of the models increases with MD and docked models the resulting ensembles become more diverse and contain more intermediates (Table 1). However, the SD for the ratio of the different conformations in these ensembles is mostly relatively high and the inclusion of the more diverse models does not improve the quality of the fits but results in a significantly increased S_free for the docked models. For the refinement against the docked models the number, accuracy and independence of the six distance distributions (including influences of the spin labels on the equilibrium of states) does not allow for an unrestrained determination of an equilibrium of different domain orientations. Thus, a decrease of restraints and increase of conformational diversity (crystal conformers → MD conformers → docked conformers) results in a more diverse final ensemble and thus larger standard deviations.

Fitting of the distance distributions with explicit full-atom spin labels

In a second approach, ensemble fitting was performed with full-atom models of MTSSL attached to the crystal structure conformers instead of using the probability function of the cone model to describe the conformational space of the label. First, the optimal w_E was determined, as was done for the cone model. Ensemble fitting with the explicit spin labels showed a higher dependency on w_E and the minimum was found at w_E = 0 (Figure 5D, Figure S5). In addition, there are three major differences compared to the fits with the cone model (Table 3): 1) the optimal weighting term was w_E = 0 , leading to an increased number of conformers in the final ensemble, 2) S was lower while S_free was higher, and 3) more intermediate conformers were used to describe the ZnAMPCP state. Although exclusion of the intermediates from the initial pool results in a worse fit (S_free= (0.59 ± 0.05) compared to S_free= (0.47 ± 0.03) with intermediate conformers), Sfree is still significantly increased compared to the fits with the cone model. Thus, we do not consider this as proof for the existence of the intermediate conformations in the ZnAMPCP state.

Table 3.

Comparison of ensemble fitting of 5NT distance distributions with explicit full-atom vs. implicit (cone model) spin labels attached to the crystal conformers

Score			No. of conformers		Explicit SL
explicit SL	implicit SL	Apo	explicit SL	implicit SL	open conf.	ratio of int. conf.	closed conf.
S = 0.1966 ± 0.0023	S = 0.2911 ± 0.0000	Six distance dist.	30.0 ± 4.2	1.0 ± 0.0	100%	0%	0%
SLOO = 0.0878 ± 0.0044	SLOO = 0.0338 ± 0.0000	LOO 124/398	32.5 ± 3.9	1.0 ± 0.0	100%	0%	0%
SLOO = 0.0510 ± 0.0070	SLOO = 0.1062 ± 0.0000	LOO 124/452	24.7 ± 4.9	1.0 ± 0.0	96%	4%	0%
SLOO = 0.0935 ± 0.0101	SLOO = 0.0315 ± 0.0000	LOO 124/532	30.1 ± 4.9	1.0 ± 0.0	100%	0%	0%
SLOO = 0.1030 ± 0.0075	SLOO = 0.0453 ± 0.0000	LOO 191/398	28.1 ± 3.0	1.0 ± 0.0	100%	0%	0%
SLOO = 0.0445 ± 0.0090	SLOO = 0.0265 ± 0.0000	LOO 191/452	25.5 ± 4.5	1.0 ± 0.0	95%	5%	0%
SLOO = 0.1591 ± 0.0087	SLOO = 0.0477 ± 0.0000	LOO 191/532	37.2 ± 5.8	1.0 ± 0.0	91%	9%	0%
Sfree = 0.5389 ± 0.0467	Sfree = 0.2910 ± 0.0000	average	29.7 ± 4.5	1.0 ± 0.0	97% ± 4%	3% ± 4%	0%
explicit SL	implicit SL	ZnAMPCP	explicit SL	implicit SL	open conf.	int. conf.	closed conf.
S = 0.1898 ± 0.0031	S = 0.3110 ± 0.0000	Six distance dist.	46.5 ± 4.2	3.4 ± 1.0	48%	32%	20%
SLOO = 0.0950 ± 0.0066	SLOO = 0.0195 ± 0.0000	LOO 124/398	44.6 ± 3.9	2.0 ± 0.0	45%	34%	20%
SLOO = 0.0618 ± 0.0039	SLOO = 0.0772 ± 0.0000	LOO 124/452	46.6 ± 6.6	2.0 ± 0.0	53%	29%	18%
SLOO = 0.1356 ± 0.0051	SLOO = 0.0594 ± 0.0000	LOO 124/532	59.7 ± 3.6	3.2 ± 1.0	53%	29%	18%
SLOO = 0.0394 ± 0.0032	SLOO = 0.0192 ± 0.0000	LOO 191/398	44.4 ± 7.5	2.0 ± 0.0	44%	40%	17%
SLOO = 0.0.093 ± 0.0092	SLOO = 0.0476 ± 0.0000	LOO 191/452	44.2 ± 4.9	2.0 ± 0.0	44%	37%	19%
SLOO = 0.0459 ± 0.0034	SLOO = 0.0884 ± 0.0006	LOO 191/532	48.2 ± 7.4	2.4 ± 0.8	51%	31%	18%
Sfree = 0.4707 ± 0.0314	Sfree = 0.3110 ± 0.0006	average	47.7 ± 5.4	2.4 ± 0.8	48% ± 4%	33% ± 4%	19% ± 1%

Results were obtained at w_E = 0 (explicit) and w_E = 40 (implicit). Given is the average S and S_LOO as well as the average number of models of the best 10% of the fits with their SD. The last column shows the conformational composition of the ensemble after fitting with explicit full-atom spin labels for the best fit.

Overall the cone model appears better suited for regularizing the fitting protocol to prevent over-fitting.

Evaluation of the labeling sites

S_LOO allows for an evaluation of the contribution of each distance distribution to the overall fit (Table 1, Table 3). It may reveal if a variant was not perfectly chosen by displaying a higher S_LOO compared to the other variants. Only the mutant 124/452 showed increased S_LOO -values for some fits (compare Table 1). A reason may be the higher mobility of the spin label probe as residue 452 is located in a flexible region and not in a secondary structure element. This is also reflected in increased residual B-factors relative to the domains (data not shown). On the other hand, 124/452 is not an outlier in all fits (compare also Table 3) and the ensembles selected in the LOO-calculations are mostly very similar (Table S3). This indicates the significance of the fits and the absence of over-fitting. Additionally, as described above the CW-EPR data (Figure S2) do not point to increased spin label flexibility and any serious problems with any of the mutants. Thus, all mutants contribute with their EPR distance distributions to the differentiation between apo and bound states.

Discussion

The conformational switch in 5NT catalysis

In the present study we demonstrate the use of distance distributions from SDSL-EPR spectroscopy to study the conformational population of the domain orientations of 5NT in solution via an ensemble fitting approach. In the apo-state, 5NT is present in open conformations. Then, the enzyme’s active site is accessible for substrate binding - the molecules are in a “ready to go”-conformation. In the presence of the inhibitor AMPCP, a mixture of different conformations is observed. About half of the enzyme is in the closed state and half in the open state. The non-hydrolyzable ADP substrate analog binds with its base to the C-terminal domain and with the phosphonate groups to the metal ion and the side chains of the N-terminal domain. Thus, the conformational change is caused by these interactions stabilizing predominantly the closed state, presumably via conformational selection. However, the present data cannot exclude that AMPCP binding contributes kinetic induced fit effects to enable the closure motion. The fact that the closed state of the enzyme could be observed in previous crystal structures in the absence of bound inhibitors (Knöfel and Sträter, 2001b) indicates that a small percentage also of the unliganded enzyme exists in the closed state. This percentage is below the detection limit achieved in this work. Furthermore, we could not find any definite indication of the existence of intermediate conformers in the apo or the ZnAMPCP bound states as the sampling of intermediate structures was always accompanied by high SD which indicated over-fitting.

Comparison of explicit vs. implicit spin labels in context of previous approaches to reproduce DEER distance distributions

Since the establishment of the four-pulsed EPR method to a more widespread application (Jeschke, 2002), it has been a major aim to describe and understand the flexibility of the MTS spin label in relation to the observed distance distributions to draw conclusions back to protein structure and dynamics. While there is only a limited number of experimentally determined spin label conformations, the conformational space accessible due to the five rotatable bonds is considerably large. To predict the flexibility and orientation of the spin label different attempts were made. This includes: a tether-in-a-cone model to produce distributions of interelectron distances in context of CW-EPR spectra (Hustedt et al., 2006), Monte Carlo conformational searching of docked spin labels in combination with MD simulations (Sale et al., 2002; Sale et al., 2005), systematic studies to ensembles of rotamers (Guo et al., 2007; Guo et al., 2008) and usage of rotamer libraries as in MMM (Polyhach et al., 2011), the PRONOX algorithm (Hatmal et al., 2012), analysis of spin label rotamers by mtsslWizard (Hagelueken et al., 2012), the restrained ensemble molecular dynamics simulation methodology (Islam et al., 2013; Roux and Islam, 2013), the knowledge-based potential of the cone model (which together with Rosetta was employed for de novo structure calculations) (Alexander et al., 2008; Hirst et al., 2011) or full-atom representations from RosettaEPR (Alexander et al., 2013; Alexander et al., 2014). In a recent study, the latter two models were compared and distance distributions were more accurately described with full-atom spin labels (Alexander et al., 2013). In addition, ensemble fitting has also been used in previous studies to characterize flexible inter-domain orientations in solution via DEER. For the Gi-protein it was shown, that the rigid-body movement of the helical domain relative to the rest of the protein increases significantly in the rhodopsin-bound state compared to the basal state (Alexander et al., 2014). Nine models were generated via rigid-body docking and ensemble fitting to describe the inter-domain mobility, which however features a less dramatic domain opening compared with the β2 adrenergic receptor-Gs crystal structure (Rasmussen et al., 2011).

In the current work, the full-atom spin label representation is better able to reproduce the experimental distance distributions, as described by S , than the cone model. However, the improvement comes at the cost of over-fitting the data. Possibly, the implicit ensemble of spin label conformations provided by the cone model prevents specific conformations of the spin label from creating well matching distances from a structure that is unknowably a sub-optimal selection overall, as could occur in the case of the explicit full-atom spin label fitting and would result in better S and worse S _free as observed.

Methodological implications and limitations

In general, the preciseness of fits to the experimental distance distributions is limited by the following factors. As described, the conformational flexibility of the spin label results in a broadening of the distance peaks. Even more problematic are effects of the local environment of the spin label that limit its flexibility. This could result in a systematically shorter or longer distance distribution compared to the cone-model that assumes a free flexibility. However, the data did not indicate such a scenario, and the use of explicit full-atom models of the spin label would result in better fitting results if the spin label motion was highly restricted.

In addition, analyzing the primary DEER data is associated with deviations in the height and positions of the peaks in the distance distribution. A further potential source of systematic errors is the influence of the spin labels on the conformational equilibrium itself. Although the specific activities of the labeled 5NT variants were comparable to the wild-type enzyme, it cannot be ruled out that the spin labels change the population of the different states compared to the wild-type enzyme. Still, the comparison of the calculated and observed distance distributions (Figure S4) indicates no large outliers among the six variants.

By the introduction of S_free it was possible to estimate the degree of over-fitting of the data. However, the significance of S_free is affected by the limited number of data points (distance distributions). Furthermore, the data points are not completely independent as each distance distributions shares one of the two label positions with another data point. If this label position influences the conformational equilibrium, the over-fitting contribution of one variant with this label position will also lower S _free since the label position is present in a second distance distribution.

We could show that it is possible to characterize the equilibrium of the three basic states (open, intermediate and closed) with six distance distributions and the influence of a substrate analog on this equilibrium. For the characterization of smaller conformational changes within the open or closed states or for a characterization of the structures without the restraints from the crystal structures (i.e. starting from the docked conformers), more distance distributions would be necessary. Model calculations are required to help to define the influence of the number of distance distributions, errors in the accuracy of the distributions and outliers (influence of the spin label on the equilibrium) on the behavior of the ensemble fits.

In summary, we presented a new approach to characterize a conformational equilibrium of a domain motion in solution by combination of EPR spectroscopy, X-ray crystal structures and computational analysis in form of the ensemble fitting. 5NT is an attractive model system to further establish and evaluate this methodology, which is particularly attractive for larger or complex systems to study structures and conformational switches of large molecular assemblies.

Experimental Procedures

Choice of spin label sites for EPR distance distribution measurements

The double cysteine mutants for SDSL-EPR distance measurements were designed to probe structure and dynamics along maximally independent distance vectors within the known open and closed state structures in order to yield optimal information on the three-dimensional inter-domain orientations. For determination of appropriate positions, the structure of PDB-ID 1HP1 was chosen as the open conformer, and 1HO5 (chain A) as the closed state. The following criteria were applied to all pairs of labeling sites selected:

• 1)C_β distances in the open and closed state needed to be between 15 and 50 Å which is the optimal range for DEER experiments thereby maximizing the accuracy of the experimental distance distributions,
• 2)the mutated residue must not be proline or cysteine (read below) to avoid disruption of the backbone conformation or an increase of flexibility of the protein,
• 3)the label must be located in an exposed position to avoid disruption of the backbone conformation of the protein,
• 4)the label should preferentially be located within a secondary structure element to minimize dynamics from conformational changes in loop regions which was not a focus of the present study,
• 5)the distance change from the open to the closed conformation was maximized in order to increase the usefulness of the experiment to monitor the conformational change,
• 6)labeling sites were reused as much as possible to limit the number of mutants that had to be created and tested,
• 7)and at the same time no two spin label pairs must connect the same two regions of the protein to avoid redundancy in the experimental setup.

Our protocol to achieve conditions 1–7 was as follows: First, all pairs of sites that fulfill criteria 1–4 were collected in a list. Next, the list was sorted by expected change in distance (criterion 5) and the top residue pair was chosen as the first double mutant. For the second distance, the list was pruned by removing pairs that did not contain one of the original labeling sites (criterion 6) and for pairs that link similar regions (criterion 7). Spin label pairs were defined as linking similar regions if the respective pairs of C_β atoms were both closer than 15 Å. From the remaining pairs of residues the one with the largest distance change was selected. This procedure was repeated until the list was empty.

An initial set of double mutants was selected and prepared. However, mutants with spin labels attached to L123C or A449C resulted in up to 80% reduced specific enzymatic activity and reduced flexibility of the spin label side chains as observed in CW-EPR experiments (data not shown). Therefore these spin label positions were excluded. The final set consisted of the six mutants T124C/G398C, T124C/Q452C, T124C/K532C, K191C/G398C, K191C/Q452C and K191C/K532C. 5NT contains a natural disulfide C258/C275 which was also present in all EPR spin label mutants. A control experiment via labeling of the wild-type enzyme showed that the background labeling of the natural disulfide C258/C275 was less than 1% and thereby not disturbing the experiments.

Preparation of MTSSL labeled 5NT mutants

The six 5NT variants each containing two additional cysteines were labeled with MTSSL. The experimental procedure is detailed in the supplement. Briefly, after expression in E. coli and chromatographic purification (Schultz-Heienbrok et al., 2004; Krug et al., 2013), a tenfold excess of MTSSL over protein was added in two steps with incubation at room temperature and 4°C. Unreacted spin label was removed by a desalting column.

Data acquisition of EPR distance distributions

CW-EPR experiments were carried out on a Bruker EMX spectrometer using a 10 mW microwave power level and a modulation amplitude of 1.6 G. DEER spectroscopy was performed on a Bruker 580 pulsed EPR spectrometer operating at Q-band frequency (33.9 GHz) with a standard four-pulse protocol at 83 K (Jeschke, 2002). Data were processed in DeerAnalysis 2011 (Jeschke et al., 2006) with Tikhonov regularization and L-curve determination of the optimal regularization parameter (Chiang et al., 2005). For 5NT sample details see supplemental experimental procedures.

Simulation of EPR distance distributions with rotamer library

A rotamer library approach as implemented in the software MMM was used to predict the conformational space of the MTSSL (Polyhach et al., 2011). Based on these spin label rotamers theoretical DEER distance distributions and expected mean distances between the MTSSL sites were predicted and compared to the experimentally obtained 5NT distance distributions.

Characterization of the inter-domain orientation

5NT conformations were characterized by a comparison to models generated along an ideal linear rotational path (i.e. rotation around a single axis) between the most open (1HP1_A, χ₁ = 97°) and the most closed conformer (1HPU_C, χ₁ = 0°). These artificial models were generated in steps of 1° rotation for a range of χ₁ from −50° to 200°. To characterize the conformational state of a given conformer relative to 1HPU_C, the conformer was superposed onto each conformer of the linear path by aligning first the N-terminal and then the C-terminal domains with the program LSQKAB (Kabsch, 1976). Thereby, a tilt angle χ₂ to each of the linear path models was calculated. Each conformer is thus finally characterized by the domain opening angle χ₁ of the closest reference state on the 1HPU_C-1HP1_A rotation and a tilt angle χ₂, which describes the deviation from the reference state (as an interdomain rotation angle). A χ₂ of 0° indicates a conformer on the 1HPU_C – 1HP1_A rotational path.

Conformers from the crystal structures

Eight crystal forms provided 16 independent 5NT conformers: PDB IDs 1USH, 2USH, 1HP1, 1OID, 1OIE, 1OI8, 1HO5, 1HPU, 4WWL (Knöfel and Sträter, 1999, 2001b, 2001a; Schultz-Heienbrok et al., 2004). They are indicated by their PDB-ID and the respective protein chain (e.g., conformer 1HPU_C is chain C of 1HPU).

Conformers from a targeted Molecular Dynamics simulation

300 conformers were taken from a targeted Molecular Dynamics (MD) simulation between the open (1USH_A) and closed form of 5NT (1HPU_D) (manuscript in preparation). The simulation results in a closure motion that runs via the crystallographically observed intermediate states.

Conformers from domain docking

Further models were created by docking of the domain structures, either from the most open (1HP1_A) or from the most closed crystallographic conformer (1HPU_C). Residues 26–353 and 363–550 were used for the N- and C-terminal domains, respectively. Docking was carried out with the Biochemical Library (BCL) using a protocol adapted from protein folding (Karakas et al., 2012) and allowed the domains to move as rigid-bodies relative to one another. The linker helix of residues 354 to 362 was omitted, but a loop score (Woetzel et al., 2012) was employed in order to ensure the domains remained within biologically probable orientations of one another during docking.

Preparation of full-atom spin label models

Fifty independent structure relaxation trajectories were conducted for each of the sixteen crystal structures using the Rosetta relaxation protocol (Bradley et al., 2005). Next, a full-atom representation of MTSSL was attached to 5NT at residue sites 124, 191, 398, 452 and 532 of the 800 different relaxed conformers (Alexander et al., 2013). The Rosetta fixed backbone design protocol was used to perform the residue mutations and to optimize conformations of all side chains in the structure (Kuhlman et al., 2003).

Ensemble fitting of protein models to EPR distance distributions

A Monte Carlo procedure was used to find the ensemble of protein models that reproduces best the experimentally measured EPR distance distributions. The models were selected from three different pools of structures: (i) the experimental crystal structures, (ii) from a targeted MD simulation between the open and closed form and (iii) from domain docking. Several copies of these conformers served as candidate pool with 1500 to 3000 protein models. The ensemble was selected from this pool. One protein model could be used several times in the final ensemble to represent an increased probability for that state.

The agreement of the ensemble with an individual EPR distance distribution is calculated based on the cumulative Euclidian distance (Kamarainen et al., 2003):

$$d=\sqrt{\frac{\sum _{b=0}^{B-1}{(\sum _{j=0}^b{\mathit{\text{Ensemble}}}_j-\sum _{j=0}^b{\mathit{\text{EPR}}}_j)}^2}{B}}.$$

Here, B is the number of bins in the histograms describing the probability distributions for a given distance; Ensemble_j and EPR_j are the distance probabilities at bins j of the model ensemble and EPR distance distribution histograms, respectively. The cumulative Euclidian distance is normalized to the number of bins, and all distance distributions were scored across a range from 0 to 90 Å.

For each EPR distance measured, a distance probability histogram for the ensemble of models is derived by implicitly representing the spin label in the protein models. For each model in the ensemble, the distance between the corresponding C_β atoms is converted into a probability distribution of likely spin label distances using the cone model and statistics previously described (Hirst et al., 2011). The ensemble distribution for a given distance is then the sum of the individual model probability distributions and corresponds to Ensemble from above. This procedure allows ensemble and EPR distances to be directly compared, since both will now correspond to spin label distances. When models with explicit spin labels are used, an ensemble’s distribution for a given distance is directly calculated from the distances between spin labels within the structures of the ensemble. The score of the ensemble compared with all the EPR distances is the summation of d for each EPR measurement, $S=\sum _{i}d$

An additional scoring term selects for small ensemble sizes. This ensures that only protein conformations critical to reproducing the experimental measurements are included in the ensemble. The ensemble size score is calculated as, $E=\frac{N}{P}$, where N is the number of models in the ensemble and P is the constant total number of models in the candidate pool of models.

The total score of the ensemble T =S+w_EE is calculated at each Monte Carlo step and determines whether an ensemble change will be accepted or rejected. The constant w_E is the weight of the size score. The smaller the total ensemble score T , the more accurately the ensemble reproduced all of the EPR measurements.

The ensemble was built-up from an initial size of between 100 and 105 models using three possible changes to the ensemble: a) adding a protein model from the pool to the current ensemble; b) removing a protein model from the current ensemble; c) swapping a protein model between the model pool and the current ensemble. At each Monte Carlo step, a change is applied and either accepted, if the move causes the ensemble to better reproduce the EPR distance distributions (reduced T ), or rejected otherwise.

A relative improvement I was calculated after each move as $I=\frac{(T_{\mathit{\text{old}}}-T_{\mathit{\text{new}}})}{T_{\mathit{\text{new}}}}$ .If a move is rejected, I is zero as T did not change. If the move is accepted I gives the fraction of the improvement relative to the new score as a positive number as T_old >T_new . The Monte Carlo procedure terminated after T did not improve by 0.01 within 1000 steps.

Leave-one-out validation score

To assess the degree of over-fitting a leave-one-out score (S_LOO ) was introduced. For this a leave-one-out-ensemble was determined by ensemble fitting against (i −1) distance distributions, i.e. against five of the six distance distributions. Then, S_LOO for the sixth (i.e. the left-out) distance distribution was determined by assessing the fit of the ensemble to the left-out distance distribution. This score describes the agreement with the distance distribution that was not used in fitting and is thus free from over-fitting to this distance distribution. A ‘free’ score value is calculated as $S_{\mathit{\text{free}}}=\sum _i{S}_{\mathit{\text{LOO}}}$ (Figure 5A).

Highlights.

• -Almost isoenergetic states of a domain motion can be characterized by EPR
• -X-ray structures are combined with spectroscopic data by ensemble fitting
• -A quantitative characterization of the equilibrium can be obtained
• -Substrate binding changes the equilibrium from the open to open and closed states

Abbreviations

5NT

E. coli 5’-nucleotidase

AMPCP

α,β-methylene-ADP

CW-EPR

continuous wave-EPR

DEER

double electron-electron resonance

EPR

electron paramagnetic resonance

MD

molecular dynamics

MTSSL

methanethiosulfonate spin label

SD

standard deviation

SDSL

site-directed spin-labeling

ZnAMPCP

inhibitor-bound state in presence of Zn²⁺