Relating microstructure to rheology of a bundled and cross-linked F-actin network in vitro

Abstract

The organization of individual actin filaments into higher-order structures is controlled by actin-binding proteins (ABPs). Although the biological significance of the ABPs is well documented, little is known about how bundling and cross-linking quantitatively affect the microstructure and mechanical properties of actin networks. Here we quantify the effect of the ABP scruin on actin networks by using imaging techniques, cosedimentation assays, multiparticle tracking, and bulk rheology. We show how the structure of the actin network is modified as the scruin concentration is varied, and we correlate these structural changes to variations in the resultant network elasticity.

F-actin is one of the most important participants in maintaining the mechanical integrity of eukaryotic cells. In vivo, actin filaments rarely exist as isolated single filaments but instead associate into bundles or networks, in concert with >60 different actin binding proteins (ABPs), to influence cell shape, division, adhesion, and motility (1–4). The elastic modulus of cytoplasmic actin gels is estimated to be of order 100–1,000 Pa (5), and the gel must be able to sustain shear stresses of up to 1,000 Pa for proper cell functions (6). This large elasticity cannot result exclusively from a network of actin alone; in vitro, solutions of entangled actin filaments are weak elastic solids. For example, a solution of actin filaments at a concentration of 24 μM has an elastic modulus of only 0.1 Pa and breaks under a shear stress of <0.1 Pa (7, 8). Therefore, the properties of the actin cytoskeleton must be regulated predominantly by ABPs. Modest changes in the concentration of ABPs can significantly modify the structure of the network because they can both bundle and cross-link the actin filaments. These structural changes can lead to concomitant change in the mechanical properties, dramatically enhancing the mechanical rigidity (9–13). The changes in structure occur over a large range of length scales, ranging from a few nanometers, the size of an ABP, to several micrometers, the length of an individual actin filament. The dearth of techniques that probe the structure and properties over this range of length scales has limited our ability to determine the modifications caused by the ABPs and to identify their critical contributions. As a result, a quantitative understanding of how the changes in mechanical stiffness are correlated with structure remains elusive.

In this study, we probe the changes in structure and mechanical properties of a F-actin network as a function of ABP concentration. We use electron microscopy (EM) to measure structural changes on the nanometer scale and confocal microscopy to measure structural changes on the micrometer scale. We exploit the technique of multiparticle tracking (MPT), by using small nonbinding particles to directly probe the variations in mesh size with changing ABP concentration, and compare the results with the analysis of images obtained with confocal microscopy. Moreover, we employ MPT to probe the local mechanical response by using particles that bind to the network, and we correlate this with measurements of the bulk rheological properties. We thereby demonstrate the versatility of the MPT technique in providing the local structural and mechanical information, provided the data are interpreted with care, and we use the MPT results to probe the properties of cross-linked actin networks. By comparing our data to predictions of a theoretical model, we show that the linear elasticity of the composite network directly reflects the properties of individual actin filaments or bundles.

We use the ABP scruin, which simultaneously bundles and cross-links the actin filaments. In vivo, scruin locks >80 actin filaments to form an ordered crystalline bundle that functions as a mechanical spring in the acrosomal process in the sperm of Limulus polyphemus (horseshoe crab) (14, 15). EM-derived structure shows that this acrosome bundle is an extensively cross-linked composite of actin filaments where scruin–calmodulin heterodimers are bound to every actin subunit with its stoichiometric ratio of 1:1 (scruin:actin) (16, 17). Scruin binds pairs of adjacent actin subunits in the same filament (16); scruin makes a variety of contacts with neighboring scruin molecules on different filaments to form a tight crystalline bundle. The Young's modulus, E, of a scruin-mediated actin bundle in vivo is similar to that of single actin filament, implying that scruin bonding is stiffer than actin (18).

In contrast, actin filaments polymerized in the presence of scruin in vitro form an isotropic, disordered 3D network of rigidly bundled and cross-linked F-actin. The scruin cross-links are both rigid and irreversible; as a result, the compliance of the network is completely determined by that of the actin filaments, unlike other cross-linking proteins, such as filamin or α-actinin (11). Thus, the actin–scruin composite network is an excellent model system with which to study the physics of cross-linked semiflexible polymer networks and the complex relationship between the microstructure and the macroscopic mechanical properties.

Materials and Methods

Protein Preparation. Actin. G-actin solutions were prepared by dissolving lyophilized G-actin in deionized water and dialyzing the solutions against fresh G-buffer (2 mM Tris·HCl/0.2 mM ATP/0.2 mM CaCl₂/0.2 mM DTT/0.005% NaN₃, pH 8.0) at 4°C for 24 hr; the buffer was replaced with fresh G-buffer every 8 hr. Solutions of G-actin were kept at 4°C and used within 7 days of preparation. Actin polymerization was initiated by adding F-buffer (2 mM Tris·HCl/2 mM MgCl₂/100 mM KCl/0.2 mM DTT/0.2 mM CaCl₂/0.5 mM ATP, pH 7.5) and mixing gently. Scruin. Scruin was purified from the acrosomal process of Limulus sperm by following the protocol published by Sun et al. (19). In the presence of high calcium, a bundle of actin filaments cross-linked by scruin–calmodulin heterodimers (hereafter referred to simply as scruin) extends from the head of the sperm to form a 60-μm-long finger of membrane called the acrosomal process. The extended acrosome bundles were sheared from the cell body and then separated from the nuclei and flagella by centrifugation. The membrane surrounding the acrosome was removed with a mild detergent, HECAMEG (38 mM methyl-6-O-(N-heptylcarbamoyl)-β-d-glucopyranoside). Scruin was solubilized from the bundle by addition of 1 M CaCl₂ and purified further by filtrations through a series that comprised a size exclusion column (AcA4), ion exchange column (MonoQ), and another size exclusion column (Superose 12). Fractions containing scruin were run on a SDS/PAGE (with a 3% stacking gel and a 12% resolving gel) to select the fraction of the best quality. The purified samples were stable at 4°C for ≈2 weeks. Before experiments, scruin was clarified by being spun at 90,000 × g for 20 min, and its integrity was checked with SDS/PAGE. Protein concentrations were determined either by the Bradford assay (with BSA as a standard) or by absorbance at 280 nm with an extinction coefficient of 1.68 × 10⁵ M^-1·cm^-1.

MPT. Micrometer-sized tracer particles were added to the solution of G-buffer, F-buffer, and scruin. Immediately after addition of G-actin, the solution was gently mixed and transferred into a 5 mm × 10 mm × 1 mm glass chamber. The chamber was sealed with high-vacuum grease to prevent evaporation, and the sample was equilibrated for 1 hr at 25°C. We imaged ≈100 spheres per field-of-view with bright field optics on an inverted microscope and recorded their dynamics at 30 frames per second by using a CCD camera with a shutter speed of 0.5 ms (20, 21). Particle centers were detected in each frame to a resolution of ≈20 nm, and the time evolution of each particle position was determined (22). To avoid wall effects, we imaged 100 μm into the sample. The particles remained in the field-of-view for at least 90 s, and we calculated the mean-squared displacement (MSD) 〈Δx ²(τ)〉 (23) of the individual particles undergoing thermal motions. Several thousand frames were captured, ensuring good statistical accuracy for time scales up to 100× the frame rate.

Thermally driven dynamics of the embedded particles depend sensitively both on the microstructure and the nature of the coupling between the particles and the network. When the particle radius, a, is significantly larger than the average mesh size of the network, ξ, or when the particles are chemically bound to the network, the particle motion probes the local mechanical response (24). In this case, MSD of individual particles in the field can be related to the frequency-dependent linear moduli by using a generalized Stokes–Einstein relation to extract frequency-dependent elastic and loss moduli; this technique is known as one-particle (1-P) microrheology (25, 26). In cases in which the particle size is much larger than all structural length scales, 1-P microrheology correctly captures bulk mechanical response. However, in materials with structural length scales similar to that of the particle size, the response probed by individual particles may not correspond to the bulk mechanical properties (27). To circumvent this problem, we examined the correlated motions of pairs of particles to examine only the stress fluctuations that propagate at large length scales; this technique is known as two-particle (2-P) microrheology (20), and it correctly probes bulk mechanical properties.

As the embedded particle radius approaches the typical mesh size of the material, ξ ∼ a, the thermal motion of the particles can be used to probe the local microstructure, assuming that the particles are not chemically bound to the network (23, 27–29). The particles explore the local structure diffusively at short time scales, whereas the steric and elastic constraints imposed by the network affect the dynamics of the network at longer time scales; thus, a plateau in the MSD of individual particles should reveal the local pore size, 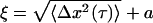for large τ (23).

In this study, we used 1-μm-diameter particles coated with either polyethylene glycol (PEG) or BSA to elucidate both the network microstructure and the local elasticity by using MPT. The PEG coating prevents scruin adsorption on the particles, enabling them to probe the changes in network microstructure (28). Although the BSA-coating is generally known to reduce the adsorption of some proteins to colloidal surfaces, scruin has been shown to readily bind to the BSA-coated particles (28), making the particles adhere to the bundles. The bound particles are sensitive to the changes in local rigidity and thus can be used as a probe to measure the elasticity of the bundled network. Thus, we used the PEG-coated particles to probe the microstructure of the network and the BSA-coated particles to probe the mechanical response, using both 1-P and 2-P microrheology.

Bulk Rheology. The bulk mechanical response of the networks was measured with a stress-controlled rheometer (CVOR, Bohlin Instruments, Malvern, U.K.) with a 40-mm parallel plate geometry and gap of 140 μm. The maximum applied strain, γ, was maintained at sufficiently low values, typically <0.02 to ensure that the measurements were in the linear elastic regime. We measured the frequency-dependent elastic modulus, G′ (ω), and loss modulus, G″ (ω), in the frequency range of ω = 0.06 - 30 rad/s. Within this range, the mechanical response of all networks is dominated by a frequency-independent elastic modulus, G′ (ω) = G_o. Additionally, we probed the elastic response as a function of strain, γ, at a fixed frequency ω = 1 rad/s, to determine the range of the linear response by determining γ_crit, the strain at which the mechanical response becomes nonlinear.

Confocal Fluorescence Microscopy. Confocal fluorescence microscopy was used to visualize the structure of the bundled and cross-linked F-actin network and to obtain ξ independently of the MPT method. We deposited a 3-μl drop of 6.6 μM Texas red phalloidin (catalog no. T7471, Molecular Probes) in methanol on a no. 1.5 glass-bottomed chamber (catalog no. P35G-1.5–14-C, Mat-Tek, Ashland, MA), and allowed it to dry at least for 1 hr. The polymerization was initiated by adding F-buffer to actin–scruin mixtures, and the samples were immediately loaded on top of the dried Texas red dye such that the final ratio of the dye to the sample was 1:200 (vol/vol). The sample was then enclosed by placing a coverslip over a spacer, a thick layer of vacuum grease laid around the sample. The actin–scruin mixture was allowed to polymerize for 1 hr at room temperature (≈25°C) and was examined with a Zeiss LSM 510-Meta confocal microscope. Laser excitation at λ = 543 nm was used with a LP 560 filter and HFT 488/543 beam splitters. For 3D imaging, a stack of 20–100 frames was collected with an interval of 100 nm between adjacent slices. Fluorescent images were deconvolved with huygens professional software (Scientific Volume Imaging, Hilversum, The Netherlands) and the images are assembled to obtain a 3D projection by using imaris software (Bitplane, Zurich). The mesh size was determined by measuring the peak-to-peak distance in the intensity profile obtained across fluorescent images.

EM. A 10-μl mixture of actin–scruin, polymerized at room temperature for 1 hr, was transferred to 400-mesh, carboncoated nickel grids (EM Science). After waiting for 30 s, the samples were negatively stained with 1% uranyl acetate by passing drops of freshly prepared uranyl acetate solution across the grid. The stained grids were air-dried and examined with a Philips EM410 transmission electron microscope. The negatives were scanned to digital images in tagged image file format (TIFF) and the thicknesses of the bundles were measured with openlab software (Improvision, Lexington, MA).

Cosedimentation Assays. Binding and polymerization assay. Cosedimentation assays were performed at high speed to check the degree of F-actin polymerization and scruin binding. Mixtures of actin and scruin at various concentrations were incubated for 1 hr at 25°C and then centrifuged at 200,000 × g for 30 min at 4°C in a TLA100 rotor (Beckman Coulter). A sample of 11.9 μM actin was also polymerized and ultracentrifuged as a control. The pellets were resuspended in 1× F-buffer. Both supernatants and pellets were run on a SDS/polyacrylamide gel (3% stacking and 12% resolving), and the gel was stained with 0.2% Coomassie brilliant blue R-250 to visualize the protein bands in the gel. Bundling assay. The assay for bundling was virtually identical to the binding assay, except that low speed sedimentation was used. Typically, bundles sediment at 10,000 × g in 15 min, but because almost no F-actin sediment at this speed, it is important to include a control sample of F-actin only. After a 1-hr incubation at room temperature, 50 μl of actin–scruin mixture was spun at 12,000 × g for 15 min with a table-top centrifuge (Model 3200, Eppendorf). The supernatant is carefully pipetted out of the tube and any remaining supernatant was removed by inverting the tube and letting the liquid drain. The pellet was the resuspended in F-buffer. Both supernatants and resuspended pellets were analyzed by SDS/PAGE.

Results

In this study, we made direct measurements of the network microstructure with confocal microscopy, EM, and MPT. To characterize the structure, we determined that the distribution of pore sizes and bundle thicknesses as the ratio of scruin to actin concentration, R = c_S/c_A, is varied. Cosedimentation assays at both high and low speed were performed to confirm that the addition of scruin had no effect on the actin filament density but only enhanced the bundling of filaments. We measured the network elasticity with MPT and bulk rheology. We compared our results to the predictions of a model of entropic elasticity for semiflexible polymer networks, and we showed that the bulk properties of the network were directly related to the properties of individual bundles and filaments at the length of the mesh size.

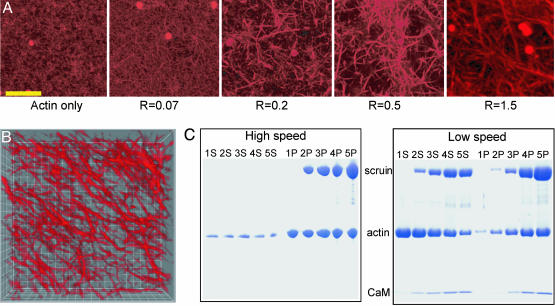
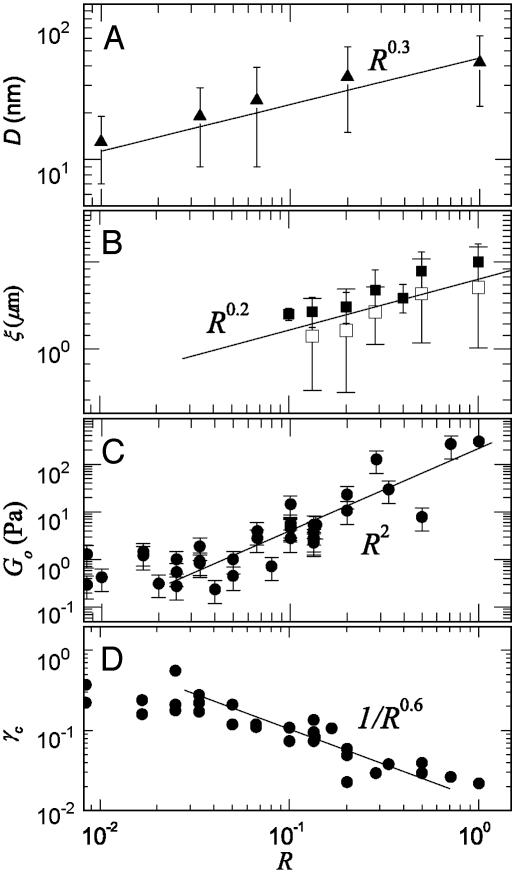
Evolution of Pore Structure. Confocal fluorescence microscopy with the labeled actin indicates that when scruin is added, actin filaments form bundles whose thickness increases with increasing concentration of scruin as shown in Fig. 1A; simultaneously, the pore size of the network becomes larger. The high-speed cosedimentation assay results confirm that the majority of actin was polymerized and that the degree of actin polymerization was independent of the presence of scruin, and the actin filament density in the network remained constant, regardless of the amount of scruin in the sample (Fig. 1C). This observation is in contrast with other ABPs, such as profilin, which control actin assembly by altering the concentration of G-actin at which polymerization to F-actin is initiated (30, 31). Moreover, all of the scruin cosedimented with F-actin, suggesting that scruin has a high affinity for filamentous actin. The low-speed cosedimentation assay results characterize the amount of scruin in the pelleted bundle and indicate that more filaments form bundles as the concentration of scruin is increased (Fig. 1C). However, this assay is not able to differentiate between the effects of bundle thickening and the increase in number of bundles. Instead, we used confocal imaging to show that the number of single filaments decreases, whereas the bundles thicken with increasing scruin concentration. At a low concentration of scruin (low R), it is more probable to form random crossover points between two filaments, leading to small loose bundles with irregularity in their structure as evidenced in EM images. As R is increased, more tightly bound individual bundles become visible in an otherwise largely homogeneous network of actin filaments; beyond a critical R, the bundles themselves become cross-linked by means of a variety of scruin–scruin interactions. The bundle thickness, D_B, at various R is visualized by transmission EM of negatively stained bundles of actin (Fig. 2A), and we find D_B/D₀ ∼ R^x, where x = 0.3 (Fig. 3A) and D₀ is the diameter of a single actin filament.

Fig. 1.

Changes in the degree of bundling at various R values. (A) Confocal images of an F-actin:scruin network at various R values. The rightmost image is an assembled 3D projection of 50 images with 100-nm intervals. (Scale bar, 10 μm.) (B) Three-dimensional deconvolved image of a 1:2 (scruin:actin) network. Each grid measures 1 μm. (C) Scanned image of a SDS/polyacrylamide gel. The sample numbers, 1, 2, 3, 4, and 5, correspond to R = 0, 0.07, 0.2, 0.5, and 1, respectively, at a fixed c_A = 11.9 μM. S, supernatant after centrifugation; P, pellet after centrifugation. High-speed cosedimentation assay data shows that the F-actin density is unaffected by the presence of scruin and that all of scruin binds to F-actin. Low-speed assay data shows the degree of bundling; although all scruin binds to F-actin, not all of the scruin-decorated F-actins assemble into thick bundles. CaM, calmodulin.

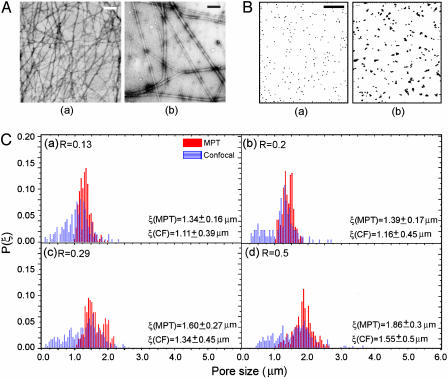
Fig. 2.

Characterization of the bundle thickness, D_B, and pore size, ξ, distribution at various R values. (A) EM images of the actin-only (a) and R = 1(b) samples. (Scale bar, 200 nm.) (B) Two-dimensional map of the particle trajectories to demonstrate ξ and the degree of heterogeneity at R = 0.03 (a) and R = 1(b). (Scale bar, 1 μm.) (C) The distribution of pore sizes at various R values for c_A = 11.9 μM measured with MPT (solid red) and confocal microscopy (CF, striated blue). We observed both the mean and the width of the distribution of ξ increasing as R increased. P(ξ), normalized probability.

Fig. 3.

The bundle thickness, mesh size, elastic modulus, and critical strain as a function of R at c_A = 11.9 μM. (A) The average D_B at various R values was measured from the digitized EM images and shows D_B ∼ R^0.3. A single actin filament is ≈7 nm in diameter, and D_B becomes as large as 65 nm at R = 1. (B) ξ is measured by using both MPT (▪) and confocal imaging (□). Results show that ξ at R = 0.1 is 2-fold larger than that predicted for an entangled actin network and follows the scaling of ξ ∼ R^0.2. (C) G_o was measured by using bulk rheology, and the best fit for the data follows G_o ∼ R² (solid line). (D) The strain at which we observe the onset of nonlinearity, γ_crit, of the actin–scruin composite networks at various R values, showing a scaling of γ_crit ∼ R^-0.6.

We quantified the pore size distribution by using both MPT and confocal microscopy. MPT is conventionally used to quantify the local elasticity, viscosity, and diffusivity of soft materials, such as gels and entangled solutions (25). This technique also offers a method to characterize the organization of polymers in solution. The distribution of particle MSD was mapped onto a 2D plane to study the degree of heterogeneity, and the magnitudes of the MSDs were used to determine the pore size distribution (Fig. 2B). We find that the average pore size, ξ, increases from 1.3 to 1.9 μm as R varies between 0.1 and 0.5; furthermore, the degree of heterogeneity in the distribution also increases with increasing R as indicated by the increased width of the distributions (Fig. 2C). The distributions of pore sizes determined by analyzing confocal images, shown by the blue columns in Fig. 2C, show a similar trend to those determined with MPT; however, the average values obtained from the confocal images are consistently ≈16% lower than those obtained from MPT. The difference arises because randomly cut cross sections of a 3D object will always be smaller than the maximum diameter of the pore. In addition, whereas the MPT method cannot measure pores smaller than the particle size (1 μm), the confocal imaging method is limited by the resolution of the optics and thus expands the distribution curve to smaller sizes. Therefore, the MPT measurements overestimate ξ, whereas the confocal imaging underestimates it. In the absence of any quantitative characterization of this difference, we used the average of these two independent measurements to determine ξ. Our experiments show that at R = 0.1, ξ has increased 2-fold over that predicted for a purely entangled actin solution; moreover, we find that the mesh size continues to increase as R increases, ξ ∼ R^x, where now x = 0.2 (Fig. 3B).

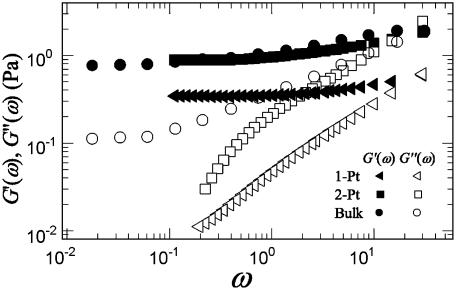
Mechanical Response. We measured the mechanical response of the composite network by using both microrheology and bulk rheology techniques. The elastic components of the moduli, G′ (ω), obtained from both the 1-P and 2-P microrheology with BSA-coated particles are in good agreement with that obtained with bulk rheology. Nevertheless, the results suggest that the 2-P microrheology is a better measure of the bulk property of the network (Fig. 4). Two-particle microrheology probes the behavior over a larger length scale; it also eliminates variations in local mechanical response caused by differences in the coupling between the embedded particles and the network. The loss moduli, G″ (ω), measured with both forms of microrheology are in poor agreement with that measured by bulk rheology. This discrepancy arises because of the uncertainties inherent in microrheology, for which only the magnitude of the complex modulus is measured, and the distinct components G′ and G″ are determined by exploiting the Kramers–Kronig relations (25); as a result, there is much more uncertainty in the subdominant component, G″ (ω).

Fig. 4.

G′ (ω) (solid symbols) and G″ (ω) (open symbols) at c_A = 11.9 μM and R = 0.03 measured with 1-P and 2-P microrheology and bulk rheology. Although the elastic moduli, G_o, measured with both 1-P and 2-P microrheology with BSA-coated particles match well with the bulk measurement, 2-P microrheology shows an excellent agreement with the bulk rheology.

Composite actin–scruin networks are predominantly elastic gels in which G′ (ω) dominates over G″ (ω) for a wide range of frequencies. As shown in Fig. 4, G′ (ω) exhibits little frequency-dependence in the range of ω = 0.03–30 rad/s, allowing us to characterize these networks with a single low-frequency plateau elastic modulus, G_o, measured at ω = 0.6 rad/s. We determined changes in both G_o and the strain at which the network response becomes nonlinear, γ_crit, as a function of filament cross-linking and bundling as we increase R at fixed c_A. The effects on the mechanical properties are significant, particularly for R > 0.03. At c_A = 11.9 μM, G_o changes by four orders of magnitude, from 0.1 to 300 Pa when R is varied from 0.01 to 1. We find G_o ∼ R² for fixed c_A and for R > 0.03 as shown in Fig. 3C. Associated with the increase of G_o is a decrease in γ_crit from 0.4 to 0.04 as R is varied from 0.04 to 1. We find γ_crit ∼ R^-0.6.

As the ratio of scruin to actin decreases, we observe a transition from a highly bundled and densely cross-linked composite network to a very weak network of actin filaments at R ∼ 0.03; the elastic modulus of this weak network is only slightly greater than that of a solution of entangled actin filaments at the same c_A. At concentrations of scruin below this bundling threshold, the gel retains its isotropic nature with a very slow change in its elastic modulus as the scruin concentration decreases (31).

Discussion

In this study, we report the changes observed in mechanical response and in local microstructure upon formation of a bundled and cross-linked actin network with increasing concentration of scruin, a rigid ABP. The modification of the microstructure arises from the fact that scruin has two types of interactions, scruin–actin and scruin–scruin interactions; scruin decorates individual actin filaments and simultaneously forms adhesive patches that can interact with one another either to form bundles of multiple filaments or cross-links between bundles of filaments, thereby forming a solid gel. To correlate the changes of the microstructures induced by the ABP to the mechanical properties of the network, we relate the elasticity of the cross-linked and bundled network to the properties of constituent individual bundles and filaments

In the absence of any ABPs, the elasticity of single actin filaments and their entangled solutions is purely entropic (32). In the presence of ABPs that lead to cross-linking, the elasticity of the resultant network of semiflexible filaments can also be entropic in origin (33, 34). We can theoretically relate the elasticity of the network to the elasticity of single entropic filaments. To accomplish this, the cross-linked network was modeled as a collection of thermally fluctuating semiflexible polymers. For such a network, the elastic modulus (see Fig. 5, which is published as supporting information on the PNAS web site, and ref. 34) is

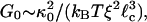[1]

where κ₀ is the bending rigidity of a single filament, ξ is the network pore size, and 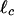is the distance between cross-links. By using the same model, we can also calculate the critical strain, γ_crit, at which the mechanical response becomes nonlinear (see Fig. 5 and ref. 34), which is

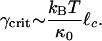[2]

For our actin–scruin composite networks, bundling and cross-linking have a large effect on both the bending rigidity, κ, and 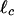; this provides a means of exploring the relationship between microscopic structure and mechanical response of the bundled and cross-linked network. To accomplish this, we investigate the changes in G_o and γ_crit as a function of R at a fixed actin concentration of c_A = 11.9 μM. Because of the compact nature and the large number of scruin–scruin interactions between adjacent filaments, scruin-mediated, in vivo actin bundles behave like homogeneous elastic rods with a Young's modulus, E, similar to that of a single actin filament (18). For such a linear, elastic, and isotropic rod, κ ∼ D⁴, where D is the diameter (35). The in vitro bundles in the network show very similar structural features, and the network breakage at high strain occurs at the value of actin-filament rupture stress rather than stress-induced cross-link unbinding; this confirms that the scruin bonds are rigid and stronger than actin filaments themselves (M.L.G., J.H.S., F. C. MacKintosh, L.M., P.M., and D.A.W., unpublished data). Therefore, we assume that the filaments in the in vitro bundles are tightly cross-linked, with no slip between individual filaments, and, thus, we infer that the bending rigidity of the composite bundle is κ_B ∼ κ₀(D_B/D₀)⁴, where D_B is the bundle diameter, D₀ is the diameter of a single actin filament, and κ₀ is the filament bending rigidity. We must also account for the effect of bundling on the mesh size. From the cosedimentation assay, we know that the total number of actin filaments remains constant, independent of R. Thus, as the bundles thicken, the average spacing between bundles must increase. Therefore, as D_B increases, the effective ξ of the network also increases, giving 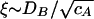. From our EM measurements, we determine the increase in bundle thickness, D_B ∼ D₀R^x, which allows us to determine the variations in both κ and ξ as a function of bundling. For the bending rigidity, we find κ_B ∼ κ₀R^4x, where x is the bundling exponent. For the mesh size, we find 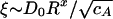. Furthermore, for a densely cross-linked network, 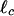is proportional to the entanglement length, 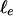(36), 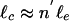. Moreover, as the degree of cross-liking increases, we expect n′ to decrease; thus, we take 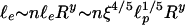, where y is a cross-linking exponent. By using Eq. 1, we predict the elastic modulus of the bundled network as a function of R,

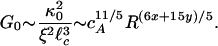[3]

This scaling relation allows us to consider the competition between bundling and cross-linking in determining the effects of elastic properties in modifications of morphology of the networks. We can directly measure the bundling exponent, x, by direct measurements from the EM images and determine the scaling of the bundle thickness, D_B ∼ D₀R^x, with x = 0.3 (Fig. 3A). This result is in good accord with our determination of the bundling exponent from the measurements of the scaling of the mesh size by using both confocal imaging and MPT, where we find ξ ∼ D₀R^x, with x = 0.2 for R > 0.03 at a fixed c_A (Fig. 3B). Thus, we show that our measurements at the nanometer scale made with EM correlate well with our measurements at the micrometer scale made with optical techniques.

We could not independently determine the value of the cross-linking exponent, y. Instead, we used our measurements of the R-dependence of G_o to determine a value for y and compared this to the resultant R-dependence of γ_crit. We observe G_o ∼ R² in our bulk measurements, as shown in Fig. 3C; thus, Eq. 3 yields the cross-linking exponent y = 0.58 by using x = 0.2. The fact that y > x may imply that the effects of cross-linking are stronger than those of bundle formation in our in vitro actin–scruin composite networks. By using Eq. 2, we obtain

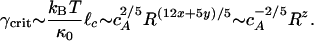[4]

By using the measured value of x and the value predicted for y, we find z ∼ -1.1. By comparison, we experimentally measure γ_crit ∼ R^-0.6 as shown in Fig. 3D. Given the inherent uncertainties and the large exponents, this agreement is reasonable. Thus, our results directly elucidate how the modifications in network morphology affect the origin of the elastic properties.

Our results confirm that the macroscopic network elasticity is directly related to structural parameters measured at the length scale of the mesh size, typically <1 μm, over a large range of cross-link densities, bundle thicknesses, and filament densities. The results also suggest that the mechanical properties of the network should be invariant from microscopic to macroscopic length scales; this is confirmed by our data showing that the elastic moduli obtained from both the 1-P and 2-P microrheology are comparable with the bulk network modulus (Fig. 4).

In summary, we use the experimentally observed scaling behavior to show that the linear elasticity of the actin–scruin composite network can be related to the properties of an individual bundle and its structural organization. The rigid, inextensible, and irreversible cross-linking provided by scruin enables us to simplify the composite system by ignoring the effects of the single-molecule elasticity of the cross-linkers. Thus, the actin–scruin composite network is an excellent model system with which to study the physics of semiflexible biopolymer networks. The results presented here provide tools to measure both the microscopic structure and the elastic properties of the network over a wide range of length scales and insights into the relationship of the mechanical properties of the disordered network to changes in its microstructure and organization.