Skip to main content
NCBI home page
Scientific Reports logoLink to Scientific Reports
. 2016 Jan 11;6:18983. doi: 10.1038/srep18983

Tunable atomic spin-orbit coupling synthesized with a modulating gradient magnetic field

Xinyu Luo 1, Lingna Wu 1, Jiyao Chen 1, Qing Guan 2, Kuiyi Gao 2, Zhi-Fang Xu 3, L You 1,4, Ruquan Wang 2,4,a
PMCID: PMC4707438  PMID: 26752786

Abstract

We report the observation of synthesized spin-orbit coupling (SOC) for ultracold spin-1 87Rb atoms. Different from earlier experiments where a one dimensional (1D) atomic SOC of pseudo-spin-1/2 is synthesized with Raman laser fields, the scheme we demonstrate employs a gradient magnetic field (GMF) and ground-state atoms, thus is immune to atomic spontaneous emission. The strength of SOC we realize can be tuned by changing the modulation amplitude of the GMF, and the effect of the SOC is confirmed through the studies of: 1) the collective dipole oscillation of an atomic condensate in a harmonic trap after the synthesized SOC is abruptly turned on; and 2) the minimum energy state at a finite adiabatically adjusted momentum when SOC strength is slowly ramped up. The condensate coherence is found to remain very good after driven by modulating GMFs. Our scheme presents an alternative means for studying interacting many-body systems with synthesized SOC.

Spin-orbit coupling (SOC), as is often referred to in condensed matter physics, couples the spin of a particle to its orbital degrees of freedom. It is believed that SOC constitutes an important ingredient for quantum simulation with ultracold atoms1,2,3,4. Research on SOC is an active area due to its ubiquitous appearance in condensed matter phenomena, such as topological insulator5,6, spin Hall effect7,8, and spintronics9. In contrast to solid-state materials, where SOC originates from the orbital motion of electrons inside a crystal’s intrinsic electric field, the coupling between atomic spin and its center of mass motion has to be engineered artificially. In recent years we have witnessed great successes of artificial atomic gauge fields10,11,12,13,14,15,16,17,18,19. A popular scheme employs Raman laser fields11 to couple two atomic ground states forming a pseudo-spin-1/2 system, leading to a SOC with equal Rashba20 and Dresselhaus21 contributions. This is routinely used nowadays for both bosonic11,14 and fermionic15,16 alkali atom species. More general forms of SOC are pursued actively in a variety of settings22,23,24,25, which together with the above well understood Raman scheme26,27,28,29,30,31 significantly expand the scopes of quantum simulation using synthetic gauge fields in ultracold atoms, fostering exciting opportunities for observing novel quantum phenomena with ultracold atoms32,33,34,35,36,37,38,39,40,41,42.

The Raman scheme, pioneered by the Spielman group11, makes use of coherent atom-light interaction. As pointed out by several authors2,4,43, spontaneous emissions, nevertheless, come into play in the presence of even far off-resonant laser fields, which give rise to heating or atom loss. The effective spontaneous emission rate (heating rate) and the effective Rabi frequency for the Raman spin flip process both scale as the ratio of laser power to detuning squared, and are respectively proportional to the excited state spontaneous emission rate and fine structure splitting. Thus spontaneous emission cannot be suppressed with increased detuning. At a fixed effective Rabi frequency, heating will be stronger for K atoms than for Rb and Cs atoms, because the excited state fine structure splitting for K atom is smaller. The situations are worse for Na and Li atoms, whose even smaller fine structure splittings essentially rule out the possibility for observing many body phenomena with SOC from the Raman scheme. Alternative ideas less affected by atomic spontaneous emissions are proposed, such as using narrow-line transitions in high spin atoms44,45 or manipulating a spin-dependent tunneling without spin-flip in an optical lattice tilted by a static gradient magnetic field (GMF)43. Besides heating from atomic spontaneous emission, the SOC strength realized in the Raman scheme is difficult to be tuned continuously in an experiment because it is determined by the photon recoil momentum and the intersection angle between the two Raman laser beams. An idea based on periodically modulating the effective Rabi frequency can reduce the synthesized SOC strength46, which is successfully realized in recent experiments47.

To overcome the restrictions due to atomic spontaneous emission and to enhance tunability, one can seek out spin-dependent interactions between atoms and magnetic fields to synthesize SOC, as was proposed by Xu et al.48 using repeated GMF pulses and by Anderson et al.49 using modulating GMFs. A GMF provides a spin-dependent force, which over times leads to a spin (atomic internal state) dependent momentum (spatial/orbital degrees of freedom) impulse, hence gives rise to SOC. An analogous protocol is also proposed to generate SOC for atoms in an optical lattice50. These ideas can be applied to all spinful atoms48,49. A modulating GMF is recently used to produce a state dependent optical lattice for ultracold fermionic atoms51. The procedure for obtaining an effective Hamiltonian from such a periodically driven quantum system is developed in ref. 52. A non-uniform magnetic field is also widely used to couple electronic spin and orbital degrees of freedom in the condensed matter systems53,54,55.

This article reports our observation of a tunable SOC with equal Rashba and Dresselhaus contributions in a spin-1 87Rb atomic Bose-Einstein condensate (BEC) synthesized by modulating a one dimensional (1D) GMF48,49. In the absence of other non-commuting interaction terms, The SOC with strengh kso we report corresponds to a spin-dependent momentum shift ∝ mFkso to the single-particle dispersion curves for spin component mF, which gives rise to the three crossing dispersion curves for the three spin components of spin-1 atoms. The synthesized SOC is confirmed through the following two observations: first, we measure the excitation of the collective dipole mode of a condensate in a harmonic trap after abruptly turning on the SOC; and second, we achieve the adiabatic loading of condensed atoms into the minimum energy state at shifted momentum when SOC is gradually turned on by slowly ramping up the amplitude of the modulating GMF.

Results

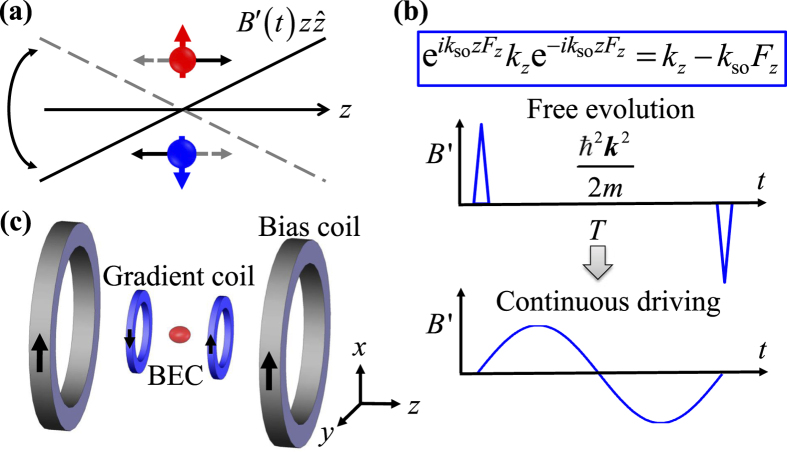
Our experiments synthesize an effective 1D SOC by applying a time-periodically modulating 1D GMF 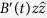Inline graphic with zero average48,49, as illustrated in Fig. 1. The GMF provides a spin-dependent force 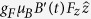Inline graphic for a spin F atom (with mass m). Here, μB is the Bohr magneton, gF is the Lande g-factor and Fx,y,z denotes the x-, y-, and z-component of spin vector F. Although the net impulse over one period is zero, the accumulated distance an atom moves depends on its spin state, which implies the atom acquires a spin dependent group velocity. Thus atomic spin and its center-of-mass motion (orbital) is coupled by GMF pulses. The origin for the synthesized 1D SOC can be understood more straightforwardly when we consider the extreme case where each period contains a pair of two opposite GMF pulses of impulse ±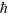Inline graphickso capping the ends of free evolution over time T. 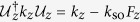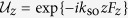These two pulses enact a unitary transformation, which displaces the canonical momentum by a spin-dependent quantity, i.e., Inline graphic where Inline graphic, as shown in Fig. 1(b). Hence, the effective Hamiltonian 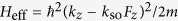Inline graphic results from a spin dependent momentum shift to the free particle Hamiltonian 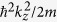Inline graphic. For the sinusoidal modulating GMF 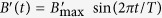Inline graphic used in our experiments, the atomic dynamics is governed by 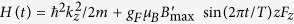Inline graphic. Based on the Floquet theory, the effective time-independent Hamiltonian Heff is given by (more details in supplementary material)

Figure 1. A schematic illustration of SOC synthesized from a periodic GMF.

Figure 1

Open in a new tab

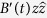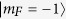(a) A periodically modulated GMF with zero average Inline graphic imparts opposite forces (black arrows or gray dashed arrows at different times) to the Inline graphic (red disk and arrow) and Inline graphic (blue disk and arrow) states of the F = 1 hyperfine manifold. (b) Each modulation period is composed of a pair of short opposite GMF pulses (blue triangles), which provide impulses ±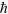Inline graphickso with free evolution sandwiched in between, translating canonical momentum kz → kz − ksoFz, leading to the SOC as shown in the blue rectangular box48. The continuous driving limit of a sinusoidal modulation with zero average is adopted in our experiment for its better technical stability49. (c) The experimental setup involves bias (gray) and gradient (blue) magnetic coils. A BEC (red football) is placed at the center of the gradient coils and aligned along the bias field.

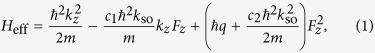graphic file with name srep18983-m10.jpg

where 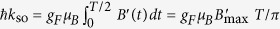Inline graphic, c1 = 1/2, and c2 = 3/8. 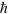Inline graphicq is the quadratic Zeeman shift (QZS) of the bias field used for selecting the 1D GMF from a 3D quadrupole magnetic field (see supplementary material). The c1 and c2 terms on the rhs of Eq. (1) describe the synthesized SOC and the effective QZS, respectively. The latter together with 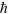Inline graphicq can be further tuned to zero or negative by an off-resonant dressing microwave field56. The above physical picture remains approximately valid in the presence of an external harmonic trap if the modulation frequency ωmod = 2π/T is far greater than the trap frequency.

Our experiments are performed in a single chamber BEC setup as described elsewhere57. We create a 87Rb BEC of 1.2 × 105 atoms in state 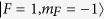Inline graphic in a crossed dipole trap with trapping frequencies 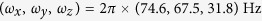Inline graphic, as illustrated in Fig. 1(c). The 1D GMF 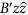Inline graphic is implemented by a combination of a 3D quadrupole magnetic field 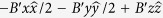Inline graphic and a 5.7 Gauss bias field 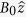Inline graphic, whose linear and quadratic Zeeman shifts are (2π) 4 MHz and (2π) 2.34 kHz, respectively (see supplementary material). The modulation frequency ωmod for the GMF is (2π) 1.0 kHz unless stated otherwise. To generate a SOC strength kso = 1 kL = 8.0554 μm−1, where 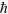Inline graphickL = 2π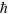Inline graphic/λL is the one photon recoil momentum at a laser wavelength λL = 780 nm, the required peak magnetic field gradient Inline graphic. The centers of the gradient field coils and the optical trap are aligned within 50 μm to minimize short-term magnetic field fluctuation during modulation (see supplementary material).

Dipole oscillations

To confirm the effect of the synthesized SOC from the modulating GMF, we first excite the collective dipole mode of a single spin component atomic condensate in a harmonic trap by abruptly turning on the modulating GMF. By rewriting the effective Hamiltonian (1) as 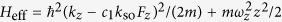Inline graphic and interchanging the roles of the conjugate variable pair kz and z, it’s easy to find that this effective Hamiltonian is equivalent to that of a particle moving in a displaced harmonic trap. Here, we neglected the extra QZS which only causes an overall energy shift. A particle displaced from the center of a harmonic trap will oscillate back and forth periodically, which is indeed what we observe. Both the position and momentum of the condensate oscillate at the trap frequency ωz. 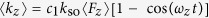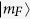Solving the Heisenberg equations of motion given by Heff, we obtain the averaged momentum Inline graphic, where Inline graphic for the Inline graphic component. The oscillation is around c1ksomF with a peak to peak amplitude 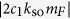Inline graphic. As shown in Fig. 2(a), in our experiments we abruptly turn on the modulating GMF, at a corresponding SOC strength of kso = 7.5 μm−1, and persist for variable hold time. After integer multiple periods of the modulation, the crossed dipole trap is turned off in less than 10 μs. Condensed atoms are expanded for about 24 ms, during which different Zeeman components are Stern-Gerlach separated by an inhomogeneous magnetic field along x-direction. For all three spin components, atomic center-of-mass momenta are derived from their shifted positions along z-direction with respect to their locations when SOC is absent. As shown in Fig. 2(c), the observed results are in good agreement with our theoretical predictions.

Figure 2. Collective dipole oscillation of a single spin component condensate observed after abruptly turning on kso = 7.5 μm−1 with ωmod = (2π) 1.0 kHz.

Figure 2

Open in a new tab

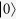(a) The time sequence of our experiments: abruptly turning on a constant amplitude modulation GMF corresponding to kso = 7.5 μm−1, followed by 24 ms of time of flight (TOF) before Stern-Gerlach imaging. (b) Absorption images of Inline graphic (top row), Inline graphic (middle row), and 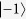Inline graphic (bottom row) components after different hold time (duration of the modulating GMF). The dashed lines are for kz = 0, or without SOC. (c) Atomic momentum for 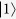Inline graphic (red squares), 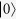Inline graphic (black rhombuses), and 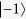Inline graphic (blue disks) spin components as a function of hold time. The rhs vertical labels are in units of kL, and solid lines denote theoretical predictions.

SOC shifted minimum energy state

As a second confirmation, we observe that the atom’s minimum energy state is adiabatically adjusted to a finite none-zero momentum kz = c1ksomF for the state 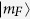Inline graphic when the modulation amplitude is slowly ramped up as shown in Fig. 3(a). In the presence of SOC, the minimum of the single-particle dispersion for the spin state 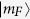Inline graphic is located at c1ksomF. According to the adiabatic theorem, if the ramp of kso is slow enough, atoms will follow the ramp and stay at the shifted minimum. 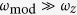In this set of experiments, atoms are prepared at the initial spin state of  Inline graphic by applying a π/2 pulse to the state (0, 0, 1)T. The modulation amplitude is then ramped up to a final value within 200 ms. After turning off the optical trap, we measure the momentum for each spin component. We find good agreement with theoretical predictions as shown in Fig. 3(c). To confirm the adiabaticity, kso is ramped up from 0 to 4.9 μm−1 in 100 ms and then back to 0 in another 100 ms. We find atomic center-of-mass momentum returns to 0 without noticeable heating. We also check the dependence of c1 on the modulation frequency ωmod and find that c1 essentially remains a constant as long as Inline graphic.

Figure 3. Atoms adiabatically follow the energy minimum shifted to finite momentum with increased SOC strength.

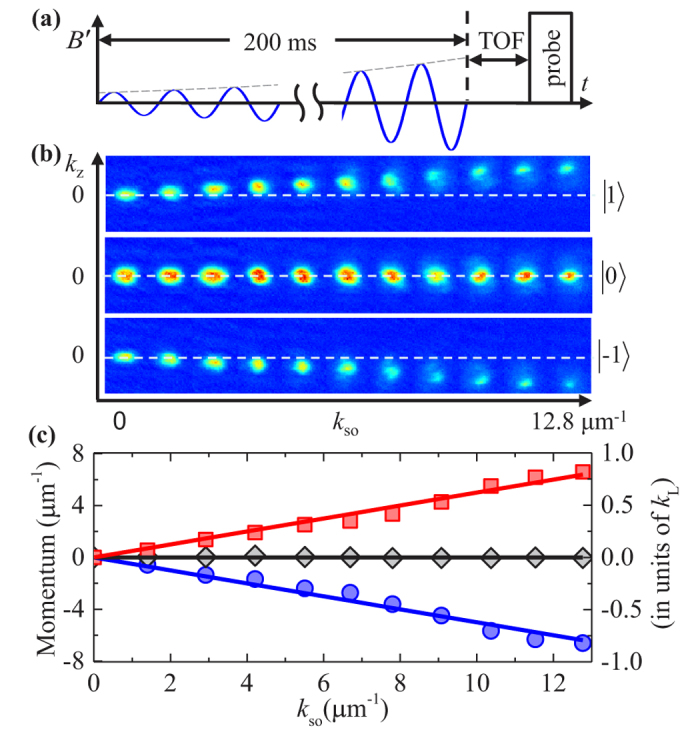
Figure 3

Open in a new tab

Here ωmod = (2π) 1.0 kHz. (a) The time sequence of our experiments: adiabatically ramping up GMF modulation amplitude to a given kso, followed by TOF before Stern-Gerlach imaging. (b) Absorption images of 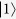Inline graphic (top row), 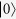Inline graphic (middle row), 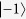Inline graphic (bottom row) components for different kso. The dashed lines are for kz = 0, or for without SOC. With the increase of SOC strength, the observed shapes for the atomic condensate cloud become increasingly distorted, indicating enhanced excitations of higher spatial modes. We believe this is due to the increased violation of the adiabatic condition when ramping the SOC strength to higher strength. Additionally, parametric heating from magnetic field gradient modulation also contributes. (c) Atomic center-of-mass momentum for 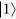Inline graphic (red squares), 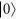Inline graphic (black rhombuses), and 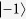Inline graphic (blue disks) spin component as a function of kso, compared with theoretical predictions (solid lines).

Discussion

The results of Fig. 3 demonstrate tunability of the SOC we synthesize. For our protocol based on temporally modulating GMFs, a point of detrimental importance concerns heating which causes relaxation and atom loss from condensates.

As mentioned before, one of the major heating mechanisms for the Raman scheme is photon scattering from the Raman laser. For different alkaline metal atoms, the situation varies significantly. A list of all alkaline metal atom data are shown in Table 1. For cesium and rubidium, the heating rate is very low, the Raman scheme works very well. For potassium, the heating will cause significant problem at the temperature scale of many quantum many body phenomenon. For sodium and lithium, the huge heating rate will quickly destroy the BEC or degenerate Fermi gas.

Table 1. The heating rate for atoms inside a harmonic trap due to spontaneous emission is estimated to be 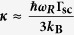Inline graphic, where ωR is the resonant photon recoil frequency, and kB is the Boltzmann constant.

Atomic species ΔFS (GHz) Γ (MHz) ωR (kHz) κ (nK/s)
133Cs 17610 5.2 2.06 0.13
87Rb 7123 6.1 3.77 1.2
40K 1730 6.0 8.49 25
23Na 516 9.8 25 1193
6Li 10 5.9 73.9 321167
Open in a new tab

The effective spontaneous emission rate 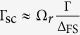Inline graphic is proportional to the Raman coupling strength Ωr, where ΔFS is the fine structure splitting in the first excited p state, and Γ is the excited state line width. The heating rate κ is calculated for Ωr ≈ ωR, which is a typical value used for studying ground state properties of the SOC Hamiltonian11.

As atomic spontaneous emission is absent in our experiments, the most likely heating mechanism comes from parametric processes associated with the temporal modulation. To minimize parametric heating, we modulate the GMF far away from the characteristic frequencies of our system. The typical trapping frequency is about (2π) 100 Hz and the mean field interaction energy is around (2π) 200 Hz. When modulated at ωmod = (2π) 1.0 kHz, heating is found to be moderate and acceptable for the reported experiments, based on the observed condensate life time. To measure the life time, we adiabatically increase the SOC strength to prepare atoms into an equilibrium state from a initial spin state 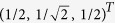Inline graphic and measure the fractions of remaining atoms as functions of time. The worst case occurs for condensates in the 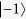Inline graphic component, whose life time is found to be around 310 ms for kso = 4.9 μm−1 corresponding to a recoil energy of 1.3 kHz, as shown in Fig. 4(a). The life time of our system is comparable to the reported values for the Raman scheme with Rb atoms11. It can be further improved by increasing the modulation frequency. Figure 4(b) displays the dependence of the atomic cloud size after 24 ms of TOF expansion on modulation frequency at a fixed kso = 4.9 μm−1. The cloud radius is found to decrease with increasing modulation frequency, which confirms the expected heating suppression with increased modulation frequency. Thus enhanced performances of the GMF scheme is expected if our experiments can be carried out with atomic chip based setups, which routinely provide higher GMFs and faster modulations58,59.

Figure 4.

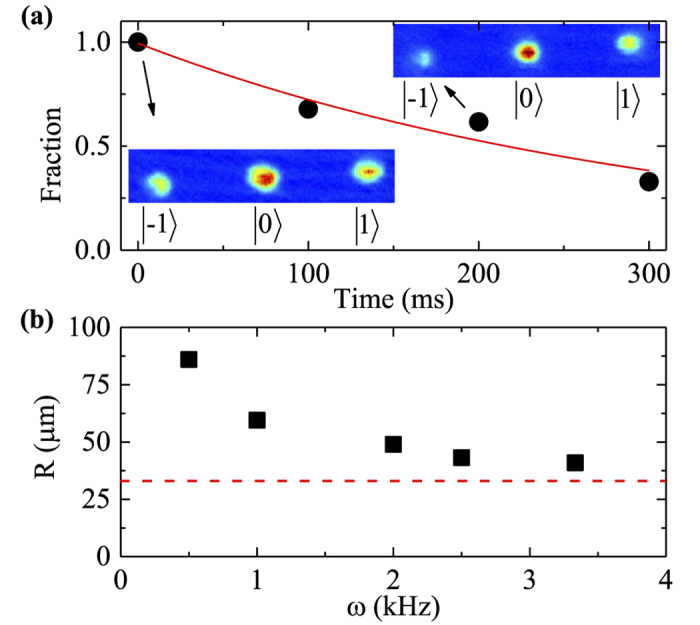
Figure 4

Open in a new tab

(a) The fraction of remaining atoms (due to heating loss from the trap) as a function of the time (after the modulating GMF is turned off) for 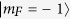Inline graphic component at kso = 4.9 μm−1. Dots denote measurement points, while the solid line is an exponential fit. The optical trap frequencies are respectively 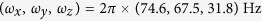Inline graphic, and ωmod = (2π) 1.0 kHz. The insert Stern-Gerlach images show the three spin components displaced along the vertical direction as a result of spin dependent momentum impulses from SOC; (b) The condensate size R (fitted radius) after 24 ms TOF expansion (black square) for 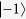Inline graphic component at kso = 4.9 μm−1 as a function of modulation frequency ωmod. The dashed line denotes the same size without SOC or at kso = 0 μm−1. Hold time is 100 ms. 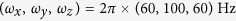The optical trap frequencies are respectively Inline graphic.

As demonstrated in our experiments, the SOC synthesized from GMF enacts spin-dependent momentum shifts to the single-particle dispersion curves, leading to curve crossings between different spin states. Inspired by the idea of ref. 50, we find that these crossings can be tuned into avoided crossings when spin flip mechanism is introduced as elaborated in more detail in the supplementary material.

In conclusion, we experimentally demonstrate a tunable SOC synthesized by a modulating GMF for a spin-1 87Rb BEC. We tune the SOC strength by changing the momentum impulse from the GMF. The observed coherence time is reasonably long compared to the Raman scheme for rubidium, and expected to be much better than the Raman scheme for sodium and lithium, pointing to promising experimental opportunities. The scheme we realized relies on spin-dependent Zeeman interactions, thus is naturally extendable to high-spin atomic states, like the spin-1 case we demonstrate here. It adds to the recent report of spin-1 SOC60 concatenated from two pseudo-spin-1/2 subsystems with Raman laser couplings. Our experiment opens up a new avenue in the synthesizing SOC with atom species not suitable with the Raman scheme, and presents an important addition to quantum simulation with tunable SOC couple strength.

Methods

Condensate production

Atomic 87Rb Bose-Einstein condensates are produced employing laser cooling followed by evaporative cooling in a single vacuum chamber, which consists of a 32 mm × 32 mm wide and 300 mm long quartz cell, a Rb reservoir, and vacuum pumps. The quartz cell is ideally suited for magnetic field modulation as it prevents eddy current, which could cause short term fluctuations to the bias field. To optimize the applications of fast and strong GMF modulation by small gradient coils and to allow for three dimensional (3D) optical access, MOT collected from background atoms are magnetically transported 10 cm to a location 8 mm away from the inside wall of the glass cell. They are first RF evaporative cooled in a hybrid trap consisting of a magnetic quadruple trap and a crossed optical dipole trap for 5 seconds. The crossed dipole trap derives from two 1064 nm laser beams (with 1/e2 Gaussian diameter 120 μm) propagating along x- and z- directions, respectively. The magnetic quadrupole field gradient is then ramped down to transfer atoms to the crossed dipole trap. Condensation occurs after a final evaporation by ramping down the power of the crossed dipole trap in 3 seconds. At the end of the final evaporation the crossed dipole trap frequencies are 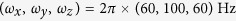Inline graphic. A condensate in 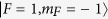Inline graphic state with 1.2 × 105 atoms is produced every 40 seconds. To minimize heating from the near-resonant driving of the modulating GMF, we further ramp down ωz to 2π × 31.8 Hz in 500 ms after BEC production, which reduces ωx and ωy respectively to 2π × 74.6 Hz and 2π × 67.5 Hz.

Magnetic field control

Three pairs of Helmholtz coils are used to control the homogeneous bias magnetic field. While transferring atoms from the hybrid trap into the crossed dipole trap, a 0.7 Gauss bias field along z-direction is simultaneously turned on in order to maintain atoms in 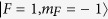Inline graphic state. In the last 1.5 seconds of evaporative cooling, we ramp up the bias field to 5.7 Gauss and hold on to this value. The Larmor frequency of the bias field is calibrated by RF driven Rabi oscillations between Zeeman sublevels. The residual magnetic field gradient is compensated to below 2 mGauss/cm by a pair of anti-Helmholtz coils along z-direction.

A pair of small anti-Helmholtz coils is used to modulate the GMF with a modulation amplitude up to 100 Gauss/cm at a frequency of (2π) 1.0 kHz. The radius for the gradient coils is 15 mm. The two coils are separated at an inner distance of 36 mm. Each coil consists of 12 turns of winding and produces an inductance of about 10 μH. The gradient coil size is much larger than the 120 μm beam waist of our dipole trap, which produces a homogeneous gradient field inside the crossed dipole trap. The coils are small enough to ensure fast and strong GMF modulation. The current for the gradient coils is regulated by a home made fast (10 μs rise time) and precise (100 ppm) linear bipolar current controller, whose phase compensation is carefully analysed and tuned for stable running with the inductive load. The gradient coil is mounted on a 3D low magnetic translation stage for precise alignment of the gradient coils. The center of the gradient field is aligned within 50 μm with the BEC, which is found to be crucial for minimizing short term bias field fluctuations during GMF modulation.

Additional Information

How to cite this article: Luo, X. et al. Tunable atomic spin-orbit coupling synthesized with a modulating gradient magnetic field. Sci. Rep. 6, 18983; doi: 10.1038/srep18983 (2016).

Supplementary Material

Supplementary Information
srep18983-s1.pdf (152KB, pdf)

Acknowledgments

This work is supported by MOST 2013CB922002 and 2013CB922004 of the National Key Basic Research Program of China, and by NSFC (No. 91121005, No. 11374176, No. 11404184, No. 11474347, and No. 11574100).

Footnotes

Author Contributions X.L. and Q.G. performed the experiment. X.L. and L.W. analysed the data. X.L., K.G., Q.G. and R.W. built the experimental setup. L.W., Z.-F.X., J.C. and L.Y. developed the theory. L.W. performed the numerical calculation. X.L., L.W., Z.-F.X., R.W. and L.Y. wrote the manuscript. L.Y. and R.W. supervised the whole research project.

References

  1. Dalibard J., Gerbier F., Juzeliūnas G. & Öhberg P. Colloquium: Artificial gauge potentials for neutral atoms. Rev. Mod. Phys. 83, 1523–1543 (2011). [Google Scholar]
  2. Galitski V. & Spielman I. B. Spin-orbit coupling in quantum gases. Nature 494, 49–54 (2013). [DOI] [PubMed] [Google Scholar]
  3. Zhang J., Hu H., Liu X.-J. & Pu H. Fermi gases with synthetic spin-orbit coupling. Annu. Rev. Cold At. Mol. 2, 81–143 (2014). [Google Scholar]
  4. Zhai H. Degenerate quantum gases with spin-orbit coupling: a review. Rep. Prog. Phys. 78, 026001 (2015). [DOI] [PubMed] [Google Scholar]
  5. Hasan M. Z. & Kane C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010). [Google Scholar]
  6. Qi X.-L. & Zhang S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011). [Google Scholar]
  7. Kato Y. K., Myers R. C., Gossard A. C. & Awschalom D. D. Observation of the spin hall effect in semiconductors. Science 306, 1910–1913 (2004). [DOI] [PubMed] [Google Scholar]
  8. Konig M. et al. Quantum spin hall insulator state in hgte quantum wells. Science 318, 766–770 (2007). [DOI] [PubMed] [Google Scholar]
  9. Žutić I., Fabian J. & Das Sarma S. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004). [Google Scholar]
  10. Lin Y.-J., Compton R. L., Jiménez-Garca K., Porto J. V. & Spielman I. B. Synthetic magnetic fields for ultracold neutral atoms. Nature 462, 628–632 (2009). [DOI] [PubMed] [Google Scholar]
  11. Lin Y.-J., Jiménez-Garca K. & Spielman I. B. Spin-orbit-coupled bose-einstein condensates. Nature 471, 83–86 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Struck J. et al. Tunable gauge potential for neutral and spinless particles in driven optical lattices. Phys. Rev. Lett. 108, 225304 (2012). [DOI] [PubMed] [Google Scholar]
  13. Jiménez-Garca K. et al. Peierls substitution in an engineered lattice potential. Phys. Rev. Lett. 108, 225303 (2012). [DOI] [PubMed] [Google Scholar]
  14. Zhang J.-Y. et al. Collective dipole oscillations of a spin-orbit coupled bose-einstein condensate. Phys. Rev. Lett. 109, 115301 (2012). [DOI] [PubMed] [Google Scholar]
  15. Wang P. et al. Spin-orbit coupled degenerate fermi gases. Phys. Rev. Lett. 109, 095301 (2012). [DOI] [PubMed] [Google Scholar]
  16. Cheuk L. W. et al. Spin-injection spectroscopy of a spin-orbit coupled fermi gas. Phys. Rev. Lett. 109, 095302 (2012). [DOI] [PubMed] [Google Scholar]
  17. Aidelsburger M. et al. Realization of the hofstadter hamiltonian with ultracold atoms in optical lattices. Phys. Rev. Lett. 111, 185301 (2013). [DOI] [PubMed] [Google Scholar]
  18. Miyake H., Siviloglou G. A., Kennedy C. J., Burton W. C. & Ketterle W. Realizing the harper hamiltonian with laser-assisted tunneling in optical lattices. Phys. Rev. Lett. 111, 185302 (2013). [DOI] [PubMed] [Google Scholar]
  19. Jotzu G. et al. Experimental realisation of the topological haldane model. Nature 515, 237 (2014). [DOI] [PubMed] [Google Scholar]
  20. Bychkov Y. A. & Rashba E. I. Oscillatory effects and the magnetic susceptibility of carriers in inversion layers. J. Phys. C 17, 6039–6045 (1984). [Google Scholar]
  21. Dresselhaus G. Spin-orbit coupling effects in zinc blende structures. Phys. Rev. 100, 580–586 (1955). [Google Scholar]
  22. Campbell D. L., Juzeliūnas G. & Spielman I. B. Realistic rashba and dresselhaus spin-orbit coupling for neutral atoms. Phys. Rev. A 84, 025602 (2011). [Google Scholar]
  23. Sau J. D., Sensarma R., Powell S., Spielman I. B. & Das Sarma S. Chiral rashba spin textures in ultracold fermi gases. Phys. Rev. B 83, 140510 (2011). [Google Scholar]
  24. Xu Z. F. & You L. Dynamical generation of arbitrary spin-orbit couplings for neutral atoms. Phys. Rev. A 85, 043605 (2012). [Google Scholar]
  25. Anderson B. M., Juzeliūnas G., Galitski V. M. & Spielman I. B. Synthetic 3d spin-orbit coupling. Phys. Rev. Lett. 108, 235301 (2012). [DOI] [PubMed] [Google Scholar]
  26. Beeler M. C. et al. The spin hall effect in a quantum gas. Nature 498, 201–204 (2013). [DOI] [PubMed] [Google Scholar]
  27. Fu Z. et al. Production of feshbach molecules induced by spin-orbit coupling in fermi gases. Nat. phys. 10, 110–115 (2014). [Google Scholar]
  28. Ji S.-C. et al. Experimental determination of the finitetemperature phase diagram of a spin corbit coupled bose gas. Nat. phys. 10, 314–320 (2014). [Google Scholar]
  29. Olson A. J. et al. Tunable landau-zener transitions in a spin-orbit-coupled bose-einstein condensate. Phys. Rev. A 90, 013616 (2014). [Google Scholar]
  30. Hamner C., Zhang Y., Khamehchi M. A., Davis M. J. & Engels P. Spin-orbit-coupled bose-einstein condensates in a one-dimensional optical lattice. Phys. Rev. Lett. 114, 070401 (2015). [DOI] [PubMed] [Google Scholar]
  31. Huang L. et al. Experimental realization of a two-dimensional synthetic spin-orbit coupling in ultracold Fermi gases. ArXiv e-prints 1506. 02861 (2015). [Google Scholar]
  32. Wu C.-J., Mondragon-Shem I. & Zhou X.-F. Unconventional bose-einstein condensations from spin-orbit coupling. Chin. Phys. Lett. 28, 97102 (2011). [Google Scholar]
  33. Wang C., Gao C., Jian C.-M. & Zhai H. Spin-orbit coupled spinor bose-einstein condensates. Phys. Rev. Lett. 105, 160403 (2010). [DOI] [PubMed] [Google Scholar]
  34. Ho T.-L. & Zhang S. Bose-einstein condensates with spin-orbit interaction. Phys. Rev. Lett. 107, 150403 (2011). [DOI] [PubMed] [Google Scholar]
  35. Xu Z. F., Lu R. & You L. Emergent patterns in a spin-orbit-coupled spin-2 bose-einstein condensate. Phys. Rev. A 83, 053602 (2011). [Google Scholar]
  36. Sinha S., Nath R. & Santos L. Trapped two-dimensional condensates with synthetic spin-orbit coupling. Phys. Rev. Lett. 107, 270401 (2011). [DOI] [PubMed] [Google Scholar]
  37. Hu H., Ramachandhran B., Pu H. & Liu X.-J. Spin-orbit coupled weakly interacting bose-einstein condensates in harmonic traps. Phys. Rev. Lett. 108, 010402 (2012). [DOI] [PubMed] [Google Scholar]
  38. Xu Z. F., Kawaguchi Y., You L. & Ueda M. Symmetry classification of spin-orbit-coupled spinor bose-einstein condensates. Phys. Rev. A 86, 033628 (2012). [Google Scholar]
  39. Vyasanakere J. P., Zhang S. & Shenoy V. B. Bcs-bec crossover induced by a synthetic non-abelian gauge field. Phys. Rev. B 84, 014512 (2011). [Google Scholar]
  40. Hu H., Jiang L., Liu X.-J. & Pu H. Probing anisotropic superfluidity in atomic fermi gases with rashba spin-orbit coupling. Phys. Rev. Lett. 107, 195304 (2011). [DOI] [PubMed] [Google Scholar]
  41. Gong M., Tewari S. & Zhang C. Bcs-bec crossover and topological phase transition in 3d spin-orbit coupled degenerate fermi gases. Phys. Rev. Lett. 107, 195303 (2011). [DOI] [PubMed] [Google Scholar]
  42. Yu Z.-Q. & Zhai H. Spin-orbit coupled fermi gases across a feshbach resonance. Phys. Rev. Lett. 107, 195305 (2011). [DOI] [PubMed] [Google Scholar]
  43. Kennedy C. J., Siviloglou G. A., Miyake H., Burton W. C. & Ketterle W. Spin-orbit coupling and quantum spin hall effect for neutral atoms without spin flips. Phys. Rev. Lett. 111, 225301 (2013). [DOI] [PubMed] [Google Scholar]
  44. Cui X., Lian B., Ho T.-L., Lev B. L. & Zhai H. Synthetic gauge field with highly magnetic lanthanide atoms. Phys. Rev. A 88, 011601 (2013). [Google Scholar]
  45. Deng Y., Cheng J., Jing H., Sun C.-P. & Yi S. Spin-orbit-coupled dipolar bose-einstein condensates. Phys. Rev. Lett. 108, 125301 (2012). [DOI] [PubMed] [Google Scholar]
  46. Zhang Y., Chen G. & Zhang C. Tunable spin-orbit coupling and quantum phase transition in a trapped bose-einstein condensate. Sci. rep. 3, 1937 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Jiménez-Garca K. et al. Tunable spin-orbit coupling via strong driving in ultracold-atom systems. Phys. Rev. Lett. 114, 125301 (2015). [DOI] [PubMed] [Google Scholar]
  48. Xu Z.-F., You L. & Ueda M. Atomic spin-orbit coupling synthesized with magnetic-field-gradient pulses. Phys. Rev. A 87, 063634 (2013). [Google Scholar]
  49. Anderson B. M., Spielman I. B. & Juzeliunas G. Magnetically generated spin-orbit coupling for ultracold atoms. Phys. Rev. Lett. 111, 125301 (2013). [DOI] [PubMed] [Google Scholar]
  50. Struck J., Simonet J. & Sengstock K. Spin-orbit coupling in periodically driven optical lattices. Phys. Rev. A 90, 031601 (2014). [Google Scholar]
  51. Jotzu G. et al. Creating state-dependent lattices for ultracold fermions by magnetic gradient modulation. Phys. Rev. Lett. 115, 073002 (2015). [DOI] [PubMed] [Google Scholar]
  52. Goldman N. & Dalibard J. Periodically driven quantum systems: Effective hamiltonians and engineered gauge fields. Phys. Rev. X 4, 031027 (2014). [Google Scholar]
  53. Tokura Y., van der Wiel W. G., Obata T. & Tarucha S. Coherent single electron spin control in a slanting zeeman field. Phys. Rev. Lett. 96, 047202 (2006). [DOI] [PubMed] [Google Scholar]
  54. Pioro-Ladriere M. et al. Electrically driven single-electron spin resonance in a slanting zeeman field. Nat. Phys. 4, 776–779 (2008). [Google Scholar]
  55. Tokura Y., Kubo T. & Munro W. J. Power dependence of electric dipole spin resonance. JPS Conference Proceedings 1, 012022 (2014).
  56. Gerbier F., Widera A., Fölling S., Mandel O. & Bloch I. Resonant control of spin dynamics in ultracold quantum gases by microwave dressing. Phys. Rev. A 73, 041602 (2006). [Google Scholar]
  57. Gao K.-Y. et al. Ultra-high efficiency magnetic transport of 87 rb atoms in a single chamber bose-einstein condensation apparatus. Chin. Phys. Lett. 31, 063701 (2014). [Google Scholar]
  58. Schumm T. et al. Matter-wave interferometry in a double well on an atom chip. Nat. Phys. 1, 57–62 (2005). [Google Scholar]
  59. Machluf S., Japha Y. & Folman R. Coherent Stern CGerlach momentum splitting on an atom chip. Nat. Commun. 4, 2424 (2013). [DOI] [PubMed] [Google Scholar]
  60. Campbell D. L. et al. Itinerant magnetism in spin-orbit coupled Bose gases. ArXiv e-prints 1501.05984 (2015).

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep18983-s1.pdf (152KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES