Abstract
Patterning of periodic stripes during development requires mechanisms to control both stripe spacing and orientation. A number of models can explain how stripe spacing is controlled, including molecular mechanisms, such as Turing’s reaction-diffusion model, as well as cell-based and mechanical mechanisms. However, how stripe orientation is controlled in each of these cases is poorly understood. Here, we model stripe orientation using a simple, yet generic model of periodic patterning, with the aim of finding qualitative features of stripe orientation that are mechanism-independent. Our model predicts three qualitatively distinct classes of orientation mechanism: gradients in production rates, gradients in model parameters, and anisotropies (e.g. in diffusion or growth). We provide evidence that the results from our minimal model may also apply to more specific and complex models, revealing features of stripe orientation that may be common to a variety of biological systems.
Graphical abstract
Introduction
Periodic patterns are found in a wide variety of different organisms, forming across a large range of time- and length-scales. Well studied examples include: the regular spacing of villi in the gut (Shyer et al. (2013)); hair follicle patterning on mammalian skin (Sick et al. (2006); Mou et al. (2006)); the formation of regularly spaced digits in the limb (Sheth et al. (2012)); branching morphogenesis in the lung (Menshykau et al. (2014)); and pigmentation patterns in a variety of animals (Kondo and Asai(1995); Nakamasu et al. (2009); Yamaguchi et al. (2007); Frohnhöfer et al. (2013)).
A number of different models have been proposed to explain the formation of these periodic patterns, most notably Turing’s ‘reaction-diffusion model’, in which periodicity is generated molecularly (Kondo and Miura(2010)). The canonical reaction-diffusion model involves two diffusing molecules: a rapidly-diffusing inhibitor molecule, and a slowly-diffusing activator molecule. Provided that the activator stimulates production of both itself and its inhibitor sufficiently strongly, and that the inhibitor diffuses sufficiently more rapidly than the activator, periodic patterns can spontaneously emerge from an initially homogeneous pattern (termed a Turing instability) (Turing(1952)).
Despite the prominence of molecular-level reaction-diffusion models, there are many other ways to generate periodic patterns – or, to put it mathematically, many other systems that exhibit Turing instabilities. These include more complex molecular circuits but importantly also a number of cell-based and mechanical models which can recapitulate periodic patterning in silico (Maini et al. (1991); Hiscock and Megason(2015); Murray and Oster(1984b); Murray et al. (1988); Myerscough et al. (1998); Lubensky et al. (2011)). The logic of each of these models is similar, but the underlying biology is different. For example, a reaction-diffusion model uses a short-ranged activator and a long-ranged inhibitor to generate a periodic pattern. An analogous cell-based model would be where cells signal to each other, using a short-ranged pro-mitotic signal, and a long-ranged anti-mitotic signal. Similarly, a mechanical model where a tissue buckles into a periodic shape consists of a short-ranged mechanical interaction - resistance to bending - and a long-ranged mechanical interaction - compression of the tissue.
Since the logic of each of these mechanisms is similar, it can be difficult to experimentally distinguish them (Hiscock and Megason(2015)). Furthermore, there is increasing evidence that cellular and mechanical processes are relevant in vivo. For example, a combination of cell-movement, cell proliferation and signalling via long, cellular protrusions has been shown to be important in patterning the stripes on the zebrafish skin (Hamada et al. (2014); Yamanaka and Kondo(2014)). Equally, tissue mechanics has been strongly implicated in forming regularly spaced villi during growth of the gut (Shyer et al. (2013)). Thus, a variety of models – spanning molecular, cellular and/or mechanical processes – must be considered if we are to understand general properties of periodic patterning.
One property that has so far received little attention and forms the focus of this work is pattern orientation. Here, we focus our discussion exclusively on striped as opposed to spotted periodic patterns, since stripe orientation is more apparently functional. As an example, stripes in animal pigment patterns often have a stereotyped direction e.g. wildtype zebrafish have stripes parallel to their long axis during normal development. However, during aberrant patterning - for example, when the pattern regenerates after damage (Yamaguchi et al. (2007)), or when the pattern proceeds in the absence of some organizing signal (Frohnhöfer et al. (2013)) - the tight regulation of pattern orientation is impaired (Figure 1).
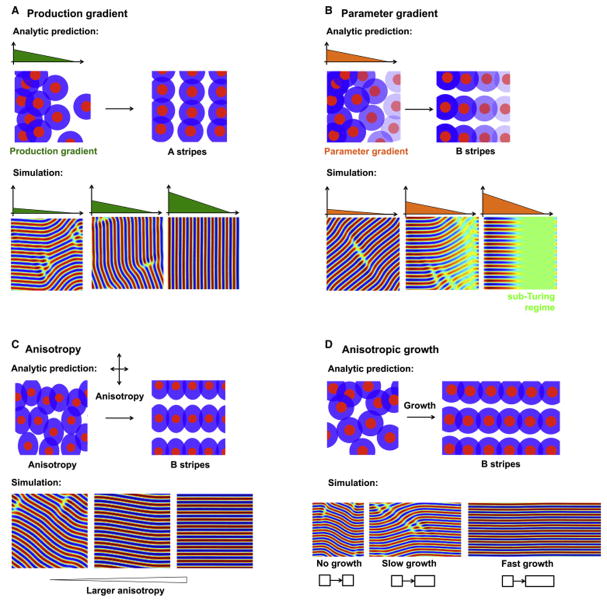
Figure 1. The phenomenology of stripe orientation.
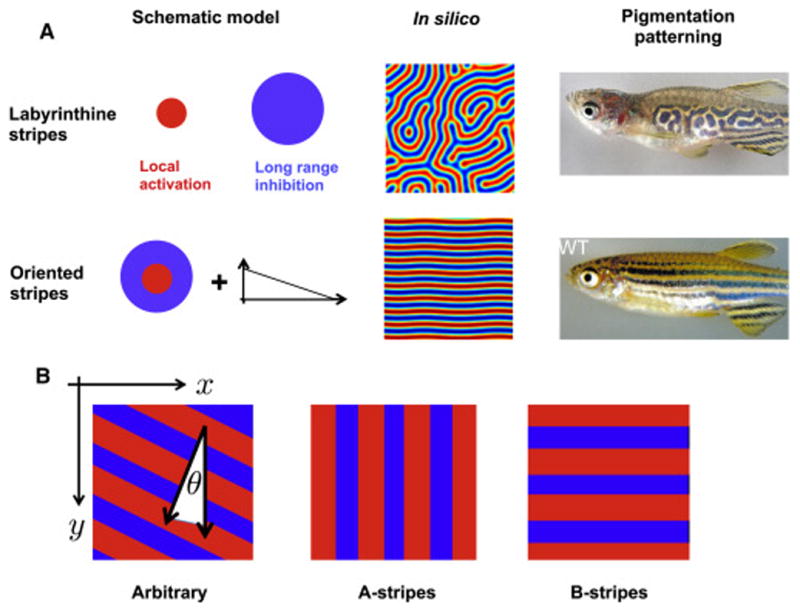
A: Left: Many periodic patterns involve local activation, long range inhibition; here, the size of the circles reflects the range of the interaction. We propose that additional mechanisms (e.g. some form of gradient, as schematized) are needed to orient stripes. Middle: In silico stripes are oriented in random directions in the absence of an orientation mechanism. Right: the zebrafish choker mutant has labryinthine stripes (adapted from Frohnhöfer et al. (2013)), in contrast to the stereotyped longitudinal stripes of wildtype adults (reproduced with permission from Rawls et al. (2001) ).
B: In this work, we use a rectangular geometry, specified by (x, y)coordinates. Stripes can either be arbitrarily oriented (left), parallel to the x axis (middle), or parallel to the y axis (right).
Several mechanisms have previously been proposed to control stripe direction. Firstly, if the initial condition of the pattern is a single stripe, then subsequent stripes will tend to form parallel to the first stripe, in which case the direction of the first stripe specifies the orientation of the entire pattern (Nakamasu et al. (2009)). Secondly, boundary conditions also influence pattern orientation (Lacalli et al. (1988); Murray(2003)) - for example, in a long, narrow geometry, stripes can only ‘fit’ in one direction (mimicking the pattern of stripes found on e.g. leopard tails (Murray(1988))). However, in many tissues, stripe orientation likely relies on multiple cues besides strong initial conditions or extreme geometry (for example, during limb patterning, discussed below). What controls pattern orientation in these cases? Two further hypotheses have been proposed: (i) a morphogen gradient interacts with a Turing system (Sheth et al. (2012); Glimm et al. (2012)); or (ii) the diffusion of Turing molecules is anisotropic (Shoji et al. (2002)). This previous work has generated a number of interesting hypotheses, but has several limitations. Firstly, these hypotheses have been generated from simulation data and thus it is difficult to generalize them, particularly to cellular and mechanical models. Secondly, the simulations do not determine the uniqueness of any particular prediction. The property of uniqueness is key, since the ability of a specific mechanism to orient stripes in silico is, by itself, not good evidence for that specific mechanism actually operating in vivo. What is needed is to show that the proposed mechanism can uniquely explain the data on orientation; or alternatively, that other plausible mechanisms cannot orient stripes in silico i.e. a ‘negative control’ model.
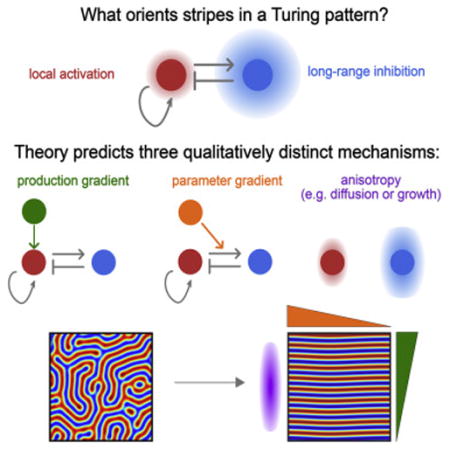
Here we seek to extract common features of stripe orientation, to generalize the results to nonmolecular models, and to determine the uniqueness of any particular result by using a simple but generic model of periodic patterning. By choosing a theoretical framework at the appropriate level of abstraction, we hope to make predictions that are generalizable to different mechanisms. The framework we used is based on a single variable description of a generic Turing instability: the Swift-Hohenberg equation (Cross and Hohenberg(1993)). This equation is based on a core set of assumptions that formally describe the shared features of Turing-like patterns which allows us to derive analytical results that could be generally applicable rather than using simulations of specific models. By analyzing this simple model, we find three qualitatively distinct ways to orient stripes and suggest the generality of our predictions by applying them to several specific examples.
Results
A generic model of stripe orientation
Most mechanisms for periodic patterning are based on a simple core logic: local activation and long-range inhibition (LALI) (Meinhardt and Gierer(2000); Meinhardt and Gierer(1974); Gierer and Meinhardt(1972)). Local activation amplifies the pattern locally to create regions of increased pattern density; long-range inhibition ensures that these high density regions are separated by a minimum distance, thereby forming a periodic pattern (Figure 1A). For different biological systems the underlying nature of these interactions might be different (e.g. molecular vs. cellular vs. mechanical interactions). However, in each case, the core LALI logic is conserved.
We thus seek a model that captures the main features of the LALI logic. To do this, we take a few simple assumptions about the patterning mechanism:
The equations should be invariant under translation and rotation.
The equations should generate stable periodic patterns from a nearly homogeneous starting point.
The amplitude of these patterns should be finite.
The stable pattern should be stripes, not spots.
Given these conditions, the simplest possible partial differential equation (PDE) model that describes the time evolution of a pattern, ϕ(x,t), in a two-dimensional space, is:
| (1) |
where a, d are constants and ℒ is a differential operator defined as:
| (2) |
This equation is known as the Swift-Hohenberg equation, and has been used extensively to understand pattern formation in a variety of contexts (Cross and Hohenberg(1993)). In Supporting Online Information, section S1A, we show that this equation can be derived simply by considering the phenomenonology of periodic patterns and by appealing to the principle that models should be simple. This approach contrasts with that of many engineering or physics models, in which the underlying processes are well-understood and the model is used to understand the consequences of these processes. In biology, however, the underlying processes are often unmeasured, sometimes unknown and almost always complex. Thus the generality and simplicity of a phenomenological model is often valuable.
Since the Swift-Hohenberg equation compresses a multivariate set of PDEs into a single variable description, it may be difficult to have an intuition of the terms in equation 1. The most non-intuitive term is the form of the operator ℒ- what is its biological interpretation? The intuition becomes clear if we remember that the operator describes a system, and not a single molecule. This is analogous to representing the complexities of molecular transport by the diffusion operator ∇2 - it is a coarse-grained approximation of a much more complex system of interactions. With this viewpoint, ℒ describes the aggregate effect of nonlocal interactions in the system. Why can a single form of ℒ describe many mechanisms? It reflects the core logic of periodic patterning i.e. ℒ is a formal description of a local activation, long-range inhibition interaction (Supporting Online Information, section S1B). For example, in a activator/inhibitor reaction-diffusion system, we can conceptualize the activator to activate itself at short distances, and inhibit itself at long distances (indirectly, via the rapidly diffusing inhibitor). The operator ℒ then describes this spatially-distributed negative feedback.
Limitations of the model
The limitation of using a simple model is that it cannot describe all the features of a more complex biological model. To understand which features it can, and can’t, describe, we can explore the relationship between the simple model, specified by equation 1, and a more complex model. When the complex model can be specified by a set of coupled PDEs, equation 1 is a reasonable description of the full set of PDEs in a parameter regime near the onset of a Turing instability, see Supporting Online Information, section S1A. Equation 1 is therefore applicable to a wide range of biological mechanisms, provided patterning is via a Turing instability. However, we stress that this condition need not always hold for striped patterns. For example, stripes of pair rule gene expression do not require a Turing instability and instead involve specifying each stripe separately (Stanojevic et al. (1991)). When Turing instabilities are not required, models based on Equation 1 are not useful. In addition, the model breaks down if there are other instabilities in addition to the Turing instability. For example, stripes may be oriented by processes that involve travelling waves (Page et al. (2005); Sheth et al. (2012)), or oscillations (Sakamoto and Miyakawa(2008)); behaviours that cannot be described by equation 1 (Supporting Online Information, section S1C). Equation 1 and thus the results in this article, hold when stripes can arise in bulk from a homogeneous initial condition and form a stable steady state, in the absence of extreme boundary effects. In short: for a given mechanism, Equation 1 can predict some ways to orient stripes. It cannot rule out other, more complicated ways to orient stripes. However, we expect these exceptions to be qualitatively distinct from a Turing instability (e.g. oscillations or travelling waves) and thus can be ruled in or out by observation of the pattern dynamics in vivo.
Solving the equation
One approach we take to solving Equation 1 is to simulate it (see Supporting Online Information, section S2 for simulation details). However, these results do not make the connection to stripe orientation transparent. Therefore, we sought an analytical solution in order to build our understanding of the problem. The goal of this approach is to understand the qualitative features of stripe orientation, namely to determine i) what types of mechanism can orient stripes, and ii) in which direction the stripes tend to be oriented. This does not require modeling stripes in all orientations. Instead, the qualitative features can be derived by considering just the two extreme stripe orientations: stripes oriented along the y-axis, ‘A-stripes’, or stripes oriented along the x-axis, ‘B-stripes’ (Figure 1). To see this, note that if both A- and B-stripes are stable, then so are all intermediate stripe orientations. In contrast, if a given mechanism causes A-stripes to be unstable, then there will be a range of stable stripe orientations that centers around B-stripes and excludes A-stripes. As the strength of the orientation mechanism increases, the range of permissible orientations will narrow until only B-stripes are robustly formed. Thus, by considering just A- and B-stripes, we can determine the main qualitative features of stripe orientation (see also Supporting Online Information, section S3,4 for an expanded discussion).
We can now solve Equation 1 by making the ansatz that the solution is a superposition of A- and B-stripes, i.e.
| (3) |
where c.c denotes the complex conjugate. In Supporting Online Information, section S5, we show that this transforms Equation 1 into two separate equations:
| (4) |
| (5) |
These equations describe the time evolution of the amplitude of A- and B-stripes respectively and, as such, are often referred to as ‘amplitude equations’ (Van Hecke et al. (1994)). The parameter r denotes the strength of the Turing instability. For r < 0, the steady state pattern is uniform in space, whereas for r > 0, we transition into the Turing regime in which periodic patterns spontaneously arise. We analyze these equations in the regime r < 0, which corresponds to the regime of straight but unoriented stripes. We expect the analysis to yield qualitative insights outside this regime, although cannot prove this formally.
Having obtained the amplitude equations, we must then solve them to determine whether A- and/or B-stripes are produced. To do this, we look for the (nonzero) steady states of Equations 4&5, which are either A-stripes, , or B-stripes, . We then examine the stability of these steady states to small variations, (δA, δB). For A-stripes, we consider . Substituting into the above equations gives:
| (6) |
| (7) |
i.e. A-stripes are a stable steady state solution. Now, the symmetry of equation 4&5 under A↔B means that B-stripes will also be a solution, meaning that Equation 1 alone cannot orient stripes along a particular direction. To successfully orient stripes, the symmetry A↔B must be broken. In the remainder of this article, we use this framework to show that many different mechanisms to orient stripes fall into three qualitatively distinct categories. In each case, the category is defined by exactly how the symmetry A↔B is broken (The details of the algebra are outlined in Supporting Online Information, section S5–9).
Stripes are oriented perpendicular to a production gradient
The first modification we consider is something we call a ‘production gradient.’ Imagine a periodic patterning mechanism that amplifies periodic disturbances in pattern density. To create a production gradient, we add a spatially varying overall bias in pattern production (Figure 2A). To formulate this mathematically, we rewrite Equation 1 as:
| (8) |
where h(x) represents the spatially varying production rate, which we assume to be a gradient oriented along the x axis. As an example, consider a canonical reaction diffusion model that generates pattern by having two diffusible molecules regulate each other’s production rates. If, in addition, these production rates are regulated by a separate, graded morphogen signal, this would be a production gradient (Glimm et al. (2012)). A cell-based example could be where the generation of a particular cell type (e.g. melanocytes in the zebrafish skin) is controlled by a gradient.
Figure 2. Stripe orientation in the Swift-Hohenberg model.
A: Stripes are oriented perpendicular to a production gradient. Upper: Pattern production varies along the x axis, as schematized by the early spatial bias in pattern density. As the pattern evolves over time, we predict that this will generate stripes parallel to the y axis. Lower: Simulation of Equation 8 shows that stripes are oriented perpendicular to the production gradient.
B: Stripes are oriented parallel to a parameter gradient. A: Interaction strength varies along the x axis, schematized by the graded transparency of the colored sections. We predict that this will generate stripes parallel to the x axis. B: Simulation of Equation 11 confirms that stripes are oriented parallel to the parameter gradient.
C: Stripes are oriented by anisotropies. Upper: A schematic of local activation, long range inhibition with anisotropic interactions. Lower: Simulation of Equation 14 confirms the ability of anisotropies to orient stripes.
D: Stripes are oriented by directional growth. Upper: A schematic of periodic patterning in the presence of uniform growth along the x axis. Lower: Simulation of Equation 1 in the presence of anisotropic growth shows stripe alignment along the direction of growth.
To solve Equation 8, we convert it to a set of amplitude equations:
| (9) |
| (10) |
Here, hA is a constant and breaks the symmetry of the equations. In Supporting Online Information, section S6, we show that when , B-stripes lose their stability. Near the transition point, hcrit, only B-stripes are unstable, and stripes that are oriented between A- and B-stripes remain stable. However, as h increases further, we expect the range of stable orientations to narrow, until stripes are robustly aligned along a single direction i.e. A-stripes.
To explore this further, we simulated Equation 8 directly. In agreement with the analytical results, we found that a production gradient tends to align stripes perpendicular to the direction of the gradient. Further, the stripes become more sharply and reliably oriented as the strength of the gradient term increases (Figure 2A). Taken together, the simulations and analysis suggest that a production gradient can orient stripes perpendicular to the gradient.
Stripes are oriented parallel to a parameter gradient
A production gradient orients stripes perpendicular to the gradient. However, others have arrived at the opposite conclusion when simulating the impact of graded Fgf signaling on digit/non-digit patterning in the mouse limb i.e. Fgf oriented stripes are parallel to the gradient (Sheth et al. (2012)). This motivated us to consider a second type of gradient, which we term a ‘parameter gradient.’ In this case, the gradient does not stimulate production of the pattern variable, independent of the periodic pattern. Instead, it causes spatial variation in some parameter of the periodic patterning mechanism, such that the system transitions from a homogeneous sub-Turing region to a periodic, Turing region. Not all parameters in the underlying model can achieve this - it is only those which control the effective Turing instability parameter, r. Mathematically, we describe this effect as:
| (11) |
For a reaction diffusion model, an example of a parameter gradient would be a gradient of reaction rate parameters, achieved, for example, if some graded signal regulated the strength of interactions between activator and inhibitor molecules. As before, we recast Equation 11 as a set of amplitude equations:
| (12) |
| (13) |
where the parameter gradient, r(x), is oriented parallel to the x axis, and α is a constant that breaks the symmetry of the equations. In Supporting Online Information, section S7, we show that, for large enough spatial variation in the parameter r, that A-stripes lose their stability. As before, we expect that intermediate stripes between A- and B-stripes may still be stable. To investigate this further, we simulated Equation 11 with different parameter gradients, a(x). We found that a steep parameter gradient (large ∂a/∂x) produces stripes that were more reliably aligned along a single direction (Figure 2B). These results suggest that parameter gradients can orient stripes parallel to the gradient.
Stripes are oriented by anisotropies
The third modification we consider is when there is some intrinsic anisotropy in the mechanism. Anisotropy means that a parameter takes a different value depending on the direction that is being considered. This can be modelled by a simple modification of the differential operator, ℒ in Equation 2. In the isotropic case, ℒ is direction-independent i.e. . To incorporate anisotropy, this condition is relaxed i.e. to represent that the operator depends on the the direction (x,y) of the change, giving:
| (14) |
An example of this is a reaction diffusion model with anistropic diffusivities, in which molecules diffuse more rapidly along certain directions than along others (Shoji et al. (2002)). Anisotropy could also be present in cell motility, in the strength of intercellular signaling via oriented cellular protrusions, or in the mechanical properties of a tissue. When we add anisotropy to the amplitude equations, we obtain:
| (15) |
| (16) |
Anisotropy is captured by the two parameters, rA, rB. As long as rA ≠ rB, the symmetry of these equations is broken. In Supporting Online Information, section S8 we show that if rB > 2rA (i.e. a sufficiently large anisotropy), then A-stripes lose their stability. Once again, near the critical point rB ≈ 2rA, we expect a large range of possible stripe orientations that becomes progressively narrower as rB increases. We observed this qualitative trend when simulating Equation 14 (Figure 2C). These results imply that anisotropies in the tissue can orient stripes, and that the stripes are oriented along the direction that maximizes the parameter r.
A slightly different, but common source of anisotropy is anisotropic tissue growth. Again, the effect of this anisotropy is to make rA ≠ rB. Simulations (Figure 2D) and analysis (Supporting Online Information, section S9) demonstrate that stripes tend to be oriented parallel to the direction of uniform tissue growth. We note that this is achieved only if the growth is fast compared to the patterning kinetics. In many cases (e.g. rugae in the palate (Economou et al. (2012))), growth occurs on a timescale much slower than patterning and so stripes need not be oriented by growth.
The simple model can correctly predict stripe orientation in more complicated models
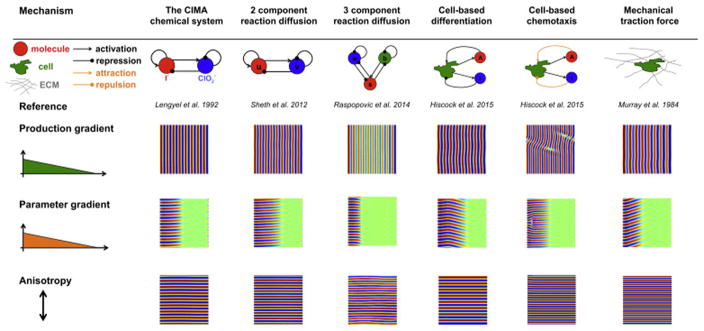
In summary, our analysis of a simple model (equation 1) predicts three ways to orient stripes. Do these results hold for more complex models? To answer this question, we took six previously published models - spanning molecular, cellular and mechanical processes - and aimed to orient stripes by introducing gradients in production, parameters, or adding anisotropies(see Supporting Online Information, section S10 for a description of each model. Particular care must be taken for the case of a parameter gradient, in which the appropriate parameter(s) are those that can transition the system from the sub-Turing to the Turing regime). In each case, we find that our simple model could correctly predict the simulation results of the more complex models (Figure 3). However, our simulations also revealed parameter regimes for which a single orientation mechanism alone can only partially orient the stripes. This suggests that some stripe-orientation mechanisms may be sensitive to exact parameter choice and further investigation is required to comment on the robustness of stripe orientation more generally.
Figure 3.
Simulations of 6 different Turing models (Lengyel and Epstein(1992), Sheth et al. (2012); Raspopovic et al. (2014); Hiscock and Megason(2015); Murray and Oster(1984a)) reveal common features of stripe orientation, that are consistent with the simpler model presented here.
Despite the diversity and complexity of the different mechanisms studied, our work shows that three types of stripe orientation appear to be common to many mechanisms in certain parameter regimes, and are consistent with a much simpler model. However, this does not rule out there being more complicated mechanisms to orient stripes that are not captured by equation 1. For example, we found parameter regimes in the CIMA system where stripes are oriented by oscillations, and in the 2 component reaction-diffusion system where stripes are oriented by travelling waves (see Supporting Online Information, section S1C). However, these are qualitatively distinct mechanisms and thus should be distinguishable by specifically designed biological experiments.
Conclusions
In this article, we have addressed the question of how Turing-like stripes are oriented. By analyzing a generic model of stripe orientation that applies given a limited set of assumptions, we have found three qualitatively distinct types of orientation mechanism. These can be concisely summarized by rewriting Equation 1 as:
| (17) |
Here, (i) h(x)is a production gradient, (ii) a(x) is a parameter gradient, and (iii) represents anisotropies. We find that (i) production gradients orient stripes perpendicular to the gradient; (ii) parameter gradients orient stripes parallel to the gradient; and (iii) anisotropies orient stripes along the direction of the anisotropy.
Overall, this analysis provides an intuition for understanding general features of stripe orientation. It can explain and unify existing results that have simulated specific models. It can also be readily applied to new biological scenarios and can be used to critically evaluate existing hypotheses. We discuss these features in the context of limb development in the case study section. We thus hope that the results in this article provide an intuition for the simple and universal features of stripe orientation amidst the complexities and variety of the underlying biology.
Supplementary Material
Limb patterning as a case study.
To illustrate how to apply our general model to a specific case, we consider an example: digit/non-digit patterning in the mouse limb. The formation of regularly spaced digits (and metacarpals) was ascribed to a Turing-like mechanism several decades ago (Newman and Frisch(1979)), with a number of candidate molecules being proposed (Badugu et al. (2012); Zhu et al. (2010; Miura and Shiota(2000)), although the hypothesis has remained controversial. Recent studies, however, strongly suggest that digit/non-digit patterning is indeed periodic, as evidenced by mouse mutants with periodic but more closely spaced digits (Sheth et al. (2012)). Further, there is data that supports a reaction diffusion model of patterning, based on Wnts and BMPs (Raspopovic et al. (2014)). This specific model has been simulated in detail and can recapitulate many features of limb patterning in silico. However, roles for alternative molecular, cellular or mechanical processes are difficult to rule out, particularly since extensive cell movement and ECM remodeling is also observed during patterning, at least in vitro (Raspopovic et al. (2014)).
If digits are patterned via a Turing-like mechanism as a set of stripes, it raises the question: what orients the stripes so that the digits always form parallel to the limb? Some hints come from an in vitro model of digit formation that lacks several important signalling centres e.g. Shh secreted posteriorly, and AER-derived Fgf. In this case, a periodic pattern still forms, although the orientation of the pattern is no longer well-defined thereby generating a labryinthine pattern (Paulsen and Solursh(1988); Miura and Shiota(2000)) (see Figure 4A).
There are several existing hypotheses for digit alignment that have been generated by simulating specific reaction-diffusion models. Sheth et al. (2012) advance the idea that a combination of Fgf and Hox gradients modulate the reaction terms in the reaction-diffusion equations and that this is sufficient to orient stripes (also reviewed in (Green and Sharpe(2015))). Raspopovic et al. (2014) use a slightly more complex reaction-diffusion model and suggest that, in addition to the Fgf and Hox gradients, anisotropic growth of the limb bud contributes to digit orientation. A third hypothesis is that the geometry of the limb dictates boundary conditions that orient stripes (Newman and Frisch(1979)). However, the work of Raspopovic et al. (2014) and Sheth et al. (2012), which use measured limb bud geometries in their simulations, suggests that boundary conditions alone are insufficient. Given this existing data - from both experiments and simulations - what can our analysis add?
The first strength of the approach presented here is that it can generalize existing hypotheses. Stripe orientation by Fgf/Hox gradients falls into the category of a parameter gradient - the gradient moves the system from sub-Turing to Turing, and orients stripes parallel to the gradient. Immediately, our analysis predicts that many other parameter gradients could also orient stripes. Table 1 gives some example hypotheses. Similarly, stripe orientation by anisotropic growth is just one example of the more general phenomenon of stripe orientation by anisotropies. Table 1 provides some other examples.
Our model also predicts the existence of a third way to orient stripes - a production gradient along the anterior-posterior axis of the limb that orients stripes perpendicular to the gradient. The obvious candidate molecule is Shh, although a Shh null mouse still has correctly oriented digits (Sheth et al. (2013); Sheth et al. (2007)) and therefore an alternative gradient must be sought.
The second strength of our approach is that it allows us to interpret existing data and hypotheses and to determine the uniqueness of any simulation results. Current data on digit alignment is largely descriptive - digits emerge as stripes that fan out radially along the PD axis of the limb bud (Figure 4B). Thus stripes must be oriented in a way that reflects this radial geometry. For this reason, alignment via a production gradient seems unlikely, since it is hard to construct a gradient along the AP axis that would respect the radial geometry. In contrast, a parameter gradient controlled by the AER is naturally in a radial orientation. Further, there is a transition from a sub-Turing no-digit regime (the zeugopod) to a Turing, digit regime (the autopod), again consistent with a parameter gradient. Orientation of digits by anisotropies is also plausible, but requires the anisotropy to be radially organized. This is certainly possible - for example, a radially directed gradient of Wnt5a regulates anisotropic cell behaviours via the PCP pathway as the digits form (Gao et al. (2011) ).
Thus, stripes are likely oriented by either a parameter gradient or by anisotropies. The specific models of Sheth et al. (2012) and Raspopovic et al. (2014) are important in that they developed specific hypotheses for what these parameter gradients and anisotropies are - namely reaction parameters and anisotropic growth in a reaction diffusion system, using a BMP- and Wnt-based model that has strongest experimental support. However, our modelling suggests that other mechanisms, within the same broad categories of parameter gradients and anisotropies, could be at play. To distinguish these models requires experiments that are specific to the proposed orientation mechanism e.g. directly perturbing the proposed reaction parameters without affecting anisotropic growth and measuring the effect on stripe orientation. In vitro chondrogenesis models (Paulsen and Solursh(1988)) are an appealing system in which to disentangle the interdependence of growth and patterning that complicate the interpretation of in vivo experiments.
In summary, we hope that this example illustrates how our simple but generic model can help to generalize and critically evaluate results from specific models and existing hypotheses.
Box A/Figure A. Applications of our results to digit/non-digit patterning in the mouse limb.
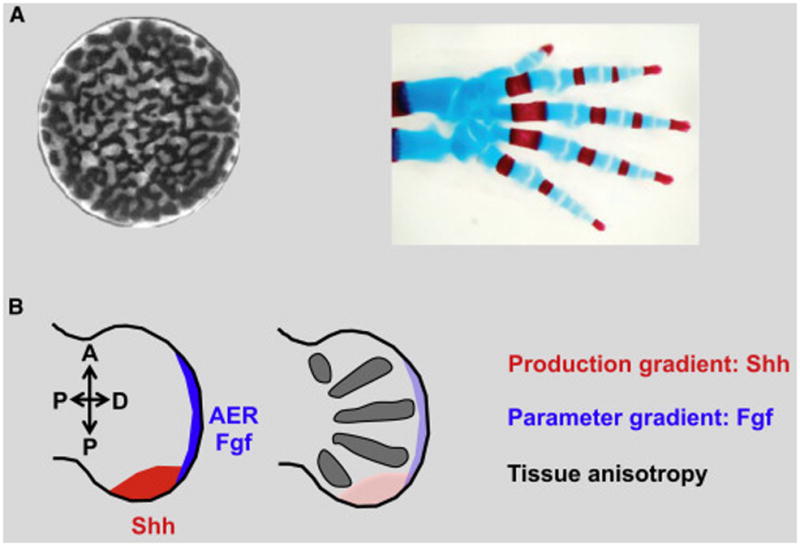
A: Left: labryinthine periodic patterns in cultured mouse limb cells (reproduced with permission from (Miura and Shiota(2000))) contrasts to robustly oriented skeletal elements of a mouse limb (adapted from Sheth et al. (2012). Reprinted with permission from AAAS.).
B: Left: The mouse limb develops under the influence of several morphogen gradients (coloured sections illustrate gradient sources) (Tickle(2006)). Right: Skeletal elements (forming the metacarpals and subsequently the digits) form with stereotyped orientation, parallel to the axis of the limb and fanning out radially.
Table A.
Hypotheses for digit orientation mechanisms for molecular, cellular and mechanical processes.
| Mechanism to orient stripes | Molecular | Type of periodic patterning mechanism | |
|---|---|---|---|
| Cell-based | Mechanical | ||
| Production gradient | Shh stimulates molecular production | Shh stimulates production of interdigit cells | Shh promotes ECM production |
| Parameter gradient | Fgf affects interactions between two molecules | Fgf modulates intercellular signaling | Fgf controls tissue stiffness |
| Tissue anisotropy | Diffusion is anisotropic | Cell motility is anisotropic | Tissue elasticity tensor is anisotropic |
Acknowledgments
Funding sources
This work is supported by the National Institutes of Health (grants R01 DC010791 and R01 GM107733). T.W.H. is also supported by the Herchel Smith Graduate Fellowship.
Footnotes
Contributions
T.W.H. and S.G.M designed the research and wrote the paper. T.W.H. performed the mathematical analysis.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Badugu A, Kraemer C, Germann P, Menshykau D, Iber D. Digit patterning during limb development as a result of the bmp-receptor interaction. Scientific reports. 2012;2 doi: 10.1038/srep00991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cross MC, Hohenberg PC. Pattern formation outside of equilibrium. Reviews of modern physics. 1993;65:851. [Google Scholar]
- De Wit A, Borckmans P, Dewel G. Instabilities and Nonequilibrium Structures IV. Springer; 1993. Turing structures in the presence of gradients; pp. 247–258. [Google Scholar]
- Economou AD, Ohazama A, Porntaveetus T, Sharpe PT, Kondo S, Basson MA, Gritli-Linde A, Cobourne MT, Green JB. Periodic stripe formation by a turing mechanism operating at growth zones in the mammalian palate. Nature genetics. 2012;44:348–351. doi: 10.1038/ng.1090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frohnhöfer HG, Krauss J, Maischein HM, Nüsslein-Volhard C. Iridophores and their interactions with other chromatophores are required for stripe formation in zebrafish. Development. 2013;140:2997–3007. doi: 10.1242/dev.096719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao B, Song H, Bishop K, Elliot G, Garrett L, English MA, Andre P, Robinson J, Sood R, Minami Y, et al. Wnt signaling gradients establish planar cell polarity by inducing vangl2 phosphorylation through ror2. Developmental cell. 2011;20:163–176. doi: 10.1016/j.devcel.2011.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gierer A, Meinhardt H. A theory of biological pattern formation. Kybernetik. 1972;12:30–39. doi: 10.1007/BF00289234. [DOI] [PubMed] [Google Scholar]
- Glimm T, Zhang J, Shen YQ, Newman SA. Reaction–diffusion systems and external morphogen gradients: The two-dimensional case, with an application to skeletal pattern formation. Bulletin of mathematical biology. 2012;74:666–687. doi: 10.1007/s11538-011-9689-6. [DOI] [PubMed] [Google Scholar]
- Green JB, Sharpe J. Positional information and reaction-diffusion: two big ideas in developmental biology combine. Development. 2015;142:1203–1211. doi: 10.1242/dev.114991. [DOI] [PubMed] [Google Scholar]
- Hamada H, Watanabe M, Lau HE, Nishida T, Hasegawa T, Parichy DM, Kondo S. Involvement of delta/notch signaling in zebrafish adult pigment stripe patterning. Development. 2014;141:318–324. doi: 10.1242/dev.099804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hiscock TW, Megason SG. Mathematically guided approaches to distinguish models of periodic patterning. Development. 2015;142:409–419. doi: 10.1242/dev.107441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondo S, Asai R. A reaction-diffusion wave on the skin of the marine angelfish pomacanthus. Nature. 1995;376:765–768. doi: 10.1038/376765a0. [DOI] [PubMed] [Google Scholar]
- Kondo S, Miura T. Reaction-diffusion model as a framework for understanding biological pattern formation. Science. 2010;329:1616–1620. doi: 10.1126/science.1179047. [DOI] [PubMed] [Google Scholar]
- Lacalli T, Wilkinson D, Harrison L. Theoretical aspects of stripe formation in relation to drosophila segmentation. Development. 1988;104:105–113. doi: 10.1242/dev.104.1.105. [DOI] [PubMed] [Google Scholar]
- Lengyel I, Epstein IR. A chemical approach to designing turing patterns in reaction-diffusion systems. Proceedings of the National Academy of Sciences. 1992;89:3977–3979. doi: 10.1073/pnas.89.9.3977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lubensky DK, Pennington MW, Shraiman BI, Baker NE. A dynamical model of ommatidial crystal formation. Proceedings of the National Academy of Sciences. 2011;108:11145–11150. doi: 10.1073/pnas.1015302108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maini P, Myerscough M, Winter K, Murray J. Bifurcating spatially heterogeneous solutions in a chemotaxis model for biological pattern generation. Bulletin of mathematical biology. 1991;53:701–719. doi: 10.1007/BF02461550. [DOI] [PubMed] [Google Scholar]
- Meinhardt H, Gierer A. Applications of a theory of biological pattern formation based on lateral inhibition. Journal of cell science. 1974;15:321–346. doi: 10.1242/jcs.15.2.321. [DOI] [PubMed] [Google Scholar]
- Meinhardt H, Gierer A. Pattern formation by local self-activation and lateral inhibition. Bioessays. 2000;22:753–760. doi: 10.1002/1521-1878(200008)22:8<753::AID-BIES9>3.0.CO;2-Z. [DOI] [PubMed] [Google Scholar]
- Menshykau D, Blanc P, Unal E, Sapin V, Iber D. An interplay of geometry and signaling enables robust lung branching morphogenesis. Development. 2014;141:4526–4536. doi: 10.1242/dev.116202. [DOI] [PubMed] [Google Scholar]
- Miura T, Shiota K. Tgfβ2 acts as an “activator” molecule in reaction-diffusion model and is involved in cell sorting phenomenon in mouse limb micromass culture. Developmental Dynamics. 2000;217:241–249. doi: 10.1002/(SICI)1097-0177(200003)217:3<241::AID-DVDY2>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- Mou C, Jackson B, Schneider P, Overbeek PA, Headon DJ. Generation of the primary hair follicle pattern. Proceedings of the National Academy of Sciences. 2006;103:9075–9080. doi: 10.1073/pnas.0600825103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray JD, Maini P, Tranquillo R. Mechanochemical models for generating biological pattern and form in development. Physics Reports. 1988;171:59–84. [Google Scholar]
- Murray JD. How the leopard gets its spots. Scientific American. 1988;258:80–87. [Google Scholar]
- Murray JD. Mathematical biology ii: Spatial models and biomedical applications. Springer; 2003. [Google Scholar]
- Murray J, Oster G. Cell traction models for generating pattern and form in morphogenesis. Journal of mathematical biology. 1984a;19:265–279. doi: 10.1007/BF00277099. [DOI] [PubMed] [Google Scholar]
- Murray J, Oster G. Generation of biological pattern and form. Mathematical Medicine and Biology. 1984b;1:51–75. doi: 10.1093/imammb/1.1.51. [DOI] [PubMed] [Google Scholar]
- Myerscough M, Maini P, Painter K. Pattern formation in a generalized chemotactic model. Bulletin of mathematical biology. 1998;60:1–26. doi: 10.1006/bulm.1997.0010. [DOI] [PubMed] [Google Scholar]
- Nakamasu A, Takahashi G, Kanbe A, Kondo S. Interactions between zebrafish pigment cells responsible for the generation of turing patterns. Proceedings of the National Academy of Sciences. 2009;106:8429–8434. doi: 10.1073/pnas.0808622106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman SA, Frisch H. Dynamics of skeletal pattern formation in developing chick limb. Science. 1979;205:662–668. doi: 10.1126/science.462174. [DOI] [PubMed] [Google Scholar]
- Page KM, Maini PK, Monk NA. Complex pattern formation in reaction–diffusion systems with spatially varying parameters. Physica D: Nonlinear Phenomena. 2005;202:95–115. [Google Scholar]
- Paulsen DF, Solursh M. Microtiter micromass cultures of limb-bud mesenchymal cells. In vitro cellular & developmental biology. 1988;24:138–147. doi: 10.1007/BF02623891. [DOI] [PubMed] [Google Scholar]
- Raspopovic J, Marcon L, Russo L, Sharpe J. Digit patterning is controlled by a bmp-sox9-wnt turing network modulated by morphogen gradients. Science. 2014;345:566–570. doi: 10.1126/science.1252960. [DOI] [PubMed] [Google Scholar]
- Rawls JF, Mellgren EM, Johnson SL. How the zebrafish gets its stripes. Developmental biology. 2001;240:301–314. doi: 10.1006/dbio.2001.0418. [DOI] [PubMed] [Google Scholar]
- Sakamoto F, Miyakawa K. Formation of somitogenesis-like pattern in a reaction–diffusion system. Journal of the Physical Society of Japan. 2008;77:083801. [Google Scholar]
- Sheth R, Bastida MF, Ros M. Hoxd and gli3 interactions modulate digit number in the amniote limb. Developmental biology. 2007;310:430–441. doi: 10.1016/j.ydbio.2007.07.023. [DOI] [PubMed] [Google Scholar]
- Sheth R, Grégoire D, Dumouchel A, Scotti M, Pham JMT, Nemec S, Bastida MF, Ros MA, Kmita M. Decoupling the function of hox and shh in developing limb reveals multiple inputs of hox genes on limb growth. Development. 2013;140:2130–2138. doi: 10.1242/dev.089409. [DOI] [PubMed] [Google Scholar]
- Sheth R, Marcon L, Bastida MF, Junco M, Quintana L, Dahn R, Kmita M, Sharpe J, Ros MA. Hox genes regulate digit patterning by controlling the wavelength of a turing-type mechanism. Science. 2012;338:1476–1480. doi: 10.1126/science.1226804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shoji H, Iwasa Y, Mochizuki A, Kondo S. Directionality of stripes formed by anisotropic reaction–diffusion models. Journal of Theoretical Biology. 2002;214:549–561. doi: 10.1006/jtbi.2001.2480. [DOI] [PubMed] [Google Scholar]
- Shyer AE, Tallinen T, Nerurkar NL, Wei Z, Gil ES, Kaplan DL, Tabin CJ, Mahadevan L. Villification: how the gut gets its villi. Science. 2013;342:212–218. doi: 10.1126/science.1238842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sick S, Reinker S, Timmer J, Schlake T. Wnt and dkk determine hair follicle spacing through a reaction-diffusion mechanism. Science. 2006;314:1447–1450. doi: 10.1126/science.1130088. [DOI] [PubMed] [Google Scholar]
- Stanojevic D, Small S, Levine M. Regulation of a segmentation stripe by overlapping activators and repressors in the drosophila embryo. Science. 1991;254:1385–1387. doi: 10.1126/science.1683715. [DOI] [PubMed] [Google Scholar]
- Tickle C. Making digit patterns in the vertebrate limb. Nature Reviews Molecular Cell Biology. 2006;7:45–53. doi: 10.1038/nrm1830. [DOI] [PubMed] [Google Scholar]
- Turing AM. The chemical basis of morphogenesis. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences. 1952;237:37–72. doi: 10.1098/rstb.2014.0218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Hecke M, Hohenberg P, Van Saarloos W. Fundamental Problems in Statistical Mechanics VIII. New York: Elsevier; 1994. Amplitude equations for pattern forming systems; pp. 245–278. [Google Scholar]
- Yamaguchi M, Yoshimoto E, Kondo S. Pattern regulation in the stripe of zebrafish suggests an underlying dynamic and autonomous mechanism. Proceedings of the National Academy of Sciences. 2007;104:4790–4793. doi: 10.1073/pnas.0607790104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamanaka H, Kondo S. In vitro analysis suggests that difference in cell movement during direct interaction can generate various pigment patterns in vivo. Proceedings of the National Academy of Sciences. 2014;111:1867–1872. doi: 10.1073/pnas.1315416111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu J, Zhang YT, Alber MS, Newman SA. Bare bones pattern formation: a core regulatory network in varying geometries reproduces major features of vertebrate limb development and evolution. PLoS One. 2010;5:e10892. doi: 10.1371/journal.pone.0010892. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.