Using Computational Modeling To Optimize the Design of Antibodies That Trap Viruses in Mucus

Abstract

Immunoglobulin G (IgG) antibodies that trap viruses in cervicovaginal mucus (CVM) via adhesive interactions between IgG-Fc and mucins have recently emerged as a promising strategy to block vaginally transmitted infections. The array of IgG bound to a virus particle appears to trap the virus by making multiple weak affinity bonds to the fibrous mucins that form the mucus gel. However, the antibody characteristics that maximize virus trapping and minimize viral infectivity remain poorly understood. Toward this goal, we developed a mathematical model that takes into account physiologically relevant spatial dimensions and time scales, binding, and unbinding rates between IgG and virions and between IgG and mucins, as well as the respective diffusivities of virions and IgG in semen and CVM. We then systematically explored the IgG–antigen and IgG–mucin binding and unbinding rates that minimize the flux of infectious HIV arriving at the vaginal epithelium. Surprisingly, contrary to common intuition that infectivity would drop monotonically with increasing affinities between IgG and HIV, and between IgG and mucins, our model suggests maximal trapping of HIV and minimal flux of HIV to the epithelium are achieved with IgG molecules that exhibit (i) rapid antigen binding (high k_on) rather than very slow unbinding (low k_off), that is, high-affinity binding to the virion, and (ii) relatively weak affinity with mucins. These results provide important insights into the design of more potent “mucotrapping” IgG for enhanced protection against vaginally transmitted infections. The model is adaptable to other pathogens, mucosal barriers, geometries, and kinetic and diffusional effects, providing a tool for hypothesis testing and producing quantitative insights into the dynamics of immune-mediated protection.

Antibodies (Abs) produced by our immune system are found in abundant quantities in both blood and mucosal secretions and serve as key molecules that help regulate numerous complex defense mechanisms against foreign pathogens.¹ For example, Abs can directly block contact between viruses and target cells, a process known as neutralization.² Abs can also facilitate other protective functions, such as ingestion and destruction of the pathogens (opsonization) or infected cells (antibody-dependent cellular cytotoxicity, or ADCC) by specialized immune cells, as well as activation of a cascade of enzymes that lead to direct lysis of the pathogen membrane (complement).³ These various protective mechanisms most certainly contribute to the robust protection observed with topically delivered Abs against mucosally transmitted infections in a multitude of animal studies.⁴

In the female reproductive tract, immunoglobulin G (IgG) is the predominant Ab secreted into cervicovaginal mucus (CVM) coating the vaginal epithelium,⁵ yet its role in protection against vaginal infections is not yet well understood. CVM is composed primarily of a heterogeneous mesh network of mucin fibers with low viscosity fluid-filled pores, most of which are larger than the majority of viruses.⁶ Indeed, HIV virions are capable of diffusing nearly unimpeded through the mucus gel.⁷ Noting the abundance of Abs produced and secreted by the immune system into mucus secretions, we hypothesized that virus-specific IgG may work in tandem with the mucin mesh to prevent infections. We recently showed that IgG can indeed trap viruses in CVM, thereby facilitating an additional and highly potent mechanism of immune protection.^5c Interestingly, the diffusivity of IgG in mucus is only slowed ~10–20% compared to in buffer;⁸ hence, individual IgG molecules must make only weak and transient bonds with mucins and thus were previously thought incapable of effectively trapping viruses in mucus gels. Nevertheless, as IgG accumulates on the virus surface, the array of virion-bound IgG can collectively form multiple weak Ab–mucin bonds between the virion and CVM, thereby generating sufficient avidity to slow or even immobilize individual virions in mucus akin to multiple weak links formed by a Velcro patch. Trapping viruses in mucus not only reduces the flux of virus reaching target cells in the vaginal epithelium, but trapped viruses are also quickly eliminated along with natural mucus clearance mechanisms, as evident by protection against vaginal herpes transmission using a non-neutralizing monoclonal IgG.^5c

Many viruses, including HIV, can rapidly diffuse through mucus gels under physiological conditions, limiting the window of opportunity for Abs to accumulate on the virus surface before the virus reaches and infects the underlying vaginal epithelium.⁹ The extent to which IgG can hinder the diffusion of viruses in mucus, and consequently the potency of protection based on IgG-mediated trapping of viruses, is thus critically dependent on whether virus-specific IgG, topically delivered or elicited by vaccine or prior infection, can accumulate rapidly enough on a virion and impart sufficient binding avidity between the virion and mucus to trap the virus before it can reach the underlying cells. We are interested in developing potent “muco-trapping” IgG (i.e., that enables effective trapping with fewer virion-bound IgG) not only because this would (i) reduce the dose of IgG needed for passive immunization of the vagina but also because this would (ii) likely improve protection against viruses, such as HIV, that have only a small number of antigens on their surface.

Our aim quickly posed a conundrum: although fewer virus-bound IgGs would be needed to trap a virus if each bound IgG binds more tightly to mucins, high IgG affinity to mucins would reduce or even prevent the diffusive mobility of IgG in the mucus gel. Because the Smoluchowski encounter rate between two diffusive species is proportional to the sum of their diffusivities, mucin-associated IgG would therefore have markedly reduced encounters with virions and, by definition, exhibit lower rates of binding to viral antigens. The IgG–mucin and IgG–antigen affinities and actual binding/unbinding rates that maximize viral trapping and protection will depend on specific characteristics of the target virus, such as its diffusivity in mucus and surface antigen density.

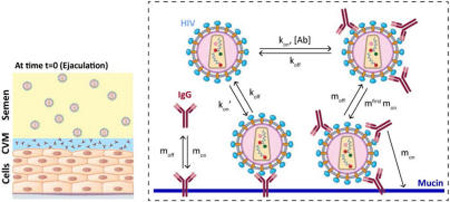
Because an empirical, experimental determination of these numerous parameters and their relative contributions to trapping and protection remains exceedingly challenging, we turned to mathematical modeling to better understand the subtle interplay between the various kinetic and diffusive processes among IgG, virions, and CVM during vaginal transmission of sexually transmitted viruses. Specifically, we consider CVM containing a specific concentration of antigen-specific IgGs that possess tunable binding and unbinding kinetics to mucins in CVM subjected to introduction of virus-laden semen (Figure 1). With a mathematical model, starting from the moment of viral deposition in the female reproductive tract, we can model the subsequent codiffusion of virions and IgG as well as the binding and unbinding kinetics among IgG molecules, viruses, and mucins and freely explore the vast parameter space in the context of physiologically relevant spatial dimensions and time scales. As a proof-of-concept, we focused on HIV, given the great need for alternative strategies to prevent vaginal HIV transmission; indeed, passive immunization has recently garnered attention as a promising approach for HIV prophylaxis.¹⁰ In turn, the model allows us to explore whether, and the extent to which, tuning IgG–mucin affinity can facilitate improved protection against vaginal HIV infection. In doing so, we report that the model suggests a “sweet spot” in the characteristics of IgG that maximize trapping and minimize infectious flux of HIV to the vaginal epithelium.

Figure 1.

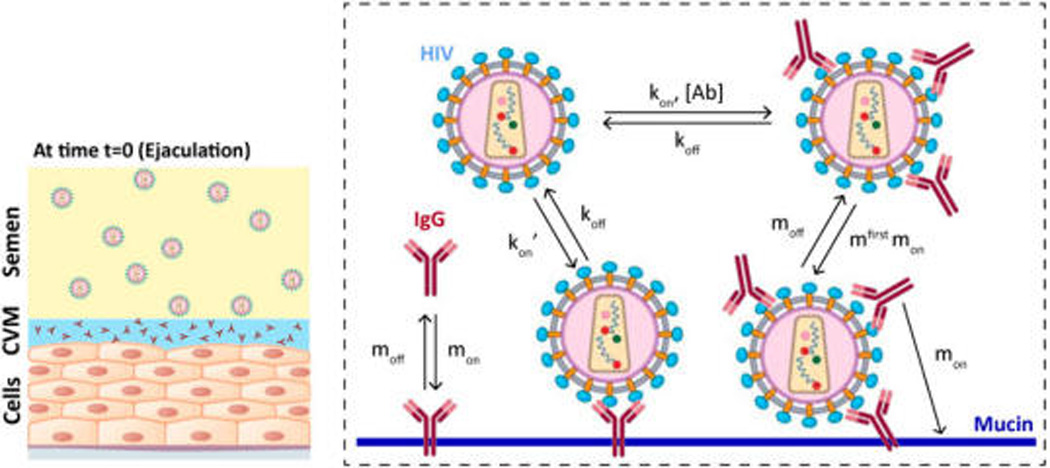
Schematic of our model that captures the dynamics of HIV from seminal fluid diffusing across a cervicovaginal mucus (CVM) layer containing HIV-binding IgG to reach the underlying vaginal epithelium. To reduce infection, IgG must bind to HIV in sufficient quantities to neutralize or to trap the virions in mucus before HIV virions successfully penetrate CVM. Our model captures the tandem effects of IgG–antigen binding kinetics (k_on, k_off) as well as IgG–mucin interactions (m_on, m_off).

RESULTS

Incorporating Mucin-Binding Kinetics into Previous Models for HIV Penetration of Ab-Laden CVM

We have previously modeled the diffusion of HIV through CVM by combining a stochastic/deterministic hybrid model for the one-dimensional Brownian movement of individual HIV virions together with a continuum model that describes the average local concentration of broadly neutralizing monoclonal IgG in CVM.¹¹ That model allowed us to show that a multitude of weak bonds between virion-bound IgG and mucins alone, defined by the ratios of IgG diffusion in mucus versus buffer (α) in the range of 0.8–0.9, is sufficient to immobilize the vast majority of HIV near the semen/CVM interface. Nevertheless, to further explore the IgG trapping potency across the full range of IgG–mucin affinity, it was necessary to incorporate additional complexity into the model. First, when modeling IgG that binds more tightly to mucins, we made the assumption that the probability of a successful bond between an IgG molecule and the corresponding viral antigen is directly proportional to the overall collision frequencies between the two bodies, which can be described by the classical Smoluchowski principle.¹² Because an IgG bound to mucins will possess a far reduced range of motion relative to that of a free, unbound IgG molecule, the bound IgG should possess a reduced k_on rate, denoted k_on′, proportional to the reduction in collision frequency with viral antigen, which in turn can be approximated by the ratios of the diffusivity of IgG versus mucins in CVM. Although the diffusivity of individual mucins in CVM remains unknown, we have previously shown that CVM is composed of heavily bundled mucins that likely reflect an exceedingly limited range of motion for individual mucins.⁶ We thus made a very conservative estimate that an IgG bound to mucin will possess a 30-fold reduced k_on rate compared to individual free IgG (i.e., k_on′ = k_on/30), which roughly equates to assuming the range of motion of mucins to match that for individual HIV virions. Although obviously an overconservative assumption, further reduction in k_on′ does not meaningfully affect estimates generated by our model (Figure S4).

A second important detail we incorporated into our model is the kinetics of IgG binding to and unbinding from mucins, which we termed m_on and m_off, respectively. Experimentally, m_on and m_off appear to be extremely transient and difficult to measure individually⁸ (see also the Supporting Information). Instead, IgG–mucin affinity is inherently reflected by the diffusion coefficients of IgG in CVM versus in buffer, which we denote α. α reflects the fraction of bound versus unbound IgG at any moment in time and is equivalent to the ratio m_off/(m_off + [M]m_on) at steady state. Assuming IgG binding to its antigen does not increase its affinity to mucins, the rates with which individual IgG can bind to mucins must be far faster than the rate of virion-associated IgG binding to mucins. We thus introduced a correction factor of ~30 for the mucin-association kinetics for virion-bound IgG, which is equivalent to the difference in diffusivities of HIV versus IgG in CVM. This correction was necessary to ensure we do not overestimate the trapping potency of viruses.

As a first step toward understanding how IgG–mucin affinity can affect trapping potency, we modeled the probability and duration of HIV–IgG complexes associating with mucins in CVM containing 1 µg/mL NIH45-46 with varying IgG–mucin affinity. Naturally, HIV with surface IgG possessing no affinity to mucins, defined by α = 1, never binds to mucins, and the HIV–IgG complex undergoes free diffusion for the entire duration (Figure 2A). When IgG–mucin affinity is slightly increased such that individual IgGs associate with mucins ~5 and 10% of the time (i.e., α = 0.95 and 0.9, respectively), the fraction of time an HIV–IgG complex spends freely diffusing in mucus begins to decrease, with a corresponding increase in the fraction of time spent associated with mucins (Figure 2B,C). Interestingly, the fraction of time the HIV–IgG complex associates with mucins appears to peak between α = 0.1 and 0.25 (Figure 2D–F). This is attributed to the facts that (i) increased IgG–mucin affinity markedly reduces the fraction of NIH45-46 that can freely diffuse and readily bind to HIV, including IgG that diffuses from CVM into the semen layer and binds to HIV virions before they enter the CVM layer (Figure S2); and (ii) mucin-associated IgG captures HIV with far lower efficiency (i.e., reduced k_on′ vs k_on). These two factors together increase the number of HIV virions with no bound IgG. With further increases of mucin affinity to α = 0.01, the amount of HIV free of bound IgG dominates relative to HIV–IgG complexes, and most HIV again undergoes Brownian motion in CVM (Figure 2G).

Figure 2.

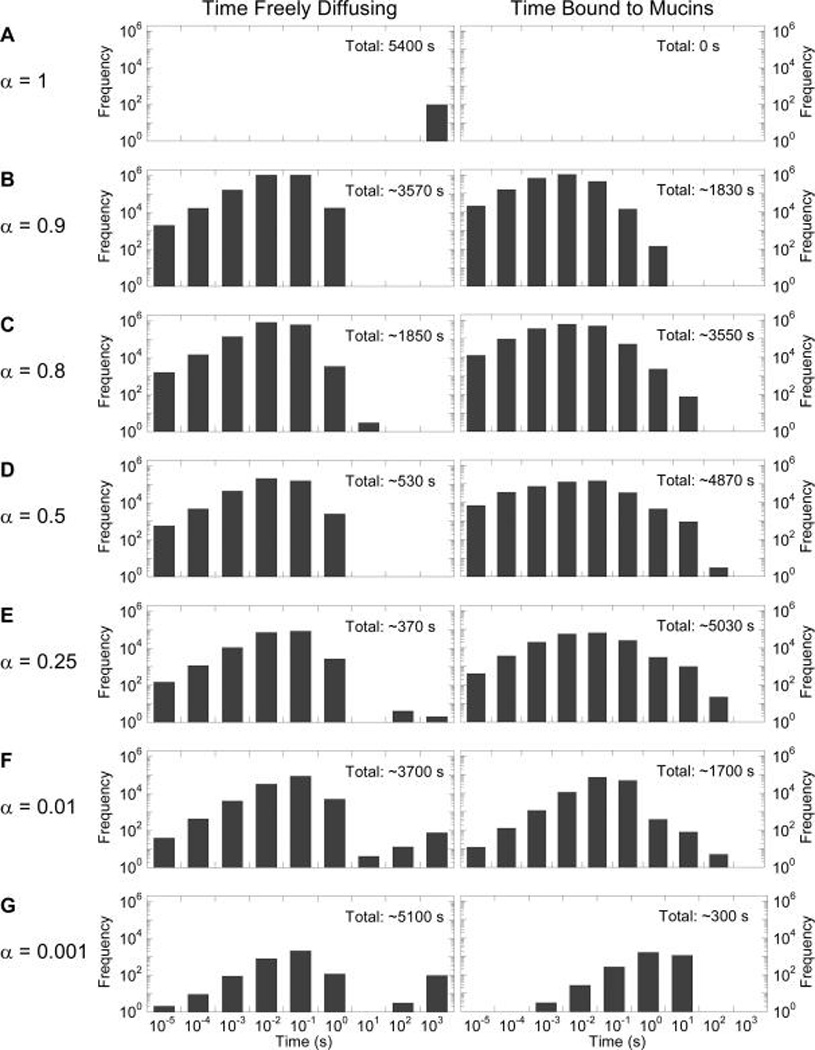
Distribution of time HIV virions spend freely diffusing or associated with mucins in CVM containing 1 µg/mL NIH45-46 with different affinity to mucins, ranging from no affinity at α = 1 to very strong affinity at α = 0.001. To minimize bias toward virions with no surface-bound IgG undergoing free diffusion, Abs are allowed to accumulate on HIV for 30 min first prior to measuring the time of free diffusion or association with mucins for the subsequent 90 min.

Influence of IgG–Mucin Affinity on Maximizing Trapping Potency and Vaginal Protection

We next quantified how the probability of HIV–mucin association affects the fraction of HIV that can penetrate CVM and reach the underlying vaginal epithelium and the corresponding reduction in infectivity based on the decrease in HIV–Env free of bound IgG on those virions.⁹ In good agreement with the estimate of the fraction of time spent associated with mucins, the maximum reduction in HIV flux reaching the vaginal epithelium peaks at IgG–mucin affinities corresponding to α = 0.25 (Figure 3A). At 5 and 10 µg/mL NIH45-46 initially present in CVM and an IgG–mucin affinity equivalent to α = 0.25, only ~3 and ~0.3% of the HIV viral load in semen, respectively, are predicted to reach the vaginal epithelium over the first 2 h post-ejaculation, equating to 10–100-fold reduced flux compared to the estimated ~30% of HIV load over the same duration in the absence of IgG–mucin affinity (Figure 3A). Under this scenario, each HIV virion on average possesses ~2 bound IgGs (Figure 3B), and the overall infectivity is reduced by 86–94% (i.e., ~7–16-fold) compared to IgG without affinity to mucins (Figure 3C,D). Note that the reduction in infectivity is less than the reduction in the flux of HIV viruses because NIH45-46 without affinity to mucins can still neutralize the virus.

Figure 3.

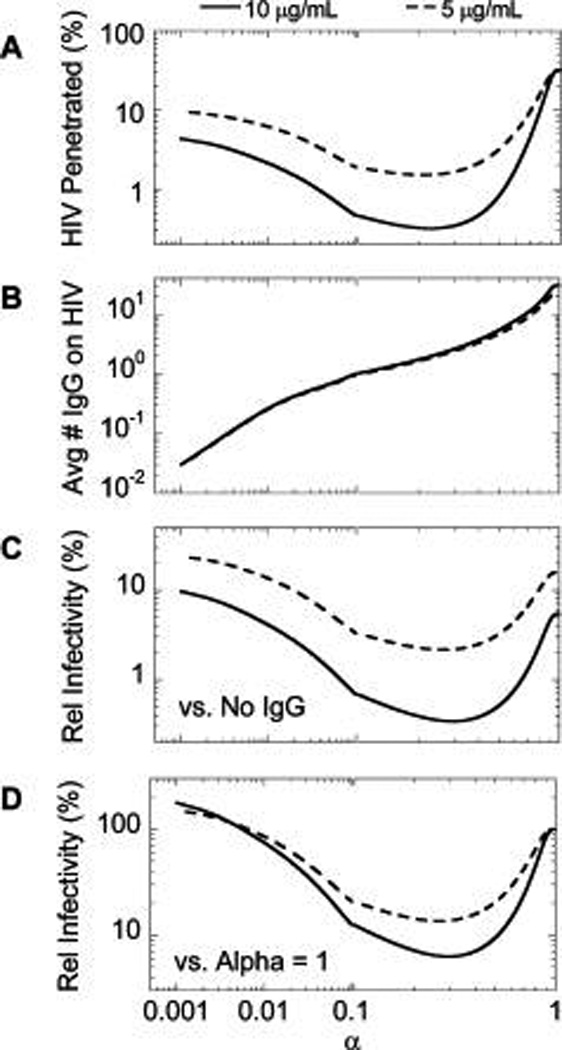
Predicted trapping potency and protection by 5 and 10 µg/mL NIH45-46 with varying affinity to mucins as characterized by α: (A) predicted fraction of HIV load initially in semen that can diffuse across CVM containing NIH45-46 over the first 2 h post-deposition; (B) average number of NIH45-46 bound to HIV arriving at the vaginal epithelium (values <1 represent HIV virions that arrive at the vaginal epithelium without any bound NIH45-46); (C, D) extent of NIH45-46-mediated protection, as quantified by infectivity relative to (C) no NIH45-46 present in CVM or (D) the same amount of NIH45-46 present but without any affinity to mucins.

When IgG–mucin affinity is further increased (i.e., lower α), the fraction of HIV reaching the vaginal epithelium begins to increase. Furthermore, there are also substantially fewer IgGs bound to HIV–Env on virions that reach the vaginal epithelium. Indeed, when α drops below 0.1, on average <1 IgG molecule is bound to each virion over the entire population of HIV virions, which implies that there must be HIV virions without any bound IgG (Figure 3B). As a result, the infectivity of HIV may actually be greater for hypothetical NIH45-46 that can bind tightly to mucins than if NIH45-46 possessed no mucin affinity at all (Figure 3C,D).

To begin to understand how to engineer more potent HIV-trapping IgG, we evaluated the relative impact of the rate of IgG binding to the virus surface compared to IgG–mucin affinity. The rate of IgG binding to HIV is the product of both the local IgG concentration and k_on, the binding kinetic constant: a doubling of IgG k_on has the same impact on IgG binding to HIV as doubling the IgG concentration. The reduction of HIV flux arriving at the vaginal epithelium and the reduction in mean number of NIH45-46-free Env proteins on HIV that reached the vaginal epithelium were sensitive to both IgG–antigen binding rate and IgG–mucin affinity (Figure 4). When IgG–mucin affinity was increased, the amount of initial NIH45-46 in CVM needed to reduce the flux of viruses arriving at the vaginal epithelium by 50% decreased from 5 to 50 µg/mL for α = 0.8–0.9 (this IgG–mucin affinity is within the range of what was previously measured for IgG in CVM) to <1 µg/mL when α = 0.25 (Figure 4A). Similarly, the amount of NIH45-46 needed to reduce the mean number of NIH45-46-free Env proteins on HIV by 80% decreased from 26 µg/mL for α = 0.8 to 3 µg/mL for α = 0.25 (Figure 4D). Overall, the amount of NIH45-46 needed to reduce infectivity by 90% decreased from 7 µg/mL when α = 1 to 2 µg/mL when α = 0.25 (Figure 4C).

Figure 4.

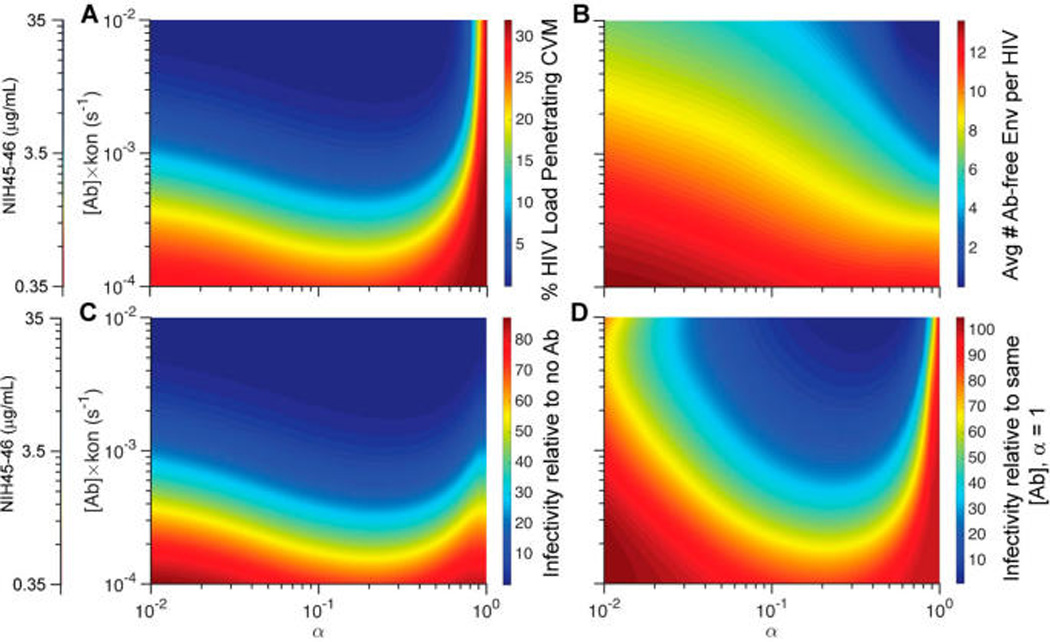
Phase diagrams mapping the predicted trapping potency and protection as a function of NIH45-46 concentration in CVM and IgG affinity to mucins as characterized by α: (A) fraction of HIV load initially in semen that can diffuse across CVM containing NIH45-46 over the first 2 h post-deposition; (B) average number of Ab-free Env trimers on HIV arriving at the vaginal epithelium; (C, D) extent of NIH45-46-mediated protection, as quantified by infectivity relative to (C) no NIH45-46 present in CVM or (D) the same amount of NIH45-46 present but without any affinity to mucins.

Influence of IgG–Antigen Binding Affinity on Maximizing Trapping Potency and Vaginal Protection

A longstanding assumption for neutralizing IgG against HIV and other viruses is that higher binding affinity between IgG and viral antigen facilitates more potent protection. However, it is important to note that high-affinity IgGs are typically identified and selected on the basis of neutralization assays in the absence of mucus coatings and with some incubation time between virus and IgG prior to exposure of the virus to target cells. Thus, we sought to quantitatively evaluate whether a high antigen–IgG affinity that typically maximizes neutralization potency in vitro would also be maximally protective against mucosal HIV transmission in our model.

Interestingly, we found that the antigen-unbinding rate k_off generally possessed only a very minor effect on increasing the fraction of HIV load that is trapped in mucus or facilitating more effective protection, especially when the IgG concentration or the k_on rate is low (Figure 5A). For example, at 1 µg/mL of IgG with k_on of 1.5 × 10⁴ M⁻¹ s⁻¹ (k_on[Ab] = 10⁻⁴ s⁻¹), improvements of k_off from 10⁻³ s⁻¹ to 10⁻⁴ s⁻¹ reduced the HIV flux arriving the vaginal epithelium by only 1.6%, and a further improvement from 10⁻⁴ s⁻¹ to 10⁻⁵ s⁻¹ essentially resulted in no appreciable difference in reduction of flux (Figure 5A). This is similarly reflected by the minimal change in the infectivity of the viruses relative to IgG with no mucin affinity from 100% with k_off = 10⁻³ s⁻¹ to 96% with k_off = 10⁻⁴ s⁻¹ to finally 92% with k_off = 10⁻⁵ s⁻¹ (Figure 5C,D). The lack of impact by k_off is directly attributed to the exceedingly limited number of IgG molecules that can accumulate on the surface of HIV either when IgG is present at low to modest concentrations or when IgG possesses inadequate binding kinetics (Figure 5B); slower unbinding kinetics simply cannot enhance HIV trapping in mucus or neutralization when few or no IgGs are bound to HIV in the first place.

Figure 5.

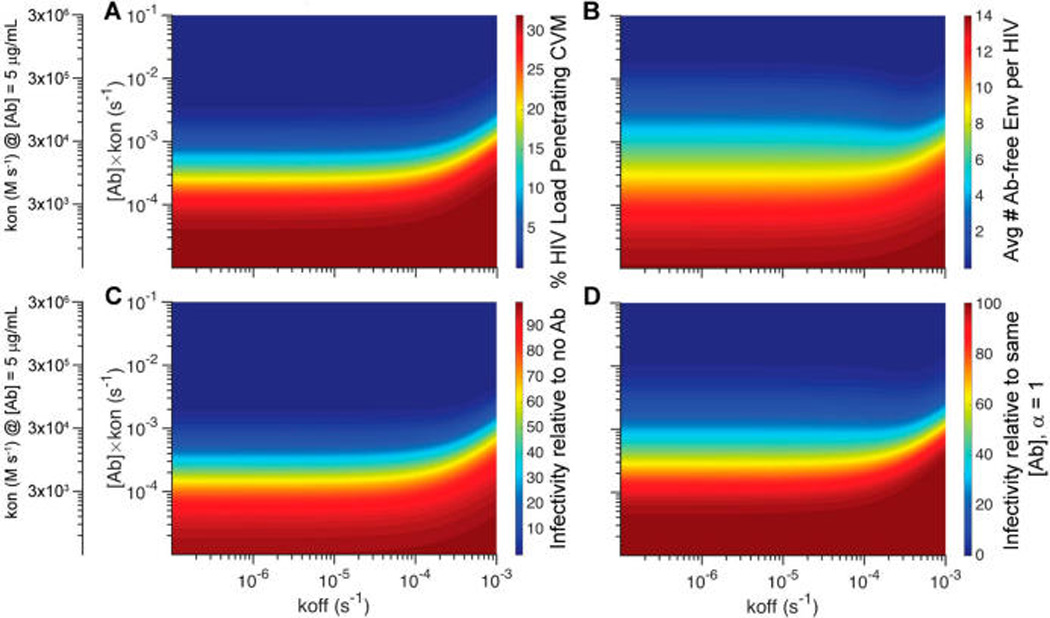
Phase diagrams mapping the predicted trapping potency and protection as a function of NIH45-46 unbinding kinetics from HIV virions (k_off) as well as accumulation kinetics on HIV virions, which is influenced by both the local NIH45-46 concentrations and the binding rate (k_on): (A) fraction of HIV load initially in semen that can diffuse across CVM containing NIH45-46 over the first 2 h post-deposition; (B) average number of Ab-free Env trimers on HIV arriving at the vaginal epithelium; (C, D) extent of NIH45-46-mediated protection, as quantified by infectivity relative to (C) no NIH45-46 present in CVM or (D) the same amount of NIH45-46 present but without any affinity to mucins.

In contrast to k_off, the IgG–antigen binding rate k_on plays a far more critical role in effective mucosal protection. Because the rate of IgG accumulation on the virion surface is the product of the IgG concentration and k_on, increasing IgG k_on by definition would have the same magnitude of impact as increasing IgG concentration. In other words, a 10-fold faster k_on would reduce the fraction of HIV reaching the vaginal epithelium and overall infectivity to the same extent as increasing the total HIV-binding IgG in CVM by 10-fold (Figure 5A), because both would result in the same increase in the number of IgG bound to HIV before the virions can reach the vaginal epithelium. Our current finding on the relative importance of k_on versus k_off is consistent with an earlier investigation that simply evaluated the kinetics of neutralization, which did not take into account IgG–mucin interactions.¹¹ Incorporating IgG–mucin affinity appears to amplify the difference, likely because rapidly binding IgG can protect by either trapping or neutralization, and viruses slowed by IgG–mucin interactions will also be more completely neutralized prior to reaching target cells underlying the vaginal epithelium.

DISCUSSION

A hallmark of HIV is its exceptionally high mutation rate, which enables the virus to readily escape antibodies generated by the immune system and prevents the host from mounting a protective immune response. Comprehensive studies of elite controllers—the rare individuals who can maintain undetectable viral load without antiretroviral therapy—led to the discovery and cloning of monoclonal antibodies that can broadly neutralize the vast majority of HIV strains. These broadly neutralizing antibodies (bnAbs) were thought to provide a template for the development of an HIV vaccine. Unfortunately, HIV vaccines, including those that can block vaginal transmission of HIV, remain elusive to date, for at least two reasons. First, bnAbs are typically highly somatically mutated, and vaccines may not be able to elicit the extent of somatic hypermutation needed in most individuals to generate the desirable bnAbs. Second, many HIV vaccine candidates are based on DNA or subunit proteins rather than attenuated virus; the durability of antibody response from subunit vaccines is generally shorter than that of vaccines based on attenuated virus, and the level of antibody titers induced in the vagina may be inadequate to block vaginal HIV transmission.

To overcome these challenges, a recently emerged strategy is to passively immunize the vagina via sustained delivery of bnAbs.^{10b, 13} By dosing the bnAbs directly into the vagina, this strategy not only bypasses the limitations of somatic hypermutation but also ensures protective levels of bnAbs are present in the vagina to block HIV transmission. Despite these important advantages, a critical shortcoming for passive immunization is the relatively high cost of maintaining protective levels of antibody in the body compared to vaccination. Much effort has been spent on reducing the costs of antibody production, such as the production of antibodies in plants,¹⁴ as well as cheaper and more efficient methods of purifying antibodies.¹⁵ Here, we introduce a novel and completely distinct approach—based on tuning IgG–mucin interactions—that could markedly reduce the dose of bnAbs needed to block vaginal HIV transmission. The majority of bnAbs against HIV appear to possess k_on in the range of 10⁴ M s⁻¹, which we previously estimated may require concentrations in excess of 5–10 µg/mL to facilitate effective protection. Although we predict enhanced vaginal protection can be accomplished with both increasing k_on and optimizing IgG–mucin affinity, bnAbs generally bind to a very unique epitope on HIV-Env that makes it unlikely that k_on can be substantially improved without compromising binding affinity (i.e., resulting in higher k_off). In contrast, simply by tuning the interactions between IgG–Fc and mucins, we can potentially reduce the required dose of bnAb for effective protection by 3.5-fold or more without jeopardizing the broad antigen coverage of bnAb. Optimizing IgG–Fc interactions with mucins thus offers a promising strategy to markedly reduce the costs for effective passive immunization of the vagina. The convergence of these various approaches may synergistically drive down costs and make passive immune protection against HIV cost-effective even in resource-poor settings.

Surprisingly, our model suggests that high-affinity IgG–mucin interactions are unlikely to enhance protection. Instead, the ideal IgG–mucin affinity that maximizes protection in our model (α ~ 0.25) is comparable to the mucin affinity previously measured for IgM molecules.⁸ It is also worth noting that IgM, due to its pentameric structure, has 10 Fab arms compared to 2 Fab arms for each IgG and hence can bind to its antigenic target and accumulate on the surface of virions with exceptional speed even if each Fab possesses relatively poor affinity compared to a fully affinity-matured IgG. Thus, an IgM molecule appears to simultaneously satisfy both of the design requirements we have identified in this study—rapid k_on and modest mucin affinity. Indeed, we recently found that IgM that binds HIV-sized nanoparticles exhibited greater mucotrapping potency than corresponding IgG (Henry et al., submitted for publication). IgM is the first antibody isotype produced by our immune system and appears early in the course of an infection. Virus-specific IgM also usually reappears upon re-infection. Although speculative, our study raises the hypothesis that an evolved effector function of IgM may be to quickly begin purging a new pathogen from mucosal surfaces that likely represent the initial site of infection early in the course of infection, and thereby minimize the viral titers that can enter the systemic circulation.

As discussed above, it is unlikely that we can markedly improve the k_on for bnAbs without potentially compromising their broad antigenic coverage. An alternative method to enhance the overall rate of IgG accumulating on the viral surface at mucosal secretions is to include IgG targeting other viral epitopes, including potentially non-neutralizing epitopes, because trapping virions in mucus requires only binding and not necessarily neutralizing IgG. It is important to note that the immune system typically generates a polyclonal Ab response against diverse epitopes, rather than solely a neutralizing Ab response against a single viral epitope. Indeed, many of the naturally produced IgG against HIV found in HIV patients associate with either the lipid membrane of HIV virions, or other parts of the gp120 site on the Env spike not directly involved in HIV infection of immune cells.¹⁶ Likewise, virtually all of the IgGs detected in the moderately successful RV144 trial were non-neutralizing.¹⁷ Such a polyclonal response would likely result in a substantially faster rate of Ab accumulation than with an individual monoclonal IgG. Thus, codelivery of multiple IgGs to enhance passive immune protection of the vagina, or inclusion of multiple immunogens (including non-neutralizing epitopes) in vaccine formulations, would both harness the same strategy our immune system has evolved to fend off foreign pathogens.

Although often under-appreciated, CVM represents the first line of defense against sexually transmitted infections in the female reproductive tract. In addition to minimizing trauma to the vaginal epithelium upon coital stirring, the presence of the CVM layer also prevents virions in semen from immediately contacting the vaginal epithelium upon ejaculation and directly reduces the virion flux and total viral load in semen that can reach target cells over time. Reinforcing the CVM barrier against sexually transmitted viral infections using virus-specific Abs that trap viruses in mucus is likely an important mechanism of the vaginal mucosal defense, but one that continues to be largely under-appreciated and under-explored. We expect that the combination of quantitative, predictive models with experimental validation will enable development of improved passive immunization as well as vaccination methods that harness the mucus barrier to reinforce mucosal defense against HIV and other sexually transmitted infections.

MATERIALS AND METHODS

Model Parameters for Vaginal Transmission of Cell-free HIV

In the female reproductive tract, mucus flows into the vagina from the cervical os, spreads over the vaginal epithelium, and is eventually cleared through the introitus. In this process, the thickness of the CVM layer likely varies within the vagina, with the thickest layer likely to be at the cervical os and vagina fornices, the thinnest near the introitus, and possibly substantial variations throughout. In the absence of experimental measurements of the thickness of the mucus layer coating the human vagina, we made the assumption that CVM approximately evenly covers the entire vaginal epithelial surface, due to spreading by repeated coital motion. We estimated the CVM layer thickness by dividing the volume of mucus (~750 µL; range typically between 500 µL and 2 mL) with the approximate surface area of the vaginal lumen (145 cm²;¹⁸ Table 1), which results in a thickness of roughly L = 50 µm. Our estimate of approximate mucus volume is based on the volume that may be collected by repeated use of a menstrual collection device, the Instead Softcup, which we have utilized in prior studies.^5c,6,7a,b,19 Although the Softcup is intended to be placed over the cervical os during menses, in our studies, donors typically insert the Softcup for only 5–10 s. Due to the limited duration of insertion, the mucus we collect reflects predominantly mucus overlaying the vaginal surface that was gathered on the SoftCup during the insertion/extraction process, rather than mucus that flowed out of the cervical os and pooled onto the cup over many hours. This procedure allows us to obtain substantial volumes of mucus that contains the same microbial communities and densities as sampling by vaginal swabs.^7b

Table 1.

Parameters and Values Incorporated into the Model

parameter	symbol	value	refs
HIV-1
diffusivity in CVM	Dv	1.27 µm2/sa	7a
diffusivity in semen		assume same as in CVM
viral load in semen		8.4 × 105 copies/ejaculateb	21, 22
no. of Env trimer spikes	N*	14 ± 7 (SD)	24
IgG
diffusivity in CVM	DAb	40 µm2/s	8
diffusivity in semen		assume same as in CVM
IgG concentration in CVM		variable
IgG–Env affinity	kon, koff	variable
IgG–mucin affinity	mon [M], moff	variable
ratio of DAb vs diffusivity in buffer	α	variable
vagina
surface area of lumen	SAvagina	145 cm2c	18a,b
volume of luminal CVM	VCVM	~750 µL	25
thickness of CVM layer	L	50 µmd
volume of semen	Vsemen	~3.0 mL	22
thickness of semen layer	d	200 µmd

^aThe geometrically averaged Deff for HIV was previously measured to be 0.25 µm²/s, but with a substantial fraction of viruses exhibiting more rapid mobility. For the current analysis, we used 1.27 µm²/s, which represents the top 25th percentile of virus mobility; this is in reasonable agreement with a more recent study of HIV diffusion in genital secretions.^7c

^bEstimated on the basis of a median semen volume of 3.0 mL²² and 2.8 × 10⁵ HIV-1 RNA copies/mL, which represents the upper limit of HIV-1 RNA copies/mL in seminal plasma from ref 21. This is in reasonable agreement with another report by Chakraboty et al., which estimated 5 × 10⁵ HIV-1 RNA copies/ejaculate, with a maximum of about 2 × 10⁷ HIV-1 RNA copies/ejaculate.²⁶

^cThe mean surface area of the vagina in the native state was previously estimated to be ~ 90 cm² by injection of vinyl polysiloxane casts vaginally. Alternatively, the surface area of vaginal lumen may also be inferred by the surface area of the erect penis (average ~200 cm²) assuming complete insertion into the vagina. We took the average from the two approaches.

^dCVM (L) and semen (d) thicknesses are estimated by V_CVM/SA_vagina and V_semen/SA_vagina, respectively.

Similar to previous studies,^9,11,20 we modeled the diffusion of HIV (D_HIV ~ 1.27 µm²/s¹¹) from a virion-rich layer of semen (8.4 × 10⁵ virions, the average viremia in semen of acutely infected males^9,21 in an ejaculate volume of ~3.0 mL²²) uniformly deposited on the luminal surface of the CVM layer. This results in a thickness of d = 200 µm for the semen layer. Neutralizing Abs (D_Ab ~ 40 µm²/s¹¹) accumulate on HIV virions at rates depending on Ab–antigen affinity, the number of available antigen sites on the virus surface, the local Ab concentration, and the diffusivity of the Abs in CVM. For a model monoclonal broadly neutralizing Ab against HIV, we focused on NIH45-46, which binds to the CD4 binding site of gp120 and whose binding affinities were previously described.²³ The number of Env spikes N_* on individual HIV virions is variable and was estimated to follow a negative binomial distribution with N_* = 14 ± 7 (range 4–35) based on cryoelectron microscopy of HIV virions.²⁴

Ab Binding to HIV Env Spikes

We assume each Env spike can bind up to three Abs without significant steric hindrance; thus, individual Abs at concentration u(z,t) can bind and unbind independently with rates k_on and k_off, and overall binding/unbinding rates depend on the number of unoccupied binding sites 3N_* −n, where n is the number of bound Ab. However, because the diffusivity for a mucin-bound Ab u_b(z,t) is reduced compared to free individual Ab, the Smoluchowski encounter rate, which describes the collision rate of two populations of spherical particles diffusing freely in three dimensions, implies that the binding rate for a mucin-bound Ab $(k_{\text{on}}^{\prime })$ to its antigen should be reduced proportionally to the difference in diffusivities of the Ab (D_Ab) and the virus (D_v); hence, $k_{\text{on}}^{\prime }=(D_{\mathrm{v}}/(D_{\mathrm{A}\mathrm{b}}+D_{\mathrm{v}}))$ k_on ≈ (1/30) k_on. The Ab–virion binding rate equations can be summarized as

(1)

where (Ab) is an unbound Ab, (Ab)ⁿZ(t) denotes a virion at Z(t) with n bound Ab, and superscript/subscript f and b denote free and bound terms, respectively. Individual Abs also bind and unbind to mucins at rates m_on[M] and m_off, where [M] is the effective concentration of Ab binding sites in the mucin network. In addition, virion-bound Abs may associate with mucins, effectively immobilizing the entire Ab–virion complex for the duration of the interaction.

HIV Diffusion through CVM

We developed two different methods to simulate HIV penetration across the vaginal mucus layer. In the first method, a stochastic particle simulation was used for virion diffusion, virion–Ab binding, and Ab–mucin interactions. Because the number of Abs is much larger than the number of virions, we utilized a diffusion partial differential equation (PDE) for the Ab concentration. Virion diffusion for a particle Z is given by the stochastic differential equation (SDE) dZ = (2D)^1/2 dW, where W is Brownian motion and $D=\{\begin{array}{cc}{D}_{\mathrm{H}\mathrm{I}\mathrm{V}}\hfill & \text{free}\hfill \\ 0,\hfill & \text{bound}\hfill \end{array}$, where “free” indicates that all virion-bound Abs are free from mucin and “bound” indicates that at least one virion-bound Ab is associated with mucin. We assume Brownian diffusion of virions based on our previous findings that HIV and other viruses and nanoparticles can diffuse nearly unobstructed in CVM.^5c,7a,b,19 Importantly, although we are measuring the rate of virus arriving the epithelium, an essentially 1D process, the actual simulated random walks are in 3D. Ab binding and unbinding to virus were simulated with a Poisson random variable with rates given by eq 1. Lastly, Ab–mucin interactions were simulated with Poisson random variables and rates dependent on the total number of virion-bound Abs and those Abs currently interacting with mucins. Due to the great computational expense involved in simulating Ab–mucin interactions, particularly when m_on[M] > m_off, we computed lookup tables giving the distributions for the time that a virion spends freely diffusing and the time that a virion spends interacting with mucins (see the Supporting Information and Figure S1). The (random) time that a virion spends freely diffusing is given by the last time that none of the surface-bound Abs associate with mucin until the next time that at least one of its associated Abs binds to mucin. Similarly, the time that a virion spends interacting with mucins is given by the last time that at least one of the virion-bound Abs associates with mucin until the next time that none of the surface-bound Abs associate with mucin. We then sampled from these lookup tables whenever a virion’s state changes (freely diffusing or bound to mucin, binding or unbinding an Ab, crossing the semen/CVM interface). These methods were used to generate data presented in Figure 2.

The second simulation method consists of a reaction–diffusion PDE to capture the average behavior of the virus population. The virus population is represented by a vector $\overrightarrow{V}(z,t)$, where the component V_n(z,t) represents the concentration of virus with n bound Abs. We previously introduced a parameter α = (m_off/(m_off + [M]m_on)) to represent the fraction of time that Abs in CVM spend freely diffusing.¹¹ Because Ab–mucin interactions likely occur at fast time scales,

$$u_{\mathrm{f}}(z,t)=\{\begin{array}{c}\hfill \alpha u(z,t),0<d<50\hfill \\ \hfill u(z,t),200<d<250\hfill \end{array}$$

and

$$u_{\mathrm{b}}(z,t)=u(z,t)-u_{\mathrm{f}}(z,t)$$

In the limit m_on, m_off → ∞ (keeping m_off/(m_off + [M]m_on) fixed), the stochastic model can thus be approximated by the reaction–diffusion system

$$\frac{\partial \stackrel{\rightharpoonup }{V}}{\partial t}=D\frac{{\partial }^2\overrightarrow{V}}{\partial z^2}+\overrightarrow{f}(\overrightarrow{V},u)-\overrightarrow{g}(\overrightarrow{V},u)$$

$$\frac{\partial u}{\partial t}={\mathit{D}}_{\mathrm{A}\mathrm{b}0}\frac{{\partial }^{2}u}{\partial z^2}$$

where the diffusion tensor D is a diagonal tensor with entries D_v0, β₁D_v0, …, β_3N* D_v0 along the diagonal (the diffusion factors β_i are determined below) for 0 < d < 50 and diagonal entries are all D_v0 for 50 < d < 250; $D_{\mathrm{A}\mathrm{b}}=\{\begin{array}{c}\hfill \alpha D_{\mathrm{A}\mathrm{b}0},0<d<50\hfill \\ \hfill D_{\mathrm{A}\mathrm{b}0},50<d<250\hfill \end{array}$; and the reaction terms $\overrightarrow{f}(\overrightarrow{V},u)$ and $\overrightarrow{g}(\overrightarrow{V},u)$ have entries $f_n=(3N_{*}-n+1)[k_{\text{on}}^f{u}_{\mathrm{f}}(z,t)+k_{\text{on}}^b{u}_{\mathrm{b}}(z,t)]V_{n-1}(z,t){\chi }_{n>0}+(n+1)k_{\text{off}}{V}_{n+1}(z,t)-{\chi }_{n<3N_{*}}$ and $g_n=(3N_{*})[k_{\text{on}}^{\mathrm{f}}{u}_{\mathrm{f}}(z,t)+k_{\text{on}}^{\mathrm{b}}{u}_b(z,t)]V_n(z,t)+n{k}_{\text{off}}{V}_n(z,t)$ for n = 0, 1, …, 3N_*, respectively, with χ denoting the indicator function.

Simultaneous Diffusion of HIV and Ab

We use a forward-time central-space scheme to model diffusion for both the virus and Ab populations in 3D, with reflecting boundary conditions at the semen/lumen interface, reflecting conditions for Ab and absorbing conditions for virus at the CVM/cell interface, and Fick’s law for the discontinuous diffusion coefficients at the semen/CVM interface. We assume that the number of Abs binding to virions is negligible compared to the overall Ab population, so there are no local depletion effects.

If each virion-bound IgG binds and unbinds to the mucin mesh independently, then the virion spends approximately a fraction αⁿ of time with all its bound Abs simultaneously free from mucin. This yields a time-averaged diffusivity for the virion of D_vn = αⁿD_v0 in CVM. One adjustment is made, however, to account for the lower diffusivity of a virion–Ab complex compared with an individual Ab. Similar to the adjustments on k_on, we define m^first = (1/30), so that initial Ab–mucin encounters occur at rate m^firstm_on[M]. For subsequent interactions of virion-bound Abs with mucin, the rate may increase because the Ab–virus complex is already located in close proximity to a mucin molecule or may decrease due to the reduced diffusivity of the Ab–virus complex associated with mucins relative to a nonassociated Ab–virus complex. Due to the lack of empirical data in the literature, we assumed other Abs bound to the same virion with at least one Ab already associating with mucins will associate with mucins with the same mucin-binding kinetics as a free Ab molecule. To calculate the diffusion factors β₁, β₂, …, β_3N*, we first neglect the factor m_first and consider the total time free_i that a virion with i bound Abs spends freely diffusing and the total time bound_i that it spends bound to mucins up to a time T. Because the Abs are assumed to bind and unbind to mucin independently, lim_T→∞(free_i/(free_i + bound_i)) = αⁱ, and thus β_i = (free_i/m^first)/(free_i/m^first + bound_i) = αⁱ/(αⁱ + m^first(1 − αⁱ)).

The stochastic simulations and the reaction–diffusion simulations show excellent agreement, particularly at rapid m_on[M] and m_off. Indeed, for m_on[M] = 10¹ s⁻¹, the difference between stochastic simulations and the reaction–diffusion simulations is on average ~8.5% and decreases to an average of ~3.5% for m_on[M] = 10² s⁻¹ (Figure S3; see the Supporting Information for theoretical estimates of m_on[M] and m_off). Hence, we used the deterministic simulations except where noted. These methods were used to generate data presented in Figures 3A,B, 4A,B, and 5A,B.

Env Neutralization by Binding Abs

In addition to measuring reduction in the flux of viruses arriving at the epithelium, we also incorporated virus infectivity and extent of Ab neutralization in our analysis. Determining the number of Abs required to neutralize a given HIV remains an active area of research, due to the difficulty in simultaneously distinguishing the number of Abs necessary to neutralize a particular Env spike and the minimum number of Ab-free Env spikes necessary for HIV to successfully infect.²⁷ It was previously proposed that the binding of a single Ab molecule to an Env spike appears to be sufficient to inactivate the infectivity associated with that spike.²⁸ The minimum number of Ab-free Env spikes and, consequently, the number of Env spikes that must be inactivated to neutralize a virion, remain more controversial. Estimates for minimum infectivity range from a single Ab-free Env spike²⁸ to many.²⁹ For our current model, we assume that each additional Ab binding to a previously unoccupied Env incrementally reduces the likelihood of infection, and we measure the overall reduction in infectivity by the reduction in number of unoccupied Env arriving at the vaginal epithelium over the first 2 h post-ejaculation. These methods were used to generate data presented in Figures 3C,D, 4C,D, and 5C,D.

ABBREVIATIONS

Ab

antibody

CVM

cervicovaginal mucus

IgG

immunoglobulin G