Probability-based particle detection that enables threshold-free and robust in vivo single-molecule tracking

Any single-molecule study starts with finding those single-molecule signals in recorded images. Currently, parameters such as filter and thresholds are user set, and errors are unknown and not observed or controlled. A framework is presented in which expert knowledge and parameter tweaking are replaced with a probability-based hypothesis test.

Abstract

Single-molecule detection in fluorescence nanoscopy has become a powerful tool in cell biology but can present vexing issues in image analysis, such as limited signal, unspecific background, empirically set thresholds, image filtering, and false-positive detection limiting overall detection efficiency. Here we present a framework in which expert knowledge and parameter tweaking are replaced with a probability-based hypothesis test. Our method delivers robust and threshold-free signal detection with a defined error estimate and improved detection of weaker signals. The probability value has consequences for downstream data analysis, such as weighing a series of detections and corresponding probabilities, Bayesian propagation of probability, or defining metrics in tracking applications. We show that the method outperforms all current approaches, yielding a detection efficiency of >70% and a false-positive detection rate of <5% under conditions down to 17 photons/pixel background and 180 photons/molecule signal, which is beneficial for any kind of photon-limited application. Examples include limited brightness and photostability, phototoxicity in live-cell single-molecule imaging, and use of new labels for nanoscopy. We present simulations, experimental data, and tracking of low-signal mRNAs in yeast cells.

INTRODUCTION

The ability to image single molecules has revolutionized the way molecular interactions can be probed, the environments in which this is possible, and the resolution that can be achieved by use of light microscopy. Although the technology is readily available, the analysis of the images often is perceived as challenging, as a fair degree of judgment is needed to choose appropriate image filter and intensity thresholds to identify potential signals. In many single-molecule fluorescence applications, such as superresolution localization microscopy and single-molecule tracking, the position and intensity of a single fluorophore need to be measured. The first analysis step is the detection of regions that could contain signal originating from single molecules. Detection is especially difficult and important for applications for which the fluorescence signal is weak, photobleaching is limiting for the observation time, or a high background noise is present, such as in vivo RNA imaging or three dimensional imaging (Yildiz et al., 2003; Juette et al., 2008; Manley et al., 2008; Tyagi, 2009; Grunwald and Singer, 2010; Hoskins et al., 2011; Cai et al., 2014). Numerous methods exist to tackle detection (Olivo-Marin, 2002; Serge et al., 2008; Smith et al., 2010; Izeddin et al., 2012). However, for all of these methods, the rate of false-positive detection events is unknown, resulting in no quantitative assessment of true and/or false detections at this very first step underlying all further analysis. Practically, even for relatively good data, such as can be expected from single-molecule fluorescence in situ hybridization (smFISH), automated detection and visual inspection of images can diverge such that the user identifies numerous signals that were missed by the automated detection. Here we present a method that uses a probability-based hypothesis test that enables a minimum number of false-negative detections, maintaining a fixed number of false- positive detections.

The two measures that generally characterize the quality of detection are the detection efficiency, Q (sometimes called sensitivity or recall), which is defined as the ratio of all detected events over the true number of events, and the false-positive rate (FP), which is defined as the ratio of all false detections over the total number of true and false detections. Q and FP can only be known in simulations or well-designed test experiments but are unknown for a real data set. Because image filters, filter settings, and intensity thresholds are determined empirically, the Q and FP of existing methods depend intricately on user-set parameters and are not observable or controllable using existing methods. This lack of direct control over Q and FP results in unreliable detection behavior, especially in photon-starved circumstances with a low signal-to-background ratio (SBR).

To overcome the user dependence of current methods, we present an alternative approach using pixel-based hypothesis testing that delivers a minimum number of false-negative detections at a controlled/fixed number of false positives. This is possible by estimating the probability that a pixel contains signal originating from a single molecule by comparing the likelihood of a foreground model (emitter present) over that of a background model (no emitter) using a generalized likelihood ratio test (GLRT; Kay, 1993, 1998). GLRT uses estimators for which we explicitly use prior knowledge of noise characteristics in light emission: the microscope point-spread function (PSF) and camera performance. The maximum likelihood of both models is computed for each pixel x, y of the image using a small region of interest around each pixel, approximately the size of the PSF (see the Supplemental Note), resulting in the following test statistic:

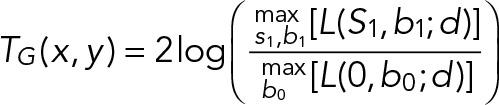where L(S, b; d) is the likelihood for a single-molecule signal intensity S and background b, given the pixel data d. The test statistic, T_G(x, y), is used to calculate the false-positive probability, P_FA(x, y), that is, the fraction of all tests (pixels) that results in a false-positive detection (Supplemental Note). The false-positive probability is corrected for the number of (dependent) hypothesis tests executed to generate a false-positive rate, FP(x, y), that gives the rate of positive tests that are incorrect. This correction is performed using a statistical tool termed false discovery rate (FDR) control (Supplemental Note; Benjamini and Yekutieli, 2001). This enables the algorithm to target a user-defined FP in experimental data without knowing the true outcome a priori, as would be the case in a simulated test data set. Regions of interest (ROIs) for localization of a potential fluorophore are identified from connected regions of pixels where the FP(x, y) is below a user-set target value. Multiple-target tracking (MTT; Serge et al., 2008) also uses GRLT for detection, but only as a quality control on ROIs that are selected with an initial detection method. Our approach removes the dependence of the arbitrary initial detection by integrating the hypothesis test into the candidate ROI selection and enables control of the number of false positives by our FDR control method.

RESULTS

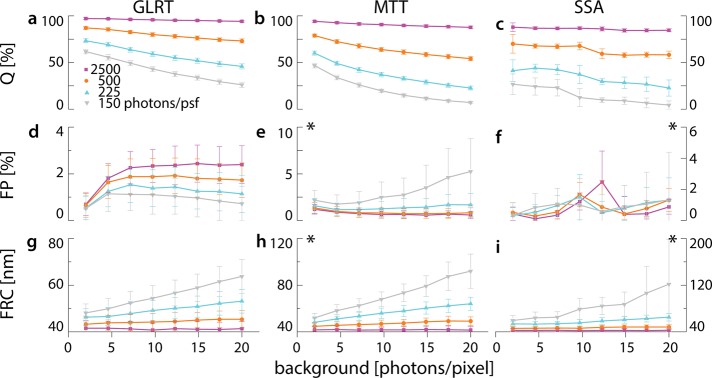
To develop a quantitative understanding of the performance of our approach, we used simulations of switching single emitters on a randomly labeled Siemens star to represent single-molecule localization–based superresolution data (Figure 1 and Supplemental Video S1). Switching of the emitters results in variation of signal strength, as the emitters can be on for the whole integration time of one frame or for parts of it (Figure 1) We compare Q and the Fourier ring correlation (FRC) resolution (Nieuwenhuizen et al., 2013) at fixed FP against the current best methods, MTT and the scale-space approach (SSA; Figure 2; Smith et al., 2010; Huang et al., 2011; Low-Nam et al., 2011; Nieuwenhuizen et al., 2013). The reason that we are able to fix FP for MTT and SSA although neither method can do so is our knowledge of ground truth in the simulations, which we use for optimizing the thresholds instead of relying on empirical settings. In contrast to the GLRT, the FP rate for the SSA and MTT in Figure 2 is bona fide fixed, which is only possible in simulations.

FIGURE 1:

Simulation object and PSF examples. (a) Superresolution reconstruction of a Siemens star as used in the simulations. Time projections in which each single molecule is replaced by its localization precision. (b) Zoom-in on a, visualizing the achieved resolution at the highest-frequency region of the object. (c) Examples of simulated single-molecule images as used in simulations with varying signal (I_max) and background rates (in photons) as indicated. An area of 12 × 12 pixels with σ_PSF = 1.39 pixels. (d) Single-molecule intensity distribution resulting from a Markov process simulation for the STORM experiment, where the maximum “on” time is >1 frame.

FIGURE 2:

Comparison of detection methods in simulations. Localization microscopy images of a Siemens star object were simulated for different levels of single-molecule and background signal. (a–c) Q, (d–f) FP, and (g–i) image resolution according to FRC for the three tested methods, demonstrating superior performance of the GLRT over MTT and SSA. Asterisk indicates a change in scale for visibility.

The intensities of the switching single molecules were set to 150, 225, 500, and 2500 photons (I_max) per PSF for the duration of a full frame (Figure 1). The PSF had a width of σ_PSF = 1.39 pixels (Supplemental Note). The background intensities varied from 2 to 20 photons/pixel (Figure 1). For MTT and SSA the FP was fixed to <5%. At 150, 225, and 500 photons, Q for GLRT was at least 10% higher than that for MTT; the detection efficiencies of GLRT and MTT were similar at 2500 photons (GLRT, 97%; MTT, 94%; Figure 2, a and b). Compared to SSA, GLRT detects 10–15% more true spots across all intensity levels (Figure 2, a and c). At low photon counts, MTT has higher detection efficiency than SSA. The detection efficiency of GLRT at 225 photons was similar to that of MTT and SSA at 500 photons at low (two photons) to medium (12 photons) background levels (Figure 2, a–c). The FP for GLRT remains well below the specified target of 5% (Figure 2d). We reconstructed images from true-positive detections of all methods and computed their FRC resolutions (Nieuwenhuizen et al., 2013). At high intensities (I = 2500), the values of FRC resolution of GLRT, MTT, and SSA were all within the uncertainty of each other. However, as the intensity decreases, the resolution for the GLRT is better, with an improvement of ∼30 nm at 150 photons (Figure 2, g–i).

The use of simulated data to test performance of multiple algorithms has the advantage that the true outcome is known and no assumptions—for example, for variables such as noise, background, and the shape of point sources—have to be made, as they can be set as desired. On the downside, the parameters chosen might not reflect the conditions of a real experiment well. Therefore, to test experimentally the performance of GLRT, MTT, and SSA at adjustable SBR levels in a realistic environment, we immobilized 100-nm-diameter fluorescent beads on a coverglass and excited them using a white-light laser (Figure 3). The first channel of the white-light laser was tuned to excite the beads, and one or more channels were tuned to overlay with the emission spectrum of the beads, acting as artificial background. Ground truth positions of the beads were found at high enough SBR to guarantee 100% detection, and beads were subsequently imaged at a constant signal level but at various background settings (Figure 3, a–l, and Supplemental Video S2). Bead data contain nonuniform image background caused by the laser in the emission band to simulate more realistic experimental conditions, as could be found, for example, during live-cell imaging. As background model, we assume a homogeneous level of background, and the signal model is an integrated Gaussian (Supplemental Note). We estimate the local background within a small box size, which is a fixed ratio to the width of the PSF (see Materials and Methods), resulting in a 12 × 12–pixel box. GLRT allows the use of other signal and background models. At background levels >7 photons/pixel, GLRT had the highest Q, followed by MTT, agreeing with our simulations (Figure 3m). For high SBRs, all methods obtained Q = 1, somewhat outperforming simulations, likely because beads in the experiment emit constantly, whereas in simulations, the duty cycle of a single fluorophore is less than the duration of a frame, as is typically the case in stochastic optical reconstruction microscopy (STORM)–like experiments. Up to background levels of 17 photons/pixel, GLRT maintains an average FP rate <5%. At higher background levels, in contrast to our simulations, the FP rate of GLRT did increase but remained well below the FP rate of MTT and SSA, in both its average and error interval (Figure 3n). We attribute the difference between simulation and experiment to the noise and background characteristics of the experimental situation compared with the uniformly distributed noise and background in our simulations. This reflects the limitations of simulations to predict the real-life performance of a method; however, the GLRT maintains its detection advantage under experimental conditions in which noise is not uniform.

FIGURE 3:

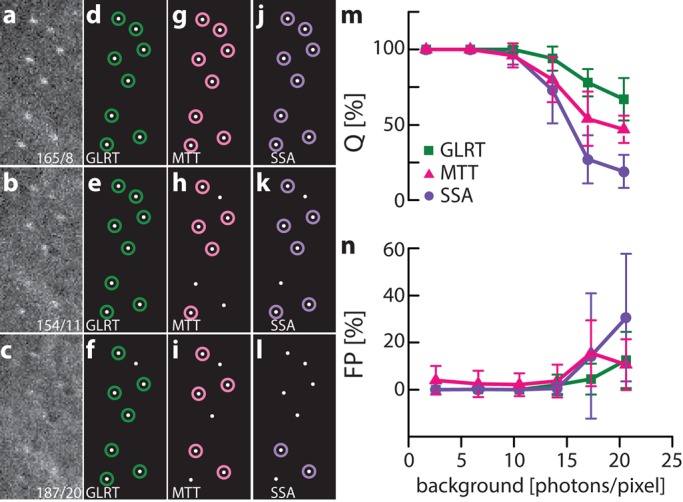
Experimental validation of single-molecule detection algorithms. The true bead positions are identified at high photon count (not shown). (a–c) Three examples of bead images. Intensity (photons) and background (photons/pixel) are indicated in raw images. Examples of detection results for GLRT (d–f), MTT (g–i), and SSA (j–l). Quantitative comparison of (m) Q and (n) FP of single-molecule detection algorithms, indicating the superior performance of GLRT, followed by MTT and SSA.

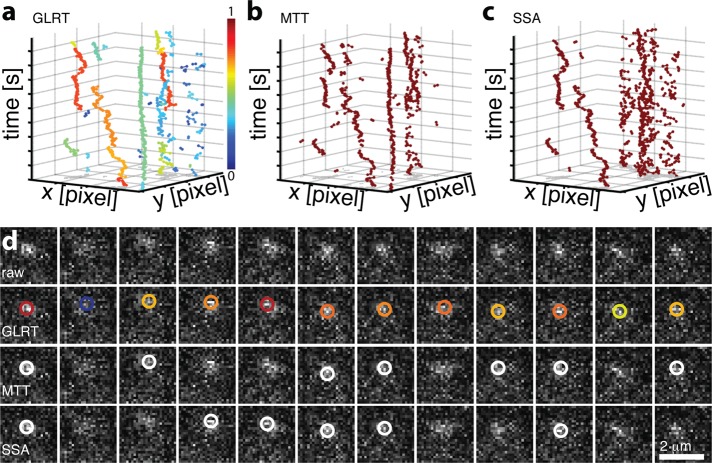
Finally, we applied GLRT, SSA, and MTT to detect single fluorescently labeled mRNAs in a living cell, a notoriously low signal (50–150 photons) situation with high background (2–10 photons/pixel; Figure 4 and Supplemental Videos S3 and S4). At the FP target of 5%, GLRT detected ∼1100 spots over 200 frames. To compare between algorithms, we set thresholds for MTT and SSA such that the same number of spots was detected. Detected spots were then linked using the same tracking algorithm (Jaqaman et al., 2008; Cutler et al., 2013). The GLRT produced longer tracks than the other methods, as the superior detection efficiency resulted in fewer track interrupts. The mean track length was 39 ± 46 frames (longest track, 185 frames) compared with 29 ± 20 frames (longest track, 69 frames) for MTT and 27 ± 23 frames (longest track, 85 frames) for SSA. These differences are significant at p < 0.05 (Mann–Whitney U test).

FIGURE 4:

Effect of GLRT detection on tracking of single mRNAs in living yeast. (a–c) Constructed traces based on 1072 ± 26 detections and identical linking parameters for (a) GLRT, (b) MTT, and (c) SSA. The color scheme in a indicates the average detection probability of the detected position underlying the tracking. (d) Sample raw data for detection of fluorescently labeled single mRNAs in a living cell using GLRT, MTT, and SSA as indicated. Color scheme of GLRT as in a.

DISCUSSION

Any single-molecule study—for example, nanoscopy, smFISH, colocalization single-molecule spectroscopy, single-molecule tracking, and so on—starts with finding those single-molecule signals in the recorded images. Single-molecule detection fundamentally suffers from false-positive and false-negative detections. With GLRT, we present a new method for the detection of single molecules that delivers a minimum number of false negatives at a fixed number of false- positive detections for the used background, noise, and PSF models. Within the GLRT framework, it is possible to treat different camera noise models (e.g., scientific complementary metal–oxide semiconductor cameras), PSFs, and experiment-specific background conditions, which results in a change of the likelihood function (Supplemental Note; Rieger and Stallinga, 2014). In other words, GLRT allows setting a target for the FP for a wide range of applications (see also Supplemental Figure S1). We showed that this target is stably achieved over a large range of SBR conditions. GLRT is based on statistical testing and significance levels, thereby replacing user-defined thresholds that have an intricate effect on FP and Q. We tested GLRT against multiple state-of-the-art methods under simulated (homogeneous background) and experimental (stochastic background and noise distribution) conditions, directly testing the predictive limits of our simulations (Figures 2 and 3). GLRT has the highest detection rate under most conditions and shows improved resolution in localization-based superresolution and tracking of single molecules (Figure 4). The robust performance of GLRT at low signal and high background allows lower excitation levels, which will improve the viability of samples during live-cell imaging (Carlton et al., 2010; Huang et al., 2013). It can also open up STORM imaging to a broader palette of fluorophores than is currently in use. In particular, the sample handling used for multiantibody labeling with Alexa Fluor 647 can be avoided (Tam et al., 2014; Valley et al., 2015). Of greatest importance, GLRT provides built-in quality control during signal detection—the first and most fundamental step of data analysis. The framework we present takes into account the whole imaging process and is easily adapted to different signal shapes—for example, a double helix—and camera types (Supplemental Note). The result of this framework is that we can robustly detect weaker signals, which opens single-molecule studies to applications that were previously not conceivable, as well as to extending observation time by reducing photobleaching.

MATERIALS AND METHODS

Single-molecule imaging

All experimental data, on live cells and beads, were acquired using an inverted fluorescence microscope equipped with a 150×/1.45 numerical aperture (NA) objective (Olympus, Tokyo, Japan) combined with 200-mm–focal length tube lenses (CVI Melles Griot, IDEX, Albuquerque, NM), resulting in an effective magnification of 167×. Images were recorded with an electron-multiplying charge-coupled device (EMCCD) camera (iXon3, 897; Andor Technology, Belfast, United Kingdom) featuring 512 × 512 pixels of size 16 × 16 μm², resulting in an effective pixel size in the image of ∼95 nm. For fluorescence excitation, 515-nm (Coherent, Carlsbad, CA) and 561-nm (Cobolt SE, Solna, Sweden) lasers were used for live-cell imaging (Saccharomyces cerevisiae) and a white-light laser (NKT Photonics, Birkerød, Denmark) for imaging of fluorescent beads (TetraSpeck microspheres, 0.1 μm, fluorescent orange; Life Technologies, Carlsbad, CA). Wavelength selection and power regulation for the imaging laser were done using an acousto-optic tunable filter (AA Optoelectronics, Orsay, France). An emission filter with central wavelength 593 nm and bandwidth 40 nm was placed between the objective and tube lens. To introduce additional background in the bead images, one or more additional wavelengths within the range of the emission filter were selected from the white-light laser. Reflection of laser light within the beam path resulted in a nonuniform intensity distribution of background signal and image noise on the camera. The ground truth positions of the beads were found at a signal of 220 photons and 2.6 photons/pixel background, yielding 100% detection (Supplemental Video S2). Beads were then detected at a signal of ∼180 photons/bead and various background settings (Figure 3 and Supplemental Video S2).

Synthetic data generation and simulation parameters

Synthetic data were generated as a Siemens star with eight arms on a field of view of 64 × 64 pixels (6.4 × 6.4 μm²). To determine Q, we produced time series of T = 100 frames with an emitter density ρ = 750 μm⁻² containing on average >500 detection events, which was repeated n = 256 times. Single-molecule switching behavior was modeled as a Markov process with a bleaching rate k_b = 0.1 frame⁻¹ and off-rate k_off = 1 frame⁻¹. On- and off-rates are coupled by the emitter density, which is approximated as ρ = k_off/(5k_on) μm⁻². The number of simulated emitters, N, is equal to the density times the area of the object (N = A_object ρ). This Markov process offers a representation of a STORM experiment but also biases the resolution calculation, since single emitters are localized more than once (Nieuwenhuizen et al., 2013). Therefore, for the resolution comparison, we performed a much longer (T = 10⁴), photoactivated localization microscopy–like simulation in which all single emitters could be localized only once, which we repeated n = 64 times. The PSF is modeled as a Gaussian with width σ_PSF = 0.3λ/(NA⋅Δx) = 0.3λ/(1.45⋅100) = 1.39 pixels (Zhang et al., 2007; Stallinga and Rieger, 2010). For our benchmark, we executed four different simulations at single-molecule intensities of 150, 225, 500, and 2500 photons of a randomly labeled Siemens star with a density ρ = 750 μm⁻² (Figure 1).

Tracking parameters

Using the bacteriophage PP7 RNA–labeling system in live S. cerevisiae cells, we followed single-molecule mRNA transport events. We used the same linking parameters for all detection algorithms and tuned the threshold of both the MTT and SSA to detect the same number of spots. The linking parameters that gave the best frame-to-frame connections are on-rate k_on = 100 frame⁻¹, off-rate k_off = 0.1 frame⁻¹, particle density ρ = (#detections)/(#frames), and diffusion constant D = 4 pixels/frame. The maximum search distance for a link was chosen as 4D, and gaps larger than a spatial jump of three pixels or temporal three frames were not allowed. These values for jump distance and time gaps were chosen to equal a distance equal to the width of one PSF at our spatial and temporal sampling rates and RNA mobility in the range of 1 μm²/s for the diffusive fraction (Politz et al., 2006). Furthermore, we weighted the candidates in the cost matrix with their detection probability for GLRT. To obtain similar performances for the MTT and SAA, we weighted candidates using a similar quantity, 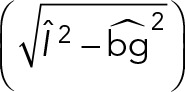, where 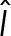is the estimated intensity, 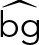is the estimated background, and 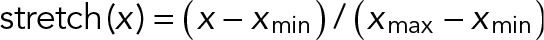, with x_max and x_min the maximum and minimum values, respectively, of all linking candidates. For comparing the three methods, we identified tracks >8 frames.

Benchmark metrics

The metric with which we judged the performance the methods is of key importance. For the GLRT, we set the target FP at 5% (near the 2σ level), since this is most often used in hypothesis testing. The actual obtained FP rate can be calculated in simulation because the true events are known. We compared the methods based on their efficiency, Q, and therefore ensured that the FP rate was comparable. Using bisectional optimization for SSA, we set the detection threshold in each video such that the maximal number of true signals was found while the FP value stayed as close as possible to the target value. To find this threshold automatically, we used eight iterations of bisectional optimization. The intensity threshold for the SSA was set such that the FP rate was matched as closely as possible to that of the GLRT, 5% FP signals. The MTT was set so that the overall average was comparable to that of the GLRT. The FP for the MTT is comparable to that of the GLRT (Figure 2, d and f) but higher for low (150) signal and high (>15) background.

Photon count calibration

The signal is detected by the camera in analogue digital units and needs to be converted into photon counts for localizations using Poisson noise characteristics (Smith et al., 2010). Conversion was done as described earlier (van Vliet et al., 1998).

Graphics processing unit implementation

We performed two maximum likelihood fits for every pixel. For a typical EMCCD, we have 512 × 512 pixels, which requires fitting 5 × 10⁵ subregions with side lengths of 3(2σ_PSF) + 1 pixels to obtain optimal localization precision (Smith et al., 2010). Per pixel, two maximum likelihood estimations (MLEs) are done: one each for the foreground model H₁ and background model H₀ (Supplemental Note). The MLEs are calculated as described earlier (Smith et al., 2010). Quantification of the speedup of MLE fitting on graphics processing units (GPUs) can be found in earlier work (Smith et al., 2010). With recent advances in GPU hardware, a 500-times speedup is feasible (Intel Core-i7-5960X vs. GeForce GTX 780 Ti; Smith et al., 2010). On a GTX 780 graphic card (Nvidia, Santa Clara, CA), the processing time per 512 × 512 pixel image is <1 s for σ_PSF = 1.39 pixels. The GPU processing was written in CUDA (Nvidia) and compiled using Visual Studio 2013. The CUDA routine was compiled as a mex-file for Matlab (MathWorks, Natick, MA) and called from Matlab. We provide a software tool and example that implements and demonstrates the detection algorithm as supplemental software, including multi-graphic card support (Supplemental Software).

Algorithmic details for detection methods

For SSA, the two different filter kernels for the noise reduction by smoothing and for background detection were uniform filters with a size of 1.5(2σ _PSF + 1) and 3(2σ _PSF + 1) pixels, respectively. The local maxima were detected using a maximum filter with a size of 3(2σ_PSF + 1) pixels, and a user-defined intensity threshold was used to create the candidate map.

Sample code and images

Additional material, the MatLab code for GLRT, simulated test data, and illustrated examples are available at www.umassmed.edu/grunwaldlab/resources/lab-code/.

Abbreviations used:

FDR

false-discovery rate

FP

false-positive rate

FRC

Fourier ring correlation

GLRT

generalized likelihood ratio test

MLE

maximum likelihood estimation

MTT

multiple-target tracking

PSF

point-spread function

ROI

region of interest

SBR

signal-to-background ratio

smFISH

single-molecule fluorescence in situ hybridization

SSA

scale-space approach.