Decentralized Multisensory Information Integration in Neural Systems

Abstract

How multiple sensory cues are integrated in neural circuitry remains a challenge. The common hypothesis is that information integration might be accomplished in a dedicated multisensory integration area receiving feedforward inputs from the modalities. However, recent experimental evidence suggests that it is not a single multisensory brain area, but rather many multisensory brain areas that are simultaneously involved in the integration of information. Why many mutually connected areas should be needed for information integration is puzzling. Here, we investigated theoretically how information integration could be achieved in a distributed fashion within a network of interconnected multisensory areas. Using biologically realistic neural network models, we developed a decentralized information integration system that comprises multiple interconnected integration areas. Studying an example of combining visual and vestibular cues to infer heading direction, we show that such a decentralized system is in good agreement with anatomical evidence and experimental observations. In particular, we show that this decentralized system can integrate information optimally. The decentralized system predicts that optimally integrated information should emerge locally from the dynamics of the communication between brain areas and sheds new light on the interpretation of the connectivity between multisensory brain areas.

SIGNIFICANCE STATEMENT To extract information reliably from ambiguous environments, the brain integrates multiple sensory cues, which provide different aspects of information about the same entity of interest. Here, we propose a decentralized architecture for multisensory integration. In such a system, no processor is in the center of the network topology and information integration is achieved in a distributed manner through reciprocally connected local processors. Through studying the inference of heading direction with visual and vestibular cues, we show that the decentralized system can integrate information optimally, with the reciprocal connections between processers determining the extent of cue integration. Our model reproduces known multisensory integration behaviors observed in experiments and sheds new light on our understanding of how information is integrated in the brain.

Introduction

Almost any behavioral task seems to require the combined effort of many brain regions working together. Information integration across distributed brain areas is thus considered of critical importance in the brain and has been described as one of the hallmarks of consciousness (Tononi and Edelman, 1998). Integration of information from different sources is essential for behavior: to obtain a reliable description for an underlying state of interest, evidence from different sources must be combined in a proper way. Accordingly, it has been found that neural systems combine information from different sensory modalities in an optimal way, as predicted by Bayesian inference. For example, while walking, the visual input (optic flow) and vestibular signal (body movement) both carry useful information about the motion direction (Bertin and Berthoz, 2004). In the brain, these visual and vestibular inputs can be fused seamlessly to give rise to a more reliable estimation of the motion direction than either of the modalities could deliver on its own (Gu et al., 2008; Chen et al., 2013). This capability of optimal multisensory integration seems ubiquitous across modalities, as has been reported, for example, for the integration of visual and auditory cues for inferring object location (Alais and Burr, 2004), motion and texture cues for depth perception (Jacobs, 1999), visual and proprioceptive cues for hand position (van Beers et al., 1999), and visual and haptic cues for object height (Ernst and Banks, 2002).

However, exactly how the brain integrates information optimally from multiple sources using synaptic communication and neural activity alone remains unresolved. A straightforward hypothesis is that a dedicated integration area, which receives feedforward inputs from all sensory modalities to be combined, pools and integrates all of the incoming information (Ma et al., 2006; Alvarado et al., 2008; Magosso et al., 2008; Ursino et al., 2009; Ohshiro et al., 2011). Although it has been shown that optimal multisensory integration could be achieved within such a dedicated area under certain conditions (Ma et al., 2006), the hypothesis does not touch upon the recent experimental findings that many interconnected multisensory areas are involved in the integration of sensory signals instead of just a single dedicated area (Gu et al., 2008; Chen et al., 2011b, 2013). Here, we argue that the existence of many multisensory areas should not be just seen as added complexity to the hypothesis of having one dedicated integration area, but instead might be at the core of how the brain coordinates the flow of information.

Using biological realistic neural network modeling, we explored theoretically how interconnected areas could integrate information in a distributed fashion. We developed a decentralized architecture for multisensory integration in which multisensory areas are connected with each other reciprocally and show that information integration can be done in an optimal manner without the need for a central area that would receive and pool all available information. As an example, we consider the task of inferring the heading direction from visual and vestibular cues and found that, when describing the interconnected multisensory areas dorsal medial superior temporal (MSTd) area and ventral intraparietal (VIP) area as a decentralized system, model predictions are in good agreement with biological observations. The decentralized system can near-optimally integrate visual and vestibular information in a wide parameter region and neural activations are consistent with the characteristic properties of neuronal responses observed during multisensory integration, including the inverse effectiveness, the spatial principle, and the reliability-based combination (Fetsch et al., 2013).

Finally, our theoretical analysis reveals that the strength of the connectivity between different multisensory areas might be related to prior knowledge about the similarity, or the probability of cooccurrence, of stimuli that are to be integrated. Therefore, our decentralized view of information integration not only provides an alternative hypothesis of how the brain might solve the challenge of integrating information, it also suggests a new interpretation of the function of connectivity within and between multisensory areas.

Materials and Methods

Neural network models for decentralized information integration.

In our study, a decentralized system consists of N (N ≥ 2) reciprocally coupled modules. Each module is modeled as a continuous attractor neural network (CANN) (Wu et al., 2008). Excitatory neurons in each CANN receive inputs from a stimulus feature θ, for example, the heading direction, and their preferred stimulus values are uniformly distributed in the parameter space (−π, π] with periodic boundary condition. Let u_l(θ, t) and r_l(θ, t) denote the synaptic input and the firing rate, respectively, of neuron θ in network l at time t. The network dynamics is given by the following:

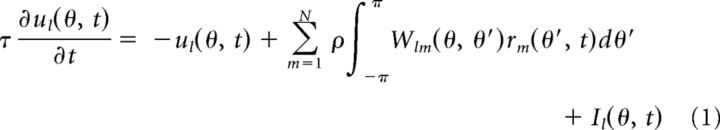where τ is a time constant and ρ is the neuronal density. W_lm(θ, θ′) represents the connection strength from neuron θ′ in network m to neuron θ in network l. I_l(θ, t) is the feedforward input from an unisensory brain area conveying the information of stimulus l.

Each CANN contains an inhibitory neuronal pool that normalizes the response of excitatory neurons divisively according to the overall activity level of the network. That is, the firing rate r_l(θ, t) of neuron θ in network l is given by the following:

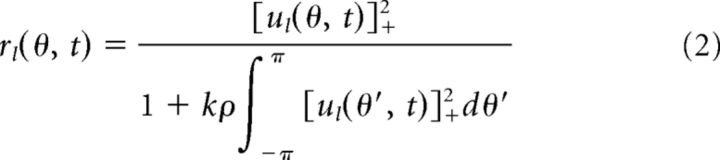where [x]₊ denotes rectification of negative values; that is, [x]₊ = 0 for x ≤ 0 and [x]₊ = x for x > 0. The parameter k controls the global inhibition strength.

The excitatory connection strength between two neurons depends on the distance of the neurons in feature space in a Gaussian manner (see Fig. 2C); that is:

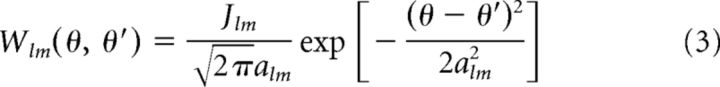where J_lm is a positive overall connection strength parameter and a_lm is the connection width in feature space. Note that W_ll denotes the recurrent connections between neurons within the same network l and W_lm, for l ≠ m, represents the reciprocal connections between neurons from different networks.

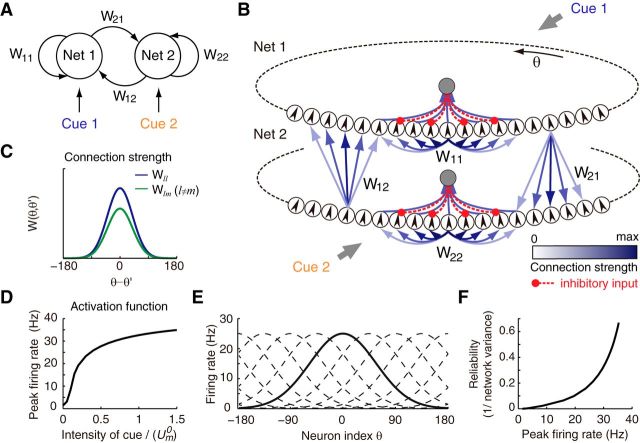
Figure 2.

Decentralized neural network model for information integration. A, Decentralized information integration system consisting of two reciprocally connected networks, each receiving an independent cue. B, Detailed network structure of the decentralized system in A. Each network module is modeled as a CANN. Small circles represent neurons with preferred feature θ indicated by the arrow inside. An inhibitory neuron pool (the gray circle in the center) sums all activities of excitatory neurons and generates divisive normalization. The blue arrows indicate translation-invariant excitatory connections, with strength represented by color; red lines are inhibitory connections. Each network module receives an independent cue as feedforward input. C, Recurrent and reciprocal connections in the system are translation-invariant; that is, the connection strength between two neurons only depends on their distance in feature space. D, Activation function of network neurons. The saturation for large synaptic input stems from the divisive normalization by the inhibitory neuron pool in each network. E, Population activity is a family of bell-shaped bumps (dashed lines), the position of which is determined by the stimulus (solid lines). F, Peak firing rate (bump height) encodes the reliability of network estimation.

When stimulus l is presented, we assume that an internal representation (also called cue) of stimulus l is generated in an unisensory cortical area; for example, the medial temporal (MT) or parieto-insular vestibular cortex (PIVC). Network l then receives the cue l as a feedforward input from the corresponding unisensory area. How the unisensory area represents the cue is largely unknown, so we follow previous approaches that the input has a Gaussian shape with multiplicative noise (Denève and Pouget, 2004; Ma et al., 2006), as follows:

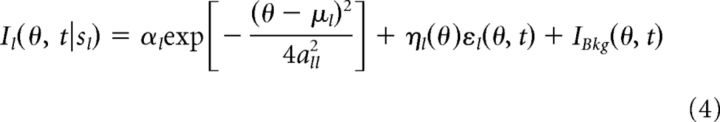where μ_l is the stimulus feature value conveyed by sensory cue l to network l. Because of the multiplicative noise, α_l is the signal strength and measures the reliability of the cue (Ma et al., 2006). The term η_l(θ)ε_l(θ, t) denotes the input noise, with noise variance η_l²(θ) = F_lα_le^{−(θ−μ_l)2/4a_ll2} proportional to the input intensity and F_l denotes the Fano factor of the input. ε_l(θ, t) is a Gaussian white noise of zero mean and unit variance. To include spontaneous activity, a background input I_Bkg(θ, t) = 〈I_Bkg〉 + $\sqrt{F_l{I}_{Bkg}}{\xi }_l$ (θ, t) is added, regardless of whether cue l is present. The mean of the background input is the same for all neurons. Input noise ε_l(θ, t) and background noise ξ_l (θ, t) are independent of each other, satisfying 〈ξ_l (θ, t)ξ_m(θ′, t′)〉 = δ_lmδ_θθ′δ(t − t′), 〈ε_l(θ, t)ε_m(θ′, t′)〉 = δ_lmδ_θθ′δ(t − t′), and 〈ξ_l(θ, t)ε_m(θ′, t′)〉 = 0, where δ_xx′ and δ(x − x′) are the Kronecker and Dirac delta functions, respectively.

Dynamics of the reciprocally coupled networks.

Because of the translational invariance of the recurrent connections in a CANN, the dynamics of a CANN is dominated by a few dynamical modes corresponding to distortions in height, position, and other higher-order features of the activity bump (Fung et al., 2010; Zhang and Wu, 2012). It was shown previously that one can project the network dynamics onto its dominant modes to simplify the mathematical analysis significantly (Fung et al., 2010). In the weak input limit (i.e., α_l is sufficiently small compared with the recurrent inputs), the change of the bump position is the dominant motion mode of the network dynamics and other distortions of the bump can be neglected. Note that the weak input limit assumption is not strictly true for all parameters considered in the Results section, where the bump height (but not the higher modes) will nevertheless be significantly affected by the input. Therefore, in addition to the following theoretical analysis, below we conducted numerical simulations in which the full dynamics were simulated and thus no assumption on the constancy of the bump height was necessary. The dominant mode corresponding to the change of the bump position is written as follows:

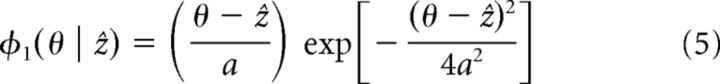where ẑ is a free parameter denoting the position of the bump and a is the width of the bump. Note that projecting a function f(θ) onto a motion mode φ(θ | ẑ) is to compute the quantity ∫_θf(θ)φ(θ | ẑ)dθ/∫_θφ(θ |ẑ)²dθ.

If only the position of the bump varies significantly with the feedforward input, then the network dynamics can be solved by using the following Gaussian ansatz:

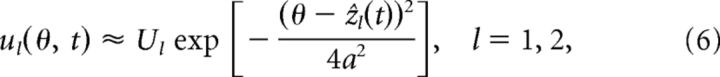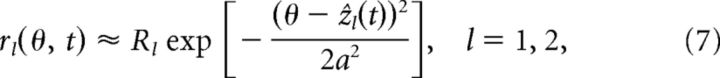where U_l and R_l represent the mean values of the bump height, which are treated unchanged in the statistically stationary state.

Taking two reciprocally connected networks as an example, we show how the projection of the network dynamics onto the dominant motion mode simplifies the description. Substituting the above Gaussian ansatz into the network dynamics (Eq. 1) and projecting it onto the motion mode (Eq. 5), we obtain the dynamics of the bump position for network 1 (the result of network 2 is the same except that the indices are interchanged), as follows:

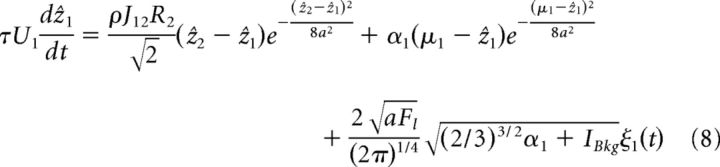For (ẑ₂ − ẑ₁)/8a² and (μ₁ − ẑ₁)/8a² sufficiently small (which is the case for the parameter regime we consider), the exponential terms can be safely ignored, and the above equation, together with the one for network 2, are further simplified to the following:

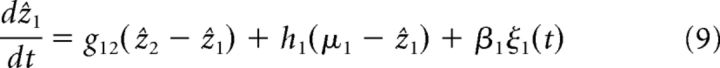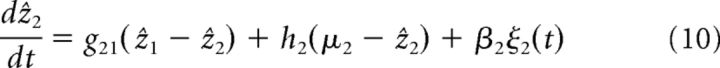where the following coefficients:

denote, respectively, the effective strengths of the reciprocal connections, the input signal, and the noise. Note that above equations are nonlinear because the effective strengths g_lm, h_l, and β_l are nonlinearly dependent with network and input parameters.

We consider the simple case that the two networks have the same parameter values and simultaneously receive identical cue intensities (but noises are independent to each other). This simplifies the notation to J_ll ≡ J_rc, J_lm ≡ J_rp(l ≠ m) and the effective parameters to g_lm ≡ g_rp, h_l ≡ h and β_l ≡ β. By this simplifying notations in Equation 9, we arrive at Equation 33.

In a general decentralized system of N reciprocally connected networks, the dynamics of the network estimations (i.e., the bump positions) can be analogously solved as follows:

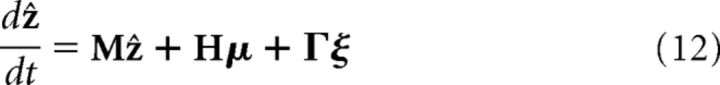where ẑ = {ẑ_l}, μ = {μ_l} and ξ = {ξ_l}, for l = 1,…, N. The system matrix is M = G − H, where G_lm = g_lm − δ_lm∑_m′g_lm′. H and Γ are diagonal matrices, with H_ll = h_l and Γ_ll = β_l. Note that if cue i is not present, then we set α_i = 0.

The steady state of the mean of ẑ is given by the following:

The covariance of ẑ in the steady state, denoted as Cov(ẑ), satisfies

To calculate Cov(ẑ), we diagonalize the matrix M as MP = PΛ, where Λ and P are the eigenvalues and eigenvectors of M, respectively. Defining y = P⁻¹ẑ, we have ΛCov(y) + [ΛCov(y)]^T = −P⁻¹ΓΓ^TP^−T, so Cov(y) can be solved as [Cov(y)]_ij = −[P⁻¹ΓΓ^TP^−T]_ij/(Λ_ii + Λ_jj). Finally, we obtain the following:

Given the number of networks and cueing conditions, the detailed expressions for the estimation mean and variance of a network can be solved by using Equations 13 and 15.

Integration performance of two reciprocally coupled networks.

It is difficult to solve analytically the integration performance of reciprocally coupled networks for more general parameter settings. We found in simulations that, over a wide range of parameters, our model achieved near Bayesian optimal performance, as shown in Figure 4. To demonstrate the underlying idea, we present below a special case in which Bayesian integration is achieved perfectly.

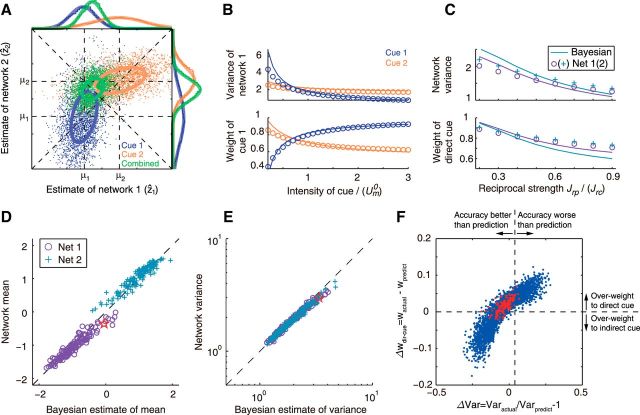
Figure 4.

Optimal information integration in two reciprocally connected networks. A, Example of joint estimations of two networks under three cueing conditions, with the marginal distributions plotted on the margin. B, Estimation variance and weight of cue 1 of network 1 when changing the intensity of either cue and fixing the intensity of another. Symbols: network results; lines: Bayesian prediction. C, Estimation variance and weight of direct cue (feedforward cue) of both networks with reciprocal connection strength. D, E, Comparisons of the mean (D) and variance (E) of the network estimate during the combined cue condition with the Bayesian prediction (Eq. 46 and 47) for different combinations of intensities for two cues (dots). Red star is an example parameter used in Figures 5, 6, and 7. F, Deviations of weight with deviations of variance of network's estimations. Red dots are deviations of network's estimations shown in D and E. Parameters: α₁, α₂ ∈ [0.4, 1.5]U_m⁰, (B–E) J_rc = 0.5J_c, J_rp ∈ 0.5J_rc; (F) J_rc = [0.4, 0.6]J_c, J_rp ∈ [0.2, 0.9]J_rc.

We consider two coupled networks that have the same parameter values. According to Equations 13 and 15, the mean and the variance of the estimate of network 1 are given by the following:

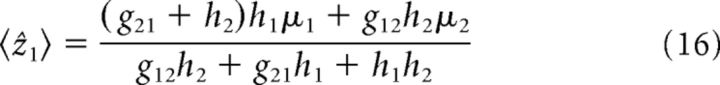where tr(M) is the trace of M; that is, tr(M) = ∑_i=1² M_ii = − (g₁₂ + g₂₁ + h₁ + h₂). To arrive at Equations 44 and 45, two approximations were made for simplification. First, we assumed that coefficients g_lm and h_l in Equations 9 and 10 are approximately unchanged with respect to stimulus conditions and abbreviate to g_lm ≡ g_rp and h_l ≡ h (α_l ≠ 0), respectively. Moreover, we assumed further that the effective noise strength β, which is the ratio of noise variance over bump height and reflects the signal-to-noise ratio of the network, is approximately unchanged across different stimulus conditions. This assumption is supported by the experimental observation that Fano factors of neural responses change insignificantly with stimulus conditions (Gu et al., 2008). With these approximations and symmetric parameter settings, it is straightforward to derive Equations 44 and 45.

Integration performance of N reciprocally coupled networks.

In a decentralized system composed of N all-to-all reciprocally connected networks, the estimation results of each network can also be calculated from Equations 13 and 15. When the N networks have same parameters and in response to N_q < N cues (suppose they are cue 1 to cue N_q for simplicity), the estimation mean and variance of network l with direct cue input l (l = 1.…, N_q) are as follows:

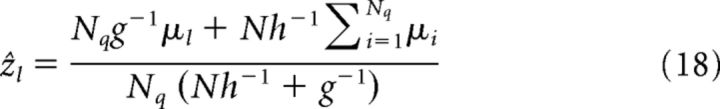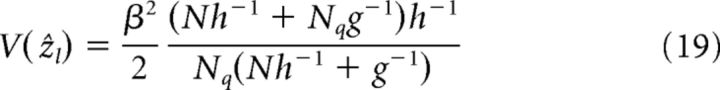Note that if only cue l is presented, it is V(ẑ_l) = β²h⁻¹/2 and the dependence on the effective reciprocal strength g vanishes, although the reciprocal connections are still there. This is because, without receiving cue inputs, other networks are unable to provide information about cue l.

The estimates of the networks without direct cue input (l = N_q + 1, … N) are as follows:

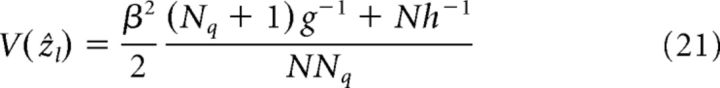A Bayesian observer of multisensory integration.

To understand the behavior of the decentralized system, the following Bayesian observer for multisensory integration is considered in this study (Bresciani et al., 2006; Ernst, 2006; Roach et al., 2006; Sato et al., 2007). Suppose that two sensory cues c₁ and c₂ are generated by two stimuli s₁ and s₂, respectively. Under the assumption that the noise processes of two cues given two stimuli are conditionally independent, the posterior distribution p(s₁, s₂ | c₁, c₂) satisfies the following:

where p(c_i | s_i) (i = 1, or 2) is the likelihood function and is modeled as a Gaussian distribution with mean μ_i and variance σ_i². p(s₁, s₂) is called the combination prior and specifies the probability of a particular combination of stimuli s₁ and s₂. Following previous studies, we choose a Gaussian function of the discrepancy between two stimuli (Shams et al., 2005; Bresciani et al., 2006; Ernst, 2006; Roach et al., 2006) as follows:

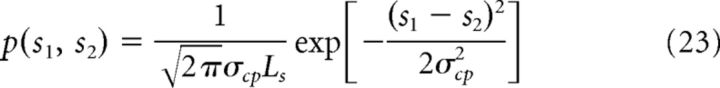where L_s is the width of the feature space; that is, L_s = 2π in case of estimating heading direction, and the parameter σ_cp measures the similarity between two stimuli. Note that the prior of each cue, p(s_i) (i = 1 or 2) has a uniform distribution across the feature space.

In the case of integrating N cues, we consider that the combination prior of the underlying stimuli is the product of the Gaussian function in the form of Equation 23 for all stimulus pairs, that is:

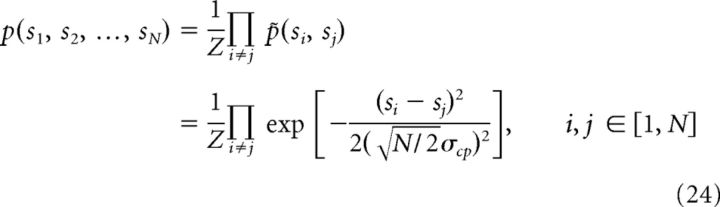where z is a normalization factor. p̃(s_i, s_j) has the same form as p(s_i, s_j) except its variance is Nσ_cp²/2. This ensures that the combination prior for s₁ and s₂ in the case of N (N > 2) cues, calculated by p_N(s₁, s₂) = ∫p(s₁, s₂, …, s_N)ds₃ds₄… ds_N equals Equation 23 in the case of N = 2. Nevertheless, the marginal distribution of each stimulus p(s_i) is still a uniform distribution.

Optimal integration in a decentralized system with N modules and N cues.

Although we show in the Results section that integration is optimal for the special case of a decentralized system of two modules and two cues, the integration of the decentralized system with N modules and N cues is generally optimal in the following sense.

Let us first consider the integration of three cues in a Bayesian observer with above joint combination prior (Eq. 24). When all three cues are simultaneously presented, the marginal posterior of s₁ can be derived as follows:

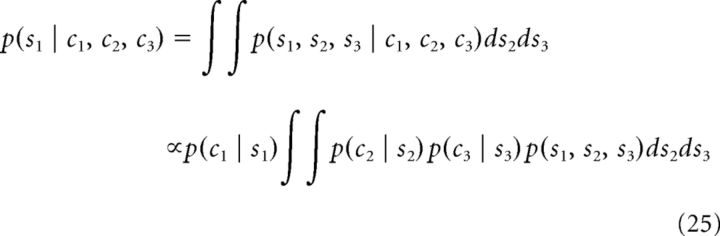Note that the last 2-fold integral in the above equation is proportional to p(s₁ | c₂, c₃). However, p(s₁ | c₂, c₃) cannot be further factorized as p(s₁ | c₂) × p(s₁ | c₃). Therefore, we have the following:

In a general integration of N cues, we found that the posterior of s₁ can be factorized as a pairwise product of the posterior under cue l and that of all other conditions excluding cue l (see also Eq. 50) as follows:

The mean and variance of the marginal posterior of the Bayesian observer can be found from Equations 18–21 by replacing h⁻¹ by σ² and g_rp⁻¹ by Nσ_cp²/2 and deleting coefficients β²/2. Therefore, in a decentralized system, network l is an optimal estimator for stimulus l by integrating its feedforward inputs from cue l and reciprocal inputs from other networks.

Evaluating the deviations of the networks' performance from the Bayesian observer.

For evaluating the optimality of the integration in the simulation, we examined the deviations of the actual mean and variance of the network estimations from the predicted mean and variance of the Bayesian observer, respectively. For the robustness against parameter variations (see Fig. 4F), we followed Fetsch et al. (2009) and used the bias of the cue weight to evaluate the bias of the mean. For example, in network 1, the bias of cue 1's weight is as follows:

where w₁^{net 1} = (〈z₁ | c₁, c₂〉 − 〈z₁ | c₂〉)/(〈z₁ | c₁〉 − 〈z₁ | c₂〉) is the actual weight of cue 1 in network 1 and ŵ₁^{net 1} V = V (z₁ | c₂)/[V(z₁ | c₁) + V(z₁ | c₂)] is the predicted value. In each network, the bias of cue 2's weight has the opposite sign of the bias of cue 1's weight; that is, Δw₁^{net 1} = − Δw₂^{net 1}, because w₁ + w₂ = 1 in the integration of two cues. Therefore, for the analysis of Figure 4F, we only calculated the bias of the weight of the direct cue Δw_dir−cue in each network. The direct cue of network l is cue l, meaning that the network receives the input of cue l directly from feedforward connections instead of via reciprocal inputs from other networks. A positive Δw_dir−cue indicates that the network's estimation is biased toward its direct cue, whereas a negative value denotes a bias to its indirect cue. The deviation of the variance was measured by the deviation between the actual variance and the predicted variance (from Eq. 46), namely:

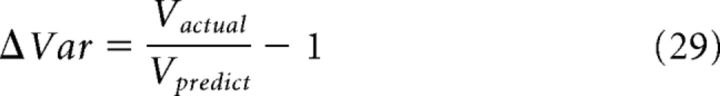A positive ΔVar indicates that the accuracy is worse than the predicted value; a negative ΔVar denotes improvement over the prediction.

Network simulations and parameters.

In the simulations, two or more CANN networks were coupled together. Each CANN consisted of 180 neurons, which were uniformly distributed in the feature space (− 180°, 180°]. The parameters of the networks were chosen symmetrically to each other; that is, all of the structural and input parameters of the networks had the same value. However, the networks received independent noise. The synaptic time constant τ was rescaled to 1 as a dimensionless number and the time step size was 0.01τ. All connections had the same width: a_lm = 40°.

In the following, we list the parameter values used if not mentioned otherwise. The recurrent connection strength J₁₁ = J₂₂ ≡ J_rc was set in the range of [0.4, 0.6]J_c, where J_c = 2 $\sqrt{2}$(2π)^1/4 $\sqrt{ka\rho }$ = 0.896 is the minimal strength for holding persistent activity. Therefore, no persistent activity occurred in a network after withdrawing the stimulus. The strength of the reciprocal connections J₁₂ = J₂₁ ≡ J_rp was in the range of [0.2, 0.9]J_rc; that is, always smaller than the recurrent connections. The input strength α was scaled relative to U_m⁰ = J_c/4ak $\sqrt{\pi }$ = 6.316 and distributed in the region of [0.4, 1.5]U_m⁰, where U_m⁰ is the synaptic bump height that a network can hold without external input when J_rc = J_c. The interval of the input strength was wide enough to cover the superadditive and nearly saturated regions. The strength of the background input was 〈I_Bkg〉 = 1 and all Fano factors of the cues and background inputs were set to 0.5. This resulted in a Fano factor of single neuron responses on the order of 1. In the simulation, the activity bump position was estimated by using a population vector; that is, calculating the center-of-mass of the activity bump. Specific parameter settings are mentioned in the figure captions.

Discrimination performance of single neurons.

To reproduce experimental findings (Gu et al., 2008), we designed a computational task to discriminate whether a stimulus value is smaller or larger than 0° based on single neuron activities. Similar to the experiment, we chose an example neuron from network 1 that preferred a heading direction of −40°. The directions of two congruent cues were simultaneously changed from −30° to 30°. In each direction, three stimulus conditions (see Fig. 3A) were applied for 50 trials and the firing rate distributions were obtained (see Fig. 5A,B). We used receiver operating characteristic (ROC) analysis (Britten et al., 1992) to compute the ability of the example neuron to discriminate between two opposite heading directions; that is, −2° versus 2°. The ROC value counts the proportion of instances in which the stimulus was correctly judged to be larger than 0°. Neurometric functions (see Fig. 5C) were constructed from these ROC values and were fitted with cumulative Gaussian functions to determine neuronal discrimination thresholds (the SD of the cumulative Gaussian function). The predicted threshold in the combined cue condition can be calculated using Bayesian inference as follows:

where σ₁ and σ₂ are the neuronal discrimination thresholds under cue 1 and cue 2, respectively.

Figure 3.

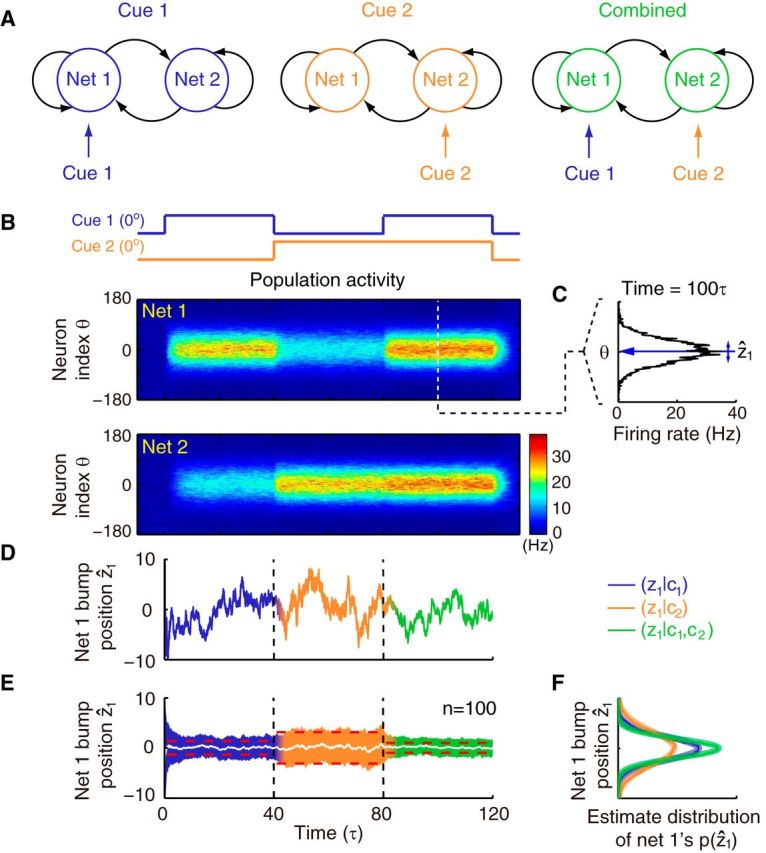
Population responses and estimation results of network modules in the decentralized system. A, Illustration of the three stimulus conditions applied to the system. Cue 1 (blue) and cue 2 (orange) are first individually presented to network 1 and network 2, respectively, and then both cues are applied simultaneously (green) in the combined cue condition. B, Averaged population activities over trials of two coupled networks when presenting the stimulus conditions from A in temporal order. Both cues are congruent and static, and centered at 0°. The color encodes firing rate of the population activity. C, Snapshot of the population activity in network 1. The position of the activity bump is considered as the current estimate of the network (ẑ₁). D, Estimate of network 1 (from the population activity shown in B, computed as indicated in C) fluctuates with time. E, Mean (white line) and SD (colored region) of network 1's estimates averaged over 100 trials. Red dashed lines are theoretical calculations of the SD, which fit well with the simulation results. Note that the variance of the network estimate when presenting two cues decreases compared with that when presenting single cues. Also note that the estimate based on the direct cue has less variance than that based on the indirect cue alone. F, Histograms and Gaussian fits of network 1's estimates under three stimulus conditions represent the posterior of the underlying state. Parameters: J_rc = 0.5J_c, J_rp = 0.5J_rc, and α = 0.5U_m⁰.

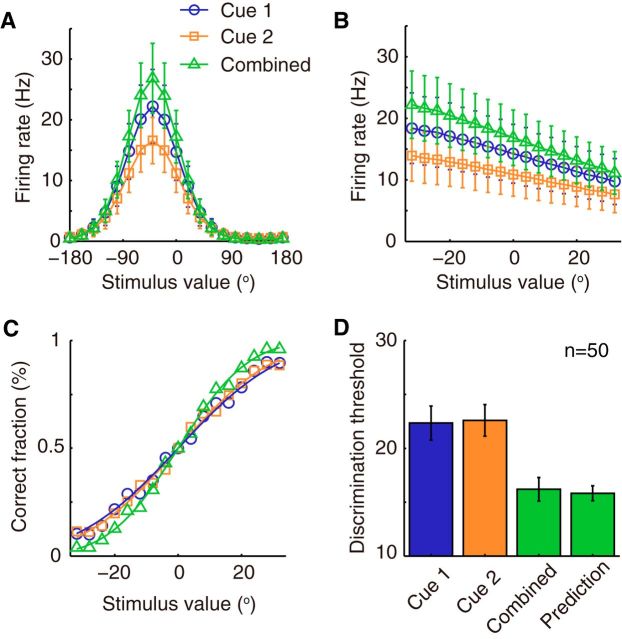
Figure 5.

Single neurons integrate information optimally. A, Tuning curve of an example neuron in network 1 for the three stimulus conditions. The example neuron prefers −40° stimulus. Error bar indicates the SD of firing rate across trials. B, Responses of the example neuron in a narrow range of stimulus values for the three stimulus conditions. The responses in this small stimulus range are used to perform ROC analysis to estimate the neurometric functions. C, Neurometric functions of the example neuron, which denotes the correct fraction of judging the stimulus to be larger than 0°. Smooth lines show the cumulative Gaussian fit of the neurometric functions. D, Average neuronal discrimination thresholds of the example neuron in three stimulus conditions compared with the Bayesian prediction (Eq. 30). The actual neuronal discrimination thresholds in the case of combined cues are comparable with the Bayesian prediction (p = 0.044, n = 50, unpaired t test). Parameters: J_rc = 0.5J_c, J_rp ∈ 0.5J_rc, α₁ = 0.4U_m⁰, α₂ = 0.9U_m⁰.

Virtual experiments reproducing empirical principles of multisensory integration.

We further performed simulations to determine whether the decentralized system can reproduce some characteristic neural response properties observed during multisensory integration, namely the inverse effectiveness, the spatial principle, and the reliability-dependent combination (Morgan et al., 2008; Fetsch et al., 2013). The neuron with feature value 0° in network 1 was used as an example neuron. Its mean firing rates under different tests are plotted in Figure 6. The virtual experiments simulated the protocols of the biological experiments. In the experiments examining the inverse effectiveness and the spatial principle, cue 1 and cue 2 had identical intensity and noise strength and the intensity increased from 0 to 1.5 U_m⁰, which produced a near saturated neuronal response. In the test of the inverse effectiveness, both cues were located at 0°, whereas in the spatial principle test, cue 1 was fixed at 0°, but cue 2 was varied from 0° to 2a, where a is the turning width of the neuron. To test the reliability-dependent combination (Morgan et al., 2008), the responses of the example neuron were measured under eight different mean values for each cue (ranging from −180° to 180° with a step size of 45°), with 64 combinations in total. The intensity of cue 1, α_1, was decreased from 0.46α₂ to 0.12α_2, which in turn decreased the reliability of cue 1 whereas the intensity of cue 2, α₂, was fixed. For each combination of two cues, the bimodal tuning curve R_bi(θ₁, θ₂) was fitted as a linear model of two unimodal tuning curves as follows:

where R_bi(θ₁, θ₂) denotes the firing rate when the two cues are located at θ₁ and θ_2, respectively. R₁(θ₁) and R₂(θ₂) are the unimodal tuning curves when only cue 1 or only cue 2 is presented, respectively. The neuronal weights w₁, w₂, and offset C were determined by minimizing the mean-squared error between the predicted bimodal responses and the measured actual neuronal responses.

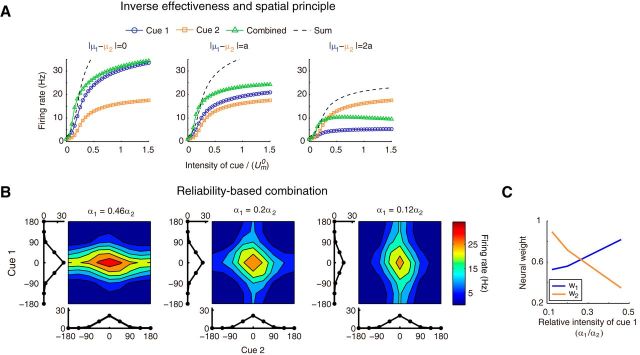
Figure 6.

Empirical principles of multisensory integration for single neurons. A, Inverse effectiveness and spatial principle. Neuronal responses in the three stimulus conditions (cue 1 or 2 alone and cue 1 and cue 2 together) are plotted as a function of cue intensity, under different disparity between two cues. The differences of two cues are varied from 0 to 2a, where a is the turning width. B, Reliability-dependent combination. The bimodal tuning curves of a probe neuron with varied cue intensities are shown as a contour plot. The two marginal curves around each contour are the unimodal tuning curves. The intensity of cue 1, α₁, decreases gradually from left to right, whereas the intensity of cue 2, α₂, is fixed. C, Bimodal turning curve fitted as a linear model of the two unimodal turning curves (Eq. 31). The plot shows the weight of the two cues with respect to the relative intensity of cue 1. Parameters are the same as in Figure 5.

Results

Decentralized architecture for information integration

In engineering applications, three principled architectures have been proposed to integrate observations (cues) from different stimuli (Durrant-Whyte and Henderson, 2008): the centralized, the distributed, and the decentralized architectures (Fig. 1). In the centralized architecture (Fig. 1A), the raw observations from sensors are sent directly into a central fusion center, which estimates the underlying state from the raw observations of all of the modalities. Although simple in structure, the centralized architecture suffers from the computational burden of the fusion center, the high communication load (because all raw observations of all modalities must be delivered into a single center), and the susceptibility of being paralyzed once the fusion center fails.

Figure 1.

Comparison of different information integration architectures. A, Centralized architecture. A central processor directly receives the raw observations from the sensors, and does all the computations to globally integrate information. B, Distributed architecture. Local processors first compute local estimates, which are subsequently integrated by a central processor to reach a global estimate. C, Decentralized architecture. No central element exists. Each processor first computes a local estimate and then propagates it to others. Information integration is done via cross talk among processors, so that each processor individually arrives at an optimally integrated estimate. D, Example of a decentralized information integration system in the cortex. MSTd and VIP are reciprocally connected with each other. Both areas can optimally integrate visual and vestibular information.

Some computational tasks can be distributed to modular local processors (Fig. 1B). The processor modules compute local estimates in parallel and then only send the results to the central processor. However, this distributed architecture also suffers from the robustness problem because a central fusion center still exists. In contrast, in a decentralized architecture (Fig. 1C), all of the processors communicate with the others directly so that a central fusion center becomes obsolete. Each processor first makes a local estimate according to its own observation and then corrects it by integrating the local estimates from the other processors to obtain a global estimate.

Would it be possible for cortical circuitry to successfully adopt a decentralized architecture to integrate multisensory information? Anatomically, there is some supportive evidence. For instance, MSTd and VIP are two brain areas that are deeply involved in the integration of visual and vestibular information for inferring the heading direction and do so optimally (Gu et al., 2008; Chen et al., 2013). There are abundant reciprocal connections between MSTd and VIP (Boussaoud et al., 1990; Baizer et al., 1991) that cause the activities of the two areas to be correlated with each other (Vincent et al., 2007). In addition, MSTd and VIP receive feedforward visual and vestibular inputs from MT cortex (Boussaoud et al., 1990) and PIVC (Lewis and Van Essen, 2000) (Fig. 1D), where MT and PIVC are unisensory regions that belong to the visual and vestibular systems, respectively. Together, MSTd and VIP appear to be good candidates for local processors within a decentralized information integration architecture (cf. Fig. 1C,D).

Biologically plausible decentralized network model for information integration

What realistic neural network model could be used to implement a local processor that allows to connect different local processors with each other as required by a decentralized architecture? Although different neural network models might be applicable in principle, we will show in the following that reciprocally interconnected CANN modules behave naturally like a decentralized information integration system that shows near-optimal cue integration over a wide parameter range in a biologically realistic manner. We first describe our model for the simplest case of two symmetrically connected processors that receive feedforward inputs (cues) from their associated stimuli (Fig. 2A) and then generalize it to multiple cues.

CANNs are widely used biologically realistic network models to implement cortical computations for continuous stimuli (Dayan and Abbott, 2001; Pouget et al., 2003), including estimating heading directions from noisy inputs (Zhang, 1996). In a typical CANN (full dynamics can be seen in Eq. 1–4), every neuron has a tuning function with respect to the same stimulus feature (Eq. 7); for example, the heading direction, but each neuron is tuned to a gradually different feature value and all neurons cover the whole feature space (Fig. 2B). The firing rate of CANNs is a nonlinear function of the input and thus neuron activations saturate in a realistic manner (Eq. 2; Fig. 2D). Because recurrent connections are translation-invariant in the space of neuronal preferred feature values (Fig. 2C), the population activity in a CANN evolves into one of many smooth bell-shaped bumps (an attractor state, solid line in Fig. 2E). Moreover, the activity bump state will be stabilized at a position (in feature space) that has maximal overlap with the input (Fig. 3C), achieving a template-matching operation that essentially infers the underlying stimulus value near a maximal likelihood estimator (Denève et al., 1999; Wu et al., 2002).

Because the position of the population activity bump can thus be interpreted as the estimate of the CANN given noisy sensory information, for example, the current guess that the neural system has about the heading direction, a CANN is an ideal implementation of a local processor in the decentralized architecture. Therefore, in our model, each local processor is modeled by a CANN that receives direct cue (feedforward) input from an unisensory brain area (Eq. 4), such as MSTd (VIP) receives feedforward inputs about visual (vestibular) information from MT (PIVC) (compare to the scheme in Fig. 2B). The feedforward inputs are localized bumps corrupted by (multiplicative) noise, so that the height of input bump α encodes the reliability of external stimulus (Eq. 4). The current estimate of a local network about the heading direction, that is, the bump position, is referred to as ẑ. Note that, in response to a localized noisy bump input, the height of network's response increases superlinearly (due to divisive normalization) with the reliability of network's estimation (Fig. 2F) (Denève et al., 2001; Denève and Pouget, 2004; Ma et al., 2006).

To achieve information exchange between local processors, we assume that CANN modules are interconnected. We show below that, if reciprocal connections between individual CANN modules are defined in a translation-invariant manner similar to the recurrent connections (Fig. 2C), the model system naturally integrates information from two cues and thus implements a decentralized information integration system. Figure 3 illustrates the dynamics of information integration in a decentralized system. To simulate a typical cue integration experiment, we first applied two single cues individually and then applied both of them simultaneously (Fig. 3A). Figure 3B shows the population activities in response to two congruent cues both centered at 0°. When two cues were simultaneously presented, the networks' responses increased compared with single-cue conditions and the variance of the networks' estimates (bump positions, Fig. 3C) in turn decreased (Fig. 3D,E), indicating that each network successfully integrated information from two sources.

To understand the network dynamics theoretically, we first looked at the dynamics of the estimation within an individual processor (CANN module) without connection to other processors. By simplifying the full network dynamics of a single processor (by ignoring distortions of the activity bump across cue conditions), we found that the current local estimate ẑ (the bump position) can be written as follows (see Eq. 5–8 in Materials and Methods):

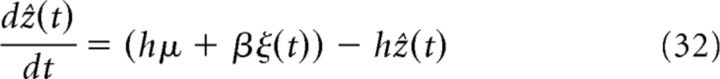where hμ + βξ(t) represents the input signal centered at μ, with the effective strength h corrupted with independent Gaussian noise ξ(t) of effective strength β. Note that the effective strengths are nonlinearly dependent on network and input parameters (see Eq. 11). From the dynamics in Equation 32, one notes that, if the current bump position corresponds to the input cue value μ, it will be only driven by noise (of zero mean) and thus on average deliver the correct estimate. If the processor's current estimate is inaccurate, it will update its estimate according to the deviation between the input and the current estimation and thus eventually arrive at the correct estimate.

If now two processors are coupled together (as in Fig. 2B), the dynamics of the estimate in network 1 can be approximated as follows (see Eq. 9 and 10 in Materials and Methods; the estimate of network 2 is obtained by relabeling):

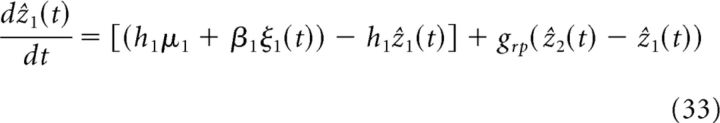The additional term in comparison with Equation 32 is related to the communication between networks. Namely, the difference between the two local estimates, g_rp[ẑ₂(t) − ẑ₁(t)] conveys the information of cue 2 and is additionally used to adjust the network's estimate (g_rp is related to the coupling strength, see Materials and Methods). Therefore, communication through reciprocal connections enables each processor to integrate information from multiple modalities.

If the information from two cues is combined together, one would expect that the reliability of the joint estimate increased. Consider that the two networks received two congruent and identical cues, that is, the cues have the same intensity h₁ = h₂ ≡ h and the same feature value μ₁ = μ₂ ≡ μ. If the networks are uncoupled (g_rp = 0), each network will deliver an unbiased estimate, 〈ẑ〉 = μ with variance V(ẑ) = β²/2h (set g_lm zero in Eq. 17). Note that the variance V(ẑ) is a decreasing function with activity bump height, indicating that the bump height encodes the reliability. When two networks are reciprocally coupled, the variance of the estimates of both networks becomes V(ẑ) = $\frac{{\beta }^2}{4}\left(\frac{1}{h}+\frac{1}{h=2g_{rp}}\right)$, which decreases with the effective reciprocal coupling strength g_rp, implying that the reciprocal connections convey the information from other cues to improve the accuracy of each network's estimate. These theoretical predictions of the variances correspond well with the simulations (red dashed line in Fig. 3E).

Together, we found that a system of interconnected CANN modules fulfills the requirements that are conceptualized in the decentralized framework of information integration: local processors compute local estimates and reciprocal interactions are used to correct the estimates by integrating information from other processors. However, whether information is integrated in an ideal way remains to be seen. We next introduce a Bayesian observer to evaluate the performance of the information integration of the decentralized system and then compare the network's estimation with the Bayesian observer in both theory and simulation.

General Bayesian observer of multisensory integration

To assess the performance of information integration in the decentralized system, a Bayesian observer is needed as a benchmark (Ernst, 2006; Clark and Yuille, 2013). We consider a Bayesian observer for a general form of multisensory integration (Shams et al., 2005; Bresciani et al., 2006; Ernst, 2006; Roach et al., 2006). In many previous studies about multisensory integration, it is assumed a priori that a single stimulus gives raise to multiple sensory representations (cues) that are then fully integrated into an unified percept (Ernst and Banks, 2002). However, more generally, sensory evidence about an entity of interest, such as the heading direction, might instead originate simultaneously from different physical sources. For instance, the optical flow of the visual field and the body acceleration are of completely different physical origin, but still simultaneously accessible by the visual system and the vestibular system, respectively. Both physical sources may only contain some partial information about the heading direction, which can nevertheless be extracted and integrated to arrive at a better estimate of the heading direction than either cue would deliver on its own. Therefore, in our framework, we suppose that two sensory cues c₁ and c₂ are generated by two distinct stimuli s₁ and s_2, respectively, and assume that these two stimuli have some systematic covariation in regard to the entity of interest. This covariation regulates the extent of how much the two cues are informative for the inference of either of the stimuli s₁ or s₂. We will see below that, if the covariation of the stimuli is weak, one cue does help little about inferring the other and both cues should be (nearly) independently processed and could give raise to two different percepts. Conversely, if both stimuli are strongly correlated, then both cues should be (nearly) fully integrated to arrive at improved estimates.

Mathematically, under the assumption that the noise processes of the two cues given two stimuli are independent with each other, the posterior distribution p(s₁, s₂ | c₁, c₂) satisfies the following:

where p(c_l | s_l) (l = 1, or 2) is the likelihood function indicating the probability that a particular value of cue c_l is generated from a given stimulus s_l and is modeled as a Gaussian distribution with mean μ_l (stimulus feature value in Eq. 4) and variance σ_l² (proportional to input intensity α_l in Eq. 4). p(s₁, s₂) is called the combination prior, which specifies the probability of the presence of s₁ and s_2. Here, we set it to be a Gaussian function of the discrepancy between two stimuli (Bresciani et al., 2006; Roach et al., 2006; Sato et al., 2007) as follows:

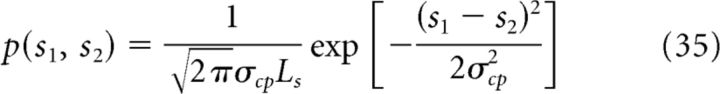L_s is the width of feature space, for example, 2π for heading direction. Note that the prior of either stimulus, p(s_l) (l = 1 or 2), is still a uniform distribution.

The combination prior given by Equation 35 specifies the a priori similarity between two stimuli that give raise to the two cues, respectively. Importantly, in the integration process, this combination prior determines the extent for the two cues to be integrated. Let us consider two extreme examples. When σ_cp = 0, p(s₁, s₂) becomes a delta function δ(s₁ − s₂), then the two marginal posterior distributions are exactly the same, that is, p(s₁ | c₁, c₂) = p(s₂ | c₁, c₂), meaning that two cues should be fully integrated into a unified percept (Ernst and Banks, 2002). In the case σ_cp = ∞, the combination prior is flat and each cue should be processed independently without any integration because no useful information can be obtained from one modality to predict the stimulus value of the other. In the case of 0 < σ_cp < ∞, two cues should be partially integrated, meaning that the estimated values of s₁ and s₂ can be different, but nevertheless the estimate of one of them uses the cue information from the other. In this study, we consider the general situation that σ_cp can take different values and treat full integration as a special case.

The posterior of stimulus 1 can be obtained by marginalizing the joint posterior distribution as follows (the posterior for stimulus 2 has similar form by interchanging indices 1 and 2):

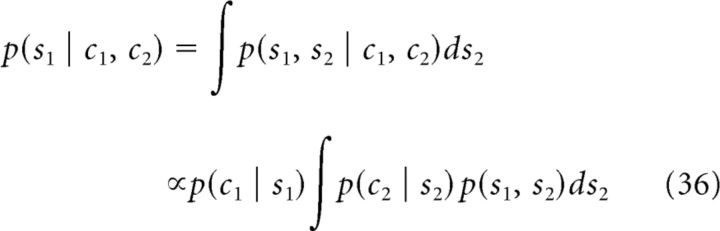Note that p(c₂ | s₁)∝ ∫ p(c₂ | s₂)p(s₁, s₂)ds₂ due to the conditional independence of two cues. Because a flat prior distribution of each stimulus and accordingly a flat prior distribution of each cue (from Eq. 35), we have the following:

Because of this factorization of the marginal posterior, the mean and variance of the estimate for each stimulus under combined cues can be derived from the mean and variance under single cues (Ernst, 2006) as follows:

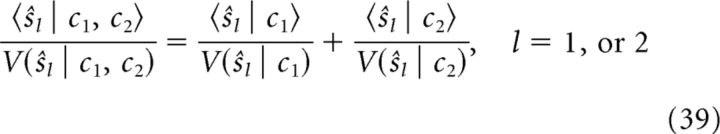In more detail, the mean and variance of s₁ and s₂ can be found as follows:

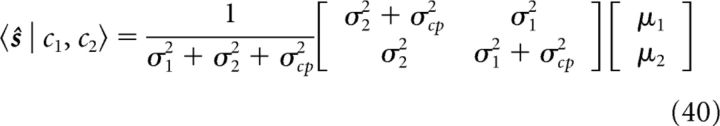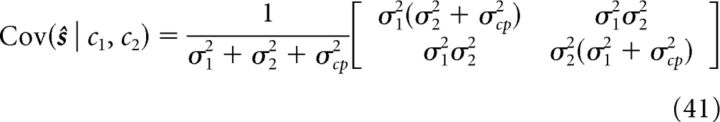where s = (s₁, s₂)^T. The mean and variance of the stimulus estimates under single-cue conditions can be found by formally letting σ₂ → ∞ (cue 1 condition) or σ₁ → ∞ (cue 2 condition). We see that the prior parameter σ_cp determines the extent of integration: when σ_cp = 0, 〈ŝ₁〉 = 〈ŝ₂〉 = (σ₂²μ₁ + σ₁²μ₂)/(σ₁² + σ₂²), the estimates of two networks are identical and full integration happens (Ernst and Banks, 2002); when σ_cp = ∞, ŝ₁ = μ₁, and ŝ₂ = μ₂, implying that the two cues are not integrated at all.

Equations 38 and 39 show how to integrate estimates under single-cue conditions optimally with associated uncertainties into combined estimates for two stimuli, which are used as the criteria for judging whether optimality is achieved in an information integration system (Ernst and Banks, 2002; Ma et al., 2006).

Decentralized system implements a general Bayesian observer

To compare the information integration of the decentralized system to the integration predicted by the Bayesian observer, we thus compared the means and variances of the network estimations in single cue and combined cue conditions. Because the dynamics of each network's estimate could be approximated in closed form (Eq. 9 and 10), we can compute the mean and variance of the estimates in analytical terms. We found that, in the case of two symmetrically connected network modules (for a general solution, see Eq. 16 and 17), the results are given by the following (to distinguish the network estimation and Bayesian observer, the estimation of network and Bayesian observer are denoted as ẑ and ŝ respectively):

If only cue 1 is presented (h₁ = h; h₂ = 0):

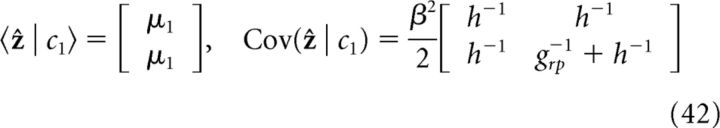Only cue 2 (h₁ = 0; h₂ = h):

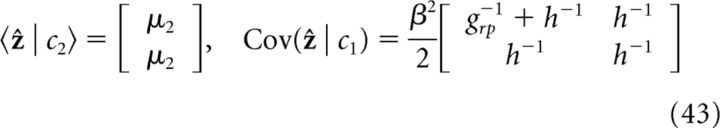Combined cues (h₁ = h₂ = h):

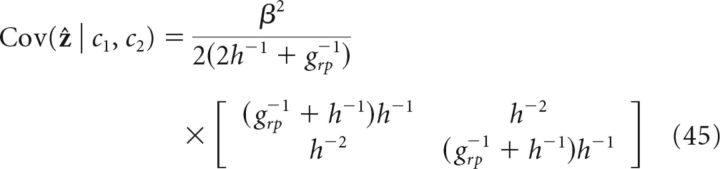It is straightforward to verify that information integration in the two coupled networks of the decentralized system (Eq. 42–45) satisfy exactly the prediction of the Bayesian observer (Eqs., 38 and 39); that is:

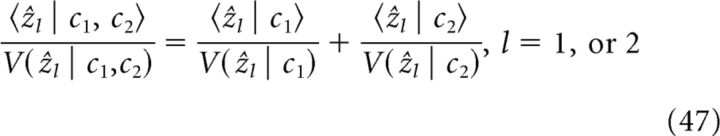Therefore, network l is an optimal estimator for stimulus l. Interestingly, by comparing estimation results of the decentralized system (Eq. 44–45) and the Bayesian observer (Eq. 40–41) with σ₁ = σ₂, we see that the reciprocal connections between the two networks encode the combination prior and thus determine the extent of integration; that is:

Similarly, the effective input strength represents the reliability of input cue:

Notably, when full Bayesian integration is considered, it requires σ_cp = 0, so g_rp = ∞; that is, the reciprocal connection strength is infinitely strong. In such a case, the two networks effectively collapse into a single network and the system becomes equivalent to a system having only a single dedicated integration area as proposed previously (Ma et al., 2006).

Although the information integration is optimal for the special case used in the theoretical analysis above, the so far approximated nonlinear dependence of the effective strengths g_rp, h, and β on network and input variables may nevertheless cause the integration in the full model to deviate from the Bayesian observer. Therefore, to determine whether optimal integration still holds without approximations and if the theoretic result generalizes to a wider parameter regime, we next performed numerical simulations.

In the simulations, for each network, the Bayesian prediction under the combined cue condition was calculated by substituting the estimates under single-cue conditions into Equations 46 and 47. This approach is similar to experimental studies in which the estimations of MSTd (VIP) neurons in the combined cue condition are predicted by using the responses of MSTd (VIP) neurons under single-cue conditions (Gu et al., 2008; Chen et al., 2013). Figure 4A shows an example of the joint estimates of both networks under all three stimulus conditions. When only cue 1 was present, the estimates of both networks were centered at μ₁ and network 1 had smaller estimation variance than network 2 because network 2 received the input indirectly via network 1. This result is in accordance with the prediction of the Bayesian observer: V(ŝ₂ | c₁) = σ₁² + σ_cp² is larger than V(ŝ₁ | c₁) = σ₁² (set σ₂ to ∞ in Eq. 41). The estimates of both networks were reversed when only cue 2 was presented. In the combined cue condition, the estimates of the two networks shifted toward a position in between μ₁ and μ₂ and had the smallest variance. Note that the means of the estimates of the two networks were different in the combined cue condition when the two cues were disparate, as required by the Bayesian observer (Eq. 40).

To determine whether the network estimation changed with cue reliability (represented by the height of the input bump), we varied the reliability of one cue while fixing the other cue as well as other network parameters (Fig. 4B). With increasing reliability of cue 1, the estimation variance of network 1 decreased (blue line in Fig. 4B top), implying that the reliability of network 1's response increased accordingly and, therefore, the weight of cue 1 in network 1 increased as well (blue line in Fig. 4B bottom). Analogous results were observed when changing the reliability of cue 2 while fixing the other parameters (orange lines in Fig. 4B).

Furthermore, we also investigated how the strength of the reciprocal connections J_rp between two networks influenced the network estimations (Fig. 4C). Increasing J_rp induced a decrease of the estimation variance and a decrease of the weight of the direct cue (the direct cue to network l is cue l) of both networks, meaning that the estimations of the two networks became closer to each other, which implies that the two cues were integrated to a larger extent (Eq. 40 and 41). This result agrees with Equation 48; that is, that the reciprocal connection strength is inversely proportional to the variance of the combination prior σ_cp².

Next, we tested the network performance under different combinations of cue intensities (see Materials and Methods for the details of the parameter settings). The cue intensities span a large interval ranging from superadditive to near-saturation regions of the neural responses. Figure 4, D and E, plots the estimation means and variances of both networks versus Bayesian predictions. Indeed, the simulation results show that each network individually achieved near optimal inference for the underlying stimulus under a wide range of parameter values (R² = 0.979 and 0.972 for the mean and variance, respectively).

We further systematically changed the network and input parameters and measured the deviations of the integration weight for the direct cue Δw_dir−cue (Eq. 28) and the deviation of estimation variance ΔVar (Eq. 29) from the Bayesian prediction (Fig. 4F). The varied parameters include reciprocal connection strengths, recurrent connection strengths, and input strengths of the two cues (see Materials and Methods for details). Expectedly, because of some nonlinear effects of the network dynamics, the integration performance deviated from Bayesian predictions for extreme parameter settings. However, in our testing parameter region, the deviations of the integration weight of the direct cue were all bounded in the region of ±0.2, and the deviations of the variance were bounded in the region of ±0.32, indicating nevertheless near optimality. Interestingly, in our system, the deviations of the weights were positively correlated with deviations of the variance, in agreement with experiments in which similar deviations from optimal behavior were observed (Fetsch et al., 2009).

Optimal information integration at the single-neuron level

Limited by the available data, electrophysiological experiments for studying cue-integration focused only on single neuron activities rather than population responses (Gu et al., 2008; Chen et al., 2013). In a heading direction discrimination task, it was found that the optimal integration of visual and vestibular inputs could be read out in single neurons' activities (Gu et al., 2008; Chen et al., 2013). To test whether similar optimal integration behaviors are achieved on a single-neuron level in our model, we mimicked the experimental setup and simulated a discrimination task in which the heading direction θ is judged as being above or below 0° based on the single neuron's activities. We investigated whether the actual discrimination performance of an example neuron during combined cues can be predicted from the single-cue conditions when using Bayesian inference (Fig. 5; see Eq. 30). Figure 5D shows the neuronal discrimination thresholds of an example neuron across trials. The threshold in the combined cue condition was significantly smaller than the threshold in cue 1 (p = 1.22 × 10⁻⁴⁰, n = 50, unpaired t test) and cue 2 conditions (p = 8.64 × 10⁻⁴⁴, n = 50, unpaired t test), indicating that the integration of two cues happened. Although the combined threshold was significantly greater than the predicted value (p = 0.044, n = 50, unpaired t test), the combined threshold was only 2% greater than the predicted one, indicating near optimal integration. This result shows that our model reproduces the experimental finding on the integration behavior of single neurons.

Empirical principles of multisensory integration

We found that our decentralized system can also reproduce some characteristic properties of neuronal responses observed during multisensory integration, including the inverse effectiveness, the spatial principle, and the reliability-based combination (Fetsch et al., 2013).

Inverse effectiveness states that the amplification effect of combined cues compared with single-cue conditions is weakened for strong input (Stein and Stanford, 2008). Figure 6A (left) displays the responses of an example neuron in three stimulus conditions with varying cue intensities (see details in Materials and Methods). With increasing cue intensities, the combined neuronal response increases, but the amplification effect of combined responses compared with the sum of single-cue responses becomes smaller, indicating that the inverse effectiveness is achieved. For weak intensity, the neuronal response to combined cues was larger than the sum of its responses to two individual cues, exhibiting a superadditive tendency, whereas, for strong inputs, the combined neuronal response was smaller than the sum of the single-cue responses, exhibiting a subadditive tendency.

This amplification of the response during combined cues is known to be modulated by the amount of disparity between two cues. This effect is called the spatial principle (Fetsch et al., 2013). Our system could reproduce this effect. When two cues were congruent, the combined neuronal response was larger than its response to either of the cues, exhibiting cross-modal enhancement (Fig. 6A, left). When the disparity of two cues was large enough, the response of the neuron became weaker than its response to the more reliable cue, exhibiting cross-modal suppression (Fig. 6A, right). This property originates from the divisive normalization in the network dynamics, as pointed out by (Ohshiro et al., 2011): when the disparity of two cues is large, cue 2 excites the example neuron weakly but still contributes effectively to the inhibitory neuron pool, which in turn more strongly suppresses the example neuron compared with the inhibition in the single-cue condition.

Finally, responses of single neurons to combined cues are reliability dependent. This effect is called reliability-based combination (Morgan et al., 2008) and could also be reproduced by our model system. Figure 6B shows the bimodal tuning curves of an example neuron in network 1 with varied cue 1 intensities while with other parameters were fixed. With a large intensity value of cue (left panel in Fig. 6B), the bimodal response of the example neuron was dominated by cue 1, meaning that the firing rate of the example neuron was affected more significantly by changing cue 1 than changing cue 2. With declining intensity of cue 1, the bimodal tuning curve of the neuron became gradually dominated by cue 2. By fitting the bimodal turning curve as a linear combination of the unimodal tuning curves of the same neuron (Eq. 31), R² is 0.96, 0.90, and 0.93 for decreasing intensity of cue 1 α₁), we found that when the reliability of cue 1 increased, the weight of cue 1 also increased; whereas the weight of cue 2 decreased.

In summary, single-neuron activities of our model system were in good agreement with a number of empirical multisensory integration principles.

Information integration of multiple cues

In reality, the brain often needs to integrate information from more than just two sensory cues (Wozny et al., 2008). A decentralized integration system is very flexible due to its modular structure and thus can be easily extended to an arbitrary number of coupled network modules with each of them receiving and processing an individual cue. For example, to integrate three cues, a third network, which receives cue 3, can be added directly to the aforementioned system (Fig. 7A). Furthermore, in the general case of integration of N cues, a decentralized system can be further extended to comprise N modules that are reciprocally connected in an all-to-all fashion and each module receives feedforward inputs from its corresponding cue. The means and variances of network estimations under all cueing conditions are derived in the Materials and Methods section (Eq. 18–21). For simplicity, we assumed that all networks and inputs have the same parameters. The results indicate that the distribution of the estimates of network l satisfies the following:

The above equation means that the distribution of the estimates of network l can be factorized as the products of the distribution under cue l condition (direct cue of network l) and the one under condition of all cues combined except cue l, p(ẑ_l | ∪_i≠lc_i). However, the latter distribution cannot be further factorized so that it is in general not proportional to Π_i≠lp(ẑ_l | c_i). This is because network l receives the information of other cues only indirectly from other networks and the reciprocal connections induce correlation between the indirect cues.

Figure 7.

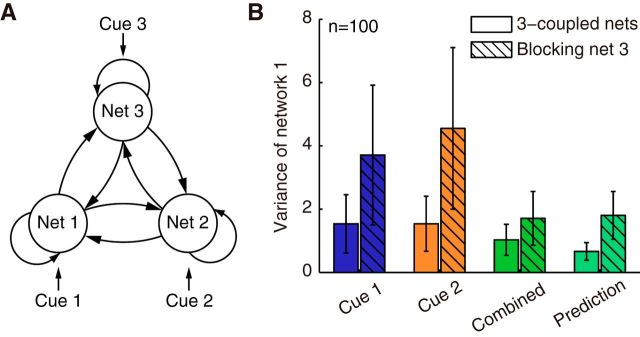
Information integration in a decentralized system with multiple reciprocally connected networks. A, Architecture of a system consisting of three reciprocally connected networks. The insertion of a third network is done simply by reciprocally connecting network 3 with other networks. B, Robust information integration in three reciprocally connected networks. After blocking network 3 (shaded bars), network 1's estimate in the combined condition is nevertheless still similar to the Bayesian estimate (no significant difference: p = 0.27, n = 80, unpaired t test), although its variance increases. Error bars plot SD of the network estimation variance obtained from 100 trials. Parameters are the same as Figure 5.

Does this incapability of factorization imply that the integration of indirect cues is suboptimal in the decentralized system? This will depend on the Bayesian observer used for the comparison. From the analysis above, we know that the reciprocal connection between network 1 and 2 represents the combination prior p(s₁, s₂) of the Bayesian observer. Because networks are only connected in a pairwise manner, prior information beyond the pairwise interaction seems impossible to represent in the network. Indeed, we found that when the combination prior of the extended Bayesian observer has the product of Gaussian form (see Eq. 24) as follows:

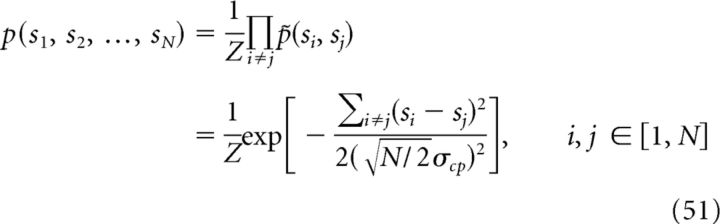where the integration of the decentralized system is still optimal, that is, network l is an opimal estimator for stimulus l through integrating its feedforward inputs from cue l and reciprocal inputs from other networks (see Eq. 18–21 and 25–27 for the derivation and unshaded bars in Figure 7B). Analogous to the system consisting of only two networks, each component of p̃(s_i, s_j) in Equation 51 is represented by the reciprocal connection between network i and network j.

Robustness against failure of modules

A key advantage of the decentralized architecture is its robustness to damage in local networks. For our model, we found that, although some cues can become inaccessible (but this problem can be resolved by cross-cue connections shown as the dashed lines in Fig. 1D), the damage of one or a few network modules does not impair the optimality of two cue integration in still intact networks, meaning that the network estimations under combined cue condition can be also predicted by using Equations 38 and 39. For example, in a system that consists of three networks receiving three cues, network 1 and 2 optimally integrated cues 1 and 2 regardless of whether network 3 was damaged; that is, p(ẑ_l | c₁, c₂)∝p(ẑ_l | c₁)p(ẑ_l | c₂), l = 1, 2 (Fig. 7B; p = 0.40 and 0.27 when comparing the network variance with the prediction with or without blocking network 3, respectively; n = 100, unpaired t test). However, the neural activity of the intact networks nevertheless changed in response to the damage. For example, a loss of network 3 caused the variance of the estimates in networks 1 and 2 to increase even though cue 3 was absent (Fig. 7B and Eq. 18–21 in Materials and Methods). This change can be understood from two perspectives. From the perspective of network dynamics, the existing connections between networks help to average out noise (Zhang and Wu, 2012; Kilpatrick, 2013). Therefore, the more excitatory connections a network module receives, the smaller the variance of its estimate, so losing a connection due to damage consequently increases the variance. Conversely, from the perspective of the Bayesian observer, the loss of network 3 changes the effective prior for the integration of cue 1 and 2, from p₃(s₁, s₂) = ∫ p(s₁, s₂, s₃)ds₃ to p̃(s₁, s₂). From Equation 24 (the case of N = 3), we see that the variance of the integration prior increases from σ_cp² to 3σ_cp²/2, thus increasing the variance of the estimation (Eq. 41). This property might explain the recent experimental finding that, whereas the integration of visual and vestibular cues can still satisfy the Bayesian prediction (Eq. 38) after blocking MSTd, the overall behavioral accuracy nevertheless decreased (Gu et al., 2012).

Discussion

In the present study, we have explored how several brain areas could work together to integrate information optimally in a decentralized manner. Decentralized computing has been favored by engineering applications due to its robustness, computational efficiency, and modularity (Durrant-Whyte and Henderson, 2008). Similar concepts, such as parallel and distributed processing, have been long proposed as the basis of brain functions (Rumelhart et al., 1988) and the idea of decentralized integration was discussed previously (Sabes, 2011). However, how decentralized information integration might be achieved in neural circuitry is not known. Here, we have shown that interconnected network modules can build up a decentralized information integration system in a biologically plausible manner. Most importantly, the resulting system is capable of integrating information from different cues and estimating multiple stimuli in a near-optimal way.

Comparison with previous approaches

In contrast to a decentralized system, a centralized architecture is similar to the hypothesis of having one dedicated multisensory area that pools incoming sensory information as assumed by a number of modeling studies on multisensory integration (Ma et al., 2006; Alvarado et al., 2008; Magosso et al., 2008; Ursino et al., 2009; Ohshiro et al., 2011). In regard to the anatomy, the finding of many interconnected multisensory areas favors the decentralized system. Taking visual–vestibular integration system as an example, not one single area, but instead many areas, including MSTd (Gu et al., 2008), VIP (Chen et al., 2013), the frontal eye field (Gu et al., 2015), and visual posterior sylvian area (Chen et al., 2011b), display integrative responses to combined visual and vestibular inputs. Apart from feedforward connections from unisensory areas, abundant reciprocal connections exist between multisensory areas (Boussaoud et al., 1990; Baizer et al., 1991).

Ma et al., 2006 found that a single dedicated network could implement a Bayesian observer with full integration as follows:

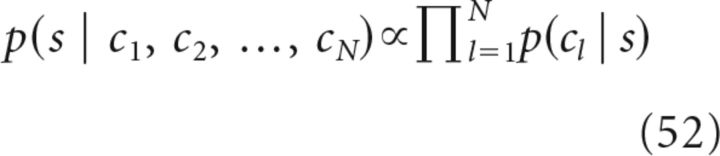where two or multiple cues are fully integrated into an unified percept. In contrast, the decentralized architecture implements a Bayesian observer of the form:

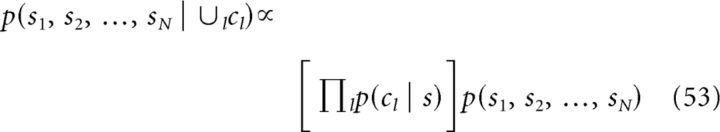which estimates the values of multiple stimuli simultaneously, integrating information from other cues to an extent that is regulated by the form of the combination prior. Whether one or the other Bayesian observer is more plausible for describing the information integration in neural systems likely depends on many aspects, such as the nature of the features to be integrated, the neural sites, and sensory modalities in questions. Human psychophysical studies suggest that, depending on cueing conditions, the brain may use different strategies to integrate multisensory information, from full to partial and to no integration at all (Hillis et al., 2002; Shams et al., 2005; Ernst, 2006). Therefore, both Bayesian observers might be offer a valid description in certain situations.

Reciprocal connections in the decentralized system

We found that the combination prior p(s₁, s₂, …, s_N) of the observer is encoded by the reciprocal connections between networks: the variance of the combination prior, σ_cp², which measures the similarity between stimuli and thus determines the extent of integration, is represented by the inverse of the effective reciprocal connection strength between networks, g_rp⁻¹. Therefore, the decentralized system gives a new explanation for the abundance of reciprocal connections between the many existent multisensory areas.

From Equations 40 and 41, we see that the conventionally used criteria for Bayesian integration are always satisfied regardless of the value of σ_cp². This raises the question of how the strength of reciprocal connections should be determined for information integration. Because the strength of the reciprocal connection regulates the integration extent in the network, it should be adjusted to match the real distribution of stimuli in the natural environment, such that the estimates of the networks are closest statistically to the true stimulus values (Körding and Wolpert, 2004; Körding et al., 2007).

Moreover, in a naturally dynamical environment, the underlying relation between two presented cues might vary over time, implying that the extent of integration, σ_cp, need to be adjusted accordingly. The decentralized system provides a promising framework to achieve this adaptability by dynamically learning or transiently modulating the effective reciprocal strength between two networks.

Reciprocal connections were also considered previously in a modeling study on coordinate transformation (Denève et al., 2001; Pouget et al., 2002; Avillac et al., 2005). However, the computations involved in coordinate transformation and multisensory integration are fundamentally different (Beck et al., 2011) and thus are not comparable to the reciprocally connected networks within the framework of decentralized information integration.

Plausibility and predictions of the model

In our framework, each network module is modeled as a CANN. CANNs have many interesting computational properties and are thus widely used to explain many cortical functions, including the population decoding of orientation (Ben-Yishai et al., 1995), spatial location (Samsonovich and McNaughton, 1997), and working memory (Compte et al., 2000). Moreover, it has been shown that a single CANN can optimally compute one sensory quantity (Denève et al., 1999; Wu et al., 2002). The recurrent connections within a CANN serve as the basis for estimating a sensory quantity from noisy inputs, whereas divisive normalization was shown to provide realistic nonlinear neural responses (Carandini et al., 1997; Ohshiro et al., 2011). Interestingly, optimal integration in a decentralized system with CANNs requires subadditivity of neuronal responses (Fig. 8A), which is in agreement with the finding of subadditive neuronal responses in multisensory areas (Morgan et al., 2008; Fetsch et al., 2013). The subadditivity in case of optimal integration in the decentralized network originates from the property that reliability increases superlinearly with bump height (Fig. 2F).

Figure 8.

A, Deviation of network variance with additivity index. The additivity index is the ratio of the peak firing rate (bump height) under combined cue condition and the sum of the two peak firing rates under both single-cue conditions. The parameters are the same as in Figure 4F. B, M-shaped covariance structure between two neurons in decentralized system, which is a symbol of CANN. θ₁ and θ₂ are the preferred direction of the two neurons. When the stimulus is in between the preferred directions, the two neurons display negative correlation; otherwise, their activities are positively correlated.

One way to test experimentally whether sensory areas might indeed be implemented by CANNs is to look for any M-shaped correlation structure between neighboring neurons' activities (Fig. 8B), a hallmark of the translation-invariant connectivity (Ben-Yishai et al., 1995; Wu et al., 2008). Recent experimental data indeed suggests an M-shaped correlation between neurons in MT (Ponce-Alvarez et al., 2013) and in the prefrontal cortex (Wimmer et al., 2014), which supports the idea that CANNs provide biologically plausible computational modules for a decentralized information integration architecture. A recent study pointed out that the M-shaped correlation limits the information capacity of a neural ensemble (Moreno-Bote et al., 2014). Certain information loss in CANNs is indeed inevitable because of their neutrally stable dynamics, which is a key property leading to many computational advantages. This neutral stability implies that noise components along the direction of bump position shift cannot be effectively averaged out, leading to potential information loss (these fluctuations can only be average out over time, not space; Wu et al., 2008). Nevertheless, for general independent noises, the information loss caused by the noise component along the direction of bump position shift is rather small, suggesting that using CANNs is still an efficient way to extract stimulus information in practice (Denève et al., 1999).

In a decentralized system, neurons in different areas are reciprocally connected, so activities of connected areas should be correlated. This prediction is supported by fMRI and EEG studies (Vincent et al., 2007; Senkowski et al., 2008). Note, however, that our framework is not restricted to model information integration across brain areas but may also be readily applied to information integration between layers or between hypercolumns within a single brain area. For instance, in the superior colliculus, where visual and auditory information are integrated (Stein and Stanford, 2008), the decentralized idea may be also applicable. Anatomically, the superficial layers of the superior colliculus receive solely visual inputs, whereas the deep layers receive solely auditory inputs. As long as the superficial and deep layers are reciprocally connected, it is possible that they constitute a decentralized integration system.

For simplicity, we ignored cross-cue connections between modules (dashed lines in Fig. 1D). Experiments found that the MSTd neurons have relatively shorter latency than VIP neurons in response to visual inputs (Gabel et al., 2002), whereas VIP neurons respond relatively faster than MSTd neurons to vestibular inputs (Chen et al., 2011a). This observation indicates that direct- and cross- feedforward connections function differently (otherwise, their response latencies would be comparable) and that, as an approximation, the contribution from the cross-feedforward connections can be regarded as included in the reciprocal connections (because they are both slower than the direct-feedforward connections and convey the same cross-cue information). Nevertheless, the cross-feedforward connections could be important in other aspects of information integration; for example, they could ensure that all cues remain accessible in case of a network module failure.

Whether MSTd and VIP and other reciprocally connected cortical areas in posterior parietal cortex constitute a decentralized system could be tested with electrophysiological experiments. According to the estimations of decentralized system (Eq. 44 and 45), when visual (vestibular) cue is presented, the discrimination thresholds of MSTd neurons should be smaller (larger) than that of VIP neurons. Another prediction is that if partial integration happens (which can only be implemented by a decentralized system), the estimation means from MSTd and VIP neurons are different when two cues are disparate (Eq. 44). This can be verified by comparing the weights of the visual cue estimated from MSTd neurons and VIP neurons.