Microfluidic sorting of protein nanocrystals by size for X-ray free-electron laser diffraction

Abstract

The advent and application of the X-ray free-electron laser (XFEL) has uncovered the structures of proteins that could not previously be solved using traditional crystallography. While this new technology is powerful, optimization of the process is still needed to improve data quality and analysis efficiency. One area is sample heterogeneity, where variations in crystal size (among other factors) lead to the requirement of large data sets (and thus 10–100 mg of protein) for determining accurate structure factors. To decrease sample dispersity, we developed a high-throughput microfluidic sorter operating on the principle of dielectrophoresis, whereby polydisperse particles can be transported into various fluid streams for size fractionation. Using this microsorter, we isolated several milliliters of photosystem I nanocrystal fractions ranging from 200 to 600 nm in size as characterized by dynamic light scattering, nanoparticle tracking, and electron microscopy. Sorted nanocrystals were delivered in a liquid jet via the gas dynamic virtual nozzle into the path of the XFEL at the Linac Coherent Light Source. We obtained diffraction to ∼4 Å resolution, indicating that the small crystals were not damaged by the sorting process. We also observed the shape transforms of photosystem I nanocrystals, demonstrating that our device can optimize data collection for the shape transform-based phasing method. Using simulations, we show that narrow crystal size distributions can significantly improve merged data quality in serial crystallography. From this proof-of-concept work, we expect that the automated size-sorting of protein crystals will become an important step for sample production by reducing the amount of protein needed for a high quality final structure and the development of novel phasing methods that exploit inter-Bragg reflection intensities or use variations in beam intensity for radiation damage-induced phasing. This method will also permit an analysis of the dependence of crystal quality on crystal size.

INTRODUCTION

X-ray free-electron laser (XFEL) technology has become popular over recent years in the field of protein crystallography.^1–3 This technology was proposed to facilitate structural studies of difficult-to-crystallize proteins^4–6 that failed to produce crystals large enough for traditional synchrotron-based crystallography where the crystal is exposed to the X-ray beam for durations longer than the onset of detrimental radiation damage. Smaller crystals grow more readily from these complex proteins and feature a low degree of long range disorder yet are damaged by the X-ray radiation dose required to collect full, high-resolution datasets using conventional methods. XFELs outrun radiation damage with pulses lasting tens of femtoseconds and thereby enable “diffraction before destruction” to solve such protein structures.^7–9 As the crystals are destroyed by the extremely intense XFEL pulse (after producing a useful diffraction pattern), the sample must be very rapidly replenished in order to collect a full dataset in a reasonable amount of time. The serial femtosecond crystallography (SFX) method has now been applied to solve the structures of many proteins,^10–13 and continued success is expected in the realm of virus complexes in the future.^14–16 However, to ensure such success, this nascent methodology requires considerable further development, from sample optimization and delivery, to detector technology and data analysis.

Two sample characteristics that significantly impact SFX data quality are crystal size and dispersity. Protein crystals smaller than the X-ray beam (generally submicron) can generate diffraction patterns with “shape transforms” or interference fringes between the Bragg spots,¹⁷ which can be used for a novel, direct phasing method.^18–20 Because SFX is a serial method where a new crystal is brought into the X-ray interaction region for each X-ray pulse, patterns from many different crystals must be indexed and their structure factors merged to reconstruct the electron density map of the molecules in the unit cell. This analysis effectively performs a Monte Carlo integration over a (typically) heterogeneous distribution of crystal sizes, shapes, and orientations, as well as the stochastically varying XFEL pulse intensity and spectrum.²¹ Narrowing the distribution of any of these fluctuating parameters would narrow the distribution of intensity samples (which are mostly partial reflections) measured for each reflection in each snapshot, to different degrees. A narrow crystal size distribution is expected to significantly decrease the number of patterns required for the determination of accurate structure factors.

Microfluidic platforms have the potential to optimize protein crystal size for SFX^22,23 since they are capable of handling small volumes of sample and allow for their manipulation in ways in which macroscale methods cannot, such as fine-tuned separations and control of chemistry. We previously demonstrated a proof-of-principle microfluidic device that can sort polystyrene particles and photosystem I (PSI) protein crystals into submicron size fractions with a narrowed size distribution.²³ The sorting principle is based on dielectrophoresis (DEP),^24,25 which has been extensively employed to manipulate particles for various applications such as size sorting,^26–28 particle trapping,^29–32 and concentration.^33–35 To induce DEP, an inhomogeneous electric field is applied to the solution, whereby gradients of the electric field ($\mathit{E}$) are formed. The DEP force (${\mathit{F}}_{\mathit{D}\mathit{E}\mathit{P}}$) acting on a spherical particle can be described as³⁶

$${\mathit{F}}_{\mathit{D}\mathit{E}\mathit{P}}=2\pi r^3{\epsilon }_m{f}_{\mathit{C}\mathit{M}}\nabla {\mathit{E}}^2,$$ (1)

where $r$ is the particle radius, ${\epsilon }_m$ is the medium permittivity, and $f_{\mathit{C}\mathit{M}}$ is the Clausius-Mossotti factor. In microfluidic devices, creative electrode patterning or the design of nonlinear channels in an insulating material such as polydimethylsiloxane (PDMS) can create $\nabla {\mathit{E}}^2$ regions where DEP acts on particles flowing through.^37,38 The latter method, known as insulator-based DEP (iDEP), is employed here as it enables simpler device fabrication for rapid replication, cost reduction, and a uniform $\nabla {\mathit{E}}^2$ along the entire channel height.^26,28,30,33 Once a DEP region is established by creating areas of high $\nabla {\mathit{E}}^2$, each particle needs to have an inherently unique ${\mathit{F}}_{\mathit{D}\mathit{E}\mathit{P}}$ in order for differential manipulation to occur for sorting. In Equation (1), the dependence of ${\mathit{F}}_{\mathit{D}\mathit{E}\mathit{P}}$ on particle radius indicates that large particles exhibit a greater ${\mathit{F}}_{\mathit{D}\mathit{E}\mathit{P}}$ response, enabling size-dependent sorting (assuming $f_{\mathit{C}\mathit{M}}$ is constant for particles with similar physicochemical properties). For protein crystal sorting, conditions are established to facilitate negative DEP,^23,26,27 whereby larger particles experiencing a higher ${\mathit{F}}_{\mathit{D}\mathit{E}\mathit{P}}$ are repelled from high $\nabla {\mathit{E}}^2$ regions more than smaller particles (details on device design can be found in the Results and Discussion section).

Since the aforementioned first-generation microsorter²³ showed the first proof-of-principle device, volume throughput was low, making it inefficient at providing the minimum sample volume (∼300 μl) needed for current XFEL liquid jet-based sample delivery methods.^39,40 To collect XFEL data using a liquid jet injector, we scaled up the size of the microsorter to increase volume throughput from ∼3 μl/h to ∼150 μl/h, which significantly reduced the time required to sort larger volumes of crystal suspensions. The particle fractions obtained were then delivered into the path of the Linac Coherent Light Source (LCLS) X-ray beam at SLAC National Accelerator Laboratory.

This paper focuses on crystal size optimization and its potential for improving data quality and facilitating new phasing methods. We further describe the second-generation microfluidic sorting device, provide a detailed sorted sample characterization using several methods, including dynamic light scattering (DLS), NanoSight particle tracking, and electron microscopy (EM), and examine diffraction patterns obtained from sorted protein nanocrystals. Additionally, simulations of SFX datasets with different levels of crystal size dispersity representing the unsorted and experimentally attained sorted crystal fractions are presented to illustrate the benefits of a narrow crystal size distribution on SFX data analysis, by comparing correlation coefficients (CC*), multiplicities, and signal-to-noise ratios (SNRs) of merged reflections.

EXPERIMENTAL

Materials and chemicals

For protein preparation and crystallization, n-dodecyl-β-maltoside (β-DDM) (D97002-C) was purchased from Glycon, Germany. 2-(N-morpholino)ethanesulfonic acid (MES), MgSO₄, CaCl₂, MgCl₂, and phenylmethanesulfonyl fluoride (PMSF) were purchased from Sigma Aldrich, USA. For sorting, platinum wire was purchased from Alfa Aesar, USA, PDMS (Sylgard 184) from Dow Corning, USA, and Tygon (1/16 in. inner diameter) and fluorinated ethylene propylene (1/32 in. inner diameter) tubing were purchased from Cole Parmer, USA.

Photosystem I purification and crystallization

All steps of isolation, purification, and crystallization were carried out in dim green light and at 4 °C. PSI was isolated and purified from Thermosynechococcus elongatus as described previously,⁴ with modifications. Cells were broken with an M-110 l microfluidizer processor (Microfluidics, Inc., USA) and inhibition of proteases was implemented by maintaining a concentration of 50 μM PMSF at all steps prior to isolation of PSI by anion exchange chromatography. Crystallization was used as a final purification step as described in Hunter et al.⁹ The PSI-containing High-Performance Liquid Chromatography (HPLC) fractions (which contain 20 mM MES, pH 6.4, 0.02% β-DDM, and 140 mM MgSO₄) were concentrated to approximately 5 ml (corresponding to 10 mM chlorophyll) and diluted with buffer without salt (5 mM MES, pH = 6.4, and 0.02% β-DDM) to obtain a concentration of 8 mM MgSO₄. Crystal growth is induced by concentrating the sample in an ultrafiltration cell. Crystals were then harvested and washed in buffer with 6 mM salt (5 mM MES, pH = 6.4, 6 mM MgSO₄, and 0.02% β-DDM) and stabilized in buffer without salt (5 mM MES, pH = 6.4, and 0.02% β-DDM). The crystal suspension was coarsely fractionated by sedimentation as follows: the suspension was aliquoted into several microcentrifuge tubes and allowed to settle for sequential steps of 10, 20, 30, and 40 min, each time removing the supernatant. All crystals were prepared within 10 days of fractionation and stored at 4 °C in the dark.

Microfluidic device fabrication and photosystem I crystal sorting

The microfluidic sorter was fabricated using standard photolithography and soft lithography techniques.^41,42 Briefly, a printed photomask containing the channel outlines was designed using AutoCAD software (AutoDesk, USA) and printed at high resolution (CAD/Art Services, Inc., USA). This mask was then patterned on a silicon wafer with SU-8 negative photoresist (MicroChem, USA) using a mask aligner (System III, Hybrid Technology Group, USA). The wafer was silanized and a 10:1 mixture of PDMS/cross-linker was poured on the wafer and cured at 80 °C for 4 h to form a negative relief of the structures. The PDMS structure was cut off the wafer and plasma treated with a glass microscope slide to form a sealed channel system. 6 mm diameter circles were punched at channel ends to form reservoirs. Platinum wire electrodes were placed in each reservoir to facilitate connection to a high voltage source (HVS448, LabSmith, USA), and tubing was placed in outlet reservoirs for connection to a negative pressure pump (MFCS-EZ, Fluigent, France) to extract sorted fractions. ∼100 μl of PSI crystal suspension (30 or 40 min settled fraction) were added to the inlet reservoir, and 500 V peak-to-peak AC potential at a frequency of 250 Hz was applied across the device with negative pressure applied to all outlet reservoirs to initiate the sorting process and maintain sample flow and extraction. Monitoring and fluorescence imaging of experiments performed at Arizona State University were done with a fluorescence microscope (IX71, Olympus, USA) equipped with appropriate bandpass filters (exciter: 470 nm, Semrock; emitter: 690 nm, Chroma) and attached CCD camera (iXon, Andor Technology, UK) controlled by Micro-Manager acquisition software (ver. 1.4, UCSF, USA). Monitoring of experiments performed at LCLS was facilitated with a portable microscope (SVM340, LabSmith, USA) equipped with an EPI-fluorescence camera module (476 nm excitation) and installed emission filter (675 nm, Edmund Optics, USA), controlled by LabSmith μScope software (ver. 1.04).

Sample characterization

To measure sample size distribution, dynamic light scattering measurements were performed using a droplet-based instrument (Spectro Size 302, Molecular Dimensions, UK) and a cuvette-based instrument (DynaPro Nanostar, Wyatt Technologies, USA). For the former, 3 μl of sample was pipetted on a siliconized glass coverslip and placed in a hanging drop-mode on top of the well of a 24-well plate, with each well containing 500 μl of buffer without salt to prevent the drop from evaporating during the DLS measurement. The sample drop was aligned to the laser and 10 DLS scans lasting 20 s each were recorded. For the latter, 60 μl of sample was placed in a UV-transparent plastic cuvette and set in the instrument from which 20 measurements lasting 10 s each were recorded. Further sample size distribution measurements were performed using a NanoSight instrument (LM10-HS, 405 nm laser, Malvern Instruments, UK), in which 300 μl of sample at a concentration of approximately 10⁸ particles/ml was injected into the sample holder cell and measured using Nanoparticle Tracking Analysis (NTA) software.

Transmission electron microscopy (TEM) imaging of PSI crystals was performed as described previously.⁴³ Briefly, 25 μl aliquots of PSI crystal sample were collected in their native buffer. The aliquot was concentrated and 8 μl of sample was applied to a pre-discharged square mesh copper grid (Electron Microscopy Sciences) and incubated for 30 s before blotting and staining with 2% (wt./vol.) uranyl acetate. TEM images were acquired using an FEI Tecnai T12 electron microscope operating at 120 kV equipped with a Gatan UltraScan 1000 CCD camera.

Serial femtosecond crystallography experiments

Sorted PSI nano- and microcrystal fractions were prepared for SFX experiments at LCLS by first concentrating them 3–4 fold by centrifugation (<300 rpm). This sample was then loaded into a stainless steel reservoir, which was then connected to the Gas Dynamic Virtual Nozzle (GDVN)^39,40 injector sample line (75 μm ID) controlled by an HPLC pressure pump. Gas to the GDVN was provided by an in-house helium gas supply at 450 psi. The sample was delivered at an average rate of 15 μl/min and jetted out of the GDVN in a stream positioned perpendicular to the XFEL beam direction (for further details on liquid-jet sample delivery, see Refs. 39 and 40). SFX data were collected at the Coherent X-ray Imaging (CXI) instrument at LCLS from sorted and unsorted PSI nano/microcrystal suspensions, with the latter serving as a reference sample to test the experimental conditions. Two Cornell-SLAC Pixel Array Detectors (CSPADs)⁴⁴ were arranged in series, for high spatial resolution on the front detector (z = 88 mm) and high angular resolution on the back detector, at very low scattering angles (z = 2.1 m). We used 9.48 keV X-ray pulses, lasting ∼40 fs each, with an average pulse energy of ∼2.2 mJ (1.4 × 10¹² photons/pulse), at a 120 Hz pulse repetition rate.

RESULTS AND DISCUSSION

Microfluidic crystal sorting

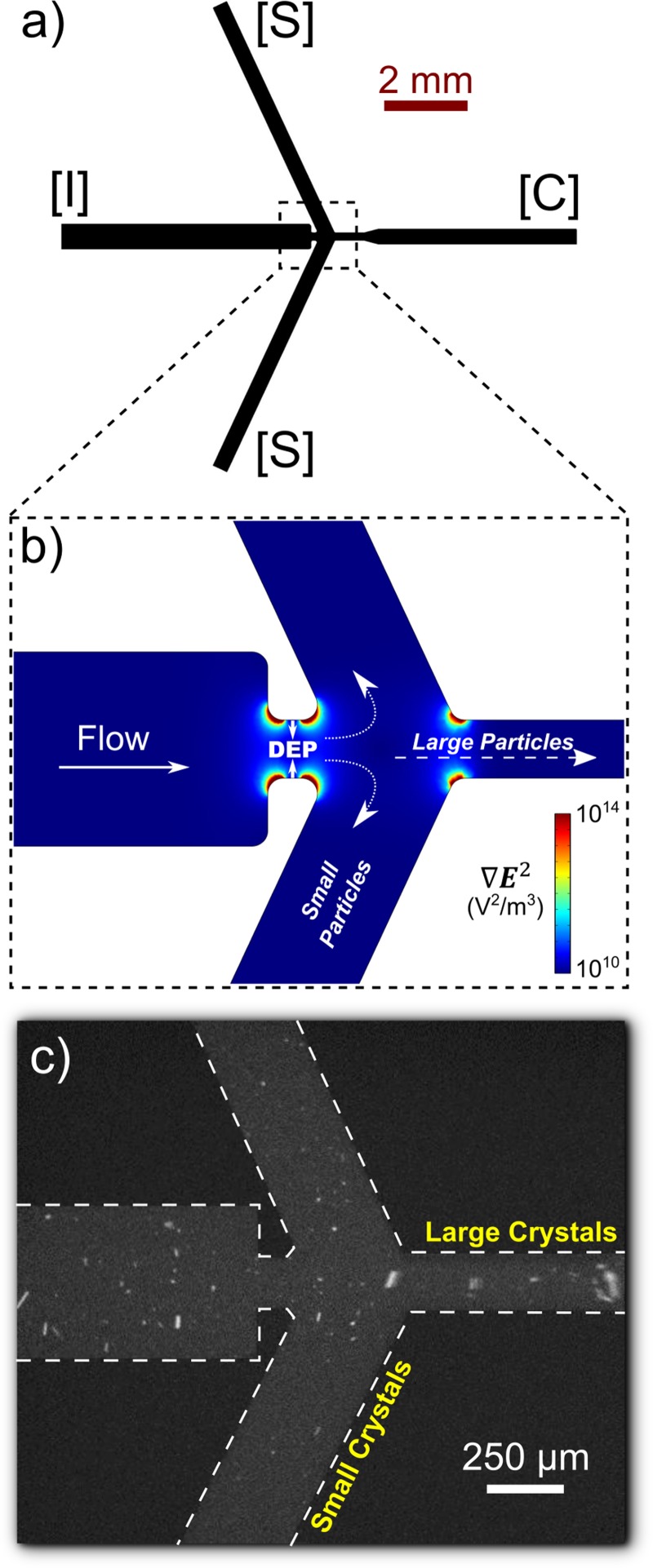
Our XFEL crystal size optimization is based on sorting a bulk PSI crystal suspension by size to isolate submicron fractions with reduced size dispersity using microfluidics. Figure 1(a) shows a schematic drawing of the microchannel design employed, which is a second-generation, scaled-up version of a microsorter we developed previously.²³ The device operates on the basis of DEP, whereby inhomogeneous electric fields form when potentials are applied across wide channels connected by a thinner constriction region. These inhomogeneities create areas of high $\nabla {\mathit{E}}^2$ within the constriction region shown in Figure 1(b), whereby a DEP force is induced as described in Equation (1). Because negative DEP prevails under the operating conditions, particles are repelled from constriction channel walls to an extent proportional to their radius (${\mathit{F}}_{\mathit{D}\mathit{E}\mathit{P}}\propto \hspace{0.17em}{r}^3$). Consequently, for sorting, large particles are focused centrally, whereas small particles do not experience significant repulsion and deflect into side channels, effectively separating the size fractions.

FIG. 1.

(a) Microfluidic sorting device schematic with labeled channels ([I] = inlet, [S] = side outlet, and [C] = center outlet). (b) Close up of the central region showing simulated $\nabla {\mathit{E}}^2$ values and differential particle deflection based on size. The DEP-active region is indicated within the constriction channel where large $\nabla {\mathit{E}}^2$ values are apparent. (c) Fluorescence microscopy imaging showing PSI crystals flowing through the device. Large crystals are seen focused into [C] and small crystals deflect into [S]. Particles flow from left to right.

This second-generation microsorter was developed to greatly increase throughput compared to the first-generation device. With the current XFEL liquid jet injection system,^39,40 the minimum loading volume is ∼300 μl which was difficult to produce with the first-generation device running at a few μl/h. We therefore targeted a large volumetric flow rate of >150 μl/h by increasing channel widths by 5× and channel depth by 10× in order to reduce experimentation time from weeks to days. The channel design was also simplified, whereby only two wide side channels ([S]) were formed in order to collect large amounts of the desired deflected submicron particles. Figure 1(c) shows a fluorescence microscopy snapshot of a sorting event, where large protein crystals are seen focusing into the [C] outlet, while small submicron crystals (mainly identified by optically unresolvable bulk fluorescence) deflect into the two [S] outlet channels. These fractions were extracted and collected for further characterization and SFX experimentation. The [C] channel crystal fraction can also be recovered from the sorting device such that virtually all crystals passing through can be collected. This fraction could then be resorted iteratively to pull out nearly all of the submicron crystals from the initial heterogeneous mixture, and the larger crystals could be dissolved and recrystallized to obtain more submicron crystals, increasing the amount of sorted crystal sample available for an SFX experiment. In principle, raw protein is not wasted during sorting due to the non-destructive, sample-conserving nature of the microfluidic sorter.

Sorted crystal size characterization

Size distributions of the crystal suspensions obtained from the sorting process were characterized using two methods: DLS and NanoSight NTA. The two techniques operate on size-dependent diffusion of particles but use different detection methods: DLS quantifies the size of particles from their diffusion coefficients by autocorrelating signal changes due to Brownian motion over time and NanoSight uses light scattering and image analysis software to individually track and monitor the scattered light from diffusing particles frame by frame to quantify size information.⁴⁵ We used both types of instruments as complementary techniques to confidently determine the size distributions of each crystal fraction (both provide size distribution and NanoSight can estimate particle concentration).

Figure 2 shows DLS data obtained from a sample droplet of the inlet PSI suspension and obtained sorted [S] fraction in the form of signal heat maps (blue = lowest, red = highest), (a) and (b), and particle count histograms, (c) and (d). From the bulk (Figures 2(a) and 2(c)), a wide crystal size distribution is present as expected, ranging from ∼200 nm to ∼20 μm. In contrast, the fraction that passed through the sorter and was collected from the [S] channel reservoirs shows a narrower, submicron size distribution (Figures 2(b) and 2(d)) with crystals ranging in size from ∼200 nm to ∼600 nm indicating that the broad bulk crystal size distribution was reduced modally and narrowed as desired (signal below 100 nm is likely from free PSI trimers and very small nanocrystals). A second cuvette-based DLS instrument was also used to measure the particle size of a sorted fraction, to confirm the droplet-based DLS results. As shown in Figure 2(e), the PSI suspension prior to sorting was again found to have a wide crystal size distribution (∼200 nm to ∼10 μm), whereas the sorted fraction (Figure 2(f)) indicated similar trends as before with a crystal size range between ∼150 nm and ∼550 nm. Any discrepancies in size measurement between the two DLS instruments most likely arise from (i) the order of magnitude difference in sample volume measured giving differences in population size and particle settling effects and/or (ii) differences in the proprietary software algorithms correlating the raw signal to an assigned particle size.

FIG. 2.

DLS heat map of (a) the PSI crystal suspension prior to fractionation, indicating a wide size distribution (∼200 nm to ∼20 μm), and (b) a PSI crystal fraction collected from the [S] channels indicating a narrowed submicron size distribution (∼200 nm to ∼600 nm). Signal increases from blue (lowest) to red (highest). (c) and (d) show DLS histograms corresponding to (a) and (b), respectively. (e) and (f) show DLS histograms of the PSI suspension prior to sorting (∼200 nm to ∼10 μm) and an [S] channel fraction (∼150 nm to ∼550 nm), respectively, measured using a cuvette-based instrument for comparison with (a)–(d), confirming the differences in the size distribution.

NanoSight NTA was also used as a supporting method to further confirm that the modal size and size distribution of the sorted [S] fraction were reduced compared to the bulk suspension shown previously. Figure 3(a) illustrates data obtained from this method as absolute particle counts versus particle diameter averaged for three scans. As shown with the DLS data, the size distribution is further confirmed to be submicron, with a major peak designating a size range of ∼125 nm to ∼300 nm and contributions up to ∼650 nm. The NanoSight detects and counts the scattered light from individual particles, where images of particle scattering can be obtained to confirm the presence of actual particles, as shown in Figure 3(b).

FIG. 3.

NanoSight NTA data of the [S] channel fraction. (a) Averaged particle size distribution for three measurements indicating a submicron size range between ∼100 nm and ∼650 nm with the majority being <300 nm. (b) Image taken of the suspended particles diffracting as they are measured by the instrument illustrating low size dispersity. Not appreciable in the image is the small particle size, which is evident in the distance traversed per frame as measured in (a).

Sorted crystal quality characterization

Two modes of characterization were performed to determine whether the sample maintained crystallinity after passing through the microfluidic channels under the applied voltage. First, second-order nonlinear imaging of chiral crystals (SONICC) was utilized due to the fact that it can exclusively detect chiral crystals (i.e., the majority of protein crystals) in a sample.^46,47 Protein molecules and amorphous precipitate are not SONICC active and thus do not emit a signal. This method is also useful for detecting crystals below the size limit of a standard optical microscope (i.e., nanocrystals) with SNRs enabling high contrast imaging. Figure 4(a) shows a brightfield image of an [S] channel-collected fraction and Figure 4(b) shows a corresponding SONICC image clearly containing a bright signal from the protein crystals in solution. This signifies that the sorted fractions contain protein crystals after passing through the microfluidic device.

FIG. 4.

PSI crystal characterization post-fractionation. (a) Brightfield image of a droplet of the [S] channel fraction. (b) SONICC image of the same droplet, indicating that crystallinity is maintained.

Second, TEM was used to examine crystal lattice quality after sorting and as a further measure to confirm the existence of protein nanocrystals in the sorted fractions.⁴³ Figure 5(a) shows an electron micrograph of heterogeneously sized PSI crystals from the bulk sample, with further magnification and corresponding fast Fourier transform (FFT) analysis (Figures 5(b) and 5(c), respectively) exhibiting the lattice structure and Bragg spots from the crystal designated with an arrow. Images were also taken of a representative submicron crystal from an [S] channel fraction (Figure 5(d)) for comparison after passing through the microfluidic device where the lattice can readily be observed. Further magnification (Figure 5(e)) clearly shows the well-ordered unit cells, while the FFT (Figure 5(f)) also features Bragg spots confirming that the well-ordered structure is maintained. Other crystals in this sample were also observed by TEM and ranged in size from ∼300 nm to ∼600 nm, which is in agreement with the size characterizations discussed previously.

FIG. 5.

(a) TEM image of PSI crystals from the bulk sample. (b) High magnification TEM image of a portion of this group, showing an intact, well-ordered lattice structure. (c) FFT from the crystal marked by the arrow in (a) and (b) illustrating a well-ordered lattice. (d) TEM image of a submicron PSI crystal from the [S] fraction. (e) Enlargement of (d), showing the well-ordered crystalline lattice is maintained. (f) Corresponding FFT with Bragg spots from the ordered lattice.

Serial femtosecond crystallography on sorted crystals

Sorted PSI crystal fractions were delivered into the XFEL for SFX experiments at LCLS as described in the experimental section. Sharp diffraction spots to 4 Å resolution were obtained from a sorted crystal fraction (Figure 6(a)) containing a submicron crystal size range as described previously, further indicating that the fragile membrane protein crystals were not damaged and remained crystalline during the sorting process. From this same crystal, shape transforms were also observed (Figure 6(b)), indicating a small crystal size and the ability to obtain shape transforms from sorted crystals, which could facilitate new phasing methods for SFX.^18–20

FIG. 6.

(a) Diffraction pattern on the front CSPAD (at a distance of ∼88 mm) from a sorted PSI crystal showing sharp spots and low mosaicity, with (b) corresponding shape transforms on the inner part of the back CSPAD (at a distance of ∼2 m), indicating a small crystal.

We note that hit rates were very low (<1%) for the sorted samples, and patterns were indexable with the expected PSI unit cell parameters. We attribute the low hit rate to low sample concentration, and the low SNR from nanocrystals (with very large unit cells) in solution. Even in the close-to-ideal conditions simulated (details below), only half of the simulated diffraction patterns from the sorted (submicron) crystals were indexable. Future experiments can be optimized for data collection from submicron crystals (higher sample concentration, thinner liquid jet, softer X-rays) and would benefit from a more intense beam (i.e., at future XFELs).

Potential for investigating crystal quality

The ability to manipulate the size distribution of protein nano- and microcrystals will enable quantitative studies of the relationship between protein crystal size and diffraction quality. Membrane protein crystals on the nanometer scale are assumed to be of superior quality to large membrane protein crystals by virtue of being smaller than a mosaic block and thus not prone to long-range disorder.^48,49 However, the increased number of surface unit cells (partial or full) to inner-crystal unit cells may lead to a limit in the quality improvement of crystallinity as a function of decreasing crystal size. This cannot be probed with a broadly disperse crystal suspension by SFX, as it is impossible to distinguish diffraction patterns from a small crystal in the center of the beam from diffraction patterns from large crystals only partially intercepted by the beam using intensity alone (i.e., without clear shape transforms to determine crystal size). Pre-sorting protein crystals with a microfluidic device will be an ideal method to answer this question by enabling systematic studies of crystal quality as a function of crystal size.

Potential for facilitating high intensity radiation damage induced phasing (HI-RIP)

The brilliance available at LCLS can also be used for HI-RIP.^50,51 In HI-RIP, the different degrees of ionization of heavy atoms, in particular, compared to a low-fluence dataset, provides a novel method for finding the molecular substructure (akin to a single-wavelength anomalous dispersion experiment). HI-RIP SFX requires the whole crystal to be exposed to sufficiently high intensity for multiple ionizations, which is difficult to achieve experimentally due to the XFEL beam with broad, low-fluence tails. By using a narrow size distribution of nano- or microcrystals matched to the size of the XFEL beam focus, it becomes much simpler to separate high intensity from low intensity data to maximize the radiation damage-induced contrast at the heavy atom positions and thus facilitate phasing.

Making more efficient use of protein crystals in SFX data collection by microfluidic sorting

We investigated the effect of crystal size distribution on merged SFX data quality by simulating PSI nano/microcrystal distributions with varying levels of size heterogeneity. PSI diffraction patterns were simulated using pattern_sim, a program in the CrystFEL software suite,⁵² considering crystals as rectangular prisms with integer numbers of unit cells, where each side length is chosen independently from a top-hat distribution between user-specified size limits. Distribution (a) was comprised of a very broad range of crystal side lengths between 0.1 and 10.0 μm, representing the unsorted fraction, and (b) comprised of crystals with side lengths of 150–550 nm, representing the sorted fraction. A histogram of simulated crystal volumes for dataset (b) is shown in Figure 7(a). The simulations used 9.5 keV X-ray pulses with a fixed flux of 6 × 10¹¹ photons/pulse, no divergence, and 1% bandwidth. (This does not reflect the shot-to-shot fluctuations in wavelength and X-ray flux at LCLS, which were ∼0.2% and ∼30%, respectively, for the SFX experiment in this study.⁵³) The detector, representing a CSPAD, had 1764 × 1764 pixels, each 110 × 110 μm², positioned at a working distance of 0.21 m (3 Å at the edge), with a two-photon, Poisson-distributed, uniform background. Scattering from the liquid jet was not included. PSI structure factors were calculated from 1JB0.pdb⁵⁴ (a = b = 281, c = 165.2 Å; α = β = 90°, and γ = 120°; in space group P6₃), using sfall, from the Collaborative Computational Project Number 4 (CCP4).^52,55,56 Three datasets were simulated, indexed, and merged: two contained 10 000 diffraction snapshots for both crystal size distributions and one contained 5000 diffraction snapshots for the “unsorted,” wide size distribution. Over 99% of the wide size distribution datasets were indexed, while only 48% of the sorted crystal size distribution dataset could be indexed due to low intensities/number of Bragg spots.

FIG. 7.

Comparison of SFX data quality by simulated diffraction from PSI crystals with size distributions representing the unsorted and sorted crystal fractions. (a) Crystal volumes from the simulated narrow submicron crystal dataset. (b) CC*⁵⁷ of merged reflections from 5000 and 10 000 crystals with side lengths of 0.1–10 μm (blue and green, respectively), and of 5000 merged, indexable patterns from ∼10 000 crystals with side lengths of 0.15–0.55 μm (orange). (c) Average multiplicity and (d) SNR of reflections in each resolution shell. A significantly smaller amount of protein is required for high quality reflection lists if the crystal size distribution is narrowed. The drop in quality at high resolution for the 0.15–0.55 μm crystal dataset is due to low signal strength at that resolution.

A robust measure of the quality of the merged reflection lists is CC*, which is an estimate of the value of CC_true (the measure of correlation between an averaged data set with a noise-free true signal that may be unknown). CC* reflects the degree of reliability of the merged reflection list and is used to determine the resolution of crystallographic datasets.⁵⁷ CC* was calculated by splitting the simulated dataset into two datasets, then comparing their independently merged reflection lists with results shown in Figure 7(b). The merged dataset from the sorted crystal fraction (5000 indexed patterns from ∼10 000 simulated patterns) has significantly higher CC* values (orange, Figure 7) than the unsorted crystal distribution with the same number of indexed patterns (blue, Figure 7). This is true even when comparing to twice the number (10 000) of indexed patterns from unsorted crystals (green, Figure 7) until resolutions higher than ∼4.5 Å where the multiplicity (the average number of times a reflection was measured) of the sorted crystal fraction drops significantly from insufficient scattering signal (Figure 7(c)). Figure 7(d) shows the average SNR of the reflections in each resolution shell, respectively, for each simulated dataset. Interestingly, despite an order of magnitude higher multiplicity (Figure 7(c)) and higher SNR in the medium resolution bins for the unsorted crystal size distribution compared to the sorted crystal size distribution, the CC* values in the latter dataset are significantly higher.

Importantly, the amount of protein that would be used in the sorted crystal fraction would be significantly lower than the unsorted fraction and could be tuned experimentally based on a target size range. In these simulations, the total volumes of crystals in samples (a) and (b) were 6.31 × 10⁵μm³ and 176 μm³, respectively, which corresponds to a ∼3500-fold decrease in protein use in the sorted fraction. These simulations demonstrate that reduced crystal size variation increases the accuracy of the merged intensities, requiring smaller datasets for accurate structure factors, while making much more efficient use of precious protein.

Experimentally, shot-to-shot fluctuations in the beam intensity and the random position of the crystal with respect to the beam inflate the distribution of intensities measured for each reflection, requiring even more data for accurate structure factors. These variations were not taken into account in these simulations, so the improved accuracy from narrowing the crystal size distribution may have a less significant effect on experimental data. However, sorting submicron crystal fractions can reduce the impact of crystal positioning in the beam path as larger micrometer crystals that match or exceed the beam diameter have a greater chance of being partially illuminated by the beam.

CONCLUSIONS

We have demonstrated a method to isolate submicron PSI protein crystal size fractions for SFX studies at an XFEL. The samples processed were awarded beam time at the LCLS XFEL at SLAC in which we were able to obtain diffraction from fractionated crystals. Several sample characterization methods were presented to study size distribution and crystal quality. Using DLS, we measured our sample sizes in the submicron regime, with a major range of ∼150 nm to ∼600 nm. NanoSight NTA was also used to support this data, whereby similar submicron size ranges were observed. In all cases, sample dispersity was narrowed and the size range of the bulk crystallization products (∼200 nm to ∼20 μm) was reduced to the submicron regime. SONICC images confirmed that protein crystals remained intact in solution after fractionation. TEM was used to examine the individual crystal lattices demonstrating that crystals remained well-ordered and of diffraction quality after fractionation. SFX data from fractionated crystals showed diffraction to ∼4 Å, with no evidence of damage to the crystals due to sorting, and concomitant shape transforms confirmed a small crystal size. Simulations show that a narrow size distribution improves the quality of SFX datasets, requiring smaller datasets. Moreover, targeting smaller crystals with microfluidic platforms that allow crystals not selected for SFX to be recovered for follow-up experiments preserves and reduces consumption of precious protein sample. Since hit rates and indexing rates are continually improving for SFX analysis (averaging 10% and up to 80%, respectively), we envision microfluidic sorting as a promising method to obtain protein crystal samples with desired size characteristics to improve data analysis efficiency (by narrowed size dispersity) and capability (small-crystal shape transforms for shape transform-based phasing). Further optimization and development of the current device will broaden its applicability and enhance its impact.