Understanding the kinetic mechanism of RNA single base pair formation

Significance

This paper addresses a long-standing unsolved issue in RNA folding, namely, the kinetics for the very elementary steps of RNA folding. Lacking the ability to identify the exact microscopic, molecular level processes has been responsible for a variety of inaccurate predictions for RNA dynamics and RNA biochemical, such as enzymatic, reactions. Unlike previous unfolding (pulling) simulations, we here perform a direct folding study for the process. The misfolded states and the kinetic role of ions discovered in the study may provide significant insights into the physical mechanism of RNA conformational changes in biology.

Abstract

RNA functions are intrinsically tied to folding kinetics. The most elementary step in RNA folding is the closing and opening of a base pair. Understanding this elementary rate process is the basis for RNA folding kinetics studies. Previous studies mostly focused on the unfolding of base pairs. Here, based on a hybrid approach, we investigate the folding process at level of single base pairing/stacking. The study, which integrates molecular dynamics simulation, kinetic Monte Carlo simulation, and master equation methods, uncovers two alternative dominant pathways: Starting from the unfolded state, the nucleotide backbone first folds to the native conformation, followed by subsequent adjustment of the base conformation. During the base conformational rearrangement, the backbone either retains the native conformation or switches to nonnative conformations in order to lower the kinetic barrier for base rearrangement. The method enables quantification of kinetic partitioning among the different pathways. Moreover, the simulation reveals several intriguing ion binding/dissociation signatures for the conformational changes. Our approach may be useful for developing a base pair opening/closing rate model.

RNAs perform critical cellular functions at the level of gene expression and regulation (1–4). RNA functions are determined not only by RNA structure or structure motifs [e.g., tetraloop hairpins (5, 6)] but also by conformational distributions and dynamics and kinetics of conformational changes. For example, riboswitches can adopt different conformations in response to specific conditions of the cellular environment (7, 8). Understanding the kinetics, such as the rate and pathways for the conformational changes, is critical for deciphering the mechanism of RNA function (9–19). Extensive experimental and theoretical studies on RNA folding kinetics have provided significant insights into the kinetic mechanism of RNA functions (19–36). However, due to the complexity of the RNA folding energy landscape (37–46) and the limitations of experimental tools (47–55), many fundamental problems, including single base flipping and base pair formation and fraying, remain unresolved. These unsolved fundamental problems have hampered our ability to resolve other important issues, such as RNA hairpin and larger structure folding kinetics. Several key questions remain unanswered, such as whether the hairpin folding is rate-limited by the conformational search of the native base pairs, whose formation leads to fast downhill folding of the whole structure, or by the breaking of misfolded base pairs before refolding to the native structure (18, 19, 54–73).

Motivated by the need to understand the basic steps of nucleic acids folding, Hagan et al. (74) performed forty-three 200-ps unfolding trajectories at 400 K and identified both on- and off-pathway intermediates and two dominant unfolding pathways for a terminal C-G base pair in a DNA duplex. In one of the pathways, base pairing and stacking interactions are broken concomitantly, whereas in the other pathway, base stacking is broken after base pairing is disrupted. Furthermore, the unfolding requires that the Cyt diffuse away from the pairing Gua to a distance such that the C-G hydrogen bond cannot reform easily. More recently, Colizzi and Bussi (75) performed molecular dynamics (MD) pulling simulations for an RNA duplex and construct free energy landscape from the pulling simulation. The simulation showed that the base pair opening reaction starts with the unbinding of the 5′-base, followed by the unbinding of the 3′-base (i.e., the 5′-base is less stable than the 3′-base). These previous unfolding simulations offered significant insights into the pathways and transition states. However, as shown below, several important issues remain.

One intriguing problem is the rate model for base pairing. There are currently three main types of models. In the first type of model, the barrier $\mathrm{\Delta }{G}_{+}^{‡}$ for closing a base pair is dominated by the entropic cost $\mathrm{\Delta }S$ for positioning the nucleotides to the base-paired configuration and the barrier $\mathrm{\Delta }{G}_{-}^{‡}$ for opening a base pair is the enthalpic cost $\mathrm{\Delta }H$ for disrupting the hydrogen bonds and base stacking interactions (18, 59, 60). In the second type of model, $\mathrm{\Delta }{G}_{+}^{‡}$ is the net free energy change for base pairing $\mathrm{\Delta }G=\mathrm{\Delta }H-T\mathrm{\Delta }S$ and $\mathrm{\Delta }{G}_{-}^{‡}$ is zero (76, 77). In the third type of model, $\mathrm{\Delta }{G}_{\pm }^{‡}=\pm \mathrm{\Delta }G/2$ is used (78). In addition to the above three main types, other models, such as more sophisticated hybrid rate models, have been proposed (29).

In this paper, we report a hybrid method (see Fig. 1) to investigate the single base pairing process. In contrast to the previous simulations for temperature- or force-induced unfolding reactions, we directly model the folding process here (i.e., the base pair closing process). Specifically, we use MD simulations to identify the conformational clusters. Based on the network of the conformational clusters as a reduced conformational ensemble, we apply kinetic Monte Carlo (KMC) and master equation (ME) methods to elucidate the detailed roles of base pairing and stacking interactions, as well as the roles of water and ions (79–82). The study reveals previously unidentified kinetics pathways, misfolded states, and rate-limiting steps. A clear understanding of the microscopic details of the elementary kinetic move is a prerequisite for further rigorous study of large-scale RNA kinetic studies. The method described here may provide a feasible way to develop a rate model for the base pair/stack-based kinetic move set. Furthermore, the mechanism of RNA single base folding may provide useful insights into many biologically significant processes, such as nucleotide flipping (83) in helicases and base pair fraying (84) (as the possible first step for nucleic duplex melting in nucleic acid enzymatic processes).

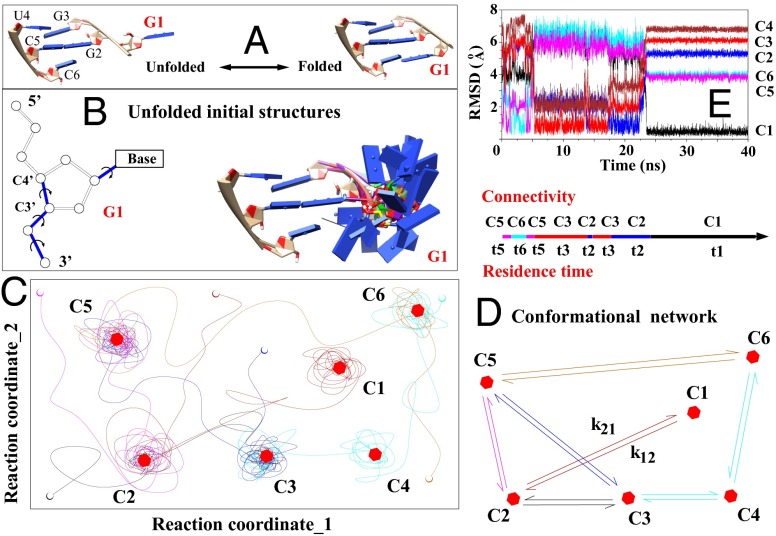
Fig. 1.

(A) Folding of a single nucleotide (G1, red) from the unfolded (Left) to the native folded (Right) state. (B) Exhaustive sampling for the (discrete) conformations of the G1 nucleotide (Right) through enumeration of the torsion angles (formed by the blue bonds). (C) Schematic plot shows the trajectories on the energy landscape (depicted with two reaction coordinates for clarity) explored by the MD simulations. The lines, open circles, and hexagons denote the trajectories; the initial states; and the (centroid structures of the) clusters, respectively. (D) Conformational network based on six clusters. (E) The rmsds to the different clusters provide information about the structural changes in a MD trajectory.

Results

Conformational Clusters.

The MD trajectories give a total of 50 clusters (Fig. 2). These 50 clusters are determined from the structural closeness as measured by the rmsd. We find we can also use three order parameters to classify the clusters: the distance $d_{12}$ between the geometric centers of all of the heavy atoms in the G1 and G2 bases and the nonbonded interaction energies $E_{12}$ and $E_{16}$ between the sequentially neighboring nucleotides G1 and G2 and between the pairing nucleotides G1 and C6, respectively. As shown in Fig. 2, the clusters can be separated by these three order parameters. It should be noted that the all-atom energy, as determined by the force field, is much more sensitive to the small changes in the bond lengths, bond angles, and torsional angles than the rmsd values. Even though conformations in the same structural cluster have small rmsds between each other, their $E_{12}$ and $E_{16}$ values may vary significantly. As a result, it might not be ideal to identify order parameters by methods like principle component analysis. In SI Appendix, we show the distributions as a function of other order parameters and the centroid structures of all of the 50 clusters.

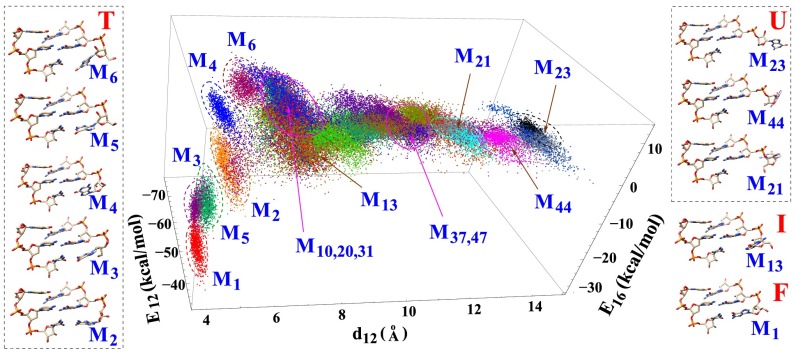
Fig. 2.

Order parameters used to classify conformations: $d_{12}$ is the distance between the geometric centers of heavy atoms between the G1 and G2 bases, and $E_{12}$ and $E_{16}$ are the nonbonded interactions (van der Waals and electrostatic energies given by VMD) between nucleotides G1 and G2 and between nucleotides G1 and C6, respectively. These energies characterize the base stacking and pairing interactions. The figure shows 1,000 randomly selected structures for each cluster. Ten centroid structures are shown for illustration. M₁ is the native folded structure. M₂₁, M₂₃, and M₄₄ are the unfolded structures with large $d_{12}$. Other structures are partially folded or misfolded structures. M₂, M₃, and M₅ have strong base stacking ($E_{12}$) and pairing ($E_{16}$) interactions. M₄ and M₁₃ have native-like backbone conformations, especially for the sugar ring atoms, but a partially unfolded base orientation. M₆ has nonnative conformations for both the base and the backbone of nucleotide G1. The magenta circles indicate the order parameters for the transition states. Structures of the other clusters, as well as the other order parameters, are shown in SI Appendix.

As illustrated in Fig. 1 C and D, with the conformational connectivity and the intercluster transition rate constants extracted from the MD trajectories, we build the cluster-based conformational network. Detailed structural analysis showed that many of the clusters were formed due to the nonnative ribose orientation of the G1 nucleotide. Unlike the native structure, which involves stabilizing stacking interactions between the G1, G2, and G3 bases, the intermediate states (clusters) have the G1 base excursion away from the native orientation, causing weaker or no stacking interactions between the bases. Furthermore, we find that a structure of an intermediate state (cluster) is usually more flexible with larger conformational fluctuations than the native cluster M₁ (Fig. 1E). The base stacking interaction ($E_{12}$) between nucleotides G1 and G2 dominates the overall stability of G1 for the folded cluster M₁ and the partially folded clusters, such as M₃ and M₅ in Fig. 2. The different structures involve competition between the different nonbonded interactions. For example, the folded cluster M₁ has the lowest value of base pairing interaction $E_{16}$ but a weaker base stacking interaction $E_{12}$. The partially folded cluster M₆ has destabilizing base pairing energy $E_{16}$ (>0) but stabilizing stacking energy $E_{12}$ (<0). We note that these energies do not include more distant interactions, such as those interactions between G1 and G3, U4, and C5 (a more detailed analysis is provided in SI Appendix).

Folding Pathway.

To validate the extracted kinetic cluster network, we first bin all of the conformations (snapshots) in the trajectories into their respective clusters. From the populations of the individual conformations, we compute the time-dependent populations for each cluster (Fig. 3A). We then use the population of each cluster at time t = 0 as the initial population and the ME method to predict the subsequent populational kinetics of the clusters (Fig. 3A). We find that such ME-predicted populational kinetics agree with the original populations from the MD trajectories. The result suggests that the conformational cluster network may be reliable.

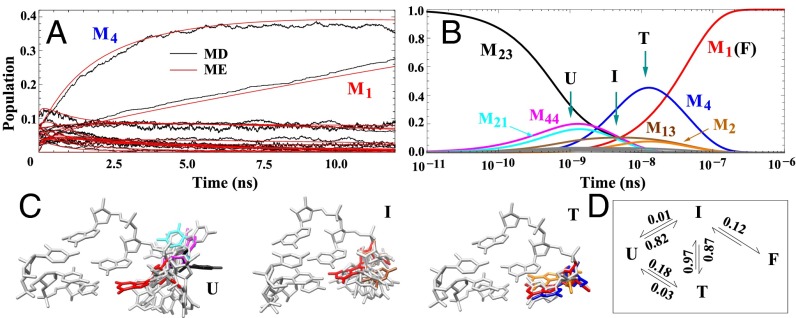
Fig. 3.

(A) Comparison between the kinetics results from MD simulations and from the ME method (red). The ME method is based on the 50-cluster conformational network. As shown in Fig. 1E, we bin the MD snapshots according to the 50 clusters to obtain the time-dependent populations for each cluster from MD (shown in black). The results support the validity of the 50-cluster network model. (B) ME-predicted, long-time, single-nucleotide folding kinetics starting from the unfolded cluster M₂₃ (black line). Based on the behavior of the populational kinetics for each cluster, we classify the 50 clusters into four states: unfolded (U), intermediate (I), trapped (T), and folded (F). (C) Typical structures of the three states are shown, with the folded state (F, in red) included for comparison. Structures of the clusters with significant populations in B are shown in C with the same color code. (D) Four-state scheme for the single-nucleotide kinetics. The numbers indicate the probabilities of the transitions between the states, (e.g., 0.87 for I → T, 0.01 for I → U, and 0.12 for I → F).

As shown in Fig. 2, cluster M₂₃ has the largest value of $d_{12}$, with the G1 base totally flipped out of the stacked position, and thus has very weak base pairing interactions $E_{16}$. We investigate the folding process starting from this unfolded cluster. We set the initial fractional population of M₂₃ to be 100%. The ME solution predicts that (Fig. 3B) through conversions with M₂₁ and M₄₄, M₂₃ quickly relaxes within ${10}^{-10}$ s. A close observation of the structures in Fig. 2 suggests that clusters M₂₁, M₂₃, and M₄₄ have similar base pairing and stacking energies, with slightly different distances of $d_{12}$. The fast conversions (details are provided in SI Appendix) between them lead to a fast preequilibration between the unfolded conformations. Following such a rapid initial relaxation, M₁₃ emerges between ${10}^{-10}$ s and ${10}^{-9}$ s. M₁₃ has the native-like backbone but nonnative base orientations. M₁₃ is a misfolded intermediate state. Subsequently, between ${10}^{-9}$ s and ${10}^{-8}$ s, part of the unfolded population is converted to M₁₃. M₁₃ reaches the maximum population of $p_{M_{13}}$ ∼ 0.1 at t ∼ 6.0 × ${10}^{-9}$ s. At around ${10}^{-9}$ s (after M₁₃ reaches its peak population), the native folded cluster M₁ emerges.

In the meantime, clusters M₄ and M₂ show a significant populational jump, with peak populations at $p_{M_4}\approx$ 0.5 and $p_{M_2}\approx$ 0.08 at t $\approx$ 1.5 × ${10}^{-8}$ s. As shown in Fig. 2, M₄ has the native-like backbone configuration and (antiparallel, partially) stacked base orientation. Similar to M₄, M₂ has a native-like (stacked) base orientation and nonnative backbone position for G1. To fold to the native folded cluster, these two states first flip out their bases so they can make necessary adjustments for their backbone conformations. After the rearrangement of the backbone conformations, the bases flip back to the native configuration. Similar to M₂ and M₄, there are also slight populational changes of M₃ and M₅. These four clusters act as trapped states for the folding reaction, because the RNA must first flip out the base (detrapping) before folding to the folded state. There are transitions from the misfolded clusters of M₂, M₄, and M₁₃ to the folded cluster M₁ in the time window from ${10}^{-8}$ s to 3.0 × ${10}^{-7}$ s. The overall folding time is about ${10}^{-6}$ s, which is consistent with the experimental results about the time of the single-strand stacking formation and helix elongation of DNA and RNA (85–88).

Based on the behavior of the time-dependent population for each cluster (details are provided in SI Appendix), we classify the 50 clusters into four states: unfolded (U), intermediate (I), trapped (T), and folded (F); several typical structures are illustrated in Fig. 3C. The U state contains unfolded clusters, such as M₂₁, M₂₃, and M₄₄. In these clusters, the base flips out and both the base and the backbone (of G1) have nonnative conformations. In the I state (e.g., M₁₃), the backbone is native-like and the base is partially flips out and is in a nonnative conformation. For such conformations, folding proceeds through rotations of the base without changing the backbone conformation and the folding is rate-limited by the process of searching for the correct (native) base conformation. For the misfolded (trapped) state, such as M₂, M₃, M₄, M₅, and M₆, the G1 base is in the stacked conformation and the backbone is in a nonnative conformation. In the folding process, to lower the overall kinetic barrier, the base stacking in a T conformation is disrupted first so that the rearrangement of the backbone conformation can occur. Indeed, we find that the G1 base flips out from the native conformation before the backbone switches to the native conformation. The overall folding kinetics can be described by the above four-state kinetic scheme (Fig. 3D).

We quantify the kinetic partitioning between the different pathways from the transition probabilities. As shown in Fig. 3D, starting from the U state, 82% of the transitions go to the I state compared with 18% to the T (trapped) state. Folding to the I and T states is rate-limited by the search for the correct (native) backbone and the base conformations, respectively. The interactions between the G1 and other atoms overcome the entropic loss involved in the G1 conformational searching process. Neither I nor T has a significant possibility to return to the U state, suggesting that the favorable interactions, such as $E_{12}$ and $E_{16}$, inhibit the G1 base from flipping back to the unfolded positions. The I → T transition, with a probability of 0.87, dominates over the I → F transition, which has a smaller probability of 0.12. The kinetic barrier difference between the two transitions is around $k_{B}T\hspace{0.17em}ln\left(\frac{0.87}{0.12}\right)\approx 2.0\hspace{0.17em}{k}_{B}T$. Here, the T state has a small rate for the exit transitions (from T to I or to U); therefore, it is indeed a trap. From the above analysis, we conclude that the overall folding process from U to F is rate-limited by the enthalpic barrier for the T → I detrapping transition and the entropic barrier for the I → F folding transition.

Transition States.

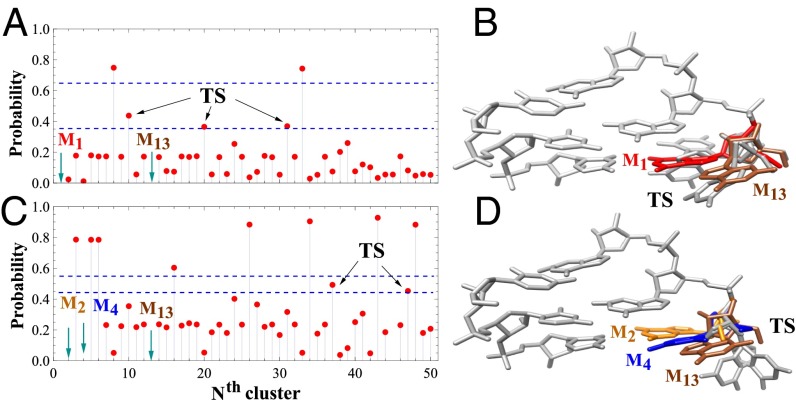
We next identify the transition states (details are provided in SI Appendix) for the two aforementioned rate-limiting transitions (T → I and I → F). We first focus on the I → F folding transition. We start from random unfolded clusters and use the KMC method to compute the probability P for a random initial cluster to enter the folded state F (structure M₁), instead of I (M₁₃) (Fig. 4A). We call the conformations with P between 0.35 and 0.65 (between the two blue lines in Fig. 4A) the “transition states.” These transition states may be close to the actual transition states that have P = 0.5. The transition states (M₁₀, M₂₀, and M₃₁ shown in gray in Fig. 4B) have native-like backbone conformations but partially folded base orientations. They all belong to the I (intermediate) state. Similar analysis gives the transition states for the detrapping transition from T (M₁₃) to I (M_2,4) (Fig. 4C). The two clusters M₃₇ and M₄₇ (Fig. 4D) in the transition state region (P = 0.45 and 0.55, respectively) have a slightly smaller probability to enter the trapped states (M₂ and M₄) instead of the intermediate state (M₁₃). We note that M₃₇ and M₄₇ also belong to the intermediate state, but with large $d_{12}$ values as shown in Fig. 2.

Fig. 4.

(A) KMC-predicted probability of falling to the folded state M₁ before reaching the intermediate state M₁₃ starting from the Nth cluster. (B) Three structures (M₁₀, M₂₀, and M₃₁ in gray) of the transition states between the folded (red) and the intermediate (brown) states obtained from A. (C) KMC-predicted probability of falling to the trapped states M₂ and M₄ before reaching the intermediate state M₁₃ starting from the Nth cluster. (D) Two structures (M₃₇ and M₄₇ in gray) of the transition states between the trapped (orange and blue) and intermediate (brown) states obtained from C. Because the kinetic cluster-based network can only give the clusters close to the transition states, we use the probability regime of (0.35, 0.65) and (0.45, 0.55) between the two dashed blue lines in A and C, respectively, to identify the transition state (TS).

Fig. 4 A (I → F) and C (I → T) shows that only a few clusters have a large forward (folding) reaction probability P (above the blue lines) and that most starting conformations would likely enter/stay in the I state. The result implies more local minima around the I state than around the U, T, and F states. The formation of the energy minima can be understood from the interaction between the G1 nucleotide and the rest of the nucleotides. For the trapped state, the G1 base is at the native-like stacked position. The fixation of the base conformation restricts the energy minima formation. For the unfolded state, the G1 base flips out; therefore, the interaction between G1 and other nucleotides is weak. The weak interaction makes the landscape less rugged. For the intermediate state, the G1 base is not fixed to the native conformation; thus, it has greater freedom and the interaction is stronger than the unfolded state, causing a bumpy energy landscape with significantly more energy minima.

Ion Effects and Kinetic Pathways.

To investigate the ion effect in the single base folding kinetics, we track the ion positions and the ion–RNA interactions in the different MD trajectories. On average, there are about six Na⁺ ions within 4 Å of the van der Waals surface of the RNA. This number of “bound” ions corresponds to nearly complete charge neutralization of the RNA backbone. Na⁺ ions mostly bind to the phosphate groups or the bases (SI Appendix, Fig. S13). The dwell time of the ions around the RNA can be as short as 5 ns. Furthermore, as shown in SI Appendix, Fig. S13, a small number of bound ions may dehydrate upon binding to RNA. For some tightly bound ions in the vicinity of the phosphate groups, we find that up to eight water molecules can be released, and three of them are from the first hydration shell of the ions.

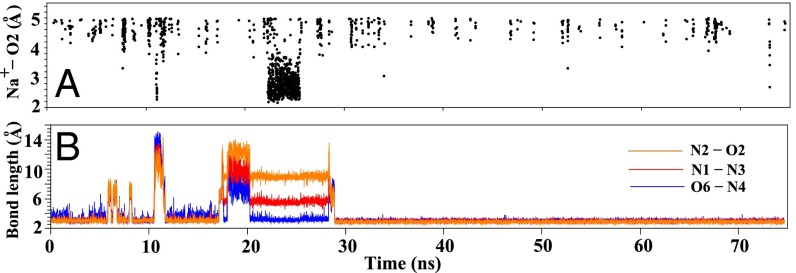
The change of ion distribution along the trajectories demonstrates that ion binding events are directly coupled to the folding events and that ion binding around the base pairing region precedes the formation of the stable G1-C6 base pair. To quantify ion–RNA association, we compute the distance between the Na⁺ ions and the O6, N1, N2, N4, N3, and O2 atoms of the G1 and C6 bases. These atoms are selected because they are directly involved in the G1-C6 base pair formation in the form of the O6-N4, N1-N3, and N2-O2 hydrogen bonding. These distances reflect the ion binding to the base.

In Fig. 5B, the O6-N4, N1-N3, and N2-O2 distances are nearly constant between t = 20 ns and t = 29 ns, suggesting the formation a stable structure during this time period. Detailed structural analysis shows that the structure is M₄ (Fig. 2), a trapped (T) state with (partially) stacked bases and a nonnative backbone conformation. Before M₄ unfolds, as shown in Fig. 5A and SI Appendix, Fig. S15, ions bind to the base pairing region to stabilize the structure. Specifically, as shown in Fig. 5A and SI Appendix, Fig. S15, from t = 22 to 27 ns, the small distances between Na⁺ and the relevant atoms in the G1 base indicate ion binding around the base. At t ≈ 27 ns, Na⁺ ions dissociate from the base and bind on and off around the backbone. The ion dissociation from the base region causes destabilization the M₄ structure. At about t = 29 ns, the structure is disrupted, as shown by the large increase of the O6-N4, N1-N3, and N2-O2 distances. Structural analysis shows a T → I transition at t = 29 ns. At about t = 30 ns, the I → F transition occurs and the final stable structure is formed. After t = 30 ns, all of the three hydrogen bonds (O6-N4, N1-N3, and N2-O2) are stabilized. The above ion-promoted folding pathway is consistent with the KMC-predicted folding pathway (additional examples for the trajectories are provided in SI Appendix, Fig. S11).

Fig. 5.

(A) Na⁺ ion distribution within a cutoff distance 5 Å from the O2 atom of C6. Ion distributions around other hydrogen bonding atoms are shown in SI Appendix, Fig. S15. (B) Donor–receptor distance distribution for the three hydrogen bonds (N2-O2, N1-N3, and O6-N4) along a typical MD simulation trajectory.

Discussion

Using an integrated approach with all-atom MD simulations, the ME method, and KMC simulations, we perform direct folding studies for single-nucleotide kinetics in a base pairing process. Based on the conformational clusters extracted from MD trajectories, we reveal a four-state kinetic mechanism. In the unfolded state U, the base of the nucleotide flips out of the folded state. In the intermediate state I, the base is in the partially unfolded conformation and the backbone is in the native orientation. In the trapped state T, the base is in the native conformation and the backbone is in the nonnative conformation. In the folded state F, both the base and the backbone are in the native state. The overall folding time (≈${10}^{-6}$ s) is consistent with the experimental results for RNA and DNA single-strand stacking formation and helix elongation (85–88).

Physically, ion binding can lower the electrostatic repulsion (and kinetic barrier) between the nucleotides, thus inducing the close approach and interaction between RNA bases/backbone. Indeed, our results demonstrate the significant role of ions in determining the kinetic pathway. We find that ion binding can initialize folding events and stabilize misfolded as well as native states at the single-nucleotide level. In particular, ion binding to the base region can stabilize base stacking interactions, and ion dissociation from the base can destabilize the base stacking interactions and trigger a detrapping transition from a misfolded state.

The four-state kinetic scheme shows that there are two dominant barriers for the overall single base folding process: (i) the entropic barrier for the search of the native-like backbone orientation (U to I) and for the search of the native-like base position (U to T), and (ii) the enthalpic barrier for the adjustment of either the backbone (T → I) or the base (I → F) conformation. The existence of the trapped state, which was missed in previous studies (74, 75), makes the overall folding process more complex. The kinetics of this elementary folding step cannot be simply described by a two-state process (i.e., the kinetics are multistate). As a result, a rate model should consider the kinetic effects from the intermediate and trapped states. The transition state of the RNA single-nucleotide folding involves partially flipped-out base conformations stabilized by weak interactions with other nucleotides. The transition state suggests that the barrier for folding/disruption of the base pair/stack is not purely entropic/enthalpic. This finding suggests that the previous simple ($\mathrm{\Delta }S,\hspace{0.17em}\mathrm{\Delta }H$)-based rate model (18, 59, 60) should be modified. The kinetic barrier is likely a combination of entropic and enthalpic contributions. In addition, to test the Metropolis ($\mathrm{\Delta }G$-based) rate model (76, 77), we need to apply our method to different RNA systems with different sequences to extract the sequence dependence of the transition states. Because the overall properties of base-base stacking and hydrogen bonding are similar for different sequences, the conclusions about the folding kinetics, such as the folding pathways, kinetic intermediates/traps, and kinetic barriers derived from the present study, may be general, even though the detailed quantitative values can be different. The method developed here can be readily extended to study the more complicated processes, such as single base flipping in the middle of RNA/DNA helices and base pair fraying with the cooperative/uncooperative flipping of the two (paired) nucleotides.

Materials and Methods

To construct an effective reduced conformational ensemble, we first extract structural clusters from MD simulation. Specifically, we first exhaustively generate all of the possible (coarse-grained) nonnative structures. We then perform MD simulations starting from each nonnative structure (as the initial state). The simulations sample hundreds of trajectories. We classify all of the snapshots in the trajectories into clusters according to the rmsd distance between the structures. We use the Visual Molecular Dynamics (VMD) (89) package to analyze the structural and energetic properties, such as the base pairing and base stacking interactions for each cluster. We implement two different nucleic acid force fields (90, 91) (AMBER ff99 and CHARMM27) with the same simulation protocol to examine the force field dependence of the predicted kinetics, and find the same general conclusions (92–94). From the kinetic connectivity between the conformations, we build a network of conformational clusters. From the KMC and ME methods for the conformational network of the clusters, we compute the detailed folding kinetics.

Initial (Unfolded) Structures.

Previous pulling simulations suggested that a 3′-base is more stable than its 5′-base pairing partner. In a folding reaction, the 3′-base is likely to fold first through single-stranded base stacking, followed by folding of the 5′-base through base pairing with the 3′-base (75, 84, 95, 96). Here, we focus on the second step, namely, the folding kinetics of the 5′-base (nucleotide G1) after the 3′-base (nucleotide C6) is folded into the native state (Fig. 1A). Because the first step is much faster than the second step, our results may provide useful information about the overall rate process for base pair formation.

Based on the 3-bp folded structure (sequence 5′GGG3′-5′UCC3′; details are provided in SI Appendix), we rotate the torsional angles of the four bonds (P-O3′, O3′-C3′, C3′-C4′, and C1′-N9), shown in Fig. 1B in blue, to generate the complete (unfolded) conformational ensemble for the nucleotide G1. Using fivefold uniform rotational angles for each bond, we generate an ensemble of $5^4$ = 625 initial structures. Excluding structures disallowed by steric clashes, we obtain 570 viable initial structures (Fig. 1B).

MD Simulations.

As illustrated in Fig. 1C, a major issue in MD simulations is that during the simulation, the sampled conformations often remain close to the initial unfolded structure. To circumvent this problem, we start from each and every unfolded conformation in the complete conformational ensemble as the initial state for the MD simulations (details are provided in SI Appendix). The use of the complete ensemble of the unfolded states is expected to enhance the completeness of the conformation sampling. For each initial structure, after a 500-step minimization for the whole system, we perform MD simulations for all of the atoms of the first (G1) nucleotide, as well as all of the water molecules and the ions. In total, we simulate 570 MD trajectories. For each trajectory, we run a 50-ns simulation. The simulation is terminated before 50 ns if the stable native structure is reached. The coordinates of all of the atoms are written to the NAMD (Nanoscale Molecular Dynamics program) dcd file every 5 ps.

Conformational Clusters.

Clusters are identified as an ensemble of kinetically connected snapshots with small rmsds between them. To determine the clusters efficiently for a large pool of conformations, we use a two-step approach. First, from the simulated trajectories, we identify the segments in the trajectories such that the rmsds between any two snapshots in the segment are less than a cutoff value, such as 1.0 Å. For each segment, we identify the centroid structure, namely, the one with the minimum total rmsd to all of the structures in the segment. We can use a segment-centroid structure to represent a segment. As a result, each trajectory can be represented as a sequence of such segment-centroid structures. Second, after removing all of the possible redundant structures and applying the same procedure to the ensemble of the (segment-centroid) structures, we obtain a set of clusters represented by the respective centroid structures (Fig. 1 C and D). Because a cluster represents a (long-lived) macrostate consisting of consecutive conformations on the trajectory, we may view a cluster as a minimum on the free energy landscape.

Kinetic Network of Conformational Clusters.

As illustrated in Fig. 1E, the rmsd values of the snapshots along a trajectory give the information about the transitions between the clusters and the residence time of each conformation. When a conformation falls in one of the clusters, its rmsd to the respective centroid structure would be smaller than the rmsds to the centroid structures of other clusters. For the case shown in Fig. 1E, the folding trajectory follows the sequential transitions of cluster C5 → cluster C6 → C5 → C3 → C2 → C3 → C2 → C1. Therefore, we can obtain the connectivities C5 ↔ C6, C5 → C3, C3 ↔ C2, and C2 → C1.

To determine the rate constants for transitions between the different clusters, for each cluster C, we first compute the mean residence time <t^C> from the MD trajectories. The inverse of <t^C> gives the total rate $k_C^{total}$ for all of the transitions leaving the cluster. The rate constant $k_{CC\prime }$ for each individual intercluster transition C → $C\prime$ can be computed from the transition frequency: $k_{CC\prime }=(N_{CC\prime }/N_C^{total})k_C^{total}$, where $N_{CC\prime }$ and $N_C^{total}$ are the numbers of occurrences for the C → $C\prime$ transition and for all of the exit transitions from cluster C, respectively (the KMC algorithm is illustrated in SI Appendix). For instance, the mean residence time for C1 is 5.9 ns. The total exit rate is $k_{C1}^{total}=\frac{1}{5.9\text{ns}}=0.17{\text{ns}}^{-1}$. Among all of the (total of 326) exit transitions for C1, there are 293 transitions to C2, 22 to C3, and 11 to C6. Therefore, the rate for the C1 → C2 transition can be estimated as $k_{12}=\frac{293}{326}\times 0.17=0.152\hspace{0.17em}{\text{ns}}^{-1}$. Once the conformational cluster network and the intercluster rates (Fig. 1D) are set up, the folding kinetics of the system can be simulated by applying the KMC and ME methods to the cluster network.

Base Pairing/Stacking Interactions Analyzed by VMD.

The stability of RNA structures is mainly influenced by three factors: base stacking, base pairing, and the chain flexibility. We used the VMD package (89) to calculate the nonbonded interactions between nucleotides G1 and G2 and between nucleotides G1 and C6 for the base primarily stacking and base pairing interactions, respectively. Furthermore, because the backbone is highly charged, metal ions and hydration effects can significantly influence the chain flexibility and the base–base and base–backbone interactions. Indeed, we find that ions play a critical role in initializing/promoting the folding process and in affecting the folding intermediate states and pathways.