Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2015 Nov 12;12(1):405–413. doi: 10.1021/acs.jctc.5b00935

CHARMM-GUI Input Generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM Simulations Using the CHARMM36 Additive Force Field

Jumin Lee †, Xi Cheng †, Jason M Swails ‡, Min Sun Yeom §, Peter K Eastman ∥, Justin A Lemkul ⊥, Shuai Wei , Joshua Buckner , Jong Cheol Jeong $, Yifei Qi †, Sunhwan Jo &, Vijay S Pande ∥, David A Case ‡, Charles L Brooks III , Alexander D MacKerell Jr ⊥, Jeffery B Klauda #, Wonpil Im †,*
PMCID: PMC4712441  PMID: 26631602

Abstract

graphic file with name ct-2015-00935e_0006.jpg

Proper treatment of nonbonded interactions is essential for the accuracy of molecular dynamics (MD) simulations, especially in studies of lipid bilayers. The use of the CHARMM36 force field (C36 FF) in different MD simulation programs can result in disagreements with published simulations performed with CHARMM due to differences in the protocols used to treat the long-range and 1-4 nonbonded interactions. In this study, we systematically test the use of the C36 lipid FF in NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM. A wide range of Lennard-Jones (LJ) cutoff schemes and integrator algorithms were tested to find the optimal simulation protocol to best match bilayer properties of six lipids with varying acyl chain saturation and head groups. MD simulations of a 1,2-dipalmitoyl-sn-phosphatidylcholine (DPPC) bilayer were used to obtain the optimal protocol for each program. MD simulations with all programs were found to reasonably match the DPPC bilayer properties (surface area per lipid, chain order parameters, and area compressibility modulus) obtained using the standard protocol used in CHARMM as well as from experiments. The optimal simulation protocol was then applied to the other five lipid simulations and resulted in excellent agreement between results from most simulation programs as well as with experimental data. AMBER compared least favorably with the expected membrane properties, which appears to be due to its use of the hard-truncation in the LJ potential versus a force-based switching function used to smooth the LJ potential as it approaches the cutoff distance. The optimal simulation protocol for each program has been implemented in CHARMM-GUI. This protocol is expected to be applicable to the remainder of the additive C36 FF including the proteins, nucleic acids, carbohydrates, and small molecules.

Introduction

Research on lipid membranes and associated proteins has broad importance in understanding various biological processes such as lipid trafficking, antibiotic resistance, drug transport, cell signaling, and lipid raft formation. Molecular dynamics (MD) simulation has become an important technique to study such systems, as computational resources and empirical force fields have advanced to allow for meaningful simulations of lipid membranes to better understand their physical properties and functions. For example, MD simulations have been used to probe details of liquid-ordered and liquid-disordered phases and also the formation of liquid-ordered rafts.1−3 There has also been a recent focus on developing accurate representations of cellular membranes based on the known diverse lipid compositions in cells and organelles.4,5 Specifically, MD simulations have been used to model the plasma membrane at a coarse-grained level3,6 to fully atomistic representations of inner and outer membranes of Gram-negative bacteria.7−10 The transport and ligand binding mechanisms for primary and secondary active transporters and binding of peripheral membrane proteins to the bilayer surface have also been studied using MD simulation techniques.11−15

Important to MD simulation is an accurate mathematical description of the relationship of conformation to energy in and between molecules, which is commonly referred to as an empirical force field (FF). For lipids, the all-atom additive CHARMM36 (C36) FF16 was developed to accurately represent a wide range of experimental bilayer properties using the constant particle number, pressure, and temperature (NPT) ensemble. The C36 FF has been extended to a wide range of lipids, e.g., sphingolipids,17 phosphoinositides,18 cardiolipin,19 bacterial lipids,7,8 ester-modified lipids,20 those with polyunsaturated chains,21 cholesterol,22 and lipopolysaccharides.9,23 Recently, the AMBER community has developed their own all-atom lipid FF (Lipid1424 and Slipids25−27) that is of comparable accuracy to that of the C36 FF. One important caveat in these FFs and their usage is that they are developed using approaches that are consistent within the family of each FF, so that it is generally desirable to remain internally consistent (within the same FF family) when studying heterogeneous systems and avoid mixing the parameters of different FFs without careful testing. Moreover, methods used for truncation of the nonbonded interaction energy should be maintained as those used during optimization of the FF to accurately represent these FFs during application studies.

The form of the potential energy function used in most biomacromolecule-based FFs are highly similar and thus allows various FFs to be used in different MD simulation programs. The C36 FF was developed by the CHARMM community initially in the context of the CHARMM program28 with the treatment of the long-range nonbonded interactions as follows. The Lennard-Jones (LJ) 6-12 (i.e., van der Waals) interactions were smoothed over the range of 10 to 12 Å using the force-based switching function,29 the particle mesh Ewald (PME) method30 was used for the long-range electrostatic interactions, and 1-4 nonbonded interactions (i.e., Coulombic and LJ interactions for atoms separated by three chemical bonds) are fully turned on (i.e., no scaling). The cutoff and 1-4 interaction scheme varies between the FFs and should be maintained when different simulation programs are used. This is particularly important with lipids, which have been shown to be particularly sensitive to the treatment of the truncation of the LJ interactions.

After the C36 FF was released, the NAMD program31 added the forced-based switching function, so that results from C36 FF simulations in NAMD and CHARMM become consistent within the differences in the simulation integrators. The GROMACS program32 has all the functionality needed to match with the C36 FF, and its single-core code is faster than CHARMM and NAMD, especially with mixed-point precision (which used to be called single-point precision). The AMBER program33 is another popular MD code, but the latest version at the time of writing (version 14) lacks the shift and switch cutoff methods, and thus one can only use a hard truncation method for the LJ term. The force-based switching function has been implemented in the development version and should improve agreement with the other programs when the next version is released. OpenMM34 has been recently developed as a toolkit for running MD simulation with graphical processing unit (GPU) accelerations. However, use of the force-based switching function is not straightforward, as the current nonbonded force calculation in OpenMM only supports the potential-based switching function.

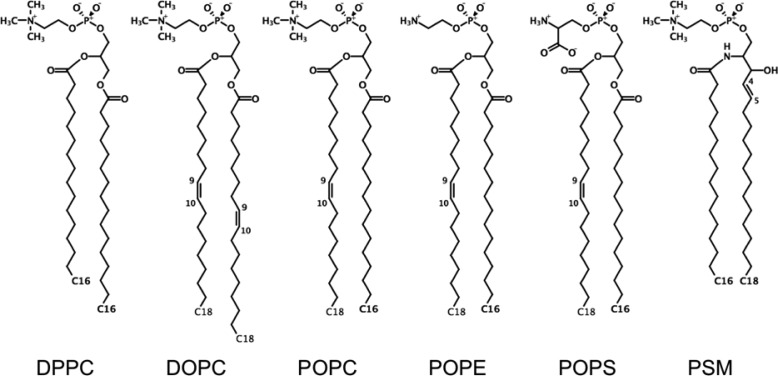
The focus of this work is to prescribe the appropriate simulation protocols to run the C36 lipid FF (and the remainder of the C36 FF including the proteins,35 nucleic acids,36 carbohydrates,37 and small organic molecules38) in a wide range of available molecular simulation software packages. Since CHARMM, NAMD, GROMACS, AMBER, and OpenMM use different algorithms for their thermostat/barostat and nonbonded interaction cutoff options, a careful study on how these differences affect bilayer properties is needed. The importance of this effort is emphasized by a recent study in which it was reported that use of the C36 lipid FF in the context of AMBER GPUs gave incorrect surface area per lipid for DPPC bilayers, which was due to the use of LJ truncation methods that were not consistent with the original parametrization.39 In the present work, we systematically identify simulation protocols for each program to best agree with C36 lipid FF simulations in CHARMM and NAMD in terms of the following three metrics: the area per lipid (lateral density), the acyl chain order parameters (lipid packing), and the area compressibility (dynamic lipid fluctuation). The CHARMM-GUI Membrane Builder(19,40−42) now incorporates the option to generate the minimization, equilibration, and production inputs (with the optimal simulation parameters resulting from this study) for each program to allow for more general use of the C36 FF. In the following sections, we describe the setup of the CHARMM-GUI Input Generator and the optimized protocol for each program in detail. To illustrate that the optimized parameters are robust and well suited for each program, we provide the results of pure lipid bilayer simulations with various lipid types (Figure 1).

Figure 1.

Figure 1

Open in a new tab

Chemical structures of lipids used for the bilayer simulations.

Methods

To determine a set of optimal simulation protocols for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM simulations using the CHARMM C36 FF, a pure DPPC bilayer system was built and simulated with the various simulation parameters available in each program. In addition, 1,2-dioleoyl-sn-phosphatidylcholine (DOPC), 1-palmitoyl-2-oleoyl-sn-phosphatidylcholine (POPC), 1-palmitoyl-2-oleoyl-sn-phosphatidylethanolamine (POPE), 1-palmitoyl-2-oleoyl-sn-phosphatidylserine (POPS), and palmitoylsphingomyelin (PSM) bilayer simulations were performed to validate the optimized protocols derived from the DPPC simulations. The procedures of building the lipid bilayer systems and the tested simulation parameters for each program are provided in detail below.

System Setups

All pure lipid bilayer systems were built using the CHARMM-GUI Membrane Builder.19,40−42 A total of 80 lipid molecules were placed in each lipid bilayer (i.e., 40 lipids in each leaflet) with its center at z = 0. A water layer of 20-Å thickness was added above and below the lipid bilayer for the DPPC, DOPC, POPC, and POPE systems and that of 40-Å thickness for the POPS and PSM systems. The corresponding hydration numbers of each membrane are 34 (DPPC), 34 (DOPC), 32 (POPC), 29 (POPE), 67 (POPS), and 58 (PSM) waters per lipid. KCl ions corresponding to 0.15 M were added in the POPS (including neutralizing ions) and PSM systems, and no ion was added in the DPPC, DOPC, POPC, and POPE systems. While CHARMM and NAMD use the origin for the periodic boundary conditions (PBC), GROMACS, AMBER, and OpenMM use the PBC center at (LX/2, LY/2, LZ/2) where LX, LY, and LZ are the system lengths along the xyz directions. Therefore, the whole system is translated by LX/2, LY/2, and LZ/2 for the GROMACS, AMBER, and OpenMM input generation in CHARMM-GUI.

Simulation Details

All simulations used the C36 FF for lipids16,17 and the CHARMM TIP3P water model.43−45 To get better sampling and check the convergence, five independent MD simulations were performed for each bilayer system using NAMD, GROMACS, AMBER, and OpenMM. The simulation temperature was maintained above the transition temperature of each bilayer: 300.0 (POPS), 303.15 (DOPC/POPC), 310.0 (POPE), and 323.15 K (DPPC/PSM). In addition, the pressure was maintained at 1 bar. PBC were employed for all simulations, and the particle mesh Ewald (PME) method30 was used for long-range electrostatic interactions. The simulation time step was set to 2 fs in conjunction with the SHAKE algorithm46 to constrain the covalent bonds involving hydrogen atoms for all programs except GROMACS in which the LINCS algorithm47 was used. After the standard Membrane Builder minimization and equilibration steps, the production run of each simulation was performed for 250 ns. The optimal parameters were determined using the most recent version of each program (NAMD 2.9, GROMACS 5.0, AMBER14, and OpenMM 6.2), such that the use of previous versions can cause some problems. For example, the semi-isotropic pressure coupling method was not implemented until version 6.2 of OpenMM. The individual simulation protocols that we tested for each MD program are summarized in Table 1 and described in detail below.

Table 1. Summary of Tested Simulation Parameters for the DPPC Bilayer Simulations.

programs conditions cut-offs (Å) abbreviations
NAMD force-based switch 8–10 N-fsw-1
8–12 N-fsw-2
10–12 N-fsw-3
GROMACS Mixed precision force-based switch 8–10 Gm-fsw-1
8–12 Gm-fsw-2
10–12 Gm-fsw-3
potential-based switch 8–10 Gm-sw-1
8–12 Gm-sw-2
10–12 Gm-sw-3
GROMACS Double precision force-based switch 8–10 Gd-fsw-1
8–12 Gd-fsw-2
10–12 Gd-fsw-3
potential-based switch 8–10 Gd-sw-1
8–12 Gd-sw-2
10–12 Gd-sw-3
AMBER truncated        tau-p = 0.5 8 A-0.5-1
10 A-0.5-2
12 A-0.5-3
truncated        tau-p = 1.0 8 A-1.0-1
10 A-1.0-2
12 A-1.0-3
OpenMM force-based switch p_freq = 5 10–12 O-fsw-5
force-based switch p_freq = 10 10–12 O-fsw-10
force-based switch p_freq =15 10–12 O-fsw-15
force-based switch p_freq = 100 10–12 O-fsw-100
CHARMM/OpenMM force-based switch 8–10 CO-fsw-1
8–12 CO-fsw-2
10–12 CO-fsw-3
potential-based switch 8–10 CO-sw-1
8–12 CO-sw-2
10–12 CO-sw-3
Open in a new tab

NAMD

The NAMD simulations were performed as a reference to compare the lipid properties with those from other simulation programs. The force-based switching function was used for the LJ interactions, and three different switching ranges (8–10, 8–12, and 10–12 Å) were examined. A semi-isotropic Nosé–Hoover Langevin-piston method48,49 with a piston period of 50 fs and a piston decay of 25 fs as well as Langevin temperature coupling with a friction coefficient of 1 ps–1 were used to control the pressure and temperature, respectively. A Python50 program was developed and used in CHARMM-GUI to convert the CHARMM parameter files to the NAMD-readable format, and it is freely available in the downloadable tarball (“download.tgz”) generated by CHARMM-GUI.

GROMACS

The force- and potential-based switching functions for the LJ interactions were tested with three different switching ranges (8–10, 8–12, and 10–12 Å). To maintain the temperature, a Nosé–Hoover temperature coupling method51,52 with a tau-t of 1 ps was used, and for pressure coupling, a semi-isotropic Parrinello–Rahman method53,54 with a tau-p of 5 ps and a compressibility of 4.5 × 10–5 bar–1 was used. Because direct reading of the CHARMM topology and parameter files is not available in GROMACS, a format conversion Python program was developed and used in CHARMM-GUI to generate the corresponding GROMACS topology and parameter files (top and itp) using the CHARMM topology and parameter files (prm, rtf, and str) as well as the psf file.

AMBER

Because AMBER does not support any switching or shifting method for LJ interactions, we examined the hard-truncation method with three different cutoff values (8, 10, and 12 Å). The temperature was maintained using Langevin dynamics with a friction coefficient of 1 ps–1. In addition, tau-p values of 0.5 and 1 ps for the semi-isotropic Berendsen pressure control55 were tested. The AMBER-readable C36 FF was prepared using ParmEd v2.0 Beta1 software.

OpenMM

OpenMM provides a library for MD simulation with GPU acceleration, so it does not have an executable program to run MD simulations. We developed a set of Python scripts that enable one to run OpenMM simulations with simple and generalized input files, and all these scripts are provided by CHARMM-GUI. Although the standard nonbonded force calculation in OpenMM only supports the potential-based switching function, we provide an implementation of the force-based switching function using OpenMM’s CustomNonbondedForce class in the scripts generated by CHARMM-GUI. The force-based switching method with the switching range of 10–12 Å for LJ interactions was used for all OpenMM simulations; other LJ interaction parameters for the DPPC bilayers were tested using CHARMM/OpenMM. Langevin dynamics was used for the temperature coupling, and friction coefficient values of 1 and 10 ps–1 were tested. A semi-isotropic Monte Carlo (MC) barostat method56,57 was used for the pressure coupling, and pressure coupling frequency values of 5, 10, 15, and 100 steps were examined. OpenMM is able to directly read the CHARMM topology and parameter files, so FF conversion was not necessary.

CHARMM/OpenMM

Because CHARMM/OpenMM uses the OpenMM library to calculate energies, the results between both programs should be identical. Therefore, the DPPC bilayer simulations to determine the LJ interaction parameters for both OpenMM and CHARMM/OpenMM were performed using CHARMM/OpenMM. The force- and potential-based switching methods were tested with switching ranges of 8–10, 8–12, and 10–12 Å. Langevin dynamics with the friction coefficient of 10 ps–1 and the semi-isotropic MC barostat with the pressure coupling frequency of 15 were used. CHARMM c39b1 with OpenMM 5.2 was used for the DPPC simulations. CHARMM/OpenMM simulations for other lipids were not performed because it is identical to OpenMM, and CHARMM-GUI provides the CHARMM/OpenMM simulation parameters that are identical to OpenMM simulations.

Analysis

The membrane properties, such as an average surface area per lipid, compressibility, and deuterium order parameters, were calculated and compared with available experimental values. The first 50 ns of each trajectory was discarded as an equilibration period, and the properties were calculated over the last 200 ns period. Most systems were equilibrated within 50 ns except for those showing the phase transition (Supporting Information Figure S1); for such systems, the data before the phase transition were discarded. The average and the standard errors were calculated from the five independent simulations.

The average surface area per lipid (AL) was calculated by simply dividing the system area (AXY) by the number of lipids in each leaflet (NL = 40). The compressibility, KA, was calculated using the following equation:58,59

graphic file with name ct-2015-00935e_m001.jpg 1

where kB is the Boltzmann constant, T is the system temperature, and ⟨δAL2⟩ is the average of the squared fluctuation of AL. The deuterium order parameters and electron density profiles (for POPS) were calculated using ST-analyzer.10 Hydrogen bonding probability was evaluated using CHARMM (COOR HBOND). The default distance cutoff of 2.4 Å between the donor H atom and the acceptor atom was used except the lipid–ion interactions calculated with the distance cutoff of 3.8 Å instead. An angular cutoff was not used.

Results and Discussion

Optimal Simulation Protocols Based on DPPC Bilayer Simulations

The bilayer properties from the DPPC simulations with various simulation parameters (Table 1) available in NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM are first presented to determine the optimal simulation protocol for each program using the C36 FF.

NAMD

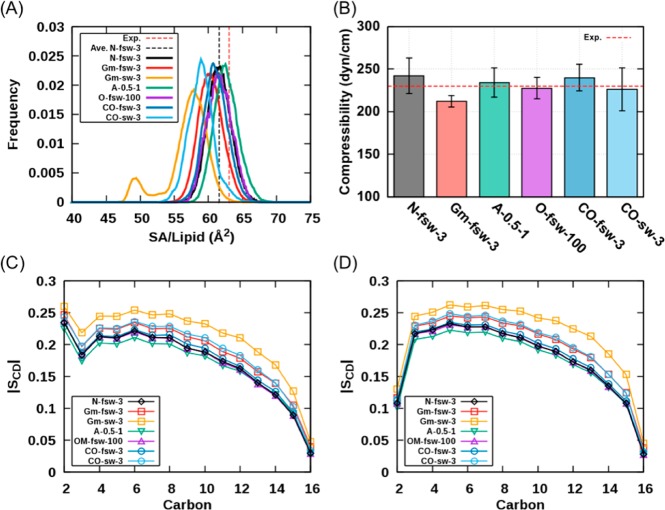
The AL values from the NAMD simulations are 64.8 ± 0.1, 62.9 ± 0.1, and 61.6 ± 0.1 Å2 for 8–10, 8–12, and 10–12 Å of the force-based switching ranges, respectively. These results are in good agreement with the experimental AL values of 63.0 ± 1.0 Å2 at 323 K.60 The KA values are 222.5 ± 9.5 (8–10 Å), 227.1 ± 7.1 (8–12 Å), and 242.4 ± 20.9 dyn/cm (10–12 Å), which are all in the range of its experimental value of 234 dyn/cm.61 Although the 8–12 Å switching range appears to yield the best AL, the 10–12 Å switching range is considered to be a standard to compare the lipid properties with other programs, as 10–12 Å is consistent with the force-based switching range used to develop the remainder of the additive CHARMM FF (for proteins, nucleic acids, carbohydrates, and small molecules). We note that use of the 8–12 Å switching range with the full additive C36 FF is likely to be satisfactory, although rigorous testing has not yet been performed using this switching scheme.

GROMACS

We first tested the influence of mixed versus double precision on the lipid properties (Supporting Information Table S1) and found no reduction in accuracy with the use of the more efficient mixed precision. Second, the influence of switching functions (potential- vs force-based) on lipid properties was investigated. Large differences were seen between these two switching functions. In general, AL values are greatly reduced with the potential-based switching function, and the 10–12 Å switching range results in a phase transition to a gel-like state. As shown in Figure 2A, the GROMACS simulation with the 10–12 Å potential-based switching function (Gm-sw-3) shows two peaks at around 49 Å2 and 58 Å2, which represent gel- and liquid-like phase states, respectively. On the other hand, the simulations with the force-based switching function show good agreement with NAMD simulation results with the slightly reduced AL values: 63.6 ± 0.1 (8–10 Å), 61.2 ± 0.1 (8–12 Å), and 60.3 ± 0.1 Å2 (10–12 Å). Most KA results are acceptable with the force-based switching simulations showing good agreement with the NAMD results: 212.6 ± 6.2 (8–10 Å), 213.9 ± 7.6 (8–12 Å), and 212.4 ± 6.8 dyn/cm (10–12 Å). The deuterium order parameter values in Figure 2C,D strongly suggest that the potential-based switching function should not be used for the GROMACS simulations with the C36 FF due to its disagreement with the NAMD results for both sn-1 and sn-2 chains. In general, these GROMACS simulations show higher order parameters than other simulations. Overall, the 8–12 Å force-based switching function shows best agreement with NAMD DPPC bilayer simulations with 10–12 Å force-based switching, but to be consistent with the remainder of the additive CHARMM FF, the 10–12 Å switching range was used for the GROMACS simulations of the other bilayer systems.

Figure 2.

Figure 2

Open in a new tab

DPPC bilayer properties from some representative simulations: (A) The distributions of surface area per lipid over the 200 ns of trajectories. (B) The compressibility properties derived from each program. (C and D) The deuterium order parameters of (C) sn-1 and (D) sn-2 chains.

AMBER

Determining an optimal protocol for AMBER was challenging due to the absence of any switching methods for LJ interactions in the current version. Therefore, the hard-truncation method with various cutoff ranges was tested. The 8-Å cutoff shows the best AL (62.6 ± 0.1 Å2), while the 12-Å cutoff shows a phase transition to a gel-like state (data is not shown). This is consistent with what was observed previously by Gould et al.39 and demonstrates the need to carefully consider the cutoff scheme in different programs. Compared to the NAMD results, the KA values are mostly in the acceptable range: 235.9 ± 12.2 (8 Å) and 228.6 ± 18.3 dyn/cm (10 Å). AMBER simulations result in slightly reduced order parameters compared to NAMD, but they are in the acceptable range. There is no considerable difference in between 0.5 and 1.0 ps for the pressure coupling time (tau-p). Thus, the 8-Å cutoff with tau-p of 0.5 ps was used for the other lipid simulations.

CHARMM/OpenMM

The cutoff methods for LJ interactions for both OpenMM and CHARMM/OpenMM were tested using CHARMM/OpenMM. Like GROMACS, the potential-based switching function reduces the AL values: 61.4 ± 0.3 (8–10 Å), 60.0 ± 0.2 (8–12 Å), and 58.9 ± 0.3 Å2 (10–12 Å). The equilibrium properties of the force-based switch function systems show good agreement with the NAMD results; the AL values are 64.6 ± 0.2 (8–10 Å), 62.5 ± 0.1 (8–12 Å), and 61.1 ± 0.2 Å2 (10–12 Å), and the KA values are 227.8 ± 14.5 (8–10 Å), 238.3 ± 13.3 (8–12 Å), and 240.0 ± 15.9 dyn/cm (10–12 Å). The deuterium order parameters of CHARMM/OpenMM simulations also show good agreement with the NAMD results except that the potential-based switch systems have higher order parameters (Figure 2C,D). For further OpenMM simulations, the 10–12 Å force-based switching function was adopted.

OpenMM

The lipid properties of the OpenMM simulations are similar to those of the NAMD simulation results (Figure 2, Supporting Information Table S1). There is no significant difference with different pressure coupling frequencies and Langevin dynamics friction coefficients. To reduce the GPU time, the pressure coupling frequency of 100 steps and the Langevin friction coefficient of 1 ps–1 were used for other lipid simulations.

Other Lipid Bilayer Properties with the Optimized Protocols

The optimal protocol for each program determined from the DPPC bilayer simulations is summarized in Table 2. To validate these protocols, we performed the DOPC, POPC, POPE, POPS, and PSM bilayer simulations and compared the lipid properties of each program.

Table 2. Optimal Protocol for Each Simulation Program Determined from DPPC Bilayer Simulations.

programs GROMACS AMBER OpenMM CHARMM/OpenMM
temp. control Nosé–Hoover Langevin Langevin Langevin
temp. constant tau-t = 1.0 gamma = 1.0 gamma = 1.0 gamma = 1.0
press. control Parrinello–Rahman Berendsen MC barostat MC barostat
press. constant tau-p = 5.0 tau-p = 0.5 p_freq = 100 p_freq = 100
vdW cutoff method force-based switch hard-truncation force-based switch force-based switch
vdW cutoff range 10–12 Å 8 Å 10–12 Å 10–12 Å
electrostatic interaction 12 Å; PME 8 Å; PME 12 Å; PME 12 Å; PME
Open in a new tab

DOPC

All programs yield similar DOPC bilayer properties with the optimal protocols. The AL values are 68.7 ± 0.1 (NAMD), 68.0 ± 0.1 (GROMACS), 69.7 ± 0.1 (AMBER), and 68.6 ± 0.2 Å2 (OpenMM), and they are in good agreement with the experimental estimate from the fully hydrated bilayer, i.e., 67.4 ± 1.0 Å2 at 303 K.60 In addition, the calculated KA values are similar among the programs: 278.0 ± 13.4 (NAMD), 255.5 ± 14.8 (GROMACS), 301.2 ± 12.3 (AMBER), and 259.5 ± 26.9 dyn/cm (OpenMM). While AMBER and OpenMM order parameters show good agreement with NAMD, GROMACS results in slightly increased order parameters for both sn-1 and sn-2 chains but they are in the acceptable range (Supporting Information Figure S2).

POPC

The experimental AL of a POPC bilayer is 68.3 ± 1.5 Å2 at 303 K,62 and NAMD shows a somewhat reduced AL of 65.0 ± 0.1 Å2. There is no significant difference between NAMD and the other programs. GROMACS results in a slightly reduced AL (64.1 ± 0.1 Å2) compared to NAMD, while AMBER shows marginally increased AL (66.0 ± 0.1 Å2). OpenMM shows the best agreement with NAMD in the AL value (64.7 ± 0.1 Å2). The KA value of each program is also in the range of the NAMD result (249.6 ± 19.7 dyn/cm): 262.5 ± 18.2 (GROMACS), 270.3 ± 18.3 (AMBER), and 274.6 ± 31.5 dyn/cm (OpenMM). Like DOPC simulation results, the GROMACS order parameters are insignificantly increased in both sn-1 and sn-2 chains compared to other programs (Supporting Information Figure S2).

POPE

The average AL value from the NAMD POPE simulation is 57.8 ± 0.1 Å2, and it shows good agreement with the experimental value of 59.75–60.75 Å2 at 308–313 K.63 Other programs also show good agreement with NAMD: 56.7 ± 0.1 (GROMACS), 58.1 ± 0.1 (AMBER), and 57.7 ± 0.1 Å2 (OpenMM). The KA values are 270.0 ± 15.8 (NAMD), 270.1 ± 8.8 (GROMACS), 254.8 ± 4.4 (AMBER), and 266.4 ± 24.5 dyn/cm (OpenMM). However, GROMACS again yields negligibly increased order parameters compared to NAMD, AMBER, and OpenMM (Supporting Information Figure S2).

POPS

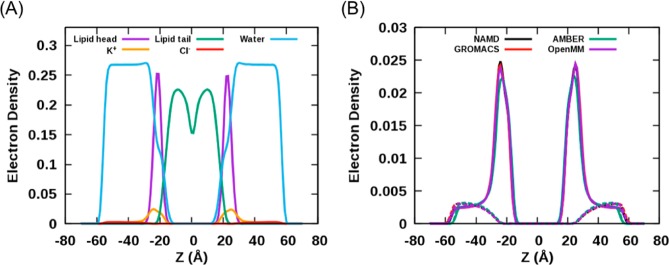
Unlike the other lipid systems described above, the AL values of the POPS bilayer systems are underestimated by ∼10% compared to its experimental AL of 62.7 Å2 at 298 K.64 NAMD yields the AL of 56.9 ± 0.2 Å2, and other programs show similar AL values as NAMD: 56.0 ± 0.4 (GROMACS) and 56.9 ± 0.5 Å2 (OpenMM) except AMBER (59.0 ± 0.1 Å2). The POPS NAMD simulation in different conditions resulted in the AL of 59.9 Å2. In this simulation, the system contained 100 POPS lipid molecules and around 5300 water molecules, and 100 K+ counterions were added.66 Thus, the slightly lower temperature with the higher ion concentration in the current simulations might account for the lower AL values. The KA values are similar among the programs: 261.1 ± 22.8 (NAMD), 262.1 ± 33.2 (GROMACS), 270.5 ± 28.5 (AMBER), and 274.0 ± 28.9 dyn/cm (OpenMM). While GROMACS shows slightly increased order parameters compared to NAMD, AMBER yields marginally reduced values (Supporting Information Figure S2). The order parameters from the OpenMM simulations show good agreement with NAMD. There is no significant difference in the density profiles of POPS bilayer systems (Figure 3) except that AMBER shows a slightly reduced hydrophobic thickness (29.8 ± 0.1 Å) compared to NAMD (31.2 ± 0.1 Å). The POPS headgroup has a peak at ±20 Å along the z-axis, and K+ ion shows the highest peak near the POPS headgroup.

Figure 3.

Figure 3

Open in a new tab

Electron density profiles of POPS bilayer simulations. (A) The NAMD results. (B) The comparison of K+ (solid lines) and Cl– (dashed lines) distributions among the programs.

PSM

Because there is no reliable experimental AL for the PSM bilayer, the GROMACS, AMBER, and OpenMM AL values are compared only with the NAMD value. While the AL values from GROMACS (54.3 ± 0.2 Å2) and OpenMM (55.7 ± 0.2 Å2) show good agreement with the NAMD AL value (55.2 ± 0.2 Å2), AMBER yields a 1.4 Å2 higher value (56.6 ± 0.3 Å2). The KA values of GROMACS (445.4 ± 13.3 dyn/cm), AMBER (392.3 ± 49.9 dyn/cm), and OpenMM (403.2 ± 49.9 dyn/cm) are in the range of the NAMD KA value (456.4 ± 64.8 dyn/cm). The GROMACS simulations result in slightly increased order parameters than NAMD in both sphingosine and N-linked acyl chains, while AMBER yields slightly reduced order parameters. (Figure 4, Supporting Information Figure S2). Generally, most programs result in good agreement in the order parameters, which are shown with the NMR data65 in Figure 4. Table 3 lists principal H-bonds in the PSM bilayer system and their probabilities obtained from each program. In general, the H-bond probabilities are similar between programs.

Figure 4.

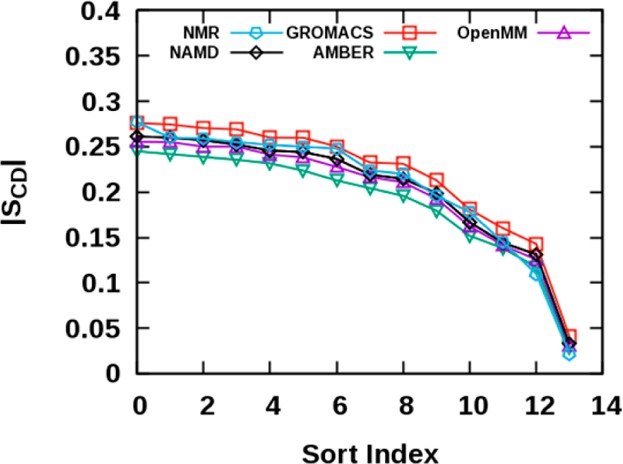
Figure 4

Open in a new tab

Value sorted SCD order parameters of PSM N-linked acyl chain from NMR and each program.

Table 3. Intra- and Intermolecular H-Bond Probabilities.
H-bond NAMD GROMACS AMBER OpenMM
Intramolecular
O—H:::O—P 0.99 ± 0.001 0.95 ± 0.001 0.99 ± 0.001 0.99 ± 0.001
O—H:::O=P 0.01 ± 0.001 0.01 ± 0.001 0.01 ± 0.001 0.01 ± 0.001
Lipid:Lipid
N—H:::O=P 0.02 ± 0.001 0.03 ± 0.002 0.02 ± 0.002 0.02 ± 0.001
N—H:::O=C 0.24 ± 0.006 0.28 ± 0.009 0.23 ± 0.008 0.23 ± 0.008
N—H:::O—C 0.15 ± 0.007 0.17 ± 0.006 0.14 ± 0.002 0.15 ± 0.004
Lipid:Water
N—H:::OH2 0.32 ± 0.007 0.34 ± 0.007 0.32 ± 0.006 0.33 ± 0.006
C=O:::HOH 0.64 ± 0.007 0.70 ± 0.007 0.64 ± 0.008 0.67 ± 0.006
C—O:::HOH 0.49 ± 0.013 0.55 ± 0.004 0.49 ± 0.004 0.51 ± 0.004
Lipid:Ion
P=O:::K+ 0.02 ± 0.001 0.02 ± 0.001 0.02 ± 0.001 0.02 ± 0.001
C=O:::K+ 0.01 ± 0.001 0.01 ± 0.002 0.01 ± 0.001 0.01 ± 0.001
C—O:::K+ 0.01 ± 0.001 0.01 ± 0.001 0.01 ± 0.001 0.01 ± 0.001
Open in a new tab

Conclusions

The use of the C36 lipid FF in various programs (NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM) has been shown to result in comparable lipid properties for DPPC, DOPC, POPC, POPE, POPS, and PSM bilayers when the optimized simulation protocols for treatment of the nonbonded interactions are applied. Since each program commonly uses different methods in dealing with LJ cutoffs, care must be taken to choose cutoff schemes that best match the approach taken during development of the C36 lipid FF using the CHARMM program. Excluding AMBER, all simulation programs have force-based switching functions that are required to properly reproduce the published C36 FF results, and, thus, the recommended cutoff scheme for these programs utilizes this approach. The lack of a switching function in AMBER has misled some researchers attempting to apply the C36 FF in this program,39 although the inclusion of the force-based switching function in upcoming versions of AMBER should ameliorate these issues in the future. As we demonstrate, using potential truncation at cutoffs >8 Å results in gel-like lipid bilayers even above the gel transition temperature. Slight changes that enhance lipid–lipid interactions will potentially result in a phase change. As described in the Results and Discussion section, the use of 8 Å hard truncation in AMBER best represents the spirit of the C36 FF, although there are slight discrepancies when applying this cutoff scheme to the other lipids tested (Supporting Information Figure S2 and Table S3). The discrepancies become larger when the system contains ions (POPS) or strongly interacting lipids (PSM). Therefore, the use of the C36 lipid FF in AMBER (versions 14 and earlier) may not agree with CHARMM/NAMD to the degree obtained with programs that contain the force-based switching function for the LJ potential.

For programs other than AMBER, the agreement with CHARMM/NAMD results for all lipid bilayers tested in this study is satisfactory. However, there are some minor differences in that the GROMACS AL values are slightly reduced and thus the order parameters are slightly higher. Although the cutoff scheme is the same between these programs, differences in other aspects of the simulation protocols, i.e., integration scheme and temperature-/pressure-coupling, can result in slight changes in lipid membrane properties. The present results indicate that the effect of different integrators and/or coupling schemes on lipid bilayer properties is smaller than that due to different cutoff schemes. The usage of different cutoff schemes can also lead to a bilayer phase change.

While the current studies are based on membrane simulations, the optimized simulation protocols should be applicable to the remainder of the C36 FF including proteins, nucleic acids, carbohydrates, and small molecules. Membrane simulations are especially sensitive to slight changes in the LJ cutoff methods, whereas other biological molecules do not have the ordered self-assembly as lipids, making them less sensitive to subtle details of the treatment of the LJ potential. The optimal simulation protocol for each program has been implemented in CHARMM-GUI. As CHARMM-GUI will convert any patch used during the system building process into appropriate simulation files, including those for GROMACS, the study of complex heterogeneous systems with the C36 FF will be readily accessible to a range of simulation packages. For example, adding carbohydrates to proteins can be easily done with CHARMM-GUI and allows for building of such systems and their proper conversion for use in GROMACS. Therefore, the simulation systems and inputs being seamlessly generated by CHARMM-GUI can be used for general research use in these simulation programs.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.5b00935.

  • Table S1, DPPC bilayer properties obtained from each program; Table S2, other lipid properties obtained from each program with the optimal protocols; Table S3, bilayer property comparison between each program and NAMD; Figure S1, The time-series of surface area per lipid properties of each simulation; and Figure S2, SCD order parameters of lipids derived from each program (PDF)

This work was supported by NSF DBI-1145987, NSF MCB-1157677, NIH U54GM087519, XSEDE MCB070009 (to W.I.), NIH R01GM072558, GM051501, GM070855 (A.D.M.), NSF MCB-1149187, NSF DBI-1145652 (J.B.K.), NIH F32GM109632 (J.A.L.), NIH GM103695, GM037554 (C.L.B.), and the National Institute of Supercomputing and Networking/Korea Institute of Science and Technology Information with supercomputing resources including technical support [KSC-2015-C3-004] (M.S.Y.).

The authors declare no competing financial interest.

Supplementary Material

ct5b00935_si_001.pdf (3.4MB, pdf)

References

  1. Rog T.; Vattulainen I. Chem. Phys. Lipids 2014, 184, 82–104. 10.1016/j.chemphyslip.2014.10.004. [DOI] [PubMed] [Google Scholar]
  2. Sodt A. J.; Sandar M. L.; Gawrisch K.; Pastor R. W.; Lyman E. J. Am. Chem. Soc. 2014, 136 (2), 725–732. 10.1021/ja4105667. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Ingolfsson H. I.; Melo M. N.; van Eerden F. J.; Arnarez C.; Lopez C. A.; Wassenaar T. A.; Periole X.; de Vries A. H.; Tieleman D. P.; Marrink S. J. J. Am. Chem. Soc. 2014, 136 (41), 14554–14559. 10.1021/ja507832e. [DOI] [PubMed] [Google Scholar]
  4. van Meer G.; Voelker D. R.; Feigenson G. W. Nat. Rev. Mol. Cell Biol. 2008, 9 (2), 112–124. 10.1038/nrm2330. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Khakbaz P.; Klauda J. B. Chem. Phys. Lipids 2015, 10.1016/j.chemphyslip.2015.08.003. [DOI] [PubMed] [Google Scholar]
  6. Qi Y.; Ingolfsson H. I.; Cheng X.; Lee J.; Marrink S. J.; Im W. J. Chem. Theory Comput. 2015, 11 (9), 4486–4494. 10.1021/acs.jctc.5b00513. [DOI] [PubMed] [Google Scholar]
  7. Lim J. B.; Klauda J. B. Biochim. Biophys. Acta, Biomembr. 2011, 1808 (1), 323–331. 10.1016/j.bbamem.2010.07.036. [DOI] [PubMed] [Google Scholar]
  8. Pandit K. R.; Klauda J. B. Biochim. Biophys. Acta, Biomembr. 2012, 1818 (5), 1205–1210. 10.1016/j.bbamem.2012.01.009. [DOI] [PubMed] [Google Scholar]
  9. Wu E. L.; Fleming P. J.; Yeom M. S.; Widmalm G.; Klauda J. B.; Fleming K. G.; Im W. Biophys. J. 2014, 106 (11), 2493–2502. 10.1016/j.bpj.2014.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Jeong J. C.; Jo S.; Wu E. L.; Qi Y.; Monje-Galvan V.; Yeom M. S.; Gorenstein L.; Chen F.; Klauda J. B.; Im W. J. Comput. Chem. 2014, 35 (12), 957–963. 10.1002/jcc.23584. [DOI] [PubMed] [Google Scholar]
  11. Stansfeld P. J.; Sansom M. S. Structure 2011, 19 (11), 1562–1572. 10.1016/j.str.2011.10.002. [DOI] [PubMed] [Google Scholar]
  12. Li J.; Wen P. C.; Moradi M.; Tajkhorshid E. Curr. Opin. Struct. Biol. 2015, 31, 96–105. 10.1016/j.sbi.2015.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Rogaski B.; Klauda J. B. J. Mol. Biol. 2012, 423 (5), 847–861. 10.1016/j.jmb.2012.08.015. [DOI] [PubMed] [Google Scholar]
  14. Pendse P. Y.; Brooks B. R.; Klauda J. B. J. Mol. Biol. 2010, 404 (3), 506–521. 10.1016/j.jmb.2010.09.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Qi Y.; Cheng X.; Lee J.; Vermaas J.; Pogorelov T.; Tajkhorshid E.; Park S.; Klauda J. B.; Im W. Biophys. J. 2015, 109, 2012. 10.1016/j.bpj.2015.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Klauda J. B.; Venable R. M.; Freites J. A.; O’Connor J. W.; Tobias D. J.; Mondragon-Ramirez C.; Vorobyov I.; MacKerell A. D. Jr.; Pastor R. W. J. Phys. Chem. B 2010, 114 (23), 7830–7843. 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Venable R. M.; Sodt A. J.; Rogaski B.; Rui H.; Hatcher E.; MacKerell A. D. Jr.; Pastor R. W.; Klauda J. B. Biophys. J. 2014, 107 (1), 134–145. 10.1016/j.bpj.2014.05.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Wu E. L.; Qi Y.; Song K. C.; Klauda J. B.; Im W. J. Phys. Chem. B 2014, 118 (16), 4315–4325. 10.1021/jp500610t. [DOI] [PubMed] [Google Scholar]
  19. Wu E. L.; Cheng X.; Jo S.; Rui H.; Song K. C.; Davila-Contreras E. M.; Qi Y.; Lee J.; Monje-Galvan V.; Venable R. M.; Klauda J. B.; Im W. J. Comput. Chem. 2014, 35 (27), 1997–2004. 10.1002/jcc.23702. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Villanueva D. Y.; Lim J. B.; Klauda J. B. Langmuir 2013, 29 (46), 14196–14203. 10.1021/la403919h. [DOI] [PubMed] [Google Scholar]
  21. Klauda J. B.; Monje V.; Kim T.; Im W. J. Phys. Chem. B 2012, 116 (31), 9424–9431. 10.1021/jp304056p. [DOI] [PubMed] [Google Scholar]
  22. Lim J. B.; Rogaski B.; Klauda J. B. J. Phys. Chem. B 2012, 116 (1), 203–210. 10.1021/jp207925m. [DOI] [PubMed] [Google Scholar]
  23. Wu E. L.; Engstrom O.; Jo S.; Stuhlsatz D.; Yeom M. S.; Klauda J. B.; Widmalm G.; Im W. Biophys. J. 2013, 105 (6), 1444–1455. 10.1016/j.bpj.2013.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Dickson C. J.; Madej B. D.; Skjevik A. A.; Betz R. M.; Teigen K.; Gould I. R.; Walker R. C. J. Chem. Theory Comput. 2014, 10 (2), 865–879. 10.1021/ct4010307. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Jämbeck J. P. M.; Lyubartsev A. P. J. Chem. Theory Comput. 2012, 8 (8), 2938–2948. 10.1021/ct300342n. [DOI] [PubMed] [Google Scholar]
  26. Jämbeck J. P. M.; Lyubartsev A. P. J. Chem. Theory Comput. 2013, 9 (1), 774–784. 10.1021/ct300777p. [DOI] [PubMed] [Google Scholar]
  27. Jämbeck J. P.; Lyubartsev A. P. J. Phys. Chem. B 2012, 116 (10), 3164–3179. 10.1021/jp212503e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Brooks B. R.; Brooks C. L. 3rd; MacKerell A. D. Jr.; Nilsson L.; Petrella R. J.; Roux B.; Won Y.; Archontis G.; Bartels C.; Boresch S.; Caflisch A.; Caves L.; Cui Q.; Dinner A. R.; Feig M.; Fischer S.; Gao J.; Hodoscek M.; Im W.; Kuczera K.; Lazaridis T.; Ma J.; Ovchinnikov V.; Paci E.; Pastor R. W.; Post C. B.; Pu J. Z.; Schaefer M.; Tidor B.; Venable R. M.; Woodcock H. L.; Wu X.; Yang W.; York D. M.; Karplus M. J. Comput. Chem. 2009, 30 (10), 1545–1614. 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Steinbach P. J.; Brooks B. R. J. Comput. Chem. 1994, 15 (7), 667–683. 10.1002/jcc.540150702. [DOI] [Google Scholar]
  30. Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. J. Chem. Phys. 1995, 103 (19), 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
  31. Phillips J. C.; Braun R.; Wang W.; Gumbart J.; Tajkhorshid E.; Villa E.; Chipot C.; Skeel R. D.; Kale L.; Schulten K. J. Comput. Chem. 2005, 26 (16), 1781–1802. 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. SoftwareX 2015, 1–2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
  33. Case D. A.; Cheatham T. E. 3rd; Darden T.; Gohlke H.; Luo R.; Merz K. M. Jr.; Onufriev A.; Simmerling C.; Wang B.; Woods R. J. J. Comput. Chem. 2005, 26 (16), 1668–1688. 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Eastman P.; Friedrichs M. S.; Chodera J. D.; Radmer R. J.; Bruns C. M.; Ku J. P.; Beauchamp K. A.; Lane T. J.; Wang L. P.; Shukla D.; Tye T.; Houston M.; Stich T.; Klein C.; Shirts M. R.; Pande V. S. J. Chem. Theory Comput. 2013, 9 (1), 461–469. 10.1021/ct300857j. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Best R. B.; Zhu X.; Shim J.; Lopes P. E.; Mittal J.; Feig M.; MacKerell A. D. Jr. J. Chem. Theory Comput. 2012, 8 (9), 3257–3273. 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Denning E. J.; Priyakumar U. D.; Nilsson L.; MacKerell A. D. Jr. J. Comput. Chem. 2011, 32 (9), 1929–1943. 10.1002/jcc.21777. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Guvench O.; Greene S. N.; Kamath G.; Brady J. W.; Venable R. M.; Pastor R. W.; MacKerell A. D. Jr. J. Comput. Chem. 2008, 29 (15), 2543–2564. 10.1002/jcc.21004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Vanommeslaeghe K.; Hatcher E.; Acharya C.; Kundu S.; Zhong S.; Shim J.; Darian E.; Guvench O.; Lopes P.; Vorobyov I.; MacKerell A. D. Jr. J. Comput. Chem. 2010, 31 (4), 671–690. 10.1002/jcc.21367. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Skjevik A. A.; Madej B. D.; Dickson C. J.; Teigen K.; Walker R. C.; Gould I. R. Chem. Commun. (Cambridge, U. K.) 2015, 51 (21), 4402–4405. 10.1039/C4CC09584G. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Jo S.; Kim T.; Im W. PLoS One 2007, 2 (9), e880. 10.1371/journal.pone.0000880. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Jo S.; Kim T.; Iyer V. G.; Im W. J. Comput. Chem. 2008, 29 (11), 1859–1865. 10.1002/jcc.20945. [DOI] [PubMed] [Google Scholar]
  42. Jo S.; Lim J. B.; Klauda J. B.; Im W. Biophys. J. 2009, 97 (1), 50–58. 10.1016/j.bpj.2009.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. J. Chem. Phys. 1983, 79 (2), 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
  44. Durell S. R.; Brooks B. R.; Ben-Naim A. J. Phys. Chem. 1994, 98 (8), 2198–2202. 10.1021/j100059a038. [DOI] [Google Scholar]
  45. Neria E.; Fischer S.; Karplus M. J. Chem. Phys. 1996, 105 (5), 1902–1921. 10.1063/1.472061. [DOI] [Google Scholar]
  46. Ryckaert J.-P.; Ciccotti G.; Berendsen H. J. C. J. Comput. Phys. 1977, 23 (3), 327–341. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
  47. Hess B.; Bekker H.; Berendsen H. J. C.; Fraaije J. G. E. M. J. Comput. Chem. 1997, 18 (12), 1463–1472. . [DOI] [Google Scholar]
  48. Martyna G. J.; Tobias D. J.; Klein M. L. J. Chem. Phys. 1994, 101 (5), 4177–4189. 10.1063/1.467468. [DOI] [Google Scholar]
  49. Feller S. E.; Zhang Y. H.; Pastor R. W.; Brooks B. R. J. Chem. Phys. 1995, 103 (11), 4613–4621. 10.1063/1.470648. [DOI] [Google Scholar]
  50. van Rossum G.; de Boer J. CWI Quarterly 1991, 4 (4), 283–303. [Google Scholar]
  51. Nose S. Mol. Phys. 1984, 52 (2), 255–268. 10.1080/00268978400101201. [DOI] [Google Scholar]
  52. Hoover W. G. Phys. Rev. A: At., Mol., Opt. Phys. 1985, 31 (3), 1695–1697. 10.1103/PhysRevA.31.1695. [DOI] [PubMed] [Google Scholar]
  53. Parrinello M.; Rahman A. J. Appl. Phys. 1981, 52 (12), 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
  54. Nose S.; Klein M. L. Mol. Phys. 1983, 50 (5), 1055–1076. 10.1080/00268978300102851. [DOI] [Google Scholar]
  55. Berendsen H. J. C.; Postma J. P. M.; Vangunsteren W. F.; Dinola A.; Haak J. R. J. Chem. Phys. 1984, 81 (8), 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
  56. Chow K. H.; Ferguson D. M. Comput. Phys. Commun. 1995, 91 (1–3), 283–289. 10.1016/0010-4655(95)00059-O. [DOI] [Google Scholar]
  57. Åqvist J.; Wennerström P.; Nervall M.; Bjelic S.; Brandsdal B. O. Chem. Phys. Lett. 2004, 384 (4–6), 288–294. 10.1016/j.cplett.2003.12.039. [DOI] [Google Scholar]
  58. Feller S. E.; Pastor R. W. J. Chem. Phys. 1999, 111 (3), 1281–1287. 10.1063/1.479313. [DOI] [Google Scholar]
  59. Kim T.; Lee K. I.; Morris P.; Pastor R. W.; Andersen O. S.; Im W. Biophys. J. 2012, 102 (7), 1551–1560. 10.1016/j.bpj.2012.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Kucerka N.; Nagle J. F.; Sachs J. N.; Feller S. E.; Pencer J.; Jackson A.; Katsaras J. Biophys. J. 2008, 95 (5), 2356–2367. 10.1529/biophysj.108.132662. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Rawicz W.; Olbrich K. C.; McIntosh T.; Needham D.; Evans E. Biophys. J. 2000, 79 (1), 328–339. 10.1016/S0006-3495(00)76295-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Kucerka N.; Tristram-Nagle S.; Nagle J. F. J. Membr. Biol. 2006, 208 (3), 193–202. 10.1007/s00232-005-7006-8. [DOI] [PubMed] [Google Scholar]
  63. Rappolt M.; Hickel A.; Bringezu F.; Lohner K. Biophys. J. 2003, 84 (5), 3111–3122. 10.1016/S0006-3495(03)70036-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Pan J.; Cheng X.; Monticelli L.; Heberle F. A.; Kucerka N.; Tieleman D. P.; Katsaras J. Soft Matter 2014, 10 (21), 3716–3725. 10.1039/c4sm00066h. [DOI] [PubMed] [Google Scholar]
  65. Konas R. M.; Daristotle J. L.; Harbor N. B.; Klauda J. B. J. Phys. Chem. B 2015, 119, 13134–13141. 10.1021/acs.jpcb.5b06066. [DOI] [PubMed] [Google Scholar]
  66. Mehnert T.; Jacob K.; Bittman R.; Beyer K. Biophys. J. 2006, 90 (3), 939–946. 10.1529/biophysj.105.063271. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct5b00935_si_001.pdf (3.4MB, pdf)

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES