Coalescent genealogy samplers: windows into population history

Abstract

Coalescent genealogy samplers attempt to estimate past qualities of a population, such as its size, growth rate, patterns of gene flow or time of divergence from another population, based on samples of molecular data. Genealogy samplers are increasingly popular because of their potential to disentangle complex population histories. In the last decade they have been widely applied to systems ranging from humans to viruses. Findings include detection of unexpected reproductive inequality in fish, new estimates of historical whale abundance, exoneration of humans for the prehistoric decline of bison and inference of a selective sweep on the human Y chromosome. This review summarizes available genealogy-sampler software, including data requirements and limitations on the use of each program.

Introduction

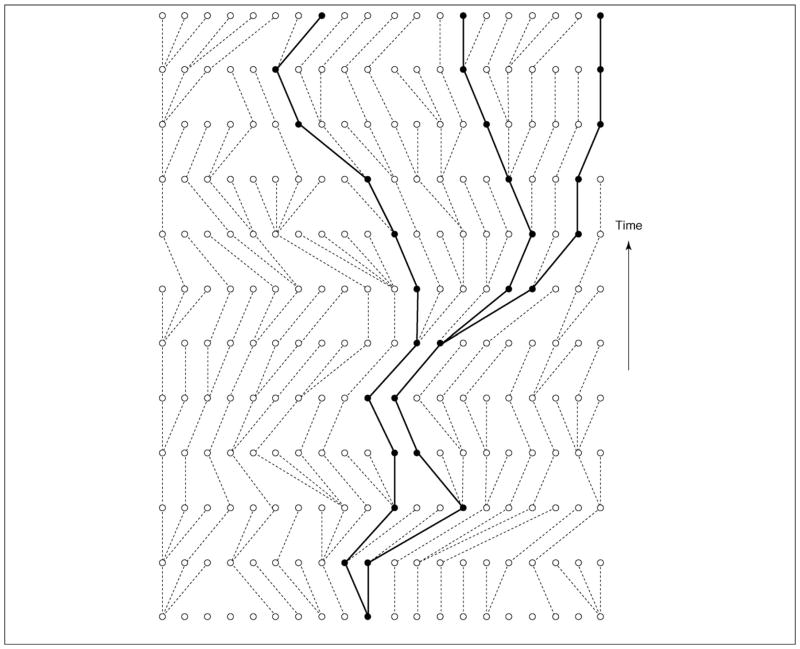
The larger a population is, the more distantly, on average, its members are related to one another. Coalescent theory quantifies this intuitive idea by relating the patterns of common ancestry within a sample to the size and structure of the overall population. Figure 1 shows a population of 20 gene copies, 3 of which have been sampled, and the points of common ancestry (called coalescences) among those samples. The distribution of common-ancestry times was originally called the n-coalescent [1,2], now usually shortened to coalescent. Today it is widely used to study historical size and other attributes of populations for which molecular sequence data are available.

Figure 1.

Coalescent embedded in population. A population of 20 gene copies showing the coalescent genealogy of 3 sampled copies. The expected time to go from k copies to k – 1 copies is exponentially distributed with a mean of Θ/[k(k – 1)], where Θ is the product of effective population size and mutation rate.

It is generally impossible to consider all possible ancestral relationships among sampled sequences. Instead, researchers have developed approaches that explore many relatively probable ancestral patterns, or genealogies. These methods can be collectively termed coalescent genealogy samplers, and have been implemented in a variety of software packages. These packages differ in how they explore genealogies, and in the population attributes and biological systems they can model.

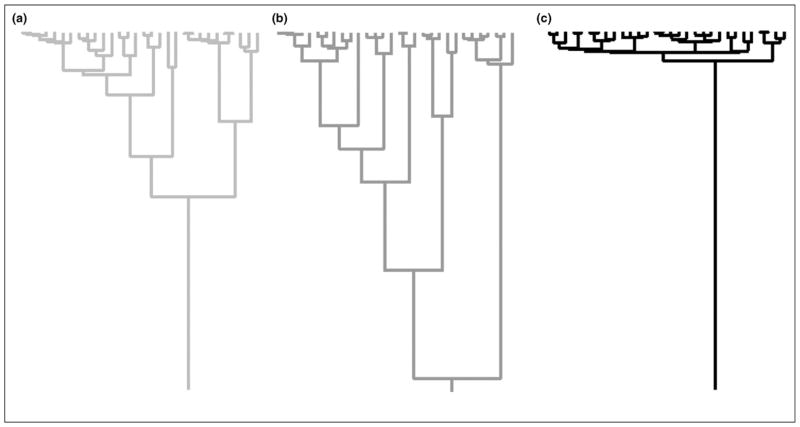
The original formulation of the coalescent could only be applied to a single, constant-size population. Researchers have since extended the coalescent to account for factors including population growth [3], population subdivision [4], genetic recombination [5] and natural selection [6]. It has also been used to infer approximate dates of mutations [7] and population divergences [8]. Figure 2 contrasts genealogies from constant-size, shrinking and growing populations, showing how the relative timing of coalescences varies with growth rate.

Figure 2.

Growth signature in genealogies. Genealogies sampled from (a) constant-size, (b) exponentially shrinking and (c) exponentially growing populations.

Coalescent genealogy samplers have been used to study diverse populations of organisms, including HIV-1 isolates from a clinical outbreak [9], rabbits in a European hybrid zone [10], Beringian bison in the Pleistocene and Holocene epochs [11] and Japanese conifers [12]. When used properly, these samplers are powerful tools for gaining insight into population histories. In this review, I will discuss the advantages of genealogy samplers over competing approaches; describe suitable data for a sampler-based study; compare the features and limitations of a variety of available samplers; and describe approaches to validating data-sampler analysis.

Why use genealogy samplers?

For many real biological systems, coalescent genealogy samplers provide more realistic estimates of historical size, expansion rate and other population parameters than summary statistics such as F_ST can. Summary statistics, although generally easier to compute and understand, are vulnerable to the presence of multiple evolutionary forces. For example, variable diversity among loci impairs the ability of F_ST to detect gene flow [13], and the presence of recombination compromises the use of Tajima’s D to detect natural selection [14]. If the researcher attempts to accommodate these complications within summary statistics, statistical power can suffer, as was seen in an attempt to infer population divergence using F_ST [15].

An alternative is to estimate the genealogy underlying a population sample and use this as the basis for parameter estimation [16–18]. However, except in a few cases of artificially manipulated populations, this genealogy cannot be known with certainty. Inferring population parameters from a single genealogy estimate, as with summary statistics, can suffer from bias and fail to provide realistic confidence intervals around estimates, especially when recombination is present [19].

By contrast, all of the genealogy samplers discussed in this review rely on making a large collection of possible genealogies and deriving parameter estimates from the collection as a whole, not from any single genealogy. Use of genealogies promises increased statistical power and robustness in complex situations; use of multiple genealogies allows accurate assessment of the potential error of the estimates. This is similar to the rationale behind Bayesian phylogenetic methods such as MRBAYES [20]. The population-genetic programs discussed here [21–28] share history, evolutionary models and, in some cases, computer code with well-developed phylogenetic methods and software which came before them.

Data requirements for genealogy samplers

All existing genealogy samplers rely on random samples from the population or populations of interest, except that the number of samples from each subpopulation can be chosen arbitrarily as it is not part of the coalescent model. Selecting particularly interesting or relevant individuals introduces a severe bias: removing all identical individuals from a sample will generally result in a huge inferred population size and confidence intervals excluding the truth. Thus, data such as a collection of type specimens for the HIV-1 serotypes will not give valid results in any current genealogy sampler.

High-quality molecular data are required: genotyping errors or incorrect sequence alignments can significantly affect parameter estimation. Table 1 shows the types of data accepted by current samplers.

Table 1.

Commonly used coalescent genealogy samplers

Program	Version reviewed	Algorithm	Data supported	Combine loci with different copy number?	Previous programs superseded
BEAST [21]	1.4.7	CS (Bayesian)	Nucleotide, amino acid, codon, two-allele	No
GENETREE [22]	9.0	IS	Nucleotide	No	ptreesim, timesim
IM, IMa [23–25]	Version of 3/2/2008	CS (Bayesian)	Nucleotide, microsatellite	Yes	MDIV
LAMARC [26]	2.1.2b	CS (Bayesian or likelihood)	Nucleotide, SNP, microsatellite, K-allele	Yes	COALESCE, FLUCTUATE, RECOMBINE
MIGRATE-N [27,28]	2.4	CS (Bayesian or likelihood)	Nucleotide, SNP, microsatellite, K-allele	Yes	MIGRATE

Abbreviations: CS, correlated sampling; IS, independent sampling.

When designing studies, researchers must choose how much effort to put into collecting more individuals, genotyping more loci or sequencing longer stretches of DNA. For the study of a single population, in the absence of recombination, the statistical power of genealogy sampling is optimized by sampling a modest number of haplotypes (as few as 8) at as many unlinked loci as possible [29]. Sequences can be fairly short, although they should be long enough to contain multiple polymorphic sites. Data requirements for multiple-population cases have not been determined, but the general principle of preferring multiple loci should still hold. With recombination, however, long sequences from a single locus can substitute for multiple loci. For summary statistics, small numbers (3–10) of very long sequences are optimal for recombination rate inference [30]; this likely holds for genealogy samplers as well. Detection of recombinations is easiest when there are distinctive sequences on both sides of the breakpoint; long sequences thus allow more recombinations to be detected.

Approaches to genealogy sampling

The quality of a genealogy is determined by the probability that the given data would have evolved on that genealogy under a specified mutational model. Genealogy inference is challenging because the ‘search space’ is very large, and no efficient algorithm is known that can guarantee finding the best genealogy. Samplers are confronted with the need to find a small number of needles (high-quality genealogies) in an enormous haystack of low-quality genealogies.

Two approaches have been used to find high-quality genealogies. The first has been called IS for ‘importance sampling,’ although ‘independent sampling’ would be a more descriptive name. This approach assumes a mutational model under which no site has mutated more than once. The simplifying effect of this infinite-sites model allows genealogies which fit the data to be rapidly and independently discovered. Unfortunately, less restrictive mutational models are difficult to incorporate into an IS sampler. Thus, IS algorithms are most applicable to low-polymorphism data such as human nuclear single-nucleotide polymorphisms (SNP).

The second approach begins with an arbitrary genealogy and makes small modifications, attempting to find high-quality genealogies ‘nearby.’ As a result, successive genealogies are correlated. This is a Markov chain Monte Carlo (MCMC) algorithm, and these methods have therefore been referred to as MCMC methods. However, IS also uses MCMC (in a substantially different way), so a clearer term is CS for ‘correlated sampling.’ CS methods permit a wider variety of mutational models, but have more difficulty producing a thorough sample of high-quality genealogies, because the correlated search can fail to find distant ‘islands’ of good genealogies. They are well suited to highly polymorphic data such as viral DNA sequences or human microsatellites.

Within the CS methods there is a further distinction between likelihood-based and Bayesian approaches. In a likelihood-based approach, genealogy sampling is guided by the fit of the genealogy to the data, and by assumed values, called ‘driving values,’ of the parameters to be estimated. A collection of genealogies is accumulated, and these are used to construct a likelihood surface, whose peak will generate new driving values. This process is repeated until the driving values stabilize. Sampling is most effective when the driving values are similar to the true underlying values, so only the final collection of genealogies, which presumably had the best driving values, is used to construct the final likelihood surface and maximum-likelihood estimate. Confidence intervals around the estimate are constructed based on the expected shape of the likelihood surface. These confidence intervals are somewhat controversial, as they involve assumptions about the shape of the likelihood surface which are fully correct only for implausibly large data sets.

In a Bayesian approach, the driving values are continually changed by sampling potential new driving values from a prior distribution and evaluating how well they fit the current genealogy. Rather than basing the final estimate on collected genealogies, a Bayesian sampler tabulates the driving values which it has visited and constructs a smoothed histogram representing the posterior distribution. The maximum of this distribution is the most probable estimate, and the area under the curve is used to construct support intervals. Bayesian estimation is also controversial, because it depends on a prior distribution which must often be chosen arbitrarily.

Two studies have compared likelihood and Bayesian analysis of the same data by the same sampler. In data-rich situations, the methods performed equally well [31]; with sparse data, Bayesian sampling performed better, apparently because the prior distribution helped constrain the search [32]. Poorly chosen priors can cause Bayesian methods to fail, whereas poorly chosen driving values can impair likelihood searches. Only two software packages offer both sampling schemes; in other cases, the choice is made implicitly when the software is chosen.

Available software

Several programs are available to perform coalescent analysis. Their authors have generally avoided duplication of effort, so that each program has clear areas of applicability. Tables 1–3 show program capabilities. Below are brief comments on each program’s particular strengths, presented in alphabetical order.

Table 3.

Assumptions of genealogy samplers

Assumption	Samplers not requiring this assumption
Random sampling
No directional or balancing selection
Random mating within subpopulations
Constant mutation rate over time	BEAST
No recombination within loci; free recombination between loci	LAMARC
Stable subpopulation structure over time	IM, IMa
Same copy number for all loci	IM, IMa, LAMARC
All samples contemporaneous	BEAST
Constant population size	BEAST, IM, LAMARC
Population growth or shrinkage is exponential	BEAST
Infinite-sites mutational model	BEAST, IM, IMa, LAMARC, MIGRATE-N

BEAST

BEAST [21] estimates effective population size, mutation rate and growth patterns for a single population. It has three unique features: a flexible model of growth based on the Bayesian skyline plot, allowing for arbitrary patterns of historical population growth; a ‘relaxed clock’ mutational model which allows the mutation rate to vary among lineages; and accommodation of samples taken at multiple time points. BEAST is particularly useful when data from multiple time points (distant enough in time to allow measurable evolution between them) are available, as with viruses or ancient DNA. Multiple time points allow the mutation rate to be estimated separately from the population size, whereas other programs are only able to estimate the composite parameter Θ, the product of effective population size and mutation rate. Multiple time points also allow greatly improved precision and detail in estimation of the population growth rate. BEAST has been used to trace cougar population demographics via molecular data from a fast-evolving feline virus [33], to infer that Beringian bison had already begun to decline before humans arrived in North America [11] and to date the origin of an HIV-1 outbreak in a Libyan hospital [9].

GENETREE

GENETREE [22] estimates Θ, migration rates and exponential growth rates for multiple stable populations. Unlike the other methods discussed here, it is an IS sampler: it constructs independent genealogies rather than repeatedly modifying a starting genealogy. This requires it to assume an infinite-sites mutational model, but renders it nearly immune to problems in which the search fails to move well among genealogies. GENETREE can provide estimates of the time back to the most recent common ancestor of a population; uniquely, it also estimates dates of specific mutations. It has been used to show that the common ancestor of human Y chromosomes was unexpectedly recent, perhaps due to a selective sweep [34].

IM and IMa

IM and IMa [23–25] consider cases in which two populations have recently diverged from a common ancestor. They estimate Θ for each population and for the common ancestor, as well as the divergence time, bidirectional migration rates among the daughter populations and (in IM only) growth rates for the daughters. They are particularly well suited for analysis of young populations and for distinguishing gene flow from retention of ancestral polymorphism. IMa, the more recent program, uses an improved search algorithm, offers likelihood ratio tests to decide among different demographic models and provides more information about the joint distribution of parameters than IM; however, it does not yet duplicate all of the features of IM. IM has been used to show that loci near the centromere show reduced gene flow compared to telomeric loci in a rabbit hybrid zone [10].

LAMARC

LAMARC [26] considers cases in which multiple populations have had stable population sizes and migration rates for a long time, and allows each population to have a separate rate of exponential growth or shrinkage. There is no theoretical limit on the number of populations, but in practice, cases with more than three or four populations take large amounts of computer time and demand extensive data for success. LAMARC allows genetic recombination within sequences and estimates an overall recombination rate. This allows use of long sequences from recombining areas of the genome, both for estimation of recombination rate and for nonconfounded estimation of other parameters. LAMARC can also perform fine-scale linkage disequilibrium mapping, relating phenotypic data to genetic variation. LAMARC has been used to show that the long-term effective population size of gray whales was substantially larger than estimated from historical whaling records, based on a mixed sample of nuclear and mitochondrial loci [35].

MIGRATE-N

MIGRATE-N [27,28] considers multiple populations using a stable-population model similar to that in LAMARC. It estimates Θ for each population and migration rates in each direction between each pair of populations. As with LAMARC, there is no set limit on the number of populations. MIGRATE-N offers detailed tests based on likelihood ratios and the Akaike information criterion (AIC) for deciding among models, such as a model of symmetrical versus unconstrained migration rates. It can also be run in parallel on multiple computers for faster analysis. MIGRATE-N has been used to show that the effective population size of red drum, a long-lived ocean fish, is three orders of magnitude smaller than its census size, suggesting highly unequal reproductive success [36].

These programs do not yet cover the full range of situations encountered by biologists. In particular, combinations such as multiple-time point sampling with recombination or population subdivision, or population divergence with recombination, are not yet possible, and none of the programs can estimate the strength of natural selection.

Frustratingly, some methods mentioned in the literature are rendered nearly unusable by lack of publicly available software, for example certain coalescent-based estimators of natural selection [6], population subdivision with multiple-time point data [37] and migration using isolation by distance (described in Ref. [38]).

Guidance and caveats on the use of genealogy samplers

Each genealogy-sampler program uses specific population models, and the biologist must carefully consider the assumptions of each model when deciding which, if any, program is appropriate. For example, LAMARC and MIGRATE-N assume the dynamics of each population have been stable for ~4N generations; when recent population divergence is likely, IM or IMa are more appropriate. Table 3 summarizes major assumptions of the programs. If these assumptions are violated, the results can be misleading. Before using any genealogy sampler, the researcher should carefully examine its documentation to understand the models it uses.

The complexity of the chosen population model considered must be weighed against the amount of data available. Attempts to estimate the 20 possible pairwise migration rates among five populations using data from a single locus will probably fail. Restricting the hypothesis–perhaps by assuming that migration is symmetrical or that certain migration routes need not be considered – will improve statistical power, but if those assumptions are incorrect, the results of the analysis will be as well. Pre-analysis of the data can help prevent the use of inappropriate population models. For example, STRUCTURE [39] can be used to determine whether there is sufficient evidence for geographic structuring to support a sampler-based subpopulation analysis. MODELTEST [40] can be used to determine the most appropriate mutation model.

Use of alternative methods can strengthen the results of a coalescent analysis. For example, a study [36] concluded that the effective population size of an ocean fish is orders of magnitude less than its census size by pairing a MIGRATE-N analysis, measuring long-term N_e, with a short-term analysis based upon allele frequency fluctuation over several years of sampling. The agreement between these unrelated methods greatly strengthened the conclusions. By contrast, agreement between multiple genealogy samplers does not strongly corroborate their results, because the underlying approaches and assumptions of the samplers are too similar.

Genealogy-sampling algorithms, when used properly, vary from slow to excruciatingly slow. It is wise to budget several months for the statistical analysis phase of a study after data collection is complete. Rushed analysis will lead to weak results. A small pilot analysis can allow the researcher to find suitable run conditions for a complete analysis without using excessive computer time. Such a pilot typically examines a single locus and a small subset of samples (8–10 randomly chosen haplotypes). A short run will then give valuable hints about how well the program performs and how long a full analysis will take.

How should sampler results be validated?

All of the genealogy samplers described in this review rely on collecting large samples of genealogies which collectively represent the genealogical information present in the data. All, therefore, are vulnerable to too-short runs or poor choices of run conditions. These can lead to too-small or unrepresentative samples of genealogies, which in turn can lead to actively misleading results and especially to overly narrow inferred confidence intervals. To get reliable results, the program user must be prepared to learn about the options and functionality of the program, and must make multiple runs to fine-tune the options.

Four basic approaches to validation are known. For all samplers, repeating the run with a different random number seed will reveal whether the results are stable. It is important to note that for some data sets, the point estimates of parameters such as growth rate can vary substantially from run to run simply because there is little information present. However, such results should be accompanied by wide, overlapping confidence intervals among the multiple runs. If the confidence intervals for multiple runs exclude one another, the runs are too short. This approach can be extended by varying the starting parameter values and starting genealogy (where possible). Small variations in the prior of a Bayesian analysis can also be tested to see whether they lead to large differences in the result; a well-behaved Bayesian run should not be highly sensitive to small variations in its prior.

For Bayesian CS samplers in particular, two useful validation capabilities are provided by the TRACER program [41], which can be used in conjunction with BEAST, LAMARC and MIGRATE-N. IM and IMa provide TRACER-like capabilities internally.

TRACER calculates the effective sample size (ESS) statistic, which gives a thumbnail diagnosis of too-short runs by revealing how much independent information is present in the sampled parameter values. High ESS values unfortunately do not prove that a program run was adequately long, but values below 200 are clear evidence that it was too short.

TRACER can also plot the changes in parameter values during the length of a run. Visual inspection of these ‘traces’ can provide important clues about run adequacy. After an initial burn-in period, traces should vary stochastically around a stable value. Long-range trends, wild oscillation or values which do not move from their starting points are clear indications of a too-short or otherwise flawed analysis.

A final approach to validation is to assess whether the whole genealogy structure has been thoroughly reconsidered, or whether there are groups of samples whose relationships have remained stuck in their initial configuration. For cases without recombination, this can be done by the AWTY program [42]. BEAST, LAMARC and MIGRATE-N produce output suitable for AWTY. Unfortunately, no equivalent tool exists for genealogies with recombination.

When a sampler run shows signs of inadequacy, it can be run longer. Alternatively, a technique called Metropolis-coupled Markov chain Monte Carlo, informally referred to as ‘heating,’ will often improve the search performance of CS genealogy samplers. It is offered by all of the CS samplers described here, and should be tried whenever multiple runs produce contradictory results, or ESS values or TRACER graphs are persistently unsatisfactory. Heating can be thought of as sending ‘scouts’ to explore distant regions of the space of possible genealogies. A search with three scouts will triple the run time, but is usually more effective than simply running the program three times as long. Heating is not applicable to IS samplers, as they are not limited to searching in the vicinity of their current genealogy. A poorly performing IS sampler should simply be run longer.

Persistent failure of a sampler to give stable results should trigger reconsideration of the study design. Are the data really suitable for this type of analysis? Are the assumptions of the program met? Is the amount of data adequate for the complexity of the model in use?

In addition to giving usage instructions, the documentation for each program generally provides guidance on how to interpret the results of the program. Internet discussion groups can be another source of useful information. Program authors and maintainers usually welcome questions about their software, and are the ultimate direct source for guidance on its use.

Conclusions

Correctly used, genealogy samplers can provide powerful and detailed insights into population history. They can help disentangle multiple evolutionary forces acting on a population, including gene flow, population growth and population divergence. Importantly, they also offer information about the degree of statistical support for their inferences.

However, genealogy samplers cannot be treated as ‘black boxes.’ A researcher planning a genealogy-sampler analysis will need a good understanding of the software and its underlying model, and also a good understanding of the study organism and its life history. Knowledge of the software is essential in choosing appropriate data, monitoring adequacy of the runs and interpreting the results. Knowledge of the biological system is essential in choosing an appropriate population model and understanding how differences between the real population and its simplified representation can affect the results of the analysis. For example, knowing the generation time of the study organism and the geological history of its habitat can suggest whether it likely has long-term stable population structure (suitable for LAMARC or MIGRATE-N) or would better be analyzed under a recent-divergence model with IM or IMa.

Steadily improving technology is allowing biologists to collect and compare more data from more complex systems than ever before. Computing resources, likewise, continue to improve in speed and availability. As coalescent genealogy samplers become easier and faster to use, the research community at large will increasingly expect these tools to be used to supplement or supersede summary-statistic calculations. These developments are spurring program authors to refine and extend their programs. As experimental biological questions continue to gain in complexity and sophistication, so too, by necessity, will the computational tools to answer them.

Table 2.

Estimation capabilities of genealogy samplers

Inference capability	BEAST	GENETREE	IM, IMa	LAMARC	MIGRATE-N
Θ (population size × mutation rate)	Yes	Yes	Yes	Yes	Yes
Migration rates		Yes	Yes	Yes	Yes
Population divergence times			Yes
Multiple sampling times	Yes
Recombination rate				Yes
Growth rate	General	Exponential	Exponential (IM only)	Exponential
Dates of common ancestors	Yes	Yes
Mutation rates	Yes
Dates of specific mutations		Yes

Glossary

AIC

Akaike information criterion, a heuristic used to determine whether the improvement in fit of a more complex model justifies the additional parameters it introduces.

Bayesian skyline plot

a graph showing the curve of inferred population size over time (and its support intervals) based on multiple sampled genealogies.

Coalescence

two lineages tracing back to a common ancestral haplotype at a particular time.

Coalescent theory

mathematics governing the expected distribution of times back to a common ancestor in a population sample.

Driving values

assumed values of the parameters to be estimated (such as Θ or migration rate) which are used to guide a likelihood-based search. Driving values too far from the unknown true values of the parameters will lead to biased estimates.

Effective population size

the size of an idealized (Wright-Fisher) population with the same rate of genetic drift as the given population. Effective population size is usually smaller than census size as a result of factors such as unequal reproductive success.

ESS

effective sample size. When data points (such as sampled genealogies) are autocorrelated, their information content is reduced. ESS estimates the size of a fully independent data set having the same information content as the given autocorrelated data. An ESS of 200 or more is recommended for genealogy sampling.

F_ST

summary statistic based on comparison of within-group and between-group genetic diversity, used to estimate population sizes and migration rates.

Genealogy

the ancestral relationship, for a particular segment of the genome, among sampled chromosomes. This takes the form of a branching tree for non-recombining data, but becomes a tangled graph (the “ancestral recombination graph”) with recombination.

Infinite-sites model

a mutational model in which no site mutates more than once in the history of the sample, thus suitable only for data in which mutations are rare.

K-allele model

a mutational model in which there are κ distinct alleles with equal chance of mutation from any allele to any other.

Migration

as used in this paper, gene flow between subpopulations.

N_e

effective population size, the size of an idealized theoretical population with the same amount of genetic drift as the given real population. In most organisms, effective size is less than census size because of factors such as overlapping generations, reproductive inequality and sex bias.

Tajima’s D

a summary statistic which detects forces such as natural selection by their effects on two different estimators of the population size.

Theta (Θ)

4N_eμ in diploids or 2N_eμ in haploids, the product of the effective population size N_e and mutation rate μ. This parameter measures the capacity of a population to maintain genetic variability. Among organisms of similar mutation rate, it functions as a measure of relative effective population size. Care should be taken when reporting or interpreting Θ because some studies use units of mutations per site, and others of mutation per locus.