SUMMARY
Most rotamer libraries are generated from subsets of the PDB and do not fully represent the conformational scope of protein side chains. Previous attempts to rectify this sparse coverage of conformational space have involved application of weighting and smoothing functions. We resolve these limitations by using physics-based molecular dynamics simulations to determine more accurate frequencies of rotameric states. This work forms part of our Dynameomics initiative and uses a set of 807 proteins selected to represent 97% of known autonomous protein folds, thereby eliminating the bias toward common topologies found within the PDB. Our Dynameomics derived rotamer libraries encompass 4.8 × 109 rotamers, sampled from at least 51,000 occurrences of each of 93,642 residues. Here, we provide a backbone-dependent rotamer library, based on secondary structure ϕ/ψ regions, and an update to our 2011 backbone-independent library that addresses the doubling of our dataset since its original publication.
Graphical abstract
INTRODUCTION
Detailed characterization of protein backbone and side-chain conformations, and the relationship between them, is necessary for improving the refinement and validation of experimentally derived structures, homology modeling, design, and prediction. The orientations and sampling of side-chain dihedral angles is not random, and propensities for certain angles have been known for some time (Bahar and Jernigan, 1996; Chandrasekaran and Ramachandran, 1970). Side-chain propensities are often referred to in terms of rotational isomers, or rotamers, defined as a combination of dihedral angles that describe a given side-chain conformation. Statistical analysis of protein structures can reveal the frequency with which individual rotamers are sampled to create libraries for selecting appropriate sidechain conformations (Ponder and Richards, 1987). As the population of some rotameric states appears to be highly correlated with protein backbone conformations (Hagarman et al., 2011; Otzen and Fersht, 1995), accurate backbone-dependent rotamer libraries are important to improve structure prediction, refinement, and design.
There are a number of rotamer libraries available, which contain rotamer probabilities computed for each residue type independent of the backbone conformation (Dunbrack and Cohen, 1997; Dunbrack and Karplus, 1993; Janin et al., 1978; Lovell et al., 2000; Scouras and Daggett, 2011), dependent on the secondary structure within which a residue is found (Janin et al., 1978; Lovell et al., 2000; McGregor et al., 1987; Schrauber et al., 1993), or with a finer detailed dependence on the local backbone (ϕ/ψ) conformation of a residue (Dunbrack and Cohen, 1997; Dunbrack and Karplus, 1993; Shapovalov and Dunbrack, 2011). There are also more specialized rotamer libraries to construct models for large-scale coarse-grained simulations (Larriva and Rey, 2014). The most popular backbone-dependent library available is from the Dunbrack Lab, which has continually improved the coverage and quality of the library over the last two decades (Dunbrack and Cohen, 1997; Dunbrack and Karplus, 1994; Shapovalov and Dunbrack, 2011). The Dunbrack rotamer library was generated by analyzing a filtered, high-quality set of crystal structures from the Protein Data Bank (PDB) (Berman et al., 2000). Indeed, all the major libraries rely on such statistical analysis of the PDB to derive rotamer probabilities (Larriva and Rey, 2014; Lovell et al., 2000; Shapovalov and Dunbrack, 2011; Xiang and Honig, 2001), yet rotamer libraries generated from the PDB have their limitations (Berman et al., 2013; Davis et al., 2007; Montelione et al., 2013).
Although the PDB is the largest repository of experimental structures, there can be extremely low or non-existent sampling of rotamers for some regions of ϕ/ψ space. A large percentage of the PDB consists of crystal structures, which depict a single structure averaged across an ensemble of crystallized protein instances (Wagner et al., 1992). Where there is mobility, B factors offer some indication of the extent of motion; however, many rotamer libraries implement a B-factor cutoff to remove residues whose positions are uncertain due to this mobility (Lovell et al., 2000). The use of such measures to obtain high-quality structural datasets from the PDB often means that dynamic rotamer conformations are expressly excluded and the full range of side-chain conformations underestimated. Furthermore, due to difficulties in crystallization of, or gaining nuclear magnetic resonance (NMR) observables from, highly flexible regions, structural data for some conformations may be unattainable.
The PDB is also not without error, nor experimental artifacts. The side-chain conformations of crystal structures can be sensitive to the crystal environment (Jacobson et al., 2002). Possible artifacts from experimental procedures include crystal contacts, inducement of ordered structure (Dobrianov et al., 1999; Kobe et al., 2008), or a general misrepresentation of the native environment due to the cryo temperatures now commonly used (Fraser et al., 2011). Often there can be incomplete or absent side-chain detail depending on the extent of structural validation prior to deposition (Chang et al., 2006; Gore et al., 2012). Even when side-chain information is present, there can be ambiguities in the electron densities (Chen et al., 2009; Lovell et al., 2000; Shapovalov and Dunbrack, 2011). Chirality and cis peptide bond errors, which affect side-chain placement and the accuracy of backbone and side-chain correlations, have also been identified within the PDB (Schreiner et al., 2011). Overall, these factors can introduce errors, much of which is incorporated directly into many of the existing rotamer libraries. Hence, refining experimental structures with statistically derived probabilities from a set of PDB structures, unless they are carefully pruned to exclude such errors, is flawed, and such static representations are not ideal for modeling, predicting, and rationalizing protein structures in solution at ambient or physiological temperatures.
Molecular dynamics (MD) simulations provide a physics-based approach from which a more exhaustive sampling of rotameric states can be acquired. Here, we use our in-house MD package, in lucem molecular mechanics (ilmm) (Beck et al., 2000–2015), based on the force field devised by Levitt et al. (Beck and Daggett, 2004; Levitt et al., 1995, 1997). Our methods differ from protocols used with other force fields, as we employ different treatments of long-range interactions; for example, particle mesh Ewald summations are not used. We also use the microcanonical ensemble to maintain energy conservation, rather than the more common isobaric-isothermal and canonical ensembles; hence, we do not use barostats and thermostats to control the macroscopic properties for what are very microscopic systems. In addition, our methods provide natural Boltzmann sampling, negating the need for weighting or culling of conformers. We have had sustained success at capturing protein dynamics in agreement with experimental observations over the last 20 years or so (Beck and Daggett, 2004; Beck et al., 2005; Rizzuti and Daggett, 2013; Schaeffer and Daggett, 2011; Schaeffer et al., 2008; Toofanny and Daggett, 2012; Towse and Daggett, 2015), with only one minor modification to our approach (Armen et al., 2005). For example, previous assessments of our simulation quality show low mean Cα root-mean-square deviations between simulation and experimental structures with good agreement with spectroscopic observables, such as nuclear Overhauser effects (NOEs) (>90%) and chemical shifts (R > 0.9) (Beck and Daggett, 2004; Beck et al., 2008). We have also predicted dynamic behaviors and structures ahead of experimental confirmation, such as the transition and intermediate states of the engrailed homeodomain (Gianni et al., 2003; Mayor et al., 2000, 2003; Religa et al., 2005), dynamic cleft formation in cytochrome b5 (Storch and Daggett, 1995; Arnesano et al., 1998; Storch et al., 1999; Hom et al., 2000), and the effects of SNPs on methyl transferases (Rutherford et al., 2006, 2008; Rutherford and Daggett, 2010). In all these cases dynamics was critical to characterize the nonnative states (the engrailed homeodomain), dynamically regulated protein-protein interactions (cytochrome b5), and subtle structural and dynamic effects linked to phenotype (methyl transferases). These are just a few examples, and each study led to unique predictions, which could not have been made with static native structures, and each was validated by experiments after the fact. Here, we draw upon our methods to introduce new dynamic rotamer libraries derived from dynamic proteins in solution.
We reduce the possibility of structural bias by beginning with a set of 807 protein structures, which represent 97% of all known autonomous protein folds, from our Consensus Domain Dictionary (CDD) (Day et al., 2003; Schaeffer and Daggett, 2011; Schaeffer et al., 2011). Extensive atomistic MD simulations of these 807 protein structures, our Dynameomics project, allow us to capture a more realistic dynamic range of side-chain conformations in solution (van der Kamp et al., 2010). Rotamer probabilities for the backbone-dependent (BBDEP) library were determined using 10° × 10° ϕ/ψ bins with a second set of probabilities determined for local backbone conformations in defined secondary structure ϕ/ψ regions, the regional secondary structure (RSS) rotamer library. Since the raw Dynameomics data have nearly doubled in size since the previous publication of our original backbone-independent (BBIND) dynamic rotamer library (Scouras and Daggett, 2011), we also provide an update of that library for comparison with our new fine- and coarse-grained backbone-dependent BBDEP and RSS libraries. All three libraries are available upon request through http://www.dynameomics.org. We provide an analysis of our data-driven approach to generating a backbone-dependent library, and discuss the preference of some rotamers for different secondary structures and the dominance of rare rotamers in narrow areas of ϕ/ψ space often coincident with high-energy ϕ/ψ conformations.
RESULTS
Generation and Experimental Validation of Backbone-Independent and Backbone-Dependent Rotamer Libraries
MD simulations of 807 representative target structures from our most current CDD were used to analyze the side-chain conformational sampling (Schaeffer et al., 2011; van der Kamp et al., 2010). The veracity of the rotamer probabilities obtained was established through comparison of calculated spectroscopic observables, reporters of the structure and dynamics captured by the MD simulations, with experiment. NMR S2 and S2-axis order parameters are experimental probes of backbone and side-chain dynamics, respectively. The reproduction of experimental S2 order parameters by the 807 simulations suggests that rotameric behaviors are faithfully captured (Figure 1A). Correspondence with experimental trends furthered the determination of relationships between rotamer occupancy and the S2 axis for different rotamers, as illustrated for Val Cγ methyl groups in Figure 1B (Scouras and Daggett, 2011).
Figure 1. NMR Order Parameters Reproduction.
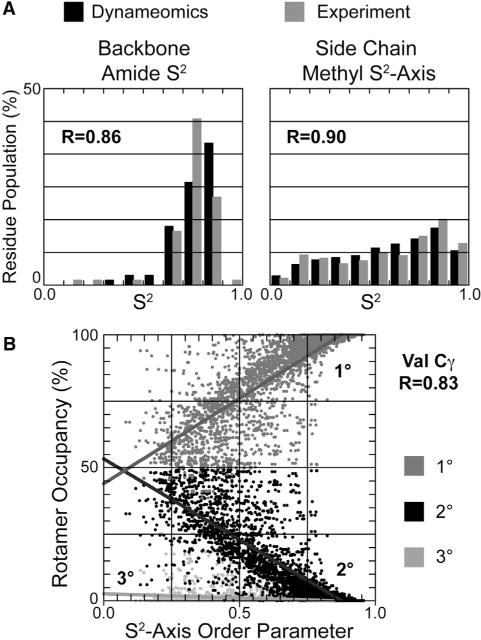
(A) Histogram of order parameters comparing experiment and calculated values from Dynameomics simulations. Correlation coefficients between experiment and simulation are inset.
(B) Example of the relationship between rotamer occupancy and order parameter for the primary, secondary, and tertiary rotamers of Val Cγ methyl groups.
A detailed example of the quantitative agreement obtained between experiment and our simulations is provided in Figures 2A and 2B. There are 2,727 NOEs available in the Biological Magnetic Resonance Bank (BMRB) (Seavey et al., 1991) for ubiquitin. When using a 5-Å cutoff, 94.4% of the NOEs are satisfied by the crystal structure of ubiquitin (PDB: 1UBQ). However, a greater number of NOEs are satisfied (95.2%) by the MD ensemble (Figure 2A). In comparing our violated NOEs more closely with experiment, we found that 185 of the NOEs have NMR upper bounds of 6.2 Å. Using the NMR upper bound for these residues results in 98.2% of the NOEs being satisfied. There are 19 violations in the X-ray structure, not present in the MD ensemble where the distance violation is more than 2 Å. In other words, beginning from the X-ray structure the protein acquired those NOEs during MD. All are long-range NOEs critical to the core and proper alignment of secondary structure.
Figure 2. Comparison between Experiment and MD and Rotamer Prediction for Ubiquitin.
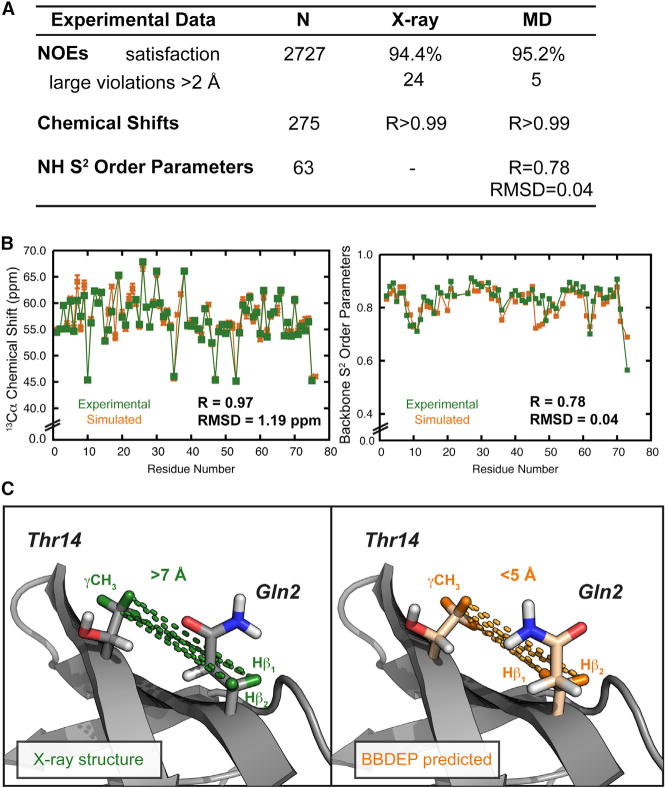
(A) Summary of experimental datasets and simulation; note that 5-Å NOE cutoff was used. RMSD, root-mean-square deviation.
(B) Experimental and simulated 13Cα chemical shifts and amide S2 order parameters. RMSD, root-mean-square deviation.
(C) Positions of the Gln2 and Thr14 side chains in the X-ray structure that fail to satisfy the NOE-derived distances (highlighted in green) and the rotamer predicted from the BBDEP library with those interactions now highlighted in orange.
Interactions between Gln2 and Thr14 provide an example of NOEs acquired during MD. The highlighted distances corresponding to gross violations of the NOE-derived distances in the X-ray structure are shown in Figure 2C. The original X-ray side chains are shaded gray with the hydrogen atoms engaged in the NOE highlighted in green. The alternative side chains predicted by the BBDEP library to be the most probable rotamers using the backbone angles of the X-ray structure, with the corresponding hydrogen atoms shaded orange, satisfy the NOEs and have χ1 angles closer to that in the MD ensemble. For example, the predicted χ1 of Gln2 taken from our rotamer library based on the ϕ/ψ angles of Gln2 is 18° from the mean χ1 angle in the MD ensemble; the difference between χ1 in the X-ray and MD ensemble is 99°. The χ1 rotamer, dictating the side-chain directionality, is crucial for satisfying this NOE. Thr14 is less mobile (χ1 SD ±34°) and the predicted rotamer is in the same rotameric bin as that present in the X-ray structure, yet it has a χ1 angle 20° closer to the MD ensemble mean. The replacement of these two side chains with the most probable rotamers from our BBDEP library generated from 807 proteins allowed the X-ray structure to satisfy this NOE (Figure 2C).
In addition, the MD ensemble can be compared with NMR chemical shifts and S2 order parameters (Figure 2B). A total of 275 chemical shifts are available for 13C, 15N, and 1H nuclei, and those calculated from the MD ensemble are in excellent agreement with experiment, with R = 0.999 (Figure 2A). Specific to the validity of our rotamer library is the recapitulation of the main-chain Cα (R = 0.97, Figure 2B) and the side-chain Cβ chemical shifts for ubiquitin (R = 0.99). Further quantitative examples supporting our experimental agreement for the D807 dataset used here regarding NOE, chemical shift, and order parameter agreement have been reported for ubiquitin (Beck et al., 2008), the engrailed homeodomain (again with excellent agreement with 99% of the 654 NOEs satisfied and R > 0.99 for the 535 chemical shifts) (Beck and Daggett, 2004), chymotrypsin inhibitor 2 (Li and Daggett, 1995), WW domains (Sharpe et al., 2007), and others (van der Kamp et al., 2010).
With our Dynameomics project we are making use of an established program and experimentally validated methods to capture protein dynamics over essentially all known protein folds. To calculate rotamer probabilities, we used the side-chain dynamics sampled through native-state MD; each structure was simulated for a minimum of 51 ns at 25°C and underwent pre- and post-simulation validation (van der Kamp et al., 2010). In total, our current Dynameomics dataset provided 4.8 × 109 samples (Table 1), where a sample is defined to be one instance of a side chain from a single time point. The current dataset is nearly double in sample size compared with our previous BBIND library (Scouras and Daggett, 2011); however, the variance in the probability distribution was minimal. There was an average variance of 0.12% with an SD of 0.30% for all BBIND rotamer representatives. The maximum change to any individual rotamer probability was 2.9%. Hence, the updated BBIND library presented here is consistent with our previous findings. Although there was a minimal impact on the BBIND statistics, the Dynameomics BBDEP library benefited from the increased information due to the number of discretized backbone conformations.
Table 1.
Statistics for the PDB-Based Dunbrack Backbone-Dependent Library RL2010 and the Dynameomics Backbone-Dependent Library
| RL2010 | Dynameomics | |
|---|---|---|
| Total samples | 6.3 × 105 | 4.8 × 109 |
| Average samples per residue | 2.9 × 104 | 2.4 × 108 |
| Average no. of populated bins per residue | 526 | 1,128 |
| Average samples per bin | 55 | 221,668 |
| Median samples per bin | 5 | 125 |
| Total φ/ψ coverage by structural dataset (%) | 52.9 | 97.0 |
| Percentage φ/ψ coverage, samples ≥50 | 23.6 | 90.6 |
A comparison with a set of high-quality X-ray crystal structures from the PDB (3,985 chains) used in creating the Dunbrack laboratory’s 2010 BBDEP rotamer library (RL2010) (Shapovalov and Dunbrack, 2011) confirms our sampling to be much more extensive and has a 104 larger sampling of rotameric states (Table 1 and Figure 3A). Rotamer probabilities were calculated using 10° × 10° ϕ/ψ bins; based on the total number of bins populated, our dataset covers 97% of the Ramachandran plot, 91% if only taking into account bins containing ≥50 samples. In comparison, 53% and 24% of ϕ/ψ space, respectively, is covered by the structural dataset used to generate the RL2010. A plot of the difference between these two datasets underscores the increased sampling and overwhelming size of the Dynameomics dataset used to construct our rotamer libraries (Figure 3A). There are 39 bins coincident with the white regions in Figure 3A not sampled due to steric conflicts by either dataset. Even with 5° × 5° bins there is no area populated by RL2010 that is not also populated by Dynameomics. Also, except for a single bin where both datasets have a single sample marked on the difference plot of Figure 3A, our dataset has more samples per bin. A quantitative examination of the maximum populations in different conformational regions confirms the degree to which our sampling exceeds that of the RL2010 dataset. In the αR region the maximum population in any one bin is 6.3 × 107 for Dynameomics versus 2.8 × 104 for RL2010 (Figure 3B). In the β region, Dynameomics has a maximum bin population of 8.6 × 106 whereas the RL2010 library contains 2,618 samples. Even in sparser regions the Dynameomics sampling dwarfs the RL2010 dataset. For example, in the reverse bridge region connecting the bottom of αR with the top of β (ϕ: −75° to −100°, ψ: −105° to −135°), the maximum bin population for the RL2010 dataset is only five samples versus 1.3 × 104 for our dataset (Figure 3).
Figure 3. Comparison of the ϕ/ψ Coverage for the Dynameomics and RL2010 Structural Datasets.
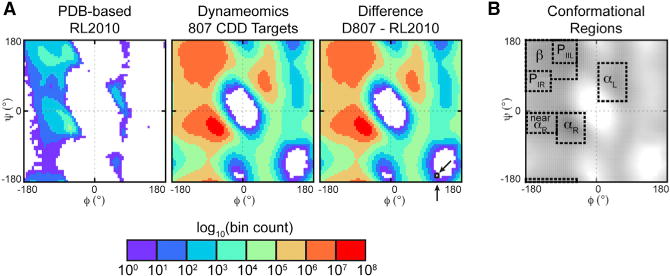
(A) Ramachandran plots for the raw structural datasets underlying the rotamer libraries and the difference between the two datasets. The unpopulated regions toward the bottom of the Dynameomics plot are only populated when including Gly and Ala, which are omitted here as they do not contribute to the rotamer library. While the difference plot appears to be the Dynameomics plot because of the much more extensive sampling in Dynameomics, there is a difference: a single bin where both datasets had only one sample, marked by arrows.
(B) Definition of secondary structure regions overlaid for the Dynameomics dataset; the ϕ/ψ limits of these regions are given in the Experimental Procedures. Dynameomics maximum populations: αR region 6.25 × 107 (bin: −62.5°, −42.5°); β region 8.62 × 106 (bin: −67.5°, 147.5°); reverse α ↔ β bridge: 1.32 × 104 (bin: −82.5°, −107.5°). RL2010 maximum populations: αR region, 2.79 × 104 (bin: −62.5°, −42.5°); β region, 2,618 (bin: −62.5°, 142.5°); reverse α ↔ β bridge: 5 (bin: −87.5°, −112.5°).
To estimate any topological bias present within our dataset, we used the proteomic Ramachandran plot (PRplot) approach (Carugo and Djinović-Carugo, 2013), whereby taking the average ϕ/ψ angles of protein structures places the different topologies across ϕ/ψ space. All-β and all-α topologies fell within the β and αR Ramachandran regions, respectively, and a histogram of the average ϕ/ψ angles for the 807 starting structures shows there is some natural bias toward all-α topologies (Figure 4). The ratio of folds taken from the all-α, all-β, and intervening mixed-α/β regions is 0.4:0.3:0.3. The PDB-based RL2010 dataset, however, showed large collections of structures in the all-β and all-α tails of the distribution, with most structures heavily concentrated in the β-region (40%) (Figure 4).
Figure 4. Topological Bias of Experimental Structures Used in Rotamer Library Creation.
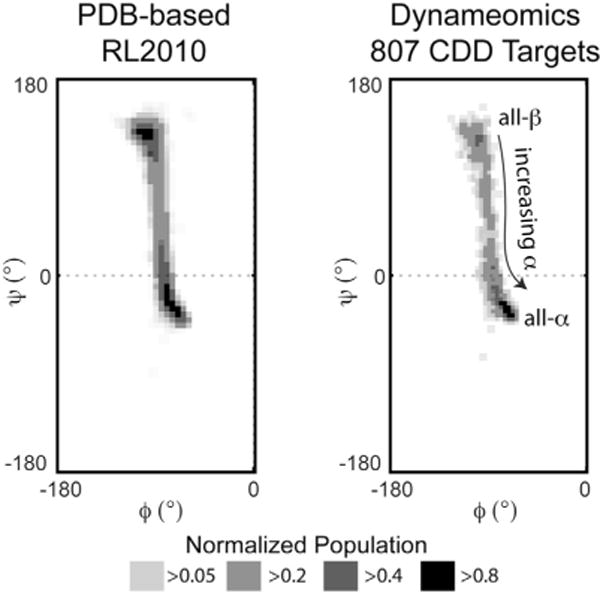
Proteomic Ramachandran plot histograms of the PDB structures used in both the RL2010 and Dynameomics rotamer libraries showing the distribution of proteins in terms of their average ϕ/ψ angles. As the coverage of ϕ/ψ space by L-amino acid-containing proteins is essentially constrained to negative values, only the left halves of the plots are shown.
Backbone-Dependent versus Independent Probabilities
The importance of taking backbone conformations into account is illustrated for Val. Independent of the backbone conformation, the most common of the three rotameric states for Val is the lower energy trans (t) rotamer, which is populated 56% of the time (Figure 5 and Table S1). Plots of dependent versus independent probabilities were used to visualize how the rotameric preferences change once backbone structure is incorporated (Figure 6). In these plots, the percentage BBDEP probabilities are given alongside the order of magnitude by which the number of instances themselves changed when compared with the BBIND library.
Figure 5. Independent Rotamer Probabilities and χ1 Dihedral Angle Distribution for Val.
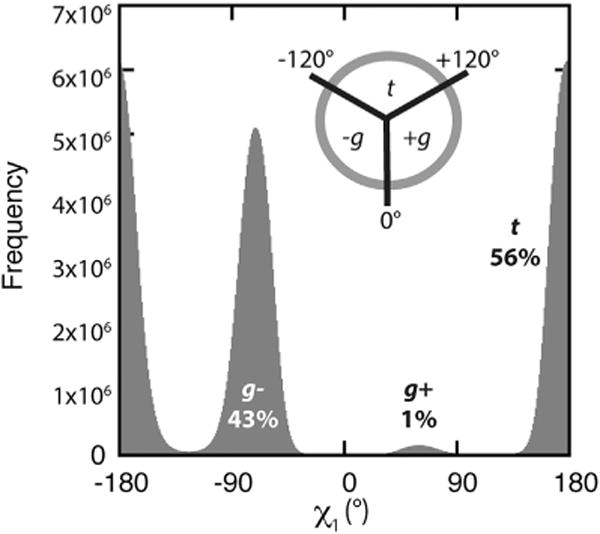
Histogram of χ1 dihedral angles for all Val residues in the Dynameomics dataset. Rotameric populations are labeled with the backbone-independent probabilities and the definition of the trans (t), gauche+ (g+), and gauche− (g−) states inset. See also Table S1.
Figure 6. Backbone-Dependent Versus Backbone-Independent Probabilities for Val.

Differences in the probabilities related to the Val ϕ/ψ distributions are given for side chains in the (A) t, (B) g−, and (C) g+ rotameric states. Well-populated regions are highlighted, and labeled and representative structures are displayed on the right. The plots range from a 0% to 100% backbone-dependent probability on a logarithmic scale, and are colored by the change in magnitude of the number of instances when compared with the backbone-independent library; e.g., pink represents a dependent probability of 0% instances of side-chain conformations. The BBDEP rotamer preferences of other residues across ϕ/ψ bins are shown in Figures S1 and S2.
When the backbone conformation is taken into account, the t rotamer is only dominant in four distinct areas around ϕ angles of [−140°, −60°] and [30°, 120°] and ψ angles of [−30°, −90°] and [90°, 120°] (Figure 6A). This is consistent with the t rotamer being the preferred side-chain conformation when the backbone is in the αR and β regions (Figure S1). The t rotamer is also extensively sampled in the lower right quadrant populated by some residues at helix termini (Figure 6A, structure A3) or those in β turns, γ turns, and inverse PIIL. In addition, this rotamer also populates an area overlapping the αL region typically sampled by residues where there has been a reverse in chain directionality, as shown for the Val residue highlighted in structure A2 in Figure 6A (Richardson, 1981). The other rotamers, lesser populated overall, have substantial populations in the ϕ/ψ areas not sampled by t, showing that these become preferred side-chain choices when the backbone is in more extended or rarer secondary structure conformations, turns, and other non-repetitive structures (Figures 6B and 6C). For example, the second most populated gauche− (g−) rotamer (43% independent probability) is occupied in more extended conformations, such as PIIL, or flexible regions and in bridge regions between energy basins (Figure 6B, areas B2 and B3; Figure S1).
Overall, the t and g− rotamers commanded 98% of the independent probability, with the third possible rotamer of Val (gauche+ [g+]) being rarely sampled (2%). Accordingly, we see that this is a consequence of the g+ rotamer being sampled over a narrower range of backbone conformations associated with the rarer observed PIR conformation and cis-proline turns (Figure 6C). Note that the color scale for Figure 6C is magnified relative to Figures 6A and 6B. Although g+ occurs in only 2% of the overall side-chain samples, it can be the predominant rotamer where the ϕ angle falls within the [−180°, −150°] and [150°, 180°] regions, at some points reaching 100% dependent probability (Figure 6C, area C1). In the proximity of ϕ = −180° and ψ = 110°, the g+ rotamer of Val is 100 times more likely to occur than the BBIND would suggest.
The preference for one rotamer over another within particular regions was not isolated to Val. Rare rotamers for other residues were also similarly dominant within a small number of ϕ/ψ locations. These regions where rare rotamers dominate coincide with higher-energy backbone conformations. The free energy landscapes constructed from the ϕ/ψ distributions showing the side-chain preferences for a given rotamer are provided in Figures S1 and S2. Note that the split rotameric bins, e.g., the g bin defined between +45° to +135° and −45° to −135° for the Phe χ2 angle (Figure 7A), are to account for indistinguishable side-chain conformations resulting from a 180° flip of the functional groups. Collective populations in these degenerate bins were used to compute the probabilities of those side-chain conformations (Table S1).
Figure 7. Rotameric Bin Definitions and Dihedral Angle Distributions.

(A) Dihedral angle ranges that define rotameric states.
(B) Polar dihedral angle distributions and rotameric bin populations from trajectories of all residues within the Dynameomics dataset. For each amino acid and side-chain dihedral angle, the polar distribution of the angle is shown surrounded by donut plots shaded by population.
See also Table S2.
Secondary Structure-Specific Differences
To assess the dependence of rotamer probabilities on the backbone conformation in a wider context, we recalculated them within defined secondary structure regions (Figure 3B) and compared the distributions against those determined for the BBIND library (Figure 5). To delineate this from the finer grained BBDEP library, where probabilities were calculated within 10° × 10° ϕ/ψ bins, we refer to this set of probabilities as the RSS rotamer library (Table S1).
The different rotamer definitions used are given in Figure 7A. As previously mentioned, Val shows distinct changes in the χ1 sampling with the t rotamer becoming more populated when Val is in αR and a population shift toward g− when the backbone is more extended (Figure 7B). Again, sampling of g+ is minimal, as this rotamer only dominates within narrow ϕ/ψ regions not coincident with regular secondary structure (Figures 6C and 7B). Comparison of Leu and Ile suggests that β branching has a strong effect on χ1, similar to that seen for the other β-branched residues, Thr and Val. However, this variation in χ1 was also seen to some extent for the smaller residues, with only one χ angle, and aromatic groups where χ1 falls between the main chain and the aromatic group. For the residues with longer side chains, e.g., Arg, secondary structure has little impact on the dihedral angle distributions. One exception is the terminal χ2 of Asn whose behavior differs even from Gln; this behavior could be due to the closer proximity of the carboxamide group to the main chain in Asn or the more frequent occurrence of this residue in helix-capping motifs (Aurora and Rose, 2013).
The changes in some of the rotamer probabilities, compared with the BBIND values, are illustrated for the β-branched residues (Figure 8). The Ramachandran plots show the distributions with the probabilities corresponding to each RSS overlaid. For simplicity, we present only the top three rotamers as ranked by their BBIND probabilities; the complete RSS and BBIND probabilities for these, and all other residues are provided in Table S1. The behavior of the residues varied from exhibiting consistent ranking of rotamers across secondary structure regions (Ser) to large departures from the backbone-independent rankings, sometimes despite modest changes in the actual probabilities (Thr). Overall, there can be striking differences in different secondary structure regions with only those for the b region consistently approaching the BBIND probabilities.
Figure 8. RSS Probabilities for Ile, Ser, and Thr Compared with the Probabilities for the Top Three BBIND Rotamers.
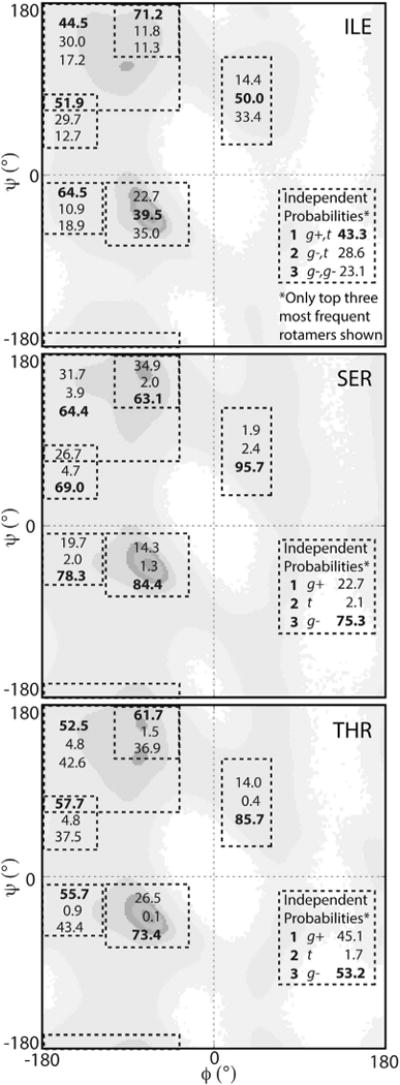
The BBIND probabilities are provided in the lower right quadrant and the RSS probabilities are inset in the same order in the appropriate secondary structural regions, as defined in Figure 4, with the most probable rotamers in bold. See also Table S1 for RSS probabilities.
In terms of which rotamer was most probable, Ser showed a consistent ordering of the top three rotamers for all secondary structure regions, matching that of the backbone-independent probability ranking (Figure 7). However, although the g− rotamer remained most probable in all secondary structure regions (Figure 8), the ratio between the probabilities shifted significantly for some regions. In particular, an increased propensity for the g− rotamer to 96% was observed for the αL region, while that of the g+ dropped to 2%, significantly lower than the backbone-independent probability of 23%. A similar consistency in the ordering of rotamers was also true of Ile, except for the decreased probabilities observed for the g+,t conformation in the αR and αL regions. In the αR region, the probability for the g+,t rotamer was 23%, nearly half that of the independent probability (43%). The difference between the probabilities was even more pronounced in the αL region, with a decrease in the g+,t probability to 14%. In both cases these decreases were offset by a substantial shift in probability toward the g−,t rotamer, which increased to 40%–50% due to a switch in preference for χ1 from g+ to g− (Figure 9).
Figure 9. Comparison of Most Probable Rotamer for all Amino Acids Taken from the BBIND and RSS Libraries.
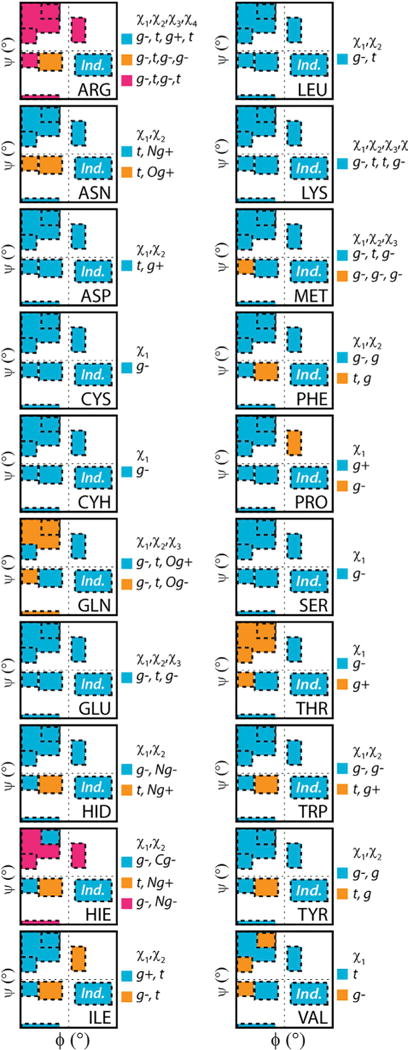
Rotamer color classifications are inset alongside the plots. Correspondence with the BBIND library is blue in each case.
Threonine, however, showed a larger departure from the independent rotamer probabilities for a number of secondary structure regions. The near αR, β, PIR, and PIIL regions all shifted toward the g+ rotameric state (Figures 8 and 9). In contrast, populations in the αL and αR regions shifted to g− (Figure 8). Unlike Ile and Ser, the most probable rotamer in the backbone-independent library was only retained in two of six regions (Figure 8). This switch between most probable rotamers is shown for other residues in Figure 9. Most residues follow Ser where, even if the probabilities themselves change, the ranking of which rotamers are most probable is retained. In rare cases, like Thr, the most probable BBIND rotamer is retained in few of the secondary structure regions (Figure 9). This behavior is most distinct for Arg; the top three rotamers, as ranked by their BBIND probabilities, are not the most probable in any of the secondary structure regions. This behavior is a consequence of the probabilities of the top rotamers in the BBIND library being sufficiently close together that the ranking of rotamers is sensitive to very small population changes.
DISCUSSION
We have presented the backbone-dependent and -independent propensities of amino acid side-chain conformations in terms of defined rotameric state populations from our Dynameomics dataset (Beck et al., 2008; Simms and Daggett, 2012; Simms et al., 2008; van der Kamp et al., 2010). Using MD simulations of 807 proteins covering essentially all known globular protein folds, we capture the dynamic range of solvated side-chain conformations at ambient temperature from which more faithful measures of both backbone-independent and -dependent probabilities could be derived. The rotameric probabilities computed in this manner complement, and in many cases rival, those determined from statistical analyses of static NMR and X-ray crystal structures. The most extensive BBDEP rotamer library to date has employed advanced statistical methods to generate a comprehensive set of probabilities using the PDB (Shapovalov and Dunbrack, 2011). However, our Dynameomics dataset possesses three main strengths that circumvent many of the limitations of PDB-based rotamer libraries.
First, our dataset has undergone extensive structural validation. Subjectivity can be difficult to eliminate from the structural determination process using experimental data (Gore et al., 2012), and retractions and fraudulent structures are not unheard of (Berman et al., 2013; Chang et al., 2006). Although there has been a recent push to improve the structural validation of both NMR and crystal structures upon deposition to the PDB (Montelione et al., 2013; Read et al., 2011), our simulation preparation and validation protocols corrected typical structural errors in the PDB and excluded erroneous structures (Davis et al., 2007). For example, a few of our originally selected targets were identified as having been poorly refined and were rejected; these structures either became rapidly distorted during our simulations or exhibited structural instability (Towse and Daggett, 2012; van der Kamp et al., 2010). These rejected targets, all NMR structures, were discarded from our dataset and replaced with equivalent higher-resolution crystal structures that did pass our validation metrics. We determined that the instability of some of the rejected structures, despite them being published with well-structured topologies in the PDB, was due to previously undetected disorder (Towse and Daggett, 2012). Moreover, as a consequence of the minimization, solvation, and equilibration routines applied to the 807 starting structures, our rotamer libraries also do not suffer the steric overlaps observed in other libraries (Lovell et al., 2000).
Second, the sample size that can be obtained from the PDB, in terms of the number of rotamer instances, is dramatically lower than that of the Dynameomics rotamer libraries (Table 1). The PDB is limited in the extent of the conformations side chains can assume, resulting in some regions being sparsely populated or lacking samples completely (Figure 3A). To generate adequate probability distributions from this sparse dataset for the RL2010 library, Bayesian statistical analysis and adaptive kernel density estimates were used to estimate rotamer probabilities (Dunbrack and Cohen, 1997; Shapovalov and Dunbrack, 2011). In contrast, our dataset is of sufficient size that, with natural Boltzmann sampling provided by the MD, we are able to obtain meaningful statistics from our raw distributions (Figure 3A).
Agreement with NMR chemical shifts, NOEs, and backbone and side-chain S2 order parameters verified our conformational sampling, and thereby the rotameric probabilities, to be a good reflection of side-chain propensities for solvated, autonomously folded protein domains at ambient temperature (Figures 1 and 2) (Beck and Daggett, 2004; Beck et al., 2008; Scouras and Daggett, 2011). One common artifact many force fields suffer from is a tendency to be overly helical. For example, a study of the polyalanine pentapeptide revealed the commonly used force fields, CHARMM27/CMAP, AMBER03, AMBER94, and AMBER99, to have helical content spanning 58%–98%, far in excess of the experimental estimate of ~20% (Best et al., 2008; Firestine et al., 2008; Jiang et al., 2013). We recently examined this behavior for our own force field using the same peptide system and confirmed our helical content to be 19%, in line with experiments (Towse et al., 2015). We have also shown that by incorporating dynamics we pick up features not well captured in the PDB, such as the differential behaviors of mobile surface residues whereby we observed flexible residues to have larger increases in the number of rotamers occupied at surfaces (+0.85 rotamers on average) than other residues (+0.10) (Scouras and Daggett, 2011). Hence, we conclude that the increased sampling achieved through the use of MD captures a realistic range of conformations.
Finally, the construction of a CDD enabled collation of a non-redundant but representative structural dataset (Day et al., 2003; Schaeffer et al., 2011). Our dataset contains 807 target structures selected to represent different fold families covering 97% of all known globular protein folds. As reported by the PDB, based on the SCOP v1.75 definitions there have been no unique protein folds deposited since 2008 (http://www.rcsb.org/pdb/statistics/contentGrowthChart.do?content=fold-scop). SCOPe has reported 11 new folds since SCOP v1.75 (2009), which are primarily membrane and large multi-domain proteins (Berman et al., 2000; Fox et al., 2014). CASP also reports the increasing difficulty to find “true new folds” for targets in their free modeling category, those available being often large and/or irregular, non-autonomous folds (Kryshtafovych et al., 2014). For globular proteins, this was anticipated (Levitt, 2007). Although new dynamic domain families are possible for disordered proteins, there is as yet no agreed categorization in place. Hence, our CDD still provides a viable consensus view of the currently classified protein fold space for globular and soluble proteins.
Due to our metafold-based selection procedure, any bias toward the more commonly found or studied topologies is minimized so that our dataset is not structurally skewed to any great degree, but we are of course biased by what is present in the PDB and downstream domain libraries, as well as our choice to focus on globular proteins. In any case, rotamer libraries that rely on statistical analyses of the PDB to derive rotamer probabilities (Larriva and Rey, 2014; Lovell et al., 2000; Shapovalov and Dunbrack, 2011; Xiang and Honig, 2001) use filtered structural subsets that are often culled further to remove sequence redundancy. This approach overlooks the occurrence of sequences with low sequence identity that still have a high degree of structural homology (Brenner et al., 1997) and potentially removes homologous protein sequences that have very different folds (Alexander et al., 2005). Hence, the probabilities for a given residue may be biased by the secondary and tertiary structural environment wherein that residue is most frequently found in the PDB rather than its true probability across protein fold space.
Our dataset mimics “true” protein fold space with the natural inclination toward mixed-α/β and mostly-a folds confirmed by other structural classification schemes (Figure 4) (Andreeva et al., 2008; Sillitoe et al., 2015), thus minimizing topological bias compared with other current libraries. In principle, our probabilities more faithfully reflect the natural structural propensities of amino acids and their side-chain conformations. Given the slow rate at which novel folds are being discovered (Levitt, 2007), neither this natural bias, nor our coverage, is likely to change for some time.
Despite the differences in the ways our library has been constructed compared with others, we agree with earlier backbone-dependent preferences for many rotameric states (Dunbrack and Cohen, 1997; Shapovalov and Dunbrack, 2011), particularly in the hydrophobic cores. For example, we observe similar side-chain behaviors for residues with similar chemistry or geometry such as the β-branched and aromatic groups. However, in determining the rotamer probabilities and their correlation to backbone propensities (Figure 6), we have identified aspects of side-chain dynamics not captured by X-ray structures. Our comparison of the differences in the BBDEP and BBIND probabilities of Val serves as an example of the importance of incorporating dynamics for proper selection of rotamers. Owing to the greater sampling of both rotamers and backbone conformations afforded by MD (Table 1), 90,034 side-chain samples were populated for the rare Val g+ conformation. Similar observations were made for the rare rotamers of other residues. This highlights just how important the minor rotamer states become for residues in certain conformations. Of note, this change in probability distribution for Val is not observed in the RL2010 library (Shapovalov and Dunbrack, 2011).
Another discrepancy raised by Shapovalov and Dunbrack (2011) as a critique of BASILISK (Harder et al., 2010) was the ranking of the Ser rotamers; the authors stated that the Ser g− rotamer was not the most probable. However, in agreement with Harder et al., we find that the g− rotamer of Ser is dominant (75%, BBIND) (Table S1; Figures 7, 8, and 9). Similarly, we find the most probable χ1 rotamer for Asp and Asn to be t and not the g− rotamer reported in RL2010. The underlying distributions in the static dataset compared with those obtained from MD, as illustrated in our previous publication (Scouras and Daggett, 2011), explains these disparities. The dynamic, solvated systems provide a more comprehensive sampling and characterization of mobile side chains on the surface of proteins.
Some of the discrepancies are also a consequence of the RL2010 library using conditional probabilities assuming that the χ2 rotamers are independent of ϕ/ψ, except for Asn and Asp (Dunbrack and Cohen, 1997). While it is known that χ1 can have a strong dependence on ϕ/ψ, we found that χ2 can also vary with ϕ/ψ. Figure 7B shows shifts in the χ2 dihedral angle distributions for some of the residues; this was most pronounced for Asn and Asp, as expected, but included other residues, such as the β-branched Ile χ2. Both the position populated within a rotameric bin, changing the average χ2-angle, and shifts in populations toward other rotameric bins are observed (Figure 7B). For example, RL2010 reports the Met g−, g−, g− rotamer to be most probable (18%). In our BBIND library, however, the most probable rotamer for Met is g−,t,g− and only within the near-αR region does the g−,g−,g− rotamer become the most frequently populated (Table S1 and Figure 9). This is an example of χ2 showing some dependence on ϕ/ψ even as the Met χ1 distribution remains relatively invariant across different secondary structure regions (Figure 7B).
For many of the residues, there was visible demarcation between collections of ϕ/ψ bins where there was preference for one rotamer over another (Figure 6). These areas of consensus often coincided with ϕ/ψ regions typical of common secondary structures. Hence, along with presenting the BBDEP and BBIND rotamer libraries, we also analyzed correlations between side-chain and backbone propensities within defined secondary structure ϕ/ψ regions (Figures 7, 8, and 9). Beyond allowing us to gain a clearer overview of how rotamer probabilities change with local backbone conformation, these RSS probabilities should prove useful for the selection of rotamers when the secondary structure of a residue is known, or has been predicted, but where the initial backbone angles are uncertain or based on a homology model.
The results presented here are available online as part of our Structural Library of Intrinsic Residue Propensities (SLIRP) at http://www.dynameomics.org/SLIRP. The updated BBIND library is also included in UCSF Chimera (Pettersen et al., 2004).
EXPERIMENTAL PROCEDURES
The Dynameomics v2009 Release Set (Schaeffer et al., 2011) (http://www.dynameomics.org) of 807 unique protein folds simulated using MD was used to generate rotamer statistics. Simulations were performed using ilmm (Beck and Daggett, 2004; Beck et al., 2000–2015) with the F3C water model (Beck et al., 2003; Levitt et al., 1997) and the Levitt force field (Levitt et al., 1995). Each structure was solvated and simulated for at least 51 ns at 25°C; the first nanosecond allowed for equilibration and was excluded from further analysis. Structures were saved every picosecond (van der Kamp et al., 2010), resulting in more than 51,000 instances for each of the 93,642 residues and totaling more than 4.8 × 109 samples. Additional details for the simulation protocols are available elsewhere (Beck and Daggett, 2004; Beck et al., 2008).
The rotamer populations, average χ angles, and associated SDs were calculated using the rotamer bin definitions in Figure 7A. For tetrameric carbons, the nomenclature used for rotameric bins was as defined by IUPAC where g+ refers to the conformation that centers on +60°and g− on −60° (Hoffman-Ostenhof et al., 1970). For non-rotameric side-chain angles, the definitions used for our earlier backbone-independent library were applied (Figure 6A) (Scouras and Daggett, 2011). Narrower rotamer bin definitions, employed elsewhere (Dunbrack and Cohen, 1997; Shapovalov and Dunbrack, 2011), split some probability distributions at the population maximum rather than capturing the energy minimum within a bin. The definitions used here accommodate the broader asymmetric and symmetric population distributions of the non-rotameric terminal χ angles; the total number of rotamers is detailed in Table S2 (Scouras and Daggett, 2011). For the terminal χ angles of the Asp, Glu, Tyr, and Phe residues, degenerate rotameric bins split about 0° and 180° angles, e.g. the two g bins of Phe χ2, were counted as a single rotameric state. These bins are associated with symmetric probability distributions where flips of the planar aromatic and carbonyl groups that alter the value of the defined χ2 or χ3, defined for specific atoms in our MD analysis, but which result in indistinguishable orientations of the side chain. To determine backbone-dependent rotamer probabilities, all residue instances were collected into 1,296 10° × 10° ϕ/ψ bins and the rotamer statistics calculated within each bin as a percentage of the total number of data points (ϕ/ψ instances) for each residue. Populations and probabilities within broader conformational regions were calculated with the secondary structure regions defined as: αR: −100°≤ φ ≤ −30°, −80° ≤ ψ ≤ −5°; near-αR: −175° ≤ φ ≤ −100°, −55° ≤ ψ ≤ −5°; αL: 5° ≤ φ ≤ 75°, 25° ≤ ψ ≤ 120°; β: −180° ≤ φ ≤ −50°, 80° ≤ ψ ≤ −170°; PIR: −180° ≤ φ ≤ −115°, 50° ≤ ψ ≤ 100°; PIIL: −110° ≤ φ ≤ −50°, 120° ≤ ψ ≤ 180° (Figure 3B).
To assess topological bias, the 807 starting structures of the Dynameomics dataset were compared with the 3,985 chains used in creating the RL2010 (Shapovalov and Dunbrack, 2011). Average ϕ/ψ angles of individual structures were computed using circular statistics, and population bias in ϕ/ψ space was then determined from histograms of the average values within the two datasets. To enable direct comparison of the two different sized datasets, fractional populations for each bin were calculated and normalized by the maximum bin population. Histograms of all the individual ϕ/ψ angles within a dataset using 5° × 5° and 10° × 10° bin widths were also generated to assess coverage. NMR S2 order parameter data used to assess backbone and side-chain dynamics and the correlation between S2 axis and multi-rotamericity populations were generated as reported previously from a set of 18 proteins (Best et al., 2004; Scouras and Daggett, 2011). Experimental data and simulation details are as previously reported for ubiquitin and were taken from BMRB entry 17439 (Beck et al., 2008).
More extensive data for the rotamer libraries described herein are available at http://www.dynameomics.org/SLIRP.
Supplementary Material
Highlights.
Improving rotamer libraries aids structure design, prediction, and modeling
Dynameomics is the simulation of solvated structures representing 97% of fold space
Dynamic rotamer libraries were created from the Boltzmann sampling of side chains
Including dynamics showed rare rotamers to be dominant in some areas of ϕ/ψ space
Acknowledgments
We are grateful for financial support provided by the NIH (GM50789 to V.D.) and by the NLM (5T15LM007442 to S.J.R.). Dynameomics simulations were performed using resources of the National Energy Research Scientific Computing (NERSC) Center offered through Production and Director Reserve Awards. NERSC is a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under contract no. DE-AC02-05CH11231. Protein images were produced using either UCSF Chimera (supported by NIH P41 RR-01081) or PyMOL (Version 1.7.4 Schrödinger LLC).
Footnotes
SUPPLEMENTAL INFORMATION
Supplemental Information includes two figures and two tables and can be found with this article online at http://dx.doi.org/10.1016/j.str.2015.10.017.
AUTHOR CONTRIBUTIONS
C.L.T. and S.J.R. performed data analysis, interpreted the results, and wrote the manuscript; I.M.V. constructed a graphical interface on Dynameomics.org and compiled downloadable libraries for external use; V.D. wrote the manuscript, and conceived of and supervised the research. All authors contributed to manuscript revisions and approved the final version.
References
- Alexander PA, Rozak DA, Orban J, Bryan PN. Directed evolution of highly homologous proteins with different folds by phage display: implications for the protein folding code. Biochemistry. 2005;44:14045–14054. doi: 10.1021/bi051231r. [DOI] [PubMed] [Google Scholar]
- Andreeva A, Howorth D, Chandonia JM, Brenner SE, Hubbard TJP, Chothia C, Murzin AG. Data growth and its impact on the SCOP database: new developments. Nucleic Acids Res. 2008;36:D419–D425. doi: 10.1093/nar/gkm993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armen RS, Bernard BM, Day R, Alonso DOV, Daggett V. Characterization of a possible amyloidogenic precursor in glutamine-repeat neurodegenerative diseases. Proc Natl Acad Sci USA. 2005;102:13433–13438. doi: 10.1073/pnas.0502068102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnesano F, Banci L, Bertini I, Felli IC. The solution structure of oxidized rat microsomal cytochrome b5. Biochemistry. 1998;37:173–184. doi: 10.1021/bi971896w. [DOI] [PubMed] [Google Scholar]
- Aurora R, Rose GD. Helix capping. Protein Sci. 2013;7:21–38. doi: 10.1002/pro.5560070103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bahar I, Jernigan RL. Coordination geometry of nonbonded residues in globular proteins. Fold Des. 1996;1:357–370. doi: 10.1016/S1359-0278(96)00051-X. [DOI] [PubMed] [Google Scholar]
- Beck DAC, Daggett V. Methods for molecular dynamics simulations of protein folding/unfolding in solution. Methods. 2004;34:112–120. doi: 10.1016/j.ymeth.2004.03.008. [DOI] [PubMed] [Google Scholar]
- Beck DAC, Alonso DOV, Daggett V. A microscopic view of peptide and protein solvation. Biophys Chem. 2003;100:221–237. doi: 10.1016/s0301-4622(02)00283-1. [DOI] [PubMed] [Google Scholar]
- Beck DAC, Armen RS, Daggett V. Cutoff size need not strongly influence molecular dynamics results for solvated polypeptides. Biochemistry. 2005;44:609–616. doi: 10.1021/bi0486381. [DOI] [PubMed] [Google Scholar]
- Beck DAC, Jonsson AL, Schaeffer RD, Scott KA, Day R, Toofanny R, Alonso DOV, Daggett V. Dynameomics: mass annotation of protein dynamics and unfolding in water by high-throughput atomistic molecular dynamics simulations. Protein Eng Des Sel. 2008;21:353–368. doi: 10.1093/protein/gzn011. [DOI] [PubMed] [Google Scholar]
- Beck DAC, McCully ME, Alonso DOV, Daggett V. in lucem molecular mechanics (il mm) University of Washington; 2000–2015. [Google Scholar]
- Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman HM, Kleywegt GJ, Nakamura H, Markley JL. How community has shaped the Protein Data Bank. Structure. 2013;21:1485–1491. doi: 10.1016/j.str.2013.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Best RB, Clarke J, Karplus M. The origin of protein sidechain order parameter distributions. J Am Chem Soc. 2004;126:7734–7735. doi: 10.1021/ja049078w. [DOI] [PubMed] [Google Scholar]
- Best RB, Buchete NV, Hummer G. Are current molecular dynamics force fields too helical? Biophys J. 2008;95:L07–L09. doi: 10.1529/biophysj.108.132696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brenner SE, Chothia C, Hubbard TJ. Population statistics of protein structures: lessons from structural classifications. Curr Opin Struct Biol. 1997;7:369–376. doi: 10.1016/s0959-440x(97)80054-1. [DOI] [PubMed] [Google Scholar]
- Carugo O, Djinović-Carugo K. A proteomic Ramachandran plot (PRplot) Amino Acids. 2013;44:781–790. doi: 10.1007/s00726-012-1402-z. [DOI] [PubMed] [Google Scholar]
- Chandrasekaran R, Ramachandran GN. Studies on the conformation of amino acids. XI. Analysis of the observed side group conformation in proteins. Int J Protein Res. 1970;2:223–233. [PubMed] [Google Scholar]
- Chang G, Roth CB, Reyes CL, Pornillos O, Chen YJ, Chen AP. Retraction. Science. 2006;314:1875. doi: 10.1126/science.314.5807.1875b. [DOI] [PubMed] [Google Scholar]
- Chen VB, Arendall WB, III, Headd JJ, Keedy DA, Immormino RM, Kapral GJ, Murray LW, Richardson JS, Richardson DC. MolProbity: all-atom structure validation for macromolecular crystallography. Acta Crystallogr D Biol Crystallogr. 2009;66:12–21. doi: 10.1107/S0907444909042073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis IW, Leaver-Fay A, Chen VB, Block JN, Kapral GJ, Wang X, Murray LW, Arendall WB, Snoeyink J, Richardson JS, et al. MolProbity: all-atom contacts and structure validation for proteins and nucleic acids. Nucleic Acids Res. 2007;35:W375–W383. doi: 10.1093/nar/gkm216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Day R, Beck DAC, Armen RS, Daggett V. A consensus view of fold space: combining SCOP, CATH, and the Dali domain dictionary. Protein Sci. 2003;12:2150–2160. doi: 10.1110/ps.0306803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobrianov I, Caylor C, Lemay SG, Finkelstein KD, Thorne RE. X-ray diffraction studies of protein crystal disorder. J Cryst Growth. 1999;196:511–523. [Google Scholar]
- Dunbrack RL, Karplus M. Backbone-dependent rotamer library for proteins. Application to side-chain prediction. J Mol Biol. 1993;230:543–574. doi: 10.1006/jmbi.1993.1170. [DOI] [PubMed] [Google Scholar]
- Dunbrack RL, Karplus M. Conformational analysis of the backbone-dependent rotamer preferences of protein sidechains. Nat Struct Mol Biol. 1994;1:334–340. doi: 10.1038/nsb0594-334. [DOI] [PubMed] [Google Scholar]
- Dunbrack RL, Cohen FE. Bayesian statistical analysis of protein side-chain rotamer preferences. Protein Sci. 1997;6:1661–1681. doi: 10.1002/pro.5560060807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Firestine AM, Chellgren VM, Rucker SJ, Lester TE, Creamer TP. Conformational properties of a peptide model for unfolded α-helices. Biochemistry. 2008;47:3216–3224. doi: 10.1021/bi702474k. [DOI] [PubMed] [Google Scholar]
- Fox NK, Brenner SE, Chandonia JM. SCOPe: structural classification of proteins–extended, integrating SCOP and ASTRAL data and classification of new structures. Nucleic Acids Res. 2014;42:D304–D309. doi: 10.1093/nar/gkt1240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraser JS, van den Bedem H, Samelson AJ, Lang PT, Holton JM, Echols N, Alber T. Accessing protein conformational ensembles using room-temperature X-ray crystallography. Proc Natl Acad Sci USA. 2011;108:16247–16252. doi: 10.1073/pnas.1111325108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gianni S, Guydosh NR, Khan F, Caldas TD, Mayor U, White GWN, Demarco ML, Daggett V, Fersht AR. Unifying features in protein-folding mechanisms. Proc Natl Acad Sci USA. 2003;100:13286–13291. doi: 10.1073/pnas.1835776100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gore S, Velankar S, Kleywegt GJ. Implementing an X-ray validation pipeline for the Protein Data Bank. Acta Crystallogr D Biol Crystallogr. 2012;68:478–483. doi: 10.1107/S0907444911050359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagarman A, Mathieu D, Toal S, Measey TJ, Schwalbe H, Schweitzer-Stenner R. Amino acids with hydrogen-bonding side chains have an intrinsic tendency to sample various turn conformations in aqueous solution. Chem Eur J. 2011;17:6789–6797. doi: 10.1002/chem.201100016. [DOI] [PubMed] [Google Scholar]
- Harder T, Boomsma W, Paluszewski M, Frellsen J, Johansson KE, Hamelryck T. Beyond rotamers: a generative, probabilistic model of side chains in proteins. BMC Bioinformatics. 2010;11:306. doi: 10.1186/1471-2105-11-306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman-Ostenhof O, Cohn WE, Braunstein AE, Karlson P, Keil B, Klyne W, Liebecq C, Slater EC, Webb EC, Whelan WJ. IUPAC-IUB commission on biochemical nomenclature. Abbreviations and symbols for the description of the conformation of polypeptide chains. J Mol Biol. 1970;52:1–17. [PubMed] [Google Scholar]
- Hom K, Wolfe G, Ma QF, Zhang H, Storch EM, Daggett V, Basus VJ, Waskell L. NMR studies of the association of cytochrome b5 with cytochrome c. Biochemistry. 2000;39:14025–14039. doi: 10.1021/bi001129o. [DOI] [PubMed] [Google Scholar]
- Jacobson MP, Friesner RA, Xiang Z, Honig B. On the role of the crystal environment in determining protein side-chain conformations. J Mol Biol. 2002;320:597–608. doi: 10.1016/s0022-2836(02)00470-9. [DOI] [PubMed] [Google Scholar]
- Janin J, Wodak S, Levitt M, Maigret B. Conformation of amino acid side-chains in proteins. J Mol Biol. 1978;125:357–386. doi: 10.1016/0022-2836(78)90408-4. [DOI] [PubMed] [Google Scholar]
- Jiang F, Han W, Wu YD. The intrinsic conformational features of amino acids from a protein coil library and their applications in force field development. Phys Chem Chem Phys. 2013;15:3413–3428. doi: 10.1039/c2cp43633g. [DOI] [PubMed] [Google Scholar]
- Kobe B, Guncar G, Buchholz R, Huber T, Maco B, Cowieson N, Martin JL, Marfori M, Forwood JK. Crystallography and protein-protein interactions: biological interfaces and crystal contacts. Biochem Soc Trans. 2008;36:1438. doi: 10.1042/BST0361438. [DOI] [PubMed] [Google Scholar]
- Kryshtafovych A, Fidelis K, Moult J. CASP10 results compared to those of previous CASP experiments. Proteins. 2014;82(Suppl 2):164–174. doi: 10.1002/prot.24448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larriva M, Rey A. Design of a rotamer library for coarse-grained models in protein-folding simulations. J Chem Inf Model. 2014;54:302–313. doi: 10.1021/ci4005833. [DOI] [PubMed] [Google Scholar]
- Levitt M. Growth of novel protein structural data. Proc Natl Acad Sci USA. 2007;104:3183–3188. doi: 10.1073/pnas.0611678104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt M, Hirshberg M, Sharon R, Daggett V. Potential energy function and parameters for simulations of the molecular dynamics of proteins and nucleic acids in solution. Comput Phys Commun. 1995;91:215–231. [Google Scholar]
- Levitt M, Hirshberg M, Sharon R, Laidig KE, Daggett V. Calibration and testing of a water model for simulation of the molecular dynamics of proteins and nucleic acids in solution. J Phys Chem B. 1997;101:5051–5061. [Google Scholar]
- Li A, Daggett V. Investigation of the solution structure of chymotrypsin inhibitor 2 using molecular dynamics: comparison to X-ray crystallographic and NMR data. Protein Eng Des Sel. 1995;8:1117–1128. doi: 10.1093/protein/8.11.1117. [DOI] [PubMed] [Google Scholar]
- Lovell SC, Word JM, Richardson JS, Richardson DC. The penultimate rotamer library. Proteins. 2000;40:389–408. [PubMed] [Google Scholar]
- Mayor U, Johnson CM, Daggett V, Fersht AR. Protein folding and unfolding in microseconds to nanoseconds by experiment and simulation. Proc Natl Acad Sci USA. 2000;97:13518–13522. doi: 10.1073/pnas.250473497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayor U, Guydosh NR, Johnson CM, Grossmann JG, Sato S, Jas GS, Freund SMV, Alonso DOV, Daggett V, Fersht AR. The complete folding pathway of a protein from nanoseconds to microseconds. Nature. 2003;421:863–867. doi: 10.1038/nature01428. [DOI] [PubMed] [Google Scholar]
- McGregor MJ, Islam SA, Sternberg MJ. Analysis of the relationship between side-chain conformation and secondary structure in globular proteins. J Mol Biol. 1987;198:295–310. doi: 10.1016/0022-2836(87)90314-7. [DOI] [PubMed] [Google Scholar]
- Montelione GT, Nilges M, Bax A, Güntert P, Herrmann T, Richardson JS, Schwieters CD, Vranken WF, Vuister GW, Wishart DS, et al. Recommendations of the wwPDB NMR validation task force. Structure. 2013;21:1563–1570. doi: 10.1016/j.str.2013.07.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otzen DE, Fersht AR. Side-chain determinants of β-sheet stability. Biochemistry. 1995;34:5718–5724. doi: 10.1021/bi00017a003. [DOI] [PubMed] [Google Scholar]
- Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. UCSF Chimera—A visualization system for exploratory research and analysis. J Comput Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- Ponder JW, Richards FM. Tertiary templates for proteins. Use of packing criteria in the enumeration of allowed sequences for different structural classes. J Mol Biol. 1987;193:775–791. doi: 10.1016/0022-2836(87)90358-5. [DOI] [PubMed] [Google Scholar]
- Read RJ, Adams PD, Arendall WB, Brunger AT, Emsley P, Joosten RP, Kleywegt GJ, Krissinel EB, Lütteke T, Otwinowski Z, et al. A new generation of crystallographic validation tools for the protein data bank. Structure. 2011;19:1395–1412. doi: 10.1016/j.str.2011.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Religa TL, Markson JS, Mayor U, Freund SMV, Fersht AR. Solution structure of a protein denatured state and folding intermediate. Nature. 2005;437:1053–1056. doi: 10.1038/nature04054. [DOI] [PubMed] [Google Scholar]
- Richardson JS. The anatomy and taxonomy of protein structure. Adv Protein Chem. 1981;34:339. doi: 10.1016/s0065-3233(08)60520-3. [DOI] [PubMed] [Google Scholar]
- Rizzuti B, Daggett V. Using simulations to provide the framework for experimental protein folding studies. Arch Biochem Biophys. 2013;531:128–135. doi: 10.1016/j.abb.2012.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rutherford K, Daggett V. Polymorphisms and disease: hotspots of inactivation in methyltransferases. Trends Biochem Sci. 2010;35:531–538. doi: 10.1016/j.tibs.2010.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rutherford K, Bennion BJ, Parson WW, Daggett V. The 108M Polymorph of human catechol O-methyltransferase is prone to deformation at physiological temperatures. Biochemistry. 2006;45:2178–2188. doi: 10.1021/bi051988i. [DOI] [PubMed] [Google Scholar]
- Rutherford K, Alphandéry E, McMillan A, Daggett V, Parson WW. The V108M mutation decreases the structural stability of catechol O-methyltransferase. Biochim Biophys Acta. 2008;1784:1098–1105. doi: 10.1016/j.bbapap.2008.04.006. [DOI] [PubMed] [Google Scholar]
- Schaeffer RD, Daggett V. Protein folds and protein folding. Protein Eng Des Sel. 2011;24:11–19. doi: 10.1093/protein/gzq096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaeffer RD, Fersht A, Daggett V. Combining experiment and simulation in protein folding: closing the gap for small model systems. Curr Opin Struct Biol. 2008;18:4–9. doi: 10.1016/j.sbi.2007.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaeffer RD, Jonsson AL, Simms AM, Daggett V. Generation of a consensus protein domain dictionary. Bioinformatics. 2011;27:46–54. doi: 10.1093/bioinformatics/btq625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrauber H, Eisenhaber F, Argos P. Rotamers: to be or not to be? an analysis of amino acid side-chain conformations in globular proteins. J Mol Biol. 1993;230:592–612. doi: 10.1006/jmbi.1993.1172. [DOI] [PubMed] [Google Scholar]
- Schreiner E, Trabuco LG, Freddolino PL, Schulten K. Stereochemical errors and their implications for molecular dynamics simulations. BMC Bioinformatics. 2011;12:190. doi: 10.1186/1471-2105-12-190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scouras AD, Daggett V. The dynameomics rotamer library: amino acid side chain conformations and dynamics from comprehensive molecular dynamics simulations in water. Protein Sci. 2011;20:341–352. doi: 10.1002/pro.565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seavey BR, Farr EA, Westler WM, Markley JL. A relational database for sequence-specific protein NMR data. J Biomol NMR. 1991;1:217–236. doi: 10.1007/BF01875516. [DOI] [PubMed] [Google Scholar]
- Shapovalov MV, Dunbrack RL. A smoothed backbone-dependent rotamer library for proteins derived from adaptive kernel density estimates and regressions. Structure. 2011;19:844–858. doi: 10.1016/j.str.2011.03.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharpe T, Jonsson AL, Rutherford TJ, Daggett V, Fersht AR. The role of the turn in β-hairpin formation during WW domain folding. Protein Sci. 2007;16:2233–2239. doi: 10.1110/ps.073004907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sillitoe I, Lewis TE, Cuff A, Das S, Ashford P, Dawson NL, Furnham N, Laskowski RA, Lee D, Lees JG, et al. CATH: comprehensive structural and functional annotations for genome sequences. Nucleic Acids Res. 2015;43:D376–D381. doi: 10.1093/nar/gku947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simms AM, Daggett V. Protein simulation data in the relational model. J Supercomput. 2012;62:150–173. doi: 10.1007/s11227-011-0692-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simms AM, Toofanny R, Kehl C, Benson NC, Daggett V. Dynameomics: design of a computational lab workflow and scientific data repository for protein simulations. Protein Eng Des Sel. 2008;21:369–377. doi: 10.1093/protein/gzn012. [DOI] [PubMed] [Google Scholar]
- Storch EM, Daggett V. Molecular dynamics simulation of cytochrome b5: implications for protein-protein recognition. Biochemistry. 1995;34:9682–9693. doi: 10.1021/bi00030a005. [DOI] [PubMed] [Google Scholar]
- Storch EM, Daggett V, Atkins WM. Engineering out motion: introduction of a de novo disulfide bond and a salt bridge designed to close a dynamic cleft on the surface of cytochrome b5. Biochemistry. 1999;38:5054–5064. doi: 10.1021/bi982158q. [DOI] [PubMed] [Google Scholar]
- Toofanny R, Daggett V. Understanding protein unfolding from molecular simulations. Wiley Interdiscip Rev Comput Mol Sci. 2012;2:405–423. [Google Scholar]
- Towse CL, Daggett V. When a domain is not a domain, and why it is important to properly filter proteins in databases. Bioessays. 2012;34:1060–1069. doi: 10.1002/bies.201200116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Towse CL, Daggett V. Modeling protein folding pathways. In: Parrill AL, Lipkowitz KB, editors. Reviews in Computational Chemistry. Vol. 28. John Wiley; 2015. pp. 87–135. [Google Scholar]
- Towse CL, Vymetal J, Vondrasek J, Daggett V. Insights into unfolded proteins from the intrinsic φ/ψ properties of the AAXAA host-guest series. Biophys J. 2015 doi: 10.1016/j.bpj.2015.12.008. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Kamp MW, Schaeffer RD, Jonsson AL, Scouras AD, Simms AM, Toofanny R, Benson NC, Anderson PC, Merkley ED, Rysavy S. Dynameomics: a comprehensive database of protein dynamics. Structure. 2010;18:423–435. doi: 10.1016/j.str.2010.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner G, Hyberts SG, Havel TF. NMR structure determination in solution: a critique and comparison with X-ray crystallography. Annu Rev Biophys Biomol Struct. 1992;21:167–198. doi: 10.1146/annurev.bb.21.060192.001123. [DOI] [PubMed] [Google Scholar]
- Xiang Z, Honig B. Extending the accuracy limits of prediction for side-chain conformations. J Mol Biol. 2001;311:421–430. doi: 10.1006/jmbi.2001.4865. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


