Exact Confidence Intervals for the Relative Risk and the Odds Ratio

Summary

For comparison of proportions there are three commonly used measurements: the difference, the relative risk and the odds ratio. Significant effort has been spent on exact confidence intervals for the difference. In this paper, we focus on the relative risk and the odds ratio when data are collected from a matched-pairs design or a two-arm independent binomial experiment. Exact one-sided and two-sided confidence intervals are proposed for each configuration of two measurements and two types of data. The one-sided intervals are constructed using an inductive order, they are the smallest under the order, and are admissible under the set inclusion criterion. The two-sided intervals are the intersection of two one-sided intervals. R codes are developed to implement the intervals. Supplementary materials for this article are available online.

1. INTRODUCTION

In medical research we often need to compare two treatments using binary data, and three parameters are commonly used: the risk difference (the difference of two proportions), the relative risk (the ratio of two proportions) and the odds ratio. The risk difference is an absolute measurement of effect, while the relative risk and the odds ratio are relative measurements for comparing outcomes. In retrospective case-control studies, the odds ratio is used because the other two parameters cannot be estimated. It is also well known that the odds ratio has a direct relationship with the regression coefficient in logistic regression. The relative risk is used in randomized controlled trials and cohort studies especially when the two relevant proportions are both small. In such a case, the risk difference is not as informative as the relative risk (see McCullagh 1980, Goodman 1985, and Agresti 2002, p.44). The relative risk and the odds ratio are comparable when the disease is rare with very low probability. For some common diseases (e.g., hypertension), the value of the odds ratio could be overestimated, and the relative risk should be used instead. It should be noted that the relative risk and the odds ratio are defined differently in Eq (3) and Eq (23) for a matched-pairs design and a two-arm independent binomial experiment. In this paper we focus on interval estimation of the relative risk and the odds ratio using data that are collected in a matched-pairs design or a two-arm independent binomial experiment, and are organized in a 2 × 2 contingency table. Results on the risk difference can be found, for example, in Wang (2010, 2012).

When no pivot quantity can be found for a discrete distribution, the coverage probability of a confidence interval is typically not a constant. Therefore, for a secure capture of the parameter of interest the coverage probability function of a desired confidence interval must be always at least the nominal level 1 − α for all parameter configurations, and we call it an exact confidence interval of level 1 − α (see Casella and Berger, 1990, p. 404). Such an interval guarantees predetermined coverage for a fixed sample size no matter where the true parameter vector is located in the parameter space. The implementation, however, is typically challenging as compared with asymptotic intervals. Some studies have shown that asymptotic intervals for proportions may have an infimum coverage probability lower than the nominal level by a fixed positive amount regardless of sample size, see Huwang (1995), Agresti and Coull (1998), Brown, Cai and DasGupta (2001), and Wang and Zhang (2014). In particular, the Wald interval, the Wilson interval (1927), and the Agresti-Coull interval (1998) for a binomial proportion are proven to have an incorrect infimum coverage even for very large sample sizes. One may turn to bootstrap intervals, especially when the parameter of interest is complicated. Such efforts can be found in, for example, Li, Taylor and Nan (2010), Lin et al. (2009) and Parzen et al. (2002). However, Wang (2013) proved that all bootstrap intervals for any function of proportions, including the relative risk and the odds ratio, always have an infimum coverage probability of zero. Therefore, practitioners are at their own risk to use these intervals, since the intervals may have a very small chance of capturing the parameter of interest, and the usage of exact intervals is justified.

Exact intervals for the relative risk and the odds ratio may be obtained by inverting exact tests in the case of two independent binomials, see for example, Gart (1971), Santner and Snell (1980), and Chan and Zhang (1999). This indirect construction may result in wider intervals. Wang (2010, 2012) proposed optimal intervals for the risk difference based on a direct analysis of coverage probability and an inductive order of the sample space. Shan and Wang (2013) developed an R-package, ExactCIdiff, to implement his intervals. This approach is now adapted to more complicated cases: the relative risk and the odds ratio. In Section 2 we describe preliminary results for the smallest one-sided interval construction. Section 3 discusses how to derive exact intervals for the relative risk and the odds ratio using a matched-pairs design and how to implement the computation. Section 4 deals with the case of a two-arm independent binomial experiment. The proposed intervals tend to be shorter than the ones from SAS (Version 9.3). Section 5 is a summary. The proofs and some figures are given in Supplementary Materials online.

2. PRELIMINARY RESULTS

Following the work by Buehler (1957), Bol’shev (1965), Chen (1993), Lloyd and Kabaila (2003), and Wang (2010) the construction of an exact one-sided confidence interval becomes automatic provided that an order (or equivalently, a rank function on a finite sample space) is specified in advance. We describe this result here, as it will be applied four times in the paper. Suppose a random vector X is observed from a finite sample space S, i.e., $S={\left\{{\underset{¯}{x}}_i\right\}}_{i=1}^n$. A rank function R(.), assuming positive integer values, is defined on S. The probability mass function of X is given by p(x; ξ), where ξ is the parameter vector belonging to a parameter space H, a subset of R^k. Suppose ξ = (θ, η) and

$$H=\{\underset{¯}{\xi }:\underset{¯}{\eta }\in D(\theta )\text{for each}\theta \in [A,B\left]\right\},$$

where θ is the parameter of interest and η is the nuisance parameter vector, [A, B] is a given interval in R¹ (A and B may be ±∞, and the interval is open when the corresponding end is infinity) and D(θ) is a subset of R^k−1 depending on θ. We are interested in searching for the smallest exact lower one-sided confidence interval [L_S(X), B] among all 1 − α intervals for θ with form [L(X), B] that satisfy

$$1\left)L\right(\underset{¯}{x})=L({\underset{¯}{x}}^{\prime }\left)\text{if}R\right(\underset{¯}{x})=R({\underset{¯}{x}}^{\prime });2)L\left(\underset{¯}{x}\right)\le L\left({\underset{¯}{x}}^{\prime }\right)\text{if}R\left({\underset{¯}{x}}^{\prime }\right)\le R\left(\underset{¯}{x}\right).$$

So a sample point x with a smaller rank has a larger confidence limit.

Lemma 1: Assume α ∈ (0, 1). For a given rank function R(.) on S and any x ∈ S, consider

$$f_{\underset{¯}{x}}{\left(\theta \right)}^{\underset{=}{\mathit{def}}}\underset{\underset{¯}{\eta }\in D\left(\theta \right)}{\inf }[1-\sum _{\{{\underset{¯}{x}}^{\prime }\in S:R({\underset{¯}{x}}^{\prime })\le R(\underset{¯}{x}\left)\right\}}p({\underset{¯}{x}}^{\prime };\underset{¯}{\xi }\left)\right]=1-\alpha .$$ (1)

If f_x(θ) is a continuous function in θ, define

$$L_s\left(\underset{¯}{x}\right)=\{\begin{array}{cc}\mathrm{the}\mathrm{smallest}\mathrm{solution}\mathrm{of}\left(1\right),\hfill & \mathrm{if}\left(1\right)\mathrm{has}a\mathrm{solution};\hfill \\ A,\hfill & \mathit{otherwise},\hfill \end{array}\phantom{\}}$$ (2)

then

• i)[L_S(X), B] is of level 1 − α and satisfies 1) and 2);
• ii)for any 1 − α interval [L(X), B] satisfying 1) and 2), L(X) ≤ L_S(X).

This lemma follows Theorem 4 in Wang (2010). Due to ii), [L_S(X), B] is the smallest interval since it is a subset of any other interval. Then it is the best under the given rank function R(.). In order to derive the smallest exact interval for parameters including the relative risk and the odds ratio with A = 0 and B = +∞, we have to resolve the following two problems for implementation:

• A)provide a reasonable rank function R(.) for each of four cases;
• B)find the infimum in Eq (1) over D(θ) and the smallest solution of Eq (1) efficiently.

For a sample space S with n sample points, there are about 2ⁿ possible rank functions on S. Some are clearly bad for interval construction. For example, the rank function R_c(.) that assumes a constant value over S (i.e., all sample points are tied) produces an interval with a constant confidence limit over S. Lemma 1 still shows that it is the smallest under R_c(.). However, such an interval is useless in practice, and can be uniformly improved by simply giving up those ties. Therefore, identifying a reasonable rank function is extremely important and also challenging, but Lemma 1 does not discuss it. One may use, for example, the maximum likelihood estimator for θ as the rank function. This, however, generates too many ties and results in a wide confidence interval. Wang (2010) proposed an inductive construction on rank function that yields an admissible interval. We apply this idea to two interesting parameters: the relative risk and the odds ratio.

Searching for the infimum of a given function is a classic, but difficult problem in numerical computation, especially for a multivariate function. A more challenging issue is that the infimum must be computed a large number of times. Programs exist for optimization, however, none is able to provide a solution precisely and quickly. Our study suggests that a two-stage grid search (explained later) for the infimum on D(θ) is an effective solution.

3. CASE I: A MATCHED-PAIRS DESIGN

In a 2 × 2 table with a matched-pairs design, suppose there are n independent and identical trials, and each trial is inspected by two criteria 1 and 2. By criterion i, each trial is classified as S_i or F_i for i = 1, 2. The numbers of trials with outcomes (S₁, S₂), (S₁, F₂), (F₁, S₂) and (F₁, F₂) are the observations, and are denoted by N₁₁, N₁₂, N₂₁ and N₂₂, respectively. Thus X_p = (N₁₁, N₁₂, N₂₁) follows a multinomial distribution with probabilities p₁₁, p₁₂, and p₂₁, respectively, denoted by Multinomial(n, p₁₁, p₁₂, p₂₁). Let p_1* = P (S₁) and p_*1 = P(S₂) be the two paired proportions. The involved items are displayed below.

	S2	F2
S1	(S1, S2), N11, p11	(S1, F2), N12, p12	p1* = p11 + p12
F1	(F1, S2), N21, p21	(F1, F2), N22, p22
	p*1 = p11 + p21		∑i,j Nij = n,∑i,j pij = 1

The relative risk θ_pr and the odds ratio θ_po are given by:

$${\theta }_{p_r}\stackrel{\mathit{def}}{=}\frac{p_{1\ast }}{p_{\ast 1}}=\frac{p_{11}+p_{12}}{p_{11}+p_{21}}\mathit{and}{\theta }_{p_o}\stackrel{\mathit{def}}{=}\frac{p_{1\ast }(1-p_{\ast 1})}{p_{\ast 1}(1-p_{1\ast })}=\frac{(p_{11}+p_{12})(1-p_{11}-p_{21})}{(p_{11}+p_{21})(1-p_{11}-p_{12})}.$$ (3)

Here, the subscripts p, r and o stand for “paired proportions”, “relative risk” and “odds ratio”, respectively. Two one-sided 1 − α confidence intervals [L(X_p), +∞) and [0, U(X_p)] and a two-sided 1 − α confidence interval [L(X_p), U(X_p)] are to be constructed for θ_pr and θ_po. To the best of our knowledge, no exact confidence intervals have been proposed for these parameters. StatXact 10 (2013) claims to compute an interval for so called “the odds ratio” (see Equations 13.17 and 13.7 in the user manual). It is indeed θ_pr, but we find that their computed interval is for p₁₂/p₂₁ not θpr. SAS (Version 9.3) does not have any discussion on exact intervals for the parameters. The sample space and the parameter space are

$$S_p=\{{\underset{¯}{x}}_p=(n_{11},n_{12},n_{21}):n_{ij}\ge 0\text{is an integer},0\le n_{11}+n_{12}+n_{21}\le n\}$$ (4)

with (n + 1)(n + 2)(n + 3)/6 sample points and

$$H_p=\left\{\right(p_{11},p_{1\ast },p_{\ast 1}):0\le p_{11}\le \min (p_{1\ast },p_{\ast 1}),0\le p_{1\ast }+p_{\ast 1}-p_{11}\le 1\},$$ (5)

respectively. The random vector X_p has a joint probability mass function

$$p_p(n_{11},n_{12},n_{21};p_{11},p_{1\ast },p_{\ast 1})=\frac{n!}{n_{11}!n_{12}!n_{21}!n_{22}!}{p}_{11}^{n_{11}}{(p_{1\ast }-p_{11})}^{n_{12}}{(p_{\ast 1}-p_{11})}^{n_{21}}{p}_{22}^{n_{22}}.$$ (6)

with n₂₂ = n−n₁₁ −n₁₂ −n₂₁ and p₂₂ = 1−(p_1* + p_*1−p₁₁). We illustrate the setting below.

Example 1. Bentur et al. (2009, p.847) conducted a study on airway hyper-responsiveness (AHR) status before and after stem cell transplantation (SCT) on 21 patients. The AHR status for each patient is assessed by a methacholine challenge test (MCT) twice, before and after SCT. The data summary is given as follows.

		Before SCT
		AHR yes	AHR no	total
After SCT	AHR yes	1(=n11), p11	7(=n12), p12	8, p1*
	AHR no	1(=n21), p21	12(=n22), p22	13
	total	2, p*1	19	21

For example, one (= n₁₁) patient has AHR before and after SCT, and p₁₁ is the probability that a patient has AHR before and after SCT. Exact confidence intervals for θ_pr and θ_po will be derived to study the effect of SCT on AHR status especially in this small sample.

3.1 INTERVALS FOR θ_pr

Three intervals (lower one-sided, upper one-sided and two-sided) are to be constructed for θ_pr. The two-sided 1 − α interval can be obtained by using the intersection of the two one-sided 1 − α/2 intervals. The next lemma discusses how to obtain an upper one-sided interval from a lower one-sided interval. Therefore, we focus on the construction of a lower one-sided 1 − α interval. Let [a, b] = [a, +∞) if b = +∞.

Lemma 2: Suppose [L(N₁₁, N₁₂, N₂₁), +∞) is a lower one-sided 1− α confidence interval for θ_pr. Then

$$[0,U(N_{11},N_{12},N_{21}\left)\right]\stackrel{\mathit{def}}{=}[0,\frac{1}{L(N_{11},N_{21},N_{12})}]$$ (7)

is an upper one-sided 1 − α confidence interval for θ_pr. Furthermore, [L(N₁₁, N₁₂, N₂₁), U(N₁₁, N₁₂, N₂₁)] is a two-sided 1 − 2α interval for θ_pr.

The parameter space H_p can be expressed in terms of (θ_pr, p₁₁, p₂₁) with

$$p_{12}=({\theta }_{p_r}-1)p_{11}+{\theta }_{p_r}{p}_{21}$$ (8)

as follows: H_pr = {(θ_pr, p₁₁, p₂₁) : (p₁₁, p₂₁) ∈ D_pr(θ_pr), ∀ θ_pr ∈ [0, +∞)}, where

$$D_{p_r}\left({\theta }_{p_r}\right)=\{\begin{array}{c}\left\{\right(p_{11},p_{12}):{\theta }_{p_r}{p}_{11}+({\theta }_{p_r}+1)p_{21}\in [0,1\left]\right\},\text{if}{\theta }_{p_r}\ge 1;\hfill \\ \left\{\right(p_{11},p_{21}):{\theta }_{p_r}{p}_{11}+({\theta }_{p_r}+1)p_{21}\in [0,1],p_{11}+p_{21}\in [0,1\left]\right\},\text{otherwise}.\hfill \end{array}\phantom{\}}$$ (9)

The first line in (9) is a triangle with three vertices, (0, 0), (1/θ_pr, 0) and (0, 1/(θ_pr + 1)), in the p₁₁-p₂₁ plane, and the second is the intersection of two triangles, one just mentioned and the other with three vertices, (0, 0), (1, 0) and (0, 1). See both cases in Figure S1 in Supplementary Materials. The joint probability mass function p_p is rewritten as

$$p_{p_r}(n_{11},n_{12},n_{21};{\theta }_{p_r},p_{11},p_{21})=p_p(n_{11},n_{12},n_{21};p_{11},p_{12},p_{21}),$$ (10)

where p_p and p₁₂ are given in (6) and (8), respectively.

As in Lemma 1, the construction of a one-sided interval [L(X_p), +∞) depends on a rank function R_pr(.) on S_p. Point x_p is large if R_pr(x_p) is small. Here are three natural rules on R_pr.

• a)R_pr(0, n, 0) = 1. i.e., point (0, n, 0) is the largest.
• b)R_pr(n₁₁, n₁₂, n₂₁) ≤ R_pr(n₁₁, n₁₂ − 1, n₂₁) for any n₁₂ ∈ [1, n − n₁₁ − n₂₁].
• c)R_pr(n₁₁, n₁₂, n₂₁ − 1) ≤ R_pr(n₁₁, n₁₂, n₂₁) for any n₂₁ ∈ [1, n − n₁₁ − n₁₂].

Rule a) follows the intuition that (0, n, 0) provides the largest estimate for θ_pr. Rules b) and c) follow the monotonicity of function θ_pr = (p₁₁ + p₁₂)/(p₁₁ + p₂₁). One would expect a similar rule for the case that n₁₂ and n₂₁ are fixed and n₁₁ varies. Both the numerator and the denominator of θ_pr include p₁₁, so it is not appropriate to propose a simple rule for n₁₁.

The rank function R_pr(.) is determined by combining Rules a), b), c) and numerical evaluation sequentially on all sample points. Again, R_pr(0, n, 0) = 1. We next describe how to assign a value for the rank function from small to large (i.e., determine sample points from large to small). Suppose that R_pr(.) has been assigned values to sets E_pr,1 through E_pr,k with values 1 through k (e.g., E_pr,1 = {(0, n, 0)}) for some k ≥ 1. i.e., set E_pr,i contains the ith largest point(s) for i ≤ k. Let $S_{p_r,k}={\cup }_{i=1}^k{E}_{p_r,i}$. Now we identify a nonempty set E_pr,k+1 in S_p that contains the (k + 1)th largest point(s). If such a set is found, then by induction, the function R_pr(.) is defined on S_p because S_pr,k is strictly increasing and S_p is finite.

For each point x_p = (n₁₁, n₁₂, n₂₁), we introduce five points: A = (n₁₁ + 1, n₁₂, n₂₁), B = (n₁₁, n₁₂ − 1, n₂₁), C = (n₁₁, n₁₂, n₂₁ + 1), D = (n₁₁ − 1, n₁₂, n₂₁), E = (n₁₁ + 1, n₁₂ − 1, n₂₁), that are next to but less than x_p. Let N_xp be the neighbor set that consists up to four points:

$$N_{{\underset{¯}{x}}_p}=\{\begin{array}{cc}\{A,B,C,D\}\cap S_p,\hfill & \text{if}A\in S_p\hfill \\ \{B,C,D,E\}\cap S_p,\hfill & \text{if}A\notin S_p.\hfill \end{array}\phantom{\}}$$ (11)

See N_xp in Figure S2 in Supplementary Materials for x_p = (3, 3, 2).

The neighbor set for S_pr,k, denoted by N_pr,k, consists of points in N_xp for any x_p ∈ S_pr,k but not in S_pr,k. i.e.,

$$N_{p_r,k}=\left({\cup }_{{\underset{¯}{x}}_p\in S_{p_r,k}}{N}_{{\underset{¯}{x}}_p}\right)\cap S_{p_r,k}^c.$$ (12)

However, some points in N_pr,k are impossible to be the (k + 1)th largest due to Rules b) and c). To eliminate them from the selection, consider a subset of N_pr,k, called the candidate set C_pr,k, given by

$$C_{p_r,k}=\left\{\right(n_{11},n_{12},n_{21})\in N_{p_r,x}:(n_{11},n_{12}+1,n_{21})\notin N_{p_r,k},(n_{11},n_{12},n_{21}-1)\notin N_{p_r,k}\}.$$ (13)

Set E_pr,k+1 is to be selected from C_pr,k, not N_pr,k. For each ${\underset{¯}{x}}_p^{\prime }=(n_{11}^{\prime },n_{12}^{\prime },n_{21}^{\prime })\in C_{p_r,k}$, consider an equation similar to (1)

$$f_{{\underset{¯}{x}}_p^{\prime }}\left({\theta }_{p_r}\right)=\underset{(p_{11},p_{12})\in D_{p_r}\left({\theta }_{p_r}\right)}{\inf }[1-\sum _{{\underset{¯}{x}}_p\in S_{p_r,k}\cup {\underset{¯}{x}}_p^{\prime }}{p}_{p_r}({\underset{¯}{x}}_p;{\theta }_{p_r},p_{11},p_{21}\left)\right]=1-\alpha ,$$ (14)

where p_pr is given in (10). Let $L^{\ast }\left({\underset{¯}{x}}_p^{\prime }\right)$ be the smallest solution to the above equation if a solution exists, and let $L^{\ast }\left({\underset{¯}{x}}_p^{\prime }\right)$ be 0 otherwise. Then define

$$E_{p_r,k+1}=\{{\underset{¯}{x}}_p\in C_{p_r,k}:L^{\ast }({\underset{¯}{x}}_p)=\max \{L^{\ast }\left({\underset{¯}{x}}_p^{\prime }\right):{\underset{¯}{x}}_p^{\prime }\in C_{p_r,k}\left\}\right\},$$ (15)

$$R_{p_r}\left({\underset{¯}{x}}_p\right)=k+1,\forall {\underset{¯}{x}}_p\in E_{p_r,k+1},\text{and}{S}_{p_r,k+1}={\cup }_{i=1}^{k+1}{E}_{p_r,i}.$$ (16)

Eq (15) assures that the rank function R_pr(.) yields the smallest (best) interval (with the largest lower confidence limit) in each step. Since E_pr,k+1 is not empty, and S_p is finite, there always exists a positive integer k_pr such that S_pr,kpr = S_p. Thus, the rank function R_pr(.) is defined on the entire S_p, and the construction for R_pr(.) is complete. Then the smallest lower one-sided 1 − α confidence interval [L_pr, +∞) for θ_pr, under the rank function R_pr(.), is derived following Lemma 1, the smallest upper one-sided 1 − α interval [0, U_pr] follows Lemma 2, and [L_pr, U_pr] is a two-sided 1 − 2α interval. If we use an existing function, e.g., the maximum likelihood estimator of θ_pr, to define an order, then many sample points, for example, the points (n₁₁, n₁₂, n₂₁) with n₁₁ + n₁₂ = n₁₁ + n₂₁, are tied since they have the same estimate, 1, for θ_pr. So, the corresponding confidence limits are equal to each other at these sample points following Lemma 1. In particular, the confidence limits at points (n₁₁, n₁₂, n₂₁) = (i, 0, 0), for i = 1, …, n, remain unchanged, indicating that the order by the maximum likelihood estimator is unreasonable.

Three facts are worth mentioning for the computation in (14) and (15). i) Find E_pr,k+1 from C_pr,k in (13) instead of N_pr,k in (12). ii) Using a two-stage grid search for the infimum in (14). i.e., for each D_pr(θ_pr) a partition is given first. We pick a point (θ_pr, p₁₁, p₁₂) in each set of the partition and identify the point that yields the minimum value of the function in (14). Then on the set of the partition that contains this point, we have another finer partition and search for the minimum again. iii) Suppose two points x_p1 and x_p2 belong to C_pr,k and we already compute L* (x_p1). If we find f_xp2(L* (x_p1)) < 1 − α, then x_p2 does not belong to E_pr,k+1 and the computation of L*(x_p2) is not needed. These three facts make the computation more efficient, and are also used for the other three cases in this paper. Next, we provide a closed form for L_pr(0, n, 0), which is useful for checking the precision of the numerical calculation.

Lemma 3: For any rank function R(.) with R(0, n, 0) = 1, let [L(N₁₁, N₁₂, N₂₁), +∞) be the smallest one-sided 1 − α interval for θ_pr under R. Then

$$L(0,n,0)=\frac{{\alpha }^{1∕n}}{1-{\alpha }^{1∕n}}.$$ (17)

Example 2. For illustration purpose, we show the construction of the largest four L_pr(x_p)’s on four sample points with ranks 1 through 4, when 1 − α = 0.95 and n = 3.

Due to a) R_pr(0, 3, 0) = 1. So L_pr(0, 3, 0) = 0.5832 following (17), or one can obtain the same result by solving a special case of (1):

$$f_{(0,3,0)}\left({\theta }_{p_r}\right)=\underset{(p_{11},p_{12})\in D_{p_r}\left({\theta }_{p_r}\right)}{\inf }[1-p_{p_r}(0,3,0;{\theta }_{p_r},p_{11},p_{12}\left)\right]=0.95.$$

To find the sample point with rank 2, we have

$$N_{(0,3,0)}=\left\{\right(0,2,0),(1,2,0\left)\right\},N_{p_r,1}=N_{(0,3,0)},\text{and}{C}_{p_r,1}=N_{p_r,1}$$

following (11), (12) and (13). Then solve (14) twice by using x′ = (0, 2, 0) and x′ = (1, 2, 0), respectively, with S_pr,1 = {(0, 3, 0)}, and obtain L*(0, 2, 0) = 0.4320 and L*(1, 2, 0) = 0.5504. Since L*(1, 2, 0) is larger than L*(0, 2, 0), set E_pr,1 = {(1, 2, 0)} and the rank function R_pr(1, 2, 0) = 2.

To find the sample points with ranks 3 and 4, repeat a similar step to the above paragraph. Then R_pr(1, 1, 0) = 3 and R_pr(2, 1, 0) = 4. The details are given in Table 1. Note that C_pr,3 is a proper subset of N_pr,3 and set E_pr,3 is found within C_pr,3 instead of E_pr,3. This would save a lot of computing time especially when n is large.

Table 1.

The details of the construction of L_pr at the four largest sample points in Example 2.

k	Epr,k	Npr,k	Cpr,k	$L^{\ast }\left({\underset{¯}{x}}_p^{\prime }\right)$	$\max \left\{L^{\ast }\right({\underset{¯}{x}}_p^{\prime }\left)\right\}$	xp	Rpr(xp)	Lpr(xp)
						(0,3,0)	1	0.5832
1	(0,3,0)	(0,2,0)	(0,2,0)	0.4320
		(1,2,0)	(1,2,0)	0.5504	0.5504	(1,2,0)	2	0.5504
2	(1,2,0)	(0,2,0)	(0,2,0)	0.4320
		(1,1,0)	(1,1,0)	0.5151	0.5151	(1,1,0)	3	0.5151
		(2,1,0)	(2,1,0)	0.4750
3	(1,1,0)	(0,2,0)	(0,2,0)	0.4104
		(1,0,0)	(1,0,0)	0.1127
		(1,1,1)	(1,1,1)	0.2169
		(0,1,0)	(2,1,0)	0.4521	0.4521	(2,1,0)	4	0.4521
		(2,1,0)
		(2,0,0)

The lower confidence limits on these four points, (0,3,0), (1,2,0), (1,1,0) and (2,1,0), are also given in Table 1 following Lemma 1 with the rank function R_pr(.) at the four points. For example, L_pr(1, 1, 0) = 0.5151 is the smallest solution of the following function of θ_pr, $\underset{(p_{11},p_{12})\in D_{p_r}\left({\theta }_{p_r}\right)}{\inf }[1-p_{p_r}(0,3,0;{\theta }_{p_r},p_{11},p_{12})-p_{p_r}(1,2,0;{\theta }_{p_r},p_{11},p_{12})-p_{p_r}(1,1,0;{\theta }_{p_r},p_{11},p_{12}\left)\right]=0.95$ which is also a special case of (1).

Example 1 (continued). Confidence intervals for θ_pr are reported in Table 2. For example, the 95% intervals [L_pr, +∞), [0, U_pr] and the 90% interval [L_pr, U_pr] for θ_pr are equal to [1.2906, +∞), [0, 15.9291] and [1.2906, 15.9291], respectively. It is clear that SCT increases the chance of having AHR because the lower-sided and two-sided intervals are inside (1, +∞). We obtain L_pr(1, 7, 1) = 1.2906 and L_pr(1, 1, 7) following Lemma 1 under the rank function R_pr(.), then U_pr(1, 7, 1) = 1/L_pr(1, 1, 7) = 15.9291 by Lemma 2. The computation takes time as the infimum in (14) is found over a two-dimensional region D_pr(θ_pr) many times.

Table 2.

Exact one-sided and two-sided intervals for θ_pr and θ_po in Example 1 when n₁₁ = 1, n₁₂ = 7, n₂₁ = 1, n₂₂ = 12.

	Two-sided 90%		Two-sided 95%
	Lower 95%	Upper 95%	Lower 97.5%	Upper 97.5%
θ pr	1.2906	15.9291	1.0448	23.0365
θ po	1.4149	26.9615	1.1956	37.4813

3.2 INTERVALS FOR θ_po

Similar to Lemma 2, we provide a one-to-one relationship between lower and upper confidence intervals for θ_po. Therefore, we only derive a lower confidence interval as upper one-sided and two-sided intervals follow Lemma 4.

Lemma 4: Suppose [L(N₁₁, N₁₂, N₂₁), +∞) is a lower one-sided 1 − α confidence interval for θ_po. Then

$$[0,U(N_{11},N_{12},N_{21}\left)\right]\stackrel{\mathit{def}}{=}[0,\frac{1}{L(N_{11},N_{21},N_{12})}]$$ (18)

is an upper one-sided 1 − α confidence interval for θ_po. Furthermore, [L(N₁₁, N₁₂, N₂₁), U(N₁₁, N₁₂, N₂₁)] is a two-sided 1 − 2α interval for θ_po.

The parameter space H_p is expressed in terms of (θ_po, p₁₁, p₂₁) with

$$p_{12}=\frac{{\theta }_{p_o}(p_{11}+p_{21})(1-p_{11})-p_{11}(1-p_{11}-p_{21})}{{\theta }_{p_o}(p_{11}+p_{21})+(1-p_{11}-p_{21})}$$ (19)

as follows: H_po = {(θ_po, p₁₁, p₂₁) : (p₁₁, p₂₁) ∈ D_po(θ_po), ∀ θ_po ∈ [0, +∞)}, where

$$D_{p_o}\left({\theta }_{p_o}\right)=\left\{\right(p_{11},p_{21}):p_{11}\le \frac{{(1-p_{21})}^2-{\theta }_{p_o}{p}_{21}^2}{1+({\theta }_{p_o}-1)p_{21}},p_{21}\le \frac{1}{\sqrt{{\theta }_{p_o}}+1}\},$$

which is a right curved triangle. See Figure S3 in Supplementary Materials for this set with different values of θ_po. The joint probability mass function p_p in (6) is rewritten as p_po(n₁₁, n₁₂, n₂₁; θ_po, p₁₁, p₂₁) = p_p(n₁₁, n₁₂, n₂₁; p₁₁, p₁₂, p₂₁), where p₁₂ is in (19).

The construction of an interval [L(X_p), +∞) depends on a rank function R_po(.) on S_p. Since θ_po and θ_pr have the same monotonicity in p₁₁, p₁₂ and p₂₁, Rules a), b) and c) for R_pr(.) in Section 3.1 are also valid for R_po(.). However, we add one more rule for R_po(.): d) R_po(n₁₁, n₁₂, n₂₁) = R_po(n₂₂, n₁₂, n₂₁), which follows that θ_po is invariant if p₁₁ and p₂₂ are exchanged. This rule in fact makes the sample space simpler. For a point x_p = (n₁₁, n₁₂, n₂₁) let ${\stackrel{‒}{x}}_p$ be a set in S_p:

$${\stackrel{‒}{x}}_p=\{\begin{array}{c}{\underset{¯}{x}}_p,\text{if}{n}_{11}=n_{22};\hfill \\ {\underset{¯}{x}}_p\cup \left\{\right(n_{22},n_{12},n_{21}\left)\right\},\text{otherwise}.\hfill \end{array}\phantom{\}}$$ (20)

By Rule d), the rank function R_po(.) assumes a constant value on set ${\stackrel{‒}{x}}_p$. Thus R_po(.) generates ties, and the confidence interval assumes a constant value on ${\stackrel{‒}{x}}_p$ that coincides with the nature of θ_po. When computing probability, each ${\stackrel{‒}{x}}_p$ is one sample point in a new sample space

$$S_p^n=\{{\stackrel{‒}{x}}_p=(n_{11},n_{12},n_{21}):n_{11}+n_{12}+n_{21}\in [0,n],n_{11}\le (n-n_{12}-n_{21})∕2\},$$ (21)

and the associated probability mass function is

$$p_{p_o}^n({\stackrel{‒}{x}}_p;{\theta }_{p_o},p_{11},p_{21})=\sum _{{\underset{¯}{x}}_p\in {\stackrel{‒}{x}}_p}{p}_{p_o}({\underset{¯}{x}}_p;{\theta }_{p_o},p_{11},p_{21}).$$ (22)

Each (n₁₁, n₁₂, n₂₁) that satisfies (21) is called the representation of ${\stackrel{‒}{x}}_p$. In this section, ${\stackrel{‒}{x}}_p$ can be the representation or the set in (20). The advantage of $S_p^n$ in (21) over S_p in (4) is that the former contains fewer elements. For example, when n = 3, there are twenty points in S_p but only thirteen points in $S_p^n$. Each set ${\stackrel{‒}{x}}_p$ and its representation are listed below:

${\stackrel{‒}{x}}_p$ in terms of (20)	the representation of ${\stackrel{‒}{x}}_p$	${\stackrel{‒}{x}}_p$ in terms of (20)	the representation of ${\stackrel{‒}{x}}_p$
{(0,0,0), (3,0,0)}	(0,0,0)	{(0,0,1), (2,0,1)}	(0,0,1)
{(0,0,2), (1,0,2)}	(0,0,2)	{(0,0,3)}	(0,0,3)
{(0,1,0),(2,1,0)}	(0,1,0)	{(0,1,1),(1,1,1)}	(0,1,1)
{(0,1,2)}	(0,1,2)	{(0,2,0),(1,2,0)}	(0,2,0)
{(0,2,1)}	(0,2,1)	{(0,3,0)}	(0,3,0)
{(1,0,0),(2,0,0)}	(1,0,0)	{(1,0,1)}	(1,0,1)
{(1,1,0)}	(1,1,0)

In the list above, for example, R_po(0, 3, 0) = 1 and R_po(0, 0, 0) = R_po(3, 0, 0).

The construction of the rank function R_po(.) is the same as R_pr(.) except that x_p and S_p in (4) and p_pr in (10) are replaced by ${\stackrel{‒}{x}}_p$ in (20), $S_p^n$ in (21) and $p_{p_o}^n$ in (22), respectively. In particular, we need to follow (12) through (16) to build up R_po(.). Once R_po(.) is defined on $S_p^n$, the smallest lower one-sided 1 − α confidence interval [L_po, +∞) for θ_po under R_po(.) is derived following Lemma 1, the smallest upper one-sided 1 − α confidence interval [0, U_po] follows Lemma 4, and [L_po, U_po] is a 1 − 2α interval.

Example 1 (continued). The three intervals above are also reported in Table 2. SCT does increase the odds of having AHR because the lower one-sided and the two-sided confidence intervals are inside (1, +∞). Again, we compute the lower one-sided interval first, then the upper one-sided and two-sided intervals follow Lemma 4.

As a closing remark for this section, the associate editor pointed out that the interval construction just developed can also be applied to the multinomial sampling in a 2 × 2 table to infer another odds ratio

$$\mathit{OR}=\frac{p_{11}{p}_{22}}{p_{12}{p}_{21}},$$

see Agresti (2002, p. 44). However, the technical details are quite different due to the structure of this odds ratio (OR), and will not be discussed in this paper.

4. CASE II: A TWO-ARM INDEPENDENT BINOMIAL EXPERIMENT

We also have a 2 × 2 table, but each row contains a binomial experiment as follows:

	S	F
experiment 1	S1, X, p1	F1, n1 − X, 1 − p1	n1
experiment 2	S2, Y, p2	F2, n2 − Y, 1 − p2	n2

where X ~ Bin(n₁, p₁) is a binomial observation with n₁ trials and a success probability p₁ and Y ~ Bin(n₂, p₂) is independent of X. The relative risk θ_ir and the odds ratio θ_io,

$${\theta }_{i_r}\stackrel{\mathit{def}}{=}\frac{p_1}{p_2}\mathit{and}{\theta }_{i_o}\stackrel{\mathit{def}}{=}\frac{p_1(1-p_2)}{p_2(1-p_1)},$$ (23)

are of interest. The subscript i stands for “independent proportions”. Compared with X_p = (N₁₁, N₁₂, N₂₁) that has three parameters p₁₁, p₁₂ and p₂₁ in Section 3, we now observe a simpler random vector X_i = (X, Y) with two parameters p₁ and p₂. In consequence, the interval construction is easier. The sample space and the parameter space are given below:

$$S_i=\{{\underset{¯}{x}}_i=(x,y):0\le x\le n_1,0\le y\le n_2,x\text{and}y\text{are integers}\},$$ (24)

and

$$H_i=\left\{\right(p_1,p_2):0\le p_1,p_2\le 1\}.$$ (25)

The joint probability mass function is

$$p_i(x,y;p_1,p_2)=\frac{n_1!}{x!(n_1-x)!}{p}_1^x{(1-p_1)}^{n_1-x}\frac{n_2!}{y!(n_2-y)!}{p}_2^y{(1-p_2)}^{n_2-y}.$$ (26)

Example 3. Consider a study in Essenberg (1952), where a two-arm randomized clinical trial was conducted for testing the effect of tobacco smoking on tumor development in mice. In the treatment (smoking) group, there were 23(= n₁) mice, and tumors were observed on 21(= x) mice; in the control group, n₂ = 32 and y = 19. Let p₁ and p₂ be the tumor rates for the treatment and control groups, respectively. A comparison between p₁ and p₂ using θ_ir and θ_io will be discussed for the smoking effect on tumor development.

4.1 INTERVALS FOR θ_ir

Similar to Lemmas 2 and 4, there exists a one-to-one relationship between lower and upper one-sided intervals.

Lemma 5: Suppose [L_n2,n1(Y, X), +∞) is a lower one-sided 1 − α confidence interval for 1/θ_ir = p₂/p₁. Then

$$[0,U(X,Y\left)\right]\stackrel{\mathit{def}}{=}[0,\frac{1}{L_{n_2,n_1}(Y,X)}]$$ (27)

is an upper one-sided 1 − α interval for θ_ir. Suppose [L_n1,n2(X, Y ), +∞) is a lower one-sided 1 − α interval for θ_ir, then [L_n1,n2(X, Y), U(X, Y)] is a two-sided 1 − 2α interval for θ_ir.

Following Lemma 5, only the construction of L_n1,n2(X, Y) for all possible n₁ and n₂ is needed. We drop the subscript and use L(X, Y) for future discussion. The interval construction depends on a rank function R_ir(.) on S_i. Here R_ir(.) should satisfy several rules that are from the monotonicity of θ_ir = p₁/p₂ as a function of p₁ and p₂.

• a)R_ir(n₁, 0) = 1. i.e., point (n₁, 0) is the largest.
• b)R_ir(x, y) ≤ R_ir(x − 1, y) for any x ∈ [1, n₁] and y ∈ [0, n₂].
• c)R_ir(x, y − 1) ≤ R_ir(x, y) for any x ∈ [0, n₁] and y ∈ [1, n₂].

These rules are shown in

$$\begin{array}{ccc}\hfill \hfill & \hfill \hfill & \hfill (x,y+1)\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \uparrow \text{Rule}\mathrm{b})\hfill \\ \hfill (x,y-1)\hfill & \hfill \stackrel{\text{Rule}\mathrm{c})}{\leftarrow }\hfill & \hfill (x,y)\hfill \end{array}$$

where “←” means “larger than or equal to”.

The parameter space H_i is rewritten in terms of (θ_ir, p₂) with p₁ = θ_irp₂ as follows:

$$H_{i_r}=\left\{\right({\theta }_{i_r},p_2):p_2\in D_{i_r}({\theta }_{i_r}\left)\stackrel{\mathit{def}}{=}\right[0,\min \{1,\frac{1}{{\theta }_{i_r}}\}],\forall {\theta }_{i_r}\in [0,+\infty \left)\right\},$$

where D_ir(θ_ir) is a line segment. See Figure S4 in Supplementary Materials. The joint probability mass function p_i for (X, Y) is rewritten as p_ir(x, y; θ_ir, p₂) = p_i(x, y; θ_irp₂, p₂), where p_i is given in (26). The construction for the rank function R_ir(.) is similar to Wang (2010). By induction, we start with R_ir(n₁, 0) = 1. Let E_pr,1 = {(n₁, 0)}. Suppose R_ir has been defined on k(≥ 1) sets E_ir,1, , , E_ir,k with values 1, 2, …, k. Let

$$N_{i_r,k}=\left\{\right(x,y)\in S_i:(x,y)\notin {\cup }_{i=1}^k{E}_{i_r,i};(x+1,y)\in {\cup }_{i=1}^k{E}_{i_r,i}\text{or}(x,y-1)\in {\cup }_{i=1}^k{E}_{i_r,i}\}$$

be the neighbor set of ${\cup }_{i=1}^k{E}_{i_r,i}$. Then, from

$$C_{i_r,k}=\left\{\right(x,y)\in N_{i_r,k}:(x+1,y)\notin N_{i_r,k}\text{and}(x,y-1)\notin N_{i_r,k}\},$$

a subset of N_ir,k, we pick the point(s) (x, y) that has the largest possible lower confidence limit to form a set E_ir,k+1 and assign a rank of R_ir(x, y) = k + 1 to any point (x, y) ∈ E_ir,k+1. This is similar to (15) and (16). Following induction, the construction of the rank function R_ir(.) is complete. Then the smallest lower one-sided 1 − α confidence interval [L_ir, +∞) under the rank function R_ir(.) is derived following Lemma 1, the smallest upper one-sided 1 − α confidence interval [0, U_ir] follows Lemma 5, and [L_ir, U_ir] is a 1 − 2α interval.

Example 3 (continued). We apply the three intervals above to Example 3 and then compare to exact intervals from SAS (Version 9.3). The intervals are reported in Table 3. For example, the 95% intervals [L_ir, +∞), [0, U_ir] and the 90% interval [L_ir, U_ir] for θ_ir are equal to [1.1671, +∞), [0, 2.0859] and [1.1671, 2.0859], respectively. The lower one-sided and two-sided intervals are subsets of (1, +∞), so the smoking group has a higher tumor rate than the control group. Regarding interval construction, we first compute L_ir = 1.1671 with n₁ = 23, n₂ = 32, x = 21 and y = 19 (using the rank function R_ir(.) and Lemma 1), then compute L_ir = 0.4794 using n₁ = 32, n₂ = 23, x = 19 and y = 21, and then U_ir = 1/0.4794 = 2.0859 (use Lemma 5). The calculation takes about 4 minutes on an HP-2760 laptop with Intel(R) Core(TM) i5=2520M CPU@2.50 GHz and 8 GB RAM using an R-code from the authors. SAS (Version 9.3) provides two exact intervals for θ_ir using “proc freq; exact relrisk;”. The first interval (default in SAS, Santner and Snell, 1980) is computed by inverting two separate one-sided exact tests that use the unstandardized relative risk as the test statistic; it is clearly too wide. The second interval (method=fmscore) also inverts tests, but uses the Farrington-Manning relative risk score statistic (Chan and Zhang, 1999), which is a less discrete statistic than the raw relative risk, and produces much sharper confidence limits (Agresti and Min, 2001) than the default. However, our two-sided intervals are shorter. See Section 4.3 for another comparison.

Table 3.

Exact one-sided and two-sided intervals for θ_ir, θ_io and p₁ − p₂ in Example 3 when n₁ = 23, x = 21, n₂ = 32, y = 19.

		Two-sided 90%		Two-sided 95%
		Lower 95%	Upper 95%	Lower 97.5%	Upper 97.5%
θ ir	Our method	1.1671	2.0859	1.1259	2.2289
	SAS(default)	0.1919	123356	0.0960	152092
	SAS(fmscore)	1.1755	2.1519	1.1204	2.2301
θ io	Our method	1.9534	33.0987	1.5832	48.5190
	SAS	1.6022	48.2034	1.3114	71.3653
p1 − p2	Wang (2010)	0.1330	0.4860	0.0947	0.5126

4.2 INTERVALS FOR θ_io

The construction of intervals [L_io, +∞), [0, U_io] and [L_io, U_io] for θ_io is similar to that for θ_ir since the monotonicity of θ_io as a function of p₁ and p₂ is the same for θ_ir.

First, we have the following and skip the proof.

Lemma 6: Suppose [L_n2,n1(Y, X), +∞) is a lower one-sided 1 − α confidence interval for 1/θ_io = p₂(1 − p₁)/[p₁(1 − p₂)]. Then

$$[0,U(X,Y\left)\right]\stackrel{\mathit{def}}{=}[0,\frac{1}{L_{n_2,n_1}(Y,X)}]$$ (28)

is an upper one-sided 1 − α interval for θ_io. Suppose [L_n1,n2(X, Y), +∞) is a lower one-sided 1 − α interval for θ_io, then [L_n1,n2(X, Y), U(X, Y)] is a two-sided 1 − 2α interval for θ_io.

Secondly, the rank function R_io(X, Y) needed for the construction of L(X, Y) satisfies the same three rules for R_ir(X, Y). However, there is a new computing issue. The parameter space H_i is rewritten in terms of (θ_io, p₂) with

$$p_1=\frac{{\theta }_{i_o}{p}_2}{1+({\theta }_{i_o}-1)p_2}$$ (29)

as follows: $H_{i_o}=\left\{\right({\theta }_{i_o},p_2):p_2\in D_{i_o}({\theta }_{i_o}\left)\stackrel{\mathit{def}}{=}\right[0,1],\forall {\theta }_{i_o}\in [0,+\infty \left)\right\}$, where D_io(θ_io) is an interval independent of θ_io. See Figure 1.

Figure 1.

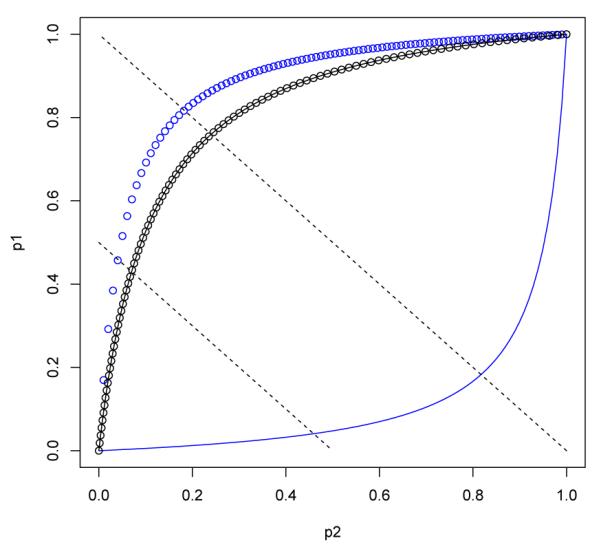
The parameter space H_io (the unit square), the sets of θ_io = 0.05 (the solid curve), θ_io = 20 with the equal p₂-spacing (the circle curve), θ_io = 10 with the equal u-spacing (the circle-line curve), two lines p₁ + p₂ = u for u = 0.5 (the dashed line, short) and u = 1 (the dashed line, long). Note θ_io ∈ [0, +∞), p₂ ∈ [0, 1] and u ∈ [0, 2].

The joint probability mass function p_i for (X, Y) is rewritten as p_io(x, y; θ_io, p₂) = p_i(x, y; p₁, p₂), where p_i and p₁ are given in (26) and (29), respectively. We need to compute probabilities on the curve of a fixed value for θ_io to find the infimum in (1) by a grid search on the curve. However, as shown in the circle curve of θ_io = 20 (Figure 1) that is obtained by partitioning [0, 1] with equal spacing in p₂, the partitioned points are clearly not evenly distributed on the curve. This is very different from Figure S4 (in Supplementary Materials), where the circle points are evenly distributed on the line of θ_ir = constant. Had we used the circle points in Figure 1 for a grid search for the infimum in (1), it would have led to an inaccurate numerical solution. So we introduce a new parameter u so that both p₁ and p₂ are functions of u ∈ [0, 2] at each fixed value of θ_io:

$$(p_2,p_1)=\{\begin{array}{c}\left(g_2\right(u),g_1(u\left)\right),\text{if}{\theta }_{i_o}\ne 1;\hfill \\ \left(\frac{u}{2},\frac{u}{2}\right),\text{otherwise},\hfill \end{array}\phantom{\}}$$ (30)

where

$$g_2\left(u\right)=\frac{u}{2}-\frac{1+{\theta }_{i_o}-\sqrt{{({\theta }_{i_o}-1)}^2{(u-1)}^2+4{\theta }_{i_o}}}{2({\theta }_{i_o}-1)},g_1\left(u\right)=\frac{{\theta }_{i_o}{g}_2\left(u\right)}{1+({\theta }_{i_o}-1)g_2\left(u\right)}.$$

This makes the selected points on the curve much more evenly distributed, as shown in the circle-line curve of θ_io = 10. More importantly, these points are symmetric about the line p₁+p₂ = 1, which does not occur for the circle points. In fact, point (p₂, p₁) is the intersection of the curve with a fixed value θ_io and the line p₁ + p₂ = u for any u ∈ [0, 2]. Therefore, we partition u on interval [0, 2] with an equal spacing instead of p₂ on interval [0, 1]. This change is clearly justified by a comparison of the two spacings in Figure 1 (θ_io = 10 vs θ_io = 20).

Lastly, we use the rank function R_io(.) to derive the smallest 1 − α interval [L_io, +∞) following Lemma 1, and obtain [0, U_io] of level 1 − α and [L_io, U_io] of level 1 − 2α by Lemma 6.

Example 3 (continued). Three proposed exact intervals and their correspondents from SAS based on Thomas (1971) (see also Gart, 1971) are reported in Table 3. Lower one-sided and two-sided intervals are inside (1, +∞) indicating that the odds of developing a tumor for the smoking group was higher than the control group. The proposed intervals are much smaller subsets of those from SAS. An R code for the proposed intervals is available. Exact intervals for p₁ − p₂ in Wang (2010) are also included in Table 3.

4.3 A SMALL COMPARISON

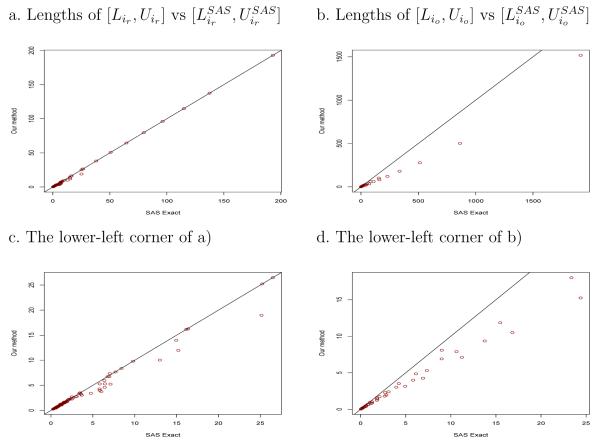
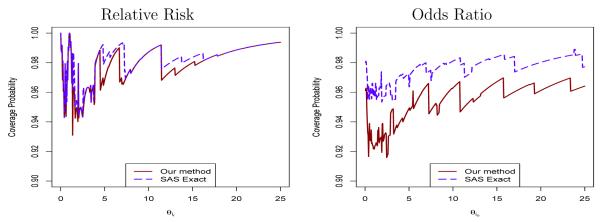
The comparison between exact and approximate intervals is not valid since they do not have the same confidence level 1 − α, even though the approximate interval claims to be of level 1 − α. Here we present a limited comparison between the proposed exact 90% confidence intervals [L_ij, U_ij] for j = r and j = o in Case II and the corresponding exact 90% intervals from SAS using “proc freq; exact relrisk(method=fmscore); exact or;”, denoted by $[L_{i_j}^{\mathit{SAS}},U_{i_j}^{\mathit{SAS}}]$. When n₁ = n₂ = 10, there are 121 intervals on all sample points. We only compare the interval lengths that are finite, and they are given in Figure 2. Each point in the plot has coordinate ($U_{i_j}^{\mathit{SAS}}-L_{i_j}^{\mathit{SAS}}$, U_ij − L_ij) at a sample point (x, y) ∈ S_i. Most points are in the lower triangle; also the average of the length ratio, $(U_{i_j}-L_{i_j})∕(U_{i_j}^{\mathit{SAS}}-L_{i_j}^{\mathit{SAS}})$, over these sample points is equal to 0.9490992 and 0.723343, respectively, for j = r and j = o. Both indicate a shorter length for the proposed intervals. Figure 3 gives the coverage probability comparison of these intervals. The left one in Figure 3, for example, is the plot of the infimum coverage probabilities of two intervals, [L_ir, U_ir] and $[L_{i_r}^{\mathit{SAS}},U_{i_r}^{\mathit{SAS}}]$, over set D_ir(θ_ir) versus θ_ir. The coverage probability of proposed intervals is closer to the nominal level than that from SAS. A similar result is expected for other sample sizes.

Figure 2.

The length comparison for the proposed two-sided 90% intervals and the 90% intervals from SAS in Case II when n₁ = n₂ = 10. The horizontal axis is the length of the SAS interval and the vertical axis is for the proposed interval. Each circle is the length of two intervals at a sample point.

Figure 3.

The coverage comparison for the proposed two-sided 90% intervals and the 90% intervals from SAS in Case II when n₁ = n₂ = 10.

5. SUMMARY

The relative risk and the odds ratio are commonly used in medical research to compare two treatments. Estimating them both with accuracy and precision is important for practitioners. In this paper, we propose twelve intervals in four sets, each set contains two one-sided intervals and one two-sided interval for each of four parameters θ_pr, θ_po, θ_ir, and θ_io. They are all of level 1 − α. The one-sided intervals are smallest under the rank functions, and are also admissible by the set inclusion criterion (see Wang, 2006). This indicates that a uniform improvement is impossible. An inductive construction is employed and in each step of the process, the shortest (best) interval is picked as shown, for example, in Eq (15). This, similar to Wang (2010, Proposition 3), indeed justifies the admissibility of the one-sided intervals. The computation time on intervals is affected by the number of nuisance parameters.