Predictions for Proteins, RNAs and DNAs with the Gaussian Dielectric Function Using DelPhiPKa

Abstract

We developed a Poisson-Boltzmann based approach to calculate the PK_a values of protein ionizable residues (Glu, Asp, His, Lys and Arg), nucleotides of RNA and single stranded DNA. Two novel features were utilized: the dielectric properties of the macromolecules and water phase were modeled via the smooth Gaussian-based dielectric function in DelPhi and the corresponding electrostatic energies were calculated without defining the molecular surface. We tested the algorithm by calculating PK_a values for more than 300 residues from 32 proteins from the PPD dataset and achieved an overall RMSD of 0.77. Particularly, the RMSD of 0.55 was achieved for surface residues, while the RMSD of 1.1 for buried residues. The approach was also found capable of capturing the large PK_a shifts of various single point mutations in staphylococcal nuclease (SNase) from PK_a -cooperative dataset, resulting in an overall RMSD of 1.6 for this set of pKa’s. Investigations showed that predictions for most of buried mutant residues of SNase could be improved by using higher dielectric constant values. Furthermore, an option to generate different hydrogen positions also improves PK_a predictions for buried carboxyl residues. Finally, the PK_a calculations on two RNAs demonstrated the capability of this approach for other types of biomolecules.

Introduction

Many biological functions of proteins are frequently affected by the ionization states of protein side-chains. Changes in the ionization states result in proton uptake/release, proton and electron transfer, and may affect protein folding, protein-ligand binding, ion transport through the channels and protein-protein interactions^1–6. These effects can be quantified by calculating the PK_a shift of ionizable residues from one state to another⁷. However, while the PK_a calculations are essential to understand all these effects, it is still challenging to accurately predict the PK_a values. The complexity stems from the coupling between ionization and conformational changes that either should be explicitly modeled or implicitly mimicked⁸.

There has been significant progress in the development of computational methods for PK_a calculations⁸. Generally, they can be grouped into two major classes: macroscopic and microscopic methods. Methods based on continuum electrostatics can be considered as being on the border between macroscopic and approaches since they use atomic presentation of the macromolecule. Macroscopic methods^9–17 are faster while microscopic methods^1,18–20 provide more details.

Among microscopic approaches, one distinguishes molecular dynamics (MD) and quantum mechanics (QM) based approaches. The MD based methods apply either constant-pH MD or free energy perturbation techniques to model the ionization states in proteins^21–26. The QM and QM/MM methods calculate the individual PK_a in the context of proteins by solving the Schrodinger equation (SE)^27–32.

Among the macroscopic methods, one distinguishes continuum electrostatics approaches and methods using empirical functions. The Poisson-Boltzmann (PB) equation based continuum electrostatics (CE) model allows the calculation of electrostatic potentials with a non-uniform distribution of dielectric medium and ionic strength^33–35. The Generalized Born (GB) based method is an alternative to provide the electrostatic energies via an analytical approximation^36,37. For the purpose of efficiency, the empirical methods were developed^38–42. The empirical methods use knowledge-based parameters for optimization and large database for training.

In the PB based methods, the macromolecule is described as a homogeneous medium with a low dielectric constant immersed in a solvent with a high dielectric constant. In this model the two major energy components affecting the pKa calculations are: the energy cost of moving a residue from water to protein interior and the screening of charge-charge interactions in the protein^43–46. In wild-type proteins, these two effects typically oppose each other. Thus, the favorable charge-charge pairwise interactions between the ionizable residues and neighboring charges and dipoles could compensate for the desolvation penalty and stabilize the buried residue in its ionized state. The outcome depends on many factors, one of which is the value of the dielectric constant of the macromolecules. Some researchers proposed the dielectric constant for proteins is as low as 4^47–49 while other values from 8 to 20^50–52. However, the appropriate dielectric constant of a protein depends on both the polarity of residues and the local protein polarizability. Many approaches were developed to improve the accuracy of calculating the electrostatics in proteins, such as using multiple dielectric constants for protein representing different types of residues⁵³, adding side-chain flexibility^54–56, changes in hydrogen bond orientations^57,58, multi-conformation and side-chain rotamers optimized in continuum electrostatics (MCCE)^50,51,59 and smooth Gaussian function representing the dielectric constant throughout the space⁶⁰. Among various means of approaches, the Gaussian-based method, which generates a smooth dielectric function for the entire space (the protein and water phase) was demonstrated to be more accurate⁶⁰. The method, which has been implemented in DelPhi program, shows that the generated smooth dielectric function results in dielectric constant of 6–7 in the protein interior and 20–30 at the protein-water interface, which is consistent with previous MD-based work⁶¹.

Here we propose a method to calculate PK_a s of ionizable groups in proteins, RNAs and single stranded DNAs. The method is implemented in an object-oriented C++ program that (1) uses Gaussian-based smooth function to mimic conformational changes associated with ionization changes and (2) calculates the electrostatic energies without defining the molecular surface. Several study cases are discussed for the validity of the program and two large dataset with different properties are used to test and benchmark the approach.

Methods

The PK_a value of an ionizable residue i in a macromolecule can be calculated either from the shift of the residue solvent reference PK_a (Eq.1), or from the one-half point of the probability of protonation states as a function of pH (titration curve).

$${\mathit{pKa}}_i(\text{protein})={\mathit{pKa}}_{i,\mathit{ref}}(\text{solvent})+\mathrm{\Delta }{\mathit{pKa}}_i(\text{solvent}\Rightarrow \text{protein})$$ (1)

However, in both approaches, calculating the electrostatic free energy of the ionizable residue in its protonated and deprotonated states is essential. Here the electrostatic energies are calculated via the modified DelPhi as a built-in module with the input structure as a 2-dimensional vector and output energy terms as an energy matrix. Below we describe the corresponding modules within the algorithm.

Protonation

Most of available structural files do not have protons and hydrogens must be generated in silico. Here a residue topology based approach is applied to generate the hydrogen positions. For each residue, the corresponding heavy atom bond connectivity, hydrogen positions and residue types are labeled in the topology file, as well as the reference PK_a value for each ionizable residue group. For PK_a calculations of RNA and single stranded DNA, the structural information of nucleic acids is also included in the topology. The structural modification for each residue or nucleic acid upon user request is allowed by revising the topology information. The adjustment of reference PK_a value for each ionizable residue can be done via editing the topology. Taking into account that the extra hydrogen of carboxyl groups (glutamic acid and aspartic acid) can be bound to either oxygen, two conformations are provided for each of those residues. An option is provided such that users are allowed to choose either of them but the default choice is set to be OE1 (Glu) and OD1 (Asp), which is selected based on the benchmarking results (Attaching the extra hydrogen to OD2/OE2 results in about 10% worse performance for both PPD and pKa-cooperative data sets). The His neutral form was considered to have proton bound at ND1.

The atomic charges and radii are accessed from pre-calculated force-field parameters. In order to be consistent with Delphi, it is designed to read the same force-field parameters as Delphi uses. Currently it supports AMBER, CHARMM and PARSE force-fields (the corresponding files can be downloaded from http://compbio.clemson.edu/delphi). The protonated structure with atomic charges and radii is not only the intermediate structure that is being subjected to the PK_a calculation, but we also provide an option to output standard Position Charge Radius (PQR) format for the setup of Poisson-Boltzmann electrostatics calculations, e.g. applied as the input of Delphi calculations.

Electrostatic free energy calculation

Smooth Gaussian based dielectric model

The smooth Gaussian function based model has been described in the previous work⁶⁰. Here we provide just the summary of the corresponding methodology. The density of the atoms is modeled as:

$${\rho }_i(r)=exp\left[-\frac{r_i^2}{{\sigma }^2·R_i^2}\right],$$ (2)

where ρ_i(r) is the atomic density at position r generated by atom i, R_i is the radius of atom i determined by the empirical force field parameter, r_i is the distance between the center of atom i and position r, and σ is the variance of Gaussian distribution.

The total atomic density can be expressed as:

$${\rho }_{\mathit{mol}}(r)=1-{\mathrm{\Pi }}_i[1-{\rho }_i(r)],$$ (3)

where the left term ρ_mol(r) represents the total atomic density at position r generated by the entire molecule, ρ_i(r) is the atomic density generated by the single atom i. And the dielectric distribution is calculated with the atomic density as:

$$\epsilon (r)={\rho }_{\mathit{mol}}(r)·{\epsilon }_{\mathit{ref}}+(1-{\rho }_{\mathit{mol}}(r))·{\epsilon }_{\mathit{water}},$$ (4)

where ε(r) represents the dielectric distribution of the molecule, ε_ref is the reference dielectric constant for protein and ε_water is the dielectric constant for water.

Determining the electrostatic free energy of each microstate

The electrostatic interactions are calculated with the Poisson-Boltzmann equation by using Delphi with smooth Gaussian dielectric function. To calculate the electrostatic energy of the ith ionizable residue, we first charge the side-chain atoms of the ith residue only and leave the rest of the structure uncharged (including the backbone of the ith residue). The electrostatic potentials generated by the charged side-chain of ionizable residue i at each atom of the protein are obtained by invoking the “site potential” (FRC) function of Delphi energy module. In this procedure, atomic charges and radii are assigned with corresponding force-field parameters. According to the input parameters ε_ref, ε_water and variance of Gaussian distribution σ, the Gaussian dielectric distribution is generated over the macromolecule with avoiding defining the molecular surface. Then three focusing calculations are performed to reach a final resolution of 4 grids/Å.

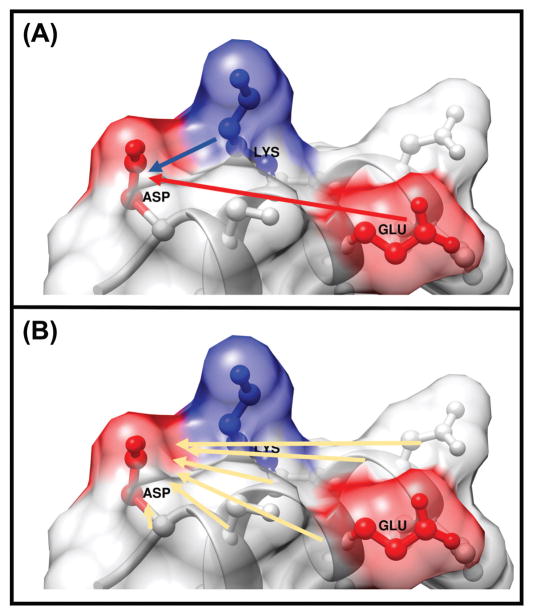
Several energy terms are calculated. The charge-charge pairwise interaction energy between the side-chain of ith residue and other ionizable residues (Fig.1A) is obtained as:

$$G_{i,j(\mathit{charged})}^{\mathit{pairwise}}={\mathrm{\sum }}_{j\in \mathit{ionizable},j\ne i}{q}_{j,\mathit{sidechain}}{\varnothing }_{j,\mathit{sidechain}}$$ (5)

where q_j,sidechain and ∅ _j,sidechain represent the atomic charges and electrostatic potentials for the side-chain atoms of ionizable residues (excluding the ith residue itself).

Figure 1.

Cartoon presentations for (A) Pairwise interaction energy of the ionizable residue ASP side-chain interacted with ionizable residue side-chains of GLU and LYS. (B) Polar energy of the residue ASP side-chain interacted with side-chains of non-ionizable residues and backbones of all residues (including the backbone of ASP itself).

The polar energy term of the electrostatic interactions between the charged residue i and other residues is obtained as:

$$G_{i,\mathit{charged}}^{\mathit{polar}}={\mathrm{\sum }}_{j\in \mathit{ionizable}}{q}_{j,\mathit{backbone}}{\varnothing }_{j,\mathit{backbone}}+{\mathrm{\sum }}_{j\notin \mathit{ionizable}}{q}_j{\varnothing }_j$$ (6)

where q_j,backbone and ∅ _j,backbone are atomic charges and electrostatic potentials for backbone atoms of ionizable residues including the ith residue itself (Fig.1B). And q_j and ∅_j are atomic charges and electrostatic potentials for the backbone and side-chain atoms of non-ionizable residues, respectively.

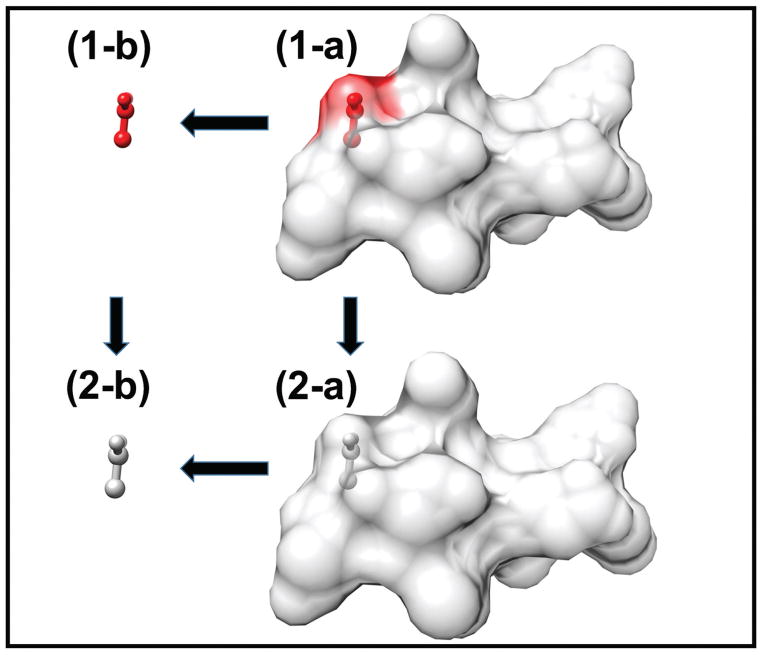
The reaction field energy $G_{i,\mathit{charged}}^{\mathit{rxn}}(\mathit{protein})$ of the ionizable residue i embedded in the protein is calculated as the total grid energy generated by DelPhi energy module as previously described⁶². In order to obtain the desolvation energy (Fig.2), we move the charged side-chain of the ith residue to the water and apply the same computational box with the same grid resolution to perform three focusing calculations again. Thus, the reaction field energy $G_{i,\mathit{charged}}^{\mathit{rxn}}(\mathit{water})$ of the ionizable residue ith in the water is obtained as the total grid energy difference from DelPhi calculation. Thus, the desolavtion energy of the residue i in its charged state is expressed as:

$$\mathrm{\Delta }{G}_{i,\mathit{charged}}^{\mathit{desol}}=G_{i,\mathit{charged}}^{\mathit{rxn}}(\mathit{protein})-G_{i,\mathit{charged}}^{\mathit{rxn}}(\mathit{water})$$ (7)

Figure 2.

Thermodynamic cycle shows the calculation of the desolvation energy of the ionizable residue side-chain. (1-a) The side-chain is protonated and embedded in the protein interior. (1-b) The side-chain is protonated in the water. (2-a) The side-chain is deprotonated and embedded in the protein interior. (2-b) The side-chain is deprotonated in the water.

Next, turning the side-chain of ith residue to its neutral state (neutral state refers to zero net charge while atoms still have partial charges) and following the same protocol, another three energy components ${\mathrm{G}}_{\mathrm{i},\text{neutral}}^{\text{polar}},{\mathrm{G}}_{\mathrm{i},\mathrm{j}(\text{neutral})}^{\text{pairwise}}$ and $\mathrm{\Delta }{G}_{i,\mathit{neutral}}^{\mathit{desol}}$ are calculated. By extracting them from the energies of charged state, 

$$\mathrm{\Delta }{G}_i^{\mathit{polar}}=G_{i,\mathit{charged}}^{\mathit{Polar}}-G_{i,\mathit{neutral}}^{\mathit{Polar}},$$ (8)

$$\mathrm{\Delta }\mathrm{\Delta }{G}_i^{\mathit{desol}}=\mathrm{\Delta }{G}_{i,\mathit{charged}}^{\mathit{desol}}-\mathrm{\Delta }{G}_{i,\mathit{neutral}}^{\mathit{desol}},$$ (9)

we obtain the total electrostatic energy shift due to the change of protonation state, which is expressed as:

$$\mathrm{\Delta }{G}_i=\gamma (i)[2.3k_{b}T(pH-{\mathit{pKa}}_i^{\mathit{ref},\mathit{solvent}})]+(\mathrm{\Delta }{G}_i^{\mathit{polar}}+\mathrm{\Delta }\mathrm{\Delta }{G}_i^{\mathit{desol}})+{\mathrm{\sum }}_{j=1,j\ne i}^N\mathrm{\Delta }{G}_{i,j}^{\mathit{pairwise}}$$ (10)

If the protein consists of many ionizable residues, the computational demand will be significant, while the calculations for each ionizable residue are independent. Thus, parallelizing these computations is a necessity to improving the efficiency. Here we report an approach that the calculation for each ionizable residue is distributed on dedicated CPUs with MPI implementation. We show that it significantly improves the performance (see performance benchmark in Result section).

Determining the probability of protonation states

The distribution of microstate electrostatic energy is used to determine the probability of ionization of the ith residue at the given pH. If the system has M microstates and with energy Gm(pH) at its mth microstate, the probability of ith residue to be ionized at particular pH is given by the Boltzmann distribution formula:

$${\mathrm{P}}_i(\text{pH})=\frac{{\mathrm{\sum }}_{m=1}^M\chi (i)·e^{-G_m(\text{pH})/kT}}{{\mathrm{\sum }}_{m=1}^M{e}^{-G_m(\text{pH})/kT}}$$ (11)

χ(i)is 1 if the ith residue is ionized and 0 if it is neutral. k is the Boltzmann constant. Then the Boltzmann distribution of ionized states is calculated as a function of pH, resulting a 2D titration curve where the residue i possesses 50% probability of being protonated is designated as the ith value. Each ionizable residue has two microstates: protonated and deprotonated. For the system with N ionizable residues, the total microstates the system possesses is M = 2^N . The Boltzmann sum needs to be calculated 2^N times per ionizable residues and 2^N for the entire system. If the system has more than 30 ionizable residues, even for the modern computer and computing clusters, it is still extremely computationally intensive and inefficient. An alternative approach is required to simplify the modeling, as described below.

Network Partition

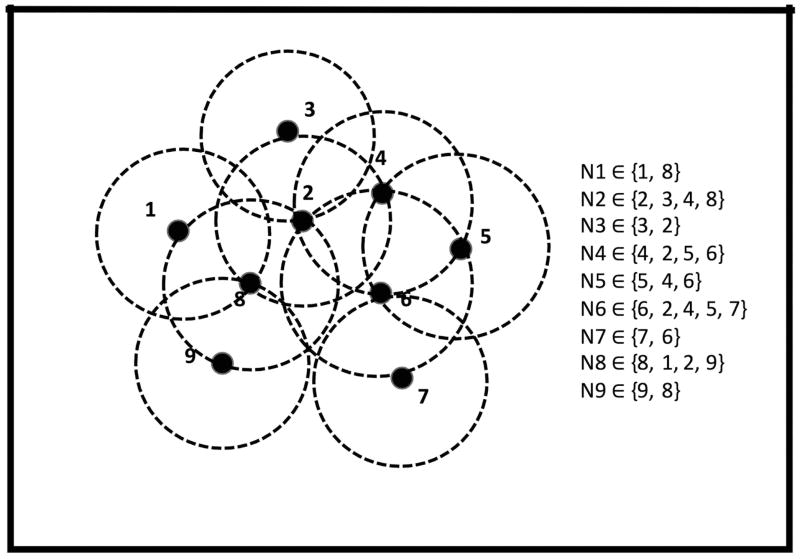
Networking is a geometrical distance based clustering protocol, which allows duplicate ionizable residues to appear in more than one partition. This eliminates the errors associated with wrong partitioning of strongly interacting groups. To partition the macromolecule with N ionizable residues into groups, we first label the geometric center of the side-chain of each ionizable residue as the representing point (RP) to obtain N RPs. The cartoon presentation (Fig. 3) demonstrates the system with 9 RPs grouped into 9 networks. Each RP locates its neighboring RPs within a given radius (a threshold that is set up by the input parameter, default value 10A) and constitutes a network. For efficiency, the ordering within each network is maintained based on the distance and the amount of RPs within a network is limited to be 20. If two networks consist of the same elements, one of them will be eliminated. The duplicate RP is tolerable within different networks. For example, P2 appears in five networks (N2, N3, N4, N6, N8). For these networks, the change of P2 protonation states will be explicitly taken into account. For the RP not in the network, its protonation state is identified by the previous calculation and the microstate is fixed with a particular energy configuration. By this protocol, the system results in 104 microstates, which is far less than the 2⁹ microstates without a partitioning algorithm.

Figure 3.

A pseudo protein molecule contains 9 ionizable residues. A representing point (RP) with labeled index represents the center of mass of each ionizable residue side-chain. Network partitioning algorithm is applied to the system and generates 9 networks based on the geometrical distance. For the residues within a network, their protonated and deprotonated states are taken into account explicitly, which results in 2^N microstates if N residues possessed by that network. For residues out of the network, the fixed microstate of protonation obtained from the previous calculation is applied.

Results and Discussion

Test case of hen egg-white lysozyme

The crystal structure of the lysozyme (PDB ID: 4lzt) is used to test the approach. Lysozyme is a small molecule with several salt-bridges and pockets. Although there are already many methods applied to calculate the PK_as of ionizable residues^59,63 and were shown to have good agreement with experimental values, still several residues are difficult to predict including buried residue Glu35 in the deep pocket and surface exposed residue Asp66.

The parameters used in DelPhiPKa are σ = 0.7, ε_ref = (optimal values obtained from the benchmark, see below), with PARSE force field for protonation and energy calculation. For comparison, two additional calculations with DelPhi homogeneous dielectric model⁶⁴ were performed with ε_protein as 4 and 8 with PARSE force-field parameter as well.

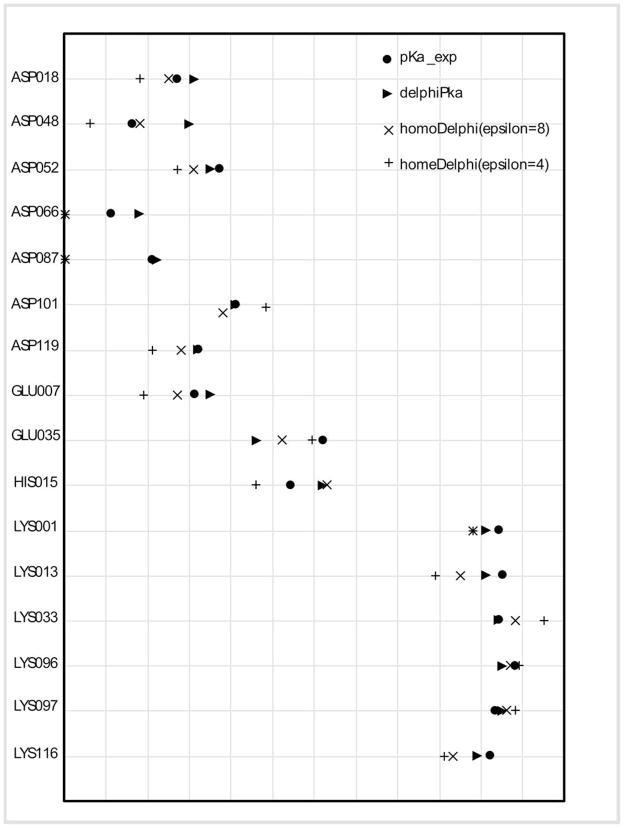
Results from homogenous dielectric model with ε_protein = 4 show that there are 14 predictions with greater than 0.5 pK units shift against experimental data (Table 1), which includes 11 residues which pKa’s are underestimated. By increasing the dielectric constant to 8, the number of outliers decreases to 10 including 8 residues with underestimated pKa’s. The results from DelPhiPKa show significant improvement over the homogenous dielectric models (Fig.4) by resulting in only 4 predictions with greater than 0.5 pK shift compared with the experimental results. Further investigations show that for buried residue Glu35 (75% buried), the PK_a value is underestimated (the calculated value as 4.6 vs. the experimental value of 6.2). However, if one increases σ to 9.0, the calculated PK_a value is 5.8, which is very close to the experimental data. In contrast, for residue Asp66 that is located on the surface, DelPhiPKa predicted PK_a value of 1.8 while other two homogeneous models both resulted in zero. However, if we decrease σ to 0.65, the prediction becomes 1.4, which is in better agreement with the experimental result. These observations show that the accuracy of predictions depends on the local dielectric constant that the Gaussian function assigns. For buried residues like Asp66, the buried side-chain and the surrounding environment make the residue less flexible and not capable in response to the local electrostatic field. Thus, the dielectric constants for those residues should be low and increasing σ causes the Gaussian function to assign a lower dielectric value. In contrast, surface residues are much more flexible and decreasing σ results in those residues being modeled with high dielectric values. Another reason that resulted in 0.7 pK of Asp66 is the hydrogen conformation. As the aspartic acid side-chain has two positions that hydrogen could be bound in its protonated state, the electrostatic energy (especially electrostatic polar energy component) is affected by this fact. Taking into account of this and assigning the proton position accordingly the predicted pKa is 1.5, which is very close to the experimental value.

Table 1.

pKa calculations with DelPhiPKa and DelPhi homogeneous dielectric model with epsilon=4 and epsilon=8 on Lysozyme (4lzt) 16 titratable residues. (Bold fonts represent that the difference between the calculated result and the measured value is greater than 0.5 pK units.)

Residue	exp. PKa	Homogeneous Delphi with εprotein = 4	Homogeneous Delphi with εprotein = 8	DelPhiPka
ASP018	2.7	1.8	2.5	3.1
ASP048	1.6	0.6	1.8	3
ASP052	3.7	3.1	2.7	3.5
ASP066	1.1	0	0	1.8
ASP087	2.1	0	0	2.2
ASP101	4.1	6.1	5.1	4.1
ASP119	3.2	2.1	2.8	3.2
GLU007	3.1	1.9	2.7	3.5
GLU035	6.2	5.93	5.2	4.6
HIS015	5.4	4.6	6.3	6.2
LYS001	10.4	9.8	9.8	10.1
LYS013	10.5	8.9	9.5	10.1
LYS033	10.4	11.5	10.8	10.4
LYS096	10.8	10.9	10.7	10.5
LYS097	10.3	10.8	10.6	10.5
LYS116	10.2	9.1	9.3	9.9

Figure 4.

Calculated pKa shifts compared with experimental measurements for 16 ionizable residues of lysozyme.

Benchmarks on two large datasets

We performed benchmarks on two large datasets in order to test the accuracy of the predictions. The first dataset contains 36 proteins with total 340 residues from Protein PK_a Database (http://pka.engr.ccny.cuny.edu/). We used only X-ray structures which are available from PDB Bank⁶⁵, which results in 32 proteins with total 302 titratable residues. All PDBs are obtained from PDB bank and fixed for missing atoms and residues by using PROFIX⁶⁶. All substrates (e.g. PO4 and SO4 groups, solvent exposed ions) and crystal waters are removed. The experimental PK_a values are from NMR measurements^67–69. The second dataset used here for benchmarking is PK_a -cooperative dataset from Garcia-Moreno’s lab^70–73, which contains a large number of PK_a values for mutants at various positions in the highly stable Δ+PHS variant of staphylococcal nuclease (SNase). There are 19 measured PK_a values from the wild-type SNase structure (PDB ID: 1stn)⁷⁴ and its variant Δ+PHS (PDB ID:3bdc)⁷². For other experimentally determined 20 PK_a values there are X-ray structures of SNase with mutations. And the rest 70 structures are artificially modeled mutants from the structure of Δ+PHS by using the SCAP program from Jackal package⁶⁶ with its built-in CHARMM heavy atom model. Among theme, 8 structures resulted in total side-chain energies greater than 1000kt due to overlaps between the mutated residue side chain and surrounding atoms, which are removed from the benchmark dataset. Thus, total 101 residues were used in the second benchmark. All structures were optimized using NAMD⁷⁵ with 5000 steps energy minimization for side-chain relaxation to reduce the clashes resulting from in silico generated mutations.

Determining optimal parameters

Since smooth Gaussian dielectric model has two adjustable parameters, the reference dielectric constant for protein (ε_ref) and the Gaussian variance (σ), the optimal values for these two parameters were investigated. The testing was performed on both datasets with AMBER, CHARMM and PARSE force-field parameters. The ε_ref was varied from 4 to 10 with an increment of 2, while σ was varied from 0.65 to 1.0 with an increment of 0.01. Total calculations generated 144 PK_a values for each individual ionizable residue and were used to compare with the experimental data. Thus, the optimal parameters were obtained by finding the set with the lowest RMSD between calculated and experimental values.

The results for PPD dataset with the AMBER force field are shown in Table 2. As ε_ref varies from 4 to 10, the calculated PK_a s become in better agreement with experimental data (smaller RMSD). With ε_ref =8, we obtained the best RMSD against experimental values. The Gaussian variance was also found to significantly affect the results (varying σ from 0.6x to 0.9x). However, the effect becomes negligible when it is varied from 0.65– 0.75. Similar investigation was done for pKa-cooperative dataset. Combining the results from three force fields, the optimal parameter σ =0.70 is found for the PPD dataset, and σ=0.93 is found for the PK_a -cooperative dataset, which is consistent with the previous work⁶⁰. The different optimal σ obtained for PPD and pKa-cooperative datasets, perhaps, indicates that σ=0.70 should be used for modeling naturally occurring titratable groups, while σ=0.93 for artificially designed mutants. These parameters will be used as default values for later benchmarks and future calculations.

Table 2.

Results of benchmarking on the PPD dataset with AMBER force field. The reference dielectric constant for the protein (ε_ref) is adjusted from 4 to 10 with an increment of 2 and the Gaussian variance (σ) is adjusted from 0.65 to 1.0 with an increment of 0.01. The lowest total RMSD of each set of parameters is listed in ascending order. For each ε_ref value, first 5 results are listed.

εref	Gaussian Variance (σ)	RMSD (TOTAL)
10	0.73	0.7947
10	0.67	0.7961
10	0.71	0.7983
10	0.70	0.7983
10	0.66	0.8002
8	0.68	0.7679
8	0.69	0.7694
8	0.70	0.7712
8	0.67	0.7725
8	0.71	0.7731
6	0.66	0.8277
6	0.69	0.8281
6	0.67	0.8287
6	0.71	0.8304
6	0.73	0.8321
4	0.65	0.8713
4	0.67	0.8746
4	0.66	0.8778
4	0.71	0.8804
4	0.69	0.8811

Statistics and benchmark results

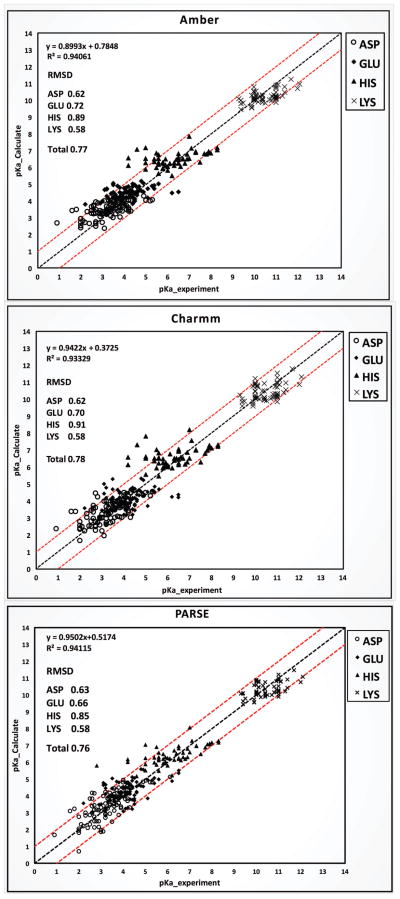
With the above-determined optimal parameters, the calculated PK_a results achieved a total RMSD less than 0.8 (Fig 5) on the PPD dataset with three force fields (RMSD=0.77 for AMBER; RMSD=0.78 for CHARMM and RMSD=0.76 for PARSE) (individual pKa’s are reported in SI). Each individual type of titratable residue achieved similar RMSD as well (RMSD≈0.6 for ASP; RMSD≈0.7 for GLU; RMSD≈0.9 for HIS; RMSD≈0.6 for LYS). The correlation coefficients were 0.94, 0.93, and 0.94 for AMBER, CHARMM and PARSE force field, respectively.

Figure 5.

Benchmark of calculated pKa values with DelPhiPKa (302 residue pKa values) with AMBER, CHARMM and PARSE force fields against experimental measured values of the PPD dataset. Total RMSD along with individual residue RMSD with each force field are marked. Red lines are +/− 1.0 pK shift compared with experimental values.

Out of 302 calculated PK_a values with PARSE force field, 180 (59.4%) RMSDs are less than 0.5 pK units (Table 3A) and 271 (89.7%) RMSDs are less than 1.0 pK unit compared with the experimental data. With other two force fields, it achieved similar results, which are 85.4% and 91.1% of predictions for the dataset are less than 1.0 pK compared with the experimental data. With all three force fields, it results in equal or less than 5 residues with calculated greater than 2.0 pK units shift against experimental values.

Table 3.

(A) Statistics of RMSD and (B) Residue positions of the PPD dataset.

(A)		Number / Percentage
		AMBER	CHARMM	PARSE
	0 < RMSD < 0.5	179 / 59.3%	178 / 58.7%	180 / 59.4%
	0.5 < RMSD < 1.0	79 / 26.2%	97 / 32.0%	91 / 30.0%
	1.0 < RMSD < 2.0	41 / 13.6%	22 / 7.3%	29 / 9.6%
	2.0 < RMSD	3 / 1.0%	5 / 1.7%	2 / 0.6%
(B)		RMSD			Number / Percentage
		AMBER	CHARMM	PARSE
	Exposed (surface)	0.58	0.55	0.53	218 / 72.2%
	Smaller than 50% Buried	0.81	0.88	0.82	53 / 17.5%
	Greater than 50% Buried	1.09	1.22	1.11	31 / 10.3%

In PPD dataset, 218 out of 302 (72.2%) residues are located on the surface and exposed to the solvent whose PK_a predictions result in an average RMSD≈0.55 with three force fields (Table 4B). However, for 31 residues (10.3%) with more than 50% of side-chain per residue buried, the average RMSD results in 1.14, which is 40% greater than the total RMSD of the dataset. Further investigations show that for buried residues, increasing σ value to 0.95 results in a slight improvement of the predictions. Although a few predictions remain unchanged or get worse, there are 20 predictions with 0.5–2.0 pK units shift towards the experimental values, which results the average RMSD of total 31 buried residues in 0.98. Histidine residues are most difficult to obtain accurate predictions. The average RMSD for His is obtained as 0.88 with three force fields, while RMSDs for other residues are between 0.6 and 0.7. Further analysis buried histidine residues with pK units shift greater than 2.0 against experimental values indicated that most of them are overestimated. Thus, an adjustment of 1.0 pK unit to the reference PK_a value of histidine residue would improve the predictions.

Table 4.

(A) Statistics of RMSD and (B) Residue positions of the pKa-cooperative dataset.

(A)		Number / Percentage
		AMBER	CHARMM	PARSE
	0 < RMSD < 1.0	54 / 53.5%	55 / 54.5%	58 / 57.4%
	1.0 < RMSD < 2.0	22 / 21.8%	31 / 30.7%	24 / 23.8%
	2.0 < RMSD < 3.0	23 / 22.8%	10 / 9.9%	15 / 14.9%
	3.0 < RMSD	2 / 2.0%	5 / 5.0%	4 / 4.0%
(B)		RMSD			Number / Percentage
		AMBER	CHARMM	PARSE
	Exposed (surface)	0.83	1.11	0.97	14 / 13.9%
	Smaller than 50% Buried	0.93	1	1.07	20 / 19.8%
	Greater than 50% Buried	1.86	1.65	1.61	67 / 66.3%

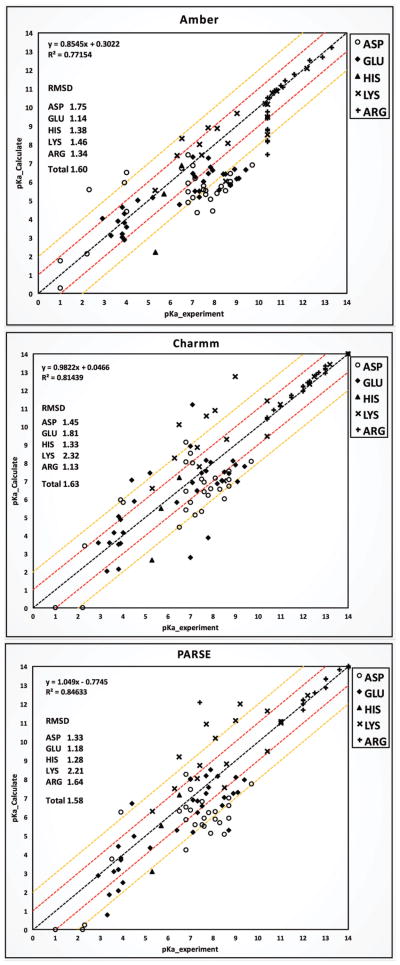
In the PK_a -cooperative dataset, 66% (Table 4B) of residue side-chains are more than 50% buried in the protein and only 14% of residues in the dataset are on the surface. We obtained the lowest total RMSD for this dataset with the optimal Gaussian variance of 0.93. Although the total RMSDs with three force fields are close (RMSD=1.60 for AMBER; RMSD=1.63 for CHARMM; RMSD=1.58 for PARSE), the RMSD for individual residue type is quite different as it is shown in Fig 6 (individual pKa’s are reported in SI). The RMSDs for ASP residues with PARSE and CHARMM achieved 1.33 and 1.45 respectively, while it is 1.75 with AMBER. The RMSDs for GLU residues with AMBER and PARSE achieved 1.14 and 1.18 respectively, but it is as large as 1.81 with CHARMM. With AMBER, the PK_a calculations for LYS achieved the best RMSD, which is 1.46. However, poor results were obtained with PARSE (RMSD=2.21) and CHARMM (RMSD= 2.32).

Figure 6.

Benchmark of calculated pKa values using DelPhiPKa with AMBER, CHARMM and PARSE force fields against experimental values of the pKa-cooperative dataset (101 residue pKa values). Total RMSD along with individual residue RMSD with each force field are marked. Red lines are +/− 1.0 pK shift compared with experimental values. Yellow lines are +/− 2.0 pK shift compared with experimental values.

About 55% of calculations on this dataset result in the RMSD less than 1.0 pK unit, however 15% to 23% of prediction are found to result in the RMSD greater than 2.0 pK (Table 4A). For 67 out of 101 (66.3%) residues buried in proteins, the RMSD is found to be 1.86 with AMBER force field and about 1.6 with CHARMM and PARSE. Since buried residue side-chains are less flexible than the ones exposed to solvent, the corresponding dielectric constants should be larger. It is found that increasing the Gaussian variance effectively favors the predictions for the buried residues, however, degrades the predictions for the exposed residues. Thus, future development of the present method could include variable Gaussian variance depending of the degree of burial of the titratable groups.

Further investigation of predictions with greater than 2.0 pK error shows that about 70% of these predictions are mutations involving carboxyl residues, such as F34D/E, L36D/E, V66D/E, V99D/E, L103D/E and V104D/E. Most of them are completely buried in the protein. Adjusting the position of hydrogen for these carboxyl residues affects the calculated PK_a values. However, until an effective protocol of determining the hydrogen conformation due to the surrounding environment is developed, it is unfair to include this “artificial” correction in the benchmark. Extending the capabilities of DelPhiPKa algorithm to include alternative hydrogen positions will alter the Gaussian-based dielectric map, even for buried residues, and because of that, such an option was not considered.

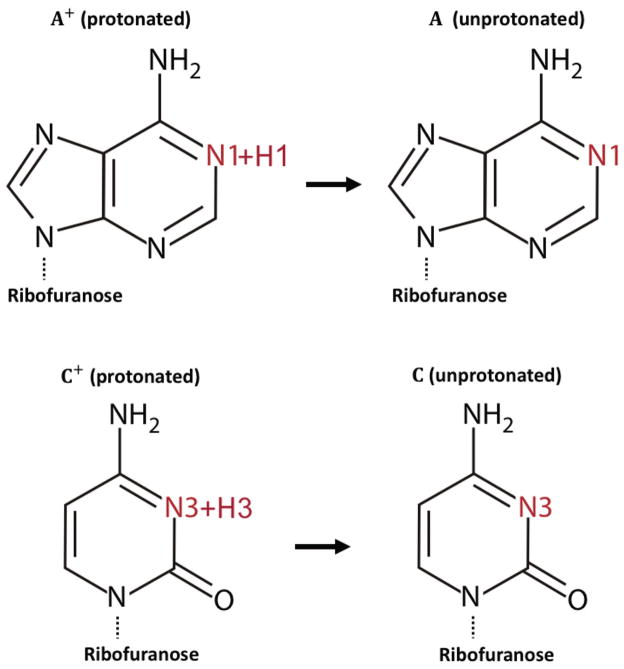
PK_a calculations for RNA

In order to make DelPhiPKa capable of calculating PK_a values of RNAs and single stranded DNAs, we extended the topology file with a new set of atomic parameters that include protonated and unprotonated structures of adenosine and cytidine (Fig.7) (similarly, one can include other nucleic bases). To validate the approach, we benchmarked the calculated PK_a values against experimental measured results of two RNAs. We also compared results with the data obtained from the previous study⁷⁶ that was calculated with DelPhi using the non-linear correction for the Poisson-Boltzmann equation. The first one is branch-point helix (BPH), which is a 21-nucleotide stem-loop structure that contains an internal asymmetric loop. In the asymmetric loop, A6 and A7 residues are stacked within the helix opposite a single uridine U16. The experiment measured the PK_a value of A7 is 6.1, while other adenosine residues in the structure have PK_a values less than 5.5 (Table 5). The second structure is lead-dependent ribozyme (LDZ), which is a 30-nucleotide stem-loop structure that also has an internal asymmetric loop. The experimental measurement shows 6 adenosine residues that have PK_as of less than 4.3 and one adenosine (A25) has PK_a value of 6.5.

Figure 7.

Adenosine and cytidine structures in their protonated and unprotonated states.

Table 5.

Comparison of calculated pKa values for adenosine residues in RNAs with NMR measured results.

Nucleotide	NMR measured PKa	Calculated PKa
Branch-point helix (BPH)
A6	<5.0	4.5±0.6
A7	6.1	5.3±0.7
A10	<5.0	4.1±0.5
A13	5.5	4.9±0.7
A17	<5.0	4.1±0.5
Lead-dependent ribozyme (LDZ)
A4	≤3.1	3.9±0.8
A8	4.3±0.3	4.7±0.5
A12	≤3.1	4.0±0.3
A16	3.8±0.4	4.3±0.7
A17	3.8±0.4	3.8±0.7
A18	3.5±0.6	4.1±0.3
A25	6.5±0.1	5.7±0.5

Calculated PK_a values are shown in Table 5. The mean±standard deviation of the calculated PK_a values are given for 12 NMR structures for BPH (PDB ID: 17ra) and 25 NMR structures for LDZ (PDB ID: 1ldz). The two nucleotides in BPH with high measured PK_a values (A7 for 6.1 and A13 for 5.5) were calculated as 5.3 and 4.9, respectively. Although the absolute pKa values calculated from DelPhiPKa were slightly different compared with the experimental data and results calculated with the non-linear correction (A7 for 6.8 and A13 for 5.3)⁷⁶, the pKa shifts are in the correct direction and the predicted PK_a values are within 1.0 pK unit compared with the experimental data. For adenosine residues in LDZ, although the prediction for A25 results in about 1.2 pK unit error (compared with 0.8 pK unit error calculated previously with the non-linear correction⁷⁶), the A25 was successfully identified as the residue with the highest PK_a value. All predictions for other residues are within less than 0.6 pK units from experimental data.

Speed performance benchmark on large-scale protein sample

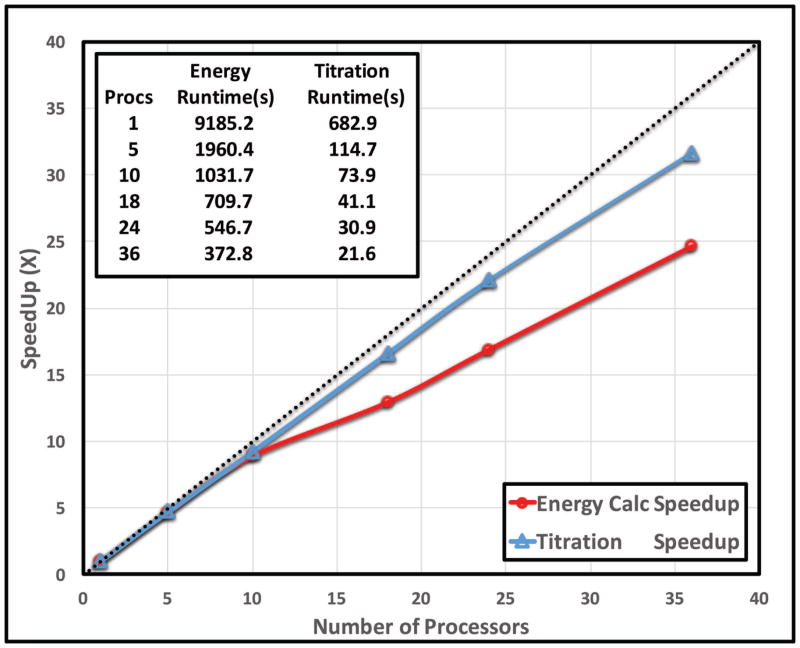
A large protein, 6-Phosphogluconate Dehydrogenase (6PGDH, PDB ID: 2zyg), is used for the speed performance benchmark. It contains 467 residues and 128 ionizable residues with a dimension of 119x113x113Å. This resulted in 1536 DelPhi runs. The benchmark was performed on the nodes with specification of AMD Opteron 2356 (8 cores and 2.3GHz) on the Palmetto cluster (http://citi.clemson.edu/palmetto/). Two parallelized modules are benchmarked, the energy calculation and the titration with the network partition. Each Delphi calculation was set for 3 focusing runs and convergence of 0.0001. The threshold value for each network was set to be 15 Å and maximum 15 residues in each network. Each calculation was performed 5 times and then we took the average runtime for benchmarking.

It is found that with 10 or less CPUs, both energy and titration modules achieve very good linear speedup (Fig 8). However, the memory usage of Delphi calculations and the communications between CPUs increased significantly with increasing the number of processors. In contrast, the speedup of parallelized titration module was only slightly affected by the increase of CPUs.

Figure 8.

Benchmark of the speed performance. The speedup vs. the number of processors utilized with the MPI parallelization.

Conclusion

An efficient method is proposed and implemented in DelPhi C++ code for PK_a calculations of proteins, RNAs and DNAs. The smooth Gaussian function based dielectric model is used for the electrostatic energy calculations instead of homogeneous dielectric model and the algorithm does not need to define molecular surface. Benchmarks were performed on two widely known datasets of experimental PK_a measurements and the predictions on both datasets showed very good agreements with experimental data. The statistics showed that PK_a predictions achieved as low as a RMSD of 0.6 for ionizable groups located on the surface. In contrast, an average RMSD of 1.8 for buried ionizable groups was obtained.

The reported approach is fast while retaining atomic information in the modeling process. This allows for analysis of the energy components and structural details causing the calculated pKa shifts. Since DelPhiPKA models proteins, RNAs and DNAs, the method can be used to study various molecular systems, including protein-DNA and protein-RNA complexes.