Abstract
As proteins evolve, amino acid positions key to protein structure or function are subject to mutational constraints. These positions can be detected by analyzing sequence families for amino acid conservation or for co-evolution between pairs of positions. Co-evolutionary scores are usually rank-ordered and thresholded to reveal the top pairwise scores, but they also can be treated as weighted networks. Here, we used network analyses to bypass a major complication of co-evolution studies: For a given sequence alignment, alternative algorithms usually identify different, top pairwise scores. We reconciled results from five commonly-used, mathematically divergent algorithms (ELSC, McBASC, OMES, SCA, and ZNMI), using the LacI/GalR and 1,6-bisphosphate aldolase protein families as models. Calculations used unthresholded co-evolution scores from which column-specific properties such as sequence entropy and random noise were subtracted; “central” positions were identified by calculating various network centrality scores. When compared among algorithms, network centrality methods, particularly eigenvector centrality, showed markedly better agreement than comparisons of the top pairwise scores. Positions with large centrality scores occurred at key structural locations and/or were functionally sensitive to mutations. Further, the top central positions often differed from those with top pairwise co-evolution scores: Instead of a few strong scores, central positions often had multiple, moderate scores. We conclude that eigenvector centrality calculations reveal a robust evolutionary pattern of constraints – detectable by divergent algorithms – that occur at key protein locations. Finally, we discuss the fact that multiple patterns co-exist in evolutionary data that, together, give rise to emergent protein functions.
Keywords: protein evolution, co-evolution, amino acid, sequence alignment, graph theory, LacI/GalR, aldolase
On-going genomic sequencing has generated a huge number of protein sequences. To place them into biological context, sequences are usually grouped into protein families that, in turn, can be used to reveal sequence/structure/function relationships. A common approach is to identify which amino acid positions are constrained during evolution. These positions are presumably crucial for the protein’s structure or function, and their mutation can provide key insights to a protein’s function. Various algorithms have been devised to detect positions that are conserved across a protein family or that vary among alternative lineages.1–13 In addition, constraints on corresponding pairs of positions can be detected using co-evolution analyses.
Co-evolutionary algorithms seek to identify pairs of positions that vary together across evolutionary time. For example, if an amino acid change at position X correlates with a change at position Y, positions X and Y are said to co-evolve. Co-evolution suggests that the two positions are linked to carry out important structural or functional roles. Such patterns can arise from short-range biophysical constraints (such as charge-charge interactions) but are also commonly observed between positions that are distant from each other on the protein structure, via mechanisms that are not yet fully understood.14–16
Several algorithms, with a range of mathematical foundations, have been devised to quantify co-evolutionary patterns in multiple sequence alignments (MSAs).17–27 These algorithms determine pairwise scores for all possible combinations of amino acid positions; the top pairwise scores indicate the strongest pattern of covariation. Despite searching for a common pattern, results from alternative algorithms seldom identify the same top pairwise scores.23,28,29 One explanation is that some algorithms have flawed predictions. On the other hand, alternative algorithms might detect distinct evolutionary signatures, each biologically important. To date, mutagenesis experiments have not identified any single algorithm as better than the others for identifying positions with co-evolutionary, mutational constraints.1
We hypothesized that deep patterns in co-evolutionary data might be robust to algorithmic details and therefore detectable by multiple algorithms. To that end, we treated unthresholded co-evolutionary scores as weighted networks (complete graphs) and used network centrality measures to identify important nodes. This allowed us to determine whether central nodes (positions) were more robustly identified by network analysis than by specific edges connecting a pair of positions.
To identify the central positions, we used the pairwise co-evolutionary scores as edges of a weighted complete graph to calculate two network centrality scores: degree centrality30 (DC) and eigenvector centrality31 (EVC). For each amino acid position (node), DC simply takes the sum of connecting edge weights, whereas EVC takes into account both the weight of its connecting edges and the centrality of its connected partners. In practice, we found little difference between these metrics; since EVC has an established history in other co-evolution studies, we focused downstream analyses on these results.
Centrality scores can be rank-ordered to reveal the most central positions of the co-evolution network. In analyzing these scores, we first considered whether the central nodes (i) were identical to positions with the highest pairwise scores, or (ii) arose from multiple, intermediate scores (Fig. 1), corresponding to multiple co-evolutionary constraints from other amino acid positions. Indeed, for the protein families of this study, positions with high EVC scores were frequently distinct from positions with the highest pairwise co-evolutionary scores. Furthermore, when results were compared among five alternative co-evolutionary algorithms, the EVC positions showed better agreement than the top pairwise positions. Comparison with experimental results showed that positions with high EVC scores have key structural and functional roles in the LacI/GalR and aldolase protein families. Thus, EVC calculations detected a robust evolutionary pattern of amino acid changes at key protein locations and can be used to guide experimental studies of protein function. Finally, we discuss the existence and interplay of multiple patterns in evolutionary data that, together, give rise to emergent protein functions.
Fig. 1. Network representation of co-evolutionary scores for the LacI/GalR family.

Note that these networks depict co-evolutionary scores, not structural contacts. (A) In this example, the ZNMI algorithm was used to calculate pairwise co-evolution scores. High scores are represented as thick edges; weak scores are represented with thin edges. Each node corresponds to an MSA column (amino acid position); node sizes and colors are scaled according to EVC scores (large, black = high, small, white = low). For figure clarity, only the top ~4% of edges are shown; however, all edge weights (co-evolution scores) were used for EVC calculations. From the network shown in A, individual nodes and their edges are highlighted in panels (B) and (C), to illustrate the difference between a top EVC position with many moderate scores (B) and a position with a high, pairwise co-evolution score but a low EVC score (C).
MATERIALS AND METHODS
Protein families, sequence alignments, and MARS software
The MSA for the LacI/GalR family was constructed in 201132 and further refined in 201328. This MSA contains 351 representative sequences from 34 ortholog groups; the full sequence set (>2000 sequences) is too large for many calculations. Sequences for the aldolase MSA were obtained by iterative rounds of PSI-BLAST33, and manually edited to remove redundant sequences. To take advantage of available sequence and structural data, a representative subset was aligned using PROMALS3D.34 The remaining sequences were clustered based on their sequence identity into groups containing at least one of the “representative” sequences in the PROMALS3D alignment. These high sequence identity clusters were re-aligned with MUSCLE.35 Group alignments were integrated into the full aldolase alignment with the custom software MARS-Prot (Supporting Information, Supplementary Methods) using the representative sequences as guides.
The MARS-Prot software is a general tool for integrating new sequences into existing sequence alignments that does not perturb the labor-intensive editing that is required to produce high quality MSAs. This tool is greatly needed: Extensive ongoing genomic sequencing requires frequent updates to existing MSAs. The MARS-Prot algorithm is described in Supplementary Methods; references cited therein are cited here.36,37 MARS-Prot is freely available under an open source license (https://github.com/djparente/MARS).
The LacI/GalR and aldolase protein alignments used in this study are available upon request. As a final check, we considered the number of sequences and phylogenetic sampling in these MSAs, which has been shown to affect MSA analyses.38,39 For example, co-evolution analyses might return biased results if one lineage of the family were oversampled. To check for this possibility, the sequence identity matrix for each MSA was manually inspected to ensure that no group of highly similar sequences was over-represented relative to the rest of the MSA. In addition, maximum-likelihood phylogenetic trees were inferred using RAxML 7.0.340 with default parameters under the PROTGAMMABLOSUM62 substitution model. Trees were visualized with PhyloWidget41 (Fig. S1). Trees for both families have a stellate appearance, indicating that many lineages are represented and that no one lineage dominated the calculation.38
Co-evolution analyses
Co-evolution scores were calculated using five alternative algorithms: Explicit Likelihood of Subset Co-variation (ELSC22), Observed Minus Expected Squared (OMES21,29), McLachlan-based Substitution Correlation (McBASC17,18,20), Statistical Coupling Analysis (SCA19), and Z-Normalized Mutual Information (ZNMI23). For ELSC, OMES, McBASC and SCA, co-evolution scores were calculated using a software implementation by Fodor et. al 22,29. For ZNMI, scores were calculated using our re-implementation of that method.28 For all algorithms, positions with >50% gaps or very high conservation (<5% sequence variability, which corresponds to sequence entropy < 0.198523), were excluded from further analysis. For ZNMI, positions with >10% gaps were further excluded, to match its initial implementation by Brown and Brown.23
All analyses were carried out using an ensemble-based approach.23,28 For the LacI/GalR MSA, 100 sub-alignments were constructed, each including 90% of the available sequences. For each sub-alignment, co-evolution scores were calculated. For each position, the scores from the 100 ensembles were averaged; these are reported as the “initial” co-evolutionary scores. The ensemble average approach limits the impact that might arise if a few sequences are misaligned. As an additional control, we generated a second ensemble containing 50% of the sequences and calculated its average co-evolution scores. If the sequences in the starting MSA are well sampled, we expect that results for the 50% ensemble will agree with those of the 90% ensemble (Table S1).
Note that the ensemble/average approach should only be used to supplement direct inspection of the sequences included in an MSA. In other analyses, we showed that this control can fail in cases of extreme over-representation, because even randomly deleting 50% of the sequences leaves a sufficient number of redundant sequences to bias the calculations. For example, 75 LacI/GalR sequences fall in the LacI subfamily; their sequence identities ranged from 37 to 99% and the subfamily phylogenetic tree had nine major branches. When these subfamily sequences were used in co-evolutionary analyses, results for the 50 and 90% ensembles were in good agreement. However, for both the pairwise and the network centrality scores, the top 20 consensus positions unexpectedly included many positions that tolerate multiple substitutions (Table S2), which indicates that they are not functionally important. Manual inspection of the LacI subfamily revealed that 41% of the sequences were >95% identical to each other. Even with a randomized, 50% sampling rate, these over-represented sequences are likely to dominate the co-evolutionary calculation, leading to the misleading results. This example shows that computed controls do not substitute for manual inspection of an MSA. Note that neither the LacI/GalR nor the aldolase families had over-represented sequences.
Like the LacI/GalR family, the aldolase family (1562 sequences) was too large for some calculations. Therefore, we constructed an ensemble of aldolase alignments, each with 500 sequences as the “90%” ensemble. A second ensemble of alignments containing 278 sequences was used for the “50%” alignment.
For both the LacI/GalR and aldolase families, the 90% and 50% scores had good agreement, which indicates that a sufficient number of sequences were included in each alignment. (Fig. S2, Table S1). Further analyses therefore focused on only the 90% ensemble.
Next, we considered that alternative co-evolutionary algorithms have divergent responses to various properties of MSA columns (such as sequence entropy or random noise) which might introduce algorithm-specific noise.29 To account for these contributions, we created shuffled alignments by independently randomizing the order of amino acids contained within each column. This maintains column properties such as amino acid distribution and sequence entropy, but destroys both phylogenetic patterns of evolutionary change and co-evolutionary relationships between pairs of positions. Shuffled alignments have been used as benchmarks for “sector” anlayses42, and various subtractions have been carried out for protein-protein co-evolution43,44. However, to the best of our knowledge, this is the first time that shuffled alignments have been used to estimate spurious signals arising in intra-protein covariation analyses. To that end, we performed “co-evolutionary” calculations on each shuffled MSA. Then, for each pair of positions, the score from the shuffled MSA was subtracted from the score of the unshuffled MSA. This calculation is a linear approximation: it assumes that initial (unshuffled) co-evolution scores were the sum of the true signals and noise. We refer to the resulting co-evolution scores as “subtracted”.
To determine consensus co-evolution scores for the initial and subtracted data sets, we used the method of Parente et al.28, with the variation of using the median Z-score, rather than the mean, to rank-order positions. (For more details, see consensus EVC scores, below.)
Z-Normalized decoy adjusted mutual information
In subtracting the MSA noise component to reveal “true” co-evolutionary components, we assumed that the magnitude of the noise was the same in the original and shuffled alignments. This assumption should hold for ELSC, McBASC, OMES and SCA, but is violated by ZNMI. For a pair of positions x and y, ZNMI scores are calculated in a three-step process23: (1) the mutual information, MI(x,y), is estimated; (2) MI(x,y) is divided by the joint sequence entropy of positions x and y to calculate the normalized mutual information, NMI(x,y); and (3) the NMI(x,y) scores are further z-normalized against the joint distribution of NMI(x,y) scores for positions x and y. Thus, the third step of this procedure scales the joint distribution of ZNMI(x,y) scores to a normal distribution with mean of 0 and variance of 1. An assumption of this procedure is that there are true co-evolutionary signals to detect: positions with high ZNMI scores are those that co-evolve strongly, relative to each position’s own NMI distribution. However, in shuffled alignments, when co-evolutionary signals have been destroyed, the ZNMI distribution is still scaled to have a normal distribution with mean 0 and variance 1. Thus, the Z-normalization step of ZNMI would spuriously scale the noise of the shuffled alignments to the same level as the co-evolutionary signal in the original alignments. Subtracting away the shuffled ZNMI score would therefore amplify, rather than eliminate, the influence of noise.
To prevent this undesirable outcome, we performed score subtraction before the Z-normalization step, by subtracting NMI of each shuffled score from the original score. This variant of the ZNMI algorithm we call the Z-Normalized Decoy Adjusted Mutual Information (ZNDAMI), mathematically defined as:
| (1) |
where NMIsub(x,y) is the subtracted NMI score2 (i.e. NMIorig(x,y) – NMIshuf(x,y)) and μxy and σxy are the mean and standard deviation of the joint NMIsub distribution for positions x and y, namely:
| (2) |
and
| (3) |
which depend on the individual distribution mean:
| (4) |
and variance:
| (5) |
where N is the number of columns in the alignment that meet the gap criterion (<10% gaps, see Methods).
Eigenvector network centrality
To identify central nodes in the ELSC, McBASC, OMES, SCA, and ZNMDAMI co-evolution networks, we calculated the eigenvector centrality31 for each position in the MSA. These calculations were performed on both the initial (unsubtracted) and subtracted pairwise co-evolutionary scores (see above). Eigenvector centrality calculations take into account both the strength of connectivity and the centrality of strongly connected partners, and has been utilized for many diverse applications, including: internet search engines45,46, social network analysis47, political analysis48, fMRI data processing49, and epidemiological disease-transmission networks50,51.
A key feature of our calculation is that we did not impose a significance threshold on the pairwise co-evolutionary data prior to EVC calculations. Although eventually necessary, we deferred thresholding until the end of analyses, which allowed us to detect positions with high EVC scores that would have otherwise been missed (Table S3 and Fig. S3). The eigenvector centrality score of the i’th position is equal to the i’th row of the dominant column eigenvector of the adjacency matrix. That is, for node si, we take
| (6) |
where Wij are entries of W, the weighted adjacency matrix, corresponding to the weight between nodes si and sj. This can be rewritten
| (7) |
where s is the eigenvector we seek, corresponding to the (necessarily) unique largest eigenvalue λ as long as the centralities are non-negative.52 Eigenvector centrality calculations were carried out using the NetworkX Python package (http://networkx.github.io/).
In practice, eigenvector centrality is computed iteratively, as follows: every node is initialized with the same starting score. Then, at subsequent iterations, the score of a node is (i) set equal to the edge-weighted sum of the current score of its neighbors, and (ii) normalized so that the squared sum of the EVC scores is constant. This process is iterated to convergence to produce a final eigenvector centrality score for each position. Informally, this procedure is analogous to first initializing every node to be equally important, reflecting our (initial) ignorance as to which nodes were more central. At every step, nodes that are strongly connected to other important nodes are preferentially selected to gain disproportionately more “importance,” allowing the iteration to uncover important nodes.
Eigenvector centrality calculations were carried out using the NetworkX python package (http://networkx.github.io/). More formally, the eigenvector centrality score of position i in the T’th iteration (si,T), in a network of N positions, is given by the iterative system:
| (8) |
| (9) |
| (10) |
where wi,j is the weight of the edges between positions i and j. For the centrality score to converge, scores must be non-negative. This is true for all algorithms except ZNMI, which transforms scores to be z-normalized with a mean of zero. Thus, for all algorithms, scores were linearly transformed to fall in the range [0,1]. The final eigenvector centrality score assigned to position i, si, is given by:
| (11) |
This procedure is identical to an algorithm called “power iteration” that calculates the dominant eigenvector of a matrix. For networks of co-evolutionary scores, power iteration is applied to the adjacency matrix of the network.
Network degree centrality
We compared EVC scores to a simpler network centrality score, degree centrality30 (Figs. S4–S5 and Table S4). This score computes the total weight of edges directly connected to each node. As with the EVC scores, weights were transformed to fall on the interval [0,1] for the calculation.
Network comparisons and consensus
In comparing various sets of results (e.g. initial versus subtracted pairwise scores, or pairwise versus EVC scores), we had no a priori reason to assume that scores should be linearly related. Thus, we used a non-parametric measure – Spearman R2 – which can detect any monotonic relationship between two variables. Similarity was quantified by calculating Spearman R2 for the edge weights assigned to each pair of positions in the network. This parameter ranges from 0.0–1.0.
For comparing EVC scores to experimental data, we determined consensus scores using results from all 5 algorithms for each position. Since each co-evolution algorithm uses a different output scale (e.g. Fig. 2A–B), each set of scores was first Z-normalized to standardize the mean and variance values. This prevents one algorithm from dominating downstream calculations. The Z-normalized EVC scores of the 5 algorithms were then used to determine a median EVC score for each position. Results were compared to crystal structures from the aldolase (PDB: 1xfb) and LacI/GalR families (PDBs: 1efa, 1wet, 1rzr, 2nzv, 3oqo, and 1byk).53–59 Molecular graphics were created using UCSF Chimera 1.8.60
Fig. 2. Eigenvector centrality scores show better correlation between co-evolution algorithms than do pairwise scores.
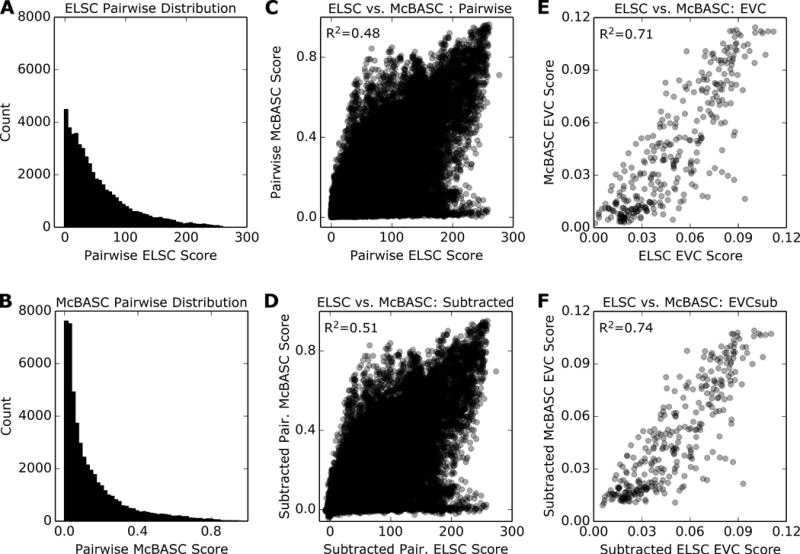
The example shown is for the aldolase family. Histograms show the distribution of co-evolutionary scores from (A) ELSC and (B) McBASC. Between these two algorithms, correlation of (C) initial (unsubtracted) or (D) subtracted pairwise co-evolution scores have modest correlations, as indicated by their Spearman R2 values. However, correlation of (E) unsubtracted or (F) subtracted EVC scores is greatly improved, as indicated by larger R2 values.
TEA-O analyses
To determine which amino acid changes in each MSA track with phylogeny, we used TEA-O analyses (http://nava.liacs.nl/kye/TEA-O/)9. Results for the LacI/GalR family were taken from Tungtur et al.32 These results were shown to be independent of the method used for generating a phylogenetic tree. Similar analyses were performed for the aldolase family, using the phylogenetic tree shown in Fig. S1.
RESULTS
For this study, we used the LacI/GalR transcription regulators and the family of 1,6-bisphosphate aldolase (“aldolase”) (Table S1). The LacI/GalR family comprises bacterial paralogs with sequence identities that range from ~19–99%.32 The aldolase family was chosen as another family with highly divergent sequence identities (~19–99%), but comprising orthologs instead of paralogs. These “class I” aldolase homologs are found in all animals, plants, and green algae.61
Analyses of co-evolutionary networks
Co-evolution analyses generate a large number of pairwise scores (N2, where N is the number of columns of amino acid positions). Most often, these scores have been rank-ordered to identify the top pairwise scores or organized into an all-vs-all heatmap (e.g.42). Alternatively, co-evolution scores have been re-cast as networks. For example, several studies imposed a threshold (such as Z ≥ 4) on the pairwise co-evolution scores and created networks in which top-scoring positions correspond to nodes and co-evolution scores correspond to edges.62–65 A useful depiction of thresholded networks is the “circos” plot.27 Recently, we used all co-evolution scores to weight the edges between all nodes to directly compare outcomes for related protein families.28 Here, we have analyzed pairwise co-evolution scores as unthresholded networks to identify features that are robustly identified by mathematically-divergent algorithms.
To identify robust features, each MSA of this study was analyzed using five common co-evolution algorithms with diverse mathematical foundations: (i) OMES measures a χ2-like goodness-of-fit parameter21,29; (ii) McBASC generalizes the correlation coefficient to categorical data17,18,20; (iii) ELSC22 and (iv) SCA19 take a perturbative approach; and (v) ZNMI23 uses an information theoretic approach to measure shared information content. As expected, for all MSAs, the five algorithms generated different rank orders for the unsubtracted pairwise scores (Table 1; Fig. 1C and Figs. S6–S9). Pairs that were assigned a high co-evolution score by one algorithm were often assigned moderate or low scores by another. When only the top score was considered for each position (in network formalism, the maximum edge weight, “MEW”), algorithm agreement did not improve (Table S5).
Table 1. Eigenvector centrality reconciles results for various co-evolution analyses.
For each pair of algorithms, non-parametric correlation coefficients (Spearman R2) are shown for pairwise co-evolution and eigenvector (EVC) scores, using either the unsubtracted (“Initial”) or subtracted (“Sub”) networks. As discussed in Methods, ZNDAMI is used in place of subtracted ZNMI.
| Algorithms | Coefficient of determination (Spearman R2)
|
|||||||
|---|---|---|---|---|---|---|---|---|
| Aldolase | LacI/GalR | |||||||
|
| ||||||||
| Pairwise | EVC | Pairwise | EVC | |||||
|
| ||||||||
| Initial | Sub | Initial | Sub | Initial | Sub | Initial | Sub | |
| ELSC vs McBASC | 0.48 | 0.51 | 0.71 | 0.74 | 0.09 | 0.11 | 0.27 | 0.50 |
| ELSC vs OMES | 0.64 | 0.65 | 0.78 | 0.78 | 0.37 | 0.42 | 0.66 | 0.73 |
| ELSC vs SCA | 0.19 | 0.23 | 0.40 | 0.43 | 0.02 | 0.14 | 0.14 | 0.32 |
| ELSC vs ZNMI | 0.44 | 0.46 | 0.78 | 0.79 | 0.23 | 0.25 | 0.45 | 0.60 |
| ELSC vs TEA-O | 0.30 | 0.54 | ||||||
| McBASC vs OMES | 0.59 | 0.63 | 0.72 | 0.75 | 0.14 | 0.20 | 0.14 | 0.38 |
| McBASC vs SCA | 0.20 | 0.23 | 0.22 | 0.26 | 0.08 | 0.13 | 0.12 | 0.36 |
| McBASC vs ZNMI | 0.48 | 0.52 | 0.65 | 0.69 | 0.18 | 0.28 | 0.05 | 0.34 |
| McBASC vs TEA-O | 0.26 | 0.38 | ||||||
| OMES vs SCA | 0.25 | 0.25 | 0.31 | 0.31 | 0.31 | 0.34 | 0.43 | 0.55 |
| OMES vs ZNMI | 0.50 | 0.54 | 0.77 | 0.85 | 0.46 | 0.50 | 0.51 | 0.69 |
| OMES vs tEA-O | 0.26 | 0.70 | ||||||
| SCA vs ZNMI | 0.35 | 0.37 | 0.60 | 0.61 | 0.18 | 0.18 | 0.33 | 0.47 |
| SCA vs TEA-O | 0.25 | 0.42 | ||||||
| ZNMI vs TEA-O | 0.34 | 0.77 | ||||||
|
| ||||||||
| Median improvement | 0.03 | 0.19 | 0.23 a | 0.05 | 0.12 | 0.29a | ||
Median improvement does not include the TEA-O comparisons.
We next attempted to reconcile results by correcting for the different algorithm sensitivities to non-coevolutionary signals, such as sequence entropy and random noise.29 To estimate these spurious signals, we created “shuffled” alignments by separately randomizing the amino acids within each column of the LacI/GalR and aldolase MSAs. This maintains column properties such as amino acid distribution and sequence entropy, but destroys both phylogenetic patterns between and co-evolutionary relationships within naturally-evolved sequences. All co-evolutionary calculations were repeated for the shuffled alignments, and for each pair of positions in the co-evolution network, the shuffled scores were subtracted from those of the unshuffled MSAs. When the final scores were compared, the subtraction process only modestly improved comparisons of pairwise scores between alternative algorithms (Table 1). However, as discussed below, subtraction improved centrality scores to a greater degree.
Notably, when comparing the pairwise scores, no single algorithm appeared to perform “better” than the others. A criterion frequently used to indicate algorithm success is mutational sensitivity of top scoring positions. For the LacI/GalR family, most of the positions with top, subtracted pairwise scores are sensitive to mutagenesis, regardless of the algorithm (Fig. S10).
Thus, we were curious whether deeper patterns in co-evolutionary data would also identify functionally important positions, and whether they would be more robustly detected by multiple algorithms. This required that we first consider how and when co-evolution scores are thresholded: Like most other metrics of evolutionary patterns in MSAs, co-evolution scores are continuous, with no clear breaks to separate “important” from “not important”. Threshold choice is always arbitrary: Conservative thresholds eliminate meaningful data; liberal thresholds may include data with no meaning. In this work, we deferred thresholding as long as possible. We chose to analyze co-evolution scores as unthresholded, weighted networks (e.g. Fig. 1A–B), using graph theory to calculate network centrality.
Network centrality can be calculated in a number of different ways.66 Most existing methods were developed for social network analyses. Methods such as “closeness” and “betweenness” centrality measure the number of steps between nodes66, and thus do not make sense for the complete graphs created by unthresholded, pairwise co-evolution scores. In contrast, both degree (DC)30 and eigenvector (EVC)31 centrality measure the effect of one node on all other nodes, based on the weights of the connecting edges. Whereas DC simply sums the weight of edges connected to each node, EVC accounts for the centrality of neighboring nodes as well. DC and EVC might identify the same nodes, but in principle EVC is sensitive to more subtle network effects. In the current study, DC results agreed strongly with EVC results (Fig. S4–S5). For simplicity, we focused remaining analyses on EVC results.
We first compared that the top EVC scores to the top pairwise co-evolutionary scores (MEW, defined above). Notably, the MEW and EVC scores do not consistently correlate, by either Spearman correlation coefficients (Table S5) or by Jaccard indices (Fig. S3). Thus, we conclude that EVC calculations for the LacI/GalR and aldolase families identify a group of amino acid positions that is distinct from the pairwise positions. That is, the centrality calculations can discriminate positions with many moderate scores from those with one strong but many weak scores (e.g., Fig. 1B vs 1C). Furthermore, if pairwise co-evolution scores were thresholded (limited to the top scores) prior to downstream analyses, several positions with high EVC scores would not be detected.
Next, we compared the EVC scores calculated by the alternative co-evolutionary algorithms. Agreement among EVC scores was greatly improved over all comparisons of pairwise scores, and across the whole range of scores. For the EVC scores determined for the initial (un-subtracted) networks, almost all comparisons showed better correlation than the pairwise co-evolutionary scores (Table 1, Fig. 2C vs Fig. 2E; Figs. S6–S49 vs. S11–S14). Subtracting noise from the co-evolution scores prior to EVC calculations usually further improved R2 values (Table 1; Fig. 2 D vs Fig 2F; Figs. S13–S14). Agreement indicates that network centrality is a robust feature of the co-evolutionary data, in contrast to the pairwise scores, which show more variability among algorithms. In addition, we noted that positions with high EVC scores were highly connected to each other within the network of co-evolution scores (e.g. Fig. 1A–B). However, like the pairwise co-evolution scores, EVC connectivity was not obligatorily related to structural proximity (Figs. 3–4).
Fig. 3. Top EVC Positions for Aldolase.
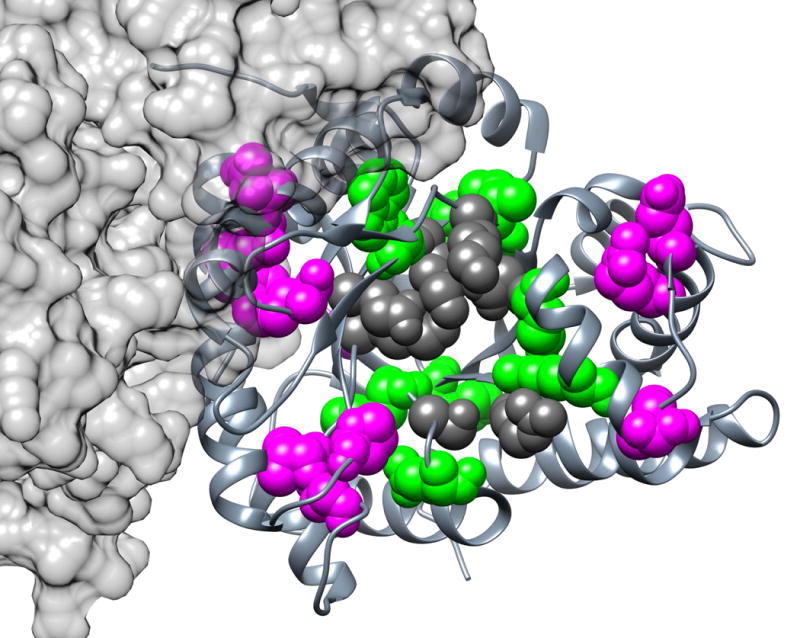
This view of aldolase is looking into the active site of one monomer. The top 20 consensus EVC positions (35, 43, 47, 53, 56, 106, 107, 122, 145, 148, 168, 169, 193, 214, 234, 237, 267, 270, 275, and 300; magenta and green spacefilled) of tetrameric human aldolase C are shown on one monomer (PDB: 1xfb58). Active site positions are highlighted in dark gray. EVC positions in contact with active site residues are highlighted in green; those without contact are highlighted in magenta.
Fig. 4. Top EVC Positions for LacI/GalR.
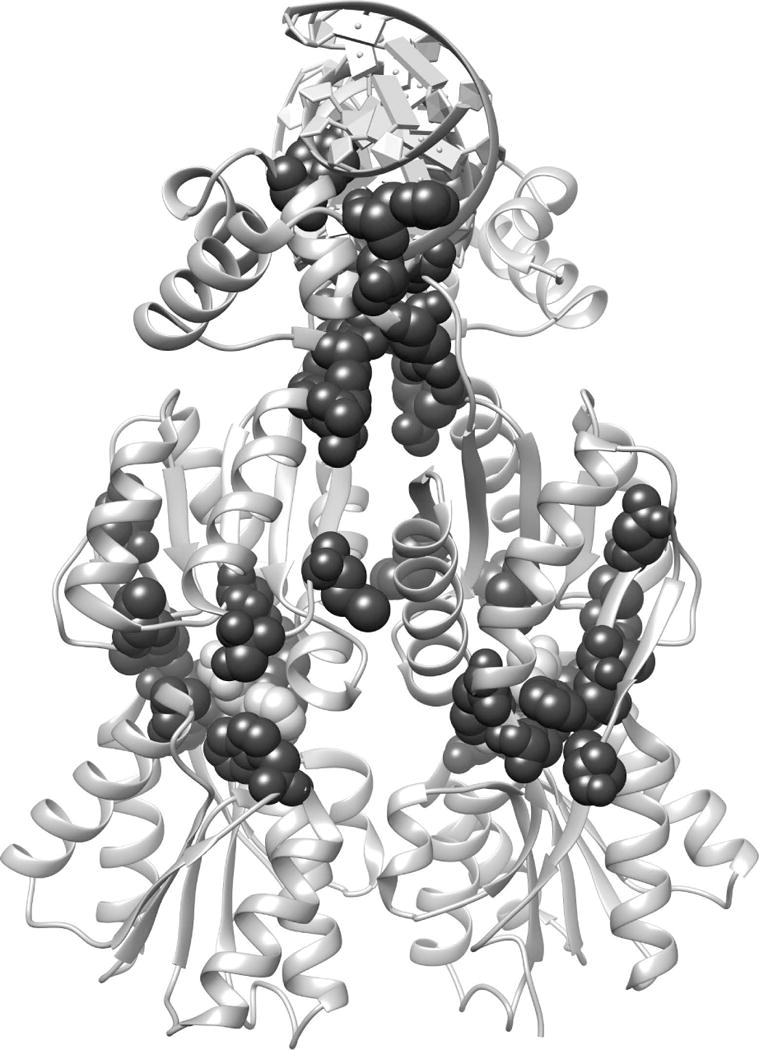
The top 20 consensus EVC positions (17, 27, 29, 51, 52, 55, 57, 98, 102, 117, 125, 150, 157, 160, 161, 193, 220, 291, 293, and 321; spacefilled black) for the LacI/GalR family were mapped onto the homodimeric structure of LacI (PDB: 1efa53). The DNA (ribbon at top of structure) and the bound allosteric effector ligand, (orthonitrophenyl-β-D-fucopyranoside, spacefilled white) are highlighted to show binding sites.
Finally, we considered an ongoing concern about co-evolution algorithms – the extent to which the covariation analyses distinguish true “co-evolution” from amino acid changes related to phylogeny.43,67,68 Similar considerations have been raised for the first eigenvector of co-evolutionary data.42,44 The rationale for our approach was that, if phylogeny is contributing a great deal to the covariation/EVC scores, then positions with top scores in phylogenetic algorithms should correlate with those identified by algorithms that are designed to identify amino acids changes that correlate with phylogenetic branches. Several algorithms have been devised to detect this pattern.1–3,9 Of these, TEA-O9 is convenient for comparison with coevolution analyses: TEA-O separately scores “specificity” positions that change at the later branches from “conserved” positions that correspond to the primary branches. Due to their conservation, most of the latter are excluded from co-evolutionary analyses.
To that end, we compared EVC scores to TEA-O scores for the LacI/GalR and aldolase families. As expected, positions with high TEA-O “conserved” scores show essentially zero correlation with EVC scores for either family (data not shown). For the LacI/GalR family, EVC scores show comparable correlations with TEA-O specificity scores as they do with each other (Table 1). However, the aldolase EVC scores show lower correlation with TEA-O (Table 1) than they do with each other.
The different correlations may arise because the LacI/GalR family is comprised of paralogs (and thus its MSA could have a stronger phylogenetic signal), whereas the aldolase family is comprised of orthologs. Such differences among protein families could help explain why estimating and correcting for the contributions of phylogeny to intra-protein covariance has been challenging. Further, the presence or absence of phylogeny in the covariation signal does not diminish the fact that the top EVC positions are important to structure and function in both LacI/GalR and aldolase families (next section). The possible implications of co-existing and overlapping patterns in evolutionary data are included below, in the Discussion.
Eigenvector central positions are important for structure and function
To assess biological significance, we compared the known structural properties and mutational sensitivities of the top 20 EVC positions. To that end, we first determined a consensus set of positions (see Methods). This was motivated by the fact that, although EVC calculations greatly improved agreement between co-evolution algorithms, agreement was never 100%. In choosing this number of sites, we also considered the problem of thresholding. The histograms of EVC scores (diagonals of Figs. S11–S14) show distinct populations of scores, and the top 20 scores fall within the top population. In many cases, the 21st (or lower-ranked) EVC position also fell within this population and might therefore also be functionally important; global analyses that avoid such thresholding are discussed below.
In the aldolase family, the top 20 EVC positions fall near (i) the active site, (ii) the inter-subunit interface or (iii) along the surface on the same face as the ligand binding pocket. (Fig. 3, magenta and green spacefilled) Eight of these positions (35, 106, 107, 145, 148, 270, 275 and 300) contact active site residues and a 9th (position 43) directly participates in catalysis. (Of the eight catalytic residues, six are highly conserved and therefore cannot co-evolve). Since these positions fall in crucial functional locations, they are likely to contribute to aldolase function. We speculate that sequence changes at these positions might fine-tune the active site geometry and catalytic parameters to the ecological niche of each organism.
In the LacI/GalR family, the top 20 positions were compared to the extensive structural, mutational and computational studies that have been performed on several paralogs. Eighteen of the top EVC positions are sensitive to mutation in LacI; 19 positions are located in structural regions that are clearly important (Fig. 4; Table S6)53–57,69–80. Indeed, the top 20 EVC positions reads as an elite list of functionally important positions: In addition to the comprehensive LacI mutagenesis study,70,79,80 many of these positions were individually targeted for mutagenesis after in-depth structure/function analyses and molecular dynamics simulations suggested (and experiments confirmed) their importance. The two positions that lack known mutational response (27 and 102) have only been mutated in LacI. These positions might be key in other LacI/GalR proteins; we recently demonstrated that mutating nonconserved positions can have widely different outcomes among homologs.77
As we noted above, setting an arbitrary threshold for top EVC positions might miss important information about other positions. To consider the full range, we color-coded each all amino acids in each structure, according to their rank-ordered EVC scores. Given the continuum of shades that represents the range of scores (Figs. 5, S15, and S16 color bars), it is striking that structural regions emerge that are dominated by one color. For the LacI/GalR family, positions assigned high EVC scores cluster in the interior of the protein (Figs. 5, white and S16, magenta), especially near the binding sites of the allosteric effector ligand and DNA operator and along the inter-monomer interface. In the aldolase family, the top 20 consensus positions were representative of the global pattern: Positions with higher centrality scores were generally found on the protein interior (Fig. S15D), at the tetramerization interaction surface (Fig. S15C), and on the same surface of the protein as the active site (Fig. S15A). In contrast, the opposite surface – far from the active site – generally had lower EVC scores (Fig. S15B).
Fig. 5. Global structural analysis LacI/GalR EVC scores.
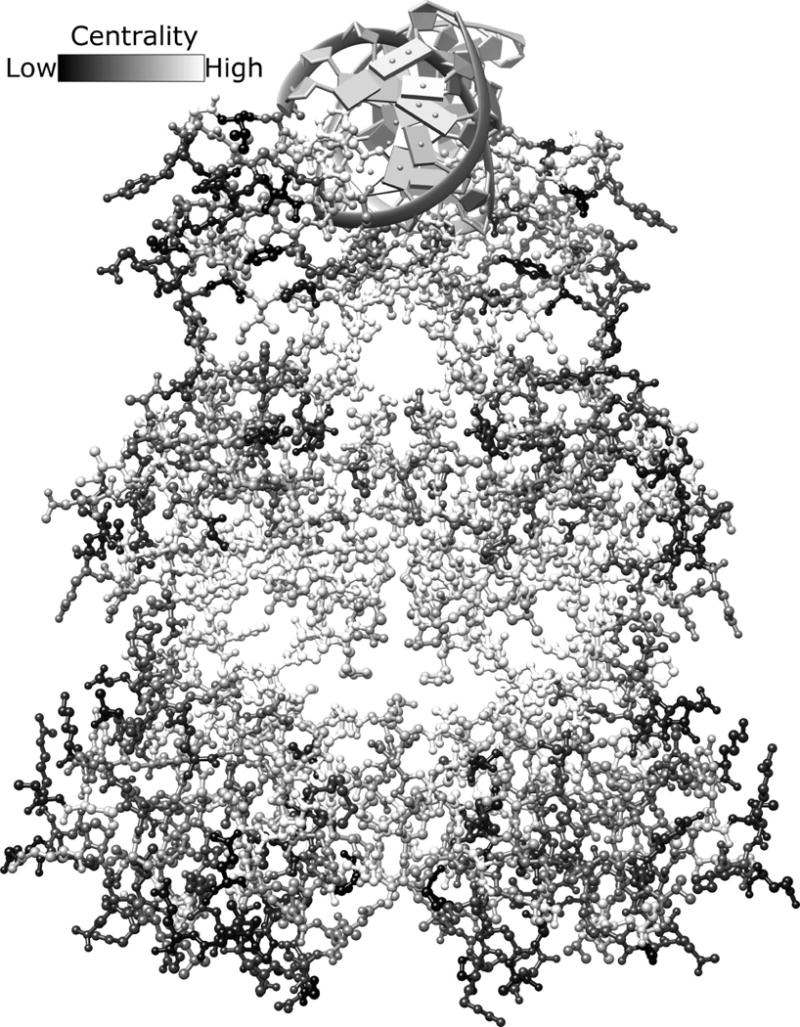
The homodimeric structure of LacI (PDB: 1efa53) is color-coded based on the rank order of each positions’ EVC score (high scores, white; low scores black). Bound DNA is shown at the top of the figure in gray. Inducer ligands bind in the central pocket of each monomer. Given the range of available scores (color bar at the top of the figure), it is striking that some structural regions are dominated by similar scores. For example, the inducer binding site is surrounded by positions with high EVC scores (very light gray and white). This figure is shown in color in Fig. S16.
DISCUSSION
Pairwise co-evolution of amino acid positions provides an incomplete view of protein evolution. Science’s common understanding of protein structure/function relationships suggests that multiple amino acids should be constrained together during evolution. Direct calculations for detecting larger groups of co-evolving positions have been limited by the sheer number of output scores, which increase exponentially. (For a protein with N positions, pairwise co-evolution calculates N2 scores; three-way co-evolution would calculate N3 scores, etc.) Thus, investigators have turned to analyses of pairwise data to identify multiply constrained positions.25,42,62,81–83 For one implementation of SCA, spectral decomposition of pairwise scores was used to determine the first eigenvector, but results were found to be heavily influenced by the sequence conservation for each position.84 Here, we have avoided such spurious signals via the use of shuffled alignments to estimate and subtract non-coevolutionary signals. Our results show that subtracted EVC scores contain information about amino acid positions key to structure and/or function of the LacI/GalR and aldolase families.
Strikingly, our analyses reconciled the contradictory results from alternative co-evolution algorithms, showing that this deeper signal of evolutionary change is robust. Other strengths of EVC calculations are that they (i) are mathematically guaranteed to have a unique top eigenvalue52, (ii) provide a tractable means to detect positions that are constrained by multiple partners, and (iii) defer problems introduced by thresholding until the final analyses. Positions with large EVC scores appear to largely follow the pattern that can be seen qualitatively in Fig. 1B: Some positions must simultaneously reconcile co-evolutionary constraints from many other positions. For these positions, no single constraint is strong, but many are moderate (Fig. 1B). This contrasts with the case illustrated in Fig. 1C: When two positions have strong co-evolutionary constraints between them, this can override the influence of most other positions (which subsequently manifests as low pairwise scores).
Despite the increased correlation over pairwise data, the EVC correlations do not perfectly reconcile the alternative algorithms. First, for aldolase, the correlations between SCA and other algorithms are lower (R2 <0.5) than the other comparisons. Perhaps SCA (i) is not an appropriate analysis for this family or (ii) detects a different evolutionary signal for this family than the other algorithms. Second, for the LacI/GalR family, half of the EVC algorithm correlations had R2 values less than 0.5 (Table 1), whereas those for aldolase (except SCA) were generally above 0.7. We speculate that this is related to the fact that the LacI/GalR family comprises paralogs, whereas the aldolase MSA contains only orthologous sequences. The lower LacI/GalR EVC correlations were not explained by the range of sequence identities in its MSA, since the aldolase MSA spans a comparable range (Table S1). Nevertheless, the EVC correlations were a significant improvement over pairwise correlations; every prior step of the calculations had much worse correlations.
In addition, we wish to stress that our results do not imply that EVC positions are a priori more important to structure or function than positions with other types of evolutionary patterns. Instead, we propose that protein evolution should be thought of as having many types of constraints that affect different groups of positions, some of which is captured by pairwise co-evolution and others by EVC calculations. Still other patterns include highly conserved positions10 and changes that track with phylogeny.1–3,9 We have also observed that, as one common scaffold evolves functional diversity, the positions under evolutionary pressure can move to different locations.28
To date, all of these evolutionary patterns appear to identify mutationally sensitive positions, and there is no reason to constrain “importance” to just one pattern of change. Indeed, our previous studies show that a large number of positions, representing a variety of evolutionary patterns, contribute to the evolution of altered LacI/GalR protein function.28,32,77 We expect similar results for other protein families. Even families that comprise a single ortholog – such as aldolase – likely evolve functional variation that is appropriate for distinct biological niches. (In the case of aldolase, the central metabolism of each organism must adapt to variations in nutrient availability.)
Finally, some positions might be described by multiple evolutionary patterns. One possibility (although not dominant in the LacI/GalR or aldolase families) is that positions with top pairwise scores are also top EVC scores. Another possible overlap is between positions with strong co-evolution and phylogenetic scores: The fact that covariation can occur from either co-evolution or phylogeny is usually seen as a drawback to these calculations, but the changes of some co-evolving pairs might also track with phylogeny. The same is true for EVC positions, as may be the case for the LacI/GalR family. Nor does the overlap diminish the functional significance of positions with top EVC scores, as shown by their sensitivity to mutagenesis and/or their key structural locations. Finally, the aldolase data show that EVC scores are not always dominated by phylogeny, because EVC and TEA-O scores show lower correlations than the EVC scores with each other (Table 1). As we noted above, each protein family may have different phylogenetic contributions to covariation scores; a strong difference could occur between families that comprise orthologs vs those comprising paralogs.
One remaining question is whether positions with different types of evolutionary patterns have different mutational responses. Conserved positions almost always exhibit what we recently called “toggle” behavior77 – at a given position, most amino acid substitutions abolish function; furthermore, compensatory changes at other positions are seldom identified. Mutational results for positions with high pairwise co-evolutionary scores have been harder to predict.77 Figure S10 shows that many of the top pairwise positions in LacI/GalR also act as functional toggles when mutated individually. For co-evolving pairs of positions, early expectations were that their mutations would compensate each other. However, results from double mutant cycles have not shown clear-cut patterns; some show no linkage between co-evolving pairs of positions62, others show epistasis (non-additivity), with the caveats that non-additivity was not always predictable or uniquely limited to the co-evolving positions.85–87
Given the high prevalence of epistasis that has been documented for changes at nonconserved positions during evolution88–91, we expect that EVC positions will also show non-additivity for combinatorial mutations. Indeed, for the LacI/GalR family, mutational epistasis has already been documented among several of the top 20 EVC positions.92 Furthermore, multiple substitutions at three top EVC positions in LacI/GalR (51, 52, and 55) reveal a “rheostat” behavior: That is, the multiple variants for one position could be rank-ordered to show a progressive effect on function that spanned orders of magnitude. It is intriguing to consider (i) whether the strong edges between high EVC positions can predict which groups of positions will show non-additivity with each other; or (ii) whether positions that have both strong EVC and strong phylogeny scores (such as in LacI/GalR) have different mutational outcomes than positions that have either strong EVC or strong phylogenetic scores (such as in aldolase).
In conclusion, EVC network centrality detects positions that can be important to protein structure and function. Furthermore, EVC calculations are more consistent between algorithms than pairwise co-evolution scores, indicating that these central nodes are a robust property of co-evolution networks.
Supplementary Material
Acknowledgments
This work was supported by the National Institutes of Health [GM079423 to LSK], by the University of Kansas Medical Center Biomedical Research Training Program to DJP, and by a K-INBRE Developmental Research Project award [P20GM103418 to JCJR].
Footnotes
Supporting software is available at:
http://sourceforge.net/projects/coevolutils/ or https://github.com/djparente/coevol-utils and https://github.com/djparente/MARS
Supporting information: Supporting information is available at Proteins online.
Some co-evolutionary algorithms and methods for constructing MSAs do appear to out-perform others in predicting direct structural contacts. However, as we noted above, this is not the sole determinant of algorithm success; long range co-evolution can also be biologically significant.
As implemented, the NMIsub is actually the original NMI score minus the average NMI score in an ensemble of ten re-shuffled alignments.
References
- 1.Mihalek I, Res I, Lichtarge O. A family of evolution-entropy hybrid methods for ranking protein residues by importance. J Mol Biol. 2004;336:1265. doi: 10.1016/j.jmb.2003.12.078. [DOI] [PubMed] [Google Scholar]
- 2.Lichtarge O, Bourne HR, Cohen FE. An Evolutionary Trace Method Defines Binding Surfaces Common to Protein Families. Journal of Molecular Biology. 1996;257:342. doi: 10.1006/jmbi.1996.0167. [DOI] [PubMed] [Google Scholar]
- 3.Gu X, Vander Velden K. DIVERGE: phylogeny-based analysis for functional–structural divergence of a protein family. Bioinformatics. 2002;18:500–501. doi: 10.1093/bioinformatics/18.3.500. [DOI] [PubMed] [Google Scholar]
- 4.Ng PC, Henikoff S. Predicting deleterious amino acid substitutions. Genome Res. 2001;11:863–874. doi: 10.1101/gr.176601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Armon A, Graur D, Ben-Tal N. ConSurf: an algorithmic tool for the identification of functional regions in proteins by surface mapping of phylogenetic information. J Mol Biol. 2001;307:447–463. doi: 10.1006/jmbi.2000.4474. [DOI] [PubMed] [Google Scholar]
- 6.Ramensky V, Bork P, Sunyaev S. Human non-synonymous SNPs: server and survey. Nucleic Acids Res. 2002;30:3894–3900. doi: 10.1093/nar/gkf493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kalinina OV, Novichkov PS, Mironov AA, Gelfand MS, Rakhmaninova AB. SDPpred: a tool for prediction of amino acid residues that determine differences in functional specificity of homologous proteins. Nucleic Acids Res. 2004;32:W424–428. doi: 10.1093/nar/gkh391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.La D, Sutch B, Livesay DR. Predicting protein functional sites with phylogenetic motifs. Proteins. 2005;58:309–320. doi: 10.1002/prot.20321. [DOI] [PubMed] [Google Scholar]
- 9.Ye K, Vriend G, AP IJ. Tracing evolutionary pressure. Bioinformatics. 2008;24:908–915. doi: 10.1093/bioinformatics/btn057. [DOI] [PubMed] [Google Scholar]
- 10.Ashkenazy H, Erez E, Martz E, Pupko T, Ben-Tal N. ConSurf 2010: calculating evolutionary conservation in sequence and structure of proteins and nucleic acids. Nucleic Acids Res. 2010;38(Suppl):W529–533. doi: 10.1093/nar/gkq399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Capra JA, Singh M. Predicting functionally important residues from sequence conservation. Bioinformatics. 2007;23:1875–1882. doi: 10.1093/bioinformatics/btm270. [DOI] [PubMed] [Google Scholar]
- 12.Chakrabarti S, Bryant SH, Panchenko AR. Functional Specificity Lies within the Properties and Evolutionary Changes of Amino Acids. J Mol Biol. 2007;373:801–810. doi: 10.1016/j.jmb.2007.08.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Valdar WS. Scoring residue conservation. Proteins. 2002;48:227–241. doi: 10.1002/prot.10146. [DOI] [PubMed] [Google Scholar]
- 14.Livesay DR, Kreth KE, Fodor AA. A critical evaluation of correlated mutation algorithms and coevolution within allosteric mechanisms. Methods Mol Biol. 2012;796:385–398. doi: 10.1007/978-1-61779-334-9_21. [DOI] [PubMed] [Google Scholar]
- 15.Burger L, van Nimwegen E. Disentangling Direct from Indirect Co-Evolution of Residues in Protein Alignments. PLoS Comput Biol. 2010;6:e1000633. doi: 10.1371/journal.pcbi.1000633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Horner DS, Pirovano W, Pesole G. Correlated substitution analysis and the prediction of amino acid structural contacts. Briefings in Bioinformatics. 2008;9:46–56. doi: 10.1093/bib/bbm052. [DOI] [PubMed] [Google Scholar]
- 17.Gobel U, Sander C, Schneider R, Valencia A. Correlated mutations and residue contacts in proteins. Proteins. 1994;18:309–317. doi: 10.1002/prot.340180402. [DOI] [PubMed] [Google Scholar]
- 18.Olmea O, Valencia A. Improving contact predictions by the combination of correlated mutations and other sources of sequence information. Fold Des. 1997;2:S25–32. doi: 10.1016/s1359-0278(97)00060-6. [DOI] [PubMed] [Google Scholar]
- 19.Lockless SW, Ranganathan R. Evolutionarily conserved pathways of energetic connectivity in protein families. Science. 1999;286:295–299. doi: 10.1126/science.286.5438.295. [DOI] [PubMed] [Google Scholar]
- 20.Olmea O, Rost B, Valencia A. Effective use of sequence correlation and conservation in fold recognition. J Mol Biol. 1999;293:1221–1239. doi: 10.1006/jmbi.1999.3208. [DOI] [PubMed] [Google Scholar]
- 21.Kass I, Horovitz A. Mapping pathways of allosteric communication in GroEL by analysis of correlated mutations. Proteins. 2002;48:611–617. doi: 10.1002/prot.10180. [DOI] [PubMed] [Google Scholar]
- 22.Dekker JP, Fodor A, Aldrich RW, Yellen G. A perturbation-based method for calculating explicit likelihood of evolutionary co-variance in multiple sequence alignments. Bioinformatics. 2004;20:1565–1572. doi: 10.1093/bioinformatics/bth128. [DOI] [PubMed] [Google Scholar]
- 23.Brown CA, Brown KS. Validation of coevolving residue algorithms via pipeline sensitivity analysis: ELSC and OMES and ZNMI, oh my! PLoS One. 2010;5:e10779. doi: 10.1371/journal.pone.0010779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Marks DS, Colwell LJ, Sheridan R, Hopf TA, Pagnani A, Zecchina R, Sander C. Protein 3D Structure Computed from Evolutionary Sequence Variation. PLoS ONE. 2011;6:e28766. doi: 10.1371/journal.pone.0028766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gloor GB, Martin LC, Wahl LM, Dunn SD. Mutual Information in Protein Multiple Sequence Alignments Reveals Two Classes of Coevolving Positions†. Biochemistry. 2005;44:7156–7165. doi: 10.1021/bi050293e. [DOI] [PubMed] [Google Scholar]
- 26.Buslje CM, Santos J, Delfino JM, Nielsen M. Correction for phylogeny, small number of observations and data redundancy improves the identification of coevolving amino acid pairs using mutual information. Bioinformatics. 2009;25:1125–1131. doi: 10.1093/bioinformatics/btp135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Simonetti FL, Teppa E, Chernomoretz A, Nielsen M, Marino Buslje C. MISTIC: mutual information server to infer coevolution. Nucleic Acids Research. 2013;41:W8–W14. doi: 10.1093/nar/gkt427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Parente DJ, Swint-Kruse L. Multiple co-evolutionary networks are supported by the common tertiary scaffold of the LacI/GalR proteins. PLoS ONE. 2013;8:e84398. doi: 10.1371/journal.pone.0084398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Fodor AA, Aldrich RW. Influence of conservation on calculations of amino acid covariance in multiple sequence alignments. Proteins. 2004;56:211–221. doi: 10.1002/prot.20098. [DOI] [PubMed] [Google Scholar]
- 30.Shaw ME. Group structure and the behavior of individuals in small groups. Journal of Psychology. 1954;38:139–149. [Google Scholar]
- 31.Bonacich P. Factoring and weighting approaches to status scores and clique identification. Journal of Mathematical Sociology. 1972;2:113–120. [Google Scholar]
- 32.Tungtur S, Parente DJ, Swint-Kruse L. Functionally important positions can comprise the majority of a protein’s architecture. Proteins. 2011;79:1589–1608. doi: 10.1002/prot.22985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Altschul SF, Madden TL, Schaffer AA, Zhang J, Zhang Z, Miller W, Lipman DJ. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Pei J, Kim BH, Grishin NV. PROMALS3D: a tool for multiple protein sequence and structure alignments. Nucleic Acids Res. 2008;36:2295–2300. doi: 10.1093/nar/gkn072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Edgar RC. MUSCLE: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 2004;32:1792–1797. doi: 10.1093/nar/gkh340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Needleman SB, Wunsch CD. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J Mol Biol. 1970;48:443–453. doi: 10.1016/0022-2836(70)90057-4. [DOI] [PubMed] [Google Scholar]
- 37.Edgar RC. MUSCLE: a multiple sequence alignment method with reduced time and space complexity. BMC Bioinformatics. 2004;5:113. doi: 10.1186/1471-2105-5-113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Benítez-Páez A, Cárdenas-Brito S, Gutiérrez AJ. A practical guide for the computational selection of residues to be experimentally characterized in protein families. Briefings in Bioinformatics. 2012;13:329–336. doi: 10.1093/bib/bbr052. [DOI] [PubMed] [Google Scholar]
- 39.Pei J. Multiple protein sequence alignment. Curr Opin Struct Biol. 2008;18:382–386. doi: 10.1016/j.sbi.2008.03.007. [DOI] [PubMed] [Google Scholar]
- 40.Stamatakis A, Ludwig T, Meier H. RAxML-III: a fast program for maximum likelihood-based inference of large phylogenetic trees. Bioinformatics. 2005;21:456–463. doi: 10.1093/bioinformatics/bti191. [DOI] [PubMed] [Google Scholar]
- 41.Jordan GE, Piel WH. PhyloWidget: web-based visualizations for the tree of life. Bioinformatics. 2008;24:1641–1642. doi: 10.1093/bioinformatics/btn235. [DOI] [PubMed] [Google Scholar]
- 42.Halabi N, Rivoire O, Leibler S, Ranganathan R. Protein sectors: evolutionary units of three-dimensional structure. Cell. 2009;138:774–786. doi: 10.1016/j.cell.2009.07.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kann MG, Shoemaker BA, Panchenko AR, Przytycka TM. Correlated Evolution of Interacting Proteins: Looking Behind the Mirrortree. Journal of Molecular Biology. 2009;385:91–98. doi: 10.1016/j.jmb.2008.09.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Sato T, Yamanishi Y, Kanehisa M, Toh H. The inference of protein–protein interactions by co-evolutionary analysis is improved by excluding the information about the phylogenetic relationships. Bioinformatics. 2005;21:3482–3489. doi: 10.1093/bioinformatics/bti564. [DOI] [PubMed] [Google Scholar]
- 45.Kleinberg JM. Authoritative sources in a hyperlinked environment. Journal of the ACM (JACM) 1999;46:604–632. [Google Scholar]
- 46.Page L, Brin S, Motwani R, Winograd T. The PageRank citation ranking: Bringing order to the web. 1999 http:ilpubsstanfordedu:8090/422/
- 47.Fowler JH, Christakis NA. Dynamic spread of happiness in a large social network: longitudinal analysis over 20 years in the Framingham Heart Study. BMJ. 2008;337:a2338. doi: 10.1136/bmj.a2338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Fowler JH. Connecting the Congress: A study of cosponsorship networks. Political Analysis. 2006;14:456–487. [Google Scholar]
- 49.Lohmann G, Margulies DS, Horstmann A, Pleger B, Lepsien J, Goldhahn D, Schloegl H, Stumvoll M, Villringer A, Turner R. Eigenvector centrality mapping for analyzing connectivity patterns in fMRI data of the human brain. PLoS One. 2010;5:e10232. doi: 10.1371/journal.pone.0010232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Gundlapalli A, Ma X, Benuzillo J, Pettey W, Greenberg R, Hales J, Leecaster M, Samore M. Social network analyses of patient-healthcare worker interactions: implications for disease transmission. AMIA Annu Symp Proc. 2009;2009:213–217. [PMC free article] [PubMed] [Google Scholar]
- 51.Fichtenberg CM, Muth SQ, Brown B, Padian NS, Glass TA, Ellen JM. Sexual network structure among a household sample of urban african american adolescents in an endemic sexually transmitted infection setting. Sex Transm Dis. 2009;36:41–48. doi: 10.1097/OLQ.0b013e3181860711. [DOI] [PubMed] [Google Scholar]
- 52.Newman MEJ. The Structure and Function of Complex Networks. SIAM Review. 2003;45:167–256. [Google Scholar]
- 53.Bell CE, Lewis M. A closer view of the conformation of the Lac repressor bound to operator. Nat Struct Biol. 2000;7:209–214. doi: 10.1038/73317. [DOI] [PubMed] [Google Scholar]
- 54.Hars U, Horlacher R, Boos W, Welte W, Diederichs K. Crystal structure of the effector-binding domain of the trehalose-repressor of Escherichia coli, a member of the LacI family, in its complexes with inducer trehalose-6-phosphate and noninducer trehalose. Protein Sci. 1998;7:2511–2521. doi: 10.1002/pro.5560071204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Schumacher MA, Glasfeld A, Zalkin H, Brennan RG. The X-ray structure of the PurR-guanine-purF operator complex reveals the contributions of complementary electrostatic surfaces and a water-mediated hydrogen bond to corepressor specificity and binding affinity. J Biol Chem. 1997;272:22648–22653. doi: 10.1074/jbc.272.36.22648. [DOI] [PubMed] [Google Scholar]
- 56.Schumacher MA, Seidel G, Hillen W, Brennan RG. Structural mechanism for the fine-tuning of CcpA function by the small molecule effectors glucose 6-phosphate and fructose 1,6-bisphosphate. J Mol Biol. 2007;368:1042–1050. doi: 10.1016/j.jmb.2007.02.054. [DOI] [PubMed] [Google Scholar]
- 57.Schumacher MA, Allen GS, Diel M, Seidel G, Hillen W, Brennan RG. Structural basis for allosteric control of the transcription regulator CcpA by the phosphoprotein HPr-Ser46-P. Cell. 2004;118:731–741. doi: 10.1016/j.cell.2004.08.027. [DOI] [PubMed] [Google Scholar]
- 58.Arakaki TL, Pezza JA, Cronin MA, Hopkins CE, Zimmer DB, Tolan DR, Allen KN. Structure of human brain fructose 1,6-(bis)phosphate aldolase: linking isozyme structure with function. Protein Sci. 2004;13:3077–3084. doi: 10.1110/ps.04915904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Schumacher MA, Sprehe M, Bartholomae M, Hillen W, Brennan RG. Structures of carbon catabolite protein A-(HPr-Ser46-P) bound to diverse catabolite response element sites reveal the basis for high-affinity binding to degenerate DNA operators. Nucleic Acids Res. 2011;39:2931–2942. doi: 10.1093/nar/gkq1177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. UCSF Chimera–a visualization system for exploratory research and analysis. J Comput Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 61.Lebherz HG, Rutter WJ. Distribution of Fructose Diphosphate Aldolase Variants in Biological Systems. Biochemistry. 1969;8:109–121. doi: 10.1021/bi00829a016. [DOI] [PubMed] [Google Scholar]
- 62.Lee Y, Mick J, Furdui C, Beamer LJ. A coevolutionary residue network at the site of a functionally important conformational change in a phosphohexomutase enzyme family. PLoS One. 2012;7:e38114. doi: 10.1371/journal.pone.0038114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Pelé J, Moreau M, Abdi H, Rodien P, Castel H, Chabbert M. Comparative analysis of sequence covariation methods to mine evolutionary hubs: Examples from selected GPCR families. Proteins. 2014 doi: 10.1002/prot.24570. In Press. [DOI] [PubMed] [Google Scholar]
- 64.Chakrabarti S, Panchenko AR. Structural and Functional Roles of Coevolved Sites in Proteins. PLoS ONE. 2010;5:e8591. doi: 10.1371/journal.pone.0008591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Lee BC, Park K, Kim D. Analysis of the residue-residue coevolution network and the functionally important residues in proteins. Proteins. 2008;72:863–872. doi: 10.1002/prot.21972. [DOI] [PubMed] [Google Scholar]
- 66.Landherr A, Friedl B, Heidemann J. A critical review of centrality measures in social networks. Business & Information Systems Engineering. 2010;2:371–385. [Google Scholar]
- 67.Talavera D, Lovell SC, Whelan S. Covariation is a poor measure of molecular coevolution. Molecular Biology and Evolution. 2015 doi: 10.1093/molbev/msv109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Dunn SD, Wahl LM, Gloor GB. Mutual information without the influence of phylogeny or entropy dramatically improves residue contact prediction. Bioinformatics. 2008;24:333–340. doi: 10.1093/bioinformatics/btm604. [DOI] [PubMed] [Google Scholar]
- 69.Choi KY, Zalkin H. Role of the purine repressor hinge sequence in repressor function. J Bacteriol. 1994;176:1767–1772. doi: 10.1128/jb.176.6.1767-1772.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Suckow J, Markiewicz P, Kleina LG, Miller J, Kisters-Woike B, Muller-Hill B. Genetic studies of the Lac repressor. XV: 4000 single amino acid substitutions and analysis of the resulting phenotypes on the basis of the protein structure. J Mol Biol. 1996;261:509–523. doi: 10.1006/jmbi.1996.0479. [DOI] [PubMed] [Google Scholar]
- 71.Falcon CM, Swint-Kruse L, Matthews KS. Designed disulfide between N-terminal domains of lactose repressor disrupts allosteric linkage. J Biol Chem. 1997;272:26818–26821. doi: 10.1074/jbc.272.43.26818. [DOI] [PubMed] [Google Scholar]
- 72.Ozarowski A, Barry JK, Matthews KS, Maki AH. Ligand-induced conformational changes in lactose repressor: a phosphorescence and ODMR study of single-tryptophan mutants. Biochemistry. 1999;38:6715–6722. doi: 10.1021/bi990242f. [DOI] [PubMed] [Google Scholar]
- 73.Swint-Kruse L, Elam CR, Lin JW, Wycuff DR, Shive Matthews K. Plasticity of quaternary structure: twenty-two ways to form a LacI dimer. Protein Sci. 2001;10:262–276. doi: 10.1110/ps.35801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Flynn TC, Swint-Kruse L, Kong Y, Booth C, Matthews KS, Ma J. Allosteric transition pathways in the lactose repressor protein core domains: asymmetric motions in a homodimer. Protein Sci. 2003;12:2523–2541. doi: 10.1110/ps.03188303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Zhan H, Camargo M, Matthews KS. Positions 94–98 of the lactose repressor N-subdomain monomer-monomer interface are critical for allosteric communication. Biochemistry. 2010;49:8636–8645. doi: 10.1021/bi101106x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Xu J, Liu S, Chen M, Ma J, Matthews KS. Altering residues N125 and D149 impacts sugar effector binding and allosteric parameters in Escherichia coli lactose repressor. Biochemistry. 2011;50:9002–9013. doi: 10.1021/bi200896t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Meinhardt S, Manley MW, Jr, Parente DJ, Swint-Kruse L. Rheostats and toggle switches for modulating protein function. PLoS One. 2013;8:e83502. doi: 10.1371/journal.pone.0083502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Zhan H, Swint-Kruse L, Matthews KS. Extrinsic interactions dominate helical propensity in coupled binding and folding of the lactose repressor protein hinge helix. Biochemistry. 2006;45:5896–5906. doi: 10.1021/bi052619p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Kleina LG, Miller JH. Genetic studies of the lac repressor. XIII. Extensive amino acid replacements generated by the use of natural and synthetic nonsense suppressors. J Mol Biol. 1990;212:295–318. doi: 10.1016/0022-2836(90)90126-7. [DOI] [PubMed] [Google Scholar]
- 80.Markiewicz P, Kleina LG, Cruz C, Ehret S, Miller JH. Genetic studies of the lac repressor. XIV. Analysis of 4000 altered Escherichia coli lac repressors reveals essential and non-essential residues, as well as “spacers” which do not require a specific sequence. J Mol Biol. 1994;240:421–433. doi: 10.1006/jmbi.1994.1458. [DOI] [PubMed] [Google Scholar]
- 81.Buck MJ, Atchley WR. Networks of Coevolving Sites in Structural and Functional Domains of Serpin Proteins. Molecular Biology and Evolution. 2005;22:1627–1634. doi: 10.1093/molbev/msi157. [DOI] [PubMed] [Google Scholar]
- 82.Xu Y, Tillier ERM. Regional covariation and its application for predicting protein contact patches. Proteins: Structure, Function, and Bioinformatics. 2010;78:548–558. doi: 10.1002/prot.22576. [DOI] [PubMed] [Google Scholar]
- 83.Fatakia SN, Costanzi S, Chow CC. Molecular Evolution of the Transmembrane Domains of G Protein-Coupled Receptors. PLoS ONE. 2011;6:e27813. doi: 10.1371/journal.pone.0027813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Teşileanu T, Colwell LJ, Leibler S. Protein Sectors: Statistical Coupling Analysis versus Conservation. PLoS Comput Biol. 2015;11:e1004091. doi: 10.1371/journal.pcbi.1004091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Gloor GB, Tyagi G, Abrassart DM, Kingston AJ, Fernandes AD, Dunn SD, Brandl CJ. Functionally Compensating Coevolving Positions Are Neither Homoplasic Nor Conserved in Clades. Molecular Biology and Evolution. 2010;27:1181–1191. doi: 10.1093/molbev/msq004. [DOI] [PubMed] [Google Scholar]
- 86.Fodor AA, Aldrich RW. On Evolutionary Conservation of Thermodynamic Coupling in Proteins. Journal of Biological Chemistry. 2004;279:19046–19050. doi: 10.1074/jbc.M402560200. [DOI] [PubMed] [Google Scholar]
- 87.Chi CN, Elfström L, Shi Y, Snäll T, Engström Å, Jemth P. Reassessing a sparse energetic network within a single protein domain. Proceedings of the National Academy of Sciences. 2008;105:4679–4684. doi: 10.1073/pnas.0711732105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Breen MS, Kemena C, Vlasov PK, Notredame C, Kondrashov FA. Epistasis as the primary factor in molecular evolution. Nature. 2012 doi: 10.1038/nature11510. advance online publication. [DOI] [PubMed] [Google Scholar]
- 89.Dawid A, Kiviet DJ, Kogenaru M, de Vos M, Tans SJ. Multiple peaks and reciprocal sign epistasis in an empirically determined genotype-phenotype landscape. Chaos. 2010;20:026105. doi: 10.1063/1.3453602. [DOI] [PubMed] [Google Scholar]
- 90.Dellus-Gur E, Elias M, Caselli E, Prati F, Salverda ML, de Visser JA, Fraser JS, Tawfik DS. Negative epistasis and evolvability in TEM-1 beta-lactamase - The thin line between an enzyme’s conformational freedom and disorder. J Mol Biol. 2015 doi: 10.1016/j.jmb.2015.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Kryazhimskiy S, Dushoff J, Bazykin GA, Plotkin JB. Prevalence of Epistasis in the Evolution of Influenza A Surface Proteins. PLoS Genet. 2011;7:e1001301. doi: 10.1371/journal.pgen.1001301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Tungtur S, Meinhardt S, Swint-Kruse L. Comparing the functional roles of nonconserved sequence positions in homologous transcription repressors: Implications for sequence/function analyses. Journal of Molecular Biology. 2010;395:785–802. doi: 10.1016/j.jmb.2009.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


