Analysis-Preserving Video Microscopy Compression via Correlation and Mathematical Morphology

Abstract

The large amount video data produced by multi-channel, high-resolution microscopy system drives the need for a new high-performance domain-specific video compression technique. We describe a novel compression method for video microscopy data. The method is based on Pearson's correlation and mathematical morphology. The method makes use of the point-spread function (PSF) in the microscopy video acquisition phase. We compare our method to other lossless compression methods and to lossy JPEG, JPEG2000 and H.264 compression for various kinds of video microscopy data including fluorescence video and brightfield video. We find that for certain data sets, the new method compresses much better than lossless compression with no impact on analysis results. It achieved a best compressed size of 0.77% of the original size, 25× smaller than the best lossless technique (which yields 20% for the same video). The compressed size scales with the video's scientific data content. Further testing showed that existing lossy algorithms greatly impacted data analysis at similar compression sizes.

INTRODUCTION

High-speed, high-resolution and high-content microscopy systems are increasing the rate and amount of video data being acquired more rapidly than the rate of increase in affordable data storage (Wollman 2007). This forces the bench scientist either to be very selective in which data sets they store or to greatly compress their data (Oh et al., 2003). At the same time, funding agencies and journals are increasingly requiring all data from published experiments be retained to enable re-analysis by others. Our goal was to develop a method that obtains high compression while preserving the information needed to perfectly reproduce analysis results.

There are a number of lossless compression techniques available that reduce the size of a data set while enabling exact reconstruction of the original file (Christopoulos et al., 2000; Wiegand, 2003; Vatolin et al., 2007; Burrows et al., 1994). Some have been developed specifically for use on images (Christopoulos et al., 2000) and video data (Wiegand, 2003; Vatolin et al., 2007). Noise in the video images combines with the requirement that every pixel be exactly reproduced in every frame to limit compression rates for these techniques.

Several high-quality image compression techniques are tuned specifically for the human visual system to produce image artifacts that are not easily seen (they are “perceptually lossless”). They achieve far greater compression rates without visible quality loss (Christopoulos et al., 2000). Similarly, a number of video-compression techniques exist, also finely tuned to avoid introducing visible artifacts (Wiegand, 2003). However these techniques are not ideal for compressing microscopy videos because of two reasons. First, human visual system and the microscopy video analysis procedure are sensitive to different sets of features in a video. Those compression techniques are designed only to address the sets of features that human visual system is sensitive to. Second, the noise in natural scene videos and microscopy videos does not have the exact same characteristics. Those compression techniques are designed in accordance with the noise in natural scene videos.

The use of three new compression techniques for single confocal fluorescence microcopy images of cells was explored by Bernas et al. (2006) to determine how much compression could be achieved based on the signal to noise ratio (SNR) of the images. They used two techniques to estimate SNR for the images (Amer et al., 2005; Nowak et al., 1999). Their spatial downsampling approach reduced image resolution to match the frequency at which the spatial intensity contrast passed below the estimated noise floor in the images. Their intensity downsampling approach reduced the number of intensities per pixel to the number of distinguishable levels based on the noise floor. Their wavelet compression approach removed wavelet coefficients that were expected to represent only noise. They achieved compression ratios of between 3 and 9 without significant reduction in three quality tests. We seek compression ratios of up to 100..

With the goal of decreasing the transmission bandwidth for time-series of confocal optical microscopy image transmission, Avinash looked at the impact of different quality levels of JPEG compression (compared to lossless compression) on the image intensity variance in single 2D images (Avitash 1995). He compared this to estimates of image noise based on the variance in visually uniform background regions. He hypothesizes that adding only slight compression noise compared to the already-present background noise may not impede quantitative analysis (20% increase in noise). He compared time-averaged versions of the same region to simulate images with different noise levels. He found that at a JPEG quality setting of 75/100, the noise variance was much higher than the difference variance (22–32× greater); at this value, the compression ratio varied between around 3 (noisy image) and 5 (less-noisy image). The compression ratio was never more than 11, even for images with significant degradation.

We describe a new method for microscopy video compression that achieves up to 100× compression, enabling high-throughput video-acquisition experiments to be stored in the same space as conventional experiments. The compression has no impact on analysis results. It achieves this by storing only the information in a video that analysis can use and averaging out noise in the background. It first separates every frame into foreground (pixels that carry information) and background (pixels that change only as a function of instrument noise) and then losslessly compresses the foreground regions. This successfully keeps all relevant data while achieving a better compression ratio. In testing, it achieved a best compressed size of 0.77% of the original size (over 100× compression) whereas the best standard technique yields 20% (~5× compression) for the same video.

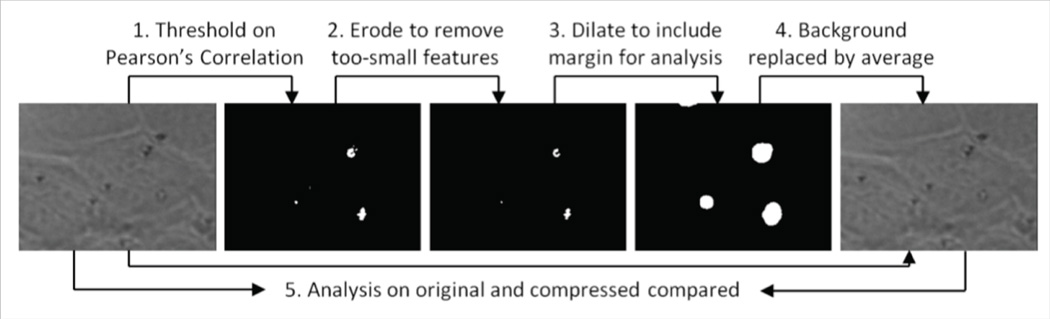
The key problem is to decide whether each pixel in each video frame is foreground or background. For microscopy video, the noise behavior is well understood to be independent between neighboring pixels, whereas blurring (convolution with the point-spread function (PSF)) will spread image brightness changes in one pixel to its neighbors (Sheppard et al., 2006). Making use of this property, we designed a correlation-based method that separates foreground from background. Fig. 1 summarizes the steps, which are further detailed below and in the Methods section.

Fig. 1.

Algorithm overview.

36×11mm (600 × 600 DPI)

The method first generates a binary segmentation of each frame into foreground and background pixels by thresholding on the maximum magnitude of the Pearson’s correlation coefficient (Stigler, 1989) between each pixel and its eight neighbors. This coefficient is computed over all frames of the video, selecting pixels whose brightness changes are correlated with those of their neighbors.

Because even independent random variables have nonzero correlations with some probability, a number of pixels are falsely labeled as foreground. These pixels are likely to be spread evenly across the image, whereas true foreground pixels will be grouped into clusters that are at least as large as the main lobe of the PSF. To remove these false positives, the binary segmentation is refined by the mathematical morphology erosion operation.

Because analysis methods make use of pixels near the foreground pixels, the resulting set of foreground pixels is dilated to include pixels that are close enough to affect analysis (this radius depends on the parameters of the analysis algorithm).

Using the refined binary segmentation, the original video has each pixel in its background regions replaced by that pixel’s time-averaged value. This removes noise, which makes the video more suitable to be compressed by a common lossless compression technique. Here we choose to use lossless H.264 compression.

To verify that the compression had no impact on analysis, the compressed video is processed by the same analysis pipeline to make sure the results exactly match those of the original video.

METHODS

The central problem in this method is to find the separation between foreground pixels (which carry information) and background pixels (which contain only noise) in microscopy video.

In general, noise can be introduced into a video at multiple stages including video acquisition, recording, processing and transmission (Amer et al., 2005). For microscopy videos, noise can be modeled by a shot noise added by white noise. Shot noise is due to the statistical variation in the number of detected photons and it obeys a Poisson distribution (Sheppard et al., 2006). White noise can be modeled by a zero-mean Gaussian distribution.

The background noise in the video can be well modeled by a Gaussian distribution with zero mean and standard deviation σ plus a Poisson distribution with mean and variance λ:

$$N(0,\sigma )+P(\lambda )$$

Importantly, neither of these terms depends on the values of neighboring pixels: they are identically randomly distributed among the pixels in the image (Sheppard et al., 2006).

Another important property of microscopy video is the mixture of values from neighboring pixels caused by the point-spread function. This causes changes in each pixel’s intensity over time to be correlated with those of neighboring pixels. As a result, in a microscopy video, time correlation of the intensity of a pixel and its neighbors tends to become nonzero whenever it is caused by changes in intensity due to specimen motion.

As detailed below, we use a sequence of steps to generate a foreground/background mask for pixels in the video. We use this map to generate another version of the video. In this new video, the foreground pixels are the same as in the original, but each background pixel is replaced in all frames by its mean value over time. The resulting video has every background pixel’s intensity constant over time, enabling it to be better compressed by lossless H.264 compression.

Step 1: Compute Correlation Scores

For each pixel in a video, we consider its intensity value over time as a vector. For a video with dimensions m×n and with k frames, we have m×n vectors. The score for each pixel is computed based on the absolute value of the Pearson’s correlation between that pixel’s intensity value vector and each of its neighbors’ vectors. We denote this value as R_i and compute it as:

$${\mathit{R}}_{\mathit{i}}=|\frac{{\mathrm{\Sigma }}_{j=1}^k(x_j-\overline{x})(y_{ij}-{ӯ}_i)}{k{\sigma }_x{\sigma }_{yi}}|$$

where x_j is the pixel intensity value for the center pixel at jth frame, x̄ is the mean pixel intensity value for the center pixel. y_ij is the pixel intensity value for the neighbor pixel at jth frame; ӯ_i is the mean pixel intensity value for the neighbor pixel. σ_x is the standard deviation of the pixel intensity value for the center pixel and σ_yi is the standard deviation of the pixel intensity value for the neighbor pixel.

We compute this value for all eight neighboring pixels. To be conservative in our estimate of foreground pixels, we compute the maximum of all neighboring pixels and use this score to determine which pixels are in the foreground.

Step 2: Determine Threshold

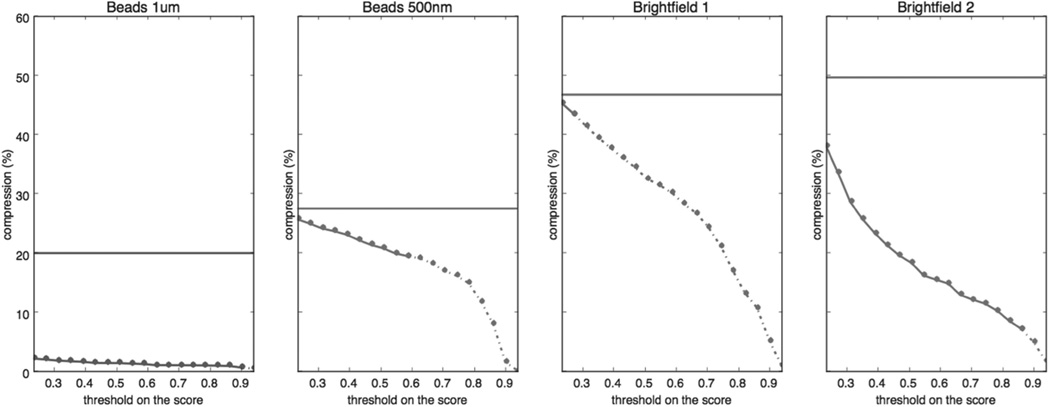
After every pixel has a score assigned to it, we must select a threshold such that all pixels whose score are above the threshold are considered foreground pixels. Fig. 3 shows the impact on compression size as this threshold is increased; fewer pixels are selected as foreground and the compression ratio improves. However, at some point this causes foreground pixels in the image to be missed, which impacts the data analysis and the compression begins to change the results of analysis. Because there is no general solution to the question “how much change to analysis values is too much”, we stop at this level we select the threshold that has the best compression without impacting analysis.

Fig. 3.

Plots of compression ratio (in percentage) vs. correlation magnitude threshold on scores for four

videos. Four plots shows the result for four test videos. Four plots share the same vertical axis. A horizontal flat line indicates the compression ratio on that video with H.264 lossless. The curves become dashed when the analysis results on compressed videos differs from the analysis result on the original, indicating the limit compression without impacting analysis results.results.

45×15mm (600 × 600 DPI)

Step 3: Remove False Positives

Even independent random variables have nonzero correlations with some probability, resulting in a number of pixels being falsely labeled as foreground. These pixels are likely to be spread evenly across the image, whereas true foreground pixels will be grouped into clusters that are at least as large as the main lobe of the PSF. To remove these false positives, the binary segmentation is refined by the mathematical morphology erosion operation (Serra, 1982).

This operation effectively places a disk on each of the foreground pixels. If all of the pixels in the disk are also foreground, the pixel is left as foreground. Otherwise it is background. We used a disk of diameter of 3 pixels for all of the videos tested. This is motivated by the extension of the point-spread function of the microscope used to collect the video.

Step 4: Include All Pixels Used by Analysis

Image analysis routines often use pixels beyond the foreground in their calculations. To ensure that they produce identical results on the compressed video, it is necessary to extend the region of foreground pixels to include these neighboring pixels. Our compression therefore expands the region by a distance in pixels specified by the scientist based on their analysis routine. This is done using the mathematical morphology dilation operation, which marks all of the pixels within a specified radius of an existing foreground pixel as also being foreground.

Our collaborators evaluate their data using the CISMM Video Spot Tracker (2015). This program uses trackers with a fixed radius. The dilation operator determines the size of neighborhood. To fit the spot tracker’s radius, a radius of 51 pixels is used. An example of a binary map before refinement and after refinement is given in Fig.1.

Software

We wrote a C++ program to implement the algorithm used to perform the experiment. Multiple publicly available compression software libraries were used. The source code of the C++ program can be obtained from https://github.com/CISMM/data_reduction. The experiment is detailed in the Results section. In the experiment, the version of the implementation of the standard libx265 is 1.3+861−86ca1de606e3. The H.264 implementation used libx264 version 0.142.50. For JPEG2000, libopenjpeg version 1.5.2 was used.

RESULTS

This method achieved much better compression than existing lossless techniques with identical analysis results in more than half of the cases tested. Perceptually-tuned lossy algorithms greatly impacted analysis when forced to achieve the same compressed size.

The data used for testing consists of six cases (Fig. 2). The first four (two fluorescence and two bright-field imaging) have 1000 frames of moving beads attached to cell membranes. The beads in the fluorescence videos have diameters of 1 µm and 500 nm. (The video with 500 nm beads has many more beads.) The fifth video shows cells moving in bright-field imaging. The sixth video consists of beads that stay mostly still for the first half of the video and then move rapidly in one direction.

Fig. 2.

Example frame from each of the videos tested, each named as in the description and tables.

361×61mm (300 × 300 DPI)

TABLE 1 compares the performance of our method against lossless H.264 compression. The usage of a more recent video compression standard H.265 was also explored and compared with H.264. Firstly, we used the two compression techniques to compress the data listed in the second column in TABLE 1, namely the fluorescence video with 1 µm-diameter beads. The data was pre-processed with our methods. In this test, H.264 outperforms H.265 by having a 0.1MB-smaller compressed video size. The same experiment was done on the cells video (Fig. 2, fifth from left). This time H.265 has a 0.1MB-smaller compressed data comparing against H.264. We are interested in the ratio between the size of compressed files with and without our method. We noticed that this ratio stays almost the same for both H.265 and H.264. More precisely, the difference stays within 1% of the range of the data size. Because H.265 does not always yield a better compression, we did most experiments using the more stable H.264 implementation. We also compared against lossless JPEG2000 and lossless JPEG, which did not perform as well.

TABLE 1.

Compression ratio for five real-world videos. Our method outperformed standard H.264 compression by large factors in three out of five test cases. In both cases, the resulting compressed video is in H.264 format so can be easily fed into analysis pipelines.

H.264 lossless	Beads 1µm	Beads 500nm	Brightfield 1	Brightfield 2	Cells
Without our method	20%	28%	47%	50%	33%
Including our method	0.77%	20%	44%	7.3%	4.8%

The size achievable before analysis is impacted scales with the information content of the video: videos with information in every pixel see no improvement. For the 500 nm video (which has more foreground) we achieve a compressed size of 19.6%, only slightly better than lossless H.264 alone. For the video with little foreground, the compressed size reaches 0.77%, 25 times better than lossless H.264 alone and an overall reduction factor of 100×.

Fig. 3 plots the compressed size vs. threshold on the scores and the maximum lossless correlation threshold in all four cases. The compression ratios using standard techniques are also displayed as horizontal lines. TABLE 1 compares our best compression ratios against those achieved by standard compression techniques. TABLE 5 shows the compression ratios for different methods for all cases.

TABLE 5.

Comparison of multiple compression methods on four of the videos shown in the main text. The left and right numbers match those in TABLE 1. Bzip2 and lossless JPEG2000 compression on the original file sequence were usually worse and never much better than lossless H.264. Lossless JPEG2000 and Bzip2 on the filtered image set were always worse than lossless H.264.

	Techniques applied with our approach			Techniques applied without our approach
Video	H.264 lossless	Bzip2	JPEG2000 lossless	JPEG2000 lossless	Bzip2	H.264 lossless
Bead 1µm	0.77%	0.79%	1.3%	24%	19%	20%
Bead 500nm	20%	21%	23%	31%	29%	28%
Brightfield 1	44%	49%	46%	47 %	51%	47%
Brightfield 2	7.3%	26%	29%	50%	54%	50%

In all the experiments described above the erosion diameter was 3 pixels (this depends on the microscope point-spread size). The dilation diameter was set to 51 pixels, which is the size of the search radius for our tracking algorithm when it is testing for beads that disappear during tracking. For experiments without disappearing beads, the diameter can be set to be 24 pixels to achieve higher compression. Dilation radius depends on how many pixels the analysis algorithm looks at beyond the pixels that are part of the objects being analyzed.

We investigated the question of how much the quality factor of H.264 lossless compression can be reduced before we saw changes in the analysis. We intended to show the relative sizes of the compressed video at the smallest H.264 lossy-compressed size that did not induce changes in the tracking compared to the size of our analysis-aware compression. However, in the four test cases (two fluorescence videos and two brightfield videos), the H.264 lossy compression changed the analysis results even at the setting that provided the least compression and gives the best video quality. This indicates that H.264 lossy compression at any level introduces changes in analysis.

We then investigated the question of how much impact the H.264 lossy compression has on tracking. This was done using a lossy compression level that matched the size of the compressed video produced by our analysis-aware compression with no loss. The metric we use for comparison is specific to our particular analysis mode, and is reported in units of fractions of the noise floor in our instrument.

TABLE 2 and TABLE 3 compare our compressed videos to videos compressed using the perceptually-tuned H.264 with its quality parameter set to make the file size match ours. (JPEG2000 was also tested and had results similar to H.264.) It is not possible to determine the impact of individual pixel-brightness values on an arbitrary analysis routine; doing this comparison requires running a particular analysis routine to see the impact. We used the video spot-tracking algorithm employed by our collaborators on both compressed and uncompressed videos and report the difference in centroid locations between the original and the compressed videos. In TABLE 2, the error metric is the squared maximum distance (in units of 0.1 pixels, which is the noise floor of the instrument) between points along bead traces, reported in units of the experiment noise floor. In TABLE 3, the error metric is the per-track mean error along with the standard deviation of the points along bead traces. Our method (by design) achieves 0 error, the perceptually-tuned videos had errors ranging from 2–50 times the noise floor and sometimes lost beads entirely.

TABLE 2.

Maximum tracking error when using lossy compression techniques and using our method in four cases (in units of the experiment noise floor, which is 1/10^th of a pixel). In one video, a bead track was lost, indicated here as infinite error. When they are forced to achieve the same compression ratios, perceptually-tuned compression techniques have a large maximum impact on analysis results.

	Beads 1µm	Beads 500nm	Brightfield 1	Brightfield 2
Lossy H.264	4.6	∞	50.3	2.6
Our method	0	0	0	0

TABLE 3.

Mean and standard deviations of tracking error when using lossy compression techniques and using our method in four cases (in units of experiment noise floor, which is 1/10^th of a pixel).

	Beads 1µm	Beads 500nm	Brightfield 1	Brightfield 2
Lossy H.264	(0.1269, 0.0568)	(∞, ∞)	(0.0468, 0.0502)	(0.1019, 0.0734)
Our method	(0, 0)	(0, 0)	(0, 0)	(0, 0)

To test the generality of the method on non-bead-based specimens, we compressed a microscopy video of moving cells (Fig. 5). Edge-length analysis was performed on this video as follows: Given a video, every frame in the video is filtered by a gauss gradient filter with a Gaussian stand derivation 1 pixel to find the high response locations that suggests existence of an edge. After thresholding, connected components analysis is run on the binary map. To remove the noise, the connected components with fewer than 90 pixels were removed.

Fig. 5.

left to right: first frame of the original video, edge detection results: original video, video with 3.5× compression, video with 4.6× compression, video with 6.8× compression

22×4mm (600 × 600 DPI)

This process was performed on both original video and compressed video. We compare the edge detection result in all frames. With the exact same edge detection result, our compression method achieved 3.5× better compression than lossless H.264 encoding alone

Even non-high-throughput cell-motion videos often use low frame rates to reduce the amount of video storage required. This causes large motion in between frames, which is challenging for vision-based tracking algorithms to handle. An increased frame rate enables storing a much finer time resolution in the same file size, potentially improving the resulting analysis.

Fast-Moving Beads Analysis

In some microscopy videos, foreground objects move quickly over time and can cover most of the frame throughout the course of the entire video. In cases such as this, our basic method does not work well because most pixels are marked as foreground. We applied our method to one such case: a microscopy video that contains 250 frames. Starting in the 100^th frame, the beads in the video start to be move rapidly over the frame. One frame of the video is shown in Fig. 4. The resulting map has most of the pixels as foreground (as expected).

Fig. 4.

left: one frame of Fastbeads video before beads move; middle: foreground/background segmentation on whole video right: fore-ground/background segmentation within a 20-frame window.

30×7mm (600 × 600 DPI)

To achieve a better compression ratio in cases like this, we added a sliding-window extension to the technique. We slide a fixed length (in time) window from the beginning of the video to the end and update the foreground and background pixels using only frames within the window.

For a video of length l and window size s, we get (l−s) different binary maps. By segmenting out only pixels with beads moving over them in a short time period, the sliding-window version of the method marks fewer pixels as foreground in each frame.

TABLE 4 shows the additional compression provided by the sliding-window technique for a video with fast-moving beads. With longer windows, the beads moved across essentially every pixel in the image, so the method produced almost no improvement over lossless H.264 alone. With very short windows, noise suppression was slightly reduced. The optimal window size for this video was 20 frames, resulting in an approximately 2× improvement in file size. A resulting map is shown in Fig. 4.

TABLE 4.

Compression ratio using the sliding window method and using lossless H.264 alone for the Fastbeads video. With longer windows, the beads moved across essentially every pixel in the image, so the method produced almost no improvement over lossless H.264 alone. With very short windows noise suppression was slightly reduced, causing an increase in file size. The optimal window size for this video was 20 frames, resulting in an approximately 2× improvement in file size. As expected, smaller dilation results in better compression (less foreground).

	Dilation Diameter 8 Pixels		Dilation Diameter 20 Pixels
Window size	With sliding window	No sliding window	With sliding window	No sliding window	Lossless H.264
100 frames	16%	35%	21%	39%	39%
50 frames	15%		21%
20 frames	14%		19%
10 frames	15%		20%
5 frames	20%		24%

Comparison with Other Techniques

TABLE 5 shows the results of doing compression tests with algorithms other than H.264 lossless. The first and sixth columns of this table match TABLE 1. Column five shows the result of using Bzip2 compression on the original files, which is usually slightly worse and in one case slightly better than lossless H.264. Column four shows the result of using lossless JPEG2000 on the original videos, which is never better than lossless H.264. Columns two and three show the results of using Bzip2 and lossless JPEG2000 on the images after our algorithm has been applied, which were always worse than using H.264 after our algorithm.

Limitations and Future Work

For the videos that were analyzed in this paper, we selected the largest threshold value that still produced analysis output identical to that from the original videos (the compression included all of the steps described below). This requires running the compression and analysis pipelines a number of times for each video, so is not efficient.

In future work, we are seeking a closed-form approach to selection of the threshold value. Ostu’s method (1979) fails in the case where there is either no foreground or no background in a given video. (Because it is forced to generate two classes, it wrongly classifies a certain portion of number of background and foreground in all cases.) We are investigating camera-noise-estimation methods to automatically determine an appropriate threshold.

CONCLUSION

In summary, we have described a new method for microscopy video compression based on correlation and mathematical morphology. Experiments on several real video data sets show that it can achieve compression ratios of >100, reducing file size by 99+%. These compression ratios correspond to file sizes that are 25× smaller than those generated by lossless compression techniques.