Improving the efficiency of estimation in the additive hazards model for stratified case-cohort design with multiple diseases

Abstract

The case-cohort study design has often been used in studies of a rare disease or for a common disease with some biospecimens needing to be preserved for future studies. A case-cohort study design consists of a random sample, called the subcohort, and all or a portion of the subjects with the disease of interest. One advantage of the case-cohort design is that the same subcohort can be used for studying multiple diseases. Stratified random sampling is often used for the subcohort. Additive hazards models are often preferred in studies where the risk difference, instead of relative risk, is of main interest. Existing methods do not use the available covariate information fully. We propose a more efficient estimator by making full use of available covariate information for the additive hazards model with data from a stratified case-cohort design with rare (the traditional situation) and non-rare (the generalized situation) diseases. We propose an estimating equation approach with a new weight function. The proposed estimators are shown to be consistent and asymptotically normally distributed. Simulation studies show that the proposed method using all available information leads to efficiency gain and stratification of the subcohort improves efficiency when the strata are highly correlated with the covariates. Our proposed method is applied to data from the Atherosclerosis Risk in Communities (ARIC) study.

1. Introduction

In large cohort studies, obtaining expensive covariate information on all members in the entire cohort could be costly and might not be feasible due to limited financial resource. In order to reduce cost, the case-cohort study design was proposed by Prentice [1]. Under the case-cohort design, covariate information is collected only from a random sample of the cohort, called the subcohort, as well as all the subjects who have the disease of interest. A key advantage for the case-cohort study is that the same subcohort can be used when several types of diseases are of interest [2]. For example, one of the goals in the Atherosclerosis Risk in Communities (ARIC) study is to investigate the association between the genetic variation in PTGS1 and coronary heart disease (CHD) as well as stroke [3]. To preserve blood specimens and reduce cost, two case-cohort studies were conducted separately using the same subcohort.

In spite of the extensive work on multiplicative hazards models for case-cohort studies, only a few methods for case-cohort studies with additive hazards models have been studied. For univariate failure time, Kulich and Lin [4] proposed semiparametric estimation and developed the asymptotic properties in additive hazards models from case-cohort data. Sun et al. [5] extended this approach to competing risks analysis in the case-cohort study. To compare the risk effect on different diseases, Kang et al. [6] proposed modeling them simultaneously using an additive hazards model for the stratified case-cohort design. However, they did not fully use all the available information on the covariate of interest. For example, in the ARIC study, the genetic variation in PTGS1 was collected from the subcohort and all subjects with CHD and/or stroke. When analysis for CHD was conducted, the PTGS1 information collected on stroke patients outside the subcohort was disregarded. This could induce loss of efficiency. Recently, Kim et al. [7] proposed the weight function to use this extra information in multiplicative hazard models for rare diseases. Similar ideas on using information from cases of other types have been proposed for nested case-control data, for example, Salim et al. (2009) [8] and Stoer and Samuelsen (2012) [9]. However, in many biomedical studies with common diseases, due to financial restrictions as well as for reserving biospecimens for future use, it is more desirable to sample a portion of the cases instead of including all the cases in the case-cohort study. Therefore, we extend Kim et al. [7]’s approach to the non-rare diseases situation in additive hazards models.

In this paper, we propose more efficient estimation methods for the additive hazards model with data from case-cohort studies by making full use of available covariate information. We also take into account two important features of the sampling in the case-cohort design. One is stratification. Stratified sampling is commonly used in survey sampling to increase the representation of the sample and to improve estimation efficiency. Due to these advantages, stratified random sample is often used in drawing the subcohort in the case-cohort design. The other feature is case sampling. We refer to the design that incorporates both features as the generalized stratified case-cohort design. We propose an estimation procedure for the parameters in the additive hazards model for the generalized stratified case-cohort design with multivariate failure times. In Section 2, we introduce the model and propose estimation procedures. Section 3 summarizes asymptotic properties for the proposed estimators and Section 4 reports simulation results to investigate the performance of the proposed estimators in finite samples. In Section 5, we illustrate the methods by analyzing data from the ARIC study. Concluding remarks are provided in Section 6.

2. Model

Suppose that a cohort study consists of n independent subjects with K diseases of interest and can be divided into L mutually exclusive strata based on available information V from all cohort members. Let T_lik and C_lik denote the potential failure time and the potential censoring time for disease k of subject i within stratum l, respectively. The failure time T_lik is assumed to be independent of C_lik given covariates. Let Z_lik(t) be a p × 1 possibly time-dependent covariate vector for disease k of subject i within stratum l at time t. We assume that time-dependent covariates are external; that is, they are not influenced by the disease processes [10]. Let X_lik = min(T_lik, C_lik) denote the observed time, Δ_lik = I(T_lik ≤ C_lik) the indicator for failure, N_lik(t) = I(X_lik ≤ t, Δ_lik = 1) the counting process, and Y_lik(t) = I(X_lik ≥ t) the at risk indicator for disease k of subject i within stratum l, where I(.) is the indicator function. Let V_i denote a discrete random variable for stratification of subject i. Let τ denote the end of study time.

Consider the following additive hazards model for T_lik given Z_lik(t)

$${\lambda }_{\mathit{lik}}\{t\mid Z_{\mathit{lik}}(t)\}={\lambda }_{0k}(t)+{\beta }_0^T{Z}_{\mathit{lik}}(t),$$ (1)

where λ_0k(t) is a baseline hazard function for disease k and β₀ is a p-vector of unknown regression parameters. Model (1) can accommodate the disease-specific effect model ${\lambda }_{\mathit{lik}}\{t\mid Z_{\mathit{lik}}^{\ast }(t)\}={\lambda }_{0k}(t)+{\beta }_k^T{Z}_{\mathit{lik}}^{\ast }(t)$ which is a special case of model (1) with ${\beta }_0^T=({\beta }_1^T,\dots ,{\beta }_k^T,\dots ,{\beta }_K^T)$ and $Z_{\mathit{lik}}{(t)}^T=[0_{li1}^T,\dots ,0_{li(k-1)}^T,{\{Z_{\mathit{lik}}^{\ast }(t)\}}^T,0_{li(k+1)}^T,\dots ,0_{\mathit{lik}}^T]$ where 0^T is a 1 × p zero vector.

Suppose that the total size n of the cohort is partitioned into groups of size n_l, l = 1, …, L. We select a fixed number ñ_l of subjects from the n_l subjects in stratum l for the subcohort by using simple random sampling. The total size of the subcohort is $\stackrel{\sim }{n}={\mathrm{\sum }}_{l=1}^L{\stackrel{\sim }{n}}_l$.

Let ξ_li be an indicator for subcohort membership for subject i in stratum l. Each subject in stratum l has the same probability α̃_l = Pr(ξ_li = 1) = ñ_l/n_l of being selected into the subcohort. The covariates Z_lik(t)(0 ≤ t ≤ τ) are measured for subjects in the subcohort and those with any disease of interest.

Under the generalized stratified case-cohort design, after selection of the subcohort, we select a fixed number m̃_lk of the cases of disease k among non-subcohort members with disease k in stratum l using simple random sampling. Denote by ${\stackrel{\sim }{m}}_k={\mathrm{\sum }}_{l=1}^L{\stackrel{\sim }{m}}_{lk}$ the total number of cases of disease k outside of the subcohort. Let η_lik be an indicator for whether subject i in stratum l is sampled as a non-subcohort subject with disease k. Let γ̃_lk = Pr (η_lik = 1|Δ_lik = 1, ξ_li = 0) = m̃_lk/(o_lk − õ_lk) denote the selection probability of subjects among non-subcohort members with disease k in stratum l, where o_lk and õ_lk denote the number of subjects with disease k in the cohort and in the subcohort within stratum l, respectively. Due to the sampling scheme, the elements in (η_l1k, …, η_lnlk) are correlated, however, (η_l1k, …, η_lnlk) is independent of (η_l′1k′, …, η_{l′nl′k′}) for k ≠ k′ or l ≠ l′.

2.1. Estimation

Suppose that there re $n={\mathrm{\sum }}_{l=1}^L{n}_l$ independent subjects with K diseases of interest. Let the independent failure time vector be T_li = (T_li1, …, T_lik) and the observed time vector be X_li = (X_li1, …, X_lik,) i = 1, …, n. Thus, for subject i in stratum l, complete observations are (X_lik, Δ_lik, ξ_li, Z_lik(t), 0 ≤ t ≤ τ, k = 1, …, K, V_i) when ξ_li = 1 or Δ_lik = 1 and (X_lik, Δ_lik, ξ_i, k = 1, …, K, V_i) when ξ_li = 0 and Δ_lik = 0.

Consider the situation with non-rare diseases of interest, but with covariate information for subjects with other diseases being available. Without using covariate information collected on subjects with other diseases, Kang et al. [6] considered the additive hazards model for generalized case-cohort designs using stratified simple random sampling. The regression parameter β₀ in (1) can be estimated by solving the estimating equation [6]:

$$\overline{U}(\beta )=\sum _{k=1}^K\sum _{l=1}^L\sum _{i=1}^{n_l}{\int }_0^{\tau }{\rho }_{ik}(t)\{Z_{\mathit{lik}}(t)-{\overline{Z}}_k(t)\}\{{dN}_{\mathit{lik}}(t)-{\beta }^T{Z}_{\mathit{lik}}(t)Y_{\mathit{lik}}(t)dt\}=0,$$ (2)

where

$${\overline{Z}}_k(t)=\frac{{\mathrm{\sum }}_{l=1}^L{\mathrm{\sum }}_{i=1}^{n_l}{\rho }_{\mathit{lik}}(t)Z_{\mathit{lik}}(t)Y_{\mathit{lik}}(t)}{{\mathrm{\sum }}_{l=1}^L{\mathrm{\sum }}_{i=1}^{n_l}{\rho }_{\mathit{lik}}(t)Y_{\mathit{lik}}(t)}$$

and ${\rho }_{\mathit{lik}}(t)=(1-{\mathrm{\Delta }}_{\mathit{lik}}){\xi }_{li}{\widehat{\alpha }}_{lk}^{-1}+{\mathrm{\Delta }}_{\mathit{lik}}{\xi }_{li}+{\mathrm{\Delta }}_{\mathit{lik}}(1-{\xi }_{li}){\eta }_{\mathit{lik}}{\widehat{q}}_{lk}^{-1}$ with ${\widehat{\alpha }}_{lk}={\mathrm{\sum }}_{i=1}^{n_l}{\xi }_{li}(1-{\mathrm{\Delta }}_{\mathit{lik}})Y_{\mathit{lik}}(t)/{\mathrm{\sum }}_{i=1}^{n_l}(1-{\mathrm{\Delta }}_{\mathit{lik}})Y_{\mathit{lik}}(t)$ and ${\widehat{q}}_{lk}={\mathrm{\sum }}_{i=1}^{n_l}{\eta }_{\mathit{lik}}(1-{\xi }_{li}){\mathrm{\Delta }}_{\mathit{lik}}{Y}_{\mathit{lik}}(t)/{\mathrm{\sum }}_{i=1}^{n_l}(1-{\xi }_{li}){\mathrm{\Delta }}_{\mathit{lik}}{Y}_{\mathit{lik}}(t)$. The time-invariant weight can involve fixed weights α̂_lk and q̂_lk with that replace α̂_lk(t) and q̂_lk(t) at t = 0. If we select all cases i.e. q̂lk(t) for all k is 1, the weight function reduces to $w_{\mathit{lik}}(t)=(1-{\mathrm{\Delta }}_{\mathit{lik}}){\xi }_{li}{\widehat{\alpha }}_{lk}^{-1}+{\mathrm{\Delta }}_{\mathit{lik}}$ in traditional case-cohort studies.

The estimator β̂ is defined as the solution to (2) and has the following explicit form:

$$\overline{\beta }={\left[\sum _{k=1}^K\sum _{l=1}^L\sum _{i=1}^{n_l}{\int }_0^{\tau }{\rho }_{\mathit{lik}}(t){\{Z_{\mathit{lik}}(t)-{\overline{Z}}_k(t)\}}^{\otimes 2}{Y}_{\mathit{lik}}(t)dt\right]}^{-1}\times \sum _{k=1}^K\sum _{l=1}^L\sum _{i=1}^{n_l}{\int }_0^{\tau }{\rho }_{\mathit{lik}}(t)\{Z_{\mathit{lik}}(t)-{\overline{Z}}_k(t)\}{dN}_{\mathit{lik}}(t),$$

where a^⊗2 = aa^T.

To make full use of covariate information collected on subjects with other diseases, we proposed the following weight function π_lik(t) when there are two diseases (i.e. K = 2):

$$\begin{array}{l}{\pi }_{\mathit{lik}}(t)={\mathrm{\Pi }}_{j=1}^2(1-{\mathrm{\Delta }}_{\mathit{lij}}){\xi }_{li}{\stackrel{\sim }{\alpha }}_{lk}^{-1}(t)+\{1-{\mathrm{\Pi }}_{j=1}^2(1-{\mathrm{\Delta }}_{\mathit{lij}})\}{\xi }_{li}\\ +{\mathrm{\Delta }}_{li1}(1-{\mathrm{\Delta }}_{li2})(1-{\xi }_{li}){\eta }_{li1}{\stackrel{\sim }{\gamma }}_{l1k}^{-1}(t)+(1-{\mathrm{\Delta }}_{li1}){\mathrm{\Delta }}_{li2}(1-{\xi }_{li}){\eta }_{li2}{\stackrel{\sim }{\gamma }}_{l2k}^{-1}(t)\\ +{\mathrm{\Delta }}_{li1}{\mathrm{\Delta }}_{li2}(1-{\xi }_{li})({\eta }_{li1}+{\eta }_{li2}-{\eta }_{li1}{\eta }_{li2}){\stackrel{\sim }{\gamma }}_{l3k}^{-1}(t),\end{array}$$ (3)

where

$$\begin{array}{ll}\hfill {\stackrel{\sim }{\alpha }}_{lk}(t)& =\sum _{i=1}^{n_l}{\mathrm{\Pi }}_{j=1}^2(1-{\mathrm{\Delta }}_{\mathit{lij}}){\xi }_{li}{Y}_{\mathit{lik}}(t)/\{\sum _{i=1}^{n_l}{\mathrm{\Pi }}_{j=1}^2(1-{\mathrm{\Delta }}_{\mathit{lij}})Y_{\mathit{lik}}(t)\}\\ \hfill {\stackrel{\sim }{\gamma }}_{l1k}(t)& =\sum _{i=1}^{n_l}{\mathrm{\Delta }}_{li1}(1-{\mathrm{\Delta }}_{li2})(1-{\xi }_{li}){\eta }_{li1}{Y}_{\mathit{lik}}(t)/\{\sum _{i=1}^{n_l}{\mathrm{\Delta }}_{li1}(1-{\mathrm{\Delta }}_{li2})(1-{\xi }_{li})Y_{\mathit{lik}}(t)\}\\ \hfill {\stackrel{\sim }{\gamma }}_{l2k}(t)& =\sum _{i=1}^{n_l}(1-{\mathrm{\Delta }}_{li1}){\mathrm{\Delta }}_{li2}(1-{\xi }_{li}){\eta }_{li2}{Y}_{\mathit{lik}}(t)/\{\sum _{i=1}^{n_l}(1-{\mathrm{\Delta }}_{li1}){\mathrm{\Delta }}_{li2}(1-{\xi }_{li})Y_{\mathit{lik}}(t)\}\\ \hfill {\stackrel{\sim }{\gamma }}_{l3k}(t)& =\sum _{i=1}^{n_l}{\mathrm{\Delta }}_{li1}{\mathrm{\Delta }}_{li2}(1-{\xi }_{li})({\eta }_{li1}+{\eta }_{li2}-{\eta }_{li1}{\eta }_{li2})Y_{\mathit{lik}}(t)/\{\sum _{i=1}^{n_l}{\mathrm{\Delta }}_{li1}{\mathrm{\Delta }}_{li2}(1-{\xi }_{li})Y_{\mathit{lik}}(t)\}.\end{array}$$

The proposed weight function uses extra covariate information collected on the selected subjects with the other disease. Specifically, subcohort subjects without either disease (i.e. ${\mathrm{\Pi }}_{j=1}^2(1-{\mathrm{\Delta }}_{\mathit{lij}}){\xi }_{li}=1$) are weighted by α̃_lk(t)⁻¹, the inverse of the estimated selection probabilities, while subjects with disease 1 or disease 2 in the subcohort (i.e. $\{1-{\mathrm{\Pi }}_{j=1}^2(1-{\mathrm{\Delta }}_{\mathit{lij}})\}{\xi }_{li}=1$) are weighted by 1. To use the information collected on the sampled subjects with disease 2, the sampled non-subcohort subjects with disease 1 (i.e. Δ_li1(1 − ξ_li)η_li1 = 1) can be decomposed into two groups: those with only disease 1 (i.e. Δ_li1(1 − Δ_li2)(1 − ξ_li)η_li1 = 1) and those with both disease 1 and disease 2 (i.e. Δ_li1Δ_li2(1 − ξ_li)η_li1 = 1). The sampled subjects in the first group (i.e. Δ_li1(1 − Δ_li2)(1 − ξ_li) = 1) are weighted by γ̃_l1k(t)⁻¹, the inverse of their estimated sampling probabilities. Similarly, the sampled non-subcohort subjects with disease 2 can also be decomposed into two groups: those with only disease 2 (i.e. Δ_li1(1 − Δ_li2)(1 − ξ_li)η_li2 =1) and those with both diseases (i.e. Δ_li1Δ_li2(1 − ξ_li)η_li2 =1). Those with only disease 2 are weighted by γ̃_l2k(t)⁻¹, the inverse of their estimated sampling probabilities. For those sampled non-subcohort subjects with both diseases, they can be weighted by ${\stackrel{\sim }{\gamma }}_{l3k}^{-1}(t)$, the inverse of the estimated sampling probabilities based on disease 1 or disease 2. Note the weight function for the traditional case-cohort design proposed by Kim et al. [7] ${\psi }_{\mathit{lik}}(t)=\{1-{\mathrm{\Pi }}_{j=1}^K(1-{\mathrm{\Delta }}_{\mathit{lij}})\}+{\mathrm{\Pi }}_{j=1}^K(1-{\mathrm{\Delta }}_{\mathit{lij}}){\xi }_{li}{\stackrel{\sim }{\alpha }}_{lk}^{-1}(t)$ is a special case of the proposed weight function (3).

We consider the following weighted estimating equation:

$$\stackrel{\sim }{U}(\beta )=\sum _{k=1}^K\sum _{l=1}^L\sum _{i=1}^{n_l}{\int }_0^{\tau }{\pi }_{\mathit{lik}}(t)\{Z_{\mathit{lik}}(t)-{\stackrel{\sim }{Z}}_k(t)\}\{{dN}_{\mathit{lik}}(t)-{\beta }^T{Z}_{\mathit{lik}}(t)Y_{\mathit{lik}}(t)dt\}=0,$$ (4)

where

$${\stackrel{\sim }{Z}}_k(t)=\sum _{l=1}^L\sum _{i=1}^{n_l}{\pi }_{\mathit{lik}}(t)Z_{\mathit{lik}}(t)Y_{\mathit{lik}}(t)/\sum _{l=1}^L\sum _{i=1}^{n_l}{\pi }_{\mathit{lik}}(t)Y_{\mathit{lik}}(t).$$

The explicit form of β̃, which is defined by the solution of the estimating equation in (4), is:

$$\stackrel{\sim }{\beta }={\left[\sum _{k=1}^K\sum _{l=1}^L\sum _{i=1}^{n_l}{\int }_0^{\tau }{\pi }_{\mathit{lik}}(t){\{Z_{\mathit{lik}}(t)-{\stackrel{\sim }{Z}}_k(t)\}}^{\otimes 2}{Y}_{\mathit{lik}}(t)dt\right]}^{-1}\times \sum _{k=1}^K\sum _{l=1}^L\sum _{i=1}^{n_l}{\int }_0^{\tau }{\pi }_{\mathit{lik}}(t)\{Z_{\mathit{lik}}(t)-{\stackrel{\sim }{Z}}_k(t)\}{dN}_{\mathit{lik}}(t).$$

Let ${\mathrm{\Lambda }}_{0k}(t)={\int }_0^{\tau }{\lambda }_{0k}(s)ds$. A Breslow-Aalen type estimator of the baseline cumulative hazard function is given by Λ̃_0k(β̃, t), where

$${\stackrel{\sim }{\mathrm{\Lambda }}}_{0k}(\beta ,t)={\int }_0^{\tau }\frac{{\mathrm{\sum }}_{l=1}^L{\mathrm{\sum }}_{i=1}^{n_l}{\pi }_{\mathit{lik}}(u)\{{dN}_{\mathit{lik}}(u)-Y_{ik}(u){\beta }^T{Z}_{\mathit{lik}}(u)du\}}{{\mathrm{\sum }}_{l=1}^L{\mathrm{\sum }}_{i=1}^{n_l}{\pi }_{\mathit{lik}}(u)Y_{\mathit{lik}}(u)}.$$ (5)

3. Asymptotic properties

In this section we present the asymptotic properties of the proposed methods. Because the traditional case-cohort study is a special case of the generalized case-cohort study, we present only the results for the generalized case-cohort study. The following theorems summarize the main results.

Theorem 3.1

Under the regularity conditions in Web appendix, β̃ converges in probability to β₀ and n^1/2(β̃ − β₀) converges in distribution to a mean zero normal distribution with covariance matrix $A{({\beta }_0)}^{-1}{\mathrm{\sum }}_{l=1}^L\mathrm{\sum }({\beta }_0)A{({\beta }_0)}^{-1}$, where

$$\begin{array}{l}A(\beta )=\sum _{k=1}^K{A}_k(\beta ),\mathrm{\sum }(\beta )=\sum _{l=1}^L{q}_l\{V_{I,l}^a(\beta )+\frac{1-{\alpha }_l}{{\alpha }_l}{V}_{II,l}^a(\beta )+(1-{\alpha }_l)\sum _{k=1}^2{V}_{\mathit{III},lk}^a(\beta )\},\\ V_{I,l}^a(\beta )=E_l{\{\sum _{k=1}^2{Q}_{l1k}(\beta )\}}^{\otimes 2},\\ V_{II,l}^a(\beta )={\mathit{Var}}_l\left[\prod _{j=1}^2(1-{\mathrm{\Delta }}_{l1j})\sum _{k=1}^2{\int }_0^{\tau }[B_{l1k}(\beta ,t)-Y_{l1k}(t)\frac{E\{{\mathrm{\Pi }}_{j=1}^2(1-{\mathrm{\Delta }}_{l1j})B_{l1k}({\beta }_0,t)\}}{E_l\{{\mathrm{\Pi }}_{j=1}^2(1-{\mathrm{\Delta }}_{l1j})Y_{l1k}(t)\}}]dt\right],\\ V_{\mathit{III},lk}^a(\beta )=Pr({\theta }_{l10})\frac{1-{\gamma }_{l1}}{{\gamma }_{l1}}{\mathit{Var}}_l\left[Q_{l1k}(\beta )-{\int }_0^{\tau }{Y}_{l1k}(t)\frac{E_l\{{dQ}_{l1k}(\beta ,t)\mid {\theta }_{l10},{\xi }_{l1}=0\}}{E_l\{Y_{l1k}(t)\mid {\theta }_{l10}\}}\mid {\theta }_{l10},{\xi }_{l1}=0\right]\\ +Pr\{{\theta }_{l01}\}\frac{1-{\gamma }_{l2}}{{\gamma }_{l2}}{\mathit{Var}}_l\left[Q_{l1k}(\beta )-{\int }_0^{\tau }{Y}_{l1k}(t)\frac{E_l\{{dQ}_{l1k}(\beta ,t)\mid {\theta }_{l01},{\xi }_{l1}=0\}}{E_l\{Y_{l1k}(t)\mid {\theta }_{l01}\}}\mid {\theta }_{l01},{\xi }_{l1}=0\right]\\ +Pr[{\theta }_{l11}][\frac{1-({\gamma }_{l1}+{\gamma }_{l2}-{\gamma }_{l1}{\gamma }_{l2})}{{\gamma }_{l1}+{\gamma }_{l2}-{\gamma }_{l1}{\gamma }_{l2}}]{\mathit{Var}}_l\left[Q_{l1k}(\beta )-{\int }_0^{\tau }{Y}_{l1k}(t)\frac{E\{{dQ}_{l1k}(\beta ,t)\mid {\theta }_{l11},{\xi }_{l1}=0\}}{E_l\{Y_{l1k}(t)\mid {\theta }_{l11}\}}\mid {\theta }_{l11},{\xi }_{l1}=0\right],\\ Q_{\mathit{lik}}(t,\beta )={\int }_0^t\{Z_{\mathit{lik}}(t)-e_k(t)\}{dM}_{\mathit{lik}}(t),q_l=lim{n}_l/n\\ B_{\mathit{lik}}(t,\beta )=\{Z_{\mathit{lik}}(t)-e_k(t)\}{Y}_{\mathit{lik}}(t)\{{\lambda }_{0k}(t)+{\beta }^T{Z}_{\mathit{lik}}(t)\},\\ e_k(t)=\frac{{\mathrm{\sum }}_{l=1}^L{q}_l{E}_l\{Y_{l1k}(t)Z_{l1k}(t)\}}{{\mathrm{\sum }}_{l=1}^L{q}_l{E}_l\{Y_{l1k}(t)\}},{\theta }_{\mathit{ljk}}=({\mathrm{\Delta }}_{li1}=j\mathit{and}{\mathrm{\Delta }}_{li2}=k).\end{array}$$

Note that Σ(β₀) consists of three parts. The first part, $V_{I,l}^a({\beta }_0)$, is the contribution to the variance from the full cohort, the second part, $V_{II,l}^a({\beta }_0)$, is due to sampling the subcohort from the full cohort, and the last part, ${\mathrm{\sum }}_{k=1}^2{V}_{\mathit{III},lk}^a({\beta }_0)$, is due to sampling a fraction of cases. If we select all cases, which is the traditional stratified case-cohort design, the last variance is zero.

We summarize the asymptotic properties of the proposed baseline cumulative hazard estimator Λ̃_0k(β̃, t) in the following theorem.

Theorem 3.2

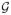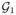Under the regularity conditions in Web appendix, Λ̃_0k(β̃, t) is a consistent estimator of Λ_0k(t) in t ∈ [0, τ] k =1, 2) and G(t)={G₁(t),G₂(t)}^T =[n^1/2{Λ̃₀₁(β̃, t) − Λ₀₁(t)}, n^1/2{Λ̃₀₂(β̃, t) − Λ₀₂(t))}]^T converges weakly to the Gaussian process (t)={ (t), 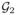(t)}^T in D[0, τ]^K with mean zero and the following covariance function 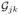(t, s) between 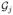(t) and 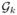(s) for j ≠ k.

$${\mathcal{G}}_{jk}(t,s)({\beta }_0)=\sum _{l=1}^L{q}_l[E_l\{{\mu }_{l1j}({\beta }_0,t){\mu }_{l1k}({\beta }_0,s)\}+\frac{1-{\alpha }_l}{{\alpha }_l}{E}_l\{w_{l1j}({\beta }_0,t)w_{l1k}({\beta }_0,s)\}+E_l\{{\nu }_{l1j}({\beta }_0,t){\nu }_{l1k}({\beta }_0,s)\}],$$

where the explicit forms of μ_lik(β, t),w_lik(β, t), and ν_lik(β, t) are given in Web Appendix.

The proof of Λ̃_0k(β̃, t) is provided in Web appendix. The proof uses Taylor expansion, the Kolmogorov-Centsov theorem, weak convergence of the baseline cumulative hazard estimator from full cohort studies with multivariate failure time, Hájek[11]’s central limit theorem for finite population sampling, and the Cramer-Wold device.

4. Simulations

We conducted simulation studies to examine the performance of the proposed methods and to compare them with the existing methods. Correlated bivariate failure time data were generated from the Clayton-Cuzick model [12]. The bivariate survival function for the bivariate survival time (T₁, T₂) given (Z_l1,Z_l2) has the following form:

$$S(t_1,t_2\mid Z_{l1},Z_{l2})={\{e^{\frac{{\int }_0^{t_1}\{{\lambda }_{01}(t)+{\beta }_1{z}_{l1}\}dt}{\theta }}+e^{\frac{{\int }_0^{t_2}\{{\lambda }_{02}(t)+{\beta }_2{z}_{l2}\}dt}{\theta }}-1\}}^{-\theta },$$

where λ_0k(t) and β_k are the baseline hazard function and the effect of the covariate for disease k, respectively, l indexes the two strata, and θ is the parameter that controls the correlation between the failure times for the two diseases. Smaller θ indicates higher correlation between the two failure times T₁ and T₂. The relationship between Kendall’s tau, τ_θ, and θ is ${\tau }_{\theta }=\frac{1}{2\theta +1}$. For θ, we used values of 0.10, 0.67, and 4 and the corresponding Kendall’s tau values are 0.83, 0.43, and 0.11, respectively. We also consider independent failure times (τ_θ =0). We set the baseline hazard function λ₀₁ =2 for the first failure event type, k =1, and λ₀₂ =4 for the second failure event type, k =2. The regression parameters considered were β₀ =0, 0.1, 0.3, and 0.5.

We generated Z from Bernouilli distribution with pr(Z =1) = 0.5 under the situation Z_l1 =Z_l2 =Z. To consider stratified subcohort sampling from two strata defined by V_i, we defined two parameters: η =Pr(V =1|Z =1) and ν =Pr(V =0|Z =0) where η is the sensitivity and ν the specificity for Z. Both η and ν greater than 0.5 indicate that V is highly correlated with Z. For stratified case-cohort studies, we set the values [η, ν]=[0.5, 0.5] and [0.7, 0.7]. Thus, a stratum variable is simulated with Pr(V =1)=(1 − ν)Pr(Z =0) + ηPr(Z =1)=0.5. Censoring times were generated from uniform distribution [0, u]where u depends on the specified level of the censoring probability.

For simulations of the traditional case-cohort design, we set event proportions of approximately 5% for k =1 and 9% for k =2. For the simulations of the generalized case-cohort design, the event proportions were set as 15% for k =1 and 26% for k =2 and we sampled half of the cases outsides the subcohort, [γ₁, γ₂]=[0.5, 0.5]. The sample size of the full cohort was set to be n =1000. For stratified sampling, we set the total subcohort sizes as 100 and 200 and sampled a subcohort of size ñ_l =ñ ×q_l from each stratum. For each configuration, we conducted 2000 simulations.

We first considered the traditional and generalized case-cohort design using unstratified sampling but with covariates available on subjects with other diseases. For generalized case-cohort design, we sampled half of the cases outside the subcohort. We examined the performance of our proposed estimator and compared our results with those in Kang et al. (2013) [6]. We fitted disease-specific model. Table 1 summarizes the results for β̃₁, β̃₂, β̂₁, and β̂₂. For different combinations of regression parameter values, event proportion, study design, subcohort sample size, and correlation, Table 1 shows the average of the estimates β̃₁ and β̃₂, the average of the estimated standard error (SE), empirical standard deviation (SD), and coverage rate (%) of the nominal 95% confidence interval (CR). The subscripts for SE and SD refer to the proposed method (Pi) for disease i and the Kang et al. (2013) [6] method (Ki) for disease i. The simulation results suggest that both methods are approximately unbiased across the setup for β₁ = β₂ =0 and [β₁, β₂]=[0.1, 0.5]. The average of the proposed estimated standard error is close to the empirical standard deviation and it is in general smaller when subcohort size are larger, as expected. The 95% confidence interval coverage rate ranges between 94% and 97%. All the sample relative efficiencies (SRE_i), defined as ${SD}_{ki}^2/{SD}_{pi}^2$ (i =1, 2), are larger than 1 which indicates that the proposed estimates are more efficient than those from Kang et al. [6]. This shows that the extra information collected on subjects with the other disease helps improve efficiency. In general, the efficiency gain is larger in situations with smaller subcohort size and smaller correlation.

Table 1.

Simulation result for the unstratified case-cohort study

[β1, β2]	Event Proportion	ñ	τθ	Proposed method				Kang et al.’s method				SRE1	Proposed method				Kang et al.’s method				SRE2
				β̃1	SEp1	SDp1	CR	β̂1	SEk1	SDk1	CR		β̃2	SEp2	SDp2	CR	β̂2	SEk2	SDk2	CR
[0, 0]	[5%, 9%] γ= [1, 1]	100	0.83	−0.02	0.73	0.75	0.94	−0.02	0.75	0.76	0.95	1.03	−0.07	1.23	1.25	0.96	−0.07	1.24	1.25	0.96	1.01
			0.43	0.00	0.73	0.73	0.95	0.00	0.74	0.74	0.95	1.04	−0.01	1.22	1.22	0.96	0.00	1.24	1.23	0.96	1.03
			0.11	0.03	0.72	0.70	0.96	0.03	0.74	0.72	0.96	1.05	0.00	1.22	1.24	0.96	0.00	1.24	1.26	0.96	1.03
			0	0.02	0.73	0.73	0.95	0.03	0.74	0.75	0.96	1.05	0.00	1.22	1.23	0.96	−0.01	1.23	1.25	0.96	1.02
		200	0.83	−0.01	0.64	0.63	0.95	−0.01	0.65	0.64	0.95	1.02	−0.02	1.01	1.01	0.96	−0.02	1.02	1.02	0.96	1.00
			0.43	0.02	0.64	0.64	0.95	0.02	0.65	0.65	0.95	1.02	−0.01	1.01	1.01	0.95	−0.02	1.02	1.02	0.95	1.02
			0.11	0.01	0.64	0.63	0.95	0.02	0.65	0.64	0.95	1.02	0.01	1.01	0.96	0.96	0.01	1.02	0.97	0.96	1.02
			0	0.00	0.64	0.64	0.95	0.00	0.65	0.64	0.95	1.02	0.01	1.00	1.01	0.96	0.01	1.01	1.02	0.96	1.02
	[15%, 26%] γ= [0.5, 0.5]	100	0.83	0.00	0.57	0.58	0.96	0.00	0.63	0.65	0.96	1.27	0.00	1.05	1.05	0.96	0.00	1.08	1.09	0.96	1.07
			0.43	−0.02	0.57	0.58	0.95	−0.01	0.63	0.64	0.96	1.20	−0.02	1.03	1.06	0.96	−0.03	1.08	1.09	0.96	1.07
			0.11	−0.01	0.56	0.57	0.95	−0.01	0.62	0.62	0.97	1.17	−0.03	1.02	1.05	0.95	−0.04	1.08	1.12	0.95	1.14
			0	0.00	0.56	0.59	0.96	0.01	0.62	0.65	0.96	1.21	−0.02	1.01	1.05	0.95	−0.01	1.07	1.12	0.95	1.13
		200	0.83	0.00	0.47	0.47	0.96	0.00	0.51	0.52	0.96	1.20	−0.03	0.81	0.81	0.95	−0.03	0.83	0.84	0.96	1.07
			0.43	0.00	0.47	0.49	0.94	0.01	0.51	0.53	0.95	1.16	−0.01	0.80	0.82	0.95	−0.01	0.83	0.85	0.96	1.07
			0.11	0.00	0.48	0.48	0.95	−0.02	0.51	0.51	0.96	1.14	−0.03	0.80	0.81	0.95	−0.03	0.83	0.84	0.95	1.08
			0	0.00	0.48	0.49	0.95	0.00	0.51	0.52	0.95	1.14	0.00	0.80	0.83	0.95	0.00	0.83	0.86	0.95	1.07
[0.1, 0.5]	[5%, 9%] γ= [1, 1]	100	0.83	0.10	0.75	0.74	0.95	0.11	0.76	0.75	0.95	1.02	0.49	1.29	1.31	0.96	0.49	1.30	1.32	0.96	1.01
			0.43	0.13	0.74	0.77	0.93	0.13	0.76	0.78	0.94	1.02	0.55	1.29	1.26	0.96	0.55	1.30	1.28	0.97	1.02
			0.11	0.11	0.74	0.75	0.95	0.12	0.76	0.77	0.95	1.06	0.49	1.29	1.27	0.96	0.49	1.31	1.30	0.96	1.04
			0	0.13	0.74	0.75	0.96	0.13	0.76	0.77	0.96	1.05	0.54	1.28	1.32	0.96	0.54	1.30	1.34	0.96	1.03
		200	0.83	0.11	0.66	0.64	0.96	0.11	0.66	0.65	0.96	1.01	0.49	1.07	1.07	0.96	0.50	1.07	1.07	0.96	1.00
			0.43	0.09	0.66	0.66	0.95	0.09	0.66	0.67	0.95	1.02	0.54	1.06	1.07	0.94	0.54	1.07	1.08	0.95	1.01
			0.11	0.10	0.65	0.66	0.95	0.09	0.66	0.66	0.95	1.02	0.48	1.05	1.07	0.95	0.48	1.06	1.08	0.95	1.03
			0	0.11	0.65	0.66	0.95	0.11	0.66	0.66	0.95	1.01	0.52	1.05	1.06	0.95	0.52	1.06	1.07	0.95	1.03
	[15%, 26%] γ= [0.5, 0.5]	100	0.83	0.12	0.58	0.59	0.96	0.11	0.64	0.66	0.96	1.23	0.52	1.11	1.17	0.95	0.52	1.14	1.20	0.95	1.05
			0.43	0.10	0.58	0.59	0.96	0.10	0.64	0.66	0.96	1.25	0.51	1.09	1.10	0.95	0.51	1.13	1.15	0.96	1.09
			0.11	0.10	0.58	0.61	0.95	0.10	0.64	0.66	0.95	1.20	0.51	1.07	1.08	0.96	0.53	1.13	1.13	0.96	1.10
			0	0.08	0.58	0.60	0.95	0.08	0.64	0.67	0.95	1.28	0.50	1.06	1.08	0.96	0.49	1.13	1.15	0.97	1.14
		200	0.83	0.09	0.48	0.49	0.95	0.09	0.53	0.54	0.94	1.22	0.52	0.85	0.86	0.96	0.52	0.88	0.89	0.95	1.07
			0.43	0.11	0.48	0.50	0.95	0.11	0.53	0.54	0.95	1.17	0.49	0.85	0.84	0.96	0.49	0.88	0.88	0.96	1.08
			0.11	0.11	0.49	0.49	0.96	0.11	0.53	0.52	0.96	1.14	0.50	0.84	0.88	0.95	0.50	0.88	0.93	0.95	1.10
			0	0.10	0.49	0.50	0.95	0.10	0.52	0.53	0.95	1.13	0.48	0.84	0.86	0.95	0.48	0.88	0.89	0.95	1.08

SE_i, the average of the estimates of standard error for β_i; SD_i, sample standard deviation for β_i; CR, the coverage rate of the nominal 95% confidence intervals; ${\mathit{SRE}}_i={SD}_{ki}^2/{SD}_{pi}^2$, sample relative efficiency

We also compared the performance of our proposed estimator to Kang et al. [7]’s estimator in stratified case-cohort studies. To mimic the situation in the ARIC study with 1) CHD and stroke and 2) diabetes and hypertension, we consider two sets: 1) event proportion for disease 1 and disease 2 to be [3%,8%]according to the baseline hazard with 1 for disease 1 and 4 for disease 2; 2) [11%,48%] according to the baseline hazard of 1 for disease 1 and 7 for disease 2. We also set the case selection probabilities for disease 1 and disease 2 to be γ =[1, 1]and γ =[0.35, 0.35], respectively. Table 2 summarizes the results. All the sample relative efficiencies for β₁ are greater than 1 which suggests that our proposed estimator for stratified case-cohort studies are more efficient than Kang et al. [6]’s estimators. The range of efficiency gain is 1% – 66%. However, efficiency gain for β₂ is small. This is expected because there are not many additional disease cases in the case-cohort sample and therefore there are not much additional information for estimating β₂. When the correlation between covariate and stratum variable is higher, sample standard deviation is smaller which indicates that more efficiency gain is associated with higher correlation between covariates and stratum variable.

Table 2.

Simulation result for comparison of two methods in stratified case-cohort study [β₁, β₂] = [0.1, 0]

Event Proportion	[ν, η]	τθ	Proposed method				Kang et al.’s method				SRE1	Proposed method				Kang et al.’s method				SRE2
			β̃1	SEp1	SDp1	CR	β̂1	SEk1	SDk1	CR		β̃2	SEp2	SDp2	CR	β̂2	SEk2	SDk2	CR
[3%, 8%] γ= [1, 1]	[0.5, 0.5]	0.83	0.12	0.45	0.47	0.92	0.12	0.46	0.47	0.93	1.02	0.00	1.18	1.21	0.96	−0.01	1.19	1.21	0.96	1.00
		0.43	0.09	0.44	0.45	0.93	0.09	0.46	0.46	0.93	1.04	−0.03	1.18	1.20	0.95	−0.03	1.19	1.20	0.95	1.01
		0.11	0.12	0.45	0.46	0.92	0.12	0.46	0.47	0.92	1.04	0.01	1.17	1.17	0.96	0.01	1.19	1.18	0.96	1.02
		0	0.10	0.45	0.45	0.93	0.10	0.46	0.46	0.93	1.04	0.00	1.17	1.19	0.96	0.00	1.19	1.21	0.96	1.03
	[0.7, 0.7]	0.83	0.11	0.44	0.44	0.92	0.11	0.45	0.45	0.93	1.03	−0.04	1.14	1.14	0.96	−0.04	1.15	1.14	0.96	1.00
		0.43	0.10	0.44	0.45	0.93	0.10	0.45	0.45	0.93	1.03	0.03	1.13	1.13	0.96	0.02	1.15	1.13	0.96	1.02
		0.11	0.11	0.44	0.46	0.92	0.11	0.45	0.47	0.92	1.03	0.02	1.13	1.14	0.95	0.02	1.14	1.15	0.96	1.01
		0	0.09	0.44	0.44	0.93	0.09	0.45	0.44	0.93	1.01	−0.02	1.12	1.12	0.96	−0.02	1.14	1.12	0.96	1.02
[11%, 50%] γ= [0.35, 0.35]	[0.5, 0.5]	0.83	0.10	0.31	0.32	0.96	0.09	0.40	0.40	0.96	1.60	0.00	1.67	1.70	0.95	0.01	1.68	1.72	0.95	1.02
		0.43	0.11	0.33	0.33	0.95	0.12	0.40	0.40	0.96	1.44	0.05	1.67	1.71	0.95	0.05	1.68	1.72	0.95	1.01
		0.11	0.11	0.35	0.34	0.95	0.11	0.40	0.40	0.96	1.41	−0.03	1.64	1.67	0.94	0.01	1.69	1.73	0.95	1.06
		0	0.11	0.34	0.34	0.96	0.10	0.40	0.40	0.95	1.42	0.00	1.62	1.63	0.95	−0.02	1.68	1.70	0.95	1.08
	[0.7, 0.7]	0.83	0.10	0.31	0.29	0.97	0.10	0.40	0.38	0.97	1.66	0.01	1.67	1.55	0.97	0.01	1.68	1.56	0.97	1.02
		0.43	0.11	0.33	0.32	0.97	0.11	0.40	0.39	0.96	1.43	0.06	1.70	1.59	0.97	0.06	1.68	1.62	0.97	1.03
		0.11	0.11	0.34	0.34	0.95	0.11	0.40	0.40	0.95	1.42	0.00	1.64	1.62	0.96	−0.02	1.67	1.65	0.96	1.05
		0	0.11	0.34	0.32	0.97	0.11	0.40	0.37	0.97	1.35	0.00	1.63	1.57	0.96	0.00	1.68	1.61	0.96	1.05

SE_i, the average of the estimates of standard error for β_i; SD_i, sample standard deviation for β_i; CR, the coverage rate of the nominal 95% confidence intervals; ${\mathit{SRE}}_i={SD}_{ki}^2/{SD}_{pi}^2$, sample relative efficiency

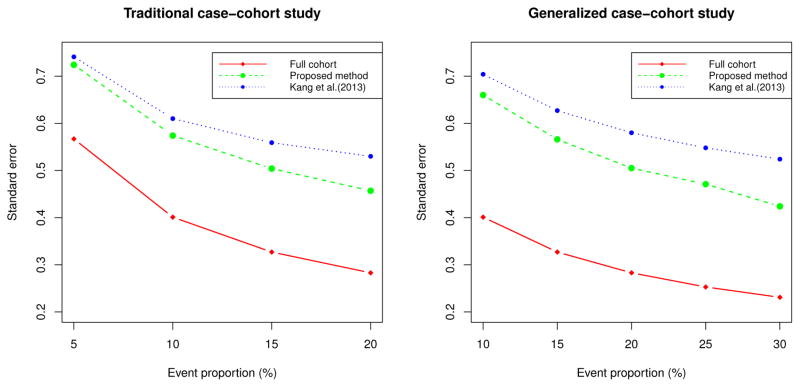
Figure 1 shows standard errors of the full cohort, our proposed method, and Kang et al. [6] for the traditional and generalized case-cohort studies. The standard errors are obtained for the setup with the subcohort size ñ =100 and τ_θ =0.43. For generalized case-cohort studies, we sampled half of the cases outside of the subcohort. Figure 1 shows that more efficiency gain compared to Kang et al. [6] is associated with higher event proportion.

Figure 1.

Comparison of standard errors

5. Data Analysis

We applied the proposed methods to two data examples from the Atherosclerosis Risk in Communities (ARIC) study for illustration under the traditional and generalized case-cohort designs. The ARIC study is a longitudinal, population-based cohort study consisting of 15,792 men and women aged from 45 to 64 years at baseline, recruited from four US communities. The first case-cohort study example is from the actual case-cohort studies in ARIC for rare diseases: incident coronary heart disease (CHD) event (7%) and stroke event (2%) [3]. To illustrate our methods for non-rare diseases, we constructed generalized case-cohort sample for incident diabetes (11%) and incident hypertension (48%). Baseline measurements were obtained during 1987–1989 and follow up for incident coronary heart disease (CHD), stroke, diabetes, and hypertension events is through 1998. Incident CHD is defined as definite or probable myocardial infarction, electrocardiographic evidence of silent myocardial infarction, definite CHD death, or coronary revascularization procedure. Incident stroke is defined as a definite or probable ischemic stroke. Incident diabetes is defined as a reported physician diagnosis, use of antidiabetes medications, a fasting (≥ 8 hours) glucose ≥ 7.0 mmol/l, or a nonfasting glucose of ≥ 11.1 mmol/l. Hypertension is defined as systolic blood pressure ≥ 140 or diastolic blood pressure ≥ 90 or used anti-hypertensive medication in the previous two weeks. We regarded the subject as censored if he or she was free of that event type by December 31, 1998 or lost to follow-up during the study.

5.1. Example 1: the traditional case-cohort studies

The primary aim of the first study example was to investigate the association between PTGS1 polymorphisms and risk of incident CHD and stroke. Cyclooxygenase-derived prostaglandins can be significant modifiers of risk of cardiovascular disease events. It has been suggested that variation in the genes encoding cyclooxygenase-derived prostaglandins (PTGS1) play an important role in cardiovascular disease risk [13, 14, 15].

Using a case-cohort design, genomic DNA genotyped for the polymorphisms in PTGS1 was available on all incident CHD and ischemic stroke cases, and the subcohort. The subcohort was selected using a stratified sampling design with three stratifying variables: age (≥ 55 or < 55 years), gender, and race (Caucasian or African American). After excluding subjects with missing genotype data or covariates, the full cohort consisted of 13,731 subjects, which included 900 subjects with only CHD, 188 subjects with only stroke, and 61 subjects with both CHD and stroke. The subcohort contained 850 disease-free subjects, 72 subjects with only CHD, 15 subject with only stroke, and 7 subjects with both CHD and stoke. The total number with assayed samples was 1,999. To adjust for confounding and other risk factors, traditional and clinical covariates related to cardiovascular diseases were used: age, gender, race, study center, current smoking status, diabetes, and hypertension.

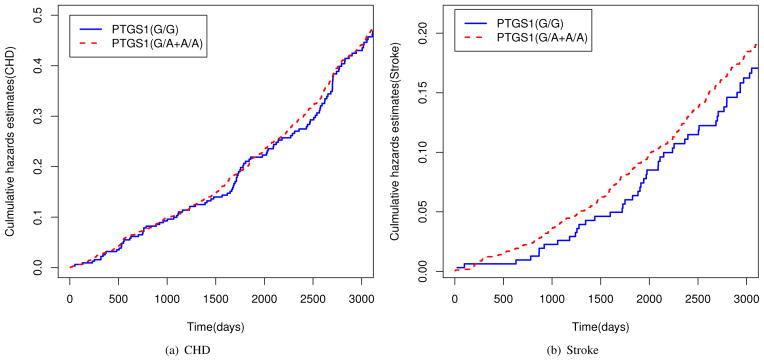
Figure 2 provides plots of the empirical cumulative hazard functions for CHD and stroke. For stroke events the difference in the cumulative hazard functions for the two genetic variation groups appear to be increasing in an approximately linear fashion, while the two functions are not very different for CHD events. Based on these plots, the additive hazards model is appropriate for studying the effects of genetic variation (PTGS1) on CHD as well as on stroke. Since all cases for CHD and stoke were selected and we are interested in comparing the risk effects on CHD and on stroke, we conducted a simultaneous analysis by using the proposed method.

Figure 2.

Plots of Nelson-Aalen cumulative hazards function estimates for genetic variation

We initially fitted the model allowing for different effects for CHD and stroke and tested whether those effects are indeed different. If we cannot reject the null hypothesis that they are the same, we use common effect for that factor for CHD and stroke. Table 3 presents the results of the final model. After adjusting for age, gender, race, study center, current smoking status, diabetes, and hypertension, presence of at least one A allele was associated with significantly higher risk of stroke compared with homozygotes. We also fitted the same model using Kang et al. [6]’s method. In general, the standard errors for the proposed estimator are slightly smaller than those for the estimator of Kang et al. [6], which provide tighter confidence intervals for the estimated parameters.

Table 3.

Analysis results for the effects of PTGS1 G/A+A/A versus G/G (×10⁻⁶)

	Variable	Proposed method			Kang et al’s method
		β̃	SE	P-value	β̂	SE	P-value
CHD	PTGS1	2.44	2.927	0.202	2.38	2.930	0.208
	Age	0.69	0.180	< 0.001	0.69	0.182	< 0.001
	Male	20.09	2.140	< 0.001	19.91	2.156	< 0.001
	Center (F)	−2.04	3.297	0.268	−2.25	3.305	0.248
	Center (J)	−8.08	5.255	0.062	−8.71	5.296	0.050
	Center (M)	−9.08	3.025	0.001	−9.03	3.046	0.002
	Current smoking	12.77	2.582	< 0.001	12.75	2.613	< 0.001
	Diabetes	22.45	5.306	< 0.001	23.04	5.441	< 0.001
	Hypertension	15.24	2.730	< 0.001	15.37	2.757	< 0.001
Stroke	PTGS1	2.85	1.470	0.026	3.01	1.529	0.024
	Age	0.33	0.073	< 0.001	0.33	0.075	< 0.001
	Male	2.36	0.800	0.002	2.30	0.815	0.002
	Center (F)	0.22	1.160	0.424	0.17	1.216	0.443
	Center (J)	6.63	4.398	0.066	6.03	4.435	0.087
	Center (M)	−0.45	0.970	0.322	−0.76	0.986	0.222
	Current smoking	4.09	1.045	< 0.001	4.38	1.089	< 0.001
	Diabetes	9.52	2.327	< 0.001	8.65	2.266	< 0.001
	Hypertension	6.20	1.102	< 0.001	6.05	1.124	< 0.001
Common effect	African	−4.74	4.218	0.131	−4.30	4.234	0.155

5.2. Example 2: the generalized case-cohort studies

To illustrate our proposed approach and compare to the approach in Kang et al. [6] in generalized case-cohort studies with some common diseases, we constructed a generalized case-cohort sample from the ARIC study based on diabetes and hypertension. We used a subcohort size of 626 stratified by race. We then sampled 35% diabetes cases and 35% hypertension cases outside of the subcohort. The final generalized case-cohort sample has 2267 subjects with 342 subjects having diabetes only, 1821 having hypertension only, and 104 having both. We applied our proposed method to study the effect of total cholesterol, HDL cholesterol, smoking status, and body mass index (BMI) on the risk of diabetes and hypertension after adjusting for age, gender, race, and study center. We also fitted the same model using Kang et al. [6]’s method. Table 4 summarized the results. All the standard errors for the proposed estimator are smaller than those for the estimator of Kang et al. [6].

Table 4.

Analysis results for Diabetes and Hypertension (×10⁻⁵)

	Variable	Proposed method			Kang et al’s method
		β̃	SE	P-value	β̂	SE	P-value
Diabetes	BMI	0.502	0.054	< 0.001	0.572	0.095	< 0.001
	Current smoking	−0.300	0.453	0.254	−0.154	0.641	0.405
Hypertension	BMI	0.087	0.034	0.005	0.138	0.055	0.006
	Current smoking	2.957	0.531	< 0.001	3.060	0.736	< 0.001
Common effect	Age	−0.090	0.011	< 0.001	−0.082	0.017	< 0.001
	African	0.004	0.005	0.198	0.015	0.008	0.032
	HDL Cholesterol	1.104	0.188	< 0.001	1.044	0.257	< 0.001
	Total Cholesterol	−1.690	1.793	0.173	−1.473	2.086	0.240
	Male	1.383	0.171	< 0.001	1.362	0.197	< 0.001
	Center (F)	17.344	2.311	< 0.001	17.438	2.546	< 0.001
	Center (J)	−0.126	0.048	0.004	−0.116	0.052	0.013
	Center (M)	0.023	0.024	0.172	0.019	0.026	0.232

6. Concluding remarks

Using a new weight function, we have proposed more efficient estimators for the additive hazards model in a stratified case-cohort design with rare or non-rare diseases. The new weight functions incorporate the extra information for subjects with other diseases, which can help to increase efficiency relative to existing methods. However, under the situation that the disease rate is low, the proposed method did not improve efficiency much, because of the small amount of extra information. Moreover, we also showed that stratified sampling for the subcohort improved efficiency when the stratum variable is correlated with covariates.

We considered both traditional and generalized case-cohort studies in additive hazards models using unstratified sampling as well as stratified sampling. We applied Kim et al. [7]’s weight function for traditional case-cohort studies to additive hazards models. Moreover, we extend it to situation with non-rare diseases. Under the unstratified sampling, our proposed estimators for both the traditional and generalized case-cohort designs are more efficient than those in Kang et al. [6].

It would be worthwhile to consider models with different associations between failure time and risk factors. We can adapt our approach to other types of models such as the proportional odds model, the accelerated failure time model, and the semiparametric transformation model by using all available information including stratum variables and covariate information for other diseases. These modifications are expected to improve efficiency.