Partial Fourier and Parallel MR Image Reconstruction with Integrated Gradient Nonlinearity Correction

Abstract

PURPOSE

To describe how integrated gradient nonlinearity (GNL) correction can be utilized within non-iterative partial Fourier (homodyne) and parallel (SENSE, GRAPPA) MR image reconstruction strategies, and demonstrate that performing GNL correction during – rather than after – these routines mitigates the image blurring and resolution loss caused by post-reconstruction image domain based GNL correction.

METHODS

Starting from partial Fourier and parallel MRI signal models that explicitly account for GNL, non-iterative image reconstruction strategies for each accelerated acquisition technique are derived under the same core mathematical assumptions as their standard counterparts. A series of phantom and in vivo experiments on retrospectively undersampled data were performed to investigate the spatial resolution benefit of integrated GNL correction over conventional post-reconstruction correction.

RESULTS

Phantom and in vivo results demonstrate that the integrated GNL correction reduces the image blurring introduced by the conventional GNL correction, while still correcting GNL-induced coarse-scale geometrical distortion. Images generated from under-sampled data using the proposed integrated GNL strategies offer superior depiction of fine image detail, e.g., phantom resolution inserts and anatomical tissue boundaries.

CONCLUSION

Non-iterative partial Fourier and parallel imaging reconstruction methods with integrated GNL correction reduce the resolution loss that occurs during conventional post-reconstruction GNL correction while preserving the computational efficiency of standard reconstruction techniques.

INTRODUCTION

Conventional image reconstruction techniques in clinical magnetic resonance imaging (MRI) typically assume that spatial encoding is performed with gradient fields that vary linearly across the entire imaging field-of-view (FOV). In practice, however, the gradient fields inevitably contain higher-order, nonlinear components due to engineering limitations, manufacturing imperfections, or to reduce peripheral nerve stimulation (1, 2). The unaccounted gradient nonlinearity (GNL) causes image geometric distortion and negatively affects applications where high geometric accuracy is required, such as large-scale longitudinal studies and pre-treatment planning (3–10).

The conventional methods to correct GNL-induced distortion are based on image-domain interpolation with the (presumed a priori known) spatial deformation mapping that results from GNL (1). Despite being able to correct coarse scale geometric distortion, such methods may introduce unnecessary blurring (11–13). Although improved image-domain interpolators can potentially reduce such blurring, they cannot completely circumvent this loss since in this case image discretization occurs before – rather than – after the correction is performed (11).

Recently, a model-based MR image reconstruction method with integrated GNL correction was reported (11). As opposed to the conventional method where distortion is corrected after image reconstruction, this model-based method prospectively accounts for the GNL effect during reconstruction and was shown to reduce the blurring and resolution loss caused by the conventional method, while still correcting the geometric correction. For acquisitions with full k-space sampling, this method can be performed non-iteratively via type-I non-uniform fast Fourier Transform (NUFFT) followed by an image intensity correction (11, 14).

In this paper, we extend the integrated GNL correction method in (11) to other widely-used reconstruction methods used for Cartesian acquisitions, including partial Fourier (15) and the parallel imaging methods of GRAPPA and SENSE (16, 17). We provide non-iterative solutions for these cases and demonstrate the feasibility of the integrated GNL with them.

THEORY

Signal Model

The Fourier domain signal measured during a Cartesian MRI acquisition with non-ideal spatial encoding gradients can be modeled as (11):

$$\mathbf{g}\left[\kappa \right]={\int }_{\Omega }f\left(\mathbf{x}\right)e^{-j\omega \left[\kappa \right]\Delta \left(\mathbf{x}\right)}d\mathbf{x}+\mathbf{n}\left[\kappa \right],$$ [1]

where f(x) is a continuous imaged object function, x is the physical position vector, Δ(x) is the (presumed a priori known) distortion field caused by GNL; Ω is the field-of-excitation; g[κ] is the κ-th signal measurement at k-space position ω[κ]; and n is the zero-mean proper complex Gaussian noise.

The problem of reconstructing the continuous image function, f(x), from a finite measurement vector, g, is intrinsically ill-posed without auxiliary assumptions about the target signal. Typically, a finite series representation of f(x) is assumed (18), i.e., $f\left(\mathbf{x}\right)\approx {\sum }_{i\in ϴ}\mathbf{u}\left[i\right]b(\mathbf{x}-\mathbf{r}\left[i\right])$, where b(x) is the (continuous) pixel basis function, r[i] is the pixel position vector, and u[i] is the corresponding display coefficient of the i-th pixel. Assuming a Dirac delta pixel model (i.e., b(x) = δ(x)), the signal model in Eq. 1 gives: $\mathbf{g}\left[\kappa \right]={\sum }_{i\in ϴ}\mathbf{u}\left[i\right]e^{-j\omega \left[\kappa \right]\cdot \Delta \left(\mathbf{r}\left[i\right]\right)}+\mathbf{n}\left[\kappa \right]$, which can be expressed in the following affine algebraic form:

$$\mathbf{g}=\mathbf{Au}+\mathbf{n},$$ [2]

where A(κ, i) = e^{−jω[κ]·Δ(r[i])} denotes the forward spatial encoding operator. In the presence of GNL, A is a mapping from a non-uniform image space grid onto a uniform k-space grid for Cartesian MRI. It can be implemented efficiently via a forward NUFFT operator of type-I (11, 14). Without GNL, A reduces to a conventional discrete Fourier transform (DFT).

Partial Fourier Homodyne Acquisition

Assuming the target signal is strictly real-valued, the partial Fourier homodyne acquisition enables up to 2× acceleration by exploiting the conjugate symmetry of k-space measurements. For homodyne acquisition, the signal model in Eq. 2 can be re-expressed as (19):

$$\mathbf{g}=\mathbf{A}\Psi {\mathbf{u}}_{\mathrm{r}}+\mathbf{n},$$ [3]

where the notation u_r denotes that the target signal is real-valued. The diagonal matrix, Ψ $({\Psi }_{i,i}=e^{j{\theta }_i})$, represents the apparent image phase that may be due to receive B₁ field inhomogeneity, off-resonance, and/or eddy current effects, which is typically estimate from a fully-sampled low-frequency region of k-space.

Standard partial Fourier methods construct method-of-moments estimates of u_r from g. Noting that the expected value $\left(\mathbb{E}\{\cdot \}\right)$ of Eq. 3 is $\mathbb{E}\left\{\mathbf{g}\right\}=\mathbb{E}\{\mathbf{A}\Psi {\mathbf{u}}_{\mathrm{r}}+\mathbf{n}\}=\mathbf{A}\Psi {\mathbf{u}}_{\mathrm{r}}$, u_r can be estimated as:

$${\mathbf{u}}_{\mathrm{r}}=\mathrm{real}\left\{{\Psi }^{\ast }{\left({\mathbf{A}}^{\ast }\mathbf{A}\right)}^{-1}{\mathbf{A}}^{\ast }\mathbf{g}\right\},$$ [4]

where the ensemble average has been replaced with the sample average or observation vector. Previous work has shown that the operator (A*A)⁻¹ can be approximated by a real-valued diagonal matrix, diag{J}, where J denotes the Jacobian determinant of the GNL-induced distortion field (11). Hence,

$${\mathbf{u}}_{\mathrm{r}}\approx \mathrm{real}\left\{{\Psi }^{\ast }\mathrm{diag}\left\{\mathbf{J}\right\}{\mathbf{A}}^{\ast }\mathbf{g}\right\}.$$ [5]

Denote Φ_L as the binary operator extracting the central, low-pass region of k-space, and Φ_H1, Φ_H2 symmetrically extracting the high-pass regions above and below the center of k-space, respectively. Then, the signal measurement vector can be split up along the phase encoding or readout direction as:

$$\begin{array}{cc}\hfill {\mathbf{u}}_{\mathrm{r}}& \approx \text{real}\left\{{\Psi }^{\ast }\mathrm{diag}\left\{\mathbf{J}\right\}{\mathbf{A}}^{\ast }({\Phi }_{\mathrm{L}}+{\Phi }_{{\mathrm{H}}_1}+{\Phi }_{{\mathrm{H}}_2})\mathrm{g}\right\}\hfill \\ \hfill & =\mathrm{real}\left\{{\Psi }^{\ast }\mathrm{diag}\left\{\mathbf{J}\right\}{\mathbf{A}}^{\ast }({\Phi }_{\mathrm{L}}+2{\Phi }_{{\mathrm{H}}_1})\mathrm{g}\right\}+\mathrm{real}\left\{{\Psi }^{\ast }\mathrm{diag}\left\{\mathbf{J}\right\}{\mathbf{A}}^{\ast }({\Phi }_{{\mathrm{H}}_2}-{\Phi }_{{\mathrm{H}}_1})\mathbf{g}\right\}\hfill \end{array}$$ [6]

Homodyne reconstruction recovers the real-valued image vector by assuming conjugate symmetry of k-space measurements (15), leading to: real $\left\{{\Psi }^{\ast }\mathrm{diag}\left\{\mathbf{J}\right\}{\mathbf{A}}^{\ast }({\Phi }_{{\mathrm{H}}_2}-{\Phi }_{{\mathrm{H}}_1})\mathbf{g}\right\}\approx 0$. Hence u_r can be reconstructed by:

$${\mathbf{u}}_{\mathrm{r}}\approx \text{real}\left\{{\Psi }^{\ast }\mathrm{diag}\left\{\mathbf{J}\right\}{\mathbf{A}}^{\ast }({\Phi }_{\mathrm{L}}+2{\Phi }_{{\mathrm{H}}_1})\mathbf{g}\right\}.$$ [7]

Similar to its original counterpart, the homodyne reconstruction described by Eq. 7 is non-iterative.

In standard partial Fourier methods, the image phase estimate Φ, is constructed from a fully-sampled low-frequency region of k-space. However, note that Eq. 3 presumes that the phase map is GNL distortion-free. Hence, this reference signal should be derived from a low-resolution image generated using integrated GNL correction, i.e.,

$${\Psi }_{i,i}=e^{j\angle {\left(\mathrm{diag}\left\{\mathbf{J}\right\}{\mathbf{A}}^{\ast }{\Phi }_{\mathrm{L}}\mathbf{g}\right)}_i},$$ [8]

where operator $\angle (\cdot )$ takes the phase map of a complex vector.

GRAPPA

GRAPPA (16) is an auto-calibrating k-space based parallel imaging method that reconstructs the full set of coil images from undersampled k-space data. Denoting G as the M × C multi-channel k-space data matrix, where M and C are the number of k-space measurements (per coil) and coils, respectively, the forward signal model of GRAPPA is:

$$\mathbf{G}=\mathbf{AU}+\mathbf{N},$$ [9]

where U is the N × C matrix (N denoting the total number of image pixels) representing the set of coil images and N is the proper Gaussian noise matrix (N × C). For parallel imaging, N ≥ M. Following auto-calibration, GRAPPA estimates missing k-space values via Fourier-domain interpolation (16). The fully-sample multi-coil k-space data matrix (N × C) estimated by GRAPPA, $\widehat{\mathbf{G}}$, is denoted as:

$$\widehat{\mathbf{G}}={\mathcal{H}}_{\mathrm{GRAPPA}}\left\{\mathbf{G}\right\},$$ [10]

where ${\mathcal{H}}_{\mathrm{GRAPPA}}\{\cdot \}$ is the k-space interpolation operator derived from auto-calibration signals (ACS).

Because GRAPPA reconstruction occurs entirely in k-space, integrated GNL correction can simply be performed while transforming the reconstruction result from k-space to the image domain in a way similar to the case of full k-space sampling:

$$\mathbf{U}={\left({\mathbf{A}}^{\ast }\mathbf{A}\right)}^{-1}{\mathbf{A}}^{\ast }\widehat{\mathbf{G}}\approx \mathrm{diag}\left\{\mathbf{J}\right\}{\mathbf{A}}^{\ast }\widehat{\mathbf{G}},$$ [11]

Again, the Jacobian determinant approximation is used. Similarly, if the target signal is presumed to be real-valued, homodyne techniques can also be incorporated into this reconstruction process to yield:

$${\mathbf{u}}_c\approx \text{real}\left\{{\Psi }_c^{\ast }\mathrm{diag}\left\{\mathbf{J}\right\}{\mathbf{A}}^{\ast }({\Phi }_{\mathrm{L}}+2{\Phi }_{{\mathrm{H}}_1}){\mathbf{g}}_c\right\},$$ [12]

where u_c, g_c, and Ψ_c denote the real-valued image, GRAPPA reconstructed k-space signal, and phase map of the c-th coil, respectively.

SENSE

SENSE (17) is another widely-used parallel imaging method, which reconstructs a single image from the measured multi-channel data set. Presuming uniform (Cartesian) under-sampling, the k-space MR signal observed during a standard SENSE acquisition can be modeled as:

$$\mathbf{g}=(\mathbf{I}\otimes \Phi \mathbf{A})\mathbf{Su}+\mathbf{n},$$ [13]

where g (MC × 1) is the multi-coil k-space data vector, S (NC × N) is a block diagonal matrix that represents the true (distortion-free) sensitivity profiles of receiving coils, Φ (M × N matrix) is a uniform under-sampling operator, u (N × 1) is the target image vector, and n (MC × 1) is the noise vector. Additionally, I denotes a C × C identity matrix and is the Kronecker product.

SENSE reconstruction estimates the target image vector, u, by solving the following regularized least-squared estimation problem:

$$\arg \underset{\mathbf{u}}{\min }{\Vert \mathbf{g}-(\mathbf{I}\otimes \Phi \mathbf{A})\mathbf{Su}\Vert }_2^2+\lambda {\Vert \mathbf{u}\Vert }_2^2,$$ [14]

where the regularization parameter, λ > 0, stabilizes the matrix inversion process implicit to this problem. As shown in (11), this problem can be solved iteratively, e.g., via conjugate gradient (CG) iteration. However, the computational efficiency of this approach may not be sufficient for routine clinical use, particularly considering that standard SENSE reconstruction (without integrated GNL correction) is non-iterative. Although CG iteration is widely used for solving quadratic estimation problems like Eq. 14, there exist many viable alternative numerical strategies. One attractive and increasingly popular optimization strategy is alternating direction method-of-multipliers (ADMM) (20), which breaks apart a compound optimization problem like Eq. 14 into a series of easier tasks.

Conventionally, a standard SENSE reconstruction is first performed on the undersampled data, after which standard image domain GNL correction is applied to the resultant image. To utilize the proposed integrated GNL correction in a similar direct manner, the uncorrected SENSE image result can instead be Fourier transformed back to k-space, and the standard integrated GNL correction process for fully-sampled data can be applied. As shown in the Appendix, this process actually corresponds to the first iteration of a particular ADMM routine for solving Eq. 14, initialized with the standard SENSE reconstruction results. Specifically, the initial standard SENSE reconstruction (i.e., without GNL correction) is performed as:

$$\mathbf{v}={\left[{\widehat{\mathbf{S}}}^{\ast }(\mathbf{I}\otimes {\mathbf{F}}^{\ast }{\Phi }^{\ast }\Phi \mathbf{F})\widehat{\mathbf{S}}+\lambda \mathbf{I}\right]}^{-1}{\widehat{\mathbf{S}}}^{\ast }(\mathbf{I}\otimes {\mathbf{F}}^{\ast }{\Phi }^{\ast })\mathbf{g},$$ [15]

where Ŝ represents the set of GNL-distorted (i.e., non-corrected) coil sensitivity profiles and F is the DFT operator. The subsequent transform and GNL correction process is:

$$\mathbf{u}=\alpha \left(\lambda \right)\mathrm{diag}\left\{\mathbf{J}\right\}{\mathbf{A}}^{\ast }\mathbf{Fv},$$ [16]

where α is a (optional) normalization constant that is a function of λ. As shown in the Appendix and Results, non-iteratively executing just a single iteration of the ADMM scheme for Eq. 14 leads to improvements in spatial resolution relative to standard reconstruction and correction pipeline.

Like GRAPPA, the homodyne strategy can also be integrated into SENSE reconstruction algorithm(21). This process mirrors Eq. 7, using the GNL-corrected SENSE reconstruction process in Eq. 16 (denoted as ${\mathcal{H}}_{\mathrm{SENSE}}\{\cdot \}$) in lieu of the integrated GNL correction process for the full-sampled data:

$${\mathbf{u}}_{\mathrm{r}}\approx \mathrm{real}\left\{{\Psi }^{\ast }{\mathcal{H}}_{\mathrm{SENSE}}\left\{({\Phi }_{\mathrm{L}}+2{\Psi }_{{\mathrm{H}}_1})\mathbf{g}\right\}\right\},$$ [17]

where the reference phase here is estimated as:

$${\Psi }_{i,i}=e^{j\angle {\left({\mathcal{H}}_{\mathrm{SENSE}}\left\{{\Phi }_{\mathrm{L}}\mathbf{g}\right\}\right)}_i},$$ [18]

Again, Eq. 17 reduces to standard SENSE with homodyne acquisition when Δ(x) = 0 (i.e., without integrated GNL correction).

METHODS

Data Acquisition

Several phantom and in vivo brain scan data sets were acquired to compare the proposed strategies with standard GNL correction. All the experiments were performed on a 3.0 T MR scanner (General Electric, Signa HDxt System, v16.0) with zoom mode gradient (slew rate = 200 T/m/s, gradient amplitude = 40 mT/m) and an 8-channel head-only receive coil.

The American College of Radiology (ACR) quality control phantom was scanned with a T₁-weighted spin echo protocol (TR = 500 ms, TE = 13 ms, FA = 90°, BW = ±15.63 kHz,matrix size = 256 × 256, FOV = 220 × 220 mm², slice thickness = 3 mm). For the sake of demonstration, the resolution insert slice of the ACR Phantom was physically centered 94 mm from the gradient isocenter along the inferior direction to ensure high GNL. Additionally, brain scans were acquired on two healthy volunteers under an IRB-approved protocol. A sagittal 2D T₂-weighted fast spin echo (FSE) sequence (TR = 4767 ms, TE = 102 ms, FA = 90°, BW = ±25.00 kHz, matrix size = 256 × 256, FOV = 220 × 220 mm², slice thickness = 4 mm, echo train length = 12) was performed on one volunteer, and an axial 3D MP-RAGE sequence (TR = 7 ms, TE = 2.9 ms, TI = 900 ms, FA = 8°, BW = ±31.25 kHz, matrix size = 256 × 256 × 240, FOV = 240 × 240 × 240 mm³, slice thickness = 1 mm) was performed on the second. For all the experiments, complete raw k-space data sets were retained and retrospectively undersampled (details below).

Image Reconstruction Experiments

Vendor-provided GNL information was used throughout the study. For all experiments in this work, 2D in-plane GNL correction (both standard and proposed methods) was performed. All the data were processed in Matlab 7.14 environment on a 4-core 3.2 GHz computer with 8 GB memory. The standard image domain GNL correction was implemented in house via conventional cubic spline interpolation in the image domain, which has been validated against the vendor-provided implementation (1). The type-I NUFFT operator was constructed using a 1.25× oversampled Fast Fourier Transform (FFT) and width J = 5 Kaiser-Bessel kernel. We note that image domain correction was not performed using a Kaiser Bessel kernel since the latter is not intrinsically interpolating (since it is non-oscillatory). This is not a problem for the NUFFT, which counters the effects of non-interpolating convolution during deapodization. Although an exhaustive evaluation of possible interpolation kernels is beyond the scope of this work, a representative result obtained with a Kaiser Bessel window is shown in Supporting Figure S1, available online. Based on our current Matlab implementation, the proposed NUFFT-based method requires 1.5 sec to correct a 256 × 256 pixels single coil image (as in the GRAPPA reconstruction example), while the standard GNL correction needs 1.0 sec. The proposed homodyne reconstruction requires the phase map to be separately corrected with the same NUFFT operator, the total time is therefore 3.0 sec (proposed) versus 1.0 sec (standard) for the equivalent matrix size.

To test the proposed partial Fourier reconstruction, the resolution insert slice of the ACR data set was selected and retrospectively undersampled (contiguously) to 63% of its original size in the phase encoding (right/left) direction according to Eq. 7. Three groups of experiments were performed: zero-filling, homodyne, and fully-sampled (for reference) reconstructions. Within each group, three different reconstructions were performed: standard reconstruction without GNL correction, standard reconstruction followed by image-domain GNL correction, and reconstruction with the integrated GNL correction. Both the standard and proposed homodyne reconstruction strategies were performed according to Eq. 7. Phase maps were computed according to Eq. 8. For the standard approach, A = F and J = 1 (i.e., no GNL) was assumed during transformation from k-space to the image domain. For the proposed approach, A was de ned as the GNL-aware type-I NUFFT operator.

To test the proposed GRAPPA reconstruction, k-space data of one slice (located at 44 mm to the right of isocenter) of the T₂-weighted FSE dataset was retrospectively 2× uniformly undersampled except within a low-pass region that remained fully-sampled for use as an ACS. A total of 36 ACS lines were preserved, leading to an effective sampling rate of 57%. The missing k-space signals were then recovered. The inverse DFT-based reconstruction was first applied to the recovered full k-space signals. Then, the standard GNL correction was applied to the reconstructed images. Next, the proposed GRAPPA with integrated GNL correction was performed according to Eq. 11. The k-space of each coil was reconstructed separately and root-sum-of-squared combined. Finally, to simulate GRAPPA with homodyne acquisition, a homodyne kernel (cutoff at 71% of total k-space) is further applied according to Eq. 7, leading to an overall undersampling rate of 43%. Then, the proposed method as in Eq. 12, along with the conventional inverse DFT-based homodyne reconstruction followed by standard GNL correction, were performed respectively.

To test the proposed SENSE reconstruction with integrated GNL correction, one slice located at −61 mm in inferior direction was selected from the MPRAGE data set and retrospectively undersampled (2×). Coil sensitivity profiles were estimated from separate calibration scan data via ESPIRiT (22). The image reconstructed by conventional SENSE was first obtained, which was then GNL-corrected using the standard image-domain method. Then, the proposed SENSE strategy with integrated GNL correction defined in Eq. 16 was directly applied to the same undersampled k-space data. λ was manually selected to be 0.025 which offered visually acceptable performance. The selection of this model parameter could potentially be automated and optimized using an objective metric like mean squared error (23), but this development is beyond the scope of this work. Finally, the k-space data were further undersampled according to homodyne acquisition (homodyne kernel cutoff at 71% of total k-space), yielding an overall undersampling rate of 36%. The proposed SENSE with homodyne acquisition (Eq. 17) was then performed. For comparison, the standard SENSE/homodyne reconstruction with and without conventional GNL correction was also performed.

RESULTS

Fig. 1 shows the images reconstructed from undersampled k-space signals by zero-padding (a-c), partial Fourier homodyne reconstruction (d-f), and images reconstructed from fully sampled k-space data (g-i). The images were sinc-interpolated (4×) for display. As expected, images reconstructed by zero-padding show blurring along the undersampling direction. The results of homodyne reconstruction exhibit comparable spatial resolution to the full k-space sampling results with an expected minor reduction in signal-to-noise ratio (SNR). Both standard and the proposed methods are able to correct the coarse scale geometrical distortion due to GNL, but the NUFFT-based homodyne reconstruction (f) shows less spatial blurring than the image after standard GNL correction (e). As shown in Fig. 1, the images after NUFFT-based correction show better depiction around the resolution inserts.

1.

The resolution insert slice of ACR phantom reconstructed by zero-padding (a-c), partial Fourier homodyne reconstruction (d-f), and from fully sampled k-space data (g-i), before and after GNL correction. a, d, and g: images without GNL correction; b, e, and h: images corrected with standard GNL correction; c, f, and i: images corrected with the proposed NUFFT-based strategy.

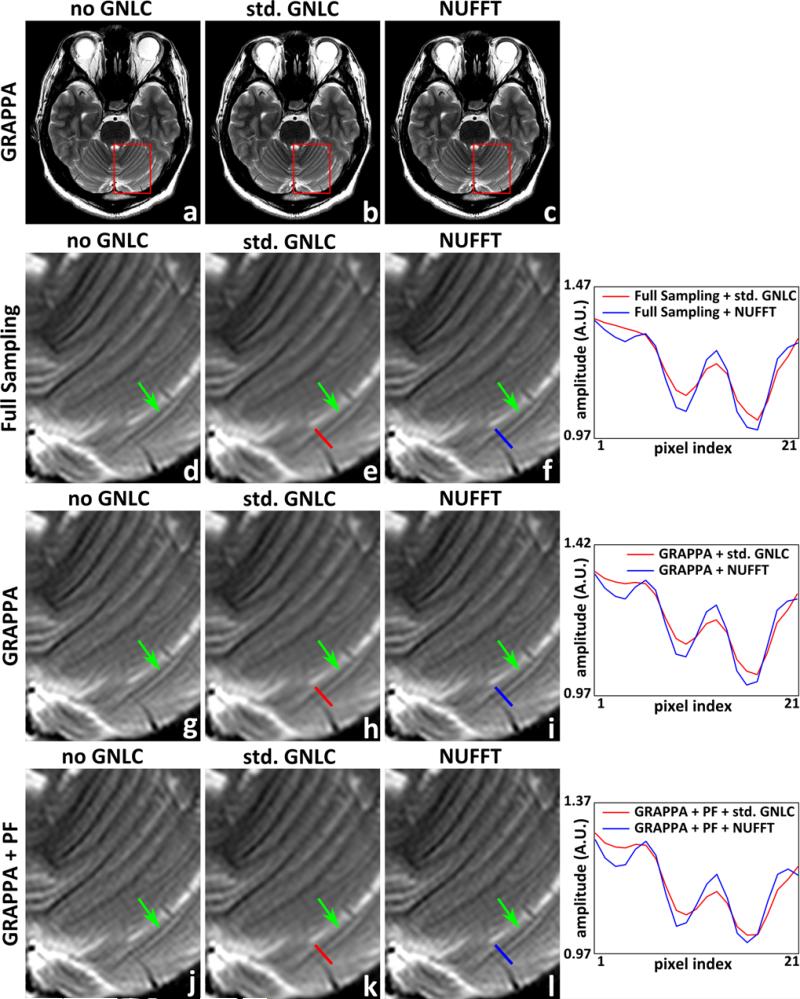
Fig. 2 shows images reconstructed via the NUFFT-based GRAPPA reconstruction, along with the standard GRAPPA reconstruction results before and after standard GNL correction. The data were sinc-interpolated (4×) for display and Fermi windowed. Both standard and NUFFT-based corrections are able to correct the geometrical distortion caused by GNL, as seen around the anterior end of Figs. 2a to 2c. Comparing between images before and after standard GNL corrections shows that the standard correction method introduces image blurring in the corrected images. This blurring is reduced by the proposed NUFFT-based correction. Shown on the right in Fig. 2 are the line profiles in the images after standard or NUFFT-based GNL correction. The line profile comparison shows that, due to the smoothing effect of interpolation, the pixel intensity change around small anatomical structures in the standard GNL correction results is reduced when compared with that in the images obtained with NUFFT-based corrections. Additional performed experiments, whose results are not shown here for brevity, suggest that the resolution preserving capability of the proposed NUFFT-based method are also retained for higher GRAPPA acceleration rates and/or fewer ACS lines, although this topic will be explored in greater depth in a separate, future study.

2.

T₂ weighed images reconstructed by conventional GRAPPA before and after the standard GNL correction, and images reconstructed by the proposed NUFFT-based GRAPPA. a-c, g-i: full scale and magnified insets of images reconstructed from k-space data with (2× retrospective) undersampling (GRAPPA); d-f, j-l: magnified insets of images reconstructed from fully sampled k-space data (Full Sampling), and that reconstructed from k-space data with uniform undersampling and partial Fourier acquisition (GRAPPA+PF), respectively. a, d, g, j: images reconstructed by conventional DFT based reconstruction before GNL correction (no GNLC); b, e, h, k: images obtained after applying standard GNL correction to a, d, g, j (std. GNLC); c, f, i, l: images reconstructed by the NUFFT-based strategies (NUFFT). The line profiles in images after the standard and proposed GNL correction are shown on the right of each row. The positions of line profiles are indicated with red (std. GNLC) or blue (NUFFT) markers.

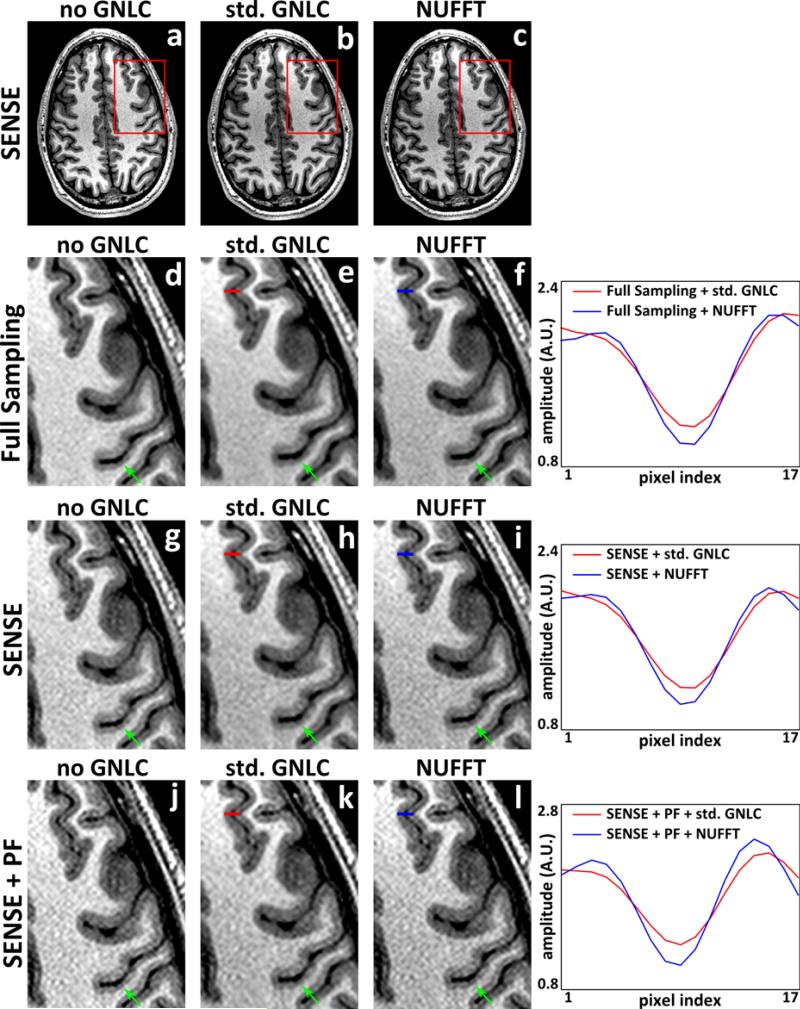
Fig. 3 shows the reconstruction results of the conventional SENSE before (a, d, g, j) and after (b, e, h, k) standard GNL correction, and the results of the proposed SENSE reconstruction with integrated GNL correction (c, f, i, l). Data were 4× sinc-interpolated for display and Fermi windowed. Similar to the observation in Figs. 1 and 2, the proposed SENSE with integrated, NUFFT-based GNL correction better preserves image details. Although the GNL distortion is relatively moderate in this example, the standard GNL correction still introduces image blurring to the anatomical boundaries and modifies noise texture. On the other hand, these boundary regions are better preserved by the proposed NUFFT-based methods. Line profiles in the images after standard and the NUFFT-based GNL corrections demonstrate the reduced blurring. These observations can be understood via the frequency spectra analysis shown in our previous work (11), which demonstrated that the power spectra of images corrected with the interpolation-based GNL correction exhibited loss of its high frequency components, similar to a low-pass filtering effect. On the contrary, the proposed NUFFT-based correction does not suffer from this loss, since the blurring introduced by interpolation in the NUFFT operators is implicitly accounted for via its integrated deconvolution.

3.

MPRAGE images reconstructed by conventional SENSE before and after the standard GNL correction, and images reconstructed by the proposed SENSE framework with integrated GNL correction. a-c, g-i: full scale and magnified insets of images reconstructed from k-space data with (2× retrospective) undersampling (SENSE); d-f, j-l: magnified insets of images reconstructed from fully sampled k-space data (Full Sampling), and that reconstructed from k-space data with uniform undersampling and partial Fourier acquisition (SENSE+PF), respectively. a, d, g, j: images reconstructed by conventional DFT based reconstruction before GNL correction (no GNLC); b, e, h, k: images obtained after applying standard GNL correction to a, d, g, j (std. GNLC); c, f, i, l: images reconstructed by the NUFFT-based strategies (NUFFT). The line profiles in images after the standard and proposed GNL correction are shown on the right of each row. The positions of line profiles are indicated with red (std. GNLC) or blue (NUFFT) markers.

DISCUSSION

We presented new methods for the combination of a recently proposed integrated GNL correction strategy with accelerated data acquisition techniques that are widely used in clinical settings, including partial Fourier homodyne and parallel imaging. Starting from the signal model for spatial encoding, the image reconstruction framework with integrated GNL correction for each strategy is constructed, from which non-iterative solutions for Cartesian MRI are derived in correspondence with their original counterparts that are routinely used in clinical settings. For SENSE, the statistical meaning in its original version as a maximum likelihood estimator is retained (17), as shown from the derivation of its reconstruction model in the Appendix. Comparison between conventional GNL correction method and the NUFFT-based corrections shows that image details are better retained by the proposed method. Although tested with 2D protocols, the proposed frameworks can be readily extended into 3D partial Fourier acquisition, and 3D GRAPPA/SENSE with two-dimensional acceleration. Other partial Fourier processing methods (e.g., POCS) are not included in this work due to their iterative nature (24, 25). Additionally, for such methods, the numerical error induced by the imperfect approximation of operator (A*A)⁻¹ by diag {J} can accumulate at each iteration, which makes the design of efficient routines challenging.

In our previous work on this topic (11), it was shown that the NUFFT-based GNL correction operator preserved the noise power spectrum of the target image. Based on this observation, and preliminary experimental results not shown here, it is hypothesized that the developed GNL correction strategies will retain their resolution preserving advantage across a broad range of SNR levels. However, extensive theoretical and experimental analysis of the effect of noise – amongst other characteristics like pixel size – on GNL-corrected image accuracy and precision is needed to rigorously validate this hypothesis. This will be the subject of a separate, future work.

The GNL distortion fields used in this work were generated using a vendor-provided 5th order spherical harmonic polynomial model of the gradient field, which is generally believed to be sufficient for conventional clinical applications (3, 4). Conventionally, these coefficients are obtained via electromagnetic field simulation based on the system specific coil design. The geometrical accuracy of GNL correction (any strategy) can potentially be improved by adopting a higher order model of the gradient field (8), and by estimating field coefficients on a system specific basis to account for manufacturing variations (26, 27). Adopting advanced calibration procedures is expected to provide overall improvements in GNL correction performance; however, the relative advantage of NUFFT-based correction over the standard image domain strategy is expected to be retained.

The proposed strategies can potentially be applied to any acquisition where the original homodyne acquisition, GRAPPA and SENSE algorithms are routinely applied. As shown in the previous work (11), the resolution retaining effect is expected to be more pronounced in region where strong GNL presents. Since the GNL distortion is usually stronger in regions away from gradient isocenter, the proposed method may particularly benefit large FOV applications such as those used in treatment planning or peripheral angiography (28). The proposed method may also be beneficial for scanners exploiting gradient coils with new, asymmetric design where gradient linearity is intentionally sacrificed in exchange for higher gradient value and slew rate, leading to stronger GNL distortion within a typical brain scan volume (29).

CONCLUSIONS

Non-iterative partial Fourier and parallel imaging reconstruction with integrated GNL correction mitigates the image blurring and resolution loss caused by conventional image domain interpolation-based GNL correction method while reducing the amount of data required to form an MR image.

APPENDIX

Here, we show that the SENSE-based GNL correction process in Eq. 16 corresponds to the first iteration of an ADMM optimization routine for solving Eq. 14,

$$\arg \underset{\mathbf{u}}{\min }{\Vert \mathbf{g}-(\mathbf{I}\otimes \Phi \mathbf{A})\mathbf{Su}\Vert }_2^2+\lambda {\Vert \mathbf{u}\Vert }_2^2.$$

Since the DFT (F) is unitary, $\mathbf{I}\otimes \Phi \mathbf{A}=(\mathbf{I}\otimes \Phi \mathbf{F})(\mathbf{I}\otimes {\mathbf{F}}^{\ast }\mathbf{A})$ and this problem can be restated as:

$$\arg \underset{\mathbf{u}}{\min }{\Vert \mathbf{g}-(\mathbf{I}\otimes \Phi \mathbf{F})(\mathbf{I}\otimes {\mathbf{F}}^{\ast }\mathbf{A})\mathbf{Su}\Vert }_2^2+\lambda {\Vert \mathbf{u}\Vert }_2^2.$$

In the above problem, coil sensitivity modulation (S) is applied before GNL-induced spatial distortion. Alternatively, this effect can be applied after distortion. Let Ŝ denote the set of GNL-distorted sensitivity profiles that satisfy $\widehat{\mathbf{S}}{\mathbf{F}}^{\ast }\mathbf{A}=(\mathbf{I}\otimes {\mathbf{F}}^{\ast }\mathbf{A})\mathbf{S}$. Then, the SENSE reconstruction problem resorts to:

$$\arg \underset{\mathbf{u}}{\min }{\Vert \mathbf{g}-(\mathbf{I}\otimes \Phi \mathbf{F})\widehat{\mathbf{S}}{\mathbf{F}}^{\ast }\mathbf{Au}\Vert }_2^2+\lambda {\Vert \mathbf{u}\Vert }_2^2.$$

The alternating direction method-of-multiplier (ADMM) algorithm (20) operates by decomposing the target optimization problem into a series of (relatively) easier tasks. To this effect, introduce an intermediary variable v = F*Au. The above (unconstrained) optimization problem can then be recast as the following (constrained) joint estimation problem:

$$\arg \underset{\mathbf{u},\mathbf{v}}{\min }{\Vert \mathbf{g}-(\mathbf{I}\otimes \Phi \mathbf{F})\widehat{\mathbf{S}}\mathbf{v}\Vert }_2^2+\lambda {\Vert \mathbf{u}\Vert }_2^2,s.t.\mathbf{v}={\mathbf{F}}^{\ast }\mathbf{Au}.$$

Note that this problem is mathematically equivalent to the original. The augmented Lagrangian functional for this constrained problem is then:

$$\mathcal{L}(\mathbf{u},\mathbf{v})={\Vert \mathbf{g}-(\mathbf{I}\otimes \Phi \mathbf{F})\widehat{\mathbf{S}}\mathbf{v}\Vert }_2^2+\lambda {\Vert \mathbf{u}\Vert }_2^2+\mu {\Vert \mathbf{v}-{\mathbf{F}}^{\ast }\mathbf{Au}-\zeta \Vert }_2^2,$$

where ζ is the Lagrangian multiplier vector and μ > 0 is an optimization constant whose value controls the rate of convergence of the iterative routine. ADMM operates by serially minimizing $\mathcal{L}(\cdot )$ with respect to u and v, independently, while updating ζ. Specifically, at the n-th ADMM iteration, the solution v_n, u_n, and ζ_n are updated as follows:

$$\begin{array}{cc}\hfill {\mathbf{u}}_n=& {\left({\mathbf{A}}^{\ast }\mathbf{A}+\frac{\lambda }{\mu }\mathbf{I}\right)}^{-1}{\mathbf{A}}^{\ast }\mathbf{F}({\mathbf{v}}_{n-1}-{\zeta }_{n-1})\hfill \\ \hfill {\mathbf{v}}_n=& {\left({\widehat{\mathbf{S}}}^{\ast }(\mathbf{I}\otimes {\mathbf{F}}^{\ast }{\Phi }^{\ast }\Phi \mathbf{F})\widehat{\mathbf{S}}+\mu \mathbf{I}\right)}^{-1}\left({\widehat{\mathbf{S}}}^{\ast }(\mathbf{I}\otimes {\mathbf{F}}^{\ast }{\Phi }^{\ast })\mathbf{g}+\mu ({\mathbf{F}}^{\ast }{\mathbf{Au}}_n+{\zeta }_{n-1})\right)\hfill \\ \hfill {\zeta }_n=& {\zeta }_{n-1}-({\mathbf{v}}_n-{\mathbf{F}}^{\ast }{\mathbf{Au}}_n).\hfill \end{array}$$

Upon inspection, the update of v_n is essentially a standard SENSE “unfolding” operation that can be solved non-iteratively (17). The Lagrange multiplier update is also straightforward. However, as previously noted for fully-sampled integrated GNL correction (11), the update of u_n cannot be computed directly.

One strategy for iteratively determining u_n is preconditioned steepest descent. At the k-th steepest descent iteration, u_n is updated as:

$${\mathbf{u}}_{n,k}={\mathbf{u}}_{n,k-1}+{\alpha }_{k-1}{\mathbf{Pr}}_{k-1},$$

where P is a Hermitian positive definite preconditioner and the residual vector

$${\mathbf{r}}_{k-1}={\mathbf{A}}^{\ast }\mathbf{F}({\mathbf{v}}_{n-1}-{\zeta }_{n-1})-\left[\left({\mathbf{A}}^{\ast }\mathbf{A}+\frac{\lambda }{\mu }\mathbf{I}\right)\right]{\mathbf{u}}_{n,k-1}.$$

Noting Eq. 5, a simple and effective preconditioner for this problem is the Jacobian determinant approximation of (A*A)⁻¹, i.e., P = diag {J}. The optimal step size is determined adaptively as:

$${\alpha }_{k-1}=\frac{{\mathbf{r}}_{k-1}^{\ast }{\mathbf{Pr}}_{k-1}}{{\mathbf{r}}_{k-1}^{\ast }\mathbf{P}({\mathbf{A}}^{\ast }\mathbf{A}+\lambda ∕\mu \mathbf{I}){\mathbf{Pr}}_{k-1}}.$$

Since steepest descent is here applied within another iterative process, it can be initialized using the final result from the previous (outer) iteration, i.e., u_n,0 = u_n–1.

With ADMM, subproblems do not need to be solved exactly to guarantee convergence – inexact solving will simply slow the overall rate of convergence (20). At minimum, a single steepest descent step can be performed, yielding the following one-step update rule for u_n at the n-th ADMM iteration:

$${\mathbf{u}}_n={\mathbf{u}}_{n-1}+{\alpha }_0{\mathbf{Pr}}_0,$$

Assume zero initial conditions for u and ζ (i.e., u₀ = ζ₀ = 0), and with v initialized as the standard SENSE reconstruction results before GNL correction, i.e.,

$${\mathbf{v}}_0={\left({\widehat{\mathbf{S}}}^{\ast }(\mathbf{I}\otimes {\mathbf{F}}^{\ast }{\Phi }^{\ast }\Phi \mathbf{F})\widehat{\mathbf{S}}+\lambda \mathbf{I}\right)}^{-1}{\widehat{\mathbf{S}}}^{\ast }(\mathbf{I}\otimes {\mathbf{F}}^{\ast }{\Phi }^{\ast })\mathbf{g}.$$

Then, the update of u at the first ADMM iteration reverts to

$${\mathbf{u}}_1={\alpha }_0\mathrm{diag}\left\{\mathbf{J}\right\}{\mathbf{A}}^{\ast }{\mathbf{Fv}}_0,$$

where

$${\alpha }_0=\frac{{\mathbf{v}}_0^{\ast }{\mathbf{F}}^{\ast }\mathbf{A}\mathrm{diag}\left\{\mathbf{J}\right\}{\mathbf{A}}^{\ast }{\mathbf{Fv}}_0}{{\mathbf{v}}_0^{\ast }{\mathbf{F}}^{\ast }\mathbf{A}\mathrm{diag}\left\{\mathbf{J}\right\}({\mathbf{A}}^{\ast }\mathbf{A}+\lambda ∕\mu \mathbf{I})\mathrm{diag}\left\{\mathbf{J}\right\}{\mathbf{A}}^{\ast }{\mathbf{Fv}}_0}.$$

Hence, the u update at the first ADMM iteration can be obtained by transforming the SENSE result back to k-space, and applies integrated GNL correction on this fully-sampled data. Thus, the expressions in Eq. 16 correspond to performing the first iteration of a specific ADMM sequence for Eq. 14.

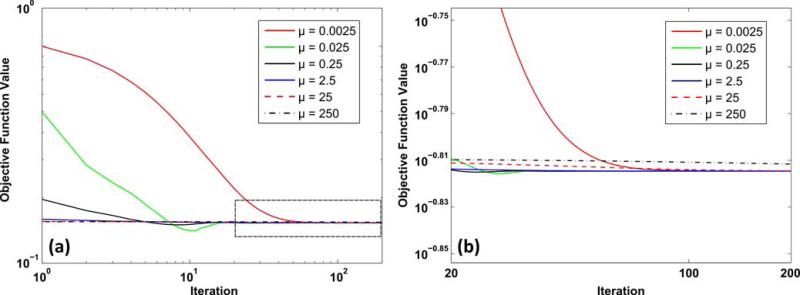
To demonstrate the efficacy and convergence of these optimization strategies, the MPRAGE data set with 2× retrospective uniform undersampling in Fig. 3 was reconstructed using the described ADMM sequence (with inexact u_n update), which was executed for 200 iterations with λ = 0.025 (manually selected). The effect of ADMM optimization constant μ was examined by performing the ADMM sequence with different values (μ = 0.0025, 0.025, 0.25, 2.5, 25, 250). As shown in Fig. 4, the objective functions (from Eq. 14) under various μ gradually converge, while the choice of μ influences the solution after the first iteration as well as the global convergence rate. When a small μ (e.g., 0.0025) is used, the ratio λ/μ is large, which diminishes the contribution of A*A in obtaining the step size α₀ and subsequently u_n, and therefore leads to a sub-optimal solution after the first iteration and decreases the global convergence rate. Although a large μ (e.g., 250) offers a good approximation after the first iteration, the strong weight set on μI during the update of v_n weakens the effect of SENSE “unfolding” operation, which also tends to slow down the rate of convergence. Finally, an intermediary value (e.g., μ = 2.5) provides a fast convergence and offers a good approximation of the nal solution after iterations, and therefore is used in Fig. 3.

4.

a Normalized objective function values of GNL-integrated SENSE reconstruction model at different numbers of ADMM iteration for a series of optimization constant μ values; b magnified inset as indicated in a.

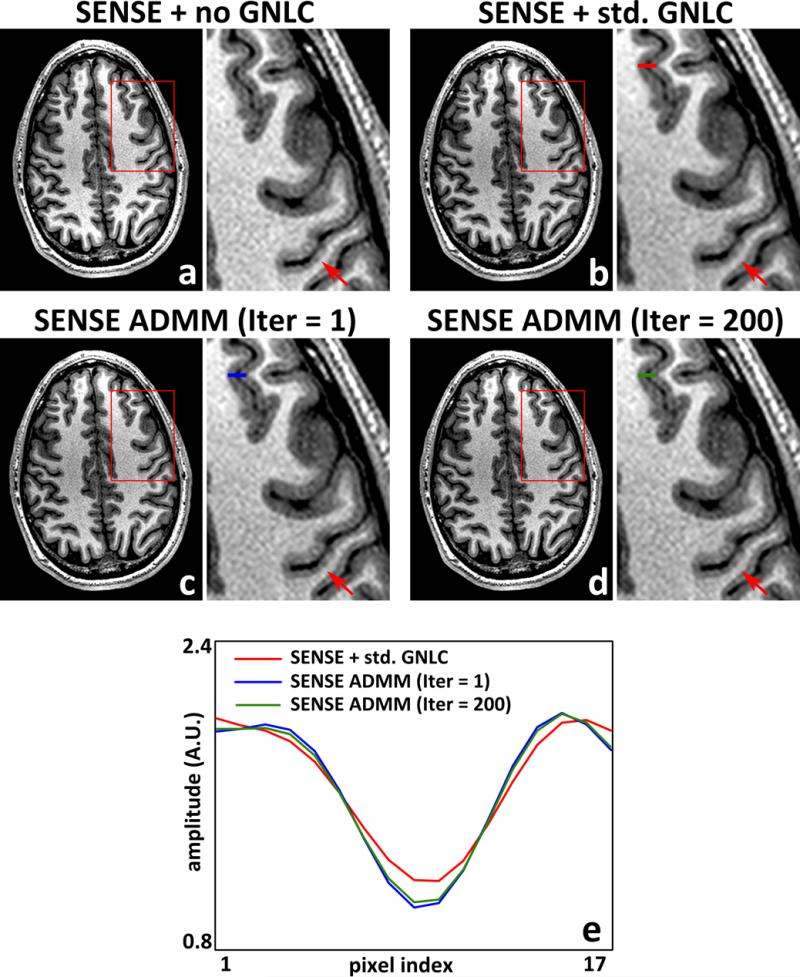
Fig. 5 compares the first iteration result of the inexact ADMM sequence described above (μ = 2.5) against the solution after 200 iterations. Note that the first iteration of the ADMM is the same as the non-iterative reconstruction solution. No substantial visual differences were observed (Figs. 5c and 5d), suggesting that performing only one ADMM iteration may be sufficient for practical application. The images with and without standard GNL correction is also shown for reference. Compared with standard GNL correction, both ADMM-based integrated GNL correction results exhibit sharper boundaries between white and gray matter (Fig. 5).

5.

MPRAGE images (and magnified insets) reconstructed using the conventional DFT based SENSE before GNL correction (a), and after standard GNL correction (b). c, d: images reconstructed using the NUFFT-based SENSE framework solved via ADMM in the 1st (c) and 200th iteration (d), respectively. Note that the 1st iteration of the ADMM is the same as the non-iterative SENSE reconstruction solution. The line profiles in images after the standard and NUFFT-based GNL correction are shown in e. The positions of line profiles are indicated with red (std. GNLC), blue (ADMM Iter = 1, non-iterative solution), or green (ADMM Iter = 200) markers.