Significance
Receptors on the surface of lymphocytes specifically recognize foreign pathogens. The diversity of these receptors sets the range of infections that can be detected and fought off. Recent experiments show that, despite the many differences between these receptors in different cell types and species, their distribution of diversity is a strikingly reproducible power law. By introducing effective models of repertoire dynamics that include environmental and antigenic fluctuations affecting lymphocyte growth or “fitness,” we show that a temporally fluctuating fitness is responsible for the observed heavy tail distribution. These models are general and describe the dynamics of various cell types in different species. They allow for the classification of the functionally relevant repertoire dynamics from the features of the experimental distributions.
Keywords: immune repertoire, population dynamics, fluctuating fitness, lymphocyte receptor, repertoire sequencing
Abstract
The adaptive immune system relies on the diversity of receptors expressed on the surface of B- and T cells to protect the organism from a vast amount of pathogenic threats. The proliferation and degradation dynamics of different cell types (B cells, T cells, naive, memory) is governed by a variety of antigenic and environmental signals, yet the observed clone sizes follow a universal power-law distribution. Guided by this reproducibility we propose effective models of somatic evolution where cell fate depends on an effective fitness. This fitness is determined by growth factors acting either on clones of cells with the same receptor responding to specific antigens, or directly on single cells with no regard for clones. We identify fluctuations in the fitness acting specifically on clones as the essential ingredient leading to the observed distributions. Combining our models with experiments, we characterize the scale of fluctuations in antigenic environments and we provide tools to identify the relevant growth signals in different tissues and organisms. Our results generalize to any evolving population in a fluctuating environment.
Antigen-specific receptors expressed on the membrane of B- and T cells (B-cell receptors, BCRs and T-cell receptors, TCRs) recognize pathogens and initiate an adaptive immune response (1). An efficient response relies on the large diversity of receptors that is maintained from a source of newly generated cells, each expressing a unique receptor. These progenitor cells later divide or die, and their offspring make up clones of cells that share a common receptor. The sizes of clones vary, as they depend on the particular history of cell divisions and deaths in the clone. The clone-size distribution thus bears signatures of the challenges faced by the adaptive system. Understanding the form of the clone-size distribution in healthy individuals is an important step in characterizing the antigenic recognition process and the functioning of the adaptive immune system. It also presents an important starting point for describing statistical deviations seen in individuals with compromised immune responses.
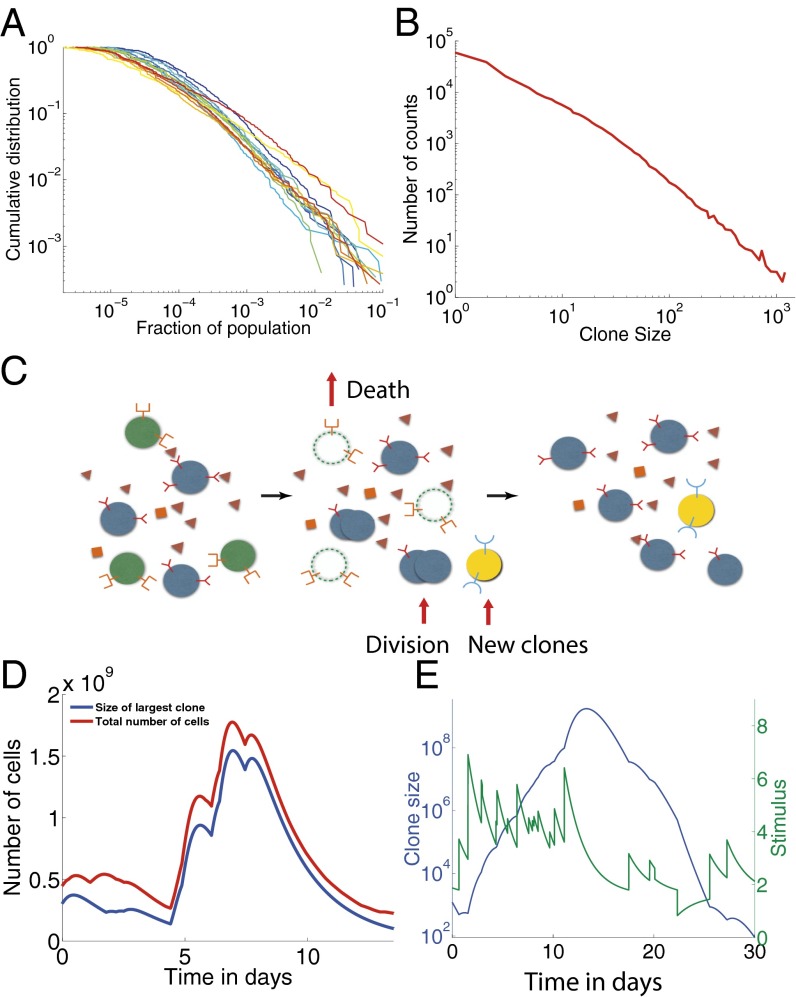
High-throughput sequencing experiments in different cell types and species (2–9) have allowed for the quantification of clone sizes and their distributions (2, 9–11). Previous population dynamics approaches to repertoire evolution have taken great care in precisely modeling these processes for each compartment of the population, through the various mechanisms by which cells grow, die, communicate, and change phenotype (12–17). However, one of the most striking properties of repertoire statistics revealed by high-throughput sequencing is the observation of power laws in clone-size distributions (Fig. 1 A and B), which holds true for various species (human, mice, zebrafish), cell type (B- and T cells), and subsets (naive and memory, CD4 and CD8), and seems to be insensitive to these context-dependent details. It remains unclear, however, what universal features of these dynamics lead to the observed power-law distributions. Here we identify the key biological parameters of the repertoire dynamics that govern its behavior.
Fig. 1.
Experimental clone-size distributions have heavy tails. (A) B-cell zebrafish experimental cumulative clone-size distribution for 14 fish as a function of the fraction of the population occupied by that clone from data in Weinstein et al. (2). (B) Clone-size distribution for murine T cells from Zarnitsyna et al. (11) (data plotted as presented in original paper). (C) The dynamics of adaptive immune cells include specific interactions with antigens that promote division and prevent cell death. New cells are introduced from the thymus or bone marrow with novel, unique receptors. Division, death, and thymic or bone marrow output on average balance each other to create a steady-state population. (D and E) Example trajectories from simulations of the immune cell population dynamics in Eq. 1. The total number of cells (D) shows large variations after an exceptional event of a large pathogenic invasion. One or a few cells that react to that specific antigen grow up to a macroscopic portion of the total population, and then decrease back to normal sizes after the invasion. A typical clone-size trajectory along with its pathogenic stimulation shows the coupling between clone growth and variations of the antigenic environment (E). Parameters used: day−1, , day−1, , day−1, , day−1, and day−1.
The wide range and types of interactions that influence a B- or T-cell fate happen in a complex, dynamical environment with inhomogeneous spatial distributions. They are difficult to measure in vivo, making their quantitative characterization elusive. Motivated by the universality of the observed clone-size distribution, we describe the effective interaction between the immune cells and their environment as a stochastic process governed by only a few relevant parameters. All cells proliferate and die depending on the strength of antigenic and cytokine signals they receive from the environment, which together determine their net growth rate (Fig. 1C). This effective fitness that fluctuates in time is central to our description. We find that its general properties determine the form of the clone-size distribution. We distinguish two broad classes of models, according to whether these fitness fluctuations are clone-specific (mediated by their specific BCR or TCR) or cell-specific (mediated by phenotypic fluctuations such as the number of cytokine receptors). We identify the models that are compatible with the experimentally observed distributions of clone sizes. These distributions do not depend on the detailed mechanisms of cell signaling and growth, but rather emerge as a result of self-organization, with no need for fine-tuned interactions. Performing a series of validated approximations, we find a simple algebraic relationship constraining the different timescales of the problem by the experimentally observed exponent of the clone-size distribution. This result allows for testable predictions and estimates of the rates that govern the diversity of a clonal distribution.
Results
Clone Dynamics in a Fluctuating Antigenic Landscape.
The fate of the cells of the adaptive immune system depends on a variety of clone-specific stimulations. The recognition of pathogens triggers large events of fast clone proliferation followed by a relative decay, with some cells being stored as memory cells to fend off future infections. Naive cells, which have not yet recognized an antigen, do not usually undergo such extreme events of proliferation and death, but their survival relies on short binding events (called “tickling”) to antigens that are natural to the organism (self-proteins) (18, 19). Because receptors are conserved throughout the whole clone (with the exception of B-cell hypermutations), clones that are better at recognizing self-antigens and pathogens will on average grow to larger populations than bad binders. By analogy to Darwinian evolution, they are “fitter” in their local, time-varying environment.
We first present a general model for clonal dynamics that accounts for the characteristics common to all cell types, following previous work by de Boer, Perelson, and collaborators (14, 20, 21). We later explore the effect of specific features such as hypermutations, memory/naive compartmentalization, and thymic output decay on the clone-size distribution.
We denote by the overall concentration of an antigen j as a function of time. We assume that after its introduction at a random time , this concentration decays exponentially with a characteristic lifetime of antigens , as pathogens are cleared out of the organism, either passively or through the action of the immune response. Lymphocyte receptors are specific to certain antigens, but this specificity is degenerate, a phenomenon referred to as cross-reactivity or polyspecificity. The extent to which a lymphocyte expressing receptor i interacts with antigen j (foreign or self) is encoded in the cross-reactivity function , which is zero if i and j do not interact, or a positive number drawn from a distribution to be specified, if they do. In general, interactions between lymphocytes and antigens effectively promote growth and suppress cell death, but for simplicity we can assume that the effect is restricted to the division rate. In a linear approximation, this influence is proportional to , i.e., the combined effect of all antigens j for which clone i is specific. This leads to the following dynamics for the evolution of the size of clone i (Fig. 1C):
| [1] |
where ν and μ are the basal division and death rates, respectively, and where is a birth–death noise of intensity , with a unit Gaussian white noise (see SI Appendix, section A for details about birth–death noise).
New clones, with a small typical initial size , are constantly produced and released into the periphery with rate (Fig. 1C). For example, a number on the order of new T cells is output by the thymus daily in humans (22). Because the total number of T cells is on the order of , this means that the net effect of cell death and proliferation results in a negative average growth rate of days−1 in homeostatic conditions (22). Because the probability of rearranging the exact same receptor independently is very low () (23), we assume that each new clone is unique and comes with its own set of cross-reactivity coefficients . Assuming a rate of new antigens, the average net growth rate in Eq. 1 is , and the stationary number of clones should fluctuate around clones. This is just an average, and treating each clone independently may lead to large variations in the total number of cells (i.e., the sum of sizes of all clones). To maintain a constant population size, clones compete with each other for specific resources (pathogens or self-antigens) and homeostatic control can be maintained by a global resource such as Interleukin 7 or Interleukin 2. Here we do not model this homeostatic control explicitly, but instead assume that the division and death rates are tuned to achieve a given repertoire size. We verified that adding an explicit homeostatic control did not affect our results (SI Appendix, Fig. S2 and SI Appendix, section B).
We simulated the dynamics of a population of clones interacting with a large population of antigens. Each antigen interacts with each present clone with probability , and with strength drawn from a Gaussian distribution of mean 1 and variance 1 (truncated to positive values). Although it has been argued that the breadth of cross-reactivity and affinity to self-antigens are correlated (24, 25), here for simplicity we draw them independently, as we do not expect this correlation to qualitatively affect the results. A typical trajectory of the antigenic stimulation undergone by a given clone, , is shown in Fig. 1E (green curve), and shows how clone growth tracks the variations of the antigenic environment. When the stimulation is particularly strong, the model recapitulates the typical behavior experimentally observed at the population level following a pathogenic invasion (26, 27), as illustrated in Fig. 1D: The population of a clone explodes (red curve), driving the growth of the total population (blue curve), while taking over a large fraction of the carrying capacity of the system, and then decays back as the infection is cleared.
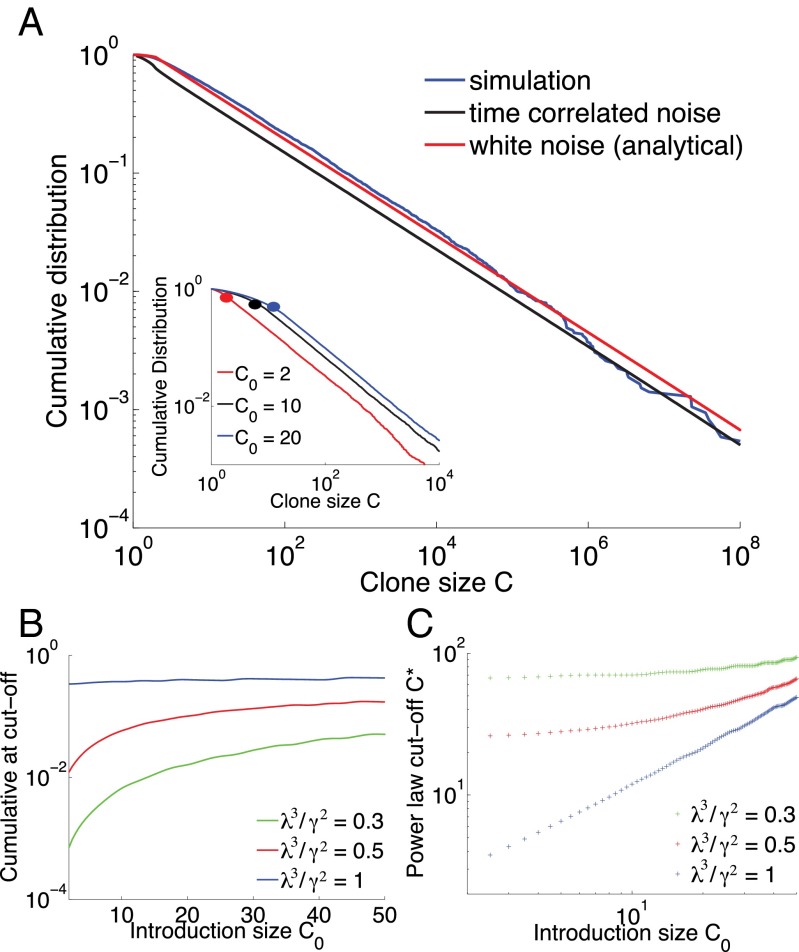
On average, the effects of division and death almost balance each other, with a slight bias toward death because of the turnover imposed by thymic or bone marrow output. However, at a given time, a clone that has high affinity for several present antigens will undergo a transient but rapid growth, whereas most other clones will decay slowly toward extinction. In other words, locally in time, the antigenic environment creates a unique “fitness” for each clone. Because growth is exponential in time, these differential fitnesses can lead to very large differences in clone sizes, even if variability in antigen concentrations or affinities is nominally small. We thus expect to observe large tails in the distribution of clone size. Fig. 2A shows the cumulative probability distribution function (CDF) of clone sizes obtained at steady state (blue curve) showing a clear power-law behavior for large clones, spanning several decades.
Fig. 2.
Clone-size distributions for populations with fluctuating antigenic, clone-specific fitness. (A) Comparison of simulations and simplified models of clone dynamics. Blue curve: cumulative distribution of clone sizes obtained from the simulation of Eq. 1. Black curve: a simplified, numerically solvable model of random clone-specific growth, also predicts a power-law behavior. Red curve: analytical solution for the Gaussian white-noise model, Eq. 4. Parameters used: day−1, day−1, day−1, day−1, , and day−1. (Inset) The exponent is independent of the initial clone size. Results from simulation with different values of the introduction clone size. The cutoff value of the power-law behavior, represented here as a dot, is strongly dependent on the value of . Parameters are day−1, day−1, day−1, day−3/2, and . (B) Value of the CDF at the point of the power-law cutoff as a function of the introduction clone size for different values of a dimensionless parameter related to the effective strength of antigen fluctuations relative to their characteristic lifetime for a fixed power-law exponent α. We use the CDF because it is robust, invariant under multiplicative rescaling of the clone sizes. This way we do not need to correct directly for PCR multiplication or sampling. Parameters for B and C are days−1, days−1, and . (C) Power-law cutoff as a function of the introduction clone size.
The exponent of the power law is independent of the introduction size of clones (Fig. 2A, Inset) and the specifics of the randomness in the environment (exponential decay, random number of partners, random interaction strength) as long as its first and second moment are kept fixed (SI Appendix, Fig. S3 and SI Appendix, section C).
Simplified Models and the Origin of the Power Law.
To understand the power-law behavior observed in the simulations, and its robustness to various parameters and sources of stochasticity, we decompose the overall fitness of a clone at a given time (its instantaneous growth rate) into a constant, clone-independent part equal to its average , and a clone-specific fluctuating part of zero mean, denoted by . This leads to rewriting Eq. 1 as
| [2] |
with .
The function encodes the fluctuations of the environment as experienced by clone i. Because antigens can be recognized by several receptors, these fluctuations may be correlated between clones. Assuming that these correlations are weak, , amounts to treating each clone independently of each other, and thus to reducing the problem to the single clone level. The stochastic process giving rise to is a sum of Poisson-distributed exponentially decaying spikes. This process is not easily amenable to analytical treatment, but we can replace it with a simpler stochastic process with the same temporal autocorrelation function. This autocorrelation is given by , with the antigenic noise strength , and where we recall that is the characteristic lifetime of antigens. The simplest process with the same autocorrelation function is given by an overdamped spring in a thermal bath, or Ornstein–Uhlenbeck process,
| [3] |
with a Gaussian white noise of intensity 1 and quantifies the strength of variability of the antigenic environment (SI Appendix, section D). This is also the process of maximum entropy or caliber (28) with that autocorrelation function (SI Appendix, section E and ref. 29).
The effect of the birth–death noise is negligible compared with the fitness variations for large clones and it has no effect on the tail (SI Appendix, Fig. S5 and SI Appendix, section F). It can thus be ignored when looking at the tail of the distribution and its power-law exponent, but it will play an important role for defining the range over which the power law is satisfied.
The population dynamics described by Eqs. 2 and 3 can be reformulated in terms of a Fokker–Planck equation for the joint abundance ρ of clones of a given log size and a given fitness f:
| [4] |
where the source term describes new clones arriving at rate with size and normally distributed fitnesses of variance . This Fokker–Planck equation can be solved numerically with finite element methods with an absorbing boundary condition at to account for clone extinction. The solution, represented by the black curve in Fig. 2A, matches closely that of the full simulated population dynamics (in blue). The power-law behavior is apparent above a transition point that depends on the distribution of introduction sizes of new clones and the parameters of the model (see below). Intuitively, the microscopic details of the noise are not expected to matter when considering long timescales, as a consequence of the central limit theorem. However, the long tails of the distribution of clone sizes involve rare events and belong to the regime of large deviations, for which these microscopic details may be important. Therefore, the agreement between the process described by the overdamped spring and the exponentially decaying, Poisson-distributed antigens is not guaranteed, and in fact does not hold in all parameter regimes (SI Appendix, Fig. S8).
We can further simplify the properties of the noise by assuming that its autocorrelation time is small compared with other timescales. This leads to taking the limit while keeping their ratio constant, so that is just a Gaussian white noise with (SI Appendix, section F and SI Appendix, Fig. S4). The corresponding Fokker–Planck equation now reads
| [5] |
with . This equation can be solved analytically at steady state, and the resulting clone-size distribution is, for ,
| [6] |
with (details in SI Appendix, section F). The full solution, represented in Fig. 2A in red, captures well the long-tail behavior of the clone-size distribution despite ignoring the temporal correlations of the noise, and approaches the solution of the colored-noise model (Eq. 3) as , as expected (Fig. 2A).
The power-law behavior and its exponent depend on the noise intensity, but are otherwise insensitive to the precise details of the microscopic noise, including its temporal properties. Fat tails (small α) are expected when the average cell lifetime is long (small ) and when the antigenic noise is high (large σ or A). The explicit expression for the exponent of the power law as a function of the biological parameters can be used to infer the antigenic noise strength directly from data. The typical net clone decay rate can be estimated from thymic output and repertoire size, as discussed earlier. The characteristic lifetime of antigens is harder to estimate, as it corresponds to the turnover time of the antigens that the body is exposed to, but is probably on the order of days or a few weeks, day−1. We estimated from the zebrafish data of Fig. 1A (2, 10) using canonical methods of power-law exponent extraction (30) (see SI Appendix, section G for details), and also found a similar value in human T cells (31). The resulting estimate, day−1, is rather striking, as it implies that fluctuations in the net clone growth rate, A, are much larger than its average .
Whereas the distribution always exhibits a power law for large clones, this behavior does not extend to clones of arbitrarily small sizes, where the details of the noise and how new clones are introduced matter. We define a power-law cutoff as the smallest clone size for which the cumulative distribution function differs from its best power-law fit by less than . Using numerical solutions to the Fokker–Planck equation associated with the colored-noise model, we can draw a map of as a function of the parameters of the system. In Fig. 2 B and C we show how varies as a function of the introduction size for different values of the dimensionless parameter related to the effective strength of antigen fluctuations relative to their characteristic lifetime at fixed power-law exponents. In principle, one can use this dependency to infer effective parameters from data. In practice, when dealing with data it is more convenient to consider the value of the cumulative distribution at , rather than itself. For example, fixing and fitting the curve of Fig. 1A with our simplified model using λ as an adjustable parameter, we obtain day−1 (SI Appendix, section G), which corresponds to a characteristic lifetime of antigens of around a week. Although this estimate must be taken with care, because of possible PCR amplification biases plaguing the small clone size end of the distribution, the procedure described here can be applied generally to any future repertoire sequencing dataset for which reliable sequence counts are available.
A Model of Fluctuating Phenotypic Fitness.
So far, we have assumed that fitness fluctuations are identical for all members of a same clone. However, the division and death of lymphocytes do not only depend on signaling through their TCR or BCR. For example, cytokines are also growth inducers and homeostatic agents (32, 33), and the ability to bind to cytokines depends on single-cell properties such as the number of cytokine receptors on the membrane of a given cell, independent of their BCR or TCR. Other stochastic single-cell factors may affect cell division and death. These signals and factors are cell-specific, as opposed to the clone-specific properties related to BCR or TCR binding. Together, they define a global phenotypic state of the cell that determines its time-varying fitness, independent of the clone and its TCR or BCR. This does not mean that these phenotypic fitness fluctuations are independent across the cells belonging to the same clone. Cells within a clone share a common ancestry, and may have inherited some phenotypic properties of their common ancestors, making their fitnesses effectively correlated with each other. However, this phenotypic memory gets lost over time, unlike fitness effects mediated by antigen-specific receptors.
We account for these phenotypic fitness fluctuations by a function quantifying how much the fitness of an individual cell c differs from the average fitness . This fitness difference is assumed to be partially heritable, which we model by
| [7] |
where is the heritability, or the typical time over which the fitness-determining trait is inherited, quantifies the variability of the fitness trait, and is a cell-specific Gaussian white noise of power 1. Despite its formal equivalence with Eq. 3, it is important to note that here the fitness dynamics occurs at the level of the single cell (and its offspring) instead of the entire clone. The dynamics of the fitness of a given clone i can be approximated from Eq. 7 by averaging the fitnesses of cells in that clone, yielding
| [8] |
| [9] |
where and are clone-specific white noise of intensity 1, and ν and μ are the average birth and death rates, respectively, so that (details in SI Appendix, section I). The difference with Eq. 3 is the prefactor in the fitness noise , which stems from the averaging of that noise over all cells in the clone, by virtue of the law of large numbers. Because of this prefactor, the fitness noise is now of the same order of magnitude as the birth–death noise, which must now be fully taken into account. Taking Eqs. 8 and 9 at the population level gives a Fokker–Planck equation with a source term accounting for the import of new clones. We verify the numerical steady-state Fokker–Planck solution against Gillespie simulations (SI Appendix, Fig. S6; see SI Appendix, section H for details).
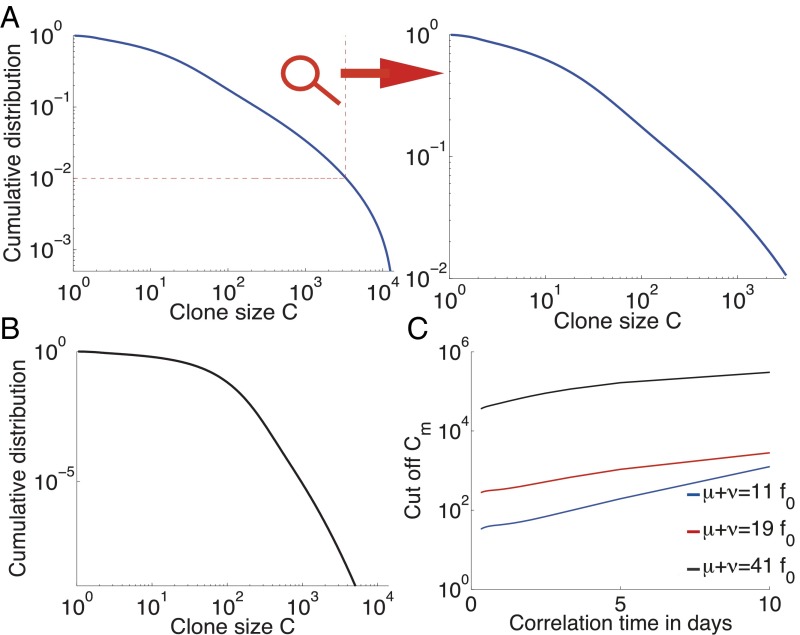
Fig. 3 A and B shows the distribution of clone sizes for different values of the phenotypic relaxation rate and environment amplitude . These distributions vary from a sharp exponential drop in the case of low heritability (large ) to heavier tails in the case of long conserved cell states (small ). To quantify the extent to which these distributions can be described as heavy-tailed, we fit them to a power law with exponential cutoff, , where is the value below which the distribution could be interpreted as an (imperfect) power law. Fig. 3C shows a strong dependency of this cutoff with the phenotypic memory . The longer the phenotypic memory , the more clone-specific the fitness looks, and the more the distribution can be mistaken for a power law in a finite-size experimental distribution. Larger birth–death noise also extends the range of validity of the power law. As a result, and despite the absence of a true power-law behavior, these models of fluctuating phenotypic fitnesses cannot be discarded based on current experimental data.
Fig. 3.
Clone-size distributions for populations with a cell-specific fluctuating phenotypic fitness. (A) Cumulative distribution of clone sizes for moderate phenotypic heritability (). The distribution is power-law–like for small clone values and drops above a cutoff around 0.01 of clone-size probability. An experiment that does not sequence the repertoire deeply enough could report a power-law behavior (see zoom). Parameters are days−1, day−1, days−1, and days−3/2. for all three graphs. (B) An example of a distribution of clone sizes from a cell-specific model with very low environmental noise, close to the pure birth–death limit. The distribution is flat () and then drops exponentially. It does not resemble experimental data. Parameters are days−1, days−1, days−1, and days−3/2. (C) Value of the cumulative distribution at the exponential cutoff as a function of the speed of environment variations , for different birth–death noise levels. Parameters are days−1 and .
The model can be solved exactly at the two extremes of the heritability parameter . In the limit of infinite heritability () the system is governed by selective sweeps. The clone with the largest fitness completely dominates the population, until it is replaced by a better one, giving rise to a trivial clone-size distribution. In the opposite limit, when heritability goes to 0 (), the Fokker–Planck equation can be solved analytically (SI Appendix, sections I and J), yielding an exact power law with exponential cutoff, , with and . The numerical solution of Fig. 3B is close to this limit. Note that even with a negligible exponential cutoff, the predicted contradicts experimental observations.
Discussion
The model introduced in this paper describes the stochastic nature of the immune dynamics with a minimal number of parameters, helping interpret the different regimes. These parameters are effective in the sense that they integrate different levels of signaling, pathways, and mechanisms, focusing on the long timescales of clone dynamics. We assumed that they are general enough that different cell types (B- and T cells) or subsets (naive or memory) can be described by the same dynamical equations despite their differences. How do refined models including these differences affect our results?
Naive and memory cells differ in their turnover rate, i.e., their death rate, memory cells being renewed at a pace 10 times faster than naive ones (34). In our model, this difference is reflected in a higher birth–death noise for memory cells. We have shown that this noise had no effect on the tail of the clone-size distribution for clone-specific fitness (SI Appendix, Fig. S5), whereas it was important for the case of a cell-specific fitness, where birth–death noise contributed to the distribution to the same extent as fitness fluctuations. However, some repertoire datasets mix both naive and memory sets, and one could wonder whether our results hold for such mixtures. To examine this question, we simulated a simple two-compartment model where naive cells get irreversibly converted into memory cells when their stimulation is above a certain threshold (see SI Appendix, section K for details). We found that when fitness was clone-specific, the clone-size distribution of the mixture and that of memory cells alone still follow a power law, whereas that of naive cells only does so when conversion to memory upon stimulation is partial (SI Appendix, Fig. S12). Repeating the same analysis for the cell-specific fitness model, we found that clone-size distributions for each phenotype differed according to their respective birth–death noises, with a longer tail for memory cells as expected from their higher turnover rate.
The main difference between B- and T cells ignored by our model is that BCRs accumulate hypermutations upon proliferation. We studied this effect by allowing proliferating clones to spawn new clones with slightly modified affinities to antigens (SI Appendix, section L). The resulting clone-size distribution still follows a power law (SI Appendix, Fig. S13), although with a slightly smaller exponent due to increased stochasticity.
Another simplifying assumption of our model is that the dynamics reaches a steady state. This may be challenged by the decay of the thymic output with age. To estimate the importance of this effect, we simulated the model of a clone-specific fitness with an exponentially decaying source term, combined with a decreasing chosen to keep the population constant on average (SI Appendix, section M). The clone-size distributions at different points in time, shown in SI Appendix, Fig. S14, still follow a power law. Interestingly, the exponent α is predicted to decrease with age, consistent with .
We showed that the relevant sources of stochasticity for the shape of the clone-size distributions fall into two main categories, depending on how cell fate is affected by the environment. Either the stochastic elements of clone growth act in a clone-specific way, through their receptor (BCR or TCR), leading to power-law distributions with exponent , or in a cell-specific way, e.g., through their variable level of sensitivity to cytokines (and more generally through any phenotypic trait affecting cell fitness), leading to exponentially decaying distributions with a power-law prefactor. These two types of signals (clone-specific and cell-specific) are important for the somatic evolution of the immune system (21, 32, 33, 35–37) and our analysis shows that the shape of the clone-size distribution is informative of their relative importance to the repertoire dynamics. It provides a first theoretical setting and an initial systematic classification for modeling immune repertoire dynamics. Our method applied to high-throughput sequencing data can be used to quantify how much each type of signal contributes to the overall dynamics, and what is the driving force for the different cell subsets. For example, although it is reasonable to speculate that clone-specific signals should dominate for memory cells (through antigen recognition), and cell-specific selection for naive cells (through cytokine-mediated homeostatic division), the relative importance of these signals for both cell types is yet to be precisely quantified, and may vary across species. A clear power law over several decades would strongly hint at dynamics dominated by interactions with antigens, whereas a faster decaying distribution would favor a scenario where individual cell fitness fluctuations dominate. Applying these methods to data from memory cells can give orders of magnitude for the division and half-life of memory lymphocytes, as well as the typical number of cells from a clone that are stored as memory following an infection.
The application of our method to data from the first immune repertoire survey [BCRs in zebrafish (2)] suggests that clone-specific noise dominates in that case, allowing us to infer a relation between the dynamical parameters of the model from the observed power-law exponent . However, there are a few issues with applying our method directly to data in the current state of the experiments. First, the counts (i.e., how many cells have the same receptor sequence and belong to the same clone) from many high-throughput repertoire sequencing experiments are imperfect because of PCR bias and sampling problems. New methods using single-molecule barcoding have been developed for RNA sequencing (8, 38, 39), but they do not solve the problem entirely, as the number of expressed mRNA molecules may not faithfully represent the cell numbers because of possible expression bias. In addition, most studies (with the exception of ref. 40) have been sequencing only one of the two chains of lymphocyte receptors, which is insufficient to determine clone identity unambiguously. As methods improve, however, our model can be applied to future data to distinguish different sources of fitness stochasticity and to put reliable constraints on biological parameters. Studying clone-size distributions in healthy individuals allows us to characterize signatures of normally functioning immune systems. By comparing them to the same properties in individuals suffering from immune diseases or cancer, our approach could be used to identify sources of anomalies.
Thanks to its generality, our model is also relevant beyond its immunological context, and follows previous attempts to explain power laws in other fields (41–43). The dynamics described here corresponds to a generalization of the neutral model of population genetics (44) where thymic or bone marrow outputs are now reinterpreted as new mutations or speciations, and where we have added a genotypic or phenotypic fitness noise (receptor or cell-specific noise, respectively). It was recently shown that such genotypic fitness noise strongly affects the fixation probability and time in a population of two alleles (45, 46). Note that, because new thymic or bone marrow clones are unrelated to existing clones, there are no lineage histories, in contrast with previous theoretical work on evolving populations in fluctuating fitness landscapes (47–49). Our main result (Eq. 6) shows how fitness noise can cause the clone-size distribution (called “frequency spectrum” in the context of population genetics) to follow a power law with an arbitrary exponent in a population of fixed size, whereas the classical neutral model gives a power law of exponent 1 with an exponential cutoff (as shown in our exact solution with ). Our results can be used to explain complex allele frequency spectra using fluctuating fitness landscapes.
Supplementary Material
Acknowledgments
This work was supported in part by Grant ERCStG 306312.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1512977112/-/DCSupplemental.
References
- 1.Janeway C. Immunobiology. Garland Science; New York: 2005. [Google Scholar]
- 2.Weinstein JA, Jiang N, White RA, 3rd, Fisher DS, Quake SR. High-throughput sequencing of the zebrafish antibody repertoire. Science. 2009;324(5928):807–810. doi: 10.1126/science.1170020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ndifon W, et al. Chromatin conformation governs T-cell receptor Jβ gene segment usage. Proc Natl Acad Sci USA. 2012;109(39):15865–15870. doi: 10.1073/pnas.1203916109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Thomas N, et al. Tracking global changes induced in the CD4 T cell receptor repertoire by immunization with a complex antigen using short stretches of CDR3 protein sequence. Bioinformatics. 2014;30(22):3181–3188. doi: 10.1093/bioinformatics/btu523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Larimore K, McCormick MW, Robins HS, Greenberg PD. Shaping of human germline IgH repertoires revealed by deep sequencing. J Immunol. 2012;189(6):3221–3230. doi: 10.4049/jimmunol.1201303. [DOI] [PubMed] [Google Scholar]
- 6.Sherwood AM, et al. Deep sequencing of the human TCR and TCR repertoires suggests that TCR rearranges after and T cell commitment. Sci Transl Med. 2011;3(90):90ra61. doi: 10.1126/scitranslmed.3002536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Robins HS, et al. Comprehensive assessment of T-cell receptor beta-chain diversity in alphabeta T cells. Blood. 2009;114(19):4099–4107. doi: 10.1182/blood-2009-04-217604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zvyagin IV, et al. Distinctive properties of identical twins’ TCR repertoires revealed by high-throughput sequencing. Proc Natl Acad Sci USA. 2014;111(16):5980–5985. doi: 10.1073/pnas.1319389111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Warren RL, et al. Exhaustive T-cell repertoire sequencing of human peripheral blood samples reveals signatures of antigen selection and a directly measured repertoire size of at least 1 million clonotypes. Genome Res. 2011;21(5):790–797. doi: 10.1101/gr.115428.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mora T, Walczak AM, Bialek W, Callan CG., Jr Maximum entropy models for antibody diversity. Proc Natl Acad Sci USA. 2010;107(12):5405–5410. doi: 10.1073/pnas.1001705107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zarnitsyna VI, Evavold BD, Schoettle LN, Blattman JN, Antia R. Estimating the diversity, completeness, and cross-reactivity of the T cell repertoire. Front Immunol. 2013;4:485. doi: 10.3389/fimmu.2013.00485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Stirk ER, Lythe G, van den Berg HA, Molina-París C. Stochastic competitive exclusion in the maintenance of the naïve T cell repertoire. J Theor Biol. 2010;265(3):396–410. doi: 10.1016/j.jtbi.2010.05.004. [DOI] [PubMed] [Google Scholar]
- 13.Stirk ER, Molina-París C, van den Berg HA. Stochastic niche structure and diversity maintenance in the T cell repertoire. J Theor Biol. 2008;255(2):237–249. doi: 10.1016/j.jtbi.2008.07.017. [DOI] [PubMed] [Google Scholar]
- 14.de Boer RJ, Freitas AA, Perelson AS. Resource competition determines selection of B cell repertoires. J Theor Biol. 2001;212(3):333–343. doi: 10.1006/jtbi.2001.2379. [DOI] [PubMed] [Google Scholar]
- 15.Almeida ARM, et al. Quorum-sensing in CD4(+) T cell homeostasis: A hypothesis and a model. Front Immunol. 2012;3:125. doi: 10.3389/fimmu.2012.00125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hapuarachchi T, Lewis J, Callard RE. A mechanistic model for naive CD4 T cell homeostasis in healthy adults and children. Front Immunol. 2013;4:366. doi: 10.3389/fimmu.2013.00366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Reynolds J, Coles M, Lythe G, Molina-París C. Deterministic and stochastic naïve T cell population dynamics: Symmetric and asymmetric cell division. Dyn Syst. 2012;27:75–103. [Google Scholar]
- 18.Troy AE, Shen H. Cutting edge: Homeostatic proliferation of peripheral T lymphocytes is regulated by clonal competition. J Immunol. 2003;170:672–676. doi: 10.4049/jimmunol.170.2.672. [DOI] [PubMed] [Google Scholar]
- 19.Mak T, Saunders M. The Immune Response: Basic and Clinical Principles. Vol 1 Elsevier/Academic; San Diego: 2006. [Google Scholar]
- 20.de Boer RJ, Perelson AS. T cell repertoires and competitive exclusion. J Theor Biol. 1994;169(4):375–390. doi: 10.1006/jtbi.1994.1160. [DOI] [PubMed] [Google Scholar]
- 21.Freitas AA, Rosado MM, Viale AC, Grandien A. The role of cellular competition in B cell survival and selection of B cell repertoires. Eur J Immunol. 1995;25(6):1729–1738. doi: 10.1002/eji.1830250636. [DOI] [PubMed] [Google Scholar]
- 22.Bains I, Antia R, Callard R, Yates AJ. Quantifying the development of the peripheral naive CD4+ T-cell pool in humans. Blood. 2009;113(22):5480–5487. doi: 10.1182/blood-2008-10-184184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Murugan A, Mora T, Walczak AM, Callan CG., Jr Statistical inference of the generation probability of T-cell receptors from sequence repertoires. Proc Natl Acad Sci USA. 2012;109(40):16161–16166. doi: 10.1073/pnas.1212755109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kosmrlj A, Jha AK, Huseby ES, Kardar M, Chakraborty AK. How the thymus designs antigen-specific and self-tolerant T cell receptor sequences. Proc Natl Acad Sci USA. 2008;105(43):16671–16676. doi: 10.1073/pnas.0808081105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kosmrlj A, et al. Effects of thymic selection of the T-cell repertoire on HLA class I-associated control of HIV infection. Nature. 2010;465(7296):350–354. doi: 10.1038/nature08997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Murali-Krishna K, et al. Counting antigen-specific CD8 T cells: A reevaluation of bystander activation during viral infection. Immunity. 1998;8(2):177–187. doi: 10.1016/s1074-7613(00)80470-7. [DOI] [PubMed] [Google Scholar]
- 27.Kaech SM, Wherry EJ, Ahmed R. Effector and memory T-cell differentiation: implications for vaccine development. Nat Rev Immunol. 2002;2(4):251–262. doi: 10.1038/nri778. [DOI] [PubMed] [Google Scholar]
- 28.Pressé S, Ghosh K, Lee J, Dill KA. Principles of maximum entropy and maximum caliber in statistical physics. Rev Mod Phys. 2013;85:1115–1141. [Google Scholar]
- 29.Cavagna A, et al. Dynamical maximum entropy approach to flocking. Phys Rev E Stat Nonlin Soft Matter Phys. 2014;89(4):042707. doi: 10.1103/PhysRevE.89.042707. [DOI] [PubMed] [Google Scholar]
- 30.Clauset A, Shalizi CR, Newman MJ. Power-law distributions in empirical data. SIAM Rev. 2009;51:661–703. [Google Scholar]
- 31.Bolkhovskaya OV, Zorin DY, Ivanchenko MV. Assessing T cell clonal size distribution: A non-parametric approach. PLoS One. 2014;9(9):e108658. doi: 10.1371/journal.pone.0108658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Schluns KS, Kieper WC, Jameson SC, Lefrançois L. Interleukin-7 mediates the homeostasis of naïve and memory CD8 T cells in vivo. Nat Immunol. 2000;1(5):426–432. doi: 10.1038/80868. [DOI] [PubMed] [Google Scholar]
- 33.Tan JT, et al. IL-7 is critical for homeostatic proliferation and survival of naive T cells. Proc Natl Acad Sci USA. 2001;98(15):8732–8737. doi: 10.1073/pnas.161126098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.de Boer RJ, Perelson AS. Quantifying T lymphocyte turnover. J Theor Biol. 2013;327:45–87. doi: 10.1016/j.jtbi.2012.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Seddon B, Zamoyska R. TCR signals mediated by Src family kinases are essential for the survival of naive T cells. J Immunol. 2002;169(6):2997–3005. doi: 10.4049/jimmunol.169.6.2997. [DOI] [PubMed] [Google Scholar]
- 36.Tanchot C, Lemonnier FA, Pérarnau B, Freitas AA, Rocha B. Differential requirements for survival and proliferation of CD8 naïve or memory T cells. Science. 1997;276(5321):2057–2062. doi: 10.1126/science.276.5321.2057. [DOI] [PubMed] [Google Scholar]
- 37.Nesić D, Vukmanović S. MHC class I is required for peripheral accumulation of CD8+ thymic emigrants. J Immunol. 1998;160(8):3705–3712. [PubMed] [Google Scholar]
- 38.Best K, Oakes T, Heather JM, Taylor JS, Chain B. 2014. Sequence and primer independent stochastic heterogeneity in PCR amplification efficiency revealed by single molecule barcoding. bioRxiv. Available at dx.doi.org/10.1101/011411.
- 39.Vollmers C, Sit RV, Weinstein JA, Dekker CL, Quake SR. Genetic measurement of memory B-cell recall using antibody repertoire sequencing. Proc Natl Acad Sci USA. 2013;110(33):13463–13468. doi: 10.1073/pnas.1312146110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.DeKosky BJ, et al. In-depth determination and analysis of the human paired heavy- and light-chain antibody repertoire. Nat Med. 2015;21(1):86–91. doi: 10.1038/nm.3743. [DOI] [PubMed] [Google Scholar]
- 41.Sornette D, Cont R. Convergent multiplicative processes repelled from zero: Power laws and truncated power laws. Journal de Physique I, EDP Sciences. 1997;7(3):431–434. [Google Scholar]
- 42.Marsili M, Maslov S, Zhang YC. Dynamical optimization theory of a diversified portfolio. Physica A. 1998;253:9. [Google Scholar]
- 43.Mitzenmacher M. A brief history of generative models for power law and lognormal distributions. Internet Math. 2004;1:226–251. [Google Scholar]
- 44.Kimura M. The Neutral Theory of Molecular Evolution. University Press; New York: 1983. [Google Scholar]
- 45.Cvijović I, Good BH, Jerison ER, Desai MM. The Fate of a Mutation in a Fluctuating Environment. 2015. preprint. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Melbinger A, Vergassola M. The impact of environmental fluctuations on evolutionary fitness functions. Scientific Reports. 2015;5:15211. doi: 10.1038/srep15211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Leibler S, Kussell E. Individual histories and selection in heterogeneous populations. Proc Natl Acad Sci USA. 2010;107(29):13183–13188. doi: 10.1073/pnas.0912538107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Mustonen V, Lässig M. Fitness flux and ubiquity of adaptive evolution. Proc Natl Acad Sci USA. 2010;107(9):4248–4253. doi: 10.1073/pnas.0907953107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Rivoire O, Leibler S. A model for the generation and transmission of variations in evolution. Proc Natl Acad Sci USA. 2014;111(19):E1940–E1949. doi: 10.1073/pnas.1323901111. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.