Slot-Mode Optomechanical Crystals: A Versatile Platform for Multimode Optomechanics

Abstract

Cavity optomechanical systems are being studied for their potential in areas such as metrology, communications, and quantum information science. For a number of recently proposed applications in which multiple optical and mechanical modes interact, an outstanding challenge is to develop multimode architectures that allow flexibility in the optical and mechanical sub-system designs while maintaining the strong interactions that have been demonstrated in single-mode systems. To that end, we demonstrate slot-mode optomechanical crystals, devices in which photonic and phononic crystal nanobeams separated by a narrow slot are coupled via optomechanical interactions. These nanobeam pairs are patterned to confine a mechanical breathing mode at the center of one beam and a low-loss optical mode in the slot between the beams. This architecture affords great design flexibility towards multimode optomechanics, as well as substantial optomechanical coupling rates. We show this by producing slot-mode devices in stoichiometric Si₃N₄, with optical modes in the 980 nm band coupled to mechanical modes at 3.4 GHz, 1.8 GHz, and 400 MHz. We exploit the Si₃N₄ tensile stress to achieve slot widths down to 24 nm, which leads to enhanced optomechanical coupling, sufficient for the observation of optomechanical self-oscillations at all studied frequencies. We then develop multimode optomechanical systems with triple-beam geometries, in which two optical modes couple to a single mechanical mode, and two mechanical modes couple to a single optical mode. Taken together, these results demonstrate great flexibility in the design of multimode chip-scale optomechanical systems with large optomechanical coupling.

I. INTRODUCTION

Sideband-resolved cavity optomechanical systems have recently demonstrated their potential in a wide variety of applications, including motion sensing [1, 2], ground state cooling [3, 4], and optomechanically-induced transparency [5, 6]. For these applications, high efficiency requires large optomechanical coupling strength in addition to sideband resolution (mechanical frequency ≫ optical linewidth). Additional phenomena have been observed in multimode cavity optomechanical systems, in which multiple optical and/or mechanical modes interact, including wavelength conversion [7–9], Raman-ratio thermometry [10], energy transfer between mechanical modes [11], and optomechanical mode mixing [12]. Phonon pair generation [13], mechanical mode entanglement [12, 14, 15], and unresolved sideband cooling [16] have also been theoretically proposed. In all these systems, improved performance and broader applicability could be achieved if the optical and mechanical modes could be independently tailored to a given application.

The slot-mode optomechanical crystal structure, in which optical and mechanical modes are confined in separate interacting beams (Fig. 1), is one way to achieve this flexibility while maintaining large optomechanical coupling strength. Simulations [17] show that, in systems in which the optomechanical interaction is dominated by moving boundaries, this geometry can significantly increase the optomechanical coupling strength relative to single nanobeam optomechanical crystals. It also provides the desired design flexibility to enable multimode applications such as optomechanical wavelength conversion.

FIG. 1.

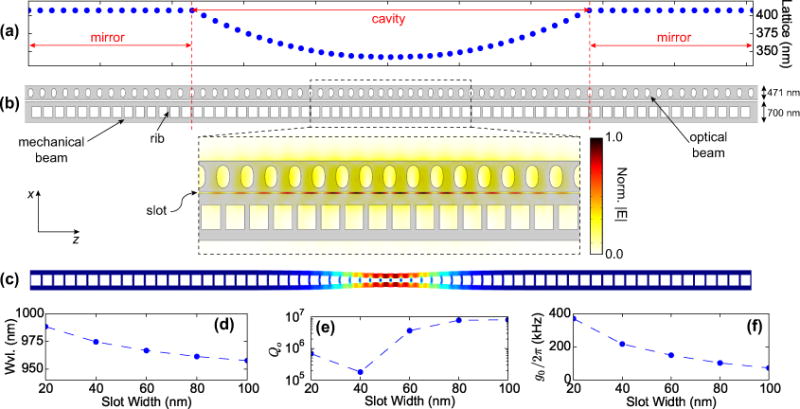
(a) Variation of the optomechanical crystal lattice constant along the length of the beams. The period is fixed in the mirror regions at the beam ends and varies quadratically in the center cavity region. (b) The slot mode optomechanical crystal is formed by parallel optical and mechanical beams that are separated by a narrow slot. The zoomed-in image of the center shows the finite element method (FEM) simulated electric field amplitude of the optical slot mode around 980 nm. (c) FEM simulation of the breathing mode of the mechanical beam (around 3.4 GHz). (d), (e), and (f): The width of the slot is varied in an FEM simulation of the (d) resonant wavelength, (e) optical quality factor (Q_o), and (f) optomechanical coupling g₀/(2π).

In this work, we experimentally demonstrate slot-mode optomechanical crystals implemented in stoichiometric Si₃N₄, a material whose broad optical transparency and large intrinsic tensile stress make it attractive for many applications. In Sec. III, we show how this intrinsic stress can be exploited to achieve slots with aspect ratios of 10:1, and in Sec. IV we demonstrate how tuning this slot width improves device performance in 3.4 GHz band devices. Sec. V shows how the mechanical mode frequency can be changed while minimally affecting the optical mode, with demonstrations of 1.8 GHz and 400 MHz band devices. Finally, in Sec. VI, we extend the slotmode optomechanical crystal concept to multimode optomechanical devices, in which two mechanical modes couple to a single optical mode, and two optical modes couple to a single mechanical mode.

II. BASIC DEVICE DESIGN

A slot-mode optomechanical crystal, shown in Fig. 1b, consists of two parallel beams separated by a narrow slot. The “optical beam” is a photonic crystal cavity designed to confine the optical mode in the slot. The “mechanical beam” is a phononic crystal resonator optimized to confine the mechanical breathing mode (Fig. 1c) while maintaining low optical loss. Both the optical and mechanical modes are confined along the z-axis by periodic patterning of holes. In the outer mirror region, the lattice spacing is constant, but it varies quadratically in the cavity region (Fig. 1a). Details on the design of this device are outlined in Ref. [17]. The devices in this work were designed for optical modes around 980 nm and mechanical breathing modes around 3.4 GHz. The optical beam is patterned with identical elliptical holes (188 nm×330 nm) along its length, while the mechanical beam holes have a constant height (370 nm) and widths that are varied such that the “ribs” between the holes align with the elliptical holes in the optical beam.

There have been several demonstrations of sideband-resolved single-nanobeam optomechanical crystals [4, 6, 7, 18, 19], in which a GHz frequency mechanical breathing mode is coupled to an optical mode localized by the same physical structure. These geometries are distinguished by the breathing mode’s high frequency (enabling sideband resolution), isolation from mechanical supports due to the phononic mirrors, and strong interaction with the optical mode. Our goal in this work is to retain these advantageous features while increasing the system’s versatility through the slot mode geometry.

Optical slot modes have been utilized before to achieve large optomechanical coupling in microrings/disks [20, 21], bilayer photonic crystal slabs [22], and photonic crystal zipper cavities [23]. These applications were lower frequency (< 150 MHz) than the 3.4 GHz band breathing modes in this work, and, thus operated in the unresolved-sideband regime (mechanical frequency < optical linewidth). In addition, previous demonstrations have not taken full advantage of the flexibility of the slot mode architecture, as the mechanical and optical modes were supported by the same structural components. Separating the optical and mechanical modes into two beams enables independent design of these modes. This opens a wide range of frequency combinations that would be difficult to access with a single optomechanical structure. The slot-mode structure also opens the possibility for additional interactions with both modes, which can be separately accessed from the beam sides opposite the slot. For example, electrodes could be added to the outside of the mechanical beam with minimal perturbation of the optical mode. Adding more optical or mechanical beams, thereby forming more slots, can also increase the device functionality by realizing multimode optomechanical systems, as discussed in Secs. VI and VII.

III. STRESS TUNING AND DEVICE FABRICATION

In addition to the design of the mechanical and optical beams, device parameters are also strongly dependent on the width of the slot between the two beams, simulated in Fig. 1d–f. Given a device with fixed design of the optical and mechanical beams, reducing the slot width red-shifts the optical resonance, and reduces Q_o somewhat (still above 10⁵). The optomechanical coupling rate g₀ increases significantly as the slot width decreases, so the slot between the optical and mechanical beams should be made as small as possible. Lithographically defining small spaces and etching high-aspect-ratio trenches are both challenging in fabrication. This can be mitigated by taking advantage of the intrinsic film stress of stoichiometric Si₃N₄ (≈ 1 GPa). An asymmetric anchoring condition in a doubly-clamped beam induces asymmetry in the stress, thereby causing it to move laterally. Long, thin tethers asymmetrically attached to the ends of parallel nanobeams have been used to shrink gaps to as small as 40 nm after release [24]. To achieve the same effect, we investigated small slits at a beam’s ends (Fig. 2a). Finite element method (FEM) simulations show that varying the width and depth of these slits controls the lateral displacement of the center of the beam (Fig. 2b). In the slot-mode device, a large initially defined and etched slot would be reduced post-release to the desired width by including these stress-tuning slits at the ends of the optical beam.

FIG. 2.

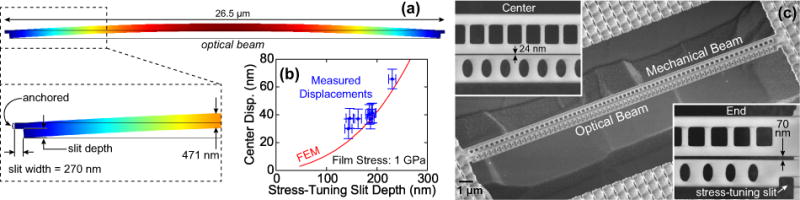
(a) FEM simulation of a tensile-stressed beam with stress-tuning slits at the ends. (b) Displacement at beam center with respect to slit depth. FEM results (line) are for a beam with the same dimensions as the optical beam of the slot-mode device. Error bars on the measured data are due to the uncertainty in the SEM measurements and are one standard deviation values. (c) Scanning electron microscope (SEM) images of a released device. Insets show the slot width at the beam end is about 70 nm, shrinking to 24 nm at the beam center.

Slot mode optomechanical crystal nanobeams were fabricated in 250 nm thick stoichiometric Si₃N₄ deposited via low-pressure chemical-vapor deposition on a bare Si substrate (tensile stress ≈ 1 GPa). Devices were patterned via electron-beam (E-beam) lithography in a positive E-beam resist and developed in hexyl acetate at 7 °C. The pattern was transferred to the Si₃N₄ using a CF₄/CHF₃ reactive ion etch. Devices were released in a 45 % KOH solution at 75 °C followed by a dip in a 1:4 HCl:H₂O solution. Finally, the devices were dried on a hotplate.

A scanning-electron microscope (SEM) image of a released device is shown in Fig. 2c. The lithographically-defined slots were between 80 nm and 120 nm, and, with the SEM, we measured stress-tuned slots as small as 24 nm at the center, an aspect ratio of about 10:1 that would be difficult to achieve with lithography alone. Fig. 2b graphs the SEM-measured displacements of the beam centers with respect to the stress-tuning slit depths. The measured trend matches well with the displacements predicted in the FEM simulations.

IV. DEMONSTRATION OF SLOT-MODE CONCEPT

The experimental setup used to characterized the Si₃N₄ slot-mode optomechanical crystals is shown in Fig. 3a, and was previously described in [18]. All measurements were taken at room temperature and pressure. Devices were characterized with a 980 nm external cavity tunable diode laser, which was coupled evanescently to the devices via a dimpled optical fiber taper waveguide (FTW) with a minimum diameter of ≈ 1 μm.

FIG. 3.

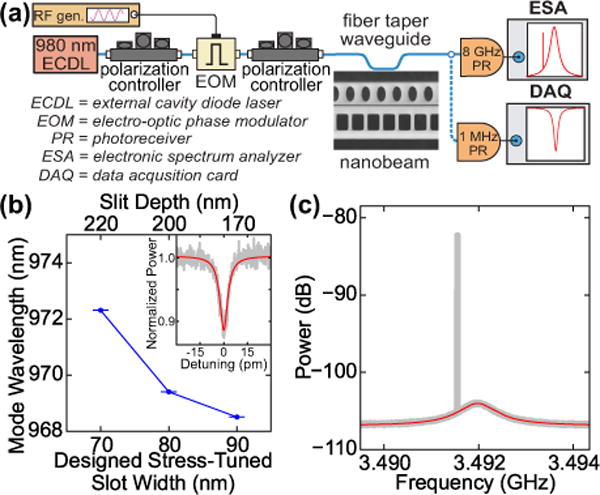
(a) Optical modes are detected by swept-wavelength spectroscopy, while mechanical modes are measured when the laser is on the blue-detuned shoulder of the optical mode. For g₀ calibration, the laser is phase-modulated. (b) Optical resonant wavelength of three devices with different stress-tuned slot widths. (inset) Optical spectrum and fit of highest measured Q_o among these devices, having designed gap of 50 nm and Q_o = (1.65 ± 0.09) × 10⁵ [25] (c) Example mechanical spectrum, including phase modulator calibration peak. This power spectral density plot is referenced to a power of 1 mW = 0 dB. Lorentzian fit of thermal noise spectrum is in red.

Among the measured devices, a device with a 50 nm stress-tuned slot had the highest intrinsic optical quality factor Q_o at (1.65 ± 0.09) × 10⁵ (linewidth of 2.0 GHz ± 0.1 GHz) [25], as shown in Fig. 3b. Q_os up to ≈ 2.4 times higher have been demonstrated in Si₃N₄ single-nanobeam optomechanical crystals [26], but it is expected that the slot mode would have lower Q_os because the geometry has more scattering sites near the optical mode. In these devices, narrower slots generally resulted in lower Q_os, with 20 nm slot devices having the lowest Q_os around 2.5 × 10⁴. With further optimization, improving Q_o in smaller slot designs is feasible.

We also used optical characterization to more precisely determine the effect of the stress tuning. Iterations of devices were made with the same optical and mechanical design but stress-tuning slits of varying depth, so that the only difference among these devices would be the final, stress-tuned slot width. An example is shown in Fig. 3b. Three devices with the same optical and mechanical design show a red shift of the optical resonance as the designed stress-tuned slot width decreases (the stress-tuning slit depth increases). This trend is expected from simulation (Fig. 1d), and was consistent in 24 of 27 unique device designs, indicating that varying this stress-tuning slit depth is a reliable technique for tuning the slot width.

For mechanical mode spectroscopy, the signal was detected with a high-bandwidth (8 GHz) photoreceiver, the output of which was sent to a real-time electronic spectrum analyzer. Optomechanical characterization required longer-term stability of the coupling, so the FTW was positioned a few hundred nanometers to the side of the device and affixed via van der Waals forces to nearby protruding parts of the Si₃N₄ film. The coupling distance was chosen for a transmission minimum around 70 %. The blue detuning of the laser further increased the measurement stability by enabling access to the thermally self-stable regime [28] so that the laser did not have to be externally locked to the cavity.

We used a calibration signal from a phase modulator to measure g₀ in a few devices [29, 30], as shown in Fig. 3c, where the phase modulator calibration tone is shown with the thermal noise spectrum of the 3.49 GHz mechanical breathing mode (quality factor Q_m ≈ 3900). For a device with a designed, stress-tuned slot width of 60 nm, we measured g₀/2π = 184 kHz ± 2 kHz, where the uncertainty comes from the uncertainty in the thermal noise spectrum fit and the measurement of the phase modulator V_π = 2.78 V ± 0.01 V (Supplement 1, Sec. S1). This value matches well with the FEM-simulated g₀ values (Fig. 1f). Another device, having a designed, stress-tuned slot width of 20 nm, had a phase-modulator-calibrated g₀/2π = 317 kHz ± 3 kHz, which also aligns with FEM simulations and confirms the significant improvement in coupling achieved by narrower slots. We note that such slot mode geometries are of particular importance for materials such as Si₃N₄, the low refractive index (vs. Si or GaAs) of which limits the achievable coupling strength in single nanobeam geometries.

In addition, with the laser blue-detuned (Δ > 0), optomechanical back-action coherently amplifies the mechanical mode, increasing the detected amplitude while decreasing the effective mechanical linewidth γ_m,eff. Assuming only optomechanical damping changes with input power, the effective linewidth is related to the optical power at the coupling point to the device P_in as follows, where κ is the intrinsic optical loss rate, κ_ex is the external coupling rate, ω_o is the optical resonant frequency, and Ω_m is the intrinsic mechanical frequency [31, 32]:

$${\gamma }_{m,\text{eff}}={\gamma }_m+\frac{g_0^2}{{\omega }_o\hslash }\frac{{\kappa }_{\text{ex}}{P}_{\text{in}}}{{\mathrm{\Delta }}^2+{(\kappa /2)}^2}\left(\frac{\kappa /2}{{(\mathrm{\Delta }+{\mathrm{\Omega }}_m)}^2+{(\kappa /2)}^2}-\frac{\kappa /2}{{(\mathrm{\Delta }-{\mathrm{\Omega }}_m)}^2+{(\kappa /2)}^2}\right)$$ (1a)

$$={\gamma }_m+g_0^2\mathrm{S}\left(\kappa ,{\kappa }_{\text{ex}},{\omega }_0,\mathrm{\Delta },{\mathrm{\Omega }}_m\right)P_{\text{in}}$$ (1b)

Thus, the effective mechanical linewidth should change linearly with respect to optical power, with the intercept indicating the intrinsic mechanical linewidth γ_m and the slope proportional to $g_0^2$. For a blue-detuned laser, this slope is negative, and when the optomechanical amplification cancels out γ_m, the device reaches the regime of regenerative self-oscillation. The P_in at which this occurs is the threshold power.

We use this relationship to determine the intrinsic Q_m of these devices by looking at the detected mechanical spectrum with respect to power. To compensate for the cavity’s power-dependent thermo-optic shift, for each input power, we adjust the laser wavelength to the optimal detuning value, which corresponds to the point at which the mechanical peak is maximized. We then linearly fit the subthreshold γ_m,eff with respect to P_in to find γ_m. This same procedure is used to compare devices with similar optical and mechanical parameters; in this case, the slope is an indicator of the relative effective g₀.

Fig. 4a and b show measurements of two such devices with similar optical and mechanical performance but different stress tuning. One device, which had a designed stress-tuned slot width of 70 nm (stress-tuning slit depth of 220 nm), had an intrinsic Q_o = (3.7 ± 0.1) × 10⁴ and an intrinsic Q_m = 2380 ± 90 [27]. The data corresponding to this device are shown in Fig. 4a and the blue data in Fig. 4c. The other device had a designed stress-tuned slot width of 20 nm (stress-tuning slit depth of 295 nm), an intrinsic Q_o = (3.2 ± 0.1) × 10⁴, and an intrinsic Q_m = 2400 ± 300. The data corresponding to this narrower-slot device are shown in Fig. 4b and the red data in Fig. 4c.

FIG. 4.

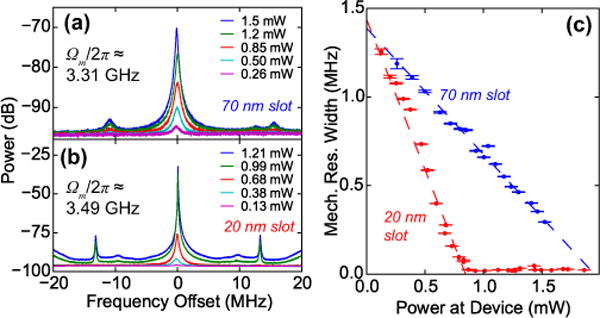
(a) Mechanical spectra at different input optical powers (P_in) for a device with a designed stress-tuned slot width of 70 nm, intrinsic Q_o = (3.7 ±0.1) × 10⁴, intrinsic Q_m = 2380±90 [27], and Ω_m/(2π) ≈ 3.31 GHz. (b) Mechanical spectra at different P_in for a device with 20 nm designed stress-tuned slot width, intrinsic Q_o = (3.2 ±0.1) × 10⁴, intrinsic Q_m = 2400 ± 300, and Ω_m/(2π) ≈ 3.49 GHz. (c) Measured γ_m,eff/(2π) of the devices from (a) (blue) and (b) (red). Error bars represent the uncertainty in the fit of the mechanical spectra to a Lorentzian. Dashed lines show weighted linear fits of the subthreshold γ_m,eff/(2π). The power spectral density plots in (a) and (b) are referenced to a power of 1 mW = 0dB.

Comparing measurements of these two devices, the mechanical mode in the 20 nm slot device is more amplified than in the 70 nm slot device. For P_in ≈ 1.2 mW, the detected mechanical peak in the 20 nm slot device is ≈ 65 dB above the noise floor, while the 70 nm slot device’s mechanical peak is only ≈ 19 dB above the noise floor. The measurements of the optomechanical narrowing of the optomechanical narrowing of the effective mechanical linewidth (Fig. 4c) show that the slope of the line for the narrower-slot device (red) is much steeper than for the wider-slot device (blue). Because they have similar optical and mechanical Qs, this suggests that the device with the 20 nm slot has a higher effective g₀. It is also noteworthy that the narrower stress-tuned slot enhances the back-action enough that it reaches self-oscillation above a threshold power of 900 μW.

Among all the devices measured, devices with more aggressive stress tuning (narrower slots) generally had steeper linewidth-narrowing slopes, implying higher effective g₀s, as expected from simulation (Fig. 1f) and confirmed by the aforementioned phase modulator calibration measurements. The most aggressively tuned devices, with slots designed to be 20 nm, had high enough effective g₀s that all but one of them reached the threshold for self-oscillation within the power range of the laser. This indicates that narrowing the slot via stress-tuning is an effective way to enhance the optomechanical coupling in slot-mode optomechanical crystal devices.

We note that the measured threshold powers are much lower, and the mechanical-linewidth-narrowing slopes much steeper, than would be expected with the g₀ values obtained from the phase modulator calibration method. This suggests other factors in the system are contributing to the effective optomechanical back-action. These could include DC optical gradient forces acting to pull the beams closer [23] and interaction of the breathing mode with the oscillating flexural beam modes.

In particular, although we designed these devices for optimal coupling to the mechanical breathing mode, and focused our measurements on characterizing it, there are other mechanical modes that couple to the optical mode. Defects in the fabricated device give rise to additional breathing-type mechanical modes [33], but the most well-coupled modes tend to be the lateral flexural beam modes. An FEM simulation of the fundamental lateral flexural beam mode (11.4 MHz) of the mechanical beam is shown in Fig. 5a. Because it is well-coupled to the optical mode and has a much lower frequency than the mechanical breathing mode, its threshold power for self-oscillation is very low; we measure it to be at P_in ≈ 150 μW. We also note that, upon detection of the optical signal modulated by self-oscillating breathing and flexural modes we observed mixing tones as sidebands of the breathing mode, as shown in Fig. 5c.

FIG. 5.

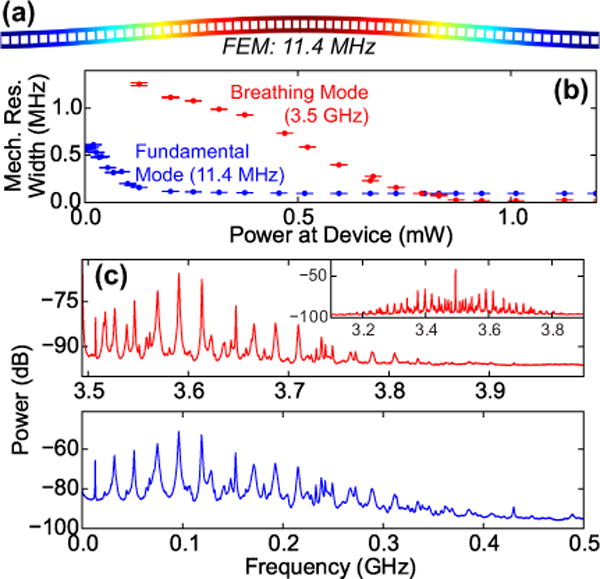
(a) FEM simulation of the fundamental lateral flexural beam mode. (b) Measured 3 dB linewidth of the fundamental flexural beam mode (blue) and the breathing mode (red) as a function of P_in. Error bars represent the uncertainty in the fit of the mechanical spectra to a Lorentzian. The fundamental mode self-oscillates at P_in ≈ 150 μW, while the breathing mode self-oscillates at P_in ≈ 900 μW. (c) Sidebands on the breathing mode (red) and the spectrum of harmonics of the lower-frequency flexural beam modes (blue) line up, indicating a mixing between the two. (inset) The full, double-sided spectrum around the self-oscillating breathing mode. All power spectral density plots in (c) are referenced to a power of 1 mW = 0 dB.

V. FLEXIBLE MECHANICAL RESONATOR DESIGN

Separating the mechanical and optical modes into two beams in the slot-mode architecture adds flexibility in designing these modes compared to a single nanobeam. By modifying the design of the mechanical beam, a wide range of mechanical frequencies can be accessed without significantly affecting the optical mode. To that end, we demonstrate lower-frequency designs around 1.8 GHz and 400 MHz. Implementing highly-localized breathing modes in various RF bands (here, the IEEE-defined UHF and L) broadens the potential application space. One way to change the mechanical frequency is simply to change the full width of the mechanical beam while keeping the same lattice variation.

For the 1.8 GHz band design, shown in Fig. 6a, the mechanical beam width was increased from 700 nm to 1.55 μm. Measurements of a fabricated device (Fig. 6b) having a designed, stress-tuned slot width of 80 nm are shown in Fig. 6c–e. The measured intrinsic Q_o = (1.01 ± 0.03) × 10⁵, and the measured intrinsic Q_m = 2130 ± 50, as derived from the weighted linear fit shown in Fig. 6e. These values are comparable to the 3.4 GHz band devices. The optomechanical coupling of this device was strong enough that we observed self-oscillation for laser powers above ≈ 2 mW (P_in is ≈ 20 % of the laser power at the FTW input). Above threshold, we also observed harmonics on the breathing mode (Fig. 6d). These arise from nonlinear modulation of the optical field due to the Lorentzian optical mode shape, as reported in other systems [34–36].

FIG. 6.

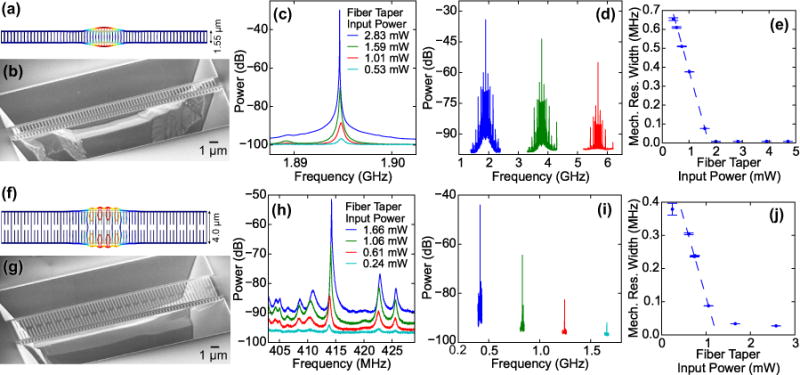
(a) FEM simulation of the 1.8 GHz band mechanical breathing mode of the 1.55 μm wide mechanical beam. (b) SEM image of a fabricated 1.8 GHz band device. (c) Detected mechanical spectra at different FTW input optical powers. (d) At a FTW input optical power of 4.7 mW, harmonics of the 1.895 GHz mechanical mode are visible. (e) Measured γ_m,eff/(2π) of the 1.895 GHz mechanical mode. Error bars represent the uncertainty in the dashed line shows the weighted linear fit of the subthreshold γ_m,eff/(2π). (f) FEM simulation of the 400 MHz band mechanical breathing mode of the 4 μm wide mechanical beam. (g) SEM image of a fabricated 400 MHz band device. (h) Mechanical spectra measured at different FTW input optical powers. (i) At a FTW input optical power of ≈ 2:6 mW, harmonics of the 414 MHz mechanical mode are visible. (j) Measured γ_m,eff/(2π) of the 414 MHz mechanical mode. Error bars represent the uncertainty in the fit of the mechanical spectra to a Lorentzian. The dashed line shows the weighted linear fit of the subthreshold γ_m,eff/(2π). The power spectral density plots in (c), (d), (h) and (i) are referenced to a power of 1 mW = 0 dB.

For the 400 MHz design, the mechanical beam width was increased to 4 μm. At this width, the mechanical mode is not well-confined for the same lattice parameters, but the “ribs” still contribute to the optical confinement. Thus, we kept the ribs to maintain high Q_o, but increased the effective mechanical lattice constants by “breaking” two-thirds of the ribs, as shown in Fig. 6f. Measurements of a fabricated device (Fig. 6g) having a slot width of 80 nm are shown in Fig. 6h–j. The measured intrinsic Q_o = (1.02 ± 0.02) × 10⁵, and the measured intrinsic Q_m = 800 ± 300, as derived from the weighted linear fit shown in Fig. 6j. The Q_o is comparable to that of the 3.4 GHz band devices, indicating that the “broken-rib” geometry minimally perturbs the optical mode. The Q_m, however, is much lower than in the 3.4 GHz band devices. This is likely due to an increase in air damping with decreased frequency [37] and an increase in anchor loss from the effective two-thirds decrease in the number of lattice periods in the mirror region of the mechanical beam. As with the other devices in this work, the mechanical spectra (Fig. 6h) include other, less-well-coupled peaks that correspond to additional breathing-type mechanical modes from defects in the fabricated device [33] or harmonics of lower-frequency flexural modes. The optomechanical coupling of the 414 MHz breathing mode of this device was strong enough that it reached self-oscillation for laser powers above ≈ 1.2 mW. As with the 1.8 GHz band device, we observed harmonics on the breathing mode above threshold (Fig. 6i).

VI. MULTIMODE OPTOMECHANICAL DEVICES

In addition to increasing flexibility in the available mechanical frequencies, the slot-mode device architecture enables new functionality in that it is straightforward to add another separate optical and/or mechanical mode. In this work, we demonstrate two cases: a single optical mode simultaneously coupled to two different mechanical beams (“M-O-M”) and a single mechanical mode coupled to two different optical modes (“O-M-O”). M-O-M devices have a variety of possible applications, with theoretical proposals including mechanical mode entanglement and phonon pair generation [12, 14] and ground-state laser cooling of an unresolved-sideband mechanical resonator [16]. Moreover, recent progress has been made in studying M-O-M devices in other platforms experimentally, including recent investigations of Bogoliubov mechanical modes [13], as well as systems showing synchronization of mechanical resonators via a travelling optical mode [38, 39]. An O-M-O slot-mode device provides a new platform for optical frequency conversion, as proposed in Ref. [17]. Unlike in previous demonstrations of optomechanically-enabled optical frequency conversion [7–9], the O-M-O device enables quasi-independent optical mode selection and independent optimization of the coupling into each optical mode.

In the example M-O-M device of this work, we surround an optical beam with a 1.8 GHz band mechanical beam (Sec. V) and a 3.4 GHz band mechanical beam, with 80 nm slots between the beams (Fig. 7b). The resultant optical mode is concentrated in both slots simultaneously (Fig. 7a). We couple to the optical mode by hovering the FTW a few hundred nanometers above the optical beam. The measured intrinsic Q_o = (1.26 ± 0.02) × 10⁵ (Fig. 7), and we simultaneously detect modulation from both the 1.8 GHz band and 3.4 GHz band mechanical modes (Fig. 7d). For the same input optical power, the detected 1.8 GHz band mode has a larger amplitude than the 3.4 GHz band mode primarily because a lower frequency mode has a larger thermal noise motional amplitude for the same temperature. With the optical quality factor in excess of 10⁵ (linewidth ≈ 2.4 GHz), this device is in the range of sideband-resolved operation for both the 3.4 GHz and 1.8 GHz band modes, suggesting that this device is a candidate for high-frequency Bogoliubov mechanical mode studies. We have also measured M-O-M devices with 1.8 GHz band and 400 MHz band mechanical breathing modes coupled to the same 981.85 nm optical mode (Supplement 1, Sec. S2).

FIG. 7.

(a) FEM simulation of the optical mode of an M-O-M device designed for coupling to 3.4 GHz band (bottom beam) and 1.8 GHz band (top beam) mechanical breathing modes. The optical mode is in both slots simultaneously. (b) SEM image of a fabricated M-O-M device. (c) Optical spectrum of M-O-M device. Measurement is in gray, and the Lorentzian fit is in red Measured intrinsic Q_o = (1.26 ± 0.02) × 10⁵ (d) Both mechanical modes measured simultaneously, FTW input power ≈ 3 mW. Data are in gray and Lorentzian fits are in red. At this optical input power, the 1.93 GHz mode has effective Q_m = 3175 ± 2, and the 3.484 GHz mode has effective Q_m = 3350 ± 10, where uncertainty comes from 95 % confidence interval of fit. (insets) FEM eigenmode simulations of corresponding mechanical breathing modes.

The O-M-O device demonstrated here comprises a mechanical beam with a 1.8 GHz band mechanical breathing mode coupled to an optical beam on each side, with 80 nm slots between the beams (Fig. 8a). The top nanobeam was made slightly wider, resulting in a red-shifted optical resonance. The top and bottom optical modes were characterized separately by repositioning the FTW, and the measured optical spectra are shown in Fig. 8b. The top mode had a measured intrinsic Q_o = (1.05 ± 0.02) × 10⁵ at 973.21 nm, and the bottom mode had a measured intrinsic Q_o = (1.1 ± 0.1) ×10⁵ at 947.34 nm.

FIG. 8.

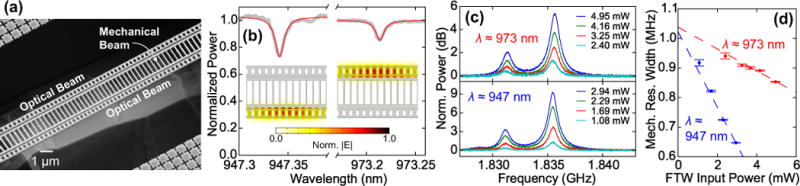
(a) SEM image of fabricated O-M-O device. (b) Separately-measured optical spectra of O-M-O device. Data are in gray, and Lorentzian fits are in red. The 947.34 nm mode (“bottom” beam) has intrinsic Q_o = (1.1 ± 0.1) × 10⁵, and the 973.21 nm mode (“top” beam) has intrinsic Q_o = (1.05 ± 0.02) × 10⁵. (insets) FEM simulations of the optical slot modes associated with bottom and top optical beams. (c) Mechanical spectra measured at different FTW input optical powers. Top spectra were acquired while optically coupled to the top beam, and bottom spectra were acquired while optically coupled to the bottom beam. (d) γ_m,eff/(2π) as measured via the top optical mode (red) and the bottom optical mode (blue) with respect to FTW input power. Dashed lines show weighted linear fits of γ_m,eff/(2π). Error bars represent the uncertainty in the fit of the mechanical spectra to a Lorentzian.

The mechanical breathing mode at ≈ 1.835 GHz was detected when coupled both to the top and to the bottom optical modes (Fig. 8c). (There is another, less-well-coupled peak at ≈ 1.831 GHz that corresponds to either an additional breathing-type mechanical mode from defects in the fabricated device [33] or a harmonic of a lower-frequency flexural mode.) We also measured γ_m,eff as a function of power for both optical modes (Fig. 8d). A weighted linear fit of these measurements indicates that the intrinsic Q_m as measured via each optical mode is in good agreement: from the top mode, Q_m = 1800 ± 100, and from the bottom mode, Q_m = 1800 ± 200. The resonant frequency also matches, as shown in Fig. 8c, implying that these two optical modes are in fact coupled to the same mechanical mode. The difference in detected mechanical peak heights and the difference in the slopes of mechanical linewidth with respect to optical power stem from the fact that the bottom optical mode at 947 nm couples more strongly to the mechanical mode.

VII. DISCUSSION

We have demonstrated slot-mode optomechanical devices in which the mechanical breathing mode of a patterned nanobeam is coupled to an optical mode that is laterally confined by a second patterned nanobeam and resides within the slot between the two beams. Along with large optomechanical coupling rates in excess of 300 kHz (as measured via phase-modulator calibration) enabled in part by narrow slot widths that can be achieved by taking advantage of the tensile film stress in Si₃N₄, this platform allows for flexible design of the optical and mechanical modes, with mechanical beams tailored to support breathing modes ranging from 400 MHz to 3.5 GHz. Moreover, this geometry can naturally be extended to multimode systems; we have shown triple-nanobeam devices with two different mechanical modes coupled to a single optical mode, as well as a triple-nanobeam device in which two different optical modes are coupled to a single mechanical mode.

Future work will focus on the use of these multimode geometries in applications such as optical wavelength conversion and Bogoliubov mechanical mode formation for phonon pair generation. Though some of the current devices are already weakly in the sideband-resolved limit (κ/2π ≈ 2 GHz < Ω_m/2π ≈ 3.4 GHz), additional improvements in Q_o would enable sideband resolution for all of the mechanical frequencies studied. Finally, the implementation of on-chip waveguides will likely be necessary to achieve long-term, stable coupling to multimoded systems.