Joint Effects of Ambient Air Pollutants on Pediatric Asthma Emergency Department Visits in Atlanta, 1998–2004

Abstract

Background

Because ambient air pollution exposure occurs as mixtures, consideration of joint effects of multiple pollutants may advance our understanding of air pollution health effects.

Methods

We assessed the joint effect of air pollutants in selected combinations (representative of oxidant gases, secondary, traffic, power plant, and criteria pollutants; constructed using combinations of criteria pollutants and fine particulate matter (PM_2.5) components) on pediatric asthma emergency department (ED) visits in Atlanta during 1998–2004. Joint effects were assessed using multi-pollutant Poisson generalized linear models controlling for time trends, meteorology and daily non-asthma upper respiratory ED visit counts. Rate ratios (RR) were calculated for the combined effect of an interquartile-range increment in each pollutant’s concentration.

Results

Increases in all of the selected pollutant combinations were associated with increases in warm-season pediatric asthma ED visits [e.g., joint effect rate ratio=1.13 (95% confidence interval 1.06–1.21) for criteria pollutants (including ozone, carbon monoxide, nitrogen dioxide, sulfur dioxide, and PM_2.5)]. Cold-season joint effects from models without non-linear effects were generally weaker than warm-season effects. Joint effect estimates from multi-pollutant models were often smaller than estimates calculated based on single-pollutant model results, due to control for confounding. Compared with models without interactions, joint effect estimates from models including first-order pollutant interactions were largely similar. There was evidence of non-linear cold-season effects.

Conclusions

Our analyses illustrate how consideration of joint effects can add to our understanding of health effects of multi-pollutant exposures, and also illustrate some of the complexities involved in calculating and interpreting joint effects of multiple pollutants.

Background

Although many air pollution health effects studies focus on individual pollutants, actual air pollution exposures are to multi-pollutant mixtures. Recognition of the importance of air pollution mixtures has led to increased interest in assessment of their health effects.^1–3 Various approaches to assessing the health effects of air pollution mixtures have been employed.^1,4 For example, some studies have assessed health effects using markers of exposure to specific mixtures, such as measures of traffic volume or proximity to roadways.⁵ Other studies have assessed health effects of mixtures characterized through source apportionment metrics,⁶ air pollution indices or sums of pollutant concentrations.^7–12 In this study we illustrate and discuss an approach to assessing air pollution mixture health effects that extends traditional single-pollutant epidemiologic models of measured pollutant concentrations by using models that include several pollutants to estimate the combined effect of multiple pollutants (i.e. joint effects).

Considering the joint effects of pollutants, rather than their individual effects, can advance our understanding of air pollutant mixture health effects. For example, considering the joint effects of groups of pollutants from particular sources may increase our understanding of important sources contributing to health effects. In addition, consideration of joint effects can address issues of confounding between pollutants and may avoid some of the difficulties involved in attempts to isolate individual effects of several correlated pollutants.^13,14

To date, joint effects have infrequently been considered in air pollution health effects studies,^15–21 with few studies assessing the precision of the joint effect estimates.^17–21 Moreover, discussion of the potential complexities involved with this approach has been limited.

In this study, we assess the joint effect of pollutants in several combinations of criteria gases, particulate matter less than 2.5 μm in diameter (PM_2.5), and PM_2.5 components, using data from a time-series study of air pollution and pediatric asthma emergency department (ED) visits in the Atlanta metropolitan area for which model performance has been previously described.²² We selected specific combinations representing pollutants with shared properties (oxidant gases and secondary pollutants) or sources (traffic and coal-fired power plant pollutants), or common air pollutants with U.S. National Ambient Air Quality Standards (NAAQS). We also discuss issues that must be considered when applying this analytic approach.

Methods

We used the data and modeling strategy applied by Strickland et al.,²² building upon previous results by considering joint effects of pollutant combinations. Methods for the original study are described in detail elsewhere.²² Briefly, daily concentrations of ambient 1-hour maximum carbon monoxide (CO), nitrogen dioxide (NO₂), and sulfur dioxide (SO₂); 8-hour maximum ozone (O₃); and 24-hour average PM_2.5 and the PM_2.5 components elemental carbon (EC), sulfate (SO₄²⁻), nitrate (NO₃⁻) and ammonium (NH₄⁺) for the period August 1, 1998 through December 31, 2004 were obtained from several ambient monitoring networks in Atlanta.^23,24 Daily pollutant measurements across monitors were combined using population weighting.²⁵ Individual-level data on ED visits during this time period were obtained from metropolitan Atlanta hospitals. Using International Classification of Diseases, 9^th Revision (ICD-9), pediatric asthma ED visits were defined as visits with a code for asthma (493.0–493.9) or wheeze (786.09 before October 1, 1998; 786.07 after October 1, 1998) that did not have a code for an external injury or poisoning (E800-E999) among children aged 5 to 17 years. ED visits for acute upper respiratory infections (codes 460.0–466.0) among children in the same age group who did not also have a code for asthma or wheeze were also identified.

We examined the joint effects of combinations of commonly measured pollutants, selected to represent oxidant gases, secondary pollutants, pollutants from traffic and coal-fired power plant sources, and criteria pollutants (Table 1). The “oxidant gases” combination included the major gaseous oxidant air pollutants (O₃, NO₂ and SO₂). The “secondary” pollutant combination included O₃ and secondary PM_2.5 (for which the concentration was calculated as the sum of the concentrations of the major inorganic PM_2.5 components SO₄²⁻, NO₃⁻, and NH₄⁺). The pollutants in the “traffic” combination were those most closely associated with traffic pollution in Atlanta (CO, NO₂ and EC).¹⁰ Organic carbon (OC) measurements were not used in these analyses because OC originates from both primary (e.g. traffic) and secondary sources, and speciated organic data needed to apportion OC to sources were available for only a limited time period. The pollutants in the “power plant” combination (SO₂ and SO₄²⁻) were selected to be relatively (although not completely) specific for pollution from coal-fired power plants.^26,27 The “criteria pollutants” combination included five of the pollutants for which NAAQS are set (including O₃, CO, NO₂, SO₂ and PM_2.5; excluding lead and particulate matter less than 10 μm in diameter). The “criteria pollutants” combination was included because of its potential regulatory significance.

Table 1.

Pollutant combinations for calculation of joint effects

Combination Name	O3	CO	NO2	SO2	PM2.5	EC	SO42−	Secondary PM2.5a
Oxidant Gases	X		X	X
Secondary	X							X
Traffic		X	X			X
Power Plant				X			X
Criteria Pollutants	X	X	X	X	X

Definition of Abbreviations: O₃=ozone, CO=carbon monoxide, NO₂=nitrogen dioxide, SO₂=sulfur dioxide, PM_2.5=particulate matter less than 2.5 μm in diameter, EC=elemental carbon component of PM_2.5, SO₄²⁻=sulfate component of PM_2.5.

^aSecondary PM_2.5 was calculated as the sum of the concentrations of selected PM_2.5 components including sulfate, nitrate, and ammonium.

We examined joint effects of pollutant combinations on pediatric asthma ED visits using Poisson generalized linear models that accounted for overdispersion. Because previous analyses showed different warm and cold-season effects,²² analyses were season-specific. We used the same general model form as Strickland et al.²² The dependent variable was the hospital-specific daily pediatric asthma ED visit count. For each pollutant in a given combination, the primary models included a linear term for the three-day moving average of pollutant concentrations [the average of the pollutant concentration on a given day (lag 0) and the previous two days (lags 1 and 2)]. Models also included a linear term for the logarithm of the daily non-asthma pediatric ED visit count for acute upper respiratory infections; cubic polynomials for day-of-season, the moving average of dew point (lags 0–2) and the moving average of minimum temperature (lags 1 and 2); indicator variables for year, month, day of week or holiday (with holidays having a separate indicator), hospital and same-day (lag 0) maximum temperature (for each degree Celsius); and interaction terms between month and year, month and lag 0 maximum temperature, and month and day of week. We estimated joint effects for an interquartile-range (IQR) increment in the three-day moving average of each pollutant concentration as the exponentiated sum (across the pollutants in the combination) of the product of each pollutant’s model coefficient and that pollutant’s IQR. Standard errors for joint effects were calculated using the variance-covariance matrices for the individual-pollutant coefficients (for a mathematical representation of models and joint effect calculations, see Supplemental Material, Model Details).

Initial models included only the pollutants in the specified combination, without interaction terms. The results of these models were compared with the results of models that also included linear terms for all first-order multiplicative interactions between the pollutants in the combination (e.g., for the oxidant gases combination, models included terms for O₃, NO₂, SO₂, and the product terms O₃*NO₂, O₃*SO₂ and NO₂*SO₂). In sensitivity analyses, we considered models with linear, quadratic and cubic terms for each pollutant, to assess the adequacy of using linear pollutant terms. In interaction models and models with quadratic and cubic terms, joint effects were calculated for a concentration change equal in magnitude to each pollutant’s IQR, starting from each pollutant’s 15^th, 25^th, or 35^th percentile levels. We also considered models that controlled for other potentially confounding pollutants.

Concurvity (the analogue of collinearity in non-linear models) was calculated for each pollutant as the correlation between observed pollutant concentrations and predicted concentrations from linear models including all other model variables (i.e., other pollutant terms, time variables and meteorological variables).²⁸ We also calculated concurvity for each pollutant in relation to only the other pollutant terms in the models (without time and meteorological variables).

Results

The distributions of the individual pollutants during the 1998–2004 warm and cold seasons are characterized in Table 2, and correlations between them are shown in Table 3. Warm-season, correlations ranged from moderately high to high (Spearman correlation coefficient (r) 0.62–0.98) among PM_2.5, secondary PM_2.5, and the PM_2.5 component SO₄²⁻. There were moderately high correlations among the traffic-related pollutants CO, NO₂, and EC (r= 0.57–0.75) in both seasons; and between PM_2.5 and O₃ (r=0.66) in the warm season. Cold-season correlations were generally lower than warm-season correlations, except for correlations between PM_2.5 and CO and PM_2.5 and EC, which were slightly higher in the cold season. For all of the pollutant combinations, all pollutants were simultaneously observed in their highest or lowest quartiles on some days in both seasons, so effect estimates for IQR increments in each pollutant represent pollutant changes that actually occur (eTable 1). The mean daily number of pediatric asthma ED visits was 26.2 (standard deviation 14.8) in the warm season and 32.5 (standard deviation 14.1) in the cold season.

Table 2.

Individual pollutant distributions, Atlanta, August 1998-December 2004

Pollutant	Season	Units	N	Mean	Standard Deviation	25th percentilea	50th percentile	75th percentilea
Ozone (8-h maximum)	WARM (May–October)	ppb	1196	53.9	19.2	39.8	53.3	67.7
Carbon monoxide (1-h maximum)		ppm	1186	0.7	0.4	0.5	0.7	0.9
Nitrogen dioxide (1-h maximum)		ppb	1196	22.3	10.2	14.8	20.5	28.7
Sulfur dioxide (1-h maximum)		ppb	1196	8.3	7.4	2.9	6.0	11.4
PM2.5 (24-h average)		μg/m³	1196	18.4	7.6	12.8	17.0	23.1
PM2.5 elemental carbon (24-h average)		μg/m³	1190	0.8	0.6	0.4	0.7	1.1
PM2.5 sulfate (24-h average)		μg/m³	1179	5.9	3.5	3.4	5.1	7.8
Secondary PM2.5b (24-h average)		μg/m³	1178	8.6	4.7	5.1	7.5	10.9
Ozone (8-h maximum)	COLD (November–April)	ppb	1148	33.6	13.9	23.4	32.6	42.7
Carbon monoxide (1-h maximum)		ppm	1137	0.9	0.5	0.5	0.7	1.1
Nitrogen dioxide (1-h maximum)		ppb	1149	25.6	9.8	18.4	24.9	31.7
Sulfur dioxide (1-h maximum)		ppb	1149	10.8	9.0	4.1	8.2	14.6
PM2.5 (24-h average)		μg/m³	1142	14.3	6.5	9.8	13.0	17.4
PM2.5 elemental carbon (24-h average)		μg/m³	1144	0.9	0.6	0.4	0.7	1.2
PM2.5 sulfate (24-h average)		μg/m³	1133	3.2	1.8	1.9	2.8	3.9
Secondary PM2.5b (24-h average)		μg/m³	1133	5.6	2.7	3.7	5.1	6.9

Definition of Abbreviations: PM_2.5=particulate matter less than 2.5 μm in diameter

^aFor comparability with previous analyses,²¹ the IQRs used in calculation of joint effects were slightly different from those reflected here, due to use of the year-round IQR during 1993–2004 for O₃, NO₂, CO and SO₂, and during August 1, 1998-December 31, 2004 for PM_2.5 and PM_2.5 components.

^bSecondary PM_2.5 was calculated as the sum of the concentrations of selected PM_2.5 components including sulfate, nitrate, and ammonium.

Table 3.

Spearman correlations between pollutants, Atlanta, August 1998-December 2004

	Season	Ozone (8-h maximum)	Carbon monoxide (1-h maximum)	Nitrogen dioxide (1-h maximum)	Sulfur dioxide (1-h maximum)	PM2.5 (24-h average)	PM2.5 elemental carbon (24-h average)	PM2.5 sulfate (24-h average)
Ozone (8-h maximum)	WARM (May–October)	1.00
Carbon monoxide (1-h maximum)		0.33	1.00
Nitrogen dioxide (1-h maximum)		0.54	0.75	1.00
Sulfur dioxide (1-h maximum)		0.27	0.32	0.44	1.00
PM2.5 (24-h average)		0.66	0.46	0.52	0.28	1.00
PM2.5 elemental carbon (24-h average)		0.39	0.73	0.68	0.31	0.53	1.00
PM2.5 sulfate (24-h average)		0.55	0.22	0.27	0.24	0.82	0.28	1.00
Secondary PM2.5a (24-h average)		0.55	0.27	0.31	0.24	0.86	0.33	0.98
Ozone (8-h maximum)	COLD (November–April)	1.00
Carbon monoxide (1-h maximum)		0.12	1.00
Nitrogen dioxide (1-h maximum)		0.30	0.74	1.00
Sulfur dioxide (1-h maximum)		0.05	0.22	0.41	1.00
PM2.5 (24-h average)		0.17	0.57	0.49	0.07	1.00
PM2.5 elemental carbon (24-h average)		0.10	0.72	0.57	0.18	0.64	1.00
PM2.5 sulfate (24-h average)		0.20	0.14	0.08	0.02	0.62	0.19	1.00
Secondary PM2.5a (24-h average)		0.07	0.16	0.12	0.08	0.67	0.24	0.92

Definition of Abbreviations: PM_2.5=particulate matter less than 2.5 μm in diameter

^aSecondary PM_2.5 was calculated as the sum of the concentrations of selected PM_2.5 components including sulfate, nitrate, and ammonium.

Daily increases in all of the selected pollutant combinations were associated with increases in daily warm-season pediatric asthma ED visit counts (Figure 1, eTable 2). Warm-season rate ratios (RR) for the joint effect of an IQR change in the three-day moving average of all pollutants in the selected combinations, in models without interactions, were 1.10 (95% confidence interval (CI)=1.04–1.16) for oxidant gases, 1.09 (95% CI=1.04–1.14) for secondary pollutants, 1.11 (95% CI=1.06–1.16) for traffic pollutants, 1.06 (95% CI=1.02–1.10) for power plant pollutants, and 1.13 (95% CI 1.06–1.21) for criteria pollutants. Warm-season joint effects were stronger than any of the single-pollutant model effects for the pollutants in each combination (eTable 3). If warm-season joint effects had been calculated using pollutant coefficients from single-pollutant models, joint effect RRs would have been overestimated (calculated RRs: oxidant gases 1.22, secondary 1.12, traffic 1.25, power plant 1.07, criteria pollutants 1.41), because single pollutant models do not control for potential confounding effects of co-varying pollutants. Cold-season joint effects varied across pollutant combinations. Overall, these were not statistically significant with the primary models, but were highest for the secondary combination (RR per IQR change=1.06, 95% CI=0.99–1.14) and the oxidant gases combination (RR per IQR change =1.05, 95% CI=0.99–1.13) (Figure 1, eTable 2). Comparison of cold-season joint effects calculated based on single-pollutant model coefficients with those from the multipollutant models is complicated by some cold-season single pollutant models indicating non-significant protective effects (eTable 3). More detailed results from the single-pollutant and primary joint effect models are shown in eTables 4 and 5 (pollutant coefficients and p-values) and eTables 6,7 (variance-covariance matrix for estimates from primary multi-pollutant models).

Figure 1. Rate ratios and 95% confidence intervals for single pollutant effects per interquartile-range increment in each pollutant from single pollutant models and for corresponding joint effects from multi-pollutant models.

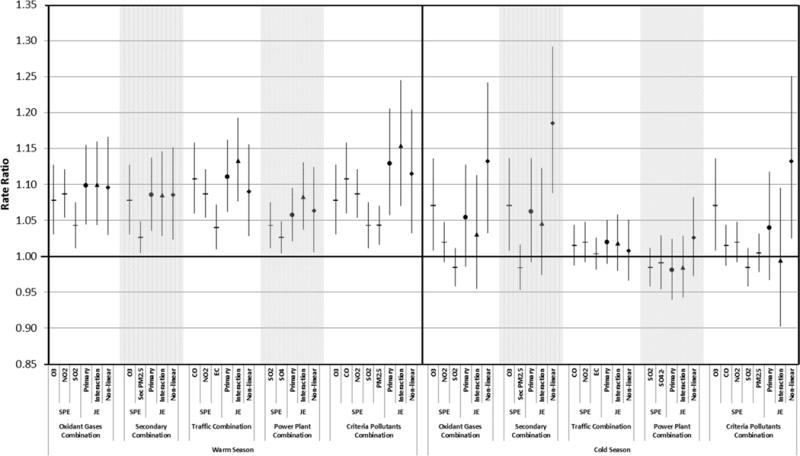
For each combination of pollutants, single-pollutant rate ratios (shown with horizontal line markers) are followed by joint effect rate ratios from the primary multi-pollutant models, which had linear pollutant terms and no interactions (“Primary”, circle markers), multi-pollutant models with linear pollutant terms and first order interactions between pollutants, with IQR increments evaluated starting at the 25^th percentile for each pollutant (“Interaction”, triangle markers), and multi-pollutant models with linear, quadratic and cubic pollutant terms and no interactions, with IQR increments evaluated starting at the 25^th percentile for each pollutant (“Non-linear”, diamond markers). For comparability with previous analyses,²² the analysis used the year-round IQR during 1993–2004 for O₃, NO₂, CO and SO₂, and during August 1, 1998-December 31, 2004 for PM_2.5 and PM_2.5 components. The IQRs used in the analysis were: O₃ 29.18 ppb, CO 0.66 ppm, NO₂ 12.87 ppb, SO₂ 10.51 ppb, PM_2.5 9.18 μg/m3, EC 0.69 μg/m3, SO₄²⁻ 3.45 μg/m3, Secondary PM_2.5 4.52 μg/m3. PM_2.5: particulate matter <2.5 μm in diameter, O₃: ozone, NO₂: nitrogen dioxide, SO₂: sulfur dioxide, Sec PM: Secondary PM_2.5, CO: carbon monoxide, EC: elemental carbon component of PM_2.5, SO₄: Sulfate component of PM_2.5. Secondary PM_2.5 was calculated as the sum of the concentrations of selected PM_2.5 components including nitrate (NO₃⁻), ammonium (NH₄⁺), and sulfate (SO₄²⁻).

Compared with joint effect estimates from models without interactions, joint effect estimates from models that included first order interactions between pollutants, with evaluation of the joint effect for a change from the 25^th to the 75^th percentile level for each pollutant, were generally not substantially different (Figure 1, eTable 2). Sensitivity analyses evaluating joint effects at other points in the pollutant distributions yielded similar conclusions relative to no-interaction models (eFigures 1 and 2). Based on consideration of individual interaction terms or consideration of likelihood ratio tests for the interaction terms together, warm-season models including first-order pollutant interactions generally did not show strong statistical evidence of important interactions (eTables 2 and 4), but cold-season models for the oxidant gases and criteria pollutants combinations did (likelihood ratio test p-values for interaction terms together <0.01, eTables 2 and 5).

In sensitivity analyses, compared with estimates from models with only linear pollutant terms, joint effect estimates for an IQR change in each pollutant (starting at the 25^th percentile) from models including quadratic and cubic pollutant terms were slightly lower for the warm-season traffic and criteria pollutant combinations; and notably higher for several cold-season combinations, particularly the oxidant gases, secondary and oxidant pollutant combinations (Figure 1). Evaluation of joint effects at other points in the pollutant distributions gave similar conclusions (eFigures 1 and 2). Dose-response curves based on the results of the models with and without non-linear terms for the oxidant gases, secondary and criteria pollutants combinations are shown in eFigure 3. Statistical evidence for the importance of the quadratic and cubic terms was observed for the warm-season traffic combination, and the cold-season secondary, criteria pollutants and power plant combinations (p-values for likelihood ratio tests for non-linear terms together <0.03, see eTable 8 for joint effect estimates and eTables 9 and 10 for detailed model results).

Joint effect estimates from models controlling for potentially confounding pollutants that were not included in calculation of joint effects were generally lower than joint effect estimates from models including only the pollutants in the joint effect (except for the traffic combination in both seasons, and the oxidant gases combination in the cold season for which estimates were not substantially different) (see eTable 8 for joint effect estimates and eTables 9, 10 for detailed model results). The difference was most marked for the warm-season secondary combination when controlling for CO, NO₂ and SO₂ (RR=1.02, 95% CI=0.96–1.08 vs. 1.09, 95% CI=1.04–1.14 in model with only O₃ and secondary PM_2.5) and for the warm-season power plant combination when controlling for O₃, CO, NO₂ and EC (RR=1.00, 95% CI 0.96–1.05 vs. 1.06, 95% CI=1.02–1.10 in model with only SO₂ and SO₄²⁻).

Measures of concurvity between pollutants and all other variables in the joint effect models were high in both seasons, ranging from 0.63 to 0.95 for the various pollutants in the models without interaction terms (eTables 4,5). Concurvity was generally lowest for SO₂ and highest for O₃. Lower, but still substantial, concurvity values were also seen for the pollutants in single-pollutant models (concurvities of 0.61–0.91), as well as for pollutants in multi-pollutant models in relation to only the other pollutants in the models (warm season 0.26–0.87, cold season 0.05–0.83 in no-interaction models). As expected, concurvities increased when first-order interaction terms were included.

Discussion

We calculated joint effects for several pollutant combinations selected based on common pollutant properties, relevance to air quality standards, or common sources. We observed warm-season joint effects representing increases of 6–13% in daily pediatric asthma ED visit rates for an IQR change in all of the pollutants in the combinations. Warm-season pediatric asthma appears to be impacted by a variety of pollutant combinations, particularly those including O₃ and/or NO₂. Joint effects for cold-season pediatric asthma showed more heterogeneity across mixtures, with strong effects observed for the oxidant gases, secondary and criteria pollutants combinations when non-linear effects were included in the models. Our results illustrated that calculation of joint effects from multi-pollutant models can avoid overestimation of joint effects that would result from their calculation based on single-pollutant model effect estimates, because single-pollutant model estimates may include some of the effect of correlated pollutants due to mutual confounding, which can be substantial. Our results also illustrate some of the complexities involved in calculating and interpreting joint effect estimates.

To calculate a joint effect, one has to calculate the effect of some specified change in each pollutant in the combination. The degree of change in each pollutant used in the calculation could be determined in several ways. We calculated the joint effect of an IQR change in each pollutant, since that has a basis in actual pollutant distributions. However, the IQR is specific to the location and time period and may vary for a given pollutant depending on the metric used (e.g., central monitor vs. population weighted average). Use of the IQR could also lead to combinations of pollutants with greater variability appearing more harmful (i.e., having a higher effect estimate per IQR change in pollutant concentrations) than combinations of pollutants with less variability, even if those combinations are not inherently more harmful. In addition, contrasts other than an IQR change may be of interest to risk assessors. To allow examination of other contrasts of interest, we have included information in the supplemental material about the individual parameter estimates (eTables 4 and 5) and the corresponding covariance matrix (eTables 6 and 7).

In sensitivity analyses, we explored the impact of several model specification decisions on the joint effect estimates. One decision relates to the approach to potential confounding by pollutants not included in the joint effect of interest. In our sensitivity analyses, models controlling for common, potentially confounding pollutants other than those in the joint effect often showed lower joint effect estimates than models that included only pollutants in the joint effect. Changes in joint effect estimates observed when including additional pollutants in the model could be due to control for confounding, but could also be due to differential measurement error. In a multi-pollutant model, measurement error can cause the effect estimate for a better-measured pollutant to represent some of the effect of a correlated but less-well-measured pollutant, making individual pollutant effect estimates less accurate.^29,30 In the presence of differential measurement error, adding other pollutants to the model could decrease the accuracy of the joint effect estimate. Differential measurement error may have impacted our joint effect estimates, with the degree of the impact depending on true pollutant effects, correlations between pollutants, relative degrees of measurement error, and correlations between measurement errors.^29,31

Other model specification issues relate to how pollutants are included in the model. Pollutants are often included in models as linear terms, as in our primary analyses. Our sensitivity analyses showed that an assumption of linear pollutant effects (on the log scale) may be inadequate. We observed statistical evidence for the importance of the quadratic and cubic terms in some cases (particularly the secondary, oxidant gases and criteria pollutants combinations in the cold season). Violation of the assumption of a log-linear effect of pollutant concentration across each pollutant’s concentration range could be magnified in a joint effect model because the assumption is made for several pollutants. Decisions also need to be made about which interactions to consider, and how to include those interactions in the model (i.e., linear terms or flexible forms). In some of our models, there was statistical evidence of important interactions. Models that include interaction terms may more accurately represent joint effects than models without interaction terms, but estimates from them may be less precise due to high correlations between model terms.

Our goal was to evaluate the joint effects approach as a method for examining air pollution mixture effects, but our analyses have limitations. Direct comparison of joint effect magnitudes across our pollutant combinations requires caution. Our combinations were carefully selected, and provided a good framework for examining issues surrounding quantification of joint effects, but they were selected for different reasons and included different numbers of pollutants (which alone can impact joint effect magnitudes). Some pollutants were in multiple combinations, which can contribute to similarities in observed joint effects. In addition, for combinations selected based on common sources, our results should be viewed as estimates of the joint effects of selected pollutants from shared sources and not as the total effects of those sources per se. Finally, results of time-series studies of acute air pollution health effects can be sensitive to model specification decisions other than those related to air pollutants. Our basic model was used in a previous study of acute air pollution effects on pediatric asthma;²² that paper presented several sensitivity analyses (controlling for pollen levels, not controlling for non-asthma upper respiratory infection ED visit counts, and using three alternate methods for time trend control) that indicated that the basic model was robust.²²

Some previous studies have used multi-pollutant models to calculate joint effects of pollutant combinations on pediatric respiratory outcomes, using approaches similar to ours. An analysis of pre-randomization-phase data from an asthma management study included estimation of the joint effect of pairs of common air pollutants on pediatric asthma exacerbations.²⁰ In that study, the strongest single-pollutant model effect estimates were observed for CO and NO₂. Joint effect estimates from models including CO and NO₂ were closer to the strongest single-pollutant model effect estimates than to an effect estimate based on the sum of single-pollutant model effects. A study of associations between PM_2.5 and O₃ and peak expiratory flow among children in Mexico City found that both pollutants were associated with decreased peak expiratory flow, but the joint effect (per IQR change) of the two pollutants was lower than the sum of their effects from single pollutant models.¹⁷

Other studies have considered air pollutant joint effects in relation to other outcomes. Roberts¹⁸ and Roberts and Martin¹⁹ modeled the total acute effect of PM₁₀, O₃, NO₂, SO₂ and CO on mortality using time-series models that calculated the overall effect of the pollutants (per standard deviation change in each pollutant), estimating the relative contribution of each pollutant to the overall effect through pollutant weights. Burnett, et al¹⁶ studied the association between particulate and gaseous air pollutants and cardiorespiratory hospitalizations in Toronto, Canada and calculated the total effect (for a change in each pollutant equal to its mean value) of pollutants selected using a forward selection procedure. In a separate study, Burnett, et al¹⁵ examined the association between daily ambient air pollution and mortality in 8 Canadian cities. They presented single-pollutant and joint effects (for a change in each pollutant equal to its mean value) for PM_2.5 and PM_10-2.5 and for a combination four gases (O₃, CO, SO₂ and NO₂). They reported that the joint effect for the gases calculated in this way was greater than the joint effects for the particles. Jerrett, et al examined the “cumulative risk index” (calculated as for our joint effects) for long-term exposure to O₃, PM_2.5 and NO₂ in relation to cardiovascular mortality.²¹ They found that the joint effect from a two-pollutant model was larger than the joint effect calculated based on single-pollutant model results. Many other studies have considered multi-pollutant models, but have focused on single pollutant effects, controlling for other pollutants, rather than on joint effects.^23,30,32,33

One reason the approach used in our analyses has not been more commonly used is concern that collinearity (also called concurvity in non-linear models) can lead to instability in effect estimates.¹ Collinearity can lead to inflation of the estimated variances of effect estimates,³⁴ and the degree of collinearity in time-series models of air pollution health effects can be substantial.²⁸ Given the need to control for confounding by variables, such as temperature, that are highly correlated with pollutant concentrations, some degree of collinearity is inevitable in time-series studies of air pollution health effects. However, collinearity must be considered in relation to power.³⁵ Our study used a long time series (6 years) with fairly high daily event counts, leading to ample power.³⁶ This may allow for a higher degree of collinearity with less adverse impact on model performance than would be the case for a study with a shorter time series or lower average daily counts. Effect estimate variances in our models did not appear severely inflated, providing some reassurance that concurvity was not excessive in relation to our study size. Nevertheless, when considering our results, one should recognize that pollutants vary in the degree to which they demonstrate collinearity with other variables in the model.²⁸ This can lead to better power for detection of effects of some pollutants, or pollutant combinations, than others.³⁶

Recognition of the importance of air pollution mixtures has led to increased interest in air pollution cumulative risk assessments (e.g., a recent risk assessment for PM_2.5 and O₃³⁷). Cumulative risk assessment considers the combined impact of multiple stressors on health outcomes, with consideration of potential interactions between stressors.^38,39 Epidemiologic studies like this one can contribute to cumulative risk assessments,⁴⁰ by providing dose-response functions. To be most useful for risk assessments, epidemiologic studies must present dose-response estimates for the same multi-pollutant contrasts considered in the risk assessment, or pollutant effect estimates from multi-pollutant models with their variance-covariance matrix to allow adaptation of results to other contrasts.^14,40 Our consideration of only commonly measured pollutants may facilitate use of our results in risk assessment. We have included information relevant to risk assessment in our supplementary material. However, individual pollutant effect estimates presented in the supplementary material are subject to the issues discussed above relating to confounding and measurement error.

In summary, our analyses illustrate the feasibility of a straightforward approach to modeling joint effects in a study of acute air pollution health effects with a long time series and fairly high average daily outcome counts. Our results shed light on pollutant combinations that may have important acute effects on pediatric asthma ED visits, and provide estimates (potentially useful for risk assessments) of the joint effects of those combinations. They also illustrate some of the complexities involved in calculating and interpreting joint effects of multiple pollutants. If the complexities are appropriately considered, calculation of joint effects is appealing because it transparently and explicitly specifies the contributions of various pollutants to the health effects of mixtures. This approach has promise for application to time-series analyses of joint effects of multiple pollutants in relation to various health endpoints in studies with sufficient power.