Sequence kernel association test of multiple continuous phenotypes

Abstract

Genetic studies often collect multiple correlated traits, which could be analyzed jointly to increase power by aggregating multiple weak effects and provide additional insights into the etiology of complex human diseases. Existing methods for multiple trait association tests have primarily focused on common variants. There is a surprising dearth of published methods for testing the association of rare variants with multiple correlated traits. In this paper, we extend the commonly used sequence kernel association test (SKAT) for single trait analysis to test for the joint association of rare variant sets with multiple traits. We investigate the performance of the proposed method through extensive simulation studies. We further illustrate its usefulness with application to the analysis of diabetes-related traits in the Atherosclerosis Risk in Communities (ARIC) Study. We identified an exome-wide significant rare variant set in the gene YAP1 worthy of further investigations.

1 Introduction

More and more large cohort studies have conducted or are conducting genome-wide association studies (GWAS) to reveal the genetic components of many complex human diseases. These large cohort studies often collected a broad array of correlated phenotypes that reflect common physiological processes. By jointly analyzing these correlated traits, we can gain more power by aggregating multiple weak effects and shed light on the mechanisms underlying complex human diseases (Solovieff et al., 2013). We propose to study multivariate test statistics to detect the joint association of a rare variant set with multiple correlated continuous traits.

Many methods have been developed for testing the association of common variants with multiple traits (see Ferreira and Purcell, 2009; Liu et al., 2009b; Yang et al., 2010; Rasmussen-Torvik et al., 2010; Avery et al., 2011; OReilly et al., 2012; Maity et al., 2012; van der Sluis et al., 2013; He et al., 2013; Schifano et al., 2013; Wu and Pankow, 2015; Hua and Ghosh, 2015, e.g.). In GWAS, identified common variants only explained a small proportion of the phenotypic variance for most complex traits studied to date. Manolio et al. (2009) have suggested that rare variants could contribute substantially to missing heritability. Individual rare variant based tests typically lack power due to low minor allele frequencies. A commonly used rare variant analysis approach is the gene-level association test that tests the joint effects of rare variants within a gene to enrich the association signal. Two commonly used rare variant set analyses are the burden test (see Morgenthaler and Thilly, 2007; Madsen and Browning, 2009; Morris and Zeggini, 2010; Price et al., 2010; Lin and Tang, 2011, e.g.) and variance component score test (see Wu et al., 2010; Neale et al., 2011; Wu et al., 2011; Lee et al., 2012, e.g.). The burden test works well for variants with similar effects and could lose substantial power with both protective and deleterious variants. The sequence kernel association test (SKAT, Wu et al., 2011) is based on the variance component score test and works well under various combinations of protective and deleterious variants, and is the most widely used approach for rare variant set association tests.

Existing methods for multi-trait association test have primarily focused on the common variants. There is a surprising dearth of published methods for analyzing rare variant set association with multiple traits. In this paper, we extend the commonly used SKAT for single trait analysis to test for the joint association of rare variant set with multiple continuous traits. We investigate the performance of the proposed method through extensive simulation studies. We further illustrate its usefulness with application to the analysis of diabetes-related traits in the Atherosclerosis Risk in Communities (ARIC) Study.

2 Methods

Consider n unrelated individuals sequenced in a region with m rare variants and K measured continuous traits. For individual i = 1, …, n, let Y_i = (y_i1, …, y_iK)^T denote the K continuous traits, X_i = (x_i1, …, x_ip) the p covariates (including the intercept) to be adjusted, and G_i = (g_i1, …, g_im) the genotypes (number of minor alleles or imputed dosage) for the m variants. Here for simplicity we have assumed a common set of covariates for all traits. The following methods can be readily adapted to the case of differing covariates.

We analyze y_ik marginally with a normal distribution with mean μ_ik = X_iα_k + G_iβ_k and variance ${\sigma }_k^2$, where α_k = (α_1k, …, α_pk)^T and β_k = (β_1k, …, β_mk)^T are coefficient vectors of length p and m respectively. Denote the correlation matrix of Y_i as Σ = (ρ_kl), where ρ_kl = Cor(y_ik, y_il). The joint association of rare variant set is testing H₀ : β₁ = … = β_K = 0 versus H_a : β_jk ≠ 0 for some j, k.

2.1 Multi-trait sequence kernel association test

For the j-th variant, we first show that its score statistics for testing β_jk across different traits have a correlation structure determined by the trait covariance matrix. Denote $\mathit{X}={({\mathit{X}}_1^T,\dots ,{\mathit{X}}_n^T)}^T$ as the n × p design matrix, and the associated hat matrix as H = X(X^TX)⁻¹ X^T.

Consider testing the association of the j-th variant and k-th trait, j = 1, …, m, k = 1, …, K. We regress the j-th variant and k-th trait on the covariate X, and define the corresponding predicted value as ${({\widehat{g}}_{1j},\dots ,{\widehat{g}}_{nj})}^T=\mathit{H}{(g_{1j},\dots ,g_{nj})}^T$, and ${({\widehat{\mu }}_{1k},\dots ,{\widehat{\mu }}_{nk})}^T=\mathit{H}{(y_{1k},\dots ,y_{nk})}^T$. Denote ${\tau }_j=\sqrt{{\sum }_{i=1}^n{(g_{ij}-{\widehat{g}}_{ij})}^2}$, j = 1, …, m, and the correlation of genotype residuals for the j-th and l-th variant as

$$r_{jl}=\frac{\sum _{i=1}^n(g_{ij}-{\widehat{g}}_{ij})(g_{il}-{\widehat{g}}_{il})}{{\tau }_j{\tau }_l},$$

which can be interpreted as the (adjusted) linkage disequilibrium (LD, genotype correlation after adjusting for covariates). For rare variants, the LD is typically small. Define a m × m (adjusted) LD matrix R = (τ_jτ_lr_jl), j = 1, …, m, l = 1, …, m.

We can check that the score statistic for testing β_jk is proportional to $U_{jk}={\sum }_{i=1}^n{g}_{ij}(y_{ik}-{\widehat{\mu }}_{ik})$ (up to a scale parameter, the estimated variance ${\sigma }_k^2$). We can further show that (see Appendix for details)

$$\mathit{Var}\left(U_{jk}\right)={\tau }_j^2{\sigma }_k^2,\mathit{Cor}(U_{jk},U_{jl})={\rho }_{kl},\mathit{Cor}(U_{jk},U_{ik})=r_{ji},\mathit{Cor}(U_{jk},U_{il})=r_{ji}{\rho }_{kl}.$$

Therefore for the same trait, score statistics of different variants are dependent with correlations reflecting their adjusted LD. For the same variant, their score statistics across different traits reflect the trait correlations. As for different variants and different traits, the correlation of their score statistics is the product of the trait correlation and adjusted variant LD. Therefore for rare variant set with small LD, the correlation of score statistics involving any two different variants is typically small.

In the same spirit as the SKAT for association test of single trait, we propose the following multi-trait sequence kernel association test for the joint effects of variant set (denoted as MSKAT)

$$Q=\sum _{j=1}^m{w}_j^2{\mathit{S}}_j^T{\widehat{\Sigma }}^{-1}{\mathit{S}}_j,$$ (1)

where w_j is a pre-specified weight (typically determined by the variant MAF; see the simulation section), and S_j = (s_j1, …, s_jK)^T with $s_{jk}=U_{jk}{\widehat{\sigma }}_k^{-1}$, k = 1, …, K. Here we have standardized the score statistics based on the trait variation, and ${\widehat{\sigma }}_k^2$ and ${\widehat{\Sigma }}_{kl}={\widehat{\rho }}_{kl}$ are all estimated under the null model

$${\widehat{\sigma }}_k^2=\frac{1}{n-p}\sum _{i=1}^n{(y_{ik}-{\widehat{\mu }}_{ik})}^2,{\widehat{\rho }}_{kl}=\sum _{i=1}^n\frac{(y_{ik}-{\widehat{\mu }}_{ik})(y_{il}-{\widehat{\mu }}_{il})}{(n-p){\widehat{\sigma }}_k{\widehat{\sigma }}_l}.$$

Define a K × m matrix S = (S₁, …, S_m). The MSKAT statistic can be written as $Q=\mathit{vec}{\left(\mathit{S}\right)}^T({\mathit{W}}^2\otimes {\widehat{\Sigma }}^{-1})\mathit{vec}\left(\mathit{S}\right)$, where W = diag(w₁, …, w_m), ⊗ means the matrix Kronecker product, and vec() is the vector operator, which stacks the columns of a matrix into a vector.

Alternatively we can consider summing over the SKAT statistics for individual trait

$$Q^{\prime }=\sum _{k=1}^K\sum _{j=1}^m{w}_j^2{s}_{jk}^2=\mathit{vec}{\left(\mathit{S}\right)}^T({\mathit{W}}^2\otimes {\mathit{I}}_K)\mathit{vec}\left(\mathit{S}\right),$$

where I_K denotes the K × K identity matrix.

A closely related approach is the multivariate kernel machine regression (MKMR) proposed by Maity et al. (2012) and further studied at Hua and Ghosh (2015). MKMR has been mainly studied for testing common variant set association. By incorporating variant weight, MKMR can be readily generalized to test rare variant set association. Both MKMR and the proposed Q/Q′ are quadratic functions of the multivariate outcomes, and hence their significance values can all be analytically and quickly computed based on the mixture of chi-square distributions. For Q/Q′, we have standardized the outcomes and worked on the individual trait-variant score statistics (hence implicitly using the linear kernel). While the MKMR has chosen to model the unscaled outcomes directly, construct the quadratic test statistic assuming a different working covariance matrix, and can use general kernel matrix for association test.

2.2 Significance p-value calculation

In the Appendix we show that the asymptotic null covariance of vec(S) is $\mathit{R}\otimes \widehat{\Sigma }$, and both Q and Q′ can be derived as a variance component score test under some working linear mixed effects model. Both Q and Q′ are constructed as quadratic functions of vec(S), and under null both Q and Q′ asymptotically follow a weighted sum of independent 1 degree of freedom (1-DF) chi-square distributions. For Q, the weights equal to λ_kj, where λ_kj = λ_j, k = 1, …, K, j = 1, …, m, and (λ₁, …, λ_m) are the eigen values of matrix W RW. For Q′, the weights equal to λ_jγ_k, j = 1, …, m, k = 1, …, K, where (γ₁, …, γ_K) are the eigen values of $\widehat{\Sigma }$.

We can quickly compute the significance p-values of Q and Q′ without the need of intensive permutations using a mix of Davies' method (Davies, 1980), and a modified scaled chi-square distribution approximation method of Liu et al. (2009a) following Wu et al. (2011); Lee et al. (2012), or the saddlepoint approximation method (Kuonen, 1999) following Chen et al. (2014); Wu et al. (2015).

3 Results

3.1 Simulation studies

We conduct simulation studies to investigate the performance of the proposed MSKAT statistics. For comparison, we included the Bonferroni corrected minimum p-value based on the individual trait SKAT significance p-values (denoted as Pmin), and the MKMR using the variant weighted linear kernel.

We simulated 1000 individuals and considered two covariates: a standard normal covariate X₁, and a binary ancestry indicator X₂ with Pr(X₂ = 1) = 0.5. We consider testing K = 4 related traits with a compound-symmetry correlation matrix: Y₁ = 1 + 0.5X₁ + 0.5X₂ + η₁ + ε₁, Y₂ = 1 + X₁ + X₂ + η₂ + ε₂, Y₃ = 1 + 0.5X₁ + 0.5X₂ + η₃ + ε₃, and Y₄ = 1 + X₁ + X₂ + η₄ + ε₄, where (ε₁, ε₂, ε₃, ε₄) are zero-mean normal with variances (${\sigma }_1^2=2$, ${\sigma }_2^2=1$, ${\sigma }_3^2=1$, ${\sigma }_4^2=1$) and correlation ρ, and (η₁, η₂, η₃, η₄) are contributions from the set of rare variants, which are simulated as follows.

Using a calibrated coalescent model (Schaffner et al., 2005), we first generated 10,000 European-like haplotypes of length 1000 kb. Each time we randomly pair the haplotypes to simulate 1000 individuals. We study those rare variants with MAF ≤ 0.01 in a randomly selected gene region of length 10 kb, denoted as (G₁, …, G_m). We model the rare variant contribution to disease risk as ${\eta }_k={\sum }_{j=1}^m{\beta }_{kj}{G}_j$, k = 1, …, K. For all methods, we assign the variant weights following Wu et al. (2011), which are the computed beta distribution density function with parameters 1 and 25 at the rare variant MAF.

We used 10 million experiments under the null to evaluate the type I error, and 10,000 experiments under various combinations of β_kj to evaluate the power. We conducted simulations for ρ = (0.2, 0.5, 0.8). We evaluated the type I error at the nominal significance level α = 10⁻⁵, 10⁻⁴, and 10⁻³, by setting all β_kj = 0. We evaluated the power under various combinations of β_kj. For each trait, we separately set their β_kj as follows. Each time we randomly selected θ proportion of rare variants and set their |β_kj| = −d log₁₀(p_j), where p_j is the rare variant MAF. The other null rare variants have zero coefficients. We have assumed that rarer variants have larger effect sizes. We conducted simulations for (1) θ = 0.25, d = 0.25, (2) θ = 0.5, d = 0.2, (3) θ = 0.75, d = 0.15. They correspond to regression coefficients of 0.5, 0.4 and 0.3 for MAF=0.01 respectively. The signs of β_kj were randomly set as 1 or −1. We also conducted simulations when all β_kj's have the same signs (see supplementary materials for complete details). We conducted simulations for four scenarios: each time only the first L traits were associated with the rare variant set, L = 1, 2, 3, 4. Intuitively in the first scenario (L = 1), where only the first trait is associated with the rare variant set, we expect that the minimum p-value based approach or testing the first trait alone will have good performance. But we will show that by simultaneously testing correlated null traits, the proposed MSKAT could actually improve the detection power compared to testing the first trait alone. When there are multiple correlated traits that are associated with the rare variant set, the proposed MSKAT could offer much improved detection power than the minimum p-value based approach.

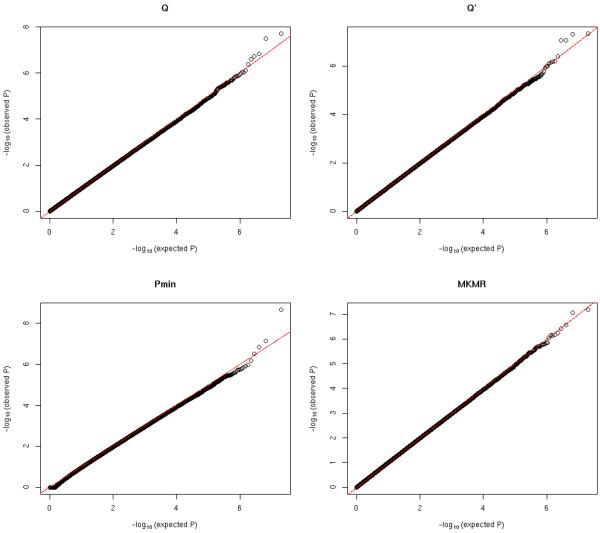
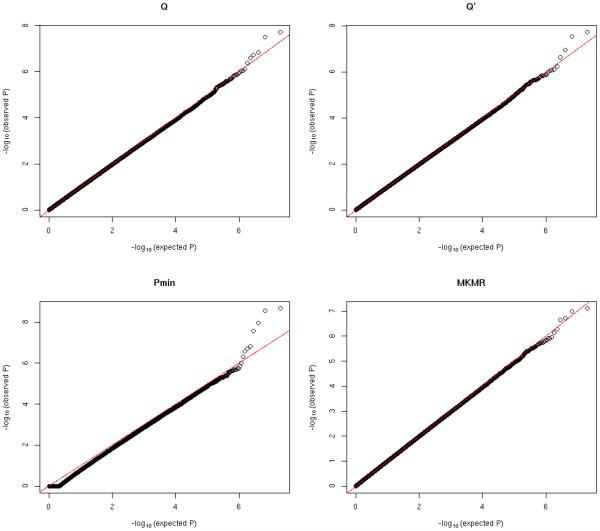
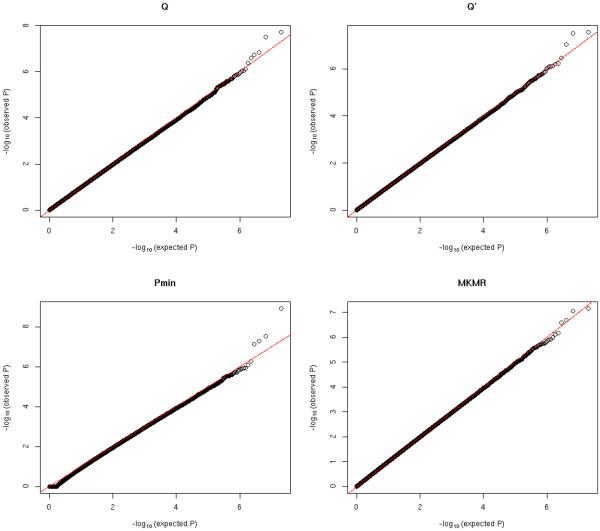
Figure 1 to 3 show the QQ plots of null significance p-values for all methods under different trait correlation ρ. Table 1 summarizes the estimated type I errors under different significance levels. Overall we can see that the Type I errors are well controlled under all considered scenarios for all methods. The Pmin is based on the Bonferroni corrected significance level and tends to be very conservative under strong trait dependence (ρ = 0.8), while the MKMR, Q and Q′ have generally more consistent performance with different trait correlations.

Figure 1.

QQ plots of null significance p-values for all methods: ρ = 0.2

Figure 3.

QQ plots of null significance p-values for all methods: ρ = 0.8

Table 1.

Type I errors (divided by the nominal significance level α) of multivariate tests for four continuous traits with pairwise correlation ρ: Q is the proposed MSKAT statistic incorporating the trait correlation, Q′ is the sum of individual trait SKAT statistics, Pmin is the Bonfferoni corrected minimum p-value based on the individual trait SKAT significance p-values, and MKMR is the multivariate kernel machine regression approach.

ρ	0.2			0.5			0.8
α	10−5	10−4	10−3	10−5	10−4	10−3	10−5	10−4	10−3
Q	0.80	0.82	0.89	0.80	0.82	0.89	0.80	0.82	0.89
Q ′	0.86	0.84	0.90	0.94	0.86	0.91	0.94	0.87	0.91
Pmin	0.70	0.81	0.89	0.77	0.82	0.88	0.77	0.70	0.73
MKMR	0.88	0.89	0.93	0.91	0.89	0.93	0.88	0.90	0.93

Table 2, 3, 4, and 5 summarize the power under significance level θ = 10⁻⁴ for L = 1, 2, 3, 4 respectively. When only the first trait is associated with the rare variant set (Table 2), Pmin performs better than MKMR, Q and Q′ under weak trait correlation (ρ = 0.2). The MKMR and MSKAT statistic Q could benefit from increased trait correlations, and offer much improved power by incorporating strongly correlated null traits.

Table 2.

Power of multivariate tests for four continuous traits with pairwise correlation ρ: Q is the proposed MSKAT statistic incorporating the trait correlation, Q′ is the sum of individual trait SKAT statistics, Pmin is the Bonferroni corrected minimum p-value based on the individual trait SKAT significance p-values, and MKMR is the multivariate kernel machine regression approach. Only the first trait is associated with the rare variant set (L = 1). The causal rare variant proportion is θ and their regression coefficient is set as −d log₁₀(MAF). The highest powered tests in each column are bold-faced.

(d, θ)	(0.25,0.25)			(0.2,0.5)			(0.15,0.75)
ρ	0.2	0.5	0.8	0.2	0.5	0.8	0.2	0.5	0.8
Q	0.016	0.038	0.204	0.024	0.054	0.280	0.017	0.036	0.205
Q ′	0.008	0.003	0.001	0.012	0.004	0.002	0.008	0.002	0.001
Pmin	0.024	0.024	0.024	0.035	0.035	0.035	0.022	0.022	0.023
MKMR	0.003	0.011	0.091	0.004	0.016	0.128	0.002	0.010	0.089

Table 3.

Power of multivariate tests for four continuous traits with pairwise correlation ρ: Q is the proposed MSKAT statistic incorporating the trait correlation, Q′ is the sum of individual trait SKAT statistics, Pmin is the Bonferroni corrected minimum p-value based on the individual trait SKAT significance p-values, and MKMR is the multivariate kernel machine regression approach. Only the first L = 2 traits are associated with the rare variant set. The causal rare variant proportion is θ and their regression coefficient is set as −d log₁₀(MAF). The highest powered tests in each column are bold-faced.

(d, θ)	(0.25,0.25)			(0.2,0.5)			(0.15,0.75)
ρ	0.2	0.5	0.8	0.2	0.5	0.8	0.2	0.5	0.8
Q	0.147	0.294	0.749	0.223	0.427	0.896	0.156	0.326	0.854
Q ′	0.085	0.029	0.012	0.136	0.048	0.019	0.088	0.030	0.012
Pmin	0.123	0.123	0.123	0.175	0.175	0.174	0.119	0.118	0.118
MKMR	0.117	0.262	0.721	0.177	0.381	0.879	0.120	0.285	0.837

Table 4.

Power of multivariate tests for four continuous traits with pairwise correlation ρ: Q is the proposed MSKAT statistic incorporating the trait correlation, Q′ is the sum of individual trait SKAT statistics, Pmin is the Bonferroni corrected minimum p-value based on the individual trait SKAT significance p-values, and MKMR is the multivariate kernel machine regression approach. Only the first L = 3 traits are associated with the rare variant set. The causal rare variant proportion is θ and their regression coefficient is set as −d log₁₀(MAF). The highest powered tests in each column are bold-faced.

(d, θ)	(0.25,0.25)			(0.2,0.5)			(0.15,0.75)
ρ	0.2	0.5	0.8	0.2	0.5	0.8	0.2	0.5	0.8
Q	0.372	0.604	0.945	0.534	0.774	0.989	0.421	0.686	0.982
Q ′	0.250	0.100	0.041	0.385	0.171	0.073	0.278	0.108	0.043
Pmin	0.206	0.206	0.204	0.283	0.281	0.276	0.199	0.196	0.193
MKMR	0.348	0.596	0.944	0.503	0.765	0.988	0.394	0.680	0.981

Table 5.

Power of multivariate tests for four continuous traits with pairwise correlation ρ: Q is the proposed MSKAT statistic incorporating the trait correlation, Q′ is the sum of individual trait SKAT statistics, Pmin is the Bonferroni corrected minimum p-value based on the individual trait SKAT significance p-values, and MKMR is the multivariate kernel machine regression approach. All L = 4 traits are associated with the rare variant set. The causal rare variant proportion is θ and their regression coefficient is set as −d log₁₀(MAF). The highest powered tests in each column are bold-faced.

(d, θ)	(0.25,0.25)			(0.2,0.5)			(0.15,0.75)
ρ	0.2	0.5	0.8	0.2	0.5	0.8	0.2	0.5	0.8
Q	0.597	0.807	0.988	0.779	0.928	0.999	0.681	0.882	0.997
Q ′	0.453	0.225	0.099	0.646	0.376	0.183	0.523	0.257	0.110
Pmin	0.277	0.275	0.271	0.376	0.372	0.366	0.266	0.262	0.257
MKMR	0.586	0.801	0.987	0.767	0.926	0.998	0.672	0.880	0.996

The statistic Q′ ignored the trait dependence by directly summing over individual trait SKAT statistics. Overall we can see that it suffered power loss with increasing trait correlations. The minimum p-value based approach Pmin had nearly constant power across different trait correlations.

When there are multiple correlated traits that are associated with the rare variant set (Table 3, 4, and 5), the MSKAT statistic Q had the overall best performance. Overall we can see that Q′ had reduced power with increasing trait correlations, and the Pmin had nearly constant power across different trait correlations. Both MKMR and the MSKAT statistic Q accounted for the trait dependence, and had improved power with increasing trait correlations.

Overall we can see that the proposed MSKAT statistic Q is an attractive approach with good power across a wide range of alternatives.

An interesting scenario is one in which only the first trait Y₁ is associated with the rare variant set and all the others are null traits (L = 1). Stephens (2013) and Wu and Pankow (2015) have reported that joint testing by incorporating a correlated null trait could improve the power for testing association of common variant. Table 6 compared the SKAT based rare variant set testing of Y₁ alone versus the joint multivariate testing under previous simulation settings. We can see that jointly testing highly correlated traits could have greater power over testing Y₁ alone. In general both MKMR and the proposed MSKAT statistic Q could benefit from the trait correlations to largely improve the detection power. The minimum p-value based approach is largely unaffected by the trait correlations.

Table 6.

Detection power incorporating correlated null traits: only the first trait Y₁ is associated with the rare variant set. The causal rare variant proportion is θ and their regression coefficient is set as −d log₁₀(MAF). We compared the multivariate trait based test approach, Q, Q′, Pmin and MKMR to the SKAT applied to testing Y₁ only, denoted as SKAT(Y₁). The highest powered tests in each row are bold-faced.

α = 10−4, d = −0.25, θ = 0.25
ρ	SKAT(Y1)	Q	Q ′	Pmin	MKMR
0.2	0.038	0.016	0.008	0.024	0.003
0.5	0.038	0.038	0.003	0.024	0.011
0.8	0.038	0.204	0.001	0.024	0.091

α = 10−4, d = −0.2, θ = 0.25
ρ	SKAT(Y1)	Q	Q ′	Pmin	MKMR
0.2	0.054	0.024	0.012	0.035	0.004
0.5	0.054	0.054	0.004	0.035	0.016
0.8	0.054	0.280	0.002	0.035	0.128

α = 10−4, d = −0.15, θ = 0.75
ρ	SKAT(Y1)	Q	Q ′	Pmin	MKMR
0.2	0.036	0.017	0.008	0.022	0.002
0.5	0.036	0.036	0.002	0.022	0.010
0.8	0.036	0.205	0.001	0.023	0.089

3.2 ARIC GWAS study

The Atherosclerosis Risk in Communities (ARIC) study (The ARIC Investigators, 1989) is a multi-center prospective investigation of atherosclerotic disease. Men and women aged 45–64 years at baseline were recruited from four U.S. communities: Forsyth County, North Carolina; Jackson, Mississippi; suburban areas of Minneapolis, Minnesota; and Washington County, Maryland. A total of 15,792 individuals participated in the baseline examination in 1987–1989. The vast majority of ARIC participants are of European (73%) or African ancestry (26%). We applied the proposed MSKAT and other competing methods in ARIC to test for association between diabetes-related traits and rare variants in each gene. Genotypes were obtained from the Illumina HumanExome BeadChip (Grove et al., 2013), which has information on 247,870 variants. We jointly analyzed fasting (≥ 8 hr) glucose levels measured at four visits each approximately three years apart in 5866 non-diabetic white participants. The ARIC Study design and methods for measurement of plasma glucose and other covariates have been described previously (Rasmussen-Torvik et al., 2010). The glucose levels had an average correlation of 0.55 between visits. We applied an additive genetic model and adjusted for age, gender and study center (population indicators).

We included rare variants with the minor allele counts larger than 1 and the MAF less than 0.01. In total we analyzed 12,439 rare variant sets in the exome-wide scan for glucose levels. We set the exome-wide significance level as 4.0 × 10⁻⁶, which is the Bonferonni corrected significance level for the total number of tested rare variant sets. When analyzing glucose at each visit separately, we did not identify any significant rare variant set at an exome-wide significance level. When the 4 visits were analyzed jointly, the MSKAT Q identified a significant set with two rare variants in the gene YAP1 (p-value = 2.4 × 10⁻⁶) that passed exome-wide significance. By contrast, the Q′, Pmin and MKMR tests did not identify any significant rare variant set. For the gene YAP1, Q′ reported a p-value of 8.8 × 10⁻³, MKMR reported a p-value of 1.5 × 10⁻⁴, and the SKAT p-values for the four measures were 0.007, 0.006, 0.216, and 0.102 respectively. The two rare YAP1 variants (rs61746398 and rs112417656) have 6 and 28 alleles detected in the samples respectively, and their estimated regression coefficients (expressed in mg/dL per copy of the minor allele) and associated p-values (listed in parentheses) at four visits are −5.0 (0.123), −11.0 (0.001), −2.7 (0.473), −11.6 (0.001) for rs61746398, and 4.0 (0.008), −3.8 (0.020), −2.3 (0.190), −1.2 (0.487) for rs112417656. Overall the rare variant effects exhibit some heterogeneity across four visits.

YAP1 is a potent oncogene and known to play a role in the development and progression of multiple cancers (Wu et al., 2010; Chen et al., 2013; Dixit et al., 2014). Common variants in YAP1 are associated with polycystic ovary syndrome (PCOS) (Louwers et al., 2013), an obesity-related endocrine disorder sharing similar epidemiological and patho-physiological features with type 2 diabetes. Among Han Chinese PCOS patients, the risk genotype for one of these common YAP1 variants (rs11225161) was also associated with higher blood glucose 30 min and 60 min after an oral glucose tolerance test (Li et al., 2012). Further research is needed on the possible role of identified rare variants in YAP1 in glucose metabolism.

4 Discussion

In the application, we have analyzed the multiple measures of fasting glucose levels over time as an illustration example. As suggested in our extensive simulation studies, the proposed methods could be useful for different correlated traits (for example, BMI and waist circumference). In our simulations, we have assumed positive correlations for traits. Since the sequence kernel association test and the proposed methods are all quadratic forms of the score statistics, they are invariant to any location and scale transformations of the outcomes. Therefore we expect that the same conclusions will hold for traits with negative correlations (for example, HDL and LDL).

In this paper we have focused on the joint analysis of multiple continuous traits. Our results have shown that joint association test can improve the variant detection power even when jointly testing additional strongly correlated null traits. It will be interesting to generalize the methods to study the joint test of mixed outcomes, which analytically and computationally are more challenging.

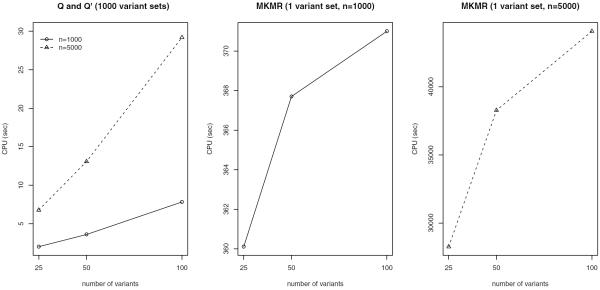
We have implemented the proposed methods in R programs posted at http://www.umn.edu/~baolin/research/mskat_Rcode.html. The proposed methods are very easy to program, and the implementations are extremely efficient: the significance p-values are analytically and quickly computed without the need of intensive permutation or random sampling. Figure 4 compares the MKMR and the proposed methods for their average CPU sec used to compute significance p-values for rare variant sets on a single Linux workstation with 2.5 GHz CPU and 24 GB memory. We follow the previous simulation setup with two covariates and four correlated traits (ρ = 0.5). We consider two sample sizes: n = 1000 and n = 5000 samples; and three variant set sizes: 25, 50 and 100 variants in each variant set. The MKMR does not scale well with the sample size and is using significantly more time than the proposed methods. Here we report the average time for one variant set using MKMR, and the average time for 1000 variant sets using the proposed methods. Overall we can see that both methods roughly scale linearly with the variant set size, and the proposed methods are very efficient and many orders of magnitude faster than MKMR.

Figure 4.

Average CPU sec used to analyze variant sets: the x-axis shows the variant set size, the y-axis shows the average CPU sec used (over 10 simulations); the first plot is for computing both p-values of Q and Q′ for 1000 variant sets, the other two plots are for computing p-values of MKMR for one variant set. To save computation time and make comparison fair, we have used the same analytical approach as the proposed methods to compute significance p-values for MKMR instead of the empirical random sampling approach as in Maity et al. (2012).

In summary, we recommend the proposed MSKAT statistic Q as a complementary approach to enhancing the detection power of rare variant set by jointly testing multiple correlated traits, which were often collected in most genetic studies.

Figure 2.

QQ plots of null significance p-values for all methods: ρ = 0.5

APPENDIX

Covariance of score statistics

Consider the score statistic $U_{jk}={\sum }_{i=1}^n{g}_{ij}(y_{ik}-{\widehat{y}}_{ik})$. Denote P = I_n − H, where I_n is a n × n identify matrix. Let ${\mathit{G}}_j^{\prime }={(g_{1j},\dots ,g_{nj})}^T$, ${\mathit{Y}}_k^{\prime }={(y_{1k},\dots ,y_{nk})}^T$. Using matrix notation, the score statistics can be written as $U_{jk}={\mathit{G}}_j^{\prime T}{\mathit{PY}}_k^{\prime }$. Therefore $\mathit{Var}\left(U_{jk}\right)={\sigma }_k^2{\mathit{G}}_j^{\prime T}{\mathit{P}}^2{\mathit{G}}_j^{\prime }={\sigma }_k^2{\tau }_j^2$, and

$$\mathit{Cov}(U_{jk},U_{jl})=\mathit{Cov}({\mathit{G}}_j^{\prime T}{\mathit{PY}}_k^{\prime },{\mathit{G}}_j^{\prime T}{\mathit{PY}}_l^{\prime })={\sigma }_k{\sigma }_l{\rho }_{kl}{\tau }_j^2,$$

$$\mathit{Cov}(U_{jk},U_{ik})=\mathit{Cov}({\mathit{G}}_j^{\prime T}{\mathit{PY}}_k^{\prime },{\mathit{G}}_i^{\prime T}{\mathit{PY}}_k^{\prime })={\sigma }_k^2{\tau }_j{\tau }_i{r}_{ji},$$

$$\mathit{Cov}(U_{jk},U_{il})=\mathit{Cov}({\mathit{G}}_j^{\prime T}{\mathit{PY}}_k^{\prime },{\mathit{G}}_i^{\prime T}{\mathit{PY}}_l^{\prime })={\sigma }_k{\sigma }_l{\rho }_{kl}{\tau }_j{\tau }_i{r}_{ji},$$

and hence

$$\mathit{Cor}(U_{jk},U_{jl})={\rho }_{kl},\mathit{Cor}(U_{jk},U_{ik})=r_{ji},\mathit{Cor}(U_{jk},U_{il})=r_{ji}{\rho }_{kl}.$$

We estimate ${\widehat{\sigma }}_k^2={\sum }_{i=1}^n{(y_{ik}-{\widehat{\mu }}_{ik})}^2∕(n-p)$, and ${\widehat{\rho }}_{kl}={\sum }_{i=1}^n(y_{ik}-{\widehat{\mu }}_{ik})(y_{il}-{\widehat{\mu }}_{il})∕(n-p)∕\left({\widehat{\sigma }}_k{\widehat{\sigma }}_l\right)$.

Variance component score test for multi-trait association

Denote the response matrix Y = (Y₁, …, Y_n) of dimension K × n. We model Y_i = (X_iα)^T + (G_iβ)^T + ϵ_i, where α = (α₁, …, α_K) and β = (β₁, …, β_K) are coefficient matrix of dimension p × K and m × K respectively. For simplicity of notation, we assume that responses have been standardized, i.e., ϵ_i ~ N(0, Σ).

Denote the vector operator as vec(), which stacks the columns of a matrix into a vector. Assume that $\mathit{vec}\left({\beta }^T\right)~N(0,{\sigma }_0^2\mathit{B})$, where B is a pre-defined matrix of dimension (mK)×(mK). Then testing the joint effects of rare variant reduces to testing $H_0:{\sigma }_0^2=0$.

Denote $\mathit{G}=({\mathit{G}}_1^T,\dots ,{\mathit{G}}_n^T)$ and E = (ϵ₁, …, ϵ_n). We have Cov(vec(E)) = I_n ⊗ Σ, and Y = (Xα)^T + β^TG + E. Note that we can write vec(β^TG) = (G^T ⊗ I_K)vec(β^T), hence $\mathit{Cov}\left[\mathit{vec}\right({\beta }^T\mathit{G}\left)\right]={\sigma }_0^2({\mathit{G}}^T\otimes {\mathit{I}}_K)\mathit{B}(\mathit{G}\otimes {\mathit{I}}_K)$. Denote A = Cov[vec(Y)]. We can check that

$$\mathit{A}={\mathit{I}}_n\otimes \Sigma +{\sigma }_0^2({\mathit{G}}^T\otimes {\mathit{I}}_K)\mathit{B}(\mathit{G}\otimes {\mathit{I}}_k),$$

and E[vec(Y)] = vec((Xα)^T). Therefore the log likelihood is proportional to

$$\ell =-\frac{1}{2}\log \mid \mathit{A}\mid -\frac{1}{2}{\left[\mathit{vec}\right(\mathit{Y})-\mathit{vec}({\left(\mathit{X}\alpha \right)}^T\left)\right]}^T{\mathit{A}}^{-1}\left[\mathit{vec}\right(\mathit{Y})-\mathit{vec}({\left(\mathit{X}\alpha \right)}^T\left)\right].$$

Note that ${\nabla }_{{\sigma }_0^2}{\mathit{A}}^{-1}=-{\mathit{A}}^{-1}\left[\right({\mathit{G}}^T\otimes {\mathit{I}}_K\left)\mathit{B}\right(\mathit{G}\otimes {\mathit{I}}_K\left)\right]{\mathit{A}}^{-1}$. Therefore the score statistic for testing ${\sigma }_0^2=0$ is proportional to

$$Q_v=\mathit{vec}{(\mathit{Y}-{\left(\mathit{X}\widehat{\alpha }\right)}^T)}^T{\mathit{A}}_0^{-1}\left[\right({\mathit{G}}^T\otimes {\mathit{I}}_K\left)\mathit{B}\right(\mathit{G}\otimes {\mathit{I}}_K\left)\right]{\mathit{A}}_0^{-1}\mathit{vec}(\mathit{Y}-{\left(\mathit{X}\widehat{\alpha }\right)}^T),$$

where ${\mathit{A}}_0={\mathit{I}}_n\otimes \widehat{\Sigma }$, and $\widehat{\alpha }$ and $\widehat{\Sigma }$ are obtained under the null model by solving

$$\underset{\alpha ,\Sigma }{\max }-\frac{1}{2}\log \mid {\mathit{I}}_n\otimes \Sigma \mid -\frac{1}{2}{\left[\mathit{vec}\right(\mathit{Y})-\mathit{vec}({\left(\mathit{X}\alpha \right)}^T\left)\right]}^T({\mathit{I}}_n\otimes {\Sigma }^{-1})\left[\mathit{vec}\right(\mathit{Y})-\mathit{vec}({\left(\mathit{X}\alpha \right)}^T\left)\right],$$

which can be solved by performing K separate linear regression models and then estimating Σ by the residual covariance matrix. Denote the projection matrix P = I_n − X(X^TX)⁻¹X^T. We can check that $\mathit{Y}-{\left(\mathit{X}\widehat{\alpha }\right)}^T=\mathit{YP}$.

Note that ${\mathit{A}}_0^{-1}={\mathit{I}}_n\otimes {\widehat{\Sigma }}^{-1}$, and ${\mathit{A}}_0^{-1}\mathit{vec}(\mathit{Y}-{\left(\mathit{X}\alpha \right)}^T)=\mathit{vec}\left({\widehat{\Sigma }}^{-1}\mathit{YP}\right)$. Therefore

$$Q_v=\mathit{vec}{\left({\widehat{\Sigma }}^{-1}YP\right)}^T\left[\right({\mathit{G}}^T\otimes {\mathit{I}}_K\left)\mathit{B}\right(\mathit{G}\otimes {\mathit{I}}_K\left)\right]\mathit{vec}\left({\widehat{\Sigma }}^{-1}YP\right).$$

Denote S = Y PG^T. Note that $(\mathit{G}\otimes {\mathit{I}}_K)\mathit{vec}\left({\widehat{\Sigma }}^{-1}\mathit{YP}\right)=\mathit{vec}\left({\widehat{\Sigma }}^{-1}\mathit{S}\right)=({\mathit{I}}_m\otimes {\widehat{\Sigma }}^{-1})\mathit{vec}\left(\mathit{S}\right)$. And hence

$$Q_v=\mathit{vec}{\left(\mathit{S}\right)}^T({\mathit{I}}_m\otimes {\widehat{\Sigma }}^{-1})\mathit{B}({\mathit{I}}_m\otimes {\widehat{\Sigma }}^{-1})\mathit{vec}\left(\mathit{S}\right).$$

We can choose $\mathit{B}={\mathit{W}}^2\otimes \widehat{\Sigma }$, where W = diag(w₁, …, w_m) is a diagonal matrix of pre-defined weights assigned to each variant. Here we assume a priori that the regression coefficients for a given variant have the same dependence structure as the covariance of the traits, and regression coefficients across different variants are independent. Then we can derive the proposed MSKAT statistic

$$Q=\mathit{vec}{\left(\mathit{S}\right)}^T({\mathit{W}}^2\otimes {\widehat{\Sigma }}^{-1})\mathit{vec}\left(\mathit{S}\right).$$

If we choose $\mathit{B}={\mathit{W}}^2\otimes {\widehat{\Sigma }}^2$, we have

$$Q^{\prime }=\mathit{vec}{\left(\mathit{S}\right)}^T({\mathit{W}}^2\otimes {\mathit{I}}_K)\mathit{vec}\left(\mathit{S}\right).$$

Asymptotic p-value computation

Note that

$$\mathit{vec}\left(\mathit{S}\right)=\mathit{vec}\left({YPG}^T\right)=(GP\otimes {\mathit{I}}_K)\mathit{vec}\left(\mathit{Y}\right).$$

Therefore vec(S) follows a multivariate normal distribution with zero null mean and asymptotical null variance

$$\mathit{Cov}\left(\mathit{vec}\right(\mathit{S}\left)\right)=(GP\otimes {\mathit{I}}_K)({\mathit{I}}_n\otimes \widehat{\Sigma })({PG}^T\otimes {\mathit{I}}_K)=\mathit{R}\otimes \widehat{\Sigma },\mathit{R}={GPG}^T.$$

We can further check that $\mathit{Cov}\left[\right(\mathit{W}\otimes {\mathit{I}}_K\left)\mathit{vec}\right(\mathit{S}\left)\right]=\left(\mathit{WRW}\right)\otimes \widehat{\Sigma }$, and $\mathit{Cov}\left[\right(\mathit{W}\otimes {\widehat{\Sigma }}^{-1∕2}\left)\mathit{vec}\right(\mathit{S}\left)\right]=\left(\mathit{WRW}\right)\otimes {\mathit{I}}_K$. Therefore for Q and Q′, their null distributions are weighted averages of 1-DF chi-square distributions, with weights being the eigen values of (W RW) ⊗ I_K and $\left(\mathit{WRW}\right)\otimes \widehat{\Sigma }$ respectively. For Kronecker product matrix, their eigen values can be computed from the crossproduct of individual matrix eigen values.