Abstract
Neuronal persistent activity has been primarily assessed in terms of electrical mechanisms, without attention to the complex array of molecular events that also control cell excitability. We developed a multiscale neocortical model proceeding from the molecular to the network level to assess the contributions of calcium regulation of hyperpolarization-activated cyclic nucleotide-gated (HCN) channels in providing additional and complementary support of continuing activation in the network. The network contained 776 compartmental neurons arranged in the cortical layers, connected using synapses containing AMPA/NMDA/GABAA/GABAB receptors. Metabotropic glutamate receptors (mGluR) produced inositol triphosphate (IP3) which caused release of Ca2+ from endoplasmic reticulum (ER) stores, with reuptake by sarco/ER Ca2+-ATP-ase pumps (SERCA), and influence on HCN channels. Stimulus-induced depolarization led to Ca2+ influx via NMDA and voltage-gated Ca2+ channels (VGCCs). After a delay, mGluR activation led to ER Ca2+ release via IP3 receptors. These factors increased HCN channel conductance and produced firing lasting for ~1 minute. The model displayed inter-scale synergies among synaptic weights, excitation/inhibition balance, firing rates, membrane depolarization, calcium levels, regulation of HCN channels, and induction of persistent activity. The interaction between inhibition and Ca2+ at the HCN channel nexus determined a limited range of inhibition strengths for which intracellular Ca2+ could prepare population-specific persistent activity. Interactions between metabotropic and ionotropic inputs to the neuron demonstrated how multiple pathways could contribute in a complementary manner to persistent activity. Such redundancy and complementarity via multiple pathways is a critical feature of biological systems. Mediation of activation at different time scales, and through different pathways, would be expected to protect against disruption, in this case providing stability for persistent activity.
Keywords: hyperpolarization-activated cyclic nucleotide-gated (HCN) channel, Ih, persistent activity, neocortex, computer simulation, multiscale modeling
1 Introduction
Computational models of functional neural activity patterns in neuronal networks have traditionally focused primarily on the role of electrical activity in shaping these patterns, neglecting the rich chemical complexity that complements electrical signaling in neurons. Persistent neuronal activity, lasting several seconds, has been proposed to underlie several functions in the central nervous system including short term working memory (Goldman-Rakic, 1995, Braver et al., 1997, Kane and Engle, 2002) and motor preparatory set (Ames et al., 2014). Additional functions probably also depend on similar mechanisms subserved by the “UP state,” identified originally in sleep and in slice but now also demonstrated in visual cortex (Cossart et al., 2003) and other brain areas (Oikonomou et al., 2014, Zhou et al., 2015, Poskanzer and Yuste, 2011, Major and Tank, 2004). Computational models of network persistent activity that have been proposed largely rely on continued interactions of neurons maintaining activity in one another through mutual synaptic activation (Lim and Goldman, 2013, Lim and Goldman, 2014, Lisman et al., 1998, Wang, 1999a, Wang, 2001).
A separate class of studies have focused on modulation of the single neuron via chemical signaling sequences (Ramakrishnan and Bhalla, 2008, Fall et al., 2005, Fall and Rinzel, 2006, Tiganj et al., 2015, Egorov et al., 2002, Fransén et al., 2006, Loewenstein and Sompolinsky, 2003, Sidiropoulou and Poirazi, 2012, Ashhad et al., 2015, Honnuraiah and Narayanan, 2013). Many of these have demonstrated that calcium signaling pathways underlie a large repertoire of cell dynamics that complements electrical signaling – interactions of chemophysiology and electrophysiology. Calcium pathways can enable persistent activity at the single cell level through effects on hyperpolarization-activated cyclic nucleotide-gated (HCN) channels (Ih) (Winograd et al., 2008, Destexhe et al., 1996). This molecular/cellular mechanism has also been proposed as one underpinning for working memory (Thuault et al., 2013). HCN channels are an important control point (Burdakov, 2005) in other respects as well, regulating somatic and dendritic responsivity and having effects on network oscillations (Neymotin et al., 2013, Kocsis and Li, 2004),
These network and molecular views of persistent activity and memory are entirely complementary. Indeed, it would be remarkable if multiple scales and multiple mechanisms were not involved in such a basic phenomenology (Lytton et al., 2014). In this paper, we combine these observations through a multiscale computer model of neocortex that ranges in scale from intracellular Ca2+ dynamics, up through cellular electrochemical coupling and on to network activity. Intracellular species simulated include Ca2+, inositol triphosphate (IP3), Ca2+ buffers, and cAMP.
Both single cells and the network produced persistent activity following excitatory stimulation. Metabotropically, the stimulus triggered an intracellular signaling cascade which caused persistent increased firing rate in the individual pyramidal cell. Placing this cell into a network with realistic connectivity produced effects augmenting and altering the persistent activity patterns through the combination of metabotropic and ionotropic recurrent activations, with non-stimulated cells suppressed via feedback inhibition. Network firing rates differed across cortical layers, and oscillation frequency shifted. The network model also demonstrated multiple roles of excitation/inhibition balance in maintaining both optimal network activation, and in controlling membrane mechanisms mediated through the voltage sensitivity of Ih. Multiple calcium sources – extracellular and intracellular – played synergistic roles in induction of persistent activity. Calcium buffer in the model was critical for regulating cytosolic free calcium, and therefore buffer level had an inverse relationship with persistent activity. By bridging multiple interacting scales and signaling modalities, electrical and chemical, our model demonstrates novel inter-scale interactions providing complementary routes for induction and maintenance of persistent activity.
2 Experimental Procedures
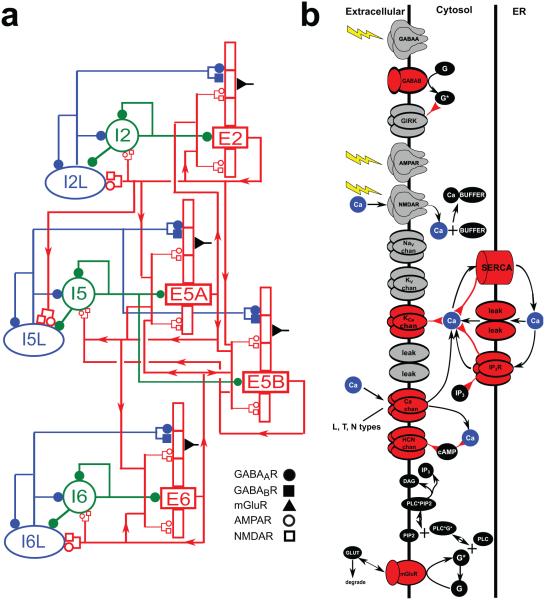
Network simulations consisted of 776 reduced compartmental cell models with single compartments for inhibitory cells and 5 compartments for pyramidal cells, arrayed by layer with connectivity taken from experimental results on motor cortex (Weiler et al., 2008) (Fig. 1a). Parallel-conductance electrophysiological simulation in the pyramidal cells was complemented by chemophysiological simulation focused on Ca2+ handling, based on a prior study (Neymotin et al., 2015) (Fig. 1b).
Figure 1. Model schematics.
(A) Schematic of neocortical network architecture. Red rectangles represent populations of 5-compartment excitatory cells (largest rectangle represents soma, 3 apical-dendrite compartments point upward, basal dendrite compartment points downward); green circles represent fast-spiking interneurons; blue ellipses represent low-threshold firing interneurons. Lines (with arrows) indicate connections between the populations. E cells synapse with AMPAR/NMDARs; I cells synapse with GABAAR / GABABRs. Filled circles represent GABAAR / GABABRs. Open circles and rectangles represent AMPAR/NMDARs. (B) Schematic of chemical signaling in pyramidal cells showing fluxes (black arrows) and second- (and third- etc) messenger modulation (red back-beginning arrows). We distinguish membrane-associated ionotropic and metabotropic receptors and ion channels involved in reaction schemes in red (in reality, it is likely that almost every membrane-bound protein is modulated). External events are represented by yellow lightning bolts – there is no extracellular diffusion; the only extracellular reaction is glutamate binding, unbinding and degradation on mGluR1 after an event. Ca2+ is shown redundantly in blue – note that there is only one Ca2+ pool for extracellular, 1 pool for cytoplasmic, and 1 pool for ER. (PLC: phospholipase C, DAg: diacyl-glycerol, cAMP: cyclic adenosine monophosphate; PIP2: phosphatidylinositol 4,5-bisphosphate).
Simulations were run in the NEURON (version 7.4) simulation environment (Carnevale and Hines, 2006) utilizing the reaction-diffusion (RxD) Python module (McDougal et al., 2013a, McDougal et al., 2013b) and NMODL (Hines and Carnevale, 2000). 16 s of simulation time took ~6 minutes using 82 nodes on a Linux cluster with parallel NEURON, run with a fixed time-step of 0.1 ms. The full model is available on ModelDB (#185858).
We describe the scales of the multiscale model sequentially from smaller to larger in the following sections. 1. The molecular scale of 10-100 microns: molecular interactions in the model primarily revolve around Ca2+ dynamics and the effects of Ca2+ on various intracellular properties, most notably on the HCN (Ih) channel. 2. The cellular scale of up to 1 mm: the description considers both cell morphology (anatomy) and electrophysiological properties. Although the primary electrophysiological mediators are ion channels at the molecular scale, they are encapsulated at the higher scale as electronic components. This encapsulation and linking across scales occurs as part of multiphysics simulation – the electrophysiological simulation based on electrical circuit theory is coupled to reaction-diffusion formalisms. 3. The local network scale of up to 1 cm. Description of the network is based on identification of synapse types. The overall simulation is multialgorithmic as well as multiphysical: event-driven algorithms for synapse and network interact with the ordinary and partial differential equation levels of electrophysiological and reaction-diffusion simulation.
2.1 Intracellular molecular scale
Our Ca2+ dynamics (Fig. 1b), similar to those used in (Neymotin et al., 2015), were derived from (Wagner et al., 2004), itself a spatial variant of (Li and Rinzel, 1994). Parameters are shown in Table 1. We modeled a one-dimensional RxD system of intracellular neuronal Ca2+ signaling in all compartments of neocortical pyramidal (PYR) neurons. Within each compartment, we modeled cytosolic and endoplasmic reticulum (ER) sub-compartments by using a fractional volume for each: for a given cell volume, fER denotes the fraction occupied by the ER, and fcyt denotes the fraction occupied by the cytosol: fcyt + fER = 1.
Table 1.
Baseline parameters.
| fcyt = 0.83 |
| fER = 0.17 |
| gIP3R = 120400.0 molecules/mM/ms |
| kIP3 = 0.00013 mM |
| kact = 0.0004 mM |
| kinh = 0.0019 mM |
| gleak = 18.06 molecules/mM/ms |
| gserca = 1.9565 molecules/ms |
| kserca = 0.0001 mM |
| τIP3 = 1000 ms |
| τIP3R = 400 ms |
| τex = 5 ms |
| D = 0.08 μm2/ms |
| D = 0.08 μm2/ms |
| DIP3 = 1.415 μm2/ms |
| DB = 0.043 μm2/ms |
| DCaB = 0.043 μm2/ms |
| FRate = 5ms−1mM−1 |
| BRate = 9.5 × 10−4ms−1 |
IP3 was produced through a reaction sequence initiated by glutamate binding to the metabotropic glutamate receptor (mGluR), based on a reaction scheme developed by (Ashhad and Narayanan, 2013) (ModelDB #150551). IP3 diffused outward from the synapse location and decayed following first-order kinetics with τIP3 of 1 s. Baseline mGluR synaptic weight was normalized to represent the increase in the amount of glutamate bound to mGluR. Extracellular glutamate did not diffuse but was represented by a local Glu value that was incremented in response to an event delivered due to a presynaptic spike. Glu showed bind/unbind kinetics on mGluR and was eliminated by first-order degradation (lower left of (Fig. 1b).
The ER Ca2+ model involves IP3 receptors (IP3Rs), SERCA pumps, and a Ca2+ leak. IP3R dynamics involved a slow Ca2+ inactivation binding site state (De Young and Keizer, 1992, Li and Rinzel, 1994). This IP3R bell-shaped dependence on calcium is evident in all mammalian isoforms of IP3Rs (Tu et al., 2005, Tu et al., 2005, Taylor and Tovey, 2010), and provides the basis of much modeling work in intracellular Ca2+ dynamics (Fall and Rinzel, 2006, Fall et al., 2004, Hartsfield, 2005, Peercy, 2008). We denote by JIP3R, JSERCA, and Jleak the mass flux per unit volume due to the IP3 receptor, SERCA pump, and leak channels, respectively. Dividing the mass flux by the volume fraction gives the change in concentration.
Cytosolic Ca2+ concentration (), ER Ca2+ concentration (), and IP3 concentration (IP3) followed:
| (1) |
| (2) |
| (3) |
Jmemb denotes the net flux into the cytosol due to channels on the plasma membrane.
Fluxes from the IP3R(JIP3R), SERCA pump (JSERCA), and leak channels (Jleak) follow:
| (4) |
| (5) |
| (6) |
Here, Ξ = NA/1018 ≈ 6.02 · 105, the number of molecules in a cubic micron at a concentration of 1 mM, where NA is Avogadro’s constant.
JIP3R has 3 gating parameters. Activation gates mCa and mIP3 are represented by their steady state values mCa∞ and mIP3∞ due to their rapid activation rates (Li and Rinzel, 1994). Inactivation via hIP3R is a slow Ca2+-dependent process with τIP3R of 400 ms.
| (7) |
| (8) |
| (9) |
| (10) |
The SERCA pump is a pump rather than a channel and so is modeled with Hill-type dynamics. Initial conditions for , , IP3, and hIP3R were set to 0.0001 mM, 1.25 mM, 0.0 mM, and 0.8, respectively. was set to 1.25 mM to reflect primed ER calcium stores. This 1.25 mM is consistent with experimentally-obtained values (Bygrave and Benedetti, 1996, Neymotin et al., 2015).
Calcium buffering followed
| (11) |
where B is diffusible buffer with diffusion coefficients D=0.043 μm2/ms for both B and CaB, about half the rate of Ca2+diffusion (Table 1) (Anwar et al., 2012). Calcium extrusion across the plasma membrane was modeled by first-order decay with τex = 5 ms except where varied in Fig. 13.
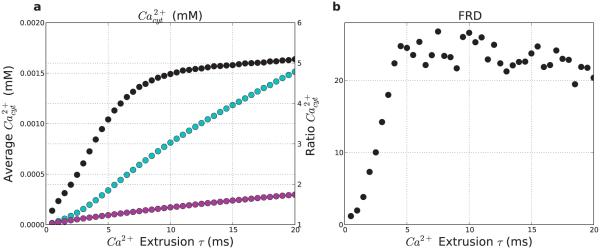
Figure 13. Slowing calcium extrusion pump allows retention of Ca2+ and increases firing-rate distinction (FRD).
(a) Average calcium concentration (left y-axis) averaged over 5 s post-stimulus. for stimulated (light-blue) and non-stimulated (purple) populations. Black points (right y-axis) show ratio. (b) Firing-rate distinction (FRD) as a function of pump speed. (n = 40)
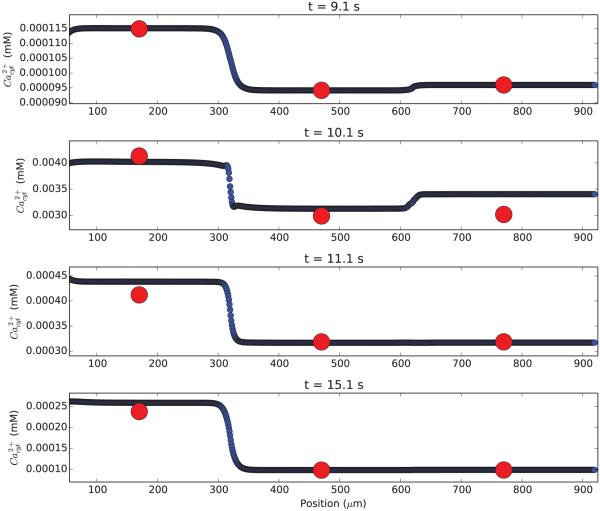
Chemical dynamics are typically slower than electrical dynamics but vary more quickly with position (less stiff in time but more stiff in space). We therefore increased chemical discretization to make sure that our baseline compartmentalization was adequate. Testing Ca2+ dynamics using 1μm subcompartments demonstrated that the calcium values were well-approximated (Fig. 2).
Figure 2. Simulation of a single neuron with high (blue; 1 μm) and low (red; 300 μm) spatial resolution shows similar calcium concentrations.
Calcium concentration is displayed as a function of position along the apical dendrite at four different times in the simulation (time from top to bottom). Excitatory stimulus at 10 s admits Ca2+ into the cytosol.
2.2 Synapses
AMPA/NMDA synapses were modeled by standard NEURON double-exponential mechanisms with parameters based on previous papers (Neymotin et al., 2013, Neymotin et al., 2011b, Neymotin et al., 2011a). All excitatory projections were mixed AMPA (rise,decay τ : 0.05,5.3 ms) and NMDA (rise,decay τ : 15,150 ms). NMDARs were scaled by 1/(1 + 0.28 · M g · exp(−0.062 · V)); M g = 1mM (Jahr and Stevens, 1990b). 13% of IN M DA was carried by Ca2+(Spruston et al., 1995). AMPA and NMDA receptors had reversal potentials of 0 mV.
Inhibitory synapses were mediated by GABAA and GABAB receptors. GABAA synapses were modeled with a double-exponential mechanism. The GABAB synapse had second messenger connectivity to a G protein-coupled inwardly-rectifying potassium channel (GIRK), as described in (Destexhe et al., 1996). LTS cells connected to apical dendrites of PYR cells using GABAA receptors (GABAAR; rise,decay τ : 0.2,20 ms) and GABAB receptors (GABABR; (Destexhe et al., 1996, Pérez-Garci et al., 2006)) and onto somata of FS and other LTS cells with GABAA Rs (rise,decay τ : 20,40 ms) (Bartos et al., 2007). GABAARs had reversal potentials of −80 mV, and GABABRs −95 mV.
2.3 Cell scale
The network consisted of pyramidal cells (PYR; 3 apical dendrite compartments, 1 basal dendrite compartment, 1 somatic compartment), fast spiking soma-targeting interneurons (FS; one compartment) , and dendrite-targeting low-threshold spiking interneurons (LTS; one compartment) (Neymotin et al., 2011b, Neymotin et al., 2011a, Wang and Buzsaki, 1996, Wang, 2002, Bartos et al., 2007, Monyer and Markram, 2004). Reaction-diffusion mechanisms (Ca2+,IP3,buffer) were restricted to the PYR cells in this network. Properties of pyramidal neurons in the different layers were identical except for apical dendrite length which is longer in deep pyramidal neurons than in superficial (Castro-Alamancos, 2013, Hay et al., 2011): 900 μm in L5-6; 450 μm in L2/3.
Voltage-gated ionic current models were based on prior models of our own and others (McCormick and Huguenard, 1992b, Migliore et al., 2004, Stacey et al., 2009, Neymotin et al., 2011b, Neymotin et al., 2011a, Neymotin et al., 2013). Voltage sensitive channels generally followed the Hodgkin-Huxley parameterization, whereby = (x∞ − x)/τx (x = m for activation particle and h for inactivation particle). Steady-state x∞ and time constant τx are either related to channel opening α(V) and closing kinetics β(V) as x∞ = α/(α + β), τx = 1/(α + β), or are directly parameterized: x∞(V), τx(V). Kinetics for channels were scaled by Q10 from an experimental temperature (where available) to simulation temperature of 37° Celsius. Q10=3 was used when no experimental value was available. All cells contained leak current, transient sodium current IN a, and delayed rectifier current IK−DR, to allow for action potential generation. Additionally, PYR cells contained in all compartments IK−A, IK−M providing firing-rate adaptation (McCormick et al., 1993). Pyramidal cells also had Ih, voltage-gated calcium channels (VGCCs) in all compartments: IL, IT , IN (McCormick and Huguenard, 1992a, Kay and Wong, 1987, Safiulina et al., 2010, Neymotin et al., 2015), and SK and BK calcium-activated potassium currents (IKCa). LTS cells contained IL, non-Ca2+-dependent Ih, SK, and Ca2+ decay. LTS Ih parameterization used Hodgkin-Huxley parameterization: = 0.00015 S/cm2k; Erev = −40 mV; with τ = 5 + 200/(exp((v + 70)/20) + exp(−(v + 70)/20)), m∞ = 1/(exp((V + 80)/10) + 1); Q10 = 2.2.
HCN channels in different cell types have somewhat different voltage dependence and different kinetics (Hagiwara and Irisawa, 1989, Wang et al., 2002, Robinson and Siegelbaum, 2003, Chen et al., 2001, Schwindt et al., 1992). The hyperpolarization-activated HCN current Ih used in pyramidal cells showed second messenger and calcium dependence taken from (Winograd et al., 2008) (ModelDB #113997; Fig. 3), modified to provide the faster voltage-sensitivity time constants found in cortex (Harnett et al., 2015). The mechanism for Ca2+ regulation of HCN channels in PYR cells in (Winograd et al., 2008) is modeled empirically in order to produce the relationship between cytosolic Ca2+ levels and Ih activation without simulating the details of Ca2+ effects on adenyl cyclase (see schematic for HCN chan in Fig. 1b). This empiric model provides combined control of conductance by cAMP (represented as a normalized level ‘p1’) and voltage using the following:
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
was 0.0025 S/cm2 in PYR soma, basal dendrites and exponentially-increasing in apical dendrites with distance from soma with 325 μm space constant, hence e-fold augmented at 325 microns as described by (Kole et al., 2006). Apical dendrite IK−DR, IK−A, IK−M density also increased with the same length constant, based on data showing HCN and Kv channel colocalization (Harnett et al., 2015, Harnett et al., 2013).
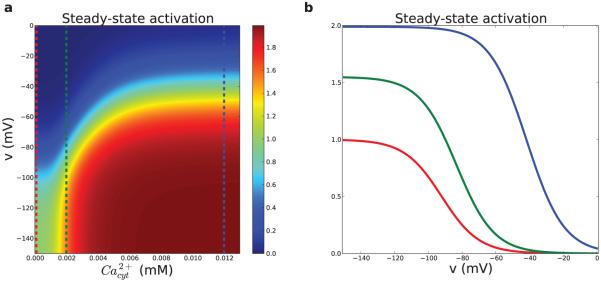
Figure 3. Pyramidal cell HCN channel activation.
(a) Steady-state HCN channel activation as a function of Ca2+ and Vmemb. Vertical lines are levels by color in (b). (b) Ihm voltage-dependence shifts right- and upward with increasing Ca2+. red: baseline at 100 nM; green: 2 μM; blue: 12 μM. Maximum steady-state activation is 2 because the second open state has twice the conductance of the first open state. At resting Ca2+ maximum steady state activation is 1.
We evaluated basic properties of the PYR model. A 0.01 nA depolarizing current provided 1.68 mV depolarization which decayed to 28% at 160 μm in apical dendrite, and 65% at 110 μm in basal dendrite (Larkum et al., 2009, Nevian et al., 2007). Rin was 54 Mohm, sag 0.28 in soma (−0.8 nA, sag = (vpeak − vsteady)/vsteady). With HCN blocked, Rin was 174 Mohm and sag was abolished (Sheets et al., 2011, Suter et al., 2013).
2.4 Network scale
The network consisted of 776 cells: 582 five-compartment pyramidal cells (PYR; 3 apical dendrite compartments, 1 basal dendrite compartment, 1 somatic compartment), 97 one-compartment fast-spiking (FS) soma-targeting interneurons, and 97 one-compartment low-threshold spiking (LTS) dendrite-targeting interneurons (Neymotin et al., 2014, Neymotin et al., 2011b, Neymotin et al., 2011a, Wang and Buzsaki, 1996, Wang, 2002, Bartos et al., 2007, Monyer and Markram, 2004). The network contained 30,486 synapses for an overall connection density of ~5% (see Table 2). PYR cells synapsed onto each-other’s dendrites. PYR-to-PYR synaptic locations on the dendrite were randomized between basal and apical compartments (Markram et al., 1997). PYR cells synapsed onto somata of FS and LTS cells (single-compartment models).
Table 2.
Network Connectivity. ij and wij are distance-independent probability of connections from Pre to Post neuronal types and synaptic weights, respectively.
| Pre | Post | ij | wij (nS) |
|---|---|---|---|
| I2L | I2L | 0.09 | 0.113 |
| I2L | I2 | 0.53 | 0.011 |
| I2L | E2 | 0.35 | 12.450 |
| I2 | I2L | 0.34 | 0.113 |
| I2 | I2 | 0.62 | 5.625 |
| I2 | E2 | 0.44 | 22.500 |
| E2 | I2L | 0.51 | 7.590 |
| E2 | I2 | 0.43 | 7.590 |
| E2 | E2 | 0.20 | 0.726 |
| E2 | I5L | 0.51 | 11.880 |
| E2 | E5A | 0.80 | 1.023 |
| E2 | E5B | 0.80 | 0.396 |
| I5L | I5L | 0.09 | 0.113 |
| I5L | I5 | 0.53 | 0.011 |
| I5L | E5A | 0.35 | 12.450 |
| I5L | E5B | 0.35 | 12.450 |
| I5 | I5L | 0.34 | 0.113 |
| I5 | I5 | 0.62 | 5.625 |
| I5 | E5A | 0.44 | 22.500 |
| I5 | E5B | 0.44 | 22.500 |
| E5A | E2 | 0.20 | 0.726 |
| E5A | I5 | 0.43 | 15.180 |
| E5A | E5A | 0.44 | 0.726 |
| E5A | E5B | 0.84 | 0.726 |
| E5A | E6 | 0.20 | 0.726 |
| E5B | E2 | 0.00 | 0.286 |
| E5B | I5 | 0.43 | 7.590 |
| E5B | E5B | 0.16 | 0.726 |
| E5B | E6 | 0.00 | 0.726 |
| I6L | I6L | 0.09 | 0.113 |
| I6L | I6 | 0.53 | 0.011 |
| I6L | E6 | 0.35 | 12.450 |
| I6 | I6L | 0.34 | 0.113 |
| I6 | I6 | 0.62 | 5.625 |
| I6 | E6 | 0.44 | 22.500 |
| E6 | E5A | 0.20 | 0.726 |
| E6 | E5B | 0.20 | 0.726 |
| E6 | I6L | 0.51 | 7.590 |
| E6 | I6 | 0.43 | 7.590 |
| E6 | E6 | 0.20 | 0.726 |
Neuronal populations were arranged by cortical layer based on our prior models (Neymotin et al., 2011, Neymotin et al., 2011a, Chadderdon et al., 2014), with additional data from direct measurements from mouse motor cortex (Weiler et al., 2008, Shipp, 2005, Hooks et al., 2013, Kiritani et al., 2012a). The network consisted of 150 layer 2/3 pyramidal cells (E2; E represents excitatory and 2 represents layer 2/3), 25 layer 2/3 fast-spiking interneurons (I2; I represents fast-spiking interneuron), 25 layer 2/3 low-threshold spiking interneurons (I2L; I2L represents low-threshold spiking interneuron in layer 2/3), 95 layer 5A pyramidal neurons (E5A), 145 layer 5B pyramidal neurons (E5B), 40 layer 5 fast-spiking interneurons (I5), 40 layer 5 low-threshold spiking interneurons (I5L), 192 layer 6 pyramidal neurons (E6), 32 layer 6 fast-spiking interneurons (I6), and 32 layer 6 low-threshold spiking interneurons (I6L).
Connection probabilities pij in the network were dependent on pre- and post-synaptic type and inversely scaled based on distance (Table 2) , in x,z plane perpendicular to the y-direction of layering, based on data from rodent motor cortex mapping (Weiler et al., 2008, Kiritani et al., 2012a). Individual neurons were placed randomly with uniform distribution. Weights from E cells displayed in Table 2 are for the AMPA synapses, with colocalized NMDA weights at 10% of AMPA weights. This provided for AMPA/NMDA current ratio of approximately 1.2, consistent with experiment (Wang et al., 2008). Since connectivity was random, specific divergence could vary. Synaptic delays were randomized between 1.8–5 ms with additional delay based on distance. Other parameters were based on the literature where available, as well as on previous models (Neymotin et al., 2013, Neymotin et al., 2011b, Neymotin et al., 2011a, Chadderdon et al., 2014, Song et al., 2013).
Background activity was simulated by excitatory and inhibitory synaptic inputs following a Poisson process, sent to all cells (Table 3), representing ongoing drive from other cortical areas and other inputs (Destexhe et al., 2003a). High background rates were required to maintain activity in the model, due to small network size (Neymotin et al., 2011a).
Table 3.
Parameters for modeling background activity. Dend indicates inputs to all dendritic compartments, consistent with experiments (Chen et al., 2013). Background inputs were not applied to GABABR synapses.
| Cell | Section | Synapse | Rise τ
(ms) |
Decay τ (ms) |
Conductance (nS) |
Rate (Hz) |
|---|---|---|---|---|---|---|
| Pyramidal | Soma | GABAAR | 0.07 | 9.1 | 0.2 | 150 |
| Pyramidal | Dend | AMPAR | 0.05 | 5.3 | 0.02 | 800 |
| Pyramidal | Dend | NMDAR | 15 | 150 | 0.02 | 300 |
| Pyramidal | Dend | GABAAR | 0.2 | 20 | 0.2 | 150 |
| Basket | Soma | AMPAR | 0.05 | 5.3 | 0.1 | 800 |
| Basket | Soma | NMDAR | 15 | 150 | 0.1 | 300 |
| Basket | Soma | GABAAR | 0.07 | 9.1 | 0.2 | 150 |
| LTS | Soma | AMPAR | 0.05 | 5.3 | 0.02 | 800 |
| LTS | Soma | NMDAR | 15 | 150 | 0.02 | 300 |
| LTS | Soma | GABAAR | 0.07 | 9.1 | 0.2 | 150 |
The synaptic stimulus used to assess persistent activity for both single cell and network simulations was provided to apical dendrites. For most simulations, a single period of stimulation was applied to 50% of PYR cells across all cortical layers. In Fig. 7, stimulation was provided selectively to a fixed number of cells in individual layers. Our current neocortical model, based on motor cortex, does not have cells in the L4 layer so that L4 inputs only synapse onto apical dendrites of L5 cells, an important part of L4 projections in sensory cortex (Shipp, 2005, Hooks et al., 2013, Suter and Shepherd, 2015).
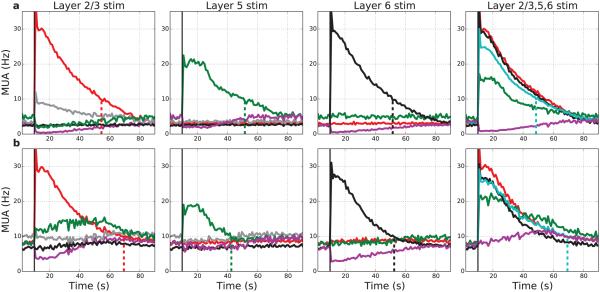
Figure 7. Targeted stimulation of individual layers produces localized persistent activity.
Activation duration of L5 cell with L5 input ~30-40 s, considerably less than the ~60 s activation duration seen in isolated L5 cell. (Layer simulation locations indicated at top of each column. Layer activity by color: E2 – red; E5 – green; E6 – black; inhibitory LTS cells in L5 – gray; within-layer non-stimulated cells – purple; stimulated cells all layers – light-blue in right column.) (a): Baseline network shows no interlaminar excitatory spread for any single layer stimulation. Layer 2/3 stimulation produces spread to L5 inhibitory cells producing reduction in firing in L5. (b): Augmented excitatory connectivity within the network (no change in strength of stimulation or background drive) produces increased durations (except paradoxical decrease with L5 stimulation) and spread of excitation from L2/3 to L5. With all-layer stimulation (right column) some spread of excitation to non-stimulated cells is also seen (purple line). (MUAs with 1000 ms bins; 75 neurons stimulated in each layer. Vertical dotted lines at times where rates drop < 10 Hz.)
To quantify the extent to which population firing rates changed during and after the stimulus, we formed multiunit activity (MUA) time-series, which count the number of spikes in each bin for a given population. We used several bin sizes (10 ms, 100 ms, 1000 ms) to display temporal activity at multiple resolutions. To quantify the efficacy of the network’s response to a stimulus we used firing-rate distinction (FRD): the average ratio of firing rates of stimulated to non-stimulated E cells using 10 ms bin size over the 5 s following the end of stimulation (measured from 0.5 s after the end of input events, to avoid ongoing effects from NMDAR activation). Average measures of calcium and HCN channel-related variables were also taken from the same period. For single cell simulations, FRD was calculated as the ratio of firing rate after the stimulus to the firing rate before the stimulus. To quantify long-term ensemble dynamics, we used population firing rate vectors formed by setting each entry in the vector as the corresponding cell’s spikes in a 1000 ms interval. To quantify similarity of these firing-rate vectors over time, we took the pairwise Pearson correlation, forming a firing-rate vector similarity matrix (Neymotin et al., 2010, Kelemen and Fenton, 2010).
3 Results
Simulation overview
Over 1600 simulations, with simulation durations of 10–245 s, were analyzed. Simulations of individual pyramidal neurons and simulations of entire networks of neurons were run. A typical simulation of 16 s of network time took ~6 minutes using 82 nodes on a Linux cluster with parallel NEURON. We ran simulations with initial calcium concentration in the ER set to 1.25 mM (Bygrave and Benedetti, 1996), to mimic the effects of ER calcium priming via prior excitatory synaptic stimulation (Fitzpatrick et al., 2009, Hong and Ross, 2007, Neymotin et al., 2015, Ross et al., 2005). This allowed the ER calcium to contribute to HCN channel regulation after mGluR stimulation.
3.1 Persistent activity in a single pyramidal neuron
A single layer 5 pyramidal neuron (E5) receiving random background synaptic activation followed by strong excitatory (AMPAR/NMDAR/mGluR) stimulation displayed a persistent increase in firing rate, via the effects of a set of molecular signaling cascades (Fig. 4). Prior to the stimulus, the E5 cell displayed a low firing rate of 1.6 Hz due to approximately balanced excitatory and inhibitory synaptic currents. After stimulation, the cytosolic calcium concentration increased due to voltage-gated calcium channel (VGCC) and NMDAR calcium influx (Fig. 4b). At the same time, the mGluR-activated cascade produced IP3 (Fig. 4c), causing Ca2+ efflux from ER to cytosol (Fig. 4d). These multiple sources of cytosolic Ca2+ augmented cAMP, an HCN channel-regulating second-messenger, over tens of seconds (Fig. 4e). Prior to the stimulation, HCN channel conductance (gh) in soma and dendrite were at similar levels (Fig. 4e), but diverged after stimulation. During the upstroke of individual action potentials, gh in the soma followed spiking rapidly while gh in dendrite did not vary as much due to more moderate alterations in dendritic voltage but showed a persistent >7× activation due to the second messenger effect (Fig. 4f). During the excitatory stimulus, Ih (Fig. 4g) briefly decreased (note negative inward current) due to membrane depolarization. Afterwards, dendritic Ih increased, following gh despite some negative feedback due to depolarization effects on both activation and driving force. The associated dendritic depolarization drove spiking in the soma (Fig. 4h). Elevated dendritic voltage lasted >65 s with somatic action potential firing increasing to 52 Hz, a 32× increase over baseline, during the 10 s after stimulation. The single cell’s firing remained elevated above 10 Hz for ~62 s after stimulation. The continued activation of Ih depended on an ongoing balance between excitation and inhibition. In the absence of inhibition, Ih turned off due to its voltage dependence (hyperpolarization activates; depolarization deactivates).
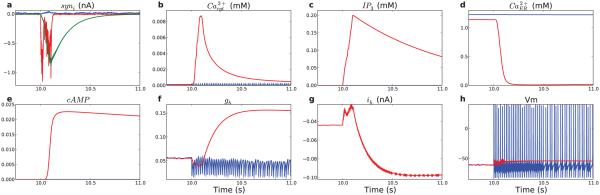
Figure 4. Isolated L5 pyramidal neuron model demonstrates persistent increase in firing after stimulation to AMPAR/NMDAR/mGLUR via a – h sequence of coupled electrical-molecular-electrical activations.
(soma levels in blue; apical dendrite levels in red, except in a) (a) Synaptic currents in apical dendrite (blue: GABAAR; red: AMPAR; green: NMDAR) (b) produces cytosolic calcium concentration increase due to calcium influx via VGCC and NMDAR, (c) while also increasing IP3 via mGluR-activated cascade, (d) which together with Ca2+ activates IP3R causing efflux of ER Ca2+. (e) cAMP is augmented by higher Ca2+ (f) persistently increasing normalized HCN conductance (gh) (g) persistently increasing Ih. (soma values out of range due to lower HCN density) (h) resulting in high rate of firing.
3.2 Persistent activity in network
Adding cell-based Ih-dependent persistent activity to a network produced a model with synergistic network- and cell/molecular-effects. Individual cells in the network model demonstrated the same pattern of persistent activity after stimulation seen in the single neuron model (Fig. 5). Activation provided augmented inhibition as well as increased excitation. This ongoing inhibition helped maintain Ih effect by preventing excessive depolarization that would deactivate Ih. The relative isolation of Ih in the dendrites also helped prevent this deactivation in the setting of high ongoing activity.
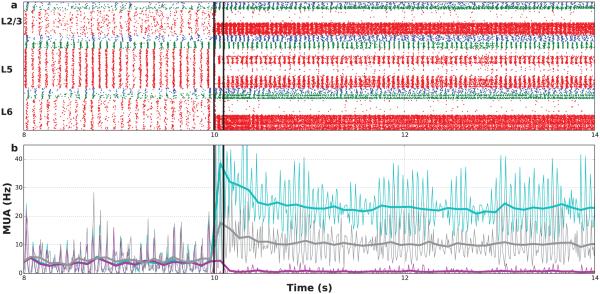
Figure 5. Network persistent activity after stimulating 50% of E-cells.
(a) Raster plot of spike times (red: PYR, blue: LTS, green: FS cells) (b) Multiunit activity (MUA; thick: 100 ms bin; thin: 10 ms bin) for stimulated E neurons (light-blue), non-stimulated E neurons (purple), interneurons (gray). (Stimulation added to background activation between black lines: 180× weight 500 Hz Poisson process.)
During baseline conditions, the average firing rates of excitatory (E) and inhibitory (I) neurons ranged between 2.5–5.4 and 2.3–9.4 Hz, respectively, with rhythmic population oscillations at a high alpha/low beta frequency of ~14 Hz. A brief, single stimulation period applied to a randomly selected 50% of the excitatory neurons across layers was used to represent the activation pattern. The immediate effects were depolarization of the stimulated cells and increase in cytosolic IP3. During stimulation, average membrane potential was increased, causing a reduction in AMPAR/NMDAR driving-force and a brief fall-off of firing rate.
After stimulation was turned off, the firing rate of stimulated E cells remained elevated for ~60 s, dropping below 10 Hz after 35 s. Rates of the stimulated pyramidal cells increased from 3.7 to 20.0 Hz while rates of the non-stimulated pyramidal cells decreased from 3.6 to 0.8 Hz. The population rhythm increased from 14 Hz to ~20 Hz. This resultant oscillation was at the firing rates of the stimulated cells, and was of lower amplitude, being carried primarily by these cells.
The network connectivity enabled several emergent effects produced via synaptic interactions. The higher activity of stimulated E cells produced increased drive from E to I cells: I rates transiently increased to ~20 Hz during stimulation (Fig. 5b gray), and then remained elevated throughout the persistent activity. This dynamic increase in inhibition throughout the network was the cause of depressed firing rates of the non-stimulated E cells (>75% reduction) which allowed the stimulated cells to dominate network dynamics. The increased activation of I cells also shortened the network’s response duration, compared to the isolated single cell.
Although the stimuli were identical across cortical layers, there was a larger post-stimulus response in layers 2/3 and 6, compared to the two E populations in layer 5 (L5A and L5B). These differences in response correlated with different ratios of convergent inhibitory inputs to convergent excitatory inputs for the E cells in the different layers (L2:0.4, L5A:0.2, L5B:0.1, L6:0.4). Higher I→ E connectivity would translate into greater hyperpolarization of E cells in a layer, greater activation of Ih, and greater activation despite the countervailing direct effect of inhibition.
3.3 Molecular cascades within cells within network
The same sequence of molecular activations that led to persistent activity in the simulation of the individual E5 cell (Fig. 4) was also seen in the E5 cells within the full network (Fig. 6). Stimulation-induced depolarization caused further opening of NMDA channels, as well as the activation of VGCCs, which admitted additional calcium into the cytosol. On average, E5 cells in the stimulated population showed a transient elevation in the cytosolic calcium of ~0.01 mM (Fig. 6a). mGluR stimulation occurred at the same time as AMPA/NMDA synapse activation and produced IP3, with subsequent IP3 binding to ER IP3Rs. Together with the available calcium, this caused the endoplasmic reticulum (ER) to release additional calcium from its stores into the cytosol after a short interval, further contributing to the population calcium increase (Fig. 6b).
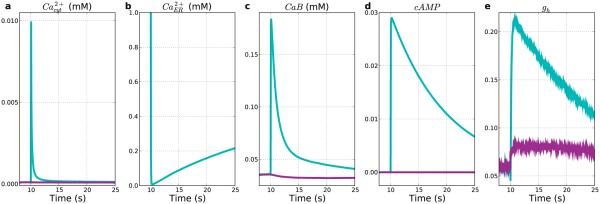
Figure 6. Stimulation produces both Ca2+ influx and release from intracellular stores.
Stimulated E5 cell averages (light-blue) vs. non-stimulated E5 cell averages (purple). (a) Transient cytosolic Ca2+ rise. (b) ER calcium depletion (non-stim value out of range). (c) Buffered Ca2+ increases in stimulated. Decrease in non-stimulated due to reduced influx with hyperpolarization. (d) cAMP. (e) Normalized HCN conductance (gh).
Upon stimulus-induced calcium influx, the level of calcium buffering proteins (B) bound to calcium (CaB) increased rapidly for the stimulated population (Fig. 6c), preventing the high levels of free cytosolic calcium which can cause excitotoxicity (Neymotin et al., 2013, Taxin et al., 2014, Seidenstein et al., 2015). After stimulation, the calcium-bound buffer levels gradually decayed as calcium was taken up into the ER and expelled via the calcium extrusion pumps. CaB for the non-stimulated population decayed due to hyperpolarization in non-stimulated cells reducing influx and decreasing intracellular calcium.
Upon stimulation, the calcium influx into the cytosol provided the preparatory steps for persistent activity, causing cAMP to increase and remain high in the stimulated population (Fig. 6d). During the stimulation itself, HCN channel conductance (gh) declined briefly due to the immediate effect of stimulus-induced depolarization (Fig. 6e). Thereafter, increased inhibition from feedback interneurons reduced stimulated-cell potential, thereby permitting rapid conductance increase, due to the quick responsivity of conductance to voltage change (Harnett et al., 2015), contrasted with the slower second messenger effects. In this way, HCN channel activation and its role in persistent dynamics was critically dependent on network effects, namely ongoing inhibition from the highly activated E → I pathway, as well as on the intrinsic chemophysiological effects of increased second messenger. Similarly, the non-stimulated population showed a slight increase in gh, caused by hyperpolarization due to augmented inhibitory input. However, in the absence of second messenger, this had little effect on the non-stimulated population.
3.4 Targeted stimulation of cortical layers
Cortical layers receive layer-specific inputs from other parts of cortex and from other brain areas (Hooks et al., 2013, Suter and Shepherd, 2015). We tested the effects of inputs into individual layers, stimulating the same number of cells in each case (Fig. 7). In the baseline simulation, activity in the stimulated layer remained confined to that layer. Duration of activity, measured by time from stimulus until the activated neuron rates dropped below 10 Hz, was about 40 s with either individual or all-layer stimulation (Fig. 7a). This differed considerably from the ~60 s seen with stimulation of an isolated L5 pyramidal cell (not shown), due to feedback inhibition in the network. Compared with the other 2 stimulation locations, L5 stimulation provided a different activation pattern with lower rate but with an initial plateau period of 15 s before activity decay. This appeared to be a network consequences of the higher density of interconnectivity among E5 cells compared to other layers. The only prominent cross-layer effect was seen with stimulation of L2/3 (Fig. 7a left column) which provided strong feedforward inhibition in L5. Activation across all layers largely overcame this downward inhibition (Fig. 7 right column). As with L5 focal stimulation, all-layer activation produced an initial plateau and abbreviated activity duration in L5..
In order to assess the influence of excitatory/inhibitory balance (Table 2) (Weiler et al., 2008), we also assessed the network with higher internal excitatory gain (Fig. 7b). This gain increase generally produced longer response durations, except that L5 stimulation paradoxically produced a weaker and shorter response (32 s) despite the increase in excitatory strength compared to the baseline network. Instead of interlayer feedforward inhibition from L2/3 to L5, this network showed feedforward excitation with interlayer activity propagation. Stimulation of all layers now produced more prolonged activation with some spread from stimulated to non-stimulated cells.
3.5 Prolonged weak stimulation also activated network
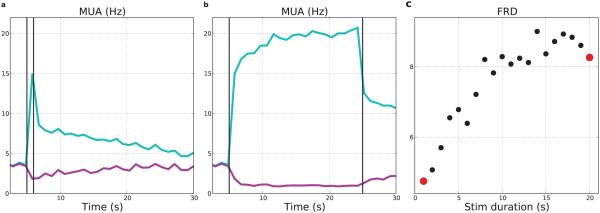
Prolonged weak (10% strength) stimulation also produced increases in the firing rate of the stimulated population with further augmentation with greater duration of stimulation (Fig. 8). Weak stimulation produced a less sharp increase in firing rates than was seen with the stronger stimulation and peak rates were reduced, even with 20 seconds of stimulation. In this low-strength case, the stimulated cells’ calcium transients were broader due to lengthier stimulation, but reached a lower peak. Post-stimulus firing-rates of stimulated neurons increased from 7.8–11.2 Hz with stimulus duration. Increased excitatory firing promoted higher firing of interneurons, which also increased slightly with stimulus duration (average from 6.0–6.8 Hz). As a result of increasing inhibition, the non-stimulated E neurons decreased their post-stimulus rates with increased duration (average 2.6–1.8 Hz). We quantified the degree of activation of the stimulated population by comparing it to the firing rate of the non-stimulated cells. We defined a firing-rate distinction (FRD) measure as the average ratio of firing rates for stimulated versus non-stimulated E cells measured by multiunit activity (MUA) over the first 5 s following stimulation (Fig. 5b). FRD increased nearly linearly over stimulus durations from 1–14 s, and then saturated with longer duration stimulation (Fig. 8c). As with the brief, strong stimulation, high firing rates persisted after the stimulation was turned off, albeit at a lower level, and produced suppression of the non-stimulated E neurons (purple line).
Figure 8. Longer-duration weak stimulation produces firing-rate distinctions.
Stimuli were 0.1× baseline strength used in other figures. (a) MUAs in response to 1 s stimulus. (b) MUAs in response to 20 s stimulus. (c) FRD in response to 1–20 s stimulus durations (red dots from (a), (b)) (50% E cells all layers; MUAs with 1000 ms bins of stimulated: light-blue; non-stimulated: purple)
3.6 Neuronal ensemble dynamics during persistent activity
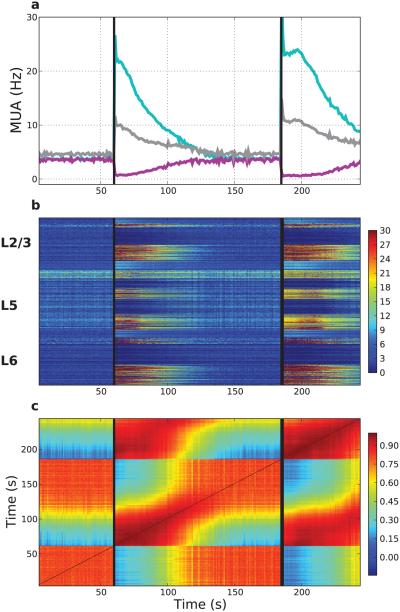
Stimulation of persistent activity was repeatable with similar overall activity as well as specific activity pattern (Fig. 9). The baseline state ensemble activity could be distinguished from that of the stimulated state by noting the change in activity vectors (Fig. 9b), with different elements and layers showing somewhat different degrees of persistence – note that the strands of activation are of different lengths in different layers. The activated state provided a reproducible firing pattern (Fig. 9c). The strong correlations in the block starting at (x, y) coordinates (185 s, 60 s) in Fig. 9c demonstrates that the activity after the second stimulation starting at 185 s is very similar to the activity after the first stimulation at 60 s. The pattern of the activated ensemble is also highly self-similar in each case (red at both the (60,60) – (100,100) block and and (185,185) – (250,250) block), demonstrating the persistent activity in the same subset of cells. Baseline activity ((0,0) – (60,60) block and (150,150) – (185,185) block) also shows self-similarity but was less stereotyped (lower overall correlation). This baseline activity was also recurrent as seen in the correlation in the block from 150,0 – 185,60. Values for the overall correlations are given in Table 4. Low similarity across pre-stimulation and post-stimulation states can be seen in the blue-green blocks – e.g., that between the first persistent-activity state (after 60 s) and the first baseline state (starting at time 0 s) is 0.45 as seen in the block from 60,0 – 80,60.
Figure 9. Network ensemble dynamics show distinct states at baseline and during expression of persistent activity.
(a) Persistent activity lasts >60 s after each identical AMPAR/NMDAR/mGLUR stimulation. Vertical lines represent the stimulus times (60, 185 s; same population of 50% of E neurons across layers). MUA created with 1 s bins. Purple (light-blue) represent stimulated (non-stimulated) E neurons; gray MUA of interneurons. (b) Firing-rate vectors (1 s intervals) transition at onset/offset of persistent activity. Color at time= x, neuron= y represents the firing rate of neuron y during the 1 s interval at time x. Neurons arranged in layers from top (L2/3) to bottom (L6). (c) Pairwise Pearson correlations between all firing rate vectors from (b). Color at times t1 = x, t2 = y indicates Pearson correlation between firing-rate vectors at those times.
Table 4.
Firing rate correlation vectors demonstrate distinct network states. Baseline and Persistent indicate baseline activity and persistent activity states, respectively. Average Pearson correlations ± standard deviation for all pairs of firing rate vectors across states are reported. × indicates value reported above.
| Time period | 0–60 (Baseline) | 60–126 (Persistent) | 126–185 (Baseline) | 185–245 (Persistent) |
|---|---|---|---|---|
| 0–60 (Baseline) | 0.808±0.053 | 0.451±0.198 | 0.797±0.054 | 0.318±0.153 |
| 60–126 (Persistent) | × | 0.844±0.125 | 0.513±0.193 | 0.819±0.135 |
| 126–185 (Baseline) | × | × | 0.809±0.037 | 0.373±0.157 |
| 185–245 (Persistent) | × | × | × | 0.909±0.068 |
3.7 Excitation/inhibition (E/I) balance modulates persistent activity
Classically E/I balance is considered as a fundamental attribute of network dynamics, balancing activity between the pathological extremes of epileptiform activity (too much E) and inactivity (too much I). This balance also plays this primary role in the current simulation. However, in addition, inhibition was permissive for stimulation-induced persistent activity due to its role in preventing deactivation of Ih through excessive depolarization due to synaptic excitation and due to depolarization from Ih itself (Eh) at −30 mV with m∞h inflection at about the same voltage location depending on [Ca++]i (Fig. 3).
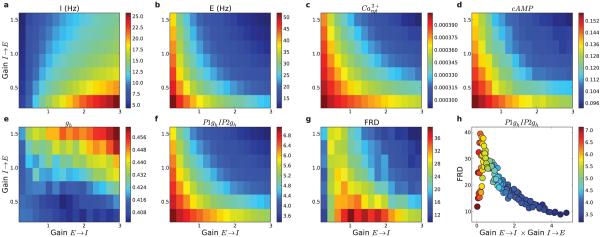
Changing the static synaptic weights from E → I neurons, and from I → E neurons, set the overall dynamic level of inhibition in the network. The dynamics of this feedback inhibition was approximately proportional to the product of E→I and I→E synaptic strengths, due to the E→I increasing I cell firing which then produced negative feedback via the I→E weights. Due to this relationship, inhibition increases from bottom-left to top-right in Fig. 10. The dynamic level of inhibition was reflected in neuronal firing rates (Fig. 10a,b) and in the overall activation of gh (Fig. 10e). Increasing the synaptic weights along the E→I pathway tended to cause the I firing rates to increase (Fig. 10a). As the E cells activated I cells more strongly, the extra feedback inhibition decreased E firing rates (Fig. 10b). Increasing synaptic weights from I→E cells hyperpolarized the E cells and dampened their activity. When weights from E→I cells were set to zero, the I firing rates were sparse.
Figure 10. Modulating E→I (15 levels) and I→E (8 levels) synaptic weights shapes firing rates and intracellular molecular activations.
(a) Interneuron and (b) excitatory neuron firing rates after stimulation. (c) Peak cytosolic calcium (mM) in stimulated excitatory cells. (d) cAMP and (e) gh of stimulated E cells. (f) Stimulated to non-stimulated gh ratio. (g) FRD (firing-rate distinction). (h) FRD as a function of network inhibition estimated by E→ I×I→ E (16 s simulations; color indicates average ratio of gh in stimulated P1 vs non-stimulated P2 populations).
The modulation of firing rates and the overall depolarization level of E cells influenced the level of stimulus-induced calcium transients via VGCCs and voltage-sensitive NMDA Ca2+ flux (Fig. 10c). Calcium transients in E cells were largest when there was minimal inhibition in the network. Elevated calcium, as a second messenger, then produced additional intracellular molecular effects. The availability of cytosolic calcium after a stimulus translated directly into the level of cAMP (Fig. 10d), with values increasing in parallel with cytosolic calcium. Once cAMP increased, it contributed to regulating HCN channel activation (gh; Fig. 10e). However, in addition to Ca2+ control, gh is also voltage-sensitive, being deactivated by depolarization. Activation of gh (Fig. 10e) therefore did not follow the patterns of cAMP (Fig. 10d) but instead nearly mirrored it, with large values at high levels of inhibition.
The ratio of gh for stimulated vs. non-stimulated cells supported stimulus-specific representations due to these molecular/cellular mechanisms (Fig. 10f). This ratio was maximally activated over a relatively narrow crescent-shaped region of E→I and I→E gains with moderate overall inhibition. At values above and to the right of the crescent, high inhibition controlled HCN channels through voltage effects so that the calcium transients no longer provided primary regulation of the HCN channel dynamics of the stimulated population.
FRD followed a similar crescent-shaped pattern, with maximal activation at moderate levels of inhibition (Fig. 10g). At these levels of inhibition, there was sufficient cytosolic calcium to regulate HCN channels in a population-specific manner, and adequate inhibition to activate HCN channels (Fig. 10f,h). At the lowest E → I synaptic weights interneuron firing rates were sparse (left-most column in Fig. 10a), and when I → E weights were also low, there was not sufficient inhibition/hyperpolarization to activate HCN channels and produce substantial FRD. Increasing I → E weights at these low E → I levels caused enhanced inhibition within the network, enhanced activation of Ih, and increased FRD (rising portion of FRD in Fig. 10h). FRD then peaked at intermediate levels of inhibition. At higher E → I weights, increasing I → E weights caused high feedback-inhibition within the network, dampening the FRD response (decaying portion of Fig. 10h).
Fig. 10h shows the discrepancy between molecular and network effects, demonstrating that the molecular effects seen in the single cell model do not fully explain the persistent activity differences in the network model. Relative activation of gh, decreasing with increasing inhibition in the network (symbol color in Fig. 10h), only partially explained FRD, shown on the y-axis of Fig. 10h. Peak FRD did not occur with lowest inhibition both because low inhibition did not adequately suppress the non-stimulated population and because excessive depolarization in the stimulated cells deactivates HCN Fig. 10e.
Stimulation of both E cells and I cells rather than E cells alone produced results qualitatively similar to Fig. 10, but with reduced FRD (peaking at 31 vs 39). Stimulating the I cells directly produced additional inhibition in the network which reduced activation of the stimulated cells and reduced Ca2+ entry, consequently reducing Ih effects.
3.8 Internal vs external calcium stores
Induction of persistent activity in our model relies on calcium, which comes to the cytosol from both extracellular stores via NMDARs and VGCCs, and from ER via IP3R. We investigated the effects of modulating the relative contribution of external and internal calcium sources by regulating the strength of stimuli influencing each store (Fig. 11) and by adjusting properties of the neurons (VGCC density, calcium in ER) that lead to different relative strengths of each calcium store (Fig. 12).
Figure 11. Persistent activity can be induced via either AMPAR/NMDAR (external stores) or mGLUR (internal store) activation.
AMPAR/NMDAR and mGLUR stimulus strength were each varied independently from 0-3× baseline (n = 31), while holding the other stimulus strength constant at 1× baseline. (a) Average cytosolic calcium in the 5 s after stimulus as a function of stimulus strength of AMPAR/NMDAR (circles) and mGLUR (triangles). (b) Ratio of stimulated to non-stimulated population firing rates (FRD) as a function of stimulus strength of AMPAR/NMDAR (circles) and mGLUR (triangles).
Figure 12. Firing-rate distinction depends on both external (VGCC) and internal (ER) calcium stores, determined respectively by voltage-gated calcium channels (VGCC) density and ER [Ca2+].
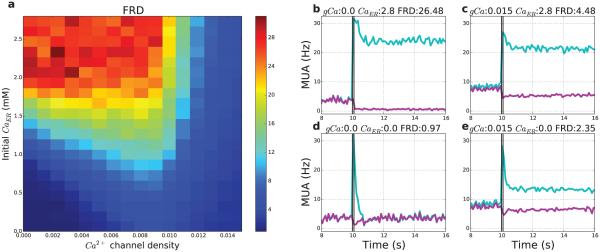
(a) N = 336 21 s simulations were run varying the density of VGCCs (x-axis) from 0–0.015 nS/cm2 (n = 16 levels), and the concentration of calcium in the ER (y-axis) from 0–2.8 mM (n = 21 levels). (b–d) Differences in MUA (light blue: stimulated; purple: non-stimulated; bin size 100 ms) and FRD; examples taken from four corners of (a). (b) High internal stores (upper left of Fig. 12): Absence of VGCCs (0.0) with high ER calcium concentration (2.8 mM) allows for high FRD (26.48); (c) High internal and external stores (upper right of Fig. 12): High density of VGCCs (0.015 nS/cm2) with high ER calcium (2.8 mM) produces moderate FRD (4.48); (d) No Ca2+ stores (lower left of Fig. 12): Absence of VGCCs with zero initial ER calcium produces low FRD (0.97); (e) High external stores (lower right of Fig. 12): High density of VGCCs (0.015 nS/cm2) with zero initial ER calcium produces moderate FRD (2.35).
Varying the strength of ionotropic (AMPAR/NMDAR) vs metabotropic (mGluR) stimulation regulated FRD (Fig. 11). The AMPAR/NMDAR stimulus strength both directly regulated depolarization/firing produced by stimulation, and also admitted calcium via both NMDARs and VGCCs, and produced augmentation of both [Ca2+] and activity. Peak [Ca2+] was less in the absence of AMPAR/NMDAR stimulus, since Ca2+ was then sourced from the limited ER stores. With increased AMPAR/NMDAR stimulus strength calcium continued to increase, whereas it plateaued with increased mGluR strength (Fig. 11a). The differences in calcium transients from differential AMPAR/NMDAR activation translated into differences in the FRD (Fig. 11b). There was a nearly linear [Ca2+] increase with AMPAR/NMDAR translated into a sigmoidal FRD while the saturating [Ca2+] response from mGluR produced a more rapid increase in FRD, with both plateauing at an FRD value of ~25. In the regime of 0-1 gain of AMPAR/NMDAR, it appeared that stimulus strength could be encoded by the FRD, the differential activation of the two populations of neurons.
Simultaneously increasing the AMPAR/NMDAR and mGluR stimulus strengths had only a small additional impact on calcium transients, with increases adding sublinearly. Increases in calcium transients at high stimulus strengths did not translate into substantial increased FRD, due to Ca2+ buffering and extrusion pumps quickly clearing cytosolic Ca2+, and preventing it from impacting HCN channel dynamics.
With low Ca2+ availability from both sources (VGCCs and ER; Fig. 12d and lower left), the FRD was low, because of insufficient calcium to trigger a post-stimulus response. High entry from external stores only (high VGCC density) produced an increase in pre-stimulus firing, a small increase in post-stimulus firing, and weak suppression of non-stimulated neuron activity, resulting in moderate FRD (lower right and Fig. 12e). High entry from from both stores (upper right and Fig. 12c) caused a substantial increase in FRD due to higher post-stimulus firing rates which led to more suppression of non-stimulated neurons. The highest FRD was seen with low flux from external and low to mid flux from internal stores (upper left, Fig. 12b and left middle), which resulted in the largest increase in stimulated neuron firing, and the largest suppression of non-stimulated neurons. Overall, FRD increased along the y-axis of Fig. 12a, in proportion to initial ER calcium levels, because ER Ca2+ only contributes to cytosolic calcium due to stimulation. In contrast, FRD tended to have an inverted-U relationship with VGCC density (x-axis around y=1.0) because increasing VGCC density allowed post-stimulus Ca2+ influx, but at high levels produced increases in baseline firing of both populations both before and after the stimulus, which reduced firing-rate distinction.
We also modified the FRD measure for use in single cell simulations by taking the ratio of post-stimulus firing rate to baseline firing rate; across the same set of variations in VGCC density and initial ER Ca2+, qualitatively similar results were found (data not shown).
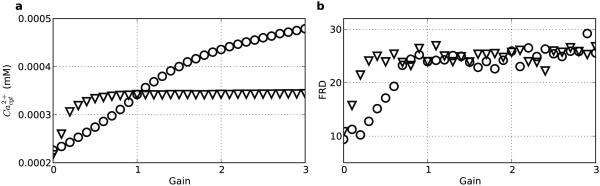
3.9 Free calcium regulates persistent activity
Modulating the plasma membrane calcium extrusion pump time constant (τex) altered calcium levels, with downstream effects on the network’s ability to display calcium-dependent persistent activity and stimulus-specific representations (Fig. 13). Both stimulation-induced calcium transients and post-stimulus calcium levels increased as the calcium extrusion pump τex increased (Fig. 13a). This pattern was evident for both the stimulated (light-blue) and non-stimulated (purple) population, although at any τex, the stimulated population had a higher calcium concentration due to stimulation it received. At a fast τex of 0.5 ms the extrusion pump cleared cytosolic calcium quickly, with pre-stimulus calcium levels for both populations being reduced to low levels. The fast action of the extrusion pump also reduced the stimulation-induced calcium transient, which was considerably smaller than at the baseline τex of 5 ms (2.5 vs 13 μM). With this fast τex, the calcium was more quickly cleared after stimulation, leaving only a small amount of calcium available to impact HCN channels, and producing a relatively low FRD (1.2). With slow calcium extrusion (τex=20 ms), pre-stimulus calcium levels were rising for both populations prior to stimulation, since the calcium clearance rate was less than the rate of cytosolic calcium entry from NMDA/VGCC/ER leak calcium channels. Stimulation also produced a large calcium transient of 50 μM, which decayed more gradually. As a result of the slow clearance rate of calcium, the calcium remained elevated in the stimulated population longer, contributing to positive feedback and increasing modulation of the stimulated population’s gh. These factors allowed the stimulated population to dominate the network dynamics, creating a large overall FRD (20). As τex increased, the ratio of calcium in the two populations showed an initial sharp rise followed by a slower rise (Fig. 13a black points). FRD, which depends on calcium-regulation of HCN channels, also showed a similar relationship with the calcium extrusion pump τex (Fig. 13b).
IP3R density increase allowed release of more Ca2+ from ER after mGluR activation (not shown). Changes between 0–3× baseline modulated calcium transients (0.003–0.014 mM) and increased FRD over a substantial range (12–28). The value with low IP3R density reflected a situation where primary Ca2+ came in from extracellular sources, less effective in the absence of any internal release as shown in Fig. 12. Increasing IP3R demonstrated a synergy between Ca2+ sources.
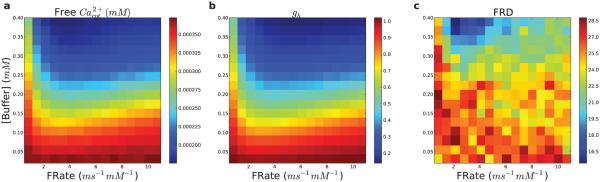
Modulating calcium buffer efficacy (F Rate× buffer concentration) altered the ability of free calcium to contribute to persistent activity (Fig. 14). Buffering affects the motility and amount of free calcium. Increased buffer prevented calcium from being taken up and stored in the ER. Overall, the amount of calcium released from the ER upon stimulation was inversely proportional to the buffer efficacy, with 1.1 vs. 1.2 mM calcium released at high and low buffering efficacy, respectively. However, with low buffering efficacy, the ER calcium levels were only slightly larger than low buffering efficacy, since ER stores were initialized to 1.25 mM and were only allowed 5 s to refill. Increased buffering efficacy meant more Ca2+ bound prior to stimulation and less available to be taken into the ER, while at the same time reducing baseline Ca2+ effects on HCN channels. Increases in buffering efficacy also decreased the Ca2+ transient with stimulation (Fig. 14a) – free Ca2+ availability was primarily a function of buffer concentration with an effect of F Rate primarily at the left margin. HCN channel activation showed a similar response profile (Fig. 14b) but FRD alterations were more patchy since FRD is based on effects on the non-stimulated as well as on the stimulated cells (Fig. 14c).
Figure 14. Ca2+ buffering alters free Ca2+ availability for modulation of Ih.
Forward rate (FRate) of binding (x-axis) and buffer concentration (y-axis) varied. (a) Cytosolic calcium transient in response to stimulus. (b) HCN activation (gh) in response to stimulus. (c) Firing-rate distinction: average ratio of firing rate of stimulated population to non-stimulated population during 5 s interval after stimulus. (n = 16 × 16)
4 Discussion
We developed a multiscale neocortical model from molecular to network level by evaluating a model of HCN modulation via a second-messenger signaling cascade at cell and network scales. This model displayed the persistent activity that has been hypothesized to contribute to cognitive, mnemonic and behavioral functions that require the maintenance of state over a period of seconds (Ames et al., 2014, Cossart et al., 2003, Goldman-Rakic, 1995, Major and Tank, 2004). The model confirmed prior simulations that showed how the molecular dynamics of calcium regulation of HCN channels Fig. 6) could produce persistent electrical activity at the single cell level (Fig. 4). Embedding these molecular models into cells within a network produced emergent effects based on interactions between excitatory and inhibitory neurons (Fig. 5, Fig. 10), and the specific details of neocortical architecture (Fig. 7).
4.1 Scale overlaps in neural systems
To a greater extent than in other bodily organ systems, the nervous system features an interplay of scales which makes encapsulation of one scale for use in a higher scale difficult. A weakness of the widely-used point-neuron model is the encapsulation of activity in a single input-output dynamic which not only omits obvious non-point interactions such as dendrodendritic synapses (Rall and Shepherd, 1968), but also subtle interactions such as that between signal integration in apical dendrite and signal integration in local microcircuit (Lytton et al., ). By contrast, the multiscale modeling approach used here builds interacting scales into a coherent model which allows us to explore these interactions across levels of organization (Sejnowski et al., 1988). In the present simulations, we focused on calcium and on multiple roles for inhibition, bridging from the molecular to cellular and network scales (Lytton and Sejnowski, 1991, Neymotin et al., 2011). Synaptic connectivity and Ca2+ handling intersected at multiple locations, including the interplay between extracellular and intracellular sources of Ca2+.
Due to these second-messenger roles, inhibition plays a major role in activity maintenance through its influence on preventing depolarization with deactivation of Ih, while at the same time contributing to activity suppression. Hence the activity maintenance that is classically attributed to excitatory/inhibitory balance is here also provided within the context of inhibitory tone (Fig. 10). We defined dynamic inhibition as a network balance which itself depends on balance provided by E → I and I → E strength across multiple cell subpopulations in neocortex, as well as on the excitability of the inhibitory cells. Changes in Vmemb alters Ca2+ flux through VGCCs based on both Vmemb and [Ca2+ ] via the Goldman-Hodgkin-Katz equation, as well as through NMDARs based on voltage sensitivity. As has been noted in other models and in tissue, synaptic bombardment greatly altered both membrane potential and input impedance with multiple subsequent effects (Bernander et al., 1991, Destexhe et al., 2003b). Overly high inhibition dampened neuronal firing while moderate inhibition was consistent with persistent activity over a wide range of parameter settings.
Calcium plays a pivotal role as a second messenger in many neural signaling pathways (Blackwell, 2013, Evans and Blackwell, 2015). Our model evaluated various scenarios regarding Ca2+ sourcing, Ca2+ removal, Ca2+ binding, and time constants of interaction with target molecules. Calcium in cytosol comes from the extracellular space, modeled here as an inexhaustible source, and from organelles which are exhaustible. Compared to mitochondria, ER is likely to be a more accessible Ca2+ source across multiple locations including spines – it spreads diffusely throughout the neuron, foliating at key points to provide additional surface area (Shemer et al., 2008, Berridge, 1998).
As part of being exhaustible, intracellular sources need to be replenished. Therefore our model implicitly required priming in order to be set up to produce Ca2+-mediated persistent activity. We predict that interventions that reduce intracellular stores or prevent their replenishment would have an adverse effect on these mechanisms. Ca2+ handling is strongly affected by binding, made more complex by the existence of different binding proteins with different affinities and mobilities, many specific to particular cell types (Schwaller, 2010). In our highly simplified model, we considered only a single diffusible binding protein. Increased binding reduced calcium availability which led to reduced priming for persistent activity as well as less availability for its direct effects after stimulation.
4.2 Predictions
Our model makes the following experimentally testable predictions.
Relative activation of E and I neurons has indirect effects on excitability via Ca2+-mediated second-messenger cascades as well as direct effects. Testable with stimulation of different subsets of neurons (i.e., E vs. I) using optogenetics (Tonnesen et al., 2009, Suter et al., 2014) while imaging calcium (and ideally cAMP as well).
Stimulus-specific persistent activity is only viable in the presence of moderate inhibition. Excessive inhibition dampens activity and prevents calcium influx from enabling persistent activity. Disinhibition produces high cytosolic calcium levels in all neurons, causing all neurons to fire at high rates, and lose stimulus-specific information. Testable in vitro by regulating excitability of localized populations of neurons via injectrode application of muscimol (GABAAR agonist) to increase inhibition or bicuculline/gabazine (GABAAR antagonists) to decrease inhibition.
In contrast to attractor network models that display a permanent up-state (Wang, 1999a, Wang, 2001), our model predicts that persistent activity will have a limited duration with an upper bound dictated by the multiple time constants associated with Ca2+ and cAMP regulation of HCN channels. Testable in vitro (Winograd et al., 2008) with intracellular recordings while providing tonic low-grade electrical stimulation followed by heightened stimulation to induce persistent activity, and measuring the duration of increased firing rates.
4.3 Compensation, complementarity and synergy
Nervous systems, and biological systems in general, utilize multiple pathways for critical functions. This multiplicity is the key to the adaptability and robustness of these complex systems. This seeming extravagance of mechanism can be arrayed along a spectrum from full redundancy at the one extreme, to the case where a separate system B with an entirely non-overlapping function can nonetheless be called into service to compensate when a system A is compromised or lost. Full redundancy provides a full backup copy – such redundancy may be present in the case of critical messenger peptides or proteins that might be produced without relevant variation from different genes to forestall disastrous mutation. Our simulations showed some degree of redundancy: activation of persistent activity depended on two stores of calcium. The internal store is potentially exhaustible; in case of failure, additional Ca2+ can be drawn from extracellular stores.
Systems that feature both compensation and complementarity rather than full redundancy are likely to be more common. Complementarity implies some degree of redundancy, but with major differences that give additional features and advantages. The simulations evinced complementarity in the ability of stronger excitatory mechanisms (Fig. 7b) to provide transfer of activation along the network circuitry, while large internal Ca2+ stores provide the substrate for activating the Ih mechanism. Additionally, the different sources of cytoplasmic calcium, intra- and extracellular, each introduced different time courses of activation that could be utilized for nuanced learning algorithms based on relative degrees of activation of ionotropic and metabotropic glutamate receptors.
Moving further along this spectrum, we can consider to what extent these systems are synergistic, working together in a way that produces advantages that neither system would provide individually. We can infer synergy from the many points of interaction between the molecular and network mechanisms which demonstrate persistent activity. For example, excitation has its effects at two very different time scales associated with the mechanisms at different spatial scales. It has immediate effects on membrane potential to activate sets of cells. This activity can then be prolonged due to the relatively long voltage-dependent currents provided by NMDARs. Still slower and longer activations can then be provided by the molecular effects via IP3 and interaction with internal stores. These activations work together synergistically, boosting the duration of persistent activity. This is still only the tip of this iceberg since the triggering of these multiple intracellular signaling pathways will produce subsequent interactions with the nucleus and genome.
4.4 Network effects
The network showed emergent effects not predictable from the single neuron simulations, through recurrent network loops that provided both excitation and inhibition. Inhibition dominated in our baseline network, strongly reducing activity in non-stimulated cells. This feedback-driven inhibition provided our simulated network with an off switch to terminate persistent activity earlier than in the single cell. Truncating the activation would also ready a network to more quickly switch internal representations, and also provide energy-saving. Differences in wiring among different layers of cortex produced longer persistent activity in L2/3 and L6 compared to L5. These differences are likely to have functional consequences due to the different sources/targets of each layer’s inputs/outputs (Hooks et al., 2011). Temporally precise interactions between excitatory and inhibitory neurons also produced alpha (14 Hz) oscillations (Lytton and Sejnowski, 1991, White et al., 2000, Neymotin et al., 2011), which shifted to beta (20 Hz) upon induction of persistent activity, due to the increased firing rates of stimulated excitatory neurons.
In addition to providing a memory mechanism, persistent activation in the network could enhance input/output for a column or for a layer in a column in a number of ways. Neurons in an activated layer are “prepared cells,” with enhanced responsiveness to subsequent synaptic inputs due to having depolarized potentials nearer to threshold and having fast time constants that enable them to respond quickly to inputs (Bernander et al., 1991). We found that individual cortical layers could also be turned on into a persistent firing state (Fig. 7). An activated layer would better respond to inputs in order to route information to its distinct cortical and subcortical targets (Hunter et al., 2006, Fukushima et al., 2012, Schroeder and Lakatos, 2012, Kumar et al., 2013).
Similarly the major interlaminar route from L2/3 to L5 could be primed and set up to permit signal flow-through. In this respect our simulated network displayed suppressive and facilitating output modes (Fig. 7 left column). The switch between modes could be effected by neuromodulation by acetylcholine which can increase excitatory tone in neocortex (Carcea and Froemke, 2013, Hasselmo and McGaughy, 2004, Hsieh et al., 2000, Giocomo and Hasselmo, 2007). Excitatory strength determined the magnitude of L5 activation, the major cortical output layer for both intratelencephalic and descending outputs (Kiritani et al., 2012b, Yamawaki and Shepherd, 2015, Anderson et al., 2010). In suppressive mode (Fig. 7a left), targeted stimulation of L2/3 suppressed L5 via strong top-down inhibition from activated E2 → I5L → E5 cells. In this mode, the cortical circuit might monitor signals arriving at L2/3, a major input layer (Petersen and Crochet, 2013) without passing that information on. Increasing E → E synaptic weights shifted the network into a facilitating mode (Fig. 7b left), which activated the strong top-down excitatory projections from L2/3 → L5 (Fig. 7b left) (Weiler et al., 2008). The network model also showed that stimulation of all cortical layers together with E → E augmentation, produced an additional degree of facilitation (Fig. 7b right).
The simulated network could also sense stimulus magnitude (Fig. 11) and duration (Fig. 8) in progressive levels of persistent activation providing further gradations of encoding. During tonic low-strength stimulation, the stimulated neurons displayed a gradual rise in firing rates, which may allow the neurons to slowly accumulate stimulus-related evidence. As stimulus-related evidence gathers in competing neuronal assemblies, the assembly with the highest firing rate could dominate cognitive representations (winner-take-all) or multiple assemblies could remain active to varying degrees.
The model demonstrated repeatable persistent activity patterns which could contribute to identifiable features of neural representation and memory function in vivo. Stimulation caused activation of an ensemble, which then represented the pattern in a reproducible ensemble activation pattern across the network (Fig. 9). This dynamic representation could be utilized as a form of short-term memory via ensemble encoding for a particular stimulation pattern (Durstewitz et al., 2000, Goldman-Rakic, 1995, Quiroga and Panzeri, 2009, Ghitza, 2011, Barbieri et al., 2005).
4.5 Inter-scale interactions produce persistent activity
Many prior models of persistent activity have focused only on cellular, or only on network, dynamics. Our model is unusual in that we develop a multiscale composite of a subcellular-scale model of calcium-induced calcium release (CICR) (Neymotin et al., 2015), a cellular-scale model of hyperpolarization-activated graded persistent activity based on Ih modulation (Winograd et al., 2008), and a network-scale neocortical model (Neymotin et al., 2011a, Chadderdon et al., 2014, Neymotin et al., 2011). The multiscale model demonstrates many points of inter-scale interaction that would not be fully captured by a series of simplifications, encapsulations and embeddings, such as the classical approach of the point-neuron approximation with its simple input/output function. Due to the inter-scale interactions, our cellular model showed additional dynamics based on the endoplasmic reticulum’s role in Ca2+ handling. Inter-scale interactions are perhaps most clearly seen where network effects meet Ca2+ effects at the nexus of Ih: calcium control of HCN is preparatory for Ih activation through relative hyperpolarization from inhibitory network effects. The network model largely followed the pattern of activity set by the cellular model, but showed additional features due to the complexities of multiple types of inputs, to the competing roles of excitation and inhibition, and to the complexity of inter-laminar wiring.
Ih, appears to have a major role to play in the dynamics of both cells and networks. In addition to the role in providing persistent activity, it also has large effects in maintaining resting potential, augmenting somatic sub-threshold resonance, and determining dendritic subthreshold responses (Accili et al., 2002, Chen et al., 2001, Santoro and Baram, 2003, Zemankovics et al., 2010, Dyhrfjeld-Johnsen et al., 2008, Dyhrfjeld-Johnsen et al., 2009, Poolos et al., 2002). Further complexity at the network levels, not explored in this study, arises from inhomogeneous distributions of HCN isoforms and HCN density in different cell types, differential dendritic expression in pyramidal neurons and colocalization with other ion channels (Accili et al., 2002, Aponte et al., 2006, Bender et al., 2001, Santoro and Baram, 2003). Additionally Ih is under subtle second messenger control, likely through more than the one effect used in this model. Multiple functions, multiple types, and multiple routes for modulation make HCN channels potent control points in the circuit.
Our model is consistent with a variety of experiments which have demonstrated that Ih contributes to neuronal persistent activity: calcium regulates HCN channels and firing dynamics in cat sensorimotor cortex neurons (Schwindt et al., 1992); blocking Ih pharmacologically with ZD7288 abolishes persistent activity in supra- and infra-granular pyramidal neurons from prefrontal cortex of ferrets and guinea pigs (Winograd et al., 2008), and in mouse prefrontal cortex pyramidal neurons (Thuault et al., 2013); HCN channels dynamically regulate resting membrane potential and cellular excitability (Thuault et al., 2013, Neymotin et al., 2013) after neuromodulators increase Ih (Heys and Hasselmo, 2012, Tsuno et al., 2013, Wang et al., 2007). However, cAMP reduced persistent activity in primates suggesting that it also has plays some countervailing roles (Arnsten et al., 2010, Wang et al., 2007). cAMP controls a number of other channels and other cytosolic processes that were not included in our model, including augmentation of K+ flux (e.g., KCNQ) that would reduce cellular excitability (Arnsten and Jin, 2012). HCN channels and certain voltage-sensitive K+ channels (Kv) are colocalized along the apical dendrites (Harnett et al., 2013) which would allow HCN and K+ channels to interact competitively, with HCN channels contributing to a neuronal excitability dampened by Kv (Poolos et al., 2002, Migliore and Migliore, 2012). Overall effects would then depend on relative sensitivity to cAMP, which could be effected through a level of meta-modulation via both intrinsic factors and external neuromodulators.
In the current study, we see how a persistent activity attractor landscape can be formed by complementing the effects of mutual excitation with the multiple complementary effects of excitatory and inhibitory interactions across cortical layers (Papoutsi et al., 2013, Papoutsi et al., 2014, Nelson et al., 2003, Marder et al., 1996). By contrast, Wang’s “bump attractor” network model was based on localized connectivity in a single layer of integrate-and-fire neurons (Compte et al., 2000, Wang, 2001). That model produced persistent activity through reverberant NMDAR excitatory activation. In that model NMDAR activation outlasted the effects of fast GABAA activation, with no slower effects from slower dendritic GABAA or from GABAB inputs. Although adding many features, our model is generally consistent with the Wang model, since it demonstrates the importance of excitatory tone in shaping the network’s response to targeted stimulation and eliciting interlayer activity propagation. However, a major difference from the bump attractor model is that our network wiring has cortical layering (y-direction) as the major geometrical feature in addition to minor lateral fall-off in connectivity (x-z plane). Our network therefore did not produce enhanced activation of a highly localized subset of strongly interconnected cells – the localized bump.
We attempted to include major neurobiological features that would allow us to assess the many inter-scale interactions that make the dynamics of the local neocortical network so complex and so fascinating. We necessarily left out many important features, both due to computational limitations and due to the fact that many of these are not understood in sufficient detail for us to adequately portray. Additionally, we of course left out many unimportant features, a key role of modeling being to eventually determine which are the important and which the unimportant parameters related to a given functional outcome. Additional features that would be valuable to more fully understand persistent activity include ICAN cationic currents (Egorov et al., 2002, Tiganj et al., 2015), persistent sodium channels (Oikonomou et al., 2014, Zhou et al., 2015), and neuromodulatory synaptic receptors such as acetylcholine and dopamine (Sawaguchi and Goldman-Rakic, 1991, Sidiropoulou et al., 2009). A further omitted feature that is believed to be important is the aforementioned distribution of HCN isoforms by cell type and location. An additional unexplored consideration is our limited approximation of Ca2+ handling due to the use of homogeneous diffusion that does not incorporate the important roles of localized subdomains due to molecular barriers, fixed buffers, and colocalizations of targets. Incorporation of some of these considerations will bring us near to the domain of molecular dynamics, a further scale of exploration that remains to be incorporated at some, perhaps remote, future date.
Acknowledgments
The authors would like to thank Ben Suter (Northwestern) for help with the model; Herman Moreno (SUNY Downstate) and Mohamed Sherif (SUNY Downstate, Yale) for discussions; Tom Morse (Yale) for ModelDB support. The authors declare no competing financial interests. Research supported by NIH grant R01 MH086638, NIH grant U01 EB017695, NIH grant T15 LM007056, NIH grant R01 NS11613, and NIH grant R01 DC012947. The NIH had no role in study design; in the collection, analysis and interpretation of data; in the writing of the report; and in the decision to submit the article for publication.
Abbreviations
- Ca
calcium
- E cell
excitatory cell
- E2/3 or E2
excitatory cell of layer 2/3, similarly E5,E6
- E/I balance
excitation/inhibition balance
- ER
endoplasmic reticulum
- FRD
firing-rate distinction
- FS cell
fast-spiking soma-targeting interneurons
- HCN channel
hyperpolarization-activated cyclic nucleotide-gated channel (with Ih current)
- IP3
inositol triphosphate
- IP3R
IP3 receptor
- I cell
inhibitory cell
- I2L
LTS inhibitory cell of layer 2/3 (similarly I5L, etc)
- I2
FS inhibitory cell of layer 2/3 (similarly I5, etc)
- LTS cell
low-threshold spiking dendrite-targeting interneurons
- mGLUR
metabotropic glutamate receptor
- PYR
neocortical pyramidal neuron
- RxD
reaction-diffusion
- SERCA
sarco/ER Ca-ATP-ase pumps
- VGCC
voltage-gated calcium channel
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Samuel A. Neymotin, Email: samn@neurosim.downstate.edu.
Robert A. McDougal, Email: robert.mcdougal@yale.edu.
Anna S. Bulanova, Email: anna.bulanova@downstate.edu.
Mustafa Zeki, Email: zeki.mustafa@gmail.com.
Peter Lakatos, Email: PLakatos@nki.rfmh.org.
David Terman, Email: terman@math.osu.edu.
Michael L. Hines, Email: michael.hines@yale.edu.
William W. Lytton, Email: billl@neurosim.downstate.edu.
References
- Accili E, Proenza C, Baruscotti M, DiFrancesco D. From funny current to HCN channels: 20 years of excitation. Physiology. 2002;17:32–37. doi: 10.1152/physiologyonline.2002.17.1.32. [DOI] [PubMed] [Google Scholar]
- Ames KC, Ryu SI, Shenoy KV. Neural dynamics of reaching following incorrect or absent motor preparation. Neuron. 2014;81:438–451. doi: 10.1016/j.neuron.2013.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson C, Sheets P, Kiritani T, Shepherd G. Sublayer-specific microcircuits of corticospinal and corticostriatal neurons in motor cortex. Nat Neurosci. 2010;13:739–744. doi: 10.1038/nn.2538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anwar H, Hong S, De Schutter E. Controlling ca2+-activated k+ channels with models of ca2+ buffering in purkinje cells. The Cerebellum. 2012;11:681–693. doi: 10.1007/s12311-010-0224-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aponte Y, Lien C, Reisinger E, Jonas P. Hyperpolarization-activated cation channels in fast-spiking interneurons of rat hippocampus. J Physiol. 2006;574:229–243. doi: 10.1113/jphysiol.2005.104042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnsten A, Jin L. Guanfacine for the treatment of cognitive disorders: a century of discoveries at Yale. Yale J Biol Med. 2012;85:45–58. [PMC free article] [PubMed] [Google Scholar]
- Arnsten A, Paspalas C, Gamo N, Yang Y, Wang M. Dynamic Network Connectivity: a new form of neuroplasticity. Trends Cogn Sci. 2010;14:365–375. doi: 10.1016/j.tics.2010.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashhad S, Johnston D, Narayanan R. Activation of InsP3 receptors is sufficient for inducing graded intrinsic plasticity in rat hippocampal pyramidal neurons. J Neurophysiol. 2015;113:2002–2013. doi: 10.1152/jn.00833.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashhad S, Narayanan R. Quantitative interactions between the A-type K+ current and inositol trisphosphate receptors regulate intraneuronal Ca2+ waves and synaptic plasticity. J Physiol. 2013;591:1645–1669. doi: 10.1113/jphysiol.2012.245688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbieri R, Wilson M, Frank L, Brown E. An analysis of hippocampal spatio-temporal representations using a Bayesian algorithm for neural spike train decoding. Ieee Trans Neural Syst Rehabil Eng. 2005;13:131–136. doi: 10.1109/TNSRE.2005.847368. [DOI] [PubMed] [Google Scholar]
- Bartos M, Vida I, Jonas P. Synaptic mechanisms of synchronized gamma oscillations in inhibitory interneuron networks. Nat. Rev. Neurosci. 2007;8:45–56. doi: 10.1038/nrn2044. [DOI] [PubMed] [Google Scholar]
- Bender R, Brewster A, Santoro B, Ludwig A, Hofmann F, Biel M, Baram T, et al. Differential and age-dependent expression of hyperpolarization-activated, cyclic nucleotide-gated cation channel isoforms 1-4 suggests evolving roles in the developing rat hippocampus. Neuroscience. 2001;106:689–698. doi: 10.1016/s0306-4522(01)00314-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernander O, Douglas R, Martin K, Koch C. Synaptic background activity influences spatio-temporal integration in single pyramidal cells. Proc Nat Acad Sci. 1991;88 doi: 10.1073/pnas.88.24.11569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berridge M. Neuronal calcium signaling review. Neuron. 1998;21:13–26. doi: 10.1016/s0896-6273(00)80510-3. [DOI] [PubMed] [Google Scholar]
- Blackwell K. Calcium: the answer to life, the universe, and everything. In: Bower J, editor. 20 Years of Computational Neuroscience. Springer; New York: 2013. pp. 141–158. chapter 6. [Google Scholar]
- Braver T, Cohen J, Nystrom L, Jonides J, Smith E, Noll D. A parametric study of prefrontal cortex involvement in human working memory. Neuroimage. 1997;5:49–62. doi: 10.1006/nimg.1996.0247. [DOI] [PubMed] [Google Scholar]
- Burdakov D. Gain control by concerted changes in IA and IH conductances. Neural Comput. 2005;17:991–995. doi: 10.1162/0899766053491841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bygrave F, Benedetti A. What is the concentration of calcium ions in the endoplasmic reticulum? Cell Calcium. 1996;19:547–551. doi: 10.1016/s0143-4160(96)90064-0. [DOI] [PubMed] [Google Scholar]
- Carcea I, Froemke R. Cortical plasticity, excitatory–inhibitory balance, and sensory perception. Prog Brain Res. 2013;207:65. doi: 10.1016/B978-0-444-63327-9.00003-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carnevale N, Hines M. The NEURON Book. Cambridge University Press; New York: 2006. [Google Scholar]
- Castro-Alamancos M. The motor cortex: a network tuned to 7-14 hz. Front Neural Circuits. 2013;7:21. doi: 10.3389/fncir.2013.00021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chadderdon G, Mohan A, Suter B, Neymotin S, Kerr C, Francis J, Shepherd G, Lytton W. Motor cortex microcircuit simulation based on brain activity mapping. Neural Comput. 2014;26:1239–1262. doi: 10.1162/NECO_a_00602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen S, Wang J, Siegelbaum S. Properties of hyperpolarization-activated pacemaker current defined by coassembly of HCN1 and HCN2 subunits and basal modulation by cyclic nucleotide. Journal Gen Physiol. 2001;117:491–504. doi: 10.1085/jgp.117.5.491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Rochefort N, Sakmann B, Konnerth A. Reactivation of the same synapses during spontaneous up states and sensory stimuli. Cell Rep. 2013;4:31–39. doi: 10.1016/j.celrep.2013.05.042. [DOI] [PubMed] [Google Scholar]
- Compte A, Brunel N, Goldman-Rakic P, Wang X. Synaptic mechanisms and network dynamics underlying spatial working memory in a cortical network model. Cereb Cortex. 2000;10:910–923. doi: 10.1093/cercor/10.9.910. [DOI] [PubMed] [Google Scholar]
- Cossart R, Aronov D, Yuste R. Attractor dynamics of network UP states in the neocortex. Nature. 2003;423:283–288. doi: 10.1038/nature01614. [DOI] [PubMed] [Google Scholar]
- De Young G, Keizer J. A single-pool inositol 1, 4, 5-trisphosphate-receptor-based model for agonist-stimulated oscillations in Ca2+ concentration. Proceedings of the National Academy of Sciences of the United States of America. 1992;89:9895–9899. doi: 10.1073/pnas.89.20.9895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destexhe A, Bal T, McCormick D, Sejnowski T. Ionic mechanisms underlying synchronized oscillations and propagating waves in a model of ferret thalamic slices. J Neurophysiol. 1996;76:2049–2070. doi: 10.1152/jn.1996.76.3.2049. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Rudolph M, Paré D. The high-conductance state of neocortical neurons in vivo. Nat Rev Neurosci. 2003a;4:739–751. doi: 10.1038/nrn1198. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Rudolph M, Paré D. The high-conductance state of neocortical neurons in vivo. Nature Reviews Neuroscience. 2003b;4:739–751. doi: 10.1038/nrn1198. [DOI] [PubMed] [Google Scholar]
- Durstewitz D, Seamans J, Sejnowski T. Neurocomputational models of working memory. Nature Neuroscience. 2000;3:1184–1191. doi: 10.1038/81460. [DOI] [PubMed] [Google Scholar]
- Dyhrfjeld-Johnsen J, Morgan R, Földy C, Soltesz I. Upregulated H-Current in hyperexcitable CA1 dendrites after febrile seizures. Front Cell Neurosci. 2008;2 doi: 10.3389/neuro.03.002.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dyhrfjeld-Johnsen J, Morgan R, Soltesz I. Double trouble? potential for hyperexcitability following both channelopathic up-and downregulation of Ih in epilepsy. Front Neurosci. 2009;3:25. doi: 10.3389/neuro.01.005.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egorov A, Hamam B, Fransén E, Hasselmo M, Alonso A. Graded persistent activity in entorhinal cortex neurons. Nature. 2002;420:173–178. doi: 10.1038/nature01171. [DOI] [PubMed] [Google Scholar]
- Evans R, Blackwell K. Calcium: amplitude, duration, or location. Biol Bull. 2015;228:75–83. doi: 10.1086/BBLv228n1p75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fall C, Lewis T, Rinzel J. Background-activity-dependent properties of a network model for working memory that incorporates cellular bistability. Biological cybernetics. 2005;93:109–118. doi: 10.1007/s00422-005-0543-5. [DOI] [PubMed] [Google Scholar]
- Fall C, Rinzel J. An intracellular Ca2+ subsystem as a biologically plausible source of intrinsic conditional bistability in a network model of working memory. Journal of Computational Neuroscience. 2006;20:97–107. doi: 10.1007/s10827-006-4791-8. [DOI] [PubMed] [Google Scholar]
- Fall C, Wagner J, Loew L, Nuccitelli R. Cortically restricted production of ip3 leads to propagation of the fertilization ca2+ wave along the cell surface in a model of the xenopus egg. Journal of theoretical biology. 2004;231:487–496. doi: 10.1016/j.jtbi.2004.06.019. [DOI] [PubMed] [Google Scholar]
- Fitzpatrick J, Hagenston A, Hertle D, Gipson K, Bertetto-D’Angelo L, Yeckel M. Inositol-1,4,5-trisphosphate receptor-mediated ca2+ waves in pyramidal neuron dendrites propagate through hot spots and cold spots. J Physiol. 2009;587:1439–1459. doi: 10.1113/jphysiol.2009.168930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fransén E, Tahvildari B, Egorov A, Hasselmo M, Alonso A. Mechanism of graded persistent cellular activity of entorhinal cortex layer V neurons. Neuron. 2006;49:735–746. doi: 10.1016/j.neuron.2006.01.036. [DOI] [PubMed] [Google Scholar]
- Fukushima M, Saunders R, Leopold D, Mishkin M, Averbeck B. Spontaneous high-gamma band activity reflects functional organization of auditory cortex in the awake macaque. Neuron. 2012;74:899–910. doi: 10.1016/j.neuron.2012.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghitza O. Linking speech perception and neurophysiology: speech decoding guided by cascaded oscillators locked to the input rhythm. Front Psychol. 2011;2:130. doi: 10.3389/fpsyg.2011.00130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giocomo L, Hasselmo M. Neuromodulation by glutamate and acetylcholine can change circuit dynamics by regulating the relative influence of afferent input and excitatory feedback. Molecular Neurobiol. 2007;36:184–200. doi: 10.1007/s12035-007-0032-z. [DOI] [PubMed] [Google Scholar]
- Goldman-Rakic P. Cellular basis of working memory. Neuron. 1995;14:477–485. doi: 10.1016/0896-6273(95)90304-6. [DOI] [PubMed] [Google Scholar]
- Hagiwara N, Irisawa H. Modulation by intracellular Ca2+ of the hyperpolarization-activated inward current in rabbit single sino-atrial node cells. J Physiol. 1989;409:121–141. doi: 10.1113/jphysiol.1989.sp017488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harnett M, Magee J, Williams S. Distribution and function of HCN channels in the apical dendritic tuft of neocortical pyramidal neurons. J Neurosci. 2015;35:1024–1037. doi: 10.1523/JNEUROSCI.2813-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harnett M, Xu N, Magee J, Williams S. Potassium channels control the interaction between active dendritic integration compartments in layer 5 cortical pyramidal neurons. Neuron. 2013;79:516–529. doi: 10.1016/j.neuron.2013.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartsfield J. A quantitative study of neuronal calcium signaling. Baylor College of Medicine; 2005. Ph.D. diss. [Google Scholar]
- Hasselmo M, McGaughy J. High acetylcholine levels set circuit dynamics for attention and encoding and low acetylcholine levels set dynamics for consolidation. Prog Brain Res. 2004;145:207–231. doi: 10.1016/S0079-6123(03)45015-2. [DOI] [PubMed] [Google Scholar]
- Hay E, Hill S, Schürmann F, Markram H, Segev I. Models of neocortical layer 5b pyramidal cells capturing a wide range of dendritic and perisomatic active properties. PLoS Comput Biol. 2011;7:e1002107. doi: 10.1371/journal.pcbi.1002107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heys J, Hasselmo M. Neuromodulation of Ih in layer II medial entorhinal cortex stellate cells: a voltage-clamp study. J Neurosci. 2012;32:9066–9072. doi: 10.1523/JNEUROSCI.0868-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hines M, Carnevale N. Expanding NEURON’s repertoire of mechanisms with NMODL. Neural Computation. 2000;12:995–1007. doi: 10.1162/089976600300015475. [DOI] [PubMed] [Google Scholar]
- Hong M, Ross W. Priming of intracellular calcium stores in rat ca1 pyramidal neurons. The Journal of Physiology. 2007;584:75–87. doi: 10.1113/jphysiol.2007.137661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honnuraiah S, Narayanan R. A calcium-dependent plasticity rule for HCN channels maintains activity homeostasis and stable synaptic learning. PloS One. 2013;8:e55590. doi: 10.1371/journal.pone.0055590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hooks B, Hires S, Zhang Y, Huber D, Petreanu L, Svoboda K, Shepherd G. Laminar analysis of excitatory local circuits in vibrissal motor and sensory cortical areas. Plos Biol. 2011;9:e1000572. doi: 10.1371/journal.pbio.1000572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hooks B, Mao T, Gutnisky D, Yamawaki N, Svoboda K, Shepherd G. Organization of cortical and thalamic input to pyramidal neurons in mouse motor cortex. J Neurosci. 2013;33:748–760. doi: 10.1523/JNEUROSCI.4338-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsieh C, Cruikshank S, Metherate R. Differential modulation of auditory thalamocortical and intracortical synaptic transmission by cholinergic agonist. Brain Res. 2000;880:51–64. doi: 10.1016/s0006-8993(00)02766-9. [DOI] [PubMed] [Google Scholar]
- Hunter M, Eickhoff S, Miller T, Farrow T, Wilkinson I, Woodruff P. Neural activity in speech-sensitive auditory cortex during silence. Proc Nat Acad Sci. 2006;103:189–194. doi: 10.1073/pnas.0506268103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jahr C, Stevens C. Voltage dependence of NMDA-activated macroscopic conductances predicted by single-channel kinetics. J Neurosci. 1990b;10:3178–3182. doi: 10.1523/JNEUROSCI.10-09-03178.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kane M, Engle R. The role of prefrontal cortex in working-memory capacity, executive attention, and general fluid intelligence: An individual-differences perspective. Psychon Bull Rev. 2002;9:637–671. doi: 10.3758/bf03196323. [DOI] [PubMed] [Google Scholar]
- Kay A, Wong R. Calcium current activation kinetics in isolated pyramidal neurones of the CA1 region of the mature guinea-pig hippocampus. J Physiol (Lond) 1987;392:603–616. doi: 10.1113/jphysiol.1987.sp016799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelemen E, Fenton A. Dynamic grouping of hippocampal neural activity during cognitive control of two spatial frames. Plos Biol. 2010;8:e1000403. doi: 10.1371/journal.pbio.1000403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiritani T, Wickersham I, Seung H, Shepherd G. Hierarchical connectivity and connection-specific dynamics in the corticospinal-corticostriatal microcircuit in mouse motor cortex. J Neurosci. 2012a;32:4992–5001. doi: 10.1523/JNEUROSCI.4759-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiritani T, Wickersham I, Seung H, Shepherd G. Hierarchical connectivity and connection-specific dynamics in the corticospinal-corticostriatal microcircuit in mouse motor cortex. J Neurosci. 2012b;32:4992–5001. doi: 10.1523/JNEUROSCI.4759-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kocsis B, Li S. In vivo contribution of h-channels in the septal pacemaker to theta rhythm generation. Eur J Neurosci. 2004;20:2149–2158. doi: 10.1111/j.1460-9568.2004.03678.x. [DOI] [PubMed] [Google Scholar]
- Kole M, Hallermann S, Stuart G. Single Ih channels in pyramidal neuron dendrites: properties, distribution, and impact on action potential output. J Neurosci. 2006;26:1677–1687. doi: 10.1523/JNEUROSCI.3664-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar S, Sedley W, Barnes G, Teki S, Friston K, Griffiths T. A brain basis for musical hallucinations. Cortex. 2013 doi: 10.1016/j.cortex.2013.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larkum M, Nevian T, Sandler M, Polsky A, Schiller J. Synaptic integration in tuft dendrites of layer 5 pyramidal neurons: a new unifying principle. Science. 2009;325:756–760. doi: 10.1126/science.1171958. [DOI] [PubMed] [Google Scholar]
- Li Y, Rinzel J. Equations for InsP3 receptor-mediated [Ca2+]i oscillations derived from a detailed kinetic model: a Hodgkin-Huxley like formalism. Journal of theoretical biology. 1994;166:461–473. doi: 10.1006/jtbi.1994.1041. [DOI] [PubMed] [Google Scholar]
- Lim S, Goldman M. Balanced cortical microcircuitry for maintaining information in working memory. Nat Neurosci. 2013;16:1306–1314. doi: 10.1038/nn.3492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lim S, Goldman M. Balanced cortical microcircuitry for spatial working memory based on corrective feedback control. J Neurosci. 2014;34:6790–6806. doi: 10.1523/JNEUROSCI.4602-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lisman J, Fellous J, Wang X. A role for NMDA-receptor channels in working memory. Nature Neuroscience. 1998;1:273–275. doi: 10.1038/1086. [DOI] [PubMed] [Google Scholar]
- Loewenstein Y, Sompolinsky H. Temporal integration by calcium dynamics in a model neuron. Nat Neurosci. 2003;6:961–967. doi: 10.1038/nn1109. [DOI] [PubMed] [Google Scholar]
- Lytton W, Arle J, Bobashev G, Ji S, Klassen T, Marmarelis V, Schwaber J, Sherif M, Sanger T, Lytton W, Neymotin S, Kerr C. Multiscale modeling for clinical translation in neuropsychiatric disease. J Comput Surgery. 2014;1:7. doi: 10.1186/2194-3990-1-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lytton W, Sejnowski T. Simulations of cortical pyramidal neurons synchronized by inhibitory interneurons. J Neurophysiol. 1991;66:1059–1079. doi: 10.1152/jn.1991.66.3.1059. [DOI] [PubMed] [Google Scholar]
- Major G, Tank D. Persistent neural activity: prevalence and mechanisms. Curr Opin Neurobiol. 2004;14:675–684. doi: 10.1016/j.conb.2004.10.017. [DOI] [PubMed] [Google Scholar]
- Marder E, Abbott L, Turrigiano G, Liu Z, Golowasch J. Memory from the dynamics of intrinsic membrane currents. Proc Nat Acad Sci. 1996;93:13481–13486. doi: 10.1073/pnas.93.24.13481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram H, Lübke J, Frotscher M, Roth A, Sakmann B. Physiology and anatomy of synaptic connections between thick tufted pyramidal neurones in the developing rat neocortex. J Physiol. 1997;500:409–440. doi: 10.1113/jphysiol.1997.sp022031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormick D, Huguenard J. A model of the electrophysiological properties of thalamocortical relay neurons. J Neurophysiol. 1992a;68:1384–1400. doi: 10.1152/jn.1992.68.4.1384. [DOI] [PubMed] [Google Scholar]
- McCormick D, Huguenard J. A model of the electrophysiological properties of thalamocortical relay neurons. J Neurophysiol. 1992b;68:1384–1400. doi: 10.1152/jn.1992.68.4.1384. [DOI] [PubMed] [Google Scholar]
- McCormick D, Wang Z, Huguenard J. Neurotransmitter control of neocortical neuronal activity and excitability. Cereb. Cortex. 1993;3:387–398. doi: 10.1093/cercor/3.5.387. [DOI] [PubMed] [Google Scholar]
- McDougal R, Hines M, Lytton W. Reaction-diffusion in the NEURON simulator. Front Neuroinform. 2013a;7:28. doi: 10.3389/fninf.2013.00028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDougal R, Hines M, Lytton W. Water-tight membranes from neuronal morphology files. J Neurosci Methods. 2013b;220:167–178. doi: 10.1016/j.jneumeth.2013.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Migliore M, Messineo L, Ferrante M. Dendritic Ih selectively blocks temporal summation of unsynchronized distal inputs in CA1 pyramidal neurons. J Comput Neurosci. 2004;16:5–13. doi: 10.1023/b:jcns.0000004837.81595.b0. [DOI] [PubMed] [Google Scholar]
- Migliore M, Migliore R. Know your current Ih: Interaction with a shunting current explains the puzzling effects of its pharmacological or pathological modulations. PLoS One. 2012;7:e36867. doi: 10.1371/journal.pone.0036867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monyer H, Markram H. Interneuron diversity series: molecular and genetic tools to study gabaergic interneuron diversity and function. Trends Neurosci. 2004;27:90–97. doi: 10.1016/j.tins.2003.12.008. [DOI] [PubMed] [Google Scholar]
- Nelson A, Krispel C, Sekirnjak C, du Lac S. Long-lasting increases in intrinsic excitability triggered by inhibition. Neuron. 2003;40:609–620. doi: 10.1016/s0896-6273(03)00641-x. [DOI] [PubMed] [Google Scholar]
- Nevian T, Larkum M, Polsky A, Schiller J. Properties of basal dendrites of layer 5 pyramidal neurons: a direct patch-clamp recording study. Nat Neurosci. 2007;10:206–214. doi: 10.1038/nn1826. [DOI] [PubMed] [Google Scholar]
- Neymotin S, Hilscher M, Moulin T, Skolnick Y, Lazarewicz M, Lytton W. Ih tunes theta/gamma oscillations and cross-frequency coupling in an in silico CA3 model. PLoS One. 2013;8:e76285. doi: 10.1371/journal.pone.0076285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neymotin S, Jacobs K, Fenton A, Lytton W. Synaptic information transfer in computer models of neocortical columns. J Comput Neurosci. 2011a;30:69–84. doi: 10.1007/s10827-010-0253-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neymotin S, Lazarewicz M, Sherif M, Contreras D, Finkel L, Lytton W. Ketamine disrupts theta modulation of gamma in a computer model of hippocampus. J Neurosci. 2011b;31:11733–11743. doi: 10.1523/JNEUROSCI.0501-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neymotin S, Lee H, Fenton A, Lytton W. Interictal EEG discoordination in a rat seizure model. J Clin Neurophysiol. 2010;27:438–444. doi: 10.1097/WNP.0b013e3181fe059e. [DOI] [PubMed] [Google Scholar]
- Neymotin S, Lee H, Park E, Fenton A, Lytton W. Emergence of physiological oscillation frequencies in a computer model of neocortex. Front Comput Neurosci. 2011;5:19. doi: 10.3389/fncom.2011.00019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neymotin S, McDougal R, Hines M, Lytton W. Calcium regulation of HCN supports persistent activity associated with working memory: a multiscale model of prefrontal cortex. BMC Neuroscience. 2014;15:P108. doi: 10.1016/j.neuroscience.2015.12.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neymotin S, McDougal R, Sherif M, Fall C, Hines M, Lytton W. Neuronal calcium wave propagation varies with changes in endoplasmic reticulum parameters: a computer model. Neural Comput. 2015;27:898–924. doi: 10.1162/NECO_a_00712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neymotin S, Taxin Z, Mohan A, Lipton P, Jaeger D, Jang R. Encyclopedia of Computational Neuroscience. Springer; 2013. Brain ischemia and stroke. [Google Scholar]
- Oikonomou K, Singh M, Sterjanaj E, Antic S. Spiny neurons of amygdala, striatum, and cortex use dendritic plateau potentials to detect network up states. Front Cell Neurosci. 2014;8:292. doi: 10.3389/fncel.2014.00292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papoutsi A, Sidiropoulou K, Cutsuridis V, Poirazi P. Induction and modulation of persistent activity in a layer V PFC microcircuit model. Front Neural Circuits. 2013;7:161. doi: 10.3389/fncir.2013.00161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papoutsi A, Sidiropoulou K, Poirazi P. Dendritic nonlinearities reduce network size requirements and mediate ON and OFF states of persistent activity in a PFC microcircuit model. PLoS Comput Biol. 2014;10:e1003764. doi: 10.1371/journal.pcbi.1003764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peercy B. Initiation and propagation of a neuronal intracellular calcium wave. J Comput Neurosci. 2008;25:334–348. doi: 10.1007/s10827-008-0082-x. [DOI] [PubMed] [Google Scholar]
- Pérez-Garci E, Gassmann M, Bettler B, Larkum M. The GABA B1b isoform mediates long-lasting inhibition of dendritic Ca2+ spikes in layer 5 somatosensory pyramidal neurons. Neuron. 2006;50:603–616. doi: 10.1016/j.neuron.2006.04.019. [DOI] [PubMed] [Google Scholar]
- Petersen C, Crochet S. Synaptic computation and sensory processing in neocortical layer 2/3. Neuron. 2013;78:28–48. doi: 10.1016/j.neuron.2013.03.020. [DOI] [PubMed] [Google Scholar]
- Poolos N, Migliore M, Johnston D. Pharmacological upregulation of h-channels reduces the excitability of pyramidal neuron dendrites. Nat Neurosci. 2002;5:767–774. doi: 10.1038/nn891. [DOI] [PubMed] [Google Scholar]
- Poskanzer K, Yuste R. Astrocytic regulation of cortical up states. Proc Natl Acad Sci U S A. 2011;108:18453–18458. doi: 10.1073/pnas.1112378108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quiroga R, Panzeri S. Extracting information from neuronal populations: information theory and decoding approaches. Nat. Rev. Neurosci. 2009;10:173–185. doi: 10.1038/nrn2578. [DOI] [PubMed] [Google Scholar]
- Rall W, Shepherd G. Theoretical reconstruction of field potentials and dendrodendritic synaptic interactions in olfactory bulb. J Neurophysiol. 1968;31:884–915. doi: 10.1152/jn.1968.31.6.884. [DOI] [PubMed] [Google Scholar]
- Ramakrishnan N, Bhalla U. Memory switches in chemical reaction space. Plos Comput Biol. 2008;4:e1000122. doi: 10.1371/journal.pcbi.1000122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson R, Siegelbaum S. Hyperpolarization-activated cation currents: from molecules to physiological function. Annu Rev Physiol. 2003;65:453–480. doi: 10.1146/annurev.physiol.65.092101.142734. [DOI] [PubMed] [Google Scholar]
- Ross WN, Nakamura T, Watanabe S, Larkum M, Lasser-Ross N. Synaptically activated Ca2+ release from internal stores in CNS neurons. Cell Mol Neurobiol. 2005;25:283–95. doi: 10.1007/s10571-005-3060-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Safiulina V, Caiati M, Sivakumaran S, Bisson G, Migliore M, Cherubini E. Control of GABA release at mossy fiber-CA3 connections in the developing hippocampus. Front Synaptic Neurosci. 2010;2 doi: 10.3389/neuro.19.001.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santoro B, Baram T. The multiple personalities of h-channels. Trends Neurosci. 2003;26:550–554. doi: 10.1016/j.tins.2003.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawaguchi T, Goldman-Rakic P. D1 dopamine receptors in prefrontal cortex: involvement in working memory. Science. 1991;251:947–950. doi: 10.1126/science.1825731. [DOI] [PubMed] [Google Scholar]
- Schroeder C, Lakatos P. The signs of silence. Neuron. 2012;74:770–772. doi: 10.1016/j.neuron.2012.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwaller B. Cytosolic Ca2+ buffers. Cold Spring Harb Perspect Biol. 2010;2 doi: 10.1101/cshperspect.a004051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwindt P, Spain W, Crill W. Effects of intracellular calcium chelation on voltage-dependent and calcium-dependent currents in cat neocortical neurons. Neuroscience. 1992;47:571–578. doi: 10.1016/0306-4522(92)90166-y. [DOI] [PubMed] [Google Scholar]
- Seidenstein A, Barone F, Lytton W. Computer modeling of ischemic stroke. Scholarpedia. 2015;10:32015. doi: 10.4249/scholarpedia.32015. revision #148671; Accessed Oct 12, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sejnowski T, Koch C, Churchland P. Computational neuroscience. Science. 1988;241:1299–1306. doi: 10.1126/science.3045969. [DOI] [PubMed] [Google Scholar]
- Sheets P, Suter B, Kiritani T, Chan C, Surmeier D, Shepherd G. Corticospinal-specific HCN expression in mouse motor cortex: Ih-dependent synaptic integration as a candidate microcircuit mechanism involved in motor control. J Neurophysiol. 2011;106:2216–2231. doi: 10.1152/jn.00232.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shemer I, Brinne B, Tegnér J, Grillner S. Electrotonic Signals along Intracellular Membranes May Interconnect Dendritic Spines and Nucleus. PLoS Computational Biology. 2008;4:e1000036. doi: 10.1371/journal.pcbi.1000036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shipp S. The importance of being agranular: a comparative account of visual and motor cortex. Philos Trans R Soc Lond B Biol Sci. 2005;360:797–814. doi: 10.1098/rstb.2005.1630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sidiropoulou K, Lu F, Fowler M, Xiao R, Phillips C, Ozkan E, Zhu M, White F, Cooper D. Dopamine modulates an intrinsic mGluR5-mediated depolarization underlying prefrontal persistent activity. Nature neuroscience. 2009;12:190. doi: 10.1038/nn.2245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sidiropoulou K, Poirazi P. Predictive features of persistent activity emergence in regular spiking and intrinsic bursting model neurons. PLoS Comput Biol. 2012;8:e1002489. doi: 10.1371/journal.pcbi.1002489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song W, Kerr C, Lytton W, Francis J. Cortical plasticity induced by spike-triggered microstimulation in primate somatosensory cortex. PLoS One. 2013;8:e57453. doi: 10.1371/journal.pone.0057453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spruston N, Schiller Y, Stuart G, Sakmann B. Activity-dependent action potential invasion and calcium influx into hippocampal CA1 dendrite. Science. 1995;8:297–300. doi: 10.1126/science.7716524. [DOI] [PubMed] [Google Scholar]
- Stacey W, Lazarewicz M, Litt B. Synaptic noise and physiological coupling generate high-frequency oscillations in a hippocampal computational model. J Neurophysiol. 2009;102:2342–2357. doi: 10.1152/jn.00397.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suter B, Migliore M, Shepherd G. Intrinsic electrophysiology of mouse corticospinal neurons: a class-specific triad of spike-related properties. Cereb Cortex. 2013;23:1965–1977. doi: 10.1093/cercor/bhs184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suter B, Shepherd G. Reciprocal interareal connections to corticospinal neurons in mouse M1 and S2. J Neurosci. 2015;35:2959–2974. doi: 10.1523/JNEUROSCI.4287-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suter B, Yamawaki N, Borges K, Li X, Kiritani T, Hooks B, Shepherd G. Neurophotonics applications to motor cortex research. Neurophotonics. 2014 doi: 10.1117/1.NPh.1.1.011008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taxin Z, Neymotin S, Mohan A, Lipton P, Lytton W. Modeling molecular pathways of neuronal ischemia. Prog Mol Biol Transl Sci. 2014;123:249–275. doi: 10.1016/B978-0-12-397897-4.00014-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor C, Tovey S. IP3 receptors: toward understanding their activation. Cold Spring Harb Perspect Biol. 2010;2 doi: 10.1101/cshperspect.a004010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thuault S, Malleret G, Constantinople C, Nicholls R, Chen I, Zhu J, Panteleyev A, Vronskaya S, Nolan M, Bruno R, Siegelbaum S, Kandel E. Prefrontal cortex HCN1 channels enable intrinsic persistent neural firing and executive memory function. J Neurosci. 2013;33:13583–13599. doi: 10.1523/JNEUROSCI.2427-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tiganj Z, Hasselmo M, Howard M. A simple biophysically plausible model for long time constants in single neurons. Hippocampus. 2015;25:27–37. doi: 10.1002/hipo.22347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tonnesen J, Sorensen A, Deisseroth K, Lundberg C, Kokaia M. Optogenetic control of epileptiform activity. Proc Nat Acad Sci. 2009;106:12162–12167. doi: 10.1073/pnas.0901915106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsuno Y, Schultheiss N, Hasselmo M. In vivo cholinergic modulation of the cellular properties of medial entorhinal cortex neurons. J Physiol. 2013;591:2611–2627. doi: 10.1113/jphysiol.2012.250431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tu H, Wang Z, Bezprozvanny I. Modulation of mammalian inositol 1,4,5-trisphosphate receptor isoforms by calcium: a role of calcium sensor region. Biophysical Journal. 2005;88:1056–1069. doi: 10.1529/biophysj.104.049601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tu H, Wang Z, Nosyreva E, De Smedt H, Bezprozvanny I. Functional characterization of mammalian inositol 1,4,5-trisphosphate receptor isoforms. Biophysical Journal. 2005;88:1046–1055. doi: 10.1529/biophysj.104.049593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner J, Fall C, Hong F, Sims C, Allbritton N, Fontanilla R, Moraru I, Loew L, Nuccitelli R. A wave of IP3 production accompanies the fertilization Ca2+ wave in the egg of the frog, Xenopus laevis: theoretical and experimental support. Cell calcium. 2004;35:433–447. doi: 10.1016/j.ceca.2003.10.009. [DOI] [PubMed] [Google Scholar]
- Wang H, Stradtman G, Wang X, Gao W. A specialized NMDA receptor function in layer 5 recurrent microcircuitry of the adult rat prefrontal cortex. Proc Nat Acad Sci. 2008;105:16791–16796. doi: 10.1073/pnas.0804318105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Chen S, Nolan M, Siegelbaum S. Activity-dependent regulation of HCN pacemaker channels by cyclic AMP: signaling through dynamic allosteric coupling. Neuron. 2002;36:451–461. doi: 10.1016/s0896-6273(02)00968-6. [DOI] [PubMed] [Google Scholar]
- Wang M, Ramos B, Paspalas C, Shu Y, Simen A, Duque A, Vijayraghavan S, Brennan A, Dudley A, Nou E, Mazer J, Arnsten A. α2a-adrenoceptors strengthen working memory networks by inhibiting cAMP-HCN channel signaling in prefrontal cortex. Cell. 2007;129:397–410. doi: 10.1016/j.cell.2007.03.015. [DOI] [PubMed] [Google Scholar]
- Wang X. Synaptic basis of cortical persistent activity: the importance of NMDA receptors to working memory. J Neurosci. 1999a;19:9587–9603. doi: 10.1523/JNEUROSCI.19-21-09587.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X. Synaptic reverberation underlying mnemonic persistent activity. Trends in Neurosciences. 2001;24:455–463. doi: 10.1016/s0166-2236(00)01868-3. [DOI] [PubMed] [Google Scholar]
- Wang X. Pacemaker neurons for the theta rhythm and their synchronization in the septohippocampal reciprocal loop. J Neurophysiol. 2002;87:889–900. doi: 10.1152/jn.00135.2001. [DOI] [PubMed] [Google Scholar]
- Wang X, Buzsaki G. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. J Neurosci. 1996;16:6402–6413. doi: 10.1523/JNEUROSCI.16-20-06402.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiler N, Wood L, Yu J, Solla S, Shepherd G. Top-down laminar organization of the excitatory network in motor cortex. Nat Neurosci. 2008;11:360–366. doi: 10.1038/nn2049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White J, Banks M, Pearce R, Kopell N. Networks of interneurons with fast and slow γ-aminobutyric acid type A (GABAA) kinetics provide substrate for mixed gamma-theta rhythm. Proc Nat Acad Sci. 2000;97:8128–8133. doi: 10.1073/pnas.100124097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winograd M, Destexhe A, Sanchez-Vives M. Hyperpolarization-activated graded persistent activity in the prefrontal cortex. Proc Natl Acad Sci USA. 2008;105:7298–7303. doi: 10.1073/pnas.0800360105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamawaki N, Shepherd G. Synaptic circuit organization of motor corticothalamic neurons. J Neurosci. 2015;35:2293–2307. doi: 10.1523/JNEUROSCI.4023-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zemankovics R, Káli S, Paulsen O, Freund T, Hájos N. Differences in subthreshold resonance of hippocampal pyramidal cells and interneurons: the role of h-current and passive membrane characteristics. J Physiol. 2010;588:2109–2132. doi: 10.1113/jphysiol.2009.185975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou W, Short S, Rich M, Oikonomou K, Singh M, Sterjanaj E, Antic S. Branch specific and spike-order specific action potential invasion in basal, oblique, and apical dendrites of cortical pyramidal neurons. Neurophotonics. 2015;2:021006. doi: 10.1117/1.NPh.2.2.021006. [DOI] [PMC free article] [PubMed] [Google Scholar]