Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Jan 27;6:19952. doi: 10.1038/srep19952

Highly Efficient Quantum Sieving in Porous Graphene-like Carbon Nitride for Light Isotopes Separation

Yuanyuan Qu 1, Feng Li 1,2, Hongcai Zhou 1, Mingwen Zhao 1,a
PMCID: PMC4728688  PMID: 26813491

Abstract

Light isotopes separation, such as 3He/4He, H2/D2, H2/T2, etc., is crucial for various advanced technologies including isotope labeling, nuclear weapons, cryogenics and power generation. However, their nearly identical chemical properties made the separation challenging. The low productivity of the present isotopes separation approaches hinders the relevant applications. An efficient membrane with high performance for isotopes separation is quite appealing. Based on first-principles calculations, we theoretically demonstrated that highly efficient light isotopes separation, such as 3He/4He, can be reached in a porous graphene-like carbon nitride material via quantum sieving effect. Under moderate tensile strain, the quantum sieving of the carbon nitride membrane can be effectively tuned in a continuous way, leading to a temperature window with high 3He/4He selectivity and permeance acceptable for efficient isotopes harvest in industrial application. This mechanism also holds for separation of other light isotopes, such as H2/D2, H2/T2. Such tunable quantum sieving opens a promising avenue for light isotopes separation for industrial application.

Light isotopes such as hydrogen and helium have been widely used in both scientific research and industrial fields. The skyrocketing demand of 3He in cryogenic industries1, neutron detection and medical lung imaging2,3, and the wide usage of D2 and T2 in nuclear technologies have made isotopes separation a pressing need. Isotopes separation is crucial and inevitable for these applications. The isotopes of an element are separable only by mass-dependent processes, e.g. thermal diffusion and quantum effect, because they have nearly identical chemical properties. Recently, membrane-based approaches with low energy consumption and easy operation have been proposed for isotopes separation. Theoretical work revealed that several membranes including porous graphene and graphene allotropes with appropriate pores may be implementable for separating 3He from 4He through quantum tunneling effect4,5,6,7,8. However, none of them is able to meet the acceptable permeance with high selectivity for industrial application9. These theoretically-designed porous structures also face the synthetic difficulties in creating the desired pores of uniform size into graphene sheets.

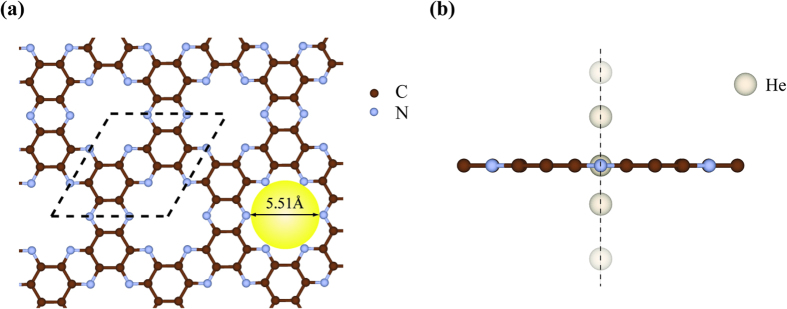
In recent years, two-dimensional (2D) carbon nitride materials, such as graphitic carbon nitride (g-C3N4)10, have attracted considerable attention due to their various potential applications in gas separation11,12, solar energy conversion13,14,15, spintronic devices16,17 and energy storage18 etc. These membranes composed of C and N atoms with intrinsic regular and uniformly distributed subnanometer pores are ideal for gas separation with designable pore sizes. Lately, a new member of carbon nitride family, the C2N-h2D membrane, have been successfully synthesized via a simple bottom-up wet-chemical reaction19. This membrane with uniformly distributed hexagonal pores (as shown in Fig. 1(a)), was proposed for promising application in electronics, sensors, catalysis, as well as gas separation11,19,20.

Figure 1.

Figure 1

Open in a new tab

(a) Top view of C2N-h2D lattice. The brown and blue balls represent the C and N atoms respectively. The unit cell is indicated by the dashed rhombus and the inscribed circle is indicated by the yellow circle. (b) Side view of the penetration path of He passing through the pore of C2N-h2D. The white ball represents the He atom.

In this paper, based on first-principles calculations, we theoretically present that under moderate tensile strain, highly efficient quantum sieving for light isotopes separation can be achieved in a porous graphene-like carbon nitride membrane (C2N-h2D) that has been synthesized in recent experiments. Both the selectivity and permeance for helium isotopes separation meet the requirement for industrial application, which is attributed to the tunable helium-membrane interaction under tensile strain. Additionally, this approach also holds for the separation of other light isotopes (e.g. H2/D2, H2/T2). The excellent mechanical property and tunable quantum sieving effect in this carbon nitride membrane opens a promising avenue for light isotopes harvest, as well as for wide range of energy or environmental applications.

Results and Discussion

Energy profiles

The optimized lattice constant for the unstrained C2N-h2D lattice is calculated to be 8.329 Å, in good agreement with experimental value19 (8.3 Å) and other theoretical values11,20 (8.354 Å or 8.32 Å). Figure 1(a) presents a top view of a fully relaxed C2N-h2D lattice, where the unit cell is indicated by a dashed rhombus. The pore size is characterized by the diameter of the inscribed circle, 5.51 Å, which is larger than the porous graphene or g-C3N4 membrane proposed for 3He separation7,12. As helium is a neutral atom without polarization, the interaction between the helium atom and the membrane is dominated by the weak vdW interaction. The lowest-energy approach to penetrate a symmetric pore is then simplified to be a straight line right through the center of the pore and perpendicular to the membrane, as shown in Fig. 1(b). Therefore, the energy profile for a helium atom passing through the pore of C2N-h2D membrane can be obtained by sequentially scanning the interaction energy between the helium atom and the membrane along the penetration path. The energy barrier along this path is mainly determined by the repulsive term of the vdW interaction, which is related to the overlap of the electron wavefunctions between the two close-shell systems due to the Pauli exclusion principle. Along this path, the maximum repulsive interaction between the helium atom and the membrane can therefore be tuned by modifying the pore size of the membrane, e.g. through applying tensile strain.

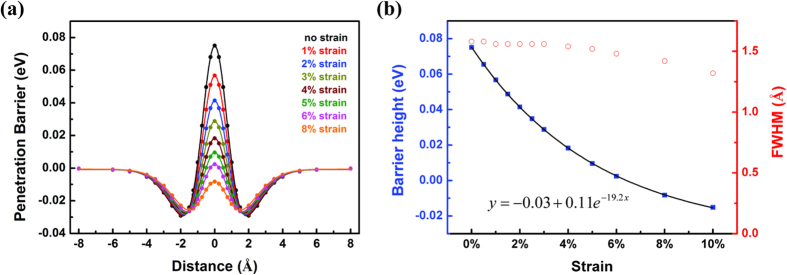
Although the vdW interaction between the helium atom and the C2N-h2D membrane has no isotope effect, isotope separation can still be achieved via quantum tunneling with appropriate potential profiles due to their different masses, as described in the following parts. The selectivity and the permeance are two key parameters for 3He/4He separation in industrial application, where the industrial-acceptable values are considered to be 6 for selectivity and 6.7 × 10−8 mol/s/cm2/bar for permeance, repectively9. To study the tensile-strain-dependent selectivity and permeance, a series of biaxial tensile strains along the primitive vectors of the unit cell were applied to the C2N-h2D membrane to enlarge the pore size for different penetration properties. The biaxial tensile strain applied to the lattice is defined as the ratio of the deformation Δa to the initial lattice constant a0, ε = Δa/a0. Therefore, the lattice constant of the C2N-h2D membrane under strain ε is a = a0(1 + ε). The penetration energy profiles under different tensile strains are plotted in Fig. 2(a). As can be seen, the penetration barrier decreases with the increase of the tensile strain, which is understandable since larger pores would reduce the repulsive interaction between the membrane and the helium atom. The barrier height exhibits an exponential decay with a decay constant of 19.2; while the full-width-at-half-maximum (FWHM) of the barrier slightly decreases with the increase of the strain as shown in Fig. 2(b).

Figure 2.

Figure 2

Open in a new tab

(a) Energy profile for He passing through the pore of the C2N-h2D membrane under different tensile strains. Colored points indicate the results obtained by first-principles calculations; while the curves show the numerically interpolated potentials. (b) The strain dependency of the penetration barrier heights and the FWHM.

Transmission probability

Based on the energy profiles under different tensile strains, we performed one-dimensional (1D) finite difference calculations21 of the quantum tunneling probability t(E) as a function of kinetic energy E for each case, as shown in Fig. 3(a). In all cases, 3He transmission (solid curves) is preferred at low kinetic energy regimes while 4He transmission (dashed curves) becomes more likely at high kinetic energy regimes. Therefore, to enhance the selectivity of 3He from 4He, it is reasonable to keep the gas at a low temperature. It should be noted that although different exchange functional forms may give different kinetic crossovers of the transmission probability of 3He and 4He, the overall trend of the tunneling probability maintains12.

Figure 3.

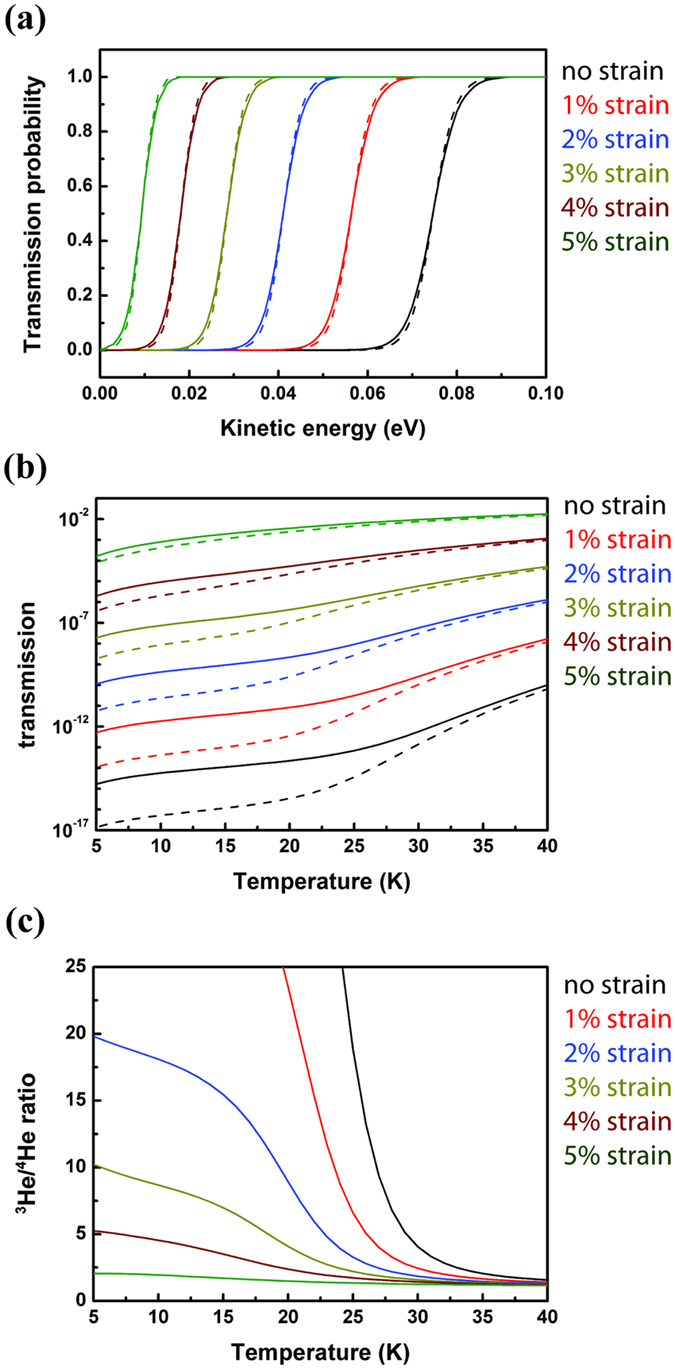
Figure 3

Open in a new tab

(a) Quantum-mechanical transmission probability of He passing through the pore of C2N-h2D membrane as a function of kinetic energy. The solid curves represent the quantum-mechanical transmission of 3He and the dashed curves represents that of 4He under different strains, respectively; (b) Thermally weighted transmission of 3He (solid curves) and 4He (dashed curves) under different strains; (c) 3He/4He transmission ratio under different strains.

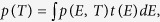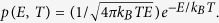The thermally weighted transmission probability p(T) can be obtained via the same strategy utilized in our previous study12, Inline graphic where Inline graphic A classical Boltzmann distribution for the velocities of both 3He and 4He is assumed for simplification as suggested by previous studies4,6,7,8,22. The thermally weighted results under different strains at low temperature regime (5–40 K) are summarized in Fig. 3(b,c), including the thermally weighted transmission probability of 3He and 4He and the 3He/4He transmission ratio. As can be seen in Fig. 3(b), in all cases, the transmission probabilities of 3He deviate from 4He, due to their different masses impact on the quantum tunneling. The 3He/4He transmission decrease drastically as temperature increase under strains below 3% as shown in Fig. 3(c).

Selectivity and permeance tuned by strain

The total flux of He atom passing though the membrane can be estimated by: 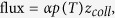Inline graphic where p(T) is the thermally weighted transmission probability, 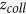Inline graphic is the collision frequency between the particle and the pore, 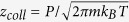Inline graphic (P is the pressure, T is the temperature, kB is the Boltzmann’s constant, m is the mass of the particle4), and α is the fraction of the area available for tunneling to occor: 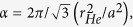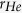Inline graphic where Inline graphic is the kinetic diameter of He atom and a is the lattice constant of the C2N-h2D membrane23. The permeance (Q) is defined as the ratio between the flux and the pressure drop across the pore, Q = flux/P, according to previous studies8,9. The selectivity and the permeance of 3He under different strains at 15 K are reported in Fig. 4, where the industrial acceptable values of the selectivity (>6) and the permeance (>6.7 × 10−8 mol/s/cm2/bar) are indicated by the blue and red dashed lines respectively9. It can be seen that at a specific temperature, the trade-off between the selectivity and the permeance can be adjusted by the strain. At 15 K, the acceptable selectivity and permeance are obtained at a strain of 3% with a selectivity of 7 and a permeance of 4 × 10−7 mol cm−2 s−1 bar−1 respectively. A more systematically scanning for the selectivities and the permeances at different temperatures can be found in Table 1, which showed that within the temperature range of 5 – 16 K, the industrial acceptable selectivity and permeance can always be satisfied by the proper adjustment of the tensile strain, where the most applicable strain for the C2N-h2D membrane is 3%, satisfying the industrial acceptable values from 5 to 16 K.

Figure 4. The 3He/4He selectivity and the 3He permeance under different strains at 15 K.

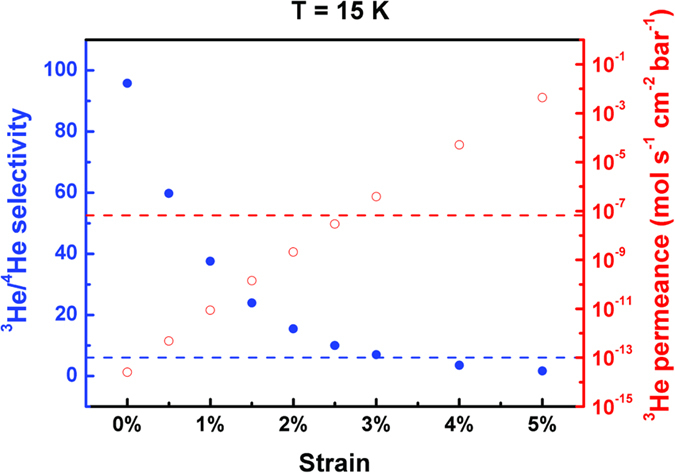
Figure 4

Open in a new tab

The blue and the red dashed lines indicate the industrial acceptable values for the selectivity (6) and the permeance (6.7 × 10−8 mol/s/cm2/bar), respectively.

Table 1. The selectivities (S) and the permeances (Q, mol/s/cm2/bar) under different strains for temperatures ranging from 4 to 17 K.

Temperature 4K 5K 8K 10K
strain S Q S Q S Q S Q
2% 20.2 2.8 × 10−10 19.8 4.3 × 10−10 18.8 8.7 × 10−10 18.1 1.2 × 10−9
2.5% 14.2 3.8 × 10−9 13.6 5.9 × 10−9 12.4 1.2 × 10−8 11.8 1.6 × 10−8
3% 10.6 4.6 × 10−8 10.2 7.1 × 10−8 9.2 1.5 × 10−7 8.7 2.0 × 10−7
4% 5.4 4.3 × 10−6 5.3 7.1 × 10−6 4.9 1.7 × 10−5 4.5 2.4 × 10−5
Temperature 12K
 15K
 16K
 17K
strain S Q S Q S Q S Q
2% 17.3 1.5 × 10−9 15.5 2.0 × 10−9 14.5 2.3 × 10−9 13.4 2.6 × 10−9
2.5% 11.2 2.0 × 10−8 10.0 2.8 × 10−8 9.4 3.2 × 10−8 8.6 3.7 × 10−8
3% 8.1 2.5 × 10−7 7.0 3.7 × 10−7 6.5 4.2 × 10−7 5.9 4.8 × 10−7
4% 4.2 3.2 × 10−5 3.5 4.7 × 10−5 3.3 5.4 × 10−5 3.0 6.3 × 10−5
Open in a new tab

The red numbers identify the conditions satisfying the industrial acceptable selectivity (>6) and permeance (>6.7 × 10−8 mol/s/cm2/bar).

The dispersion interactions are critical for the potential energy barrier, we therefore calculated the penetration barriers based on the DFT-D324 and DFT-D3(BJ)25 correction schemes (Supplementary Methods) for comparison (Supplementary Fig. S1 in SI). It is found that although different correction schemes did qualitatively change the potential energy barrier, the tensile strains that lead to the industrial acceptable selectivity and permeance are very close (Supplementary Table S1 and S2 in SI). The calculations based on the DFT-D3 scheme show that under a tensile strain of 2–3%, highly efficient 3He/4He separation at an industrial-acceptable level can be obtained at temperature ranging from 2 to 21 K; while for the DFT-D3(BJ) scheme, the most applicable strain becomes 3.5% with a temperature window of 5 to 16 K. Although the predicted strains and temperature windows slightly depend on the correction strategy of the dispersion interactions, the tunability of the penetration barrier and the selectivity by the tensile strain offer a promising approach for achieving highly efficient quantum sieving for light isotopes separation.

Stability of the C2N-h2D membrane

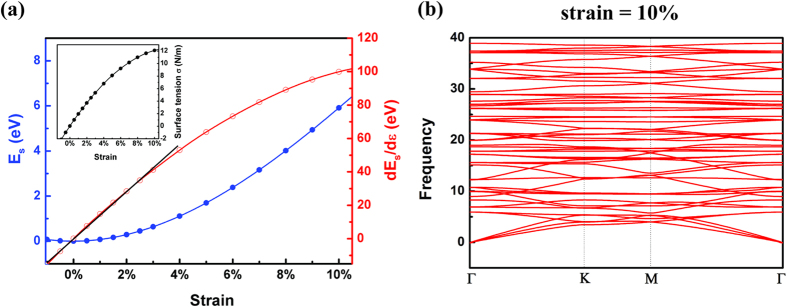
The stability of the C2N-h2D membrane under strain has also been examined by investigating the mechanical properties of the membrane, which can be revealed from the strain energy, Es = E(ε) − E(0), where E(ε) represents the energy under strain ε and E(0) represents the energy under no strain. The strain energy Es and its first derivative under different strains are plotted in Fig. 5(a). As can be seen, the strain energy increases as the increase of the tensile strain. The derivative dEs/dε increases linearly with respect to the strain for strains below 3% (black line in Fig. 5(a)), corresponding to the harmonic region. This indicates that the C2N-h2D membrane under strain below 3% undergoes the elastic deformation, thus is quite stable. The surface tension σ increases to 12 N/m at a tensile strain of 10%, as shown in the insert panel of Fig. 5(a) (see the “Supplementary Equations” for the deduction of surface tension σ). To double check the stability of the C2N-h2D membrane, we also calculated the vibration frequencies of the phonon modes for a (3 × 3 × 1) supercell under strain of 10% as shown in Fig. 5(b), which indicated that even at tensile strain up to 10%, there is no imaginary frequency modes, implying the remarkable stability of C2N-h2D membrane under tensile strain.

Figure 5.

Figure 5

Open in a new tab

(a) Strain dependency of the strain energy Es and its first derivative of the unit cell of the C2N-h2D lattice under different strains; the insert panel is the strain dependency of the surface tension σ. (b) Phonon spectra analysis of the C2N-h2D membrane under strain of 10%.

Finally, we should emphasize that although we focus on helium isotopes separation in above discussion, the tunable quantum sieving mechanism also holds for other light isotopes separation, such as H2/D2, H2/T2. For instance, our calculations indicate that under tensile strain of about 3.5%, the selectivity and permeance for H2/D2 separation are able to meet the requirement for industrial application at low temperatures regime (below 30 K). Therefore, tensile strain can serve as a promising means to tune the efficiency of membranes for light isotopes separation and the porous graphene-like carbon nitrides would be ideal candidate materials to reach the goal.

Methods

The first-principles calculations were performed within the density functional theory (DFT) using the plane-wave pseudopotential approach, implemented in the Vienna Ab initio Simulation Package (VASP)26,27,28. The electron-electron interactions are treated using a generalized gradient approximation (GGA) in the form of Perdew-Burke-Ernzerhof (PBE) for the exchange-correlation functional29. The van der Waals (vdW) interactions were included explicitly by using the empirical correction scheme of Grimme (DFT-D2)30. The energy cutoff of the plane waves was set to 520 eV with an energy precision of 10−8 eV. The atomic coordinates were fully relaxed using a conjugate gradient scheme without any symmetry restrictions until the maximum force on each ion was smaller than 0.001 eV/Å. Vacuum space larger than 15 Å was used to avoid the interaction between adjacent images. The Monkhorst-Pack meshes of 9 × 9 × 1 were used in sampling the Brillouin zone for the C2N-h2D lattice. In the subsequent calculations of the potential energy profiles for He atom penetrating the membrane pore, the z-coordinates of the atoms of C2N-h2D were kept fixed.

The quantum tunneling probability calculation was based on 1D finite difference calculations21, where the grid density was chosen to be 0.01 Å and a region of 1 Å located 7 Å away from the peak of the barrier was chosen for the incident planewaves as the barriers decrease below 0.001 eV at 6 Å away from the barrier peak.

Additional Information

How to cite this article: Qu, Y. et al. Highly Efficient Quantum Sieving in Porous Graphene-like Carbon Nitride for Light Isotopes Separation. Sci. Rep. 6, 19952; doi: 10.1038/srep19952 (2016).

Supplementary Material

Supplementary Information
srep19952-s1.pdf (238.6KB, pdf)

Acknowledgments

This work is supported by the National Basic Research Program of China (No. 2012CB932302), the National Natural Science Foundation of China (Nos. 91221101, 21433006, 11504204), the 111 project (Grant No. B13029), the Fundamental Research Funds of Shandong University (Grant No. 2015HW012), the Technological Development Program in Shandong Province Education Department (Grant No. J14LJ03), and the National Super Computing Centre in Jinan.

Footnotes

Author Contributions Y.Q., F.L. and H.Z. performed the calculations and analyzed the data. Y.Q. and M.Z. conceived the research. Y.Q. and M.Z. wrote the paper.

References

  1. Cho A. Helium-3 Shortage Could Put Freeze On Low-Temperature Research. Science 326, 778–779 (2009). [DOI] [PubMed] [Google Scholar]
  2. Salerno M. et al. Hyperpolarized noble gas MR imaging of the lung: potential clinical applications. Eur. J. Radiol. 40, 33–44 (2001). [DOI] [PubMed] [Google Scholar]
  3. Cai J. et al. Dynamic MRI of grid-tagged hyperpolarized helium-3 for the assessment of lung motion during breathing. Int.J. Radiat. Oncol. Biol. Phys. 75, 276–284 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Hauser A. W., Schrier J. & Schwerdtfeger P. Helium Tunneling through Nitrogen-Functionalized Graphene Pores: Pressure- and Temperature-Driven Approaches to Isotope Separation. J. Phys. Chem. C 116, 10819–10827 (2012). [Google Scholar]
  5. Mandrà S., Schrier J. & Ceotto M. Helium Isotope Enrichment by Resonant Tunneling through Nanoporous Graphene Bilayers. J. Phys. Chem. A 118, 6457–6465 (2014). [DOI] [PubMed] [Google Scholar]
  6. Hauser A. W. & Schwerdtfeger P. Nanoporous Graphene Membranes for Efficient 3He/4He Separation. J. Phys. Chem. Lett. 3, 209–213 (2012). [Google Scholar]
  7. Schrier J. Helium Separation Using Porous Graphene Membranes. J. Phys. Chem. Lett. 1, 2284–2287 (2010). [Google Scholar]
  8. Bartolomei M. et al. Graphdiyne Pores:‘Ad Hoc’Openings for Helium Separation Applications. J. Phys. Chem. C 118, 29966–29972 (2014). [Google Scholar]
  9. Zhu Z. Permeance should be used to characterize the productivity of a polymeric gas separation membrane. J. Membr. Sci. 281, 754–756 (2006). [Google Scholar]
  10. Guo Q., Yang Q., Yi C., Zhu L. & Xie Y. Synthesis of carbon nitrides with graphite-like or onion-like lamellar structures via a solvent-free route at low temperatures. Carbon 43, 1386–1391 (2005). [Google Scholar]
  11. Xu B. et al. Two-dimensional graphene-like C2N: an experimentally available porous membrane for hydrogen purification. Phys. Chem. Chem. Phys. 17, 15115–15118 (2015). [DOI] [PubMed] [Google Scholar]
  12. Li F., Qu Y. & Zhao M. Efficient helium separation of graphitic carbon nitride membrane. Carbon 95, 51–57 (2015). [Google Scholar]
  13. Zhao Z., Sun Y. & Dong F. Graphitic carbon nitride based nanocomposites: a review. Nanoscale 7, 15–37 (2015). [DOI] [PubMed] [Google Scholar]
  14. Cao S. & Yu J. g-C3N4-Based Photocatalysts for Hydrogen Generation. J. Phys. Chem. Lett. 5, 2101–2107 (2014). [DOI] [PubMed] [Google Scholar]
  15. Du A. et al. Hybrid graphene and graphitic carbon nitride nanocomposite: gap opening, electron–hole puddle, interfacial charge transfer, and enhanced visible light response. J. Am. Chem. Soc. 134, 4393–4397 (2012). [DOI] [PubMed] [Google Scholar]
  16. Zhang X., Zhao M., Wang A., Wang X. & Du A. Spin-polarization and ferromagnetism of graphitic carbon nitride materials. J. Mater. Chem. C 1, 6265–6270 (2013). [Google Scholar]
  17. Ghosh D., Periyasamy G. & Pati S. K. Transition Metal Embedded Two-Dimensional C3N4–Graphene Nanocomposite: A Multifunctional Material. J. Phys. Chem. C 118, 15487–15494 (2014). [Google Scholar]
  18. Wu M., Wang Q., Sun Q. & Jena P. Functionalized graphitic carbon nitride for efficient energy storage. J. Phys. Chem. C 117, 6055–6059 (2013). [Google Scholar]
  19. Mahmood J. et al. Nitrogenated holey two-dimensional structures. Nat. Commun. 6, 6468, 10.1038/ncomms7486 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Zhu L. et al. C2N: an excellent two-dimensional monolayer membrane for He separation. J. Mater. Chem. A 3, 21351–21356, 10.1039/C5TA05700K (2015). [DOI] [Google Scholar]
  21. Cedillo A. Quantum Mechanical Tunneling through Barriers: A Spreadsheet Approach. J. Chem. Education 77, 528–531, 10.1021/ed077p528 (2000). [DOI] [Google Scholar]
  22. Brockway A. M. & Schrier J. Noble Gas Separation using PG-ESX (X = 1, 2, 3) Nanoporous Two-Dimensional Polymers. J. Phys. Chem. C 117, 393–402 (2013). [Google Scholar]
  23. Nada M., Sheng D. & De-En J. Quantum mechanical basis for kinetic diameters of small gaseous molecules. J. Phys. Chem. A 118, 1150–1154 (2014). [DOI] [PubMed] [Google Scholar]
  24. Grimme S., Antony J., Ehrlich S. & Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104, 10.1063/1.3382344 (2010). [DOI] [PubMed] [Google Scholar]
  25. Grimme S., Ehrlich S. & Goerigk L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 32, 1456–1465 (2011). [DOI] [PubMed] [Google Scholar]
  26. Kohn W. & Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 140, 1133–1138 (1965). [Google Scholar]
  27. Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996). [DOI] [PubMed] [Google Scholar]
  28. Hohenberg P. & Kohn W. Inhomogeneous Electron Gas. Phys. Rev. 136, B864–B871 (1964). [Google Scholar]
  29. Perdew J., Burke K. & Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
  30. Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 27, 1787–1799 (2006). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep19952-s1.pdf (238.6KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES