Design Principles for Metal Oxide Redox Materials for Solar-Driven Isothermal Fuel Production

Abstract

The performance of metal oxides as redox materials is limited by their oxygen conductivity and thermochemical stability. Predicting these properties from the electronic structure can support the screening of advanced metal oxides and accelerate their development for clean energy applications. Specifically, reducible metal oxide catalysts and potential redox materials for the solar-thermochemical splitting of CO₂ and H₂O via an isothermal redox cycle are examined. A volcano-type correlation is developed from available experimental data and density functional theory. It is found that the energy of the oxygen-vacancy formation at the most stable surfaces of TiO₂, Ti₂O₃, Cu₂O, ZnO, ZrO₂, MoO₃, Ag₂O, CeO₂, yttria-stabilized zirconia, and three perovskites scales with the Gibbs free energy of formation of the bulk oxides. Analogously, the experimental oxygen self-diffusion constants correlate with the transition-state energy of oxygen conduction. A simple descriptor is derived for rapid screening of oxygen-diffusion trends across a large set of metal oxide compositions. These general trends are rationalized with the electronic charge localized at the lattice oxygen and can be utilized to predict the surface activity, the free energy of complex bulk metal oxides, and their oxygen conductivity.

1 Introduction

Utilizing the full spectrum of sunlight on a large scale requires technologies for the concentration and storage of this dilute and intermittent energy resource.¹ Concentrated solar radiation can be used as the source of high-temperature heat to drive thermochemical redox cycles for splitting H₂O and CO₂ and produce H₂ and CO.^2–5 Syngas (a mixture of H₂ and CO) is the building block of a plethora of chemical commodities, such as liquid hydrocarbon fuels produced via commercial Fischer–Tropsch technology. The ability to efficiently convert solar energy to chemical energy is determined by the ability of the solar receiver–reactor technology to absorb concentrated solar radiation in the form of high-temperature process heat and by the reactive material to utilize this heat to generate the fuel.⁶ In the present article, we develop design principles^6–9 for metal oxide redox materials for an energy-efficient isothermal solar fuel synthesis. However, the reported thermochemical and electronic-structure calculations screen for trends in the surface activity and oxygen ion conductivity across the periodic table that can also be useful for the development of non-noble metal catalysts for photochemical water oxidation,¹⁰ electrocatalysts for CO₂ reduction,¹¹ catalysts for the oxygen reduction reaction and oxygen evolution reaction,^8,12 and oxygen conductors for solid oxide fuel cells (SOFC).^13,14

To store solar energy chemically, a highly stable molecule such as CO₂ or H₂O is cleaved in two reaction steps of which at least one is endothermic and driven by concentrated solar heat. Conceptually, CO₂ or H₂O is first reduced to CO or H₂ (Equation 1 or 2) respectively by the oxidation of a reduced metal oxide (metal oxide oxidation):

1

2

where M is a metal, a, b, c, and d are metal-specific stoichiometric coefficients (i.e., b = 2−δ for nonstoichiometric CeO_2−δ),^2,4,15 and x and y are reaction coefficients determined by a, b, c, and d.

In a separate endothermic reaction step referred to as metal oxide reduction, the oxygen is abstracted from the solid at an elevated temperature with concentrated solar energy (in the range of about 1000 °C–1700 °C) and at low partial O₂ pressures (Equation 3 or in the presence of a reducing gas to produce further quantities of syngas (Equation 4):

3

4

Overall, without consuming solid material, the process enables the utilization of the full spectrum of solar radiation for the production of syngas from CO₂ and H₂O. If one can conduct both reaction steps at the same temperature (i.e., isothermal operation), it may be possible to circumvent energetic inefficiencies associated with large temperature swings between the reduction and oxidation steps as well as mechanical stress arising from rapid temperature changes.^15,16 During isothermal operation, product formation is driven via partial-pressure changes, i.e., high concentrations of the oxidant (CO₂ or H₂O) during the metal oxide oxidation and efficient removal of O₂ during the metal oxide reduction. The promise of such an operation was shown recently for water-splitting (Equation 2 and (3)), in which a ferrite-based reactant operated isothermally at 1350 °C was reported to yield at least three times more hydrogen (liberated at a peak rate of 0.74 mL H₂ g⁻¹ reactant min⁻¹) relative to a temperature swing between 1000 °C and 1350 °C.¹⁶

Designing optimized metal oxide reactants for the synthesis of solar fuels involves balancing material properties such as redox characteristics, reaction kinetics, volatility, phase stability, and thermal expansion, some of which may be antagonistic towards one another. Traditionally, this has been addressed by the use of thermochemical equilibrium computations.^6,17 Since an isothermal solar-thermochemical process imposes different constraints on a reactive material, relative to an isobaric operation, we begin our analysis by quantifying the trade-off of redox properties under isothermal conditions, first employing literature-based thermochemical equilibrium calculations for the descriptor-based design^6–9 of metal oxide reactants in Section 2.1.

Since such data derived from experiments are limited, in Sections 2.2 and 2.3 we use electronic-structure theory to develop key descriptors and establish trends in the thermochemical stability and oxygen conductivity of metal oxides; this provides guidance for undertaking massive materials screening in silico. We will show that the free energy of forming oxygen vacancies at the surface correlates with the free energy of formation of the bulk metal oxides. This trend can be employed to predict the thermochemical stability of bulk metal oxides and is rationalized with the amount of charge that is transferred per vacancy formed. Analogously, we compute the free energy of the transition state for oxygen-vacancy conduction that will be seen to correlate with the experimental oxygen self-diffusion constants, indicating their predictive value. For prospective rapid screening of oxygen-diffusion trends, we establish a pseudotransition-state energy for the oxygen conduction in a large set of metal oxide compositions.

2 Results and Discussion

2.1 Thermochemical Stability of Bulk Metal Oxide

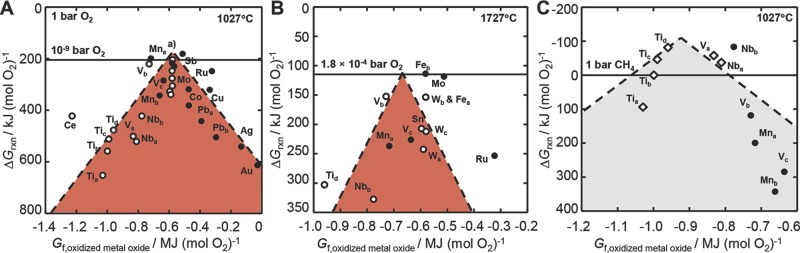
In analogy to the Sabatier principle in heterogeneous catalysis,⁹ the trade-off of the redox potential for a set of bulk metal oxides is quantified in this section to guide the choice of the redox material for an isothermal solar-driven syngas production. Figure 1 shows the Gibbs free energy of the metal oxide oxidation (Equation 1) and metal oxide reduction reactions (Equations 3 and 4) at constant temperature for 26 solid metal oxide and 3 metal/metal oxide pairs as a function of the thermochemical oxide stability. An isothermal operation requires a metal oxide that can be oxidized exergonically at a given temperature with CO₂ while its oxidized surface can be reduced at the same temperature and low partial O₂ pressure. Either one of these two reactions is slightly more endergonic, thereby limiting the equilibrium yield of the cycle. Therefore, Figure 1 shows only the limiting (most endergonic) free energies of reaction. The volcano-shaped correlation points towards the ideal material for an isothermal CO₂ reduction, that is, a metal oxide that binds oxygen just strong enough to cleave CO₂ but weak enough to facilitate the metal oxide reduction at moderate temperature and partial O₂ pressure. The optimum oxide compositions are where these effects balance, located near the intersection of a linear regression of the free energies of the metal oxide oxidation and reduction. We note although the data are computed at thermodynamic equilibrium which may only be approached during the fuel synthesis in a reactor that is open to mass exchange, the analysis is a quantitative design principle for metal oxide redox materials since the redox trends in a system that is open to mass exchange can be expected to be preserved.

Figure 1.

Volcano-type plots for isothermal redox cycles with solid metal oxides. A) The limiting free energy of oxidizing a metal oxide with CO₂ (filled circles, Equation 1 and reducing a metal oxide in an inert atmosphere (empty circles, Equation 3 is plotted versus the formation energy of the oxidized metal oxide. The analysis indicates increased reaction yields (less endergonic redox cycles at the top of the volcano) when B) increasing the temperature and decreasing the partial O₂ pressure or C) coupling the metal oxide reduction with reforming of methane (empty diamonds, Equation 4. The metal oxide pairs are (Ti_a) TiO/Ti₂O₃, (Ti_b) Ti₂O₃/Ti₃O₅, (Ti_c) Ti₃O₅/Ti₄O₇, (Ti_d) Ti₄O₇/r-TiO₂, (V_a) VO/V₂O₃, (V_b) V₂O₃/V₂O₄, (V_c) V₂O₄/V₂O₅, (Mn_a) MnO/Mn₃O₄, (Mn_b) Mn₃O₄/Mn₂O₃, (Fe_a) FeO/Fe_0.947O, (Fe_b) FeO/Fe₃O₄, (F_c) Fe₃O₄/Fe₂O₃, (Co) CoO/Co₃O₄, (Cu) Cu₂O/CuO, (Nb_a) NbO/NbO₂, (Nb_b) NbO₂/Nb₂O₅, (Mo) MoO₂/MoO₃, (Ru) Ru/RuO₂, (Ag) Ag/Ag₂O, (Sn) SnO/SnO₂, (Sb) c-Sb₂O₃/SbO₂, (Ce) Ce₂O₃/CeO₂, (W_a) WO₂/WO_2.72, (W_b) WO_2.72/WO_2.9, (W_c) WO_2.9/WO_2.96, (W_d) WO_2.96/WO₃, (Au) Au/Au₂O₃, (Pb_a) PbO/Pb₃O₄, (Pb_b) Pb₃O₄/PbO₂. a) Starting with the most endergonic cycle, W_a, Sn, W_c, Fe_b, W_b, Fe_c, Fe_a, and W_d. Dashed lines are linear fits.

Ideally, the top of the volcano curve for an isothermal CO₂ reduction corresponds to negative free energies of the metal oxide oxidation and reduction reactions. This can be achieved with materials such as Mn₃O₄, WO₃, and MoO₃ at low partial O₂ pressure (Figure 1A), with, e.g., Fe₂O₃ at intermediate partial O₂ pressure and high temperature (Figure 1B), or with relatively stable metal oxides such as CeO₂, Ti₃O₅, Ti₄O₇, TiO₂, V₂O₃, NbO₂, and Nb₂O₅ that are reduced in a reducing atmosphere¹⁴ (Figure 1C). While the use of methane is only one of several options to conduct the metal oxide reduction in a reducing atmosphere, integrating methane reforming into the process allows for upgrading the heating value of natural gas with solar energy which may increase the viability of this process. We note that use of WO₃ and MoO₃ would require means to avoid significant metal oxide volatilization.

While the volcano points towards metal oxides that are currently studied for isobaric solar-thermochemical applications, such as ceria and ferrites,^2,4,6,15,18 the analysis identifies the free energy of formation of a metal oxide as a quantitative descriptor for the rational design of metal oxides^6–9 for solar fuel production. For instance, an ideal metal oxide for a solar-driven isothermal CO₂ reduction at 1027 °C and 1 bar CO₂/air can be identified with a free energy of bulk formation of 300–500 kJ mol⁻¹ O₂. The present work shows how this information can be estimated from density functional theory (DFT) computations for complex metal oxides, such as perovskites,^5,18–20 where experimental data are scarce. While the analysis focuses on solar-thermochemical applications, the presented principles are also useful for the development of SOFC and mixed ionic-electronic conducting materials.^8,12–14

2.2 Oxygen-Vacancy Formation

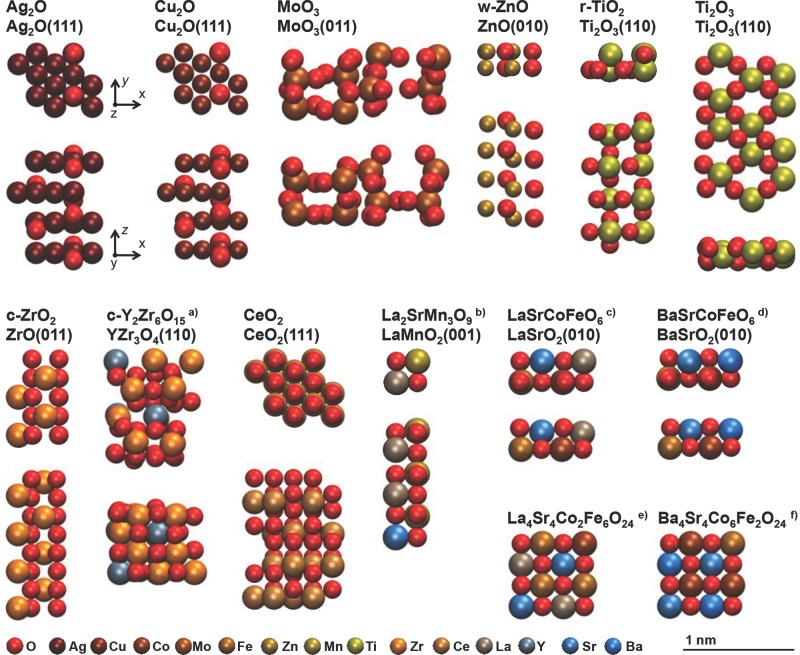
To screen for descriptors of the surface activity and oxygen conduction in metal oxides, 12 metal oxides shown structurally in Figure 2 are modeled via density functional theory. We have selected these structurally and electronically different metal oxides due to the interest in these materials for solar-driven redox cycles,^2,5,6,16 fuel cell applications,^8,12–14 electrocatalytic CO₂ reduction,¹¹ and photocatalytic H₂O oxidation.¹⁰ Computing thermodynamic properties such as the free energy of bulk formation for solids from first principles requires a combination of DFT and phonon calculations that can be costly for complex structures such as many metal oxides.²¹ This section shows how the free energy of formation of a bulk metal oxide scales with the energy of forming surface oxygen vacancies, indicating that the vacancy formation energy can be used both as a direct measure of the surface activity and as an estimate of the reducibility of the bulk oxide.

Figure 2.

Optimized surface geometries with bulk stoichiometry (top line) and surface stoichiometry and facet (second line) indicated above each model. a) 25-YSZ (i.e., 25 mol% Y, metal basis), b) La_0.67Sr_0.33MnO₃ (LSM), c) La_0.5Sr_0.5Co_0.5Fe_0.5O₃, d) Ba_0.5Sr_0.5Co_0.5Fe_0.5O₃, e) La_0.5Sr_0.5Co_0.25Fe_0.75O₃ bulk, f) Ba_0.5Sr_0.5Co_0.75Fe_0.25O₃ bulk.

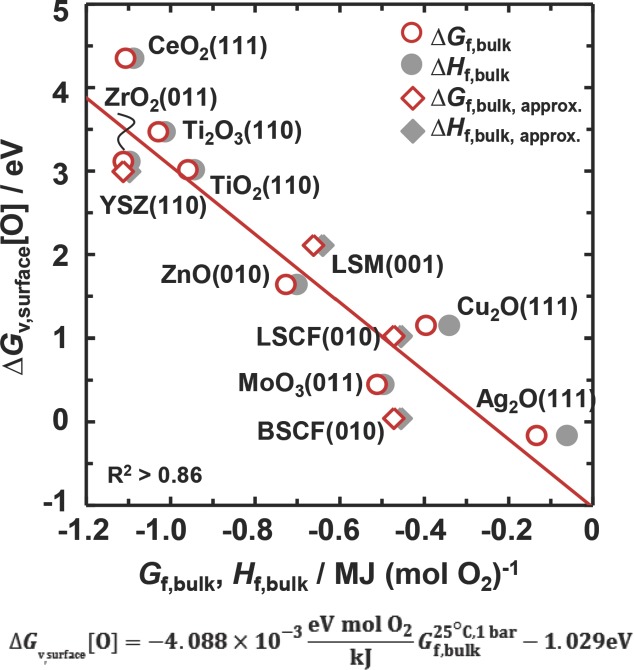
Figure 3 plots the free energy of forming oxygen vacancies at a metal oxide surface, ΔG_v,surface[O] versus the free energy and enthalpy of formation of the bulk oxide, where the bulk-formation energies are taken from the experimental literature.²² These energies of bulk formation determine the activity of the metal oxides in isothermal high-temperature CO₂ reduction, but are not always experimentally available. The plot shows a linear correlation that is essentially unaffected by entropic contributions (i.e., H_{f,bulk oxide} and G_{f,bulk oxide} differ only slightly) which indicates that the scaling is due to the enthalpy required for breaking the bonds formed between the lattice oxygen and the metal atoms. This correlation can be employed to obtain a first estimate of the free energy of formation for complex bulk metal oxides. This can be achieved by using the available thermodynamic data for metal oxides²² (or JANAF tables),²³ the presented scaling relation of the free energy of bulk formation or the free energy of reaction (shown in Figure S2, Supporting Information) at a desired temperature and pressure and DFT to determine ΔG_v,surface[O] without the need for costly phonon calculations.

Figure 3.

The DFT-calculated free energy of forming oxygen vacancies at a metal oxide surface versus the experimental²² free energy (G_{f,bulk oxide}) and enthalpy (H_{f,bulk oxide}) of formation of the bulk oxide at 25 °C and 1 bar. A linear regression is marked with a solid line. ΔG_v,surface for the highly oxidized MoO₃ was taken as the average of ΔG_v,surface in the range of −0.69–1.59 eV. The mixed metal oxides, i.e., BSCF, LSCF, LSM, and YSZ, are approximations (shown with diamonds), as described in Supporting Information.

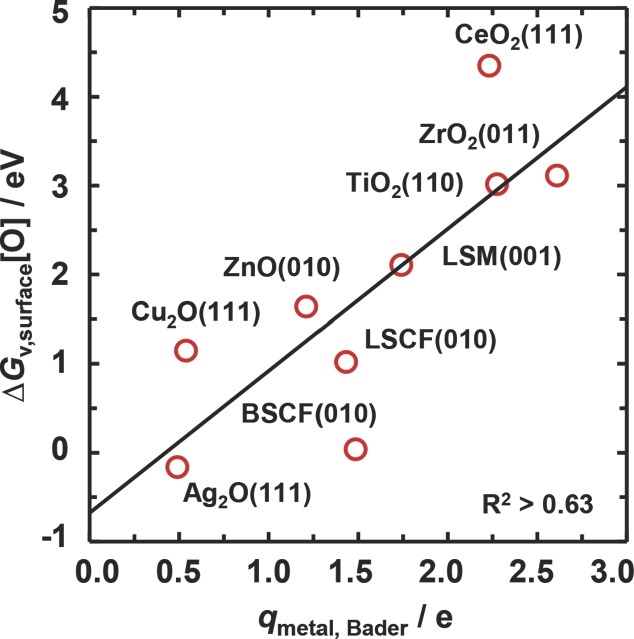
We suggest that Figure 3 shows a strong correlation as a result of the energy required to break the bonds formed between the lattice oxygen and the metal atoms. This is further confirmed via plotting ΔG_v,surface[O] versus the partial charge of the metal atoms, which we show in Figure 4. This suggests that when forming an oxygen vacancy, if a larger amount of electronic density needs to be transferred from the lattice oxygen to the bulk, the oxygen-vacancy formation will be more endergonic and a more stable metal oxide will result. While the relative endergonic ΔG_v,surface[O] for CeO₂(111) may be related to the use of VASP (Vienna Ab-Initio Simulation Package) code versus DACAPO code for all other data, the deviation of Ba_0.5Sr_0.5Co_0.5Fe_0.5O₃ (BSCF) can be understood due to the lower amount of charge localized on the lattice oxygen [e.g., −1.17 e for La_0.5Sr_0.5Co_0.5Fe_0.5O₃ (LSCF) vs −1.05 e for BSCF]. Dependent on the operation conditions, this makes BSCF potentially interesting for applications at lower temperatures versus LSCF for higher temperatures (Figure 1).

Figure 4.

The free energy of forming oxygen vacancies at the surface versus the average cation charge of the bulk metal oxides. For the perovskites, the average cation charge is computed for the metal at which the oxygen vacancy is formed, i.e., Co, Co, and Mn for BSCF, LSCF, and LSM respectively. The solid line is a linear regression.

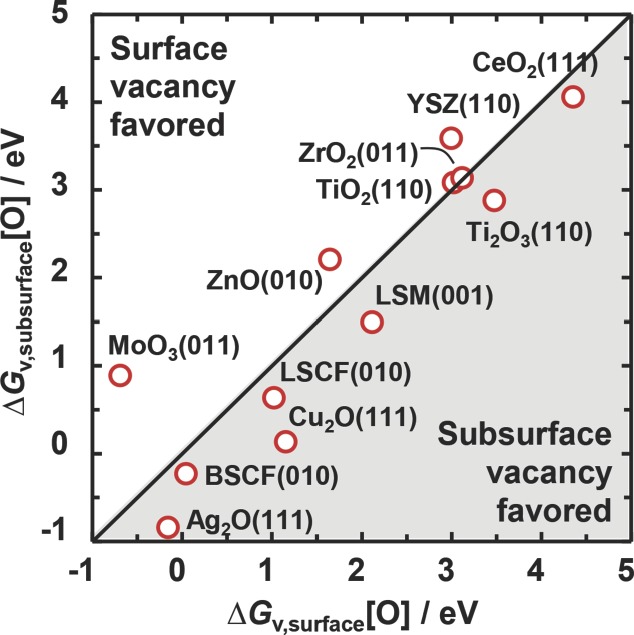
To assess the thermodynamic tendency of oxygen vacancies to diffuse into the bulk, Figure 5 shows the free energy of forming oxygen vacancies in the first subsurface layer, ΔG_v,subsurface[O], versus ΔG_v,surface[O]. At equilibrium, the vacancies favor the bulk over the surface if ΔG_v,subsurface[O] < ΔG_v,surface[O]. In this sense, if the migration of the oxygen vacancies into the bulk is desirable, materials that show that this inequality holds are interesting outliers. These include the surfaces of all studied perovskites and CeO₂, that is, currently studied solar-thermochemical redox^4,18 and SOFC materials.^13,14

Figure 5.

The free energy of forming oxygen vacancies below the surface versus the free energy of forming oxygen vacancies at the surface. The solid line marks parity.

2.3 Oxygen-Vacancy Conduction

In practice, many solar-thermochemical redox materials are limited by internal diffusion of oxygen vacancies.^5,6,24 This suggests that in addition to the thermodynamic quantities described above, a major parameter that controls the use of a metal oxide for solar-driven isothermal CO₂ reduction relates to the kinetics of the oxygen-vacancy conduction. As understood most simply with an Eyring–Polanyi equation, the rate of oxygen diffusion depends exponentially on the free energy of the vacancy conduction, which in basic transition-state theory can be quantified with the saddle-point energy for a vacancy diffusion process computed from first principles via the nudged elastic band (NEB) method.²⁵ The concepts discussed in this section are useful for estimating the intrinsic diffusion kinetics of metal oxides prior to the need for costly experimental studies.

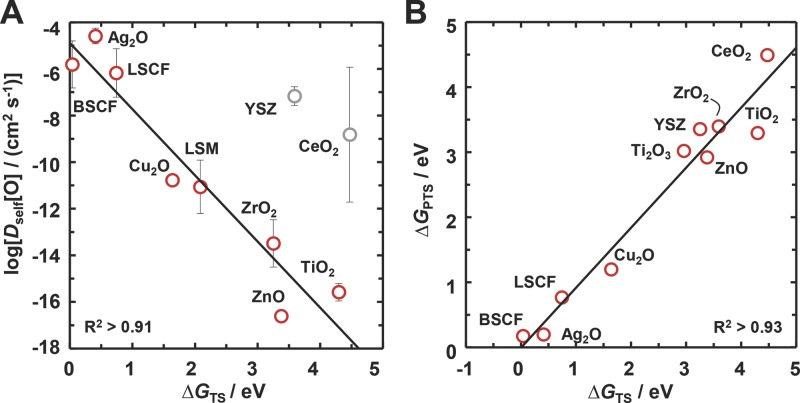
To demonstrate the use of the DFT-calculated free energies of the oxygen conduction, Figure 6 A shows the average experimental oxygen self-diffusion constant as a function of the transition-state energy. Considering the analytical uncertainty of the experimental values and the varying temperature conditions of the measurements, generally the correlation confirms the predictive power of the presented surface calculations over a range of more than 10 orders of magnitude. The deviation of yttria-stabilized zirconia (YSZ) and CeO₂ from this correlation can be understood due to the large amount of energy that is required to form the vacancies. Figure S6 (Supporting Information) shows that a correlation of the experimental oxygen self-diffusion constants with the energetic differences between the transition state and the vacancy formation captures the trend for these materials.

Figure 6.

Modeling the kinetics of the oxygen-vacancy conduction. A) The average oxygen self-diffusion constant at 771 ± 36 °C for TiO₂,^26–28 LSM,^29,30 BSCF,³¹ LSCF,^29,32 Cu₂O (extrapolated),³³ ZnO,^34,35 ZrO₂,^26,36 YSZ,^26,36–39 Ag₂O,^40–42 and CeO₂^37,43,44 versus the free energy of the transition state, ΔG_TS. One standard deviation is shown with error bars. The solid line is a linear regression (without YSZ and CeO₂). Details are given in Supporting Information. B) Correlation the pseudotransition-state energy for the oxygen-vacancy conduction, ΔG_PTS, with ΔG_TS. The solid line is a linear regression.

While an estimate of the transition-state energy is central for predicting the oxygen-diffusion kinetics in metal oxides, computing this value via the NEB method is computationally demanding even for moderately complex materials. To simplify the analysis, Brønsted–Evans–Polanyi (BEP) relations have been used successfully in heterogeneous catalysis to show that the transition-state energy of a surface reaction scales with the reaction energy.⁹ While the concept has been applied to describe surface reactions at structurally similar metal oxide surfaces,⁴⁵ we find that a simple BEP relation does not describe the oxygen conduction across the discussed metal oxides (Figure S3, Supporting Information) which can be understood due to a lack of self-similarity in a large set of structurally different metal oxide surfaces. Alternatively, we define a pseudotransition-state energy as the energy of forming a surface with both surface vacancy and subsurface vacancy and an oxygen atom fixed half-way between the two vacancies. Figure 6B shows that the pseudotransition-state energy scales linearly with the transition-state energy. While deviations, such as observed for TiO₂ and YSZ, indicate the approximate value of the pseudotransition state that is not confirming the location of the saddle point, the analysis suggests the use of the pseudotransition state in future screening studies for the oxygen-conduction characteristics of complex metal oxide compositions.

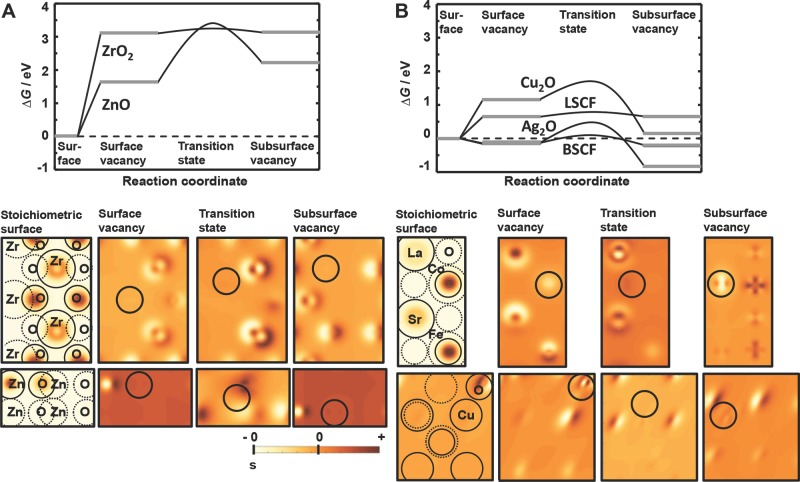
To understand the origin of the diffusion barrier that is described by the transition state, Figure 7 shows a free energy diagram for the oxygen-vacancy formation at the surface and conduction into the subsurface layer. This is representative of metal oxide reduction, and since the process is isothermal the reverse is metal oxide oxidation. In this figure, we show four representative metal oxide surfaces discussed below. We propose that the metal oxides can be classified into two groups: one group with a highly endergonic diffusion path (with transition-state energies above about 2.9 eV, Figure 7A) and a second group with a less endergonic diffusion path (with transition-state energies less than about 1.6 eV, Figure 7B). The latter value of the transition-state energy translates into a reaction rate of approximately 0.11 μmol H₂ g⁻¹ LSCF s⁻¹ liberated via splitting of 0.506 bar H₂O at 1350 °C (Supporting Information), which is of the same order of magnitude as a peak formation rate of 0.55 μmol H₂ g⁻¹ s⁻¹ reported for isothermal H₂O splitting at 1350 °C with a hercynite reactant (composed of 19.8 wt% CoFe₂O₄ on Al₂O₃).¹⁶ Thus, the latter group is of particular interest for CO₂ and H₂O splitting applications since these materials may facilitate the oxygen-vacancy formation and conduction at relatively low temperatures. An overview of all computed energy values is given in Figure S4 (Supporting Information) which shows expected features such as the facile oxygen-diffusion properties of CeO₂ indicated by a low transition state relative to the energy that is required to form the surface and subsurface oxygen vacancies.^15,37,43,44 Augmented diffusion kinetics when doping ZrO₂ with Y₂O₃ are indicated as well.^26,36–39

Figure 7.

Free energy diagrams for the formation and diffusion of oxygen vacancies (negative free energies, below the dashed line, indicate spontaneous processes). All energies are relative to the stoichiometric surface and oxygen in the form of water in the gas phase. The correlating charge density of the stoichiometric surface and charge-density differences (the position of the vacancy is marked with a circle) are shown below for ZnO, ZrO₂, Cu₂O, and LSCF. Charge density is given in units of the elementary charge per ų at the height of the vacancy (shown qualitatively with a scale bar that indicates 0; s marks 0 for the stoichiometric surface).

As we seek optimal metal oxides for high-temperature isothermal CO₂ reduction, we search for the ideal case where all energy values are close to zero, such as shown by LSCF and BSCF (Figure 7B) at the computed conditions. Additionally, the relatively facile formation of oxygen vacancies at the surface of LSCF and BSCF relative to La_0.67Sr_0.33MnO₃ (LSM) for instance is in agreement with the reported low thermal stability of LSCF and BSCF.¹⁴ This and the promising oxygen-conduction energetics make perovskites^5,18,19 such as LSCF and BSCF ideal candidates for solar-thermochemical H₂O and CO₂ splitting.

If one compares ZnO and ZrO₂ from Figure 7A, we see a higher energetic barrier of the oxygen conduction for ZnO. This is true both of the absolute value of the transition-state energy and the relative barrier height, or the difference between the transition-state energy and either stable state surrounding it. To understand the origin of these differences in activated oxygen-vacancy diffusion at our metal oxide surfaces, the charge-density difference between the surface with an oxygen vacancy and the stoichiometric surface (with the balance of oxygen in the gas phase) was computed and is shown in Figure 7. We can see an accumulation of charge density near the oxygen vacancy at the transition state for ZnO (dark-colored regions of the charge-density plots), while the oxygen vacancy at the transition state of ZrO₂ is surrounded by regions with decreased charge density (light-colored regions of the charge-density plots, Figure 7). In other words, charge density at the metal atoms surrounding the vacancy is removed, which creates a relatively positively charged environment for the conduction of the negatively charged vacancies. The same feature can be observed when comparing Cu₂O and LSCF (Figure 7) or Ag₂O and BSCF (Figure S5, Supporting Information) from the group of metal oxide surfaces with an only slightly endergonic diffusion path. Promotion of the vacancy conduction by a decreased charge density near the diffusing vacancy at the transition state may partly explain the geometric effect of the crystal lattice geometry on the oxygen-conduction properties reported for perovskites for instance¹⁴ and may aid the rational design of optimized oxygen conductors.^6–9

3 Conclusions

To guide the rational design of metal oxides for the solar-driven isothermal splitting of CO₂ and H₂O, we have developed a thermochemical rationale for choosing metal oxide redox materials. Since the underpinning thermochemical data are only available for a limited number of solid metal oxide solutions, a descriptor-based approach was established for estimating thermochemical properties at low computational cost via electronic-structure calculations. The free energy of forming oxygen vacancies and the transition-state energy of the oxygen conduction were identified as two major descriptors for the activity of metal oxides in splitting of CO₂ and H₂O, while the strength of the CO adsorption at the surface was found too weak to identify promising redox materials (Supporting Information). The utility of the reported correlations lies in the use of the free energy of forming oxygen vacancies at a metal oxide surface as a direct measure of the surface activity as well as the use of the available thermodynamic data and the presented linear scaling relations for estimating the free energy of bulk formation and the free energy of reaction for complex bulk metal oxides at a given temperature and pressure. The transition state of the oxygen conduction was shown to correlate with the experimental diffusion characteristics of a wide range of metal oxides. This and the established pseudotransition-state energy can be employed for a rapid screening of oxygen-diffusion trends across a large set of metal oxides for the development of advanced redox materials, metal oxide catalysts, and SOFC materials.

4 Experimental Section

Thermodynamic Equilibrium Calculations: A volcano-like plot⁹ was constructed as a guide for the design of metal oxide redox materials. The thermochemical equilibrium of various bulk metal oxides and their reaction products was determined as a function of temperature and pressure from tabulated free energy data.²² Per convention, negative free energy differences mark exergonic reactions.

Electronic-Structure Calculations: The most stable surfaces of 12 representative metal oxides (Table 1 and Figure 2) are modeled via DFT, performed with the open-source planewave pseudopotential electronic-structure code DACAPO.^46–48 Atomic configurations were handled in the Atomic Simulation Environment (ASE).⁴⁹ Exchange-correlation interactions were treated by the revised Perdew–Burke–Ernzerhof (PBE) functional of Hammer, Hansen, and Nørskov derived in the generalized gradient approximation.⁵⁰ Bulk structures were modeled with a k-point sampling of 4 × 4 × 4 (periodic boundary conditions in all directions), while the Brillouin zone of surface models (slabs periodically repeated in the directions parallel to the surface) was sampled with 4 × 4 × 1 k-points. A Fermi–Dirac smearing of 0.1 eV was used to achieve convergence, and results were extrapolated to 0 K. The linesearch BFGS algorithm was employed to optimize the atomic geometries until the maximum force was less than 0.05 eV Å⁻¹. To avoid reminiscent stress in the calculations, the lattice constants were chosen as the DFT-calculated bulk lattice constants, which are in average within 1.9% of the experimental values (Table1). The ferromagnetic spin configuration⁵¹ of BSCF and LSCF and the half metallicity of LSM⁵² were modeled with spin-polarized calculations. All calculations for CeO₂ were performed using the planewave-based VASP⁵³ and the PBE exchange-correlation functional.

Table 1.

Calculated and experimental lattice constants

Oxide	Crystal structurea)	Calculated (U = 0)			(U > 0)	Experimental			Reference
		a/Å	b/Å	c/Å	a/Å	a/Å	b/Å	c/Å
TiO2b)	tetragonal (136)	4.682		2.971		4.594		2.959	54
Ti2O3	trigonal (167)	5.138		14.088		5.163		13.624	55
Cu2O	cubic (224)	4.413				4.270			56
ZnOc)	hexagonal (186)	3.305		5.355		3.250		5.207	57
ZrO2d)	cubic (225)	5.142				5.110			58
YSZ d,e)	cubic (225)	5.194				5.153			58
Ag2O	cubic (224)	4.877				4.731			59
MoO3	orthorhombic (62)	14.866	3.792	4.158		13.855	3.696	3.963	60
CeO2d)	cubic (225)	5.470			5.650	5.411			61
BSCFf)	cubic (221)	3.903			4.058	4.000			62
LSCFg)	cubic (221)	3.903			4.022	3.874			63
LSM	cubic (221)	3.915			3.960	3.870			64

^a)Space group in parentheses;

^b)rutile;

^c)wurtzite structure;

^d)fluorite structure;

^e)25-YSZ, i.e., Y₂Zr₆O₁₅;

^f)a given for Ba_0.5Sr_0.5Co_0.75Fe_0.25O₃ (a = 3.925 Å for Ba_0.5Sr_0.5Co_0.5Fe_0.5O₃), while the experimental value is for Ba_0.5Sr_0.5Co_0.8Fe_0.2O₃;

^g)a given for La_0.5Sr_0.5Co_0.25Fe_0.75O₃ (a = 3.888 Å for La_0.5Sr_0.5Co_0.5Fe_0.5O₃), while the experimental value is for Sr_0.6Sr_0.4Co_0.2Fe_0.8O₃.

Although the utility of the Hubbard U model to account for the Coulombic repulsion of valance electrons in metal oxides is not determined in general and has been found to be not necessary for many metal oxides,^65–67 we have calculated the density of states (DOS), orbital occupancy, and Bader charges⁶⁸ (as well as the energies of the oxygen-vacancy formation and CO adsorption at CeO₂(111)) as criteria for determining the use of a U parameter.⁶⁷ The values of U, i.e., 3.0 eV for Mn 3d,⁵² 3.3 eV for Co 3d and 4.0 eV for Fe 3d in BSCF⁵¹ and LSCF⁶⁹ and 5 eV for Ce 4f electrons⁷⁰ are taken from the literature. Using the computational setups described above, the additional DFT +U calculations (including U = 0 as reference) were performed with the GPAW (grid-based projector-augmented wave) code^71,72 and Dudarev's implementation of the Hubbard U model.⁷³

The surface energies of the various terminations of the (001), (010), (100), (011), (101), (110), and (111) facets were computed (Table S1, Supporting Information) to determine the thermodynamically most stable surface. While most surface models consisted of 2 × 2 × 4 metal atoms in the x, y, and z directions (plus the stoichiometric amount of oxygen), the number of metal oxide layers was decreased in some cases due to the large size of certain surface models (Figure 2). The surfaces were modeled with 10 Å of vacuum perpendicular to the surface and approximately the lower half of the contained atoms constrained to the bulk geometry (i.e., in most cases the lower two layers of the slab) while the remaining atoms were allowed to optimize their positions. The interaction between the dipole moments of surfaces was decoupled via a dipole layer in the vacuum between the slabs. Figure 2 shows the most stable surface configurations.

Free energies at 25 °C and 1.013 bar total pressure, G_i, were calculated via⁷⁴

5

where T and P are the absolute temperature and pressure, N_i is the number of atoms of the chemical species i, μ_i is the chemical potential, E_i is the electronic energy determined from DFT-based structure optimization, U_ZPE,i is the zero-point vibrational energy, and S_i is the entropy. Gases are assumed to be ideal, while adsorbates and removed lattice oxygen are treated using the harmonic approximation where all degrees of freedom are treated as frustrated harmonic vibrations and PV contributions are neglected. Thermodynamic properties were calculated from vibrational frequencies and standard statistical mechanical equations evaluated through ASE.⁴⁹ Free energy corrections of the solids are neglected.²⁰

The free energy of forming oxygen vacancies, ΔG_v,j[O] at the surface (j = surface) or the first subsurface layer (j = subsurface), was computed via

6

where G_{surf with vac}, G_surf, and G_O^r are the free energies of the surface with the oxygen vacancy, the stoichiometric surface, and the reference energy of the removed lattice oxygen (taken as the energy difference of stable H₂O and H₂ in the gas phase), such that negative free energies indicate exergonic reactions. The quantities were determined for all non-symmetric lattice oxygen and are given relative to a specific surface model. Figure 2 can be used to account for the difference in monolayer vacancy concentrations (i.e., the number of oxygen vacancies relative to the amount of lattice oxygen at the surface).

Similarly, the transition-state energy for a vacancy diffusion process was computed from first principles via the climbing-image NEB method,²⁵ converged to within 0.04 eV Å⁻¹. The values were compared to a pseudotransition-state energy for the oxygen conduction, defined as the energy of forming both surface and subsurface vacancies and an oxygen atom that is fixed half-way between the vacancies (offset by further (0, −0.5, 0.5) Å for BSCF and LSCF to account for the vicinity to the bulk layer).

The effect of spin polarization⁷⁰ was found negligible for non-perovskites (i.e., differences of up to 0.15 meV, which is below a general uncertainty of the presented DFT calculations of about 50 meV). Similarly, the lattice constant of 25-YSZ (with 6.25% natural oxygen vacancies) was not effected by spin-polarized calculations.

Calculation Accuracy and Sensitivity to the Hubbard U Parameter: Modeling of metal oxides with DFT is complicated by their correlated electronic structures with partly localized electrons.⁷⁵ This aspect of the electronic structure is responsible for the semiconducting or insulating character of some metal oxides, i.e., the presence of a band gap. To account for this, the Hubbard U model is commonly used to modulate the electronic structure with an additional term that describes on-site Coulomb repulsion and exchange interactions and thereby correct the self-interaction errors.^75–77 Although the U parameter can be determined self-consistently,⁷⁷ commonly the value of U is chosen to fit the experimental band gap. While fitting procedures may be generally uncertain, the use of the Hubbard U model has been found unnecessary for certain semiconducting and insulating metal oxides, including TiO₂,⁶⁵ MoO₃,⁶⁶ and perovskites.⁶⁷ To test for the effect of U on the present surface calculations, we applied the Hubbard U model to selected metal oxides and compared the lattice constants, the DOS, and the orbital occupancy.⁶⁷ We find that the studied metal oxides are satisfactorily described without the Hubbard U model. Since we are interested in the surface activity of metal oxides, we further verified this by comparing the CO adsorption energy and the oxygen-vacancy-formation energy at CeO₂(111), which deviated by in average ±31 meV when including U = 5 eV for the Ce f states.

The DFT-optimized lattice constants with U = 0 are in average 1.94% above the experimental values. This is comparable to an overestimation by 1.09%–2.31% for metal carbides.^74,78 Computing the lattice constants for selected metal oxides with U > 0 generally increased the degree of overestimation. Further improvement of the lattice constants was obtained only for BSCF (underestimation of 2.43% with U = 0 versus overestimation of 1.45% with U > 0) while larger deviations were obtained for LSCF, LSM, and CeO₂ (overestimation of 0.75%, 1.16%, and 1.09% with U = 0 vs 3.82%, 2.33%, and 4.42% with U > 0, respectively).

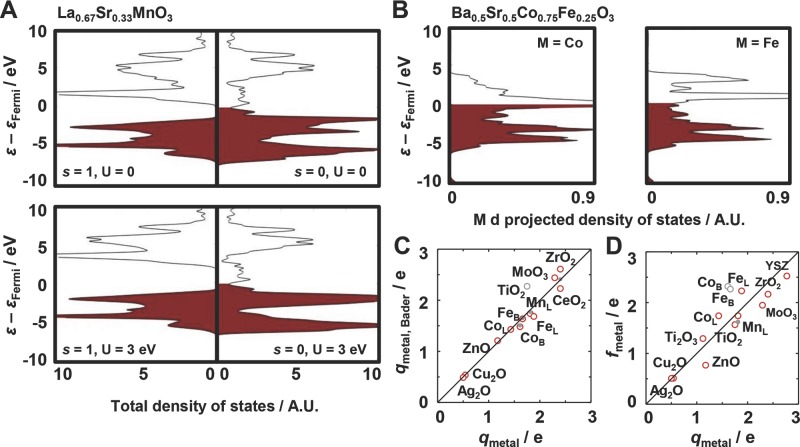
Generally, the DOS computed with U = 0 agrees with the electronic structure reported in the literature. For example, Figure 8 shows the DOS for LSM that captures the half metallicity of this perovskite (i.e., a spin-dependent conductive/insulating character) (Figure 8A).^52,79 As expected, computing the DOS with U = 3 eV for the Mn d states shifts the unoccupied states by 1–2 eV further above the Fermi level (effectively increasing the size of the band gap) and convolutes the occupied states for the other spin.⁵² Similarly, the structure of the Co d and Fe d states of BSCF with U = 0 (Figure 8B) agrees well with the DOS reported previously.⁵¹ Figure S1 (Supporting Information) gives a complete overview of the DOS.

Figure 8.

Testing the sensitivity to the Hubbard U. DOS plots for A) LSM and B) BSCF perovskite bulk structure that show the materials-specific physical properties reported in the literature. C) The partial average charge of the metal atom computed via the Bader method and D) the fractional band filling versus the charge of the metal cations as reported in the literature (mostly Bader charges) for TiO₂,⁸⁰ Ti₂O₃,⁸¹ Mn in LSM (Mn_L),⁷⁹ Fe in BSCF (Fe_B),⁸² Fe in LSCF (Fe_L),⁶⁹ Co in BSCF (Co_B),⁸² Co in LSCF (Co_L),⁶⁹ Cu₂O,⁸³ ZnO,⁸⁴ ZrO₂,⁸⁵ YSZ,^85,86 MoO₃,⁸⁷ Ag₂O,⁸⁸ and CeO₂.⁸⁹ Empty light gray circles mark data points that deviate by more than C) 0.20 or D) 0.35 e from parity (solid line); filled circles mark computations with U > 0.

To quantify the orbital occupancy, Figure 8C compares the Bader charges computed with U = 0 for the metal cations to the charges reported in the literature. The computed values agree generally well with the literature, with the exception of an overestimation of 0.52 e (elementary charges) for TiO₂, a metal oxide that has been modeled satisfactorily without the Hubbard U model.⁶⁵ Including the Hubbard U for selected metal oxides, such as CeO₂, may however slightly improve modeling of the electronic structure (Figure 8C).

Additionally, Figure 8D compares the fractional band filling (at infinite cutoff), f_metal:

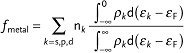7

where n_k is the number of s, p, and d valance electrons, ρ_k is the density of the metal-projected states and ε_k−ε_F is the energy of the states of a band relative to the Fermi level. While the match of f_metal with the partial cation charge is inferior compared to the Bader charges, the data show the expected trend of increasing fractional band filling with increasing partial cation charge, i.e., increasing electron localization. This indicates that the Bader charges can be used as first indicator of the orbital occupancy. Furthermore, Figure 8D shows that metal oxides with a relatively large ionic character such as ZrO₂, YSZ, and LSM are modeled well without U.

Supporting Information

Supporting Information is available from the Wiley Online Library or from the author.

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary