Semiparametric Estimation in the Secondary Analysis of Case-Control Studies

Abstract

We study the regression relationship among covariates in case-control data, an area known as the secondary analysis of case-control studies. The context is such that only the form of the regression mean is specified, so that we allow an arbitrary regression error distribution, which can depend on the covariates and thus can be heteroscedastic. Under mild regularity conditions we establish the theoretical identifiability of such models. Previous work in this context has either (a) specified a fully parametric distribution for the regression errors, (b) specified a homoscedastic distribution for the regression errors, (c) has specified the rate of disease in the population (we refer this as true population), or (d) has made a rare disease approximation. We construct a class of semiparametric estimation procedures that rely on none of these. The estimators differ from the usual semiparametric ones in that they draw conclusions about the true population, while technically operating in a hypothetic superpopulation. We also construct estimators with a unique feature, in that they are robust against the misspecification of the regression error distribution in terms of variance structure, while all other nonparametric effects are estimated despite of the biased samples. We establish the asymptotic properties of the estimators and illustrate their finite sample performance through simulation studies, as well as through an empirical example on the relation between red meat consumption and heterocyclic amines. Our analysis verified the positive relationship between red meat consumption and two forms of HCA, indicating that increased red meat consumption leads to increased levels of MeIQA and PhiP, both being risk factors for colorectal cancer. Computer software as well as data to illustrate the methodology are available at http://wileyonlinelibrary.com/journal/rss-datasets.

1 Introduction

Population-based case-control designs, hereafter called case-control designs, are popularly used for studying risk factors for rare diseases, such as cancers. The idealized set up of such designs is as follows. At a given time, there is an underlying base population, which we refer to as the true population throughout the paper. Within the true population, there are two subpopulations, those with the disease, called cases, and those without the disease, called controls. Separately, a random sample is taken from the case subpopulation, and a random sample is taken from the control subpopulation. Data on various covariates are then collected in a retrospective fashion, so that they reflect history prior to the disease. Nested case-control studies and case-cohort or case-base studies are variations of the retrospective case-control design.

The primary purpose of case-control designs is to understand the relation between disease occurrence and the covariates. The secondary analysis of such case-control data (Jiang et al., 2006; Lin and Zeng, 2009; Li, et al., 2010; Wei, et al., 2012, He et al., 2012) is based on the realization that the data further provide information about the relationship among the covariates. The relation between covariates are often of interest as well, as they can reveal associations between various covariates such as gene-environment, gene-gene and environment-environment associations. These analyses become especially important when, as is the case of retrospective sampling, a random sample from the true population is not available; see the secondary analysis literature mentioned above for more examples. If we seek to understand the regression relationship between covariates Y and X in the true population, we generally cannot use the case-control data set as if it were a random sample from the true population. Indeed, unless disease is independent of Y given X, the regression of Y on X based on the case-control sample will lead to a relationship different from that in the true population.

To see this numerically, we first define our notation. There are N₀ cases and N₁ controls, with N = N₀ + N₁. Suppose that N₀ = N₁ = 500, and that disease status D is related to covariates (Y, X) in the true population through the linear logistic model

$$\text{pr}(D=d|\mathbf{X}=x,Y=y)=f_{D|X,Y}^{\text{true}}(d,\mathbf{x},y)=H(d,\mathbf{x},y,\mathit{\alpha })=\frac{exp\{d({\alpha }_c+{\mathbf{x}}^{\mathrm{T}}{\mathit{\alpha }}_1+y{\alpha }_2)\}}{1+exp({\alpha }_c+{\mathbf{x}}^{\mathrm{T}}{\mathit{\alpha }}_1+y{\alpha }_2)},$$ (1)

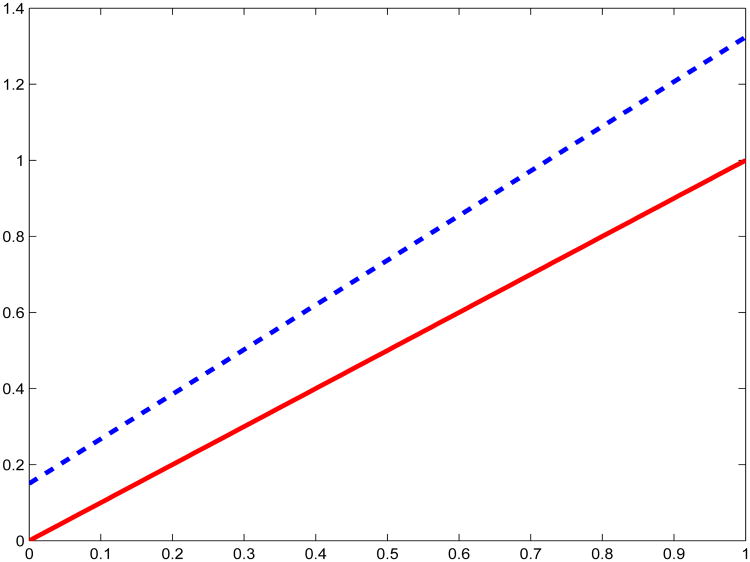
where for this illustration, α = (α_c, α₁, α₂) = (−5.5, 1.0, 0.5). Suppose further that the regression relationship in the true population is that Y = β_c + Xβ + ε, with β_c = 0, β = 1 and ε ∼ Normal(0, 1). In addition, in the true population, X ∼ Uniform(0, 1). In this setup, suppose the disease is rare, with pr(D = 1) ≈ 0.01. Thus, while controls are 99% of the true population, they are only 50% of the case-control study. To understand the bias induced by ignoring the case-control sampling scheme, we generated 3,000 case-control studies with intercept β_c = 0 and slope β = 1, and computed the intercept and slope estimates using all the data. Simply regressing Y on X and ignoring the case-control sampling scheme, the mean estimated intercept and slope across the 3,000 simulated data sets were 0.150 and 1.174, respectively, reflecting considerable bias, which leads to a coverage rate of only 67% for a nominal 95% confidence interval. Figure 1 shows the attained regression function compared to the true regression function. Using the method that we develop in this paper, our method yields the average intercept and slope estimates of 0.0024 and 1.0035, thus eliminating the bias caused by ignoring the case-control sampling scheme.

Figure 1.

Illustration of the bias induced by the case-control sampling scheme. The red solid line is the true regression function, while the blue dashed line is the regression function when using all the data and ignoring the case-control sampling scheme.

The bias in the secondary analysis is in stark contrast to what happens in the primary analysis, where estimating (α₁, α₂) is of interest. It is well known that α₁ and α₂ can be estimated consistently via ordinary logistic regression of D on (Y, X) by treating the case-control sample as if it were a random sample of the true population (Prentice and Pyke, 1979).

Our goal is to estimate the regression of Y on X in the true population, using case-control data, where for a function m(·) known up to a parameter β,

$$Y=m(\mathbf{X},\mathit{\beta })+\epsilon ,$$ (2)

where we make only the assumption that E(ε|X) = 0. Two solutions to estimating β have been proposed in the literature. (Lin and Zeng, 2009) and, obliquely, (Chen et al., 2008) proposed to assume a particular fully parametric distribution for ε and then perform a semi-parametric efficient analysis, where the distribution of X is nonparametric. There is excellent software for this problem in the case that ε = Normal(0, σ²), i.e., homoscedastic and normally distributed (http://www.bios.unc.edu/∼lin/software/SPREG/). To implement this software, however, one must either specify the disease rate pr(D = 1) in the true population or one must make a “rare-disease” assumption, which is implemented by assuming pr(D = 1) < 0.01. When the disease rate is known, reweighting the observations also corrects the biases (Scott and Wild, 2002). Wei, et al. (2012) dispense with the normality assumption, but still assume a homoscedastic distribution for ε independent of X and make a rare disease approximation.

In practice, the disease rate in the population being sampled is not known. In addition, it might not be rare. As an example, in Section 6, we use data from a case-control study of colorectal adenoma, a precursor to colorectal cancer, relating measures of heterocyclic amines to red meat consumption. While colorectal cancer is rare, colorectal adenomas are not, being on the order of 7% or more depending on the population being sampled (Yamaji et al., 2004; Corley et al., 2014). In this data set, one of the regressions is also heavily heteroscedastic. We will demonstrate that both approaches mentioned above have problems when some of the assumptions, such as the rare disease assumption, the known disease rate assumption and the known error distribution assumption, are violated (Tables 1-6).

Table 1.

Results of the simulation study with n₁ = 500 cases and n₀ = 500 controls, disease rate of approximately 4.5%, with homoscedastic errors. Here “Normal” means that ε = Normal(0, 1), while “Gamma” means that ε is a centered and scale Gamma random variable with shape 0.4, mean zero and variance one. The analyses performed were using controls only (“Controls”), the semiparametric efficient method that assumes normality and homoscedasticity (“Param”), the method of Wei, et al. (2012), (“Robust”), and our method (“Semi”). Over 1,000 simulations, we computed the mean estimated β (“Mean”), its standard deviation (“s.d.”), the mean estimated standard deviation (“Est. sd”), the coverage for a nominal 90% confidence interval (“90%”), the coverage for a nominal 95% confidence interval (“95%”), and the mean squared error efficiency compared to using only the controls (“MSE Eff”).

	Normal				Gamma
α2 = 0.00	Controls	Param	Robust	Semi	Controls	Param	Robust	Semi
Mean	0.998	0.998	1.001	1.008	0.996	1.000	0.997	1.001
s.d.	0.151	0.110	0.114	0.109	0.155	0.110	0.120	0.110
Est. sd	0.155	0.110	0.122	0.130	0.154	0.110	0.122	0.116
90%	0.903	0.900	0.921	0.910	0.898	0.894	0.910	0.912
95%	0.952	0.955	0.957	0.959	0.958	0.954	0.956	0.959
MSE Eff		1.878	1.734	1.909		1.966	1.663	1.987
α2 = 0.25	Controls	Param	Robust	Semi	Controls	Param	Robust	Semi
Mean	0.980	0.983	0.976	0.998	0.977	0.962	0.961	0.993
s.d.	0.151	0.113	0.116	0.113	0.151	0.139	0.115	0.093
Est. sd	0.154	0.111	0.119	0.115	0.148	0.140	0.120	0.103
90%	0.906	0.878	0.895	0.900	0.895	0.902	0.895	0.912
95%	0.947	0.939	0.953	0.966	0.939	0.948	0.943	0.963
MSE Eff		1.785	1.663	1.816		1.129	1.599	2.682
α2 = 0.50	Controls	Param	Robust	Semi	Controls	Param	Robust	Semi
Mean	0.974	0.969	0.946	0.992	0.954	0.799	0.958	1.002
s.d.	0.146	0.106	0.119	0.116	0.139	0.179	0.133	0.099
Est. sd	0.154	0.112	0.122	0.126	0.139	0.173	0.132	0.103
90%	0.918	0.909	0.884	0.915	0.885	0.681	0.892	0.917
95%	0.961	0.955	0.943	0.964	0.934	0.787	0.943	0.961
MSE Eff		1.780	1.270	1.627		0.295	1.092	2.186

Table 6.

Results of the simulation study with n₁ = 334 cases and n₀ = 666 controls, α₂ = 0.5, heteroscedastic errors. Here “Normal” means that ε = Normal(0, 1), while “Gamma” means that ε is a centered and scale Gamma random variable with shape 0.4, mean zero and variance one. The analyses performed were using controls only (“Controls”), the semiparametric efficient method that assumes normality and homoscedasticity (“Param”), the method of Wei, et al. (2012), (“Robust”), and our method (“Semi”). Over 1,000 simulations, we computed the mean estimated β (“Mean”), its standard deviation (“s.d.”), the mean estimated standard deviation (“Est. sd”), the coverage for a nominal 90% confidence interval (“90%”), the coverage for a nominal 95% confidence interval (“95%”), and the mean squared error efficiency compared to using only the controls (“MSE Eff”).

	Normal				Gamma
	disease rate 4.5%
α2 = 0.50	Controls	Param	Robust	Semi	Controls	Param	Robust	Semi
Mean	0.977	1.052	0.961	0.996	0.961	1.085	0.926	0.994
s.d.	0.084	0.070	0.063	0.077	0.083	0.087	0.066	0.082
Est. sd	0.087	0.072	0.064	0.083	0.08	0.087	0.067	0.090
90%	0.883	0.825	0.859	0.913	0.827	0.735	0.702	0.918
95%	0.939	0.892	0.930	0.952	0.905	0.831	0.806	0.954
MSE Eff		0.998	1.382	1.276		0.568	0.855	1.244
	disease rate 10%
α2 = 0.50	Controls	Param	Robust	Semi	Controls	Param	Robust	Semi
Mean	0.911	0.909	1.021	1.001	0.956	0.937	1.027	1.000
s.d.	0.072	0.064	0.080	0.079	0.084	0.066	0.070	0.087
Est. sd	0.072	0.065	0.080	0.076	0.087	0.065	0.072	0.094
90%	0.654	0.595	0.895	0.901	0.867	0.772	0.877	0.906
95%	0.749	0.700	0.949	0.951	0.927	0.851	0.933	0.952
MSE Eff		1.058	1.915	2.099		1.080	1.597	1.188
	disease rate 0.5%
α2 = 0.50	Controls	Param	Robust	Semi	Controls	Param	Robust	Semi
Mean	0.997	1.073	0.979	1.007	0.994	1.189	0.920	0.997
s.d.	0.088	0.073	0.066	0.078	0.084	0.100	0.071	0.070
Est. sd	0.087	0.072	0.063	0.086	0.085	0.099	0.073	0.069
90%	0.891	0.728	0.871	0.901	0.899	0.384	0.725	0.911
95%	0.950	0.820	0.929	0.952	0.953	0.539	0.829	0.960
MSE Eff		0.727	1.616	1.264		0.155	0.620	1.445

In order to relax such assumptions, novel methods are needed. In this paper, we do not assume any distributional form for ε or ε | X, we do not assume that the regression is homoscedastic, we do not require the disease rate to be known and we do not make a rare disease approximation. We do this by adopting the concept of a superpopulation (Ma, 2010): a similar idea is called an alternative characterization of the case-control study by Chen et al. (2009).

The main idea behind a superpopulation is to enable us to view the case-control sample as a sample of independent and identically distributed (iid) observations from the superpopulation. Conceptually, superpopulation is simply a proportional expansion of the case-control sample to infinity. Why a superpopulation constructed through such expansion achieves the purpose of viewing the case-control sample as an iid sample is studied carefully Ma (2010). The ability of viewing the case-control sample as a random sample permits us to use classical semiparametric approaches (Bickel et al., 1993; Tsiatis, 2006), regardless if the disease rate in the real population is rare or not, or is known or not.

We derive a class of semiparametric estimators and identify the efficient member. We further construct a member of the family that is relatively simple to compute, and illustrate how to construct the efficient estimator, applicable to both rare and common diseases. The derivation of semiparametric estimators in this context is challenging because the calculations must use quantities defined in the unknown true population to perform analysis in the superpopulation, since the models under the true population and the superpopulation share common parameters. In addition, as established in Ma (2010), the resulting semiparametric estimators further retain asymptotic consistency, a root-n convergence rate, asymptotic normality and semiparametric efficiency with respect to the true population as well. For example, our efficient estimator has the usual property that its asymptotic variance cannot be further reduced by any other device or by taking into account the case-control sampling structure.

The rest of the paper is organized as follows. Under conditions, we first establish the technical identifiability of our problem in Section 2. In Section 3, we formulate the problem into a classic semiparametric one by using the superpopulation notion and carry out analytic calculations to prepare for the estimation procedure. In Section 4, we describe details of implementation and the asymptotic theory. Simulation studies are performed in Section 5 to illustrate the finite sample performance of the procedure, showing that our method is robust, efficient and maintains nominal coverage for confidence intervals. An empirical analysis is provided in Section 6. Section 7 contains a short discussion. Technical details are given in an Appendix, as well as in the Supplementary Material. Computer code and data to illustrate our method are available http://wileyonlinelibrary.com/journal/rss-datasets.

2 The Superpopulation Model Framework

The primary disease model is the linear logistic model (1), with $\mathit{\alpha }={({\alpha }_c,{\mathit{\alpha }}_1^{\mathrm{T}},{\alpha }_2)}^{\mathrm{T}}$. Here and throughout the text, we use superscript “true” to represent quantities or operations related to the underlying true population, and also to distinguish it from a superpopulation that will be formally introduced later. In addition, in this underlying true population, Y is believed to be related to X through (2), which we rewrite as the regression model

$$f_{Y|X}^{\text{true}}(\mathbf{x},y)={\eta }_2\{y-m(\mathbf{x},\mathit{\beta }),\mathbf{x}\},$$ (3)

where m(·) is the regression mean function known up to the parameter β and η₂ is an unknown probability density function that has mean zero given X. Defining ε = Y − m(X, β), then E(ε | X) = 0. The distribution of ε, whether conditional on X or marginally, is left unspecified. In particular, heteroscedasticity is allowed. Making the identification η₂(ε, X) = η₂{Y − m(X, β), X}, this means that η₂ ≥ 0 satisfies ∫ εη₂(ε, x)dμ(ε) = 0 and ∫ η₂(ε, x)dμ(ε) = 1, but its form is unknown. Here and throughout the text, we use μ(·) to denote a Lebesgue measure for a continuous random variable and a counting measure for a discrete random variable. The distribution of the covariate X in the underlying true population is also unspecified, and its density or mass function is $f_{\mathbf{x}}^{\text{true}}(\mathbf{x})={\eta }_1(\mathbf{x})$, where η₁ ≥ 0 satisfies ∫ η₁(x)dμ(x) = 1.

The superpopulation framework of Ma (2010) is that one can think of the case-control sample as a random sample from an imaginary infinite superpopulation, in which the disease to non-disease ratio is N₁/N₀. Let N_d = N₀ when d = 0 and N_d = N₁ when D = 1. Define the true probability that D = d as $p_D^{\text{true}}(d,\mathit{\alpha },\mathit{\beta },{\eta }_1,{\eta }_2)=\int {\eta }_1(\mathbf{x}){\eta }_2(\epsilon ,\mathbf{x})H(d,\mathbf{x},y,\mathit{\alpha })d\mu (\mathbf{x})d\mu (y)$. The density of (D, Y, X) in the superpopulation is defined as

$$f_{X,Y,D}(\mathbf{x},y,d)=\frac{N_d}{N}\frac{{\eta }_1(\mathbf{x}){\eta }_2(\epsilon ,\mathbf{x})H(d,\mathbf{x},y,\mathit{\alpha })}{p_D^{\text{true}}(d,\mathit{\alpha },\mathit{\beta },{\eta }_1,{\eta }_2)}.$$ (4)

Although β appears in ε, for notational brevity, we do not explicitly write ε(β). In the secondary analysis framework, the main interest is β. However we formally treat θ = (α^T, β^T)^T as the parameter of interest. We treat η₁(·) and η₂(·,·) as the infinite dimensional nuisance parameters, thus bypassing the need to estimate them.

Remark 1. When no assumptions are made about the relationship between Y and X in the true population, the logistic intercept α_c is not identified (Prentice and Pyke, 1979), and neither is the regression of Y on X. Thus, if consistency of estimation is desired, truly nonparametric regression in a case-control study of our type is not possible. We believe that the key to identification lies in placing a restriction on the joint distribution of (Y, X) in the base population. For example, Chatterjee and Carroll (2005) show that if Y and X are independent, then α_c is generally identified, and they show this explicitly when one of the two is discrete. In our case, the restriction is a parametric model for E(Y|X). It is a reasonable conjecture that such a restriction is enough for the identifiability of α_c, a conjecture that we confirm next.

2.1 Identifiability

We first establish identifiability of the parameters α, β in the superpopulation. For greater generality, we consider the slightly more flexible model H(d, x, y) = exp[d{α_c + u(x, y, α₁, α₂)}]/[1+exp{α_c + u(x, y, α₁, α₂)}, where u(0, 0, α₁, α₂) = 0 for all α₁, α₂. Obviously, this model contains the original linear logistic model we are studying. We assume that there is no ${({\mathit{\alpha }}_1^{\mathrm{T}},{\alpha }_2)}^{\mathrm{T}}\ne {({\stackrel{\sim }{\mathit{\alpha }}}_1^{\mathrm{T}},{\stackrel{\sim }{\alpha }}_2)}^{\mathrm{T}}$ such that for all (x, y), u(x, y, α₁, α₂) = u(x, y, α̃₁, α̃₂). These are natural minimal conditions that are usually satisfied automatically as long as the parameterizations of u and m are not redundant. We also assume the following two conditions.

Assumption 1. Assume that the second moment of ε is bounded marginally and η₂ is a bounded function, i.e., E(ε²) < ∞ and sup_x,ε η₂(ε, x) < ∞. For any fixed parameters α₁, α₂, β, and any δ > 0, there exists a constant vector c₁, a constant c₂ ∈ [0, 1] and a region 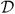with complement 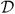^c such that when x → c₁,

$$\underset{\epsilon \in {\mathcal{D}}^c}{sup}\underset{\mathbf{x}\to {\mathbf{c}}_1}{lim}|{(1+exp[{\alpha }_c+u\{\mathbf{x},m(\mathbf{x},\mathit{\beta })+\epsilon ,{\mathit{\alpha }}_1,{\alpha }_2\}])}^{-1}-c_2|=0,$$

and lim_x→c1 pr(ε ∈ 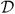| X = x)<δ. In addition, for any element e ∈ 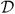, |e| ≥ 1. Typically we expect 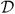^c = [−K, K] for some large K, c₁ = ∞ or −∞ or contains ±∞ as components, and c₂ = 0 or 1, although this is not required.

Assumption 2. c(β, β̃) = lim_x→c1{m(x, β̃) − m(x, β)} ≠ 0 for β̃ ≠ β.

Remark 2. Assume that pr(|ε| > K|X = x) → 0 as K → ∞ uniformly in x. We can easily verify that when both m and u are linear functions, where we write m(x, β) = x^Tβ₁ + β_c, both assumptions are satisfied except when α₁ + β₁α₂ = 0. When this happens, u{m(x, β), α₁, α₂} degenerates to a constant, and we can verify that although β₁ is still identifiable, β_c and α_c are no longer identifiable, see the Supplementary Material for details of verification of both the identifiability and the non-identifiability verification.

We state the identifiability result in Proposition 1 and provide the proof in Appendix A.1.

Proposition 1. Make Assumptions 1-2. Also assume that there are constants (C₁, C₂) such that 0 < C₁ < N₀/N₁ < C₂ < ∞. Then the parameters α and β are identifiable.

Remark 3. Identifiability under some specific situations has been considered in the literature. For example, Chatterjee and Carroll (2005), Chatterjee et al. (2006) and Chen et al. (2009) considered the case that X and Y are independent, while Chen et al. (2008) and Lin and Zeng (2009) explicitly studied the identifiability issue when the disease rate model is linear logistic and the secondary model is fully parametric. The model we consider here is more general, in that only a mean function is assumed for the secondary model. These authors all note that while in practice, it may be difficult to estimate α_c, estimation of the other parameters can still be performed effectively, see also Lobach et al. (2008).

3 Analytic Derivations

3.1 True and Conjectured Models

The major point of our article is that we only propose a model for E(Y | X), denoted m(X, β), and we specifically want to avoid positing a model for the density function of the regression errors ε = Y − m(X, β) conditional on X. We will accomplish this by a two-step process. First, in Section 3.2, we will derive the semiparametric efficient estimating equation in the superpopulation for estimating (α, β) when the density of Y given X in the true population is known. Recognizing that we do not want to make such an assumption, in Section 4, we will show how to modify the estimating equation so that it has mean zero asymptotically, even if the conjectured model for the regression errors is false, thus resulting in model-robust consistent estimation.

3.2 Analysis Under a True Model

As described in Section 3.1, here we will derive the form of the semiparametric efficient estimating equation when the conjectured model for the regression errors in (3) is true. Later in Section 4, we will modify the estimating function to make it model-robust.

Viewing the observations as randomly sampled from the superpopulation, we can perform a conventional semiparametric analysis. Of course, all the calculations need to be done with respect to the superpopulation, and all the probability statements need to be with respect to Lebesgue measure for continuous random variables and counting measure for discrete random variables in the superpopulation, and they will be if not otherwise pointed out. The functions (η₁, η₂, H), which are probability density/mass functions in the true population, do not represent the corresponding probabilities density/mass functions in the superpopulation. They are merely functions that satisfy η₁(x) ≥ 0, ∫ η₁(x) dμ (x) = 1, η₂(ε, x) ≥ 0, ∫ η₂(ε, x)dμ(ε) = 1, ∫ εη₂(ε, x)dμ(ε) = 0, H(d, x, y) ≥ 0, H(0, x, y) + H(1, x, y) = 1. In fact, we introduced these symbols to discourage the mistake of automatically viewing them as the corresponding density or mass functions in the superpopulation.

Using model (4), calculating the partial derivative of the loglikelihood with respect to α and β, it is easy to see that the score function has the form S_θ(X, Y, D, θ) = S(X, Y, D, θ) − E(S | D), where θ = (α^T, β^T)^T, ${\mathbf{S}}_{\theta }={({\mathit{S}}_{\alpha }^{\mathrm{T}},{\mathbf{S}}_{\beta }^{\mathrm{T}})}^{\mathrm{T}}$, and

$$\mathbf{S}(\mathbf{x},y,d,\mathit{\theta })=\left\{\begin{array}{c}\partial log\{H(d,\mathbf{x},y,\mathbf{\alpha })\}/\partial \mathit{\alpha }\\ \partial log\{{\eta }_2(\epsilon ,\mathbf{x})\}/\partial \mathit{\beta }\end{array}\right\}.$$ (5)

Explicitly,

$${\mathbf{S}}_{\alpha }(\mathrm{X},Y,D,\mathit{\theta })=\partial log\{H(D,\mathbf{X},Y,\mathit{\alpha })\}/\partial \mathit{\alpha }-E[\partial log\{H(D,\mathbf{X},Y,\mathit{\alpha })\}/\partial \mathit{\alpha }|D];$$

$${\mathbf{S}}_{\beta }(\mathbf{X},Y,D,\mathit{\theta })=\partial log\{{\eta }_2(\epsilon ,\mathbf{X})\}/\partial \mathit{\beta }-E[\partial log\{{\eta }_2(\epsilon ,\mathbf{X})\}/\partial \mathit{\beta }|D].$$

In Appendix A.2, we further derive the nuisance tangent space Λ and its orthogonal complement space Λ^⊥ as

$$\mathrm{\Lambda }=\{\mathbf{g}(\epsilon ,\mathbf{X})-E(\mathbf{g}|D):E_{\text{true}}(\mathbf{g})=E_{\text{true}}(\epsilon \mathbf{g}|\mathbf{X})=\mathbf{0}\mathrm{a}.\mathrm{s}.\};$$

$${\mathrm{\Lambda }}^{\perp }=[\mathbf{h}(D,\epsilon ,\mathbf{X}):E(\mathbf{h})=\mathbf{0},E\{\mathbf{h}-E(\mathbf{h}|D)|\epsilon ,\mathbf{X}\}\times \sum _d(N_d/N)H(d,\mathbf{X},y)/p_D^{\text{true}}(d)=\epsilon \mathbf{a}(\mathbf{X})\mathrm{a}.\mathrm{s}.],$$

where g(ε, x) and h(D, ε, x) are arbitrary functions that satisfy their respective constraints described above, a(x) is an arbitrary function of x, and a.s. stands for almost surely with respect to the true superpopulation distribution.

Having obtained both the score function and the two spaces Λ and Λ^⊥, conceptually, we only need to project the score function onto Λ^⊥ to obtain the efficient score S_eff. Doing this is, however, extraordinarily technical, and hence we defer the details to the Supplementary Material. Here we merely state the result in Proposition 2, which requires a series of definitions, as follows.

$$\begin{array}{c}\text{Define}{\pi }_0=p_d^{\text{true}}(0)=\int {\eta }_1(\mathbf{x}){\eta }_2(\epsilon ,\mathbf{x})H(0,\mathbf{x},y)d\mu (\mathbf{x})d\mu (y);\\ {\pi }_1=p_d^{\text{true}}(1)=\int {\eta }_1(\mathbf{x}){\eta }_2(\epsilon ,\mathbf{x})H(1,\mathbf{x},y)d\mu (\mathbf{x})d\mu (y);\\ b_0=E\{f_{D|\mathbf{X},Y}(1,\mathbf{X},Y)|D=0\};b_1=E\{f_{D|\mathbf{X},Y}(0,\mathbf{X},Y)|D=1\};\\ {\mathbf{c}}_0=E(\mathbf{S}|D=0)-E\{E(\mathbf{S}|\epsilon ,\mathbf{X})|D=0\};\\ {\mathbf{c}}_1=E(\mathbf{S}|D=1)-E\{E(\mathbf{S}|\epsilon ,\mathbf{X})|D=1\};\\ \kappa (\mathbf{x},y)={[{\sum }_{d=0}^1\{N_{d}H(d,\mathrm{x},y)\}/(N{\pi }_d)]}^{-1};t_1(\mathbf{X})={[E_{\text{true}}\{{\epsilon }^2\kappa (\mathbf{X},Y)|\mathbf{X}\}]}^{-1};\\ {\mathbf{t}}_2(\mathbf{X})=E_{\text{true}}\{\epsilon E(\mathbf{S}|\epsilon ,\mathbf{X})|\mathbf{X}\}-({\mathbf{c}}_0/b_0)E_{\text{true}}\{\epsilon f_{D|X,Y}(0,\mathbf{X},Y)|\mathbf{X}\};\\ t_3(\mathbf{X})=-b_0^{-1}{E}_{\text{true}}\{\epsilon f_{D|X,Y}(0,\mathbf{X},Y)|\mathbf{X}\};\mathbf{a}(\mathbf{x})=t_1(\mathbf{x})\{{\mathbf{t}}_2(\mathbf{x})+t_3(\mathbf{x}){\mathbf{u}}_0\};\\ {\mathbf{u}}_0={(1-E[\epsilon t_1(\mathbf{X})t_3(\mathbf{X})\kappa (\mathbf{X},Y)|D=0])}^{-1}E[\epsilon t_1(\mathbf{X}){\mathbf{t}}_2(\mathbf{X})\kappa (\mathbf{X},Y)|D=0];\\ {\mathbf{u}}_1=-(N_0/N_1){\mathbf{u}}_0;{\mathbf{v}}_0=({\pi }_1/b_0)({\mathbf{u}}_0+{\mathbf{c}}_0);{\mathbf{v}}_1=-({\pi }_0/b_0)({\mathbf{u}}_0+{\mathbf{c}}_0);\\ \mathbf{g}(\epsilon ,\mathbf{x})=E(\mathbf{S}|\epsilon ,\mathbf{X}=\mathbf{x})-\epsilon \mathbf{a}(\mathbf{x})\kappa (\mathbf{x},y)-{\mathbf{v}}_0{f}_{D|X,Y}(0,\mathbf{x},y)-{\mathbf{v}}_1{f}_{D|X,Y}(1,\mathbf{x},y).\end{array}$$ (6)

Proposition 2. Make the definitions (6). In the superpopulation, the semiparametric efficient score function is S(X_i, Y_i, D_i) − g{Y_i − m(X_i, β), X_i} − (N₀/N)v₀ − (N₁/N)v₁. The semiparametric efficient estimator is obtained by solving

$${\sum }_{i=1}^N[\mathbf{S}({\mathbf{X}}_i,Y_i,D_i)-\mathbf{g}\{Y_i-m({\mathbf{X}}_i,\mathit{\beta }),{\mathbf{X}}_i\}-(1-D_i){\mathbf{v}}_0-D_i{\mathbf{v}}_1]=0.$$ (7)

We emphasize here that the estimator in Proposition 2 is not only efficient with respect to the superpopulation, it is also efficient with respect to the true population. This is a direct consequence of the general result that if an estimator is efficient with respect to the superpopulation, it is also efficient with respect to the true population. A careful justification of this claim is given in Ma (2010). Logically, this result can be understood because if we could find a more efficient estimator with respect to the true population, this estimator would also be more efficient with respect to the superpopulation, which causes a contradiction. Intuitively, the special sampling strategy is in fact already absorbed into the formulation when we construct the superpopulation, hence no information has been lost during the conversion between populations.

4 Estimator Construction

4.1 Basic Calculations

The estimating equation (7) derived in Proposition 2 is not useful however, because it involves various calculations that rely on the unknown η₁ and η₂, which were assumed to be correctly conjectured in Section 3. If either are misspecified, the corresponding calculation will lead to inconsistent estimation of θ. The purpose of this section is to define estimators that are consistent for estimating θ based upon a posited score function, which we denote by S*. As it turns out, if the posited score function is correct, then in addition to being consistent, the estimator of θ has the additional property of being efficient. If the posited score function is incorrect, then the estimator of θ is still consistent. So our method can be thought of as a locally efficient estimator.

A careful inspection of the estimation procedure given in Proposition 2 and the definition of the related quantities suggests that the critical points lie in obtaining π₀ and π₁, in calculating E(h | ε, X) and E(h | D) for any function h(D, X, Y), and in calculating E_true(h | X) for any function h(D, X, Y).

Our algorithm is detailed as Algorithm 1, and is based upon the following considerations.

• First, we have that

  $$N_d=N{p}_D(d)=N\int f_{\mathbf{X},Y}(\mathbf{x},y)f_{D|X,Y}(d,\mathbf{x},y)d\mu (\mathbf{x})d\mu (y)=N\int f_{\mathbf{X},Y}(\mathbf{x},y)(N_{d}H/N{\pi }_d){\{{\sum }_d(N_{d}H)/(N{\pi }_d)\}}^{-1}d\mu (\mathbf{x})d\mu (y).$$

  If we estimate the last term by ${\sum }_{i=1}^N\{N_{d}H(d,{\mathbf{X}}_i,Y_i)/N{\pi }_d\}{\{{\sum }_d\{N_{d}H(d,{\mathbf{X}}_i,Y_i)/(N{\pi }_d)\}}^{-1}$ and remember that π₀ + π₁ = 1, we see that we can estimate π₀ by solving

  $${\pi }_0={\sum }_{i=1}^{N}H(0,{\mathbf{X}}_i,Y_i){[{\sum }_d{N}_{d}H(d,{\mathbf{X}}_i,Y_i)/\{{\pi }_0^{1-d}(1-{\pi }_0)\}{\pi }_d]}^{-1}.$$

Algorithm 1: Computing the Locally Efficient Score Function

The first two steps are done only once.

Posit a model for η2(ε, x) which has mean zero, and calculate (5), calling the result S*(X, Y, D). Use S*(·) in place of S(·) in (6)-(7). Estimate fX|D(x, d) by a kernel density estimate among the data with Di = d, with result f̂x|D(x, d).

The rest of the steps are done iteratively in the estimation algorithm.

Solve ${\widehat{\pi }}_0={\sum }_{i=1}^{N}H(0,{\mathbf{X}}_i,Y_i){\{N_{0}H(0,{\mathbf{X}}_i,Y_i)/{\widehat{\pi }}_0+N_{1}H(1,{\mathbf{X}}_i,Y_i)/(1-{\widehat{\pi }}_0)\}}^{-1}$ to obtain π̂0 and set π̂1 = 1 − π̂0. In the definition of κ(x, y) in (6), form κ̂(x, y) by replacing πd by π̂d. Define κ̂i = κ̂(Xi, Yi). Define f̂di = f̂D|X, Y(d, Xi, Yi) = NdH(d, Xi, Yi)κ̂i/(Nπ̂d). For any function h(d, x, y) in (6), estimate E{h(D, X, Y) | X, D = d) by nonparametric regression among observations with Di = d. For any function h(d, x, y) in (6), estimate E{h(D, X, Y) | D = d) as $\widehat{E}\{h(D,\mathbf{X},Y)|D=d)={\sum }_{i=1}^{N}h(d,{\mathbf{X}}_i,Y_i){\widehat{f}}_{\mathit{\text{di}}}/{\sum }_{i=1}^N{\widehat{f}}_{\mathit{\text{di}}}$. For any function h(d, x, y) in (6), estimate E{h(D, Y, X)|ε, X} by $\widehat{E}\{h(D,Y,\mathbf{X})|\epsilon ,\mathbf{X}\}={\sum }_{d=0}^1{N}_{d}H(d,\mathbf{X},Y)h(d,Y,\mathbf{X})\widehat{\kappa }(\mathbf{X},Y)/(N{\widehat{\pi }}_d)$. For any function h(d, x, y) in (6), estimate Etrue{h(D, X, Y) | X) by ${\widehat{E}}_{\text{true}}\{h(D,\mathbf{X},Y)|\mathbf{X})={\sum }_{d=0}^1{\widehat{\pi }}_d\widehat{E}\{h(d,\mathbf{X},Y)|\mathbf{X},D=d){\widehat{f}}_{\mathbf{X}|D}(\mathbf{X},d)/{\sum }_{d=0}^1{\widehat{\pi }}_d{\widehat{f}}_{\mathbf{X}|D}(\mathbf{X},d)$.

Application to the terms in (6) yields ĝ(εi, Xi) and v̂d, and we then form ${\widehat{\mathbf{S}}}_{\text{eff}}^{\ast }(D,{\mathbf{X}}_i,Y_i)={\mathbf{S}}^{\ast }(\mathbf{X},Y,D)-\widehat{\mathbf{g}}(\epsilon ,\mathbf{X})-(1-D){\widehat{\mathbf{v}}}_0-D{\widehat{\mathbf{v}}}_1$.

We have described the algorithm when X is continuous. When X is discrete, one simply replaces the density estimators and various nonparametric regressions with the corresponding averages associated with the different x values.

• Next we have that

  $$E(\mathbf{h}|\epsilon ,\mathbf{X})={\sum }_d\mathbf{h}{f}_{D|X,Y}(d,\mathbf{X},Y)={\sum }_d\{N_{d}H(d,\mathbf{X},Y)\mathbf{h}(d,\mathbf{X},Y)/(N{\pi }_d)\}{\{{\sum }_d{N}_{d}H(d,\mathbf{X},Y)/(N{\pi }_d)\}}^{-1}.$$

• In addition,

  $$E_{\text{true}}(\mathbf{h}|\mathbf{X})=\frac{\int \mathbf{h}{\sum }_d{\pi }_d{f}_{X,Y|D}^{\text{true}}(\mathbf{X},y,d)d\mu (y)}{\int {\sum }_d{\pi }_d{f}_{X,Y|D}^{\text{true}}(\mathbf{X},y,d)d\mu (y)}=\frac{\int \mathbf{h}{\sum }_d{\pi }_d{f}_{X,Y|D}(\mathbf{X},y,d)d\mu (y)}{\int {\sum }_d{\pi }_d{f}_{X,Y|D}(\mathbf{X},y,d)d\mu (y)}=\frac{{\sum }_d{\pi }_d\int \mathbf{h}{f}_{X,Y|D}(\mathbf{X},y,d)d\mu (y)}{{\sum }_d{\pi }_d{f}_{\mathbf{X}|D}(\mathbf{X},d)}=\frac{{\sum }_d{\pi }_d\int \mathbf{h}{f}_{Y|\mathbf{X},D}(\mathbf{X},y,d)d\mu (y)f_{\mathbf{X}|D}(\mathbf{X},d)}{{\sum }_d{\pi }_d{f}_{\mathbf{X}|D}(\mathbf{X},d)}={\sum }_d{\pi }_{d}E(\mathbf{h}|\mathbf{X},d)f_{\mathbf{X}|D}(\mathbf{X},d)/{\sum }_d{\pi }_d{f}_{\mathbf{X}|D}(\mathbf{X},d),$$

  where in the last expression, both f_X|D(x, d) and E(h | x, d) need to be estimated nonparametrically.

• Finally, we have

  $$E(\mathbf{h}|D=d)=\frac{\int f_{\mathbf{x},y}(\mathbf{x},y)\mathbf{h}(d,\mathbf{x},y)f_{D|X,Y}(d,\mathbf{x},y)d\mu (\mathbf{x})d\mu (y)}{\int f_{\mathbf{x},y}(\mathbf{x},y)f_{D|X,Y}(d,\mathbf{x},y)d\mu (\mathbf{x})d\mu (y)},$$

  which can be estimated as

  $$\widehat{E}(\mathbf{h}|D=d)={\sum }_{i=1}^N\mathbf{h}(d,{\mathbf{X}}_i,Y_i)f_{D|X,Y}(d,{\mathbf{X}}_i,Y_i)/{\sum }_{i=1}^N{f}_{D|X,Y}(d,{\mathbf{X}}_i,Y_i).$$

4.2 Distribution Theory

Because the locally efficient estimator is derived from well-established semiparametric procedures, while replacing the unknown quantities with nonparametric estimation in the proposed model, it is not surprising that it is asymptotically normally distributed with standard parametric rates of convergence. In addition, it achieves the semiparametric efficiency if the proposed model is correct. We describe the asymptotic properties of our estimator in Theorems 1, and provide a sketch of the proof for Theorem 1 in the Appendix. We first list the set of regularity conditions that Theorem 1 requires.

• C1: There exists constants 0 < C < ∞ such that lim_N→∞N₁/N₂ = C. In addition, the identifiability Assumptions 1 and 2 hold.

• C2: The univariate kernel function is a function that integrates to 1 and has support (−1, 1) and order r, i.e., ∫ K(x)x^tdx = 0 if 1 ≤ t < r and ∫ K(x)x^rdx ≠ 0. The d-dimensional kernel function, still represented with K, is a product of d univariate kernel functions, that is, $K(\mathbf{x})={\prod }_{i=1}^{d}K(x_i)$ for a d-dimensional x.

• C3: For d = 1, 0, f_X|D(x | D = d), E(ε²κ | X, D = d), E(εμ_s | X, D = d), E(εf₀ | X, D = d), E(εf₁ | X, D = d) have compact support and have continuous r^th derivatives.

• C4: The bandwidth h = N^−τ where 1/(2p) > τ > 1/(4r), where p is the dimension of x. This includes the optimal bandwidth h = O(N^−1/(2r+p)) as long as we choose a kernel of order 2r > p.

Condition C1 ensures that there are a sufficient number of both cases and controls in the sample, which occurs in all case-control studies of the type we are studying (see the introductory paragraph). Conditions C2 and C4 are standard requirements on an rth order kernel function and on the bandwidth in the kernel smoothing literature (Ma and Zhu, 2013). Condition C3 is not the weakest possible. We impose this condition to simplify the technical proof. It can be replaced with weaker conditions in the region where ‖x‖ is large, at the expense of a more tedious technical treatment.

Theorem 1. We emphasize that for any random vector S(D, Y, X), expectation and co-variance in the superpopulation is linked to expectation and covariance in the case-control sampling scheme (conditional on disease status) through

$$\begin{array}{c}E\{\mathbf{S}(D,Y,X)\}={\sum }_{d=0}^1(N_d/N)E\{\mathbf{S}(D,Y,X)|D=d\}\\ cov\{\mathbf{S}(D,Y,X)\}={\sum }_{d=0}^1(N_d/N)cov\{\mathbf{S}(D,Y,X)|D=d\}.\end{array}$$

Under the regularity conditions C1-C4, in the case-control study, as N → ∞, the estimator θ̂ obtained from solving the estimating equation ${\sum }_{i=1}^N{\widehat{\mathbf{S}}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,\widehat{\mathit{\theta }})=0$ satisfies

$$N^{1/2}(\widehat{\mathit{\theta }}-{\mathit{\theta }}_0)\to \text{Normal}\{\mathbf{0},{\mathbf{A}}^{-1}\mathbf{B}{({\mathbf{A}}^{-1})}^{\mathrm{T}}\}$$

where $\mathbf{A}=E\{\partial {\mathbf{S}}_{\text{eff}}^{\ast }(D,\mathbf{X},Y,{\mathit{\theta }}_0)/\partial {\mathit{\theta }}^{\mathrm{T}}\}$ and $\mathbf{B}=cov\{{\mathbf{S}}_{\text{eff}}^{\ast }(D,\mathbf{X},Y,{\mathit{\theta }}_0)\}$.

5 Simulations

5.1 Setup

We performed a series of simulation studies in order to evaluate the finite sample performance of the various methods. In total, we considered 72 different cases. First, we considered a balanced design, where N₀ = N₁ = 500, and an imbalanced design with N₀ = 666 and N₁ = 334, i.e., 2 controls for every case. Second, we considered 3 disease rates: a relatively rare disease rate of 4.5%, an extremely rare disease rate of 0.5% and a common disease rate of 10%. The balanced design in rare or extremely rare disease cases is representative of a typical case-control study.

Third, we considered three settings for the logistic regression. We generated X from a Uniform(0, 1) distribution. The logistic regression model was pr(D = 1|Y, X) = H(α_c + α₁X + α₂Y), where α₁ = 1 and we varied α₂ = 0.00, 0.25, 0.50. The regression model for Y given X is Y = β₁+β₂X + ε, with β₁ = 0 and β₂ = 1.

Finally, we varied the distribution of the regression errors and whether they were ho-moscedastic or not, as follows.

• In the first set of simulations, we generated homoscedastic errors ε. The distribution of ε was either Normal(0, σ²) with σ² = 1 or is a centered and standardized Gamma distribution with shape parameter 0.4, normalized to have mean zero and variance σ² = 1. To achieve an approximate 4.5% disease rate, for α₂ = (0.00, 0.25, 0.50) we set α_c = (−3.6, −3.8, −4.0). To achieve an approximate 0.5% disease rate, for α₂ = (0.00, 0.25, 0.50) we set α_c = (−5.8, −6.0, −6.2). To achieve an approximate 10% disease rate, for α₂ = (0.00, 0.25, 0.50) we set α_c = (−2.7, −2.9, −3.1).

• In the second set of simulations, we generated heteroscedastic errors as follows. The same distributions for ε were used, except that ε was multiplied by (1 + X²)^3/4/2 in all the cases, so that var(ε|X) = (1 + X²)^3/2/4. To achieve an approximate 4.5% disease rate, for α₂ = (0.00, 0.25, 0.50) we set α_c = (−3.60, −3.75, −3.95). To achieve an approximate 0.5% disease rate, for α₂ = (0.00, 0.25, 0.50) we set α_c = (−5.8, −5.95, −6.2). To achieve an approximate 10% disease rate, for α₂ = (0.00, 0.25, 0.50) we set α_c= (−2.7, −2.9, −3.1).

With respect to the method described in Section 4.1, we mention the following details. The posited model ${\eta }_2^{\ast }$ being a standard normal model in step 1. This yields the second component in S* as (y−β₁−β₂x)(1, x)^T. In performing the many nonparametric calculations in steps 4, 5, 6, 7, we used a kernel estimates with a same bandwidth h throughout. We set the bandwidth at $h=c{n}_0^{-1/3}$, and experimented with different values c between c = 0.5 and c = 2.0, with little change in the results. To assess variability, we used the asymptotic results in Theorem 1, with the A and B matrices replaced by their corresponding sample averages evaluated at the estimated parameter values.

We compared our method with three others. The first was ordinary least squares among the controls, with sandwich standard errors: the sandwich method is used to adjust confidence intervals for possible heteroscedasticity. The second was the semiparametric efficient method that assumes normality and homoscedasticity, with standard errors obtained by inverting the Hessian of the loglikelihood (Lin and Zeng (2009)). The third was the method of Wei et al. (2013) that assumes homoscedasticity, but otherwise does not specify any particular error distribution model: we used the bootstrap to obtain standard errors for this method.

A striking conclusion of these simulations is that our methods, which assumes none of rare disease, normal errors or homoscedasticity, uniformly has coverage probabilities that achieve the nominal rates.

5.2 Homoscedastic Case

Results for the homoscedastic case are given in Tables 1-3. We display the mean estimate, the standard deviation across the simulations, the mean estimated standard deviation, coverage probabilities for nominal 90% and 95% confidence intervals, and the mean squared error efficiency of the methods relative to using only the controls.

Table 3.

Results of the simulation study with n₁ = 334 cases and n₀ = 666 controls, α₂ = 0.5, homoscedastic errors. Here “Normal” means that ε = Normal(0, 1), while “Gamma” means that ε is a centered and scale Gamma random variable with shape 0.4, mean zero and variance one. The analyses performed were using controls only (“Controls”), the semiparametric efficient method that assumes normality and homoscedasticity (“Param”), the method of Wei, et al. (2012), (“Robust”), and our method (“Semi”). Over 1,000 simulations, we computed the mean estimated β (“Mean”), its standard deviation (“s.d.”), the mean estimated standard deviation (“Est. sd”), the coverage for a nominal 90% confidence interval (“90%”), the coverage for a nominal 95% confidence interval (“95%”), and the mean squared error efficiency compared to using only the controls (“MSE Eff”).

	Normal				Gamma
	disease rate 4.5%
α2 = 0.50	Controls	Param	Robust	Semi	Controls	Param	Robust	Semi
Mean	0.962	0.960	0.956	0.994	0.951	0.856	0.936	0.996
s.d.	0.133	0.106	0.108	0.113	0.128	0.153	0.123	0.101
Est. sd	0.133	0.110	0.113	0.121	0.120	0.152	0.120	0.108
90%	0.892	0.884	0.893	0.901	0.845	0.751	0.844	0.916
95%	0.957	0.943	0.954	0.952	0.925	0.848	0.910	0.960
MSE Eff		1.491	1.407	1.494		0.426	0.977	1.839
	disease rate 10%
α2 = 0.50	Controls	Param	Robust	Semi	Controls	Param	Robust	Semi
Mean	0.921	0.850	0.831	0.991	0.937	0.879	0.927	1.060
s.d.	0.106	0.114	0.134	0.082	0.129	0.117	0.107	0.082
Est. sd	0.103	0.113	0.136	0.080	0.133	0.117	0.110	0.077
90%	0.797	0.621	0.673	0.900	0.872	0.739	0.840	0.908
95%	0.881	0.752	0.780	0.949	0.932	0.845	0.909	0.949
MSE Eff		0.492	0.375	2.568		0.727	1.228	1.996
	disease rate 0.5%
α2 = 0.50	Controls	Param	Robust	Semi	Controls	Param	Robust	Semi
Mean	1	0.997	0.991	1.004	0.997	0.901	1.018	1.000
s.d.	0.133	0.107	0.113	0.110	0.129	0.191	0.134	0.100
Est. sd	0.134	0.111	0.111	0.113	0.130	0.190	0.142	0.099
90%	0.904	0.911	0.894	0.904	0.890	0.858	0.925	0.897
95%	0.944	0.959	0.943	0.945	0.947	0.921	0.966	0.953
MSE Eff		1.544	1.377	1.460		0.360	0.911	1.665

The case α₂ = 0.00 is interesting, because here Y is independent of D given X. Hence, all methods should achieve nominal coverage probabilities for estimating β, which is indeed seen in Table 1. Surprisingly, our method, which assumes neither normality nor homoscedasticity, is as efficient in terms of mean squared error as the semiparametric efficient method that assumes both, and is of course much more efficient than using only the controls.

For α₂ ≠ 0, and when ε is normally distributed, our method remains comparably as efficient as the semiparametric efficient method which assumes both normality and homoscedasticity. However, when the errors were not normally distributed, our method has much smaller bias and is much more efficient. In addition, the semiparametric efficient method has poor coverage probabilities when α₂ = 0.50. While the method of Wei et al. (2013) maintains good coverage probabilities in all cases, our methods also maintains coverage, has smaller bias and is much more efficient.

5.3 Heteroscedastic Case

The results for the heteroscedastic case, with various disease rates and equal or unequal case-control rations are given in Tables 4-6.

Table 4.

Results of the simulation study with n₁ = 500 cases and n₀ = 500 controls, disease rate of approximately 4.5%, with heteroscedastic errors. Here “Normal” means that ε = Normal(0, 1), while “Gamma” means that ε is a centered and scale Gamma random variable with shape 0.4, mean zero and variance one. The analyses performed were using controls only (“Controls”), the semiparametric efficient method that assumes normality and homoscedasticity (“Param”), the method of Wei, et al. (2012), (“Robust”), and our method (“Semi”). Over 1,000 simulations, we computed the mean estimated β (“Mean”), its standard deviation (“s.d.”), the mean estimated standard deviation (“Est. sd”), the coverage for a nominal 90% confidence interval (“90%”), the coverage for a nominal 95% confidence interval (“95%”), and the mean squared error efficiency compared to using only the controls (“MSE Eff”).

	Normal				Gamma
α2 = 0.00	Controls	Param	Robust	Semi	Controls	Param	Robust	Semi
Mean	0.996	0.996	1.000	1.005	0.992	0.994	1.000	1.002
s.d.	0.099	0.071	0.071	0.076	0.099	0.070	0.073	0.077
Est. sd	0.096	0.070	0.072	0.082	0.096	0.070	0.071	0.078
90%	0.887	0.892	0.895	0.898	0.887	0.903	0.893	0.898
95%	0.932	0.953	0.949	0.950	0.944	0.946	0.947	0.951
MSE Eff		1.948	1.961	1.692		1.971	1.847	1.663
α2 = 0.25	Controls	Param	Robust	Semi	Controls	Param	Robust	Semi
Mean	0.986	1.044	0.973	0.997	0.983	1.063	0.964	0.995
s.d.	0.100	0.072	0.066	0.077	0.094	0.082	0.069	0.071
Est. sd	0.096	0.071	0.070	0.081	0.094	0.083	0.072	0.074
90%	0.880	0.838	0.907	0.912	0.894	0.825	0.863	0.904
95%	0.936	0.907	0.953	0.959	0.946	0.900	0.934	0.950
MSE Eff		1.415	1.984	1.717		0.852	1.516	1.801
α2 = 0.50	Controls	Param	Robust	Semi	Controls	Param	Robust	Semi
Mean	0.972	1.088	0.949	0.991	0.962	1.145	0.906	0.993
s.d.	0.099	0.072	0.068	0.083	0.095	0.096	0.076	0.082
Est. sd	0.096	0.072	0.071	0.102	0.090	0.100	0.076	0.105
90%	0.877	0.664	0.842	0.897	0.857	0.591	0.655	0.900
95%	0.936	0.789	0.914	0.946	0.909	0.714	0.756	0.935
MSE Eff		0.816	1.479	1.519		0.343	0.717	1.546

The results are much in line with the homoscedastic case, with a few important exceptions. The semiparametric efficient method, which assumes both homoscedasticity and normality, has a noticeable loss of coverage probability when α₂ ≠ 0, largely caused by bias. Because they used a bootstrap to compute standard errors, the method of Wei et al. (2013) maintains good coverage probability except when α₂ = 0.50, where the bias causes deterioration in the coverage rates. Our method maintains good coverage probabilities in all cases, and because of its lack of bias, noticeably increased mean squared error efficiency.

6 Empirical Example

Epidemiological studies have led to the general belief that heterocyclic amines (HCA), such as MelQx and PhlP, are significant risk factors associated with various forms of cancers, including colorectal cancer and breast cancer (Barrett et al., 2003; Sinha et al., 2001; De Stefani et al., 1997). One of the important food sources contributing to carcinogenic HCA, among many other potential sources, is red meat, which produces the agents during the cooking process. In addition, red meat contains other nutrients such as saturated fat which is also believed to relate to the occurrence of cancer. Due to this link, epidemiological and nutritional studies of cancer often include both red meat consumption and HCA as covariates to assess the risk of developing cancer, while simultaneously studying the relation between HCA amount and red meat consumption. Understanding this relation helps to understand the health impact of red meat consumption and is important in formulating food consumption guidelines for the general public.

We implemented our method on a data set involving colorectal adenoma, with 640 cases and 665 controls. The cases and controls were defined by the occurrence of colorectal adenoma (D). In our analysis, X is red meat consumption in grams. We used two different versions of Y, namely the heterocyclic amines MeIQx and PhIP that are produced during the cooking of meat.

PhIP, MeIQx and red meat were transformed by adding 1.0 and taking logarithms to alleviate the heavy skewness of these measurements on the original scale. We also analyzed the subset of the study who were smokers. For the controls-only analysis, standard errors of the slope estimate were computed using the usual formula for least squares and also by the sandwich method. For our semiparametric analysis, we computed standard errors by the asymptotic formula of Theorem 1 and by the bootstrap, with 1,000 bootstrap samples. Given the results of the simulation, we do not expect any significant difference between these two estimates of standard errors for our method, with the asymptotic formula being much faster computationally.

We performed a preliminary analysis using only the controls. In the original data scale, all the covariates (PhiP, MelPx and red meat consumption) are very skewed and heavy-tailed, see Figures S.1-S.2 in the Supplementary Material. The transformed data were much better behaved, see Figures S.3-S.4 in the Supplementary Material. Numerically, the skewness of MeIQx in the original and transformed data scales are 3.46 and -0.19, respectively. The skewness of PhIP in the original and transformed data scales are 7.93 and -0.20, respectively. Finally, the skewness of Red Meat in the original and transformed data scales are 1.78 and -0.58, respectively. These numbers and the plots indicate that the transformation did an acceptable to very good job of removing skewness.

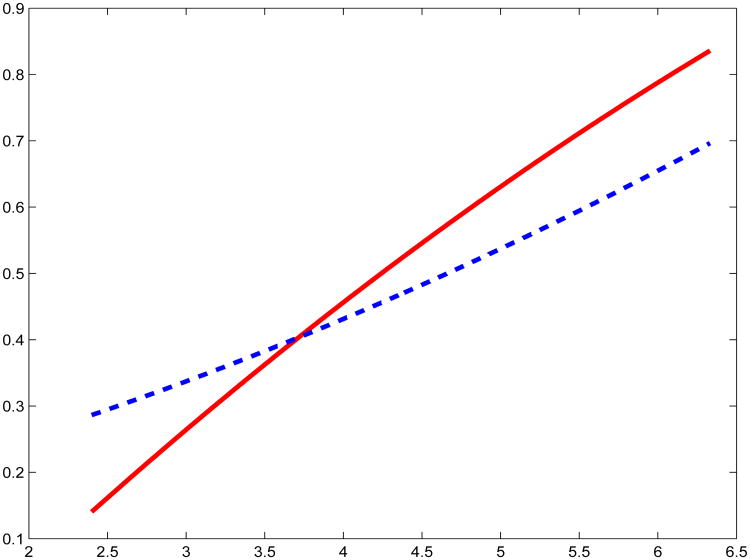
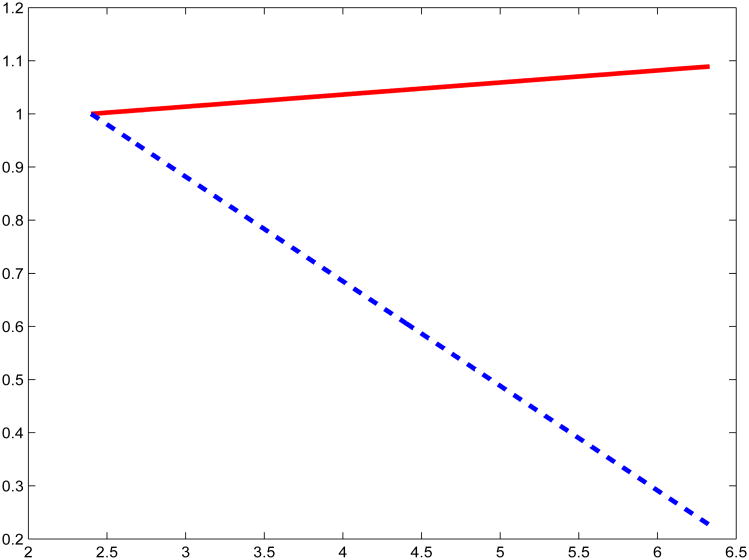
Further preliminary analysis of the controls included scatterplots of the transformed data, both of which were reasonably well-behaved and indicated an increasing trend for increasing red meat consumption, consistent with a linear trend, see Figure S.5 in the Supplementary Material. To check this, we fit a quadratic model to the transformed data: in both cases, the p-value for the quadratic term exceeded 0.20, see Figure 2. Thus, we adopted a linear function for the mean m(·) in the subsequent secondary analysis. In addition, the regression of PhIP on red meat consumption is heavily heteroscedastic, while the regression of MeIQx on red meat is passably homoscedastic. This is shown in Figure 3, where we fit a regression of the absolute residuals from a quadratic fit against red meat consumption (Davidian and Carroll, 1987): the plots from a linear regression are essentially the same.

Figure 2.

The fitted curves from a quadratic regression of MeIQx (solid red line) and PhIP (dashed blue line) on red meat consumption, using the controls. The fitted values were normalized to fit on the same plot. Neither have a statistically significant quadratic term.

Figure 3.

Plots to diagnose heteroscedasticity, with the curves representing relative standard deviation as a function of red meat consumption. Plotted are the fitted curves from a linear regression of the absolute residuals of the regression of MeIQx (solid red line) and PhIP (dashed blue line) on red meat consumption, using the controls. The fitted values were normalized to be equal at the minimum value of red meat consumption. The essentially flat curve for MeIQx indicates homoscedasticity, while that for PhIP is very strongly heteroscedastic. The latter has implications for data analysis, see Table 7 and the discussion in Section 6.

The results of this secondary analysis are given in Table 7. For MeIQx, the ordinary least squares standard errors when using only the controls are roughly the same and that of the sandwich method, which makes sense since the regression is homoscedastic. In this case, as expected from the theory, our semiparametric approach has smaller standard errors, with the least squares standard errors being approximately 30% larger. For PhIP, where the regression is distinctly homoscedastic, the sandwich standard errors for ordinary least squares among the controls is roughly 30% larger than the standard error that assumes homoscedasticity, and roughly 40% larger than our semiparametric approach. As expected from the theory, where homoscedasticity is not assumed, the standard errors for our semiparametric approach are nearly the same using either the asymptotic formula or the bootstrap.

Table 7.

Results of data analysis when Y is either MeIQx or PhIP. For the controls only, “OLS se” is the ordinary least squares standard error estimate, while “Sandwich se” is the sandwich method standard error estimate. For the parametric and semiparametric analysis, “Asymptotic se” is the standard error estimate from asymptotic theory, while “Bootstrap se” is the bootstrap standard error. For the robust analysis, only bootstrap standard error is available. The regression of PhIP on red meat (X) is heteroscedastic, reflected in the difference between the OLS standard error and the Sandwich standard error for the controls only analysis, as well as the difference between the asymptotic standard error and the bootstrap standard error of the parametric estimator.

	All Data
	Controls only			Parametric
	Estimate	OLS se	Sandwich se	Estimate	Asymptotic se	Bootstrap se
MeIQx	0.868	0.034	0.035	0.862	0.026	0.026
PhIP	0.742	0.064	0.080	0.751	0.046	0.056
	Robust			Semiparametric
	Estimate		Bootstrap se	Estimate	Asymptotic se	Bootstrap se
MeIQx	0.862		0.028	0.862	0.027	0.027
PhIP	0.751		0.057	0.750	0.057	0.058
	Smokers only
	Controls only			Parametric
	Estimate	OLS se	Sandwich se	Estimate	Asymptotic se	Bootstrap se
MeIQx	0.816	0.050	0.057	0.847	0.036	0.037
PhIP	0.619	0.095	0.132	0.737	0.063	0.080
	Robust			Semiparametric
	Estimate		Bootstrap se	Estimate	Asymptotic se	Bootstrap se
MeIQx	0.847		0.038	0.846	0.036	0.039
PhIP	0.737		0.084	0.736	0.082	0.087

As a comparison, we also implemented the parametric method of Lin and Zeng (2009) as well as the robust method by Wei et al. (2013). Standard errors of the former were assessed both by using the inverse of the Hessian of the loglikelihood and by the bootstrap, while standard errors of the latter were assessed by the bootstrap alone. The parametric method's asymptotic standard error clearly under-estimates the variability for PhIP when compared to the bootstrap, something expected because of the heteroscedasticity in PhIP. For MeIQx, where the error is homoscedastic, the parametric method, the robust method and our semiparametric approach are almost identical.

In summary, in analyzing this data set, we verified the previous observation based on the control only data that the regression error from MeIQx and red meat consumption has homoscedastic error, while that from the PhIP and red meat consumption has heteroscedastic error. Our analysis also verified the positive relationship between red meat consumption and these two forms of HCA, indicating that increased red meat consumption leads to increased levels of MeIQA and PhiP, both being risk factors for colorectal cancer. The first order accuracy of the variability of the estimated slope for our method is validated though its near-identical result with the bootstrap, and of course through the simulation results.

7 Discussion

We have developed a locally efficient semiparametric estimator for the secondary analysis of case-control studies, where only a mean model is specified to describe the relationship between the covariates. Despite this relatively weak assumption, we have shown that the problem is still identifiable under certain conditions. Through introducing the notion of a superpopulation, we are able to establish an estimation methodology via a conceptually tractable semiparametric procedure, although the derivation is highly non-standard and not trivial. The locally efficient estimator provides consistent estimation, and can achieve optimal efficiency if a posited regression error model happens to be true. Although the analysis is performed under the superpopulation concept, the general statements of consistency and local efficiency are valid in the case-control sampling scheme (Ma, 2010). In addition, the general methodology is applicable even if the linear logistic model (1) is replaced by other parametric models such as probit model, etc., as long as identifiability can be established.

Implementing the locally efficient estimator via Algorithm 1 requires several nonparametric regressions conditional on the covariates, which may be difficult when the dimension of the covariates increases. In such situations, dimension reduction techniques can be a good choice to achieve a balance between model flexibility and feasibility of parameter estimation and inference (Ma and Zhu, 2012). Further exploration of this is needed.

Table 2.

Results of the simulation study with n₁ = 500 cases and n₀ = 500 controls, α₂ = 0.5, homoscedastic errors. Here “Normal” means that ε = Normal(0, 1), while “Gamma” means that ε is a centered and scale Gamma random variable with shape 0.4, mean zero and variance one. The analyses performed were using controls only (“Controls”), the semiparametric efficient method that assumes normality and homoscedasticity (“Param”), the method of Wei, et al. (2012), (“Robust”), and our method (“Semi”). Over 1,000 simulations, we computed the mean estimated β (“Mean”), its standard deviation (“s.d.”), the mean estimated standard deviation (“Est. sd”), the coverage for a nominal 90% confidence interval (“90%”), the coverage for a nominal 95% confidence interval (“95%”), and the mean squared error efficiency compared to using only the controls (“MSE Eff”).

	Normal				Gamma
	disease rate 10%
α2 = 0.50	Controls	Param	Robust	Semi	Controls	Param	Robust	Semi
Mean	0.913	0.876	0.784	0.979	0.885	0.885	0.929	0.993
s.d.	0.120	0.121	0.159	0.117	0.124	0.124	0.108	0.109
Est. sd	0.119	0.123	0.154	0.117	0.153	0.126	0.110	0.109
90%	0.806	0.746	0.600	0.893	0.870	0.792	0.847	0.897
95%	0.867	0.837	0.723	0.956	0.926	0.891	0.908	0.948
MSE Eff		0.731	0.305	1.554		0.951	1.628	2.279
	disease rate 0.5%
α2 = 0.50	Controls	Param	Robust	Semi	Controls	Param	Robust	Semi
Mean	0.991	0.996	0.987	1.010	0.978	0.854	1.029	0.991
s.d.	0.165	0.114	0.118	0.121	0.148	0.231	0.155	0.097
Est. sd	0.155	0.112	0.120	0.122	0.149	0.223	0.160	0.096
90%	0.876	0.893	0.904	0.898	0.902	0.830	0.904	0.895
95%	0.925	0.942	0.949	0.938	0.945	0.904	0.950	0.945
MSE Eff		2.099	1.938	1.852		0.300	0.900	2.359

Table 5.

Results of the simulation study with n₁ = 500 cases and n₀ = 500 controls, α₂ = 0.5, heteroscedastic errors. Here “Normal” means that ε = Normal(0, 1), while “Gamma” means that ε is a centered and scale Gamma random variable with shape 0.4, mean zero and variance one. The analyses performed were using controls only (“Controls”), the semiparametric efficient method that assumes normality and homoscedasticity (“Param”), the method of Wei, et al. (2012), (“Robust”), and our method (“Semi”). Over 1,000 simulations, we computed the mean estimated β (“Mean”), its standard deviation (“s.d.”), the mean estimated standard deviation (“Est. sd”), the coverage for a nominal 90% confidence interval (“90%”), the coverage for a nominal 95% confidence interval (“95%”), and the mean squared error efficiency compared to using only the controls (“MSE Eff”).

	Normal				Gamma
	disease rate 10%
α2 = 0.50	Controls	Param	Robust	Semi	Controls	Param	Robust	Semi
Mean	0.905	0.897	1.078	0.990	0.950	0.931	1.065	1.001
s.d.	0.083	0.073	0.091	0.117	0.101	0.073	0.071	0.108
Est. sd	0.083	0.072	0.089	0.115	0.100	0.072	0.072	0.111
90%	0.676	0.600	0.770	0.895	0.847	0.765	0.781	0.895
95%	0.766	0.698	0.850	0.947	0.914	0.851	0.859	0.955
MSE Eff		0.998	1.107	1.154		1.258	1.370	1.089
	disease rate 0.5%
α2 = 0.50	Controls	Param	Robust	Semi	Controls	Param	Robust	Semi
Mean	0.997	1.113	0.973	1.007	0.991	1.296	0.890	0.995
s.d.	0.098	0.073	0.067	0.082	0.102	0.113	0.087	0.072
Est. sd	0.101	0.072	0.070	0.088	0.098	0.112	0.084	0.071
90%	0.906	0.541	0.892	0.897	0.895	0.145	0.630	0.907
95%	0.951	0.663	0.957	0.942	0.937	0.231	0.745	0.941
MSE Eff		0.531	1.842	1.419		0.104	0.533	2.013

Appendix: Sketch of Technical Arguments

A.1 Proof of Proposition 1

Assume the contrary. That is, assume the problem is not identifiable. This means we can find parameters α_c, α₁, α₂, β, η₂, η₁ and α̃_c, α̃₁, α̃₂, β̃, η̃₂, η̃₁ so that, denoting ε̃ = Y − m(x, β̃),

$$\begin{array}{c}{\pi }_d=\int {\eta }_1(\mathbf{x}){\eta }_2\{y-m(\mathbf{x},\mathit{\beta }),\mathbf{x}\}\frac{exp\{d{\alpha }_c+du(\mathbf{x},y,{\mathit{\alpha }}_1,{\alpha }_2,)\}}{1+exp\{{\alpha }_c+u(\mathbf{x},y,{\mathit{\alpha }}_1,{\alpha }_2)\}}d\mu (\mathbf{x})d\mu (y);\\ {\stackrel{\sim }{\pi }}_d=\int {\stackrel{\sim }{\eta }}_1(\mathbf{x}){\stackrel{\sim }{\eta }}_2\{y-m(\mathbf{x},\stackrel{\sim }{\mathit{\beta }}),\mathbf{x}\}\frac{exp\{d{\stackrel{\sim }{\alpha }}_c+du(\mathbf{x},y,{\stackrel{\sim }{\mathit{\alpha }}}_1,{\overline{\alpha }}_2)\}}{1+exp\{{\stackrel{\sim }{\alpha }}_c+u(\mathbf{x},y,{\stackrel{\sim }{\mathit{\alpha }}}_1,{\alpha }_2)\}}d\mu (\mathbf{x})d\mu (y),\end{array}$$

we have that

$$\frac{1}{{\pi }_d}{\eta }_1(\mathbf{x}){\eta }_2\{y-m(\mathbf{x},\mathit{\beta }),\mathbf{x}\}\frac{exp\{d{\alpha }_c+du(\mathbf{x},y,{\mathit{\alpha }}_1,{\alpha }_2)\}}{1+exp\{{\alpha }_c+u(\mathbf{x},y,{\mathit{\alpha }}_1,{\alpha }_2)\}}=\frac{1}{{\stackrel{\sim }{\pi }}_d}{\stackrel{\sim }{\eta }}_1(\mathbf{x}){\stackrel{\sim }{\eta }}_2\{y-m(\mathbf{x},\stackrel{\sim }{\mathit{\beta }}),\mathbf{x}\}\frac{exp\{d{\stackrel{\sim }{\alpha }}_c+du(\mathbf{x},y,{\stackrel{\sim }{\mathit{\alpha }}}_1,{\stackrel{\sim }{\alpha }}_2)\}}{1+exp\{{\stackrel{\sim }{\alpha }}_c+u(\mathbf{x},y,{\stackrel{\sim }{\mathit{\alpha }}}_1,{\stackrel{\sim }{\alpha }}_2)\}}$$ (A.1)

for all (x, y, d). Take the ratio of the above expression at d = 1 and d = 0 respectively, we obtain that for all (x, y),

$$\frac{{\pi }_0}{{\pi }_1}exp\{{\alpha }_c+u(\mathbf{x},y,{\mathit{\alpha }}_1,{\alpha }_2)\}=\frac{{\stackrel{\sim }{\pi }}_0}{{\stackrel{\sim }{\pi }}_1}exp\{{\stackrel{\sim }{\alpha }}_c+u(\mathbf{x},y,{\stackrel{\sim }{\mathit{\alpha }}}_1,{\stackrel{\sim }{\alpha }}_2)\}.$$

This yields that u(x, y, α₁,α₂) − u(x, y, α̃₁, α̃₂) is a constant. Since it is zero at (x, y) = 0, hence we have u(x, y, α₁, α₂) − u(x, y, α̃₁, α̃₂) ≡ 0. Thus, α₁, α₂ = α̃₁, α̃₂, exp(α_c)π₀/π₁ = exp(α̃_c)π̃₀/π̃₁ and

$$\frac{1}{{\pi }_0}\frac{{\eta }_1(\mathbf{x}){\eta }_2\{y-m(\mathbf{x},\mathit{\beta }),\mathbf{x}\}}{1+exp\{{\alpha }_c+u(\mathbf{x},y,{\mathit{\alpha }}_1,{\alpha }_2)\}}=\frac{1}{{\stackrel{\sim }{\pi }}_0}\frac{{\stackrel{\sim }{\eta }}_1(\mathbf{x}){\stackrel{\sim }{\eta }}_2\{y-m(\mathbf{x},\stackrel{\sim }{\mathit{\beta }}),\mathbf{x}\}}{1+exp\{{\stackrel{\sim }{\alpha }}_c+u(\mathbf{x},y,{\mathit{\alpha }}_1,{\alpha }_2)\}}$$

for all (x, y). This gives

$${\stackrel{\sim }{\eta }}_1(\mathbf{x}){\stackrel{\sim }{\eta }}_2\{y-m(\mathbf{x},\stackrel{\sim }{\mathit{\beta }}),\mathbf{x}\}=\frac{{\stackrel{\sim }{\pi }}_0}{{\pi }_0}\frac{1+exp\{{\stackrel{\sim }{\alpha }}_c+u(\mathbf{x},y,{\mathit{\alpha }}_1,{\alpha }_2)\}}{1+exp\{{\alpha }_c+u(\mathbf{x},y,{\mathit{\alpha }}_1,{\alpha }_2)\}}{\eta }_1(\mathbf{x}){\eta }_2\{y-m(\mathbf{x},\mathit{\beta }),\mathbf{x}\}.$$ (A.2)

Integrating (A.2) and the product of (A.2) and y with respect to y, we obtain

$$\begin{array}{c}{\stackrel{\sim }{\eta }}_1(\mathbf{x})=\frac{{\stackrel{\sim }{\pi }}_0}{{\pi }_0}{\eta }_1(\mathbf{x})\int \frac{1+exp\{{\stackrel{\sim }{\alpha }}_c+u(\mathbf{x},y,{\mathit{\alpha }}_1,{\alpha }_2)\}}{1+exp\{{\alpha }_c+u(\mathbf{x},y,{\mathit{\alpha }}_1,{\alpha }_2)\}}{\eta }_2\{y-m(\mathbf{x},\mathit{\beta }),\mathbf{x}\}dy;\\ {\stackrel{\sim }{\eta }}_1(\mathbf{x})m(\mathbf{x},\stackrel{\sim }{\mathit{\beta }})=\frac{{\stackrel{\sim }{\pi }}_0}{{\pi }_0}{\eta }_1(\mathbf{x})\int \frac{1+exp\{{\stackrel{\sim }{\alpha }}_c+u(\mathbf{x},y,{\mathit{\alpha }}_1,{\alpha }_2)\}}{1+exp\{{\alpha }_c+u(\mathbf{x},y,{\mathit{\alpha }}_1,{\alpha }_2)\}}{\eta }_2\{y-m(\mathbf{x},\mathit{\beta }),\mathbf{x}\}ydy\end{array}$$

respectively. Further taking ratios, we find

$$\int \frac{1+exp\{{\stackrel{\sim }{\alpha }}_c+u(\mathbf{x},y,{\mathit{\alpha }}_1,{\alpha }_2)\}}{1+exp\{{\alpha }_c+u(\mathbf{x},y,{\mathit{\alpha }}_1,{\alpha }_2)\}}{\eta }_2\{y-m(\mathbf{x},\mathit{\beta }),\mathbf{x}\}ydy=m(\mathbf{x},\stackrel{\sim }{\mathit{\beta }})\int \frac{1+exp\{{\stackrel{\sim }{\alpha }}_c+u(\mathbf{x},y,{\mathit{\alpha }}_1,{\alpha }_2)\}}{1+exp\{{\alpha }_c+u(\mathbf{x},y,{\mathit{\alpha }}_1,{\alpha }_2)\}}{\eta }_2\{y-m(\mathbf{x},\mathit{\beta }),\mathbf{x}\}dy.$$

If α_c = α̃_c, then we obtain m(x, β) = m(x, β̃), hence β = β̃. We also obtain η̃₁(x) = η₁(x)π̃₀/π₀. Since both η̃₁(x) and η₁(x) are valid density functions, we have η̃₁(x) = η₁(x) and π₀ = π̃₀, π₁ = π̃₁. This subsequently yields η₂ = η̃₂ contradicting our assumptions. Thus we obtain that α_c ≠ α̃_c.

Denote

$$r(\epsilon ,\mathbf{x})=\frac{1+exp[{\stackrel{\sim }{\alpha }}_c+u\{\mathbf{x},m(\mathbf{x},\mathit{\beta })+\epsilon ,{\mathit{\alpha }}_1,{\alpha }_2\}]}{1+exp[{\alpha }_c+u\{\mathbf{x},m(\mathbf{x},\mathit{\beta })+\epsilon ,{\mathit{\alpha }}_1,{\alpha }_2\}]}\{\epsilon -m(\mathbf{x},\stackrel{\sim }{\mathit{\beta }})+m(\mathbf{x},\mathit{\beta })\}=exp({\stackrel{\sim }{\alpha }}_c-{\alpha }_c)\{\epsilon -m(\mathbf{x},\stackrel{\sim }{\mathit{\beta }})+m(\mathbf{x},\mathit{\beta })\}+(1-exp({\stackrel{\sim }{\alpha }}_c-{\alpha }_c))\frac{\epsilon -m(\mathbf{x},\stackrel{\sim }{\mathit{\beta }})+m(\mathbf{x},\mathit{\beta })}{1+exp[{\alpha }_c+u\{\mathbf{x},m(\mathbf{x},\mathit{\beta })+\epsilon ,{\mathit{\alpha }}_1,{\alpha }_2\}]}.$$

By definition, η₂ is a valid conditional density function and it satisfies ∫ εη₂(ε, x)dε = 0, and we have that

$$0=\int r(\epsilon ,\mathbf{x}){\eta }_2(\epsilon ,\mathbf{x})d\epsilon =-exp({\stackrel{\sim }{\alpha }}_c-{\alpha }_c)\{m(\mathbf{x},\stackrel{\sim }{\mathit{\beta }})-m(\mathbf{x},\mathit{\beta })\}+(1-exp({\stackrel{\sim }{\alpha }}_c-{\alpha }_c))\int \frac{\epsilon -m(\mathbf{x},\stackrel{\sim }{\mathit{\beta }})+m(\mathbf{x},\mathit{\beta })}{1+exp[{\alpha }_c+u\{\mathbf{x},m(\mathbf{x},\mathit{\beta })+\epsilon ,{\mathit{\alpha }}_1,{\alpha }_2\}]}{\eta }_2(\epsilon ,\mathbf{x})d\epsilon$$

for all x. This means

$$\frac{\{m(\mathbf{x},\stackrel{\sim }{\mathit{\beta }})-m(\mathbf{x},\mathit{\beta })\}exp({\stackrel{\sim }{\alpha }}_c-{\alpha }_c)}{1-exp({\stackrel{\sim }{\alpha }}_c-{\alpha }_c)}=\int \frac{\epsilon {\eta }_2(\epsilon ,\mathbf{x})}{(1+exp[{\alpha }_c+u\{\mathbf{x},m(\mathbf{x},\mathit{\beta })+\epsilon ,{\mathit{\alpha }}_1,{\alpha }_2\}])}d\epsilon -\int \frac{\{m(\mathbf{x},\stackrel{\sim }{\mathit{\beta }})-m(\mathbf{x},\mathit{\beta })\}{\eta }_2(\epsilon ,\mathbf{x})}{1+exp[{\alpha }_c+u\{\mathbf{x},m(\mathbf{x},\mathit{\beta })+\epsilon ,{\mathit{\alpha }}_1,{\alpha }_2\}]}d\epsilon$$

for all x. If we let x → c₁, then

$$\frac{c(\mathit{\beta },\stackrel{\sim }{\mathit{\beta }})exp({\stackrel{\sim }{\alpha }}_c-{\alpha }_c)}{1-exp({\stackrel{\sim }{\alpha }}_c-{\alpha }_c)}=c_2{\int }_{{\mathcal{D}}^c}\epsilon {\eta }_2(\epsilon ,{\mathbf{c}}_1)d\epsilon -c_{2}c(\mathit{\beta },\stackrel{\sim }{\mathit{\beta }}){\int }_{{\mathcal{D}}^c}{\eta }_2(\epsilon ,{\mathbf{c}}_1)d\epsilon +\underset{\mathbf{x}\to {\mathbf{c}}_1}{lim}{\int }_{\mathcal{D}}\frac{\epsilon {\eta }_2(\epsilon ,\mathbf{x})}{1+exp[{\alpha }_c+u\{\mathbf{x},m(\mathbf{x},\mathit{\beta })+\epsilon ,{\mathit{\alpha }}_1,{\alpha }_2\}]}d\epsilon -\underset{\mathbf{x}\to {\mathbf{c}}_1}{lim}{\int }_{\mathcal{D}}\frac{c(\mathit{\beta },\stackrel{\sim }{\mathit{\beta }}){\eta }_2(\epsilon ,\mathbf{x})}{1+exp[{\alpha }_c+u\{\mathbf{x},m(\mathbf{x},\mathit{\beta })+\epsilon ,{\mathit{\alpha }}_1,{\alpha }_2\}]}d\epsilon =-c_{2}c(\mathit{\beta },\stackrel{\sim }{\mathit{\beta }})-c_2{\int }_{\mathcal{D}}\epsilon {\eta }_2(\epsilon ,{\mathbf{c}}_1)d\epsilon +c_{2}c(\mathit{\beta },\stackrel{\sim }{\mathit{\beta }}){\int }_{\mathcal{D}}{\eta }_2(\epsilon ,{\mathbf{c}}_1)d\epsilon +\underset{\mathbf{x}\to {\mathbf{c}}_1}{lim}{\int }_{\mathcal{D}}\frac{\epsilon {\eta }_2(\epsilon ,\mathbf{x})}{1+exp[{\alpha }_c+u\{\mathbf{x},m(\mathbf{x},\mathit{\beta })+\epsilon ,{\mathit{\alpha }}_1,{\alpha }_2\}]}d\epsilon -\underset{\mathbf{x}\to {\mathbf{c}}_1}{lim}{\int }_{\mathcal{D}}\frac{c(\mathit{\beta },\stackrel{\sim }{\mathit{\beta }}){\eta }_2(\epsilon ,\mathbf{x})}{1+exp[{\alpha }_c+u\{\mathbf{x},m(\mathbf{x},\mathit{\beta })+\epsilon ,{\mathit{\alpha }}_1,{\alpha }_2\}]}d\epsilon .$$

Thus,

$$|\frac{exp({\stackrel{\sim }{\alpha }}_c-{\alpha }_c)}{1-exp({\stackrel{\sim }{\alpha }}_c-{\alpha }_c)}+c_2|=|-c_2{\int }_{\mathcal{D}}\frac{\epsilon {\eta }_2(\epsilon ,{\mathbf{c}}_1)}{c(\mathit{\beta },\stackrel{\sim }{\mathit{\beta }})}d\epsilon +c_2{\int }_{\mathcal{D}}{\eta }_2(\epsilon ,{\mathbf{c}}_1)d\epsilon +\underset{\mathbf{x}\to {\mathbf{c}}_1}{lim}{\int }_{\mathcal{D}}\frac{\epsilon {\eta }_2(\epsilon ,\mathbf{x})/c(\mathit{\beta },\stackrel{\sim }{\mathit{\beta }})}{1+exp[{\alpha }_c+u\{\mathbf{x},m(\mathbf{x},\mathit{\beta })+\epsilon ,{\mathit{\alpha }}_1,{\alpha }_2\}]}d\epsilon -\underset{\mathbf{x}\to {\mathbf{c}}_1}{lim}{\int }_{\mathcal{D}}\frac{{\eta }_2(\epsilon ,\mathbf{x})}{1+exp[{\alpha }_c+u\{\mathbf{x},m(\mathbf{x},\mathit{\beta })+\epsilon ,{\mathit{\alpha }}_1,{\alpha }_2\}]}d\epsilon |\le \frac{2}{|c(\mathit{\beta },\stackrel{\sim }{\mathit{\beta }})|}{\int }_{\mathcal{D}}|\epsilon |{\eta }_2(\epsilon ,{\mathbf{c}}_1)d\epsilon +2{\int }_{\mathcal{D}}{\eta }_2(\epsilon ,{\mathbf{c}}_1)d\epsilon \le \frac{2}{|c(\mathit{\beta },\stackrel{\sim }{\mathit{\beta }})|}{[E\{{\epsilon }^{2}I(\epsilon \in \mathcal{D})|{\mathbf{c}}_1\}\text{pr}(\epsilon \in \mathcal{D}|{\mathbf{c}}_1)]}^{1/2}+2\text{pr}(\epsilon \in \mathcal{D}|{\mathbf{c}}_1)\le \frac{2}{|c(\mathit{\beta },\stackrel{\sim }{\mathit{\beta }})|}{\{E({\epsilon }^2)\delta \}}^{1/2}+2\delta .$$

We can make the upper bound of the above expression arbitrarily small by choosing δ arbitrarily close to zero, while the quantity on the left had side is a constant. Hence we in fact have obtained

$$\frac{exp({\stackrel{\sim }{\alpha }}_c-{\alpha }_c)}{1-exp({\stackrel{\sim }{\alpha }}_c-{\alpha }_c)}=-c_2$$

However, −c₂ is between −1 and 0, simple calculation shows that these two constants cannot be equal, hence our problem is indeed identifiable.

A.2 Derivation of Λ and Λ^⊥

Consider the nuisance tangent space associated with η₁ and η₂ respectively, we have

$$\begin{array}{c}{\mathrm{\Lambda }}_1=\{\mathbf{g}(\mathbf{x})-E(\mathbf{g}|d):\forall \mathbf{g}\text{such that}{E}_{\text{true}}(\mathbf{g})=\mathbf{0}\};\\ {\mathrm{\Lambda }}_2=\{\mathbf{g}(\epsilon ,\mathbf{x})-E(\mathbf{g}|d):\forall \mathbf{g}\text{such that}{E}_{\text{true}}(\mathbf{g}|\mathbf{X})=E_{\text{true}}(\epsilon \mathbf{g}|\mathbf{X})=\mathbf{0}\mathrm{a}.\mathrm{s}.\}.\end{array}$$

Hence Λ = Λ₁ + Λ₂ = {g(ε, x) − E(g | d) : ∀g such that E_true(g) = E_true(εg | X) = 0 a.s.}. It is easily seen that ${\mathrm{\Lambda }}_1^{\perp }=[\mathbf{h}:E(\mathbf{h})=\mathbf{0},E\{\mathbf{h}-E(\mathbf{h}|D)|\mathbf{X}\}=\mathbf{0}$ a.s.]. This is because from

$$0=E[{\mathbf{h}}^{\mathrm{T}}\{\mathbf{g}(\mathbf{X})-E(\mathbf{g}|D)\}]=E[{\{\mathbf{h}-E(\mathbf{h}|D)\}}^{\mathrm{T}}\{\mathbf{g}(\mathbf{X})-E(\mathbf{g}|D)\}]=E[{\{\mathbf{h}-E(\mathbf{h}|D)\}}^{\mathrm{T}}\mathbf{g}]=E(E[{\{\mathbf{h}-E(\mathbf{h}|D)\}}^{\mathrm{T}}|\mathbf{X}]\mathbf{g}),$$

we obtain E{h − E(h | D) | X}Σ_d ∫ f_X,Y,D (X, y, d)dμ(y)/η₁(X) = c a.s. for some constant c. Since E[E{h − E(h | D) | X}] = 0 a.s., we obtain

$$\mathbf{0}=\int E\{\mathbf{h}-E(\mathbf{h}|D)|\mathbf{x}\}{\sum }_d\int f_{X,Y,D}(\mathbf{x},y,d)d\mu (y)d\mu (\mathbf{x})=\int \mathbf{c}{\eta }_1(\mathbf{x})d\mu (\mathbf{x})=\mathbf{c}\mathrm{a}.\mathrm{s}\mathrm{..}$$

Hence c = 0 and E{h − E(h | D) | X} ${\sum }_{d=0}^1\int f_{X,Y,D}(\mathbf{X},y,d)d\mu (y)/{\eta }_1(\mathbf{X})=\mathbf{0}$ a.s., which yields E{h −E(h|D)|X} = 0 a.s..

Now we are in position to show

$${\mathrm{\Lambda }}^{\perp }={\mathrm{\Lambda }}_1^{\perp }\cap {\mathrm{\Lambda }}_2^{\perp }=[\mathbf{h}(d,\epsilon ,\mathbf{x}):E(\mathbf{h})=\mathbf{0},E\{\mathbf{h}-E(\mathbf{h}|D)|\epsilon ,\mathbf{X}\}\times {\sum }_d\frac{N_d}{N}\frac{H(d,\mathbf{X},Y)}{p_D^{\text{true}}(d)}=\epsilon \mathbf{a}(\mathbf{X})\mathrm{a}.\mathrm{s}.],$$

where a(x) is an arbitrary function of x. This is because for any $\mathbf{h}\in {\mathrm{\Lambda }}_1^{\perp }$, $\mathbf{h}\in {\mathrm{\Lambda }}_2^{\perp }$ is equivalent to

$$0=E[{\mathbf{h}}^{\mathrm{T}}\{\mathbf{g}(\epsilon ,\mathbf{X})-E(\mathbf{g}|D)\}]=E[{\{\mathbf{h}-E(\mathbf{h}|D)\}}^{\mathrm{T}}\{\mathbf{g}(\epsilon ,\mathbf{X})-E(\mathbf{g}|D)\}]=E[{\{\mathbf{h}-E(\mathbf{h}|D)\}}^{\mathrm{T}}\mathbf{g}]=E(E[{\{\mathbf{h}-E(\mathbf{h}|D)\}}^{\mathrm{T}}|\epsilon ,\mathbf{X}]\mathbf{g}).$$

Hence E{h − E(h | D) | ε, X}Σ_df_{X, Y, D}(X, Y, d)/{η₁(X)η₂(ε, X)} = εa(X) + c(X) a.s.. Because $\mathbf{h}\in {\mathrm{\Lambda }}_1^{\perp }$, we have E[E{h − E(h | D) | ε, X} | X] = 0 a.s.. Hence

$$\mathbf{0}=\int E\{\mathbf{h}-E(\mathbf{h}|D)|\epsilon ,\mathbf{X}\}\frac{{\sum }_d{f}_{X,Y,D}(\mathbf{X},y,d)}{\int {\sum }_d{f}_{X,Y,D}(\mathbf{X},y,d)d\mu (y)}d\mu (y)=\frac{\int \{\epsilon \mathbf{a}(\mathbf{X})+\mathbf{c}(\mathbf{X})\}{\eta }_1(\mathbf{x}){\eta }_2(\epsilon ,\mathbf{x})d\mu (y)}{\int {\sum }_d{f}_{X,Y,D}(\mathbf{X},y,d)d\mu (y)}=\frac{\mathbf{c}(\mathbf{x}){\eta }_1(\mathbf{X})}{\int \sum _d{f}_{X,Y,D}(\mathbf{X},y,d)d\mu (y)}\mathrm{a}.\mathrm{s}.,$$

hence c(X) = 0 a.s. and E{h − E(h | D) | ε, X}Σ_df_X,Y,D(X, Y, d)/{η₁(X)η₂(ε, X)} = εa(X) a.s.. This means that E{h − E(h | D) | ε, X} ${\sum }_d(N_d/N)H(d,\mathbf{X},Y)/p_D^{\text{true}}(d)=\epsilon \mathbf{a}(\mathbf{X})$ a.s..

A.3 Sketch of Proof of Theorem 1

For simplicity of proof, we split the N observations randomly into two sets. The first set contains n₁ = N − N^1−δ observations and the second set contains n₂ = N^1−δ observations, where δ is a small positive number. We form and solve the estimating equation using data in the first set, while calculating all the hatted quantities described in the algorithm using data in the second set. We use this only as a technical device, although in our simulations and empirical example we used all the data.

In the algorithm, the approximations involve either replacing expectation with averaging, or standard kernel regression estimation or kernel density estimation, hence the differences between the quantities with hat and without hat have either mean zero, standard deviation $O(n_2^{-1/2})$, or mean O(h^r), standard deviation O{(n₂h^p)^−1/2}. In particular, ${\widehat{\mathbf{S}}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0)-{\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0)$ has bias O(h^r) and standard deviation O{(n₂h^p)^−1/2}. Recall the definition of expectation and covariance in the superpopulation explicitly written out in the statement of Theorem 1. Then

$$\mathbf{0}=n_1^{-1/2}\sum _{i=1}^{n_1}{\widehat{\mathbf{S}}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,\widehat{\mathit{\theta }})=n_1^{-1/2}\sum _{i=1}^{n_1}{\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0)+n_1^{-1/2}\sum _{i=1}^{n_1}\{{\widehat{\mathbf{S}}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0)-{\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0)\}+E\{\frac{\partial {\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0)}{\partial {\mathit{\theta }}^{\mathrm{T}}}+o_p(1)\}{n}_1^{1/2}(\widehat{\mathit{\theta }}-{\mathit{\theta }}_0)=n_1^{-1/2}\sum _{i=1}^{n_1}{\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0)+E\left\{\frac{\partial {\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0)}{\partial {\mathit{\theta }}^{\mathrm{T}}}\right\}{n}_1^{1/2}(\widehat{\mathit{\theta }}-{\mathit{\theta }}_0)+n_1^{-1/2}\sum _{i=1}^{n_1}\{{\widehat{\mathbf{S}}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0)-{\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0)\}+o_p(1).$$

We see that ${\widehat{\mathbf{S}}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0)$ differs from ${\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0)$ in that all the unknown quantities, except S*, are estimated. This is equivalent to estimating the unknown functions η₁(x), η₂(ε, x) in (4) and using the estimate η̂₁(x), η̂₂(ε, x) in calculating ${\mathbf{S}}_{\text{eff}}^{\ast }$ from the posited S*. Thus, denoting η̂ = (η̂₁, η̂₂), we can approximate

$$n_1^{-1/2}\sum _{i=1}^{n_1}\{{\widehat{\mathbf{S}}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0)-{\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0)\}=n_1^{-1/2}\sum _{i=1}^{n_1}\{{\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0,\widehat{\eta })-{\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0,{\eta }_0)\}=\{n_1^{-1/2}\sum _{i=1}^{n_1}\partial {\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0,{\eta }_0)/\partial \eta \}(\widehat{\eta }-{\eta }_0)+O_p\{n_1^{1/2}{(\widehat{\eta }-{\eta }_0)}^2\}+o_p(1),$$ (A.3)

where $\partial {\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0,{\eta }_0)/{\partial }_{\eta }$ is pathwise derivative. However, ${\mathbf{S}}_{\text{eff}}^{\ast }$ is the projection of S* to Λ^⊥ so ${\mathbf{S}}_{\text{eff}}^{\ast }\in {\mathrm{\Lambda }}^{\perp }$. Thus, for any parametric submodel of η involving parameter γ, we have

$$E\{\partial {\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0,\gamma )/\partial {\gamma }^{\mathrm{T}}\}=\int \frac{\partial {\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0,\gamma )}{\partial {\gamma }^{\mathrm{T}}}{f}_{X,Y,D}(x,y,d)d\mu (x)\mu (y)d\mu (d)=-\int {\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0,\gamma )\frac{\partial log\{f_{X,Y,D}(x,y,d)\}}{\partial {\gamma }^{\mathrm{T}}}{f}_{X,Y,D}(x,y,d)d\mu (x)\mu (y)d\mu (d)=-E\{{\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0,\gamma ){\mathbf{S}}_{\gamma }^{\mathrm{T}}\}=\mathbf{0}.$$

The last equality is because by definition S_γ ∈ Λ which is orthogonal to Λ^⊥ and ${\mathbf{S}}_{\text{eff}}^{\ast }\in {\mathrm{\Lambda }}^{\perp }$. Here, f_X,Y,D (x, y, d) is defined in (4). Because γ is parameter of any arbitrary submodel of η, we actually have obtained

$$E\{\partial {\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0,{\eta }_0)/\partial \eta \}=-E\{{\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0,{\eta }_0){\mathbf{S}}_{\eta }^{\mathrm{T}}\}=\mathbf{0},$$

where Sη is the nuisance score function along the arbitrarily chosen specific path of the pathwise derivative. Thus, the first term of (A.3) is of order o_p(1). On the other hand, $O_p\{n_1^{1/2}{(\widehat{\eta }-{\eta }_0)}^2\}=O_p\{n_1^{1/2}{h}^{2r}+n_1^{1/2}{(n_2{h}^p)}^{-1}\}=o_p(1)$. We therefore obtain

$$\mathbf{0}=n_1^{-1/2}\sum _{i=1}^{n_1}{\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0)+E\left\{\frac{\partial {\mathbf{S}}_{\text{eff}}^{\ast }(D_i,{\mathbf{X}}_i,Y_i,{\mathit{\theta }}_0)}{\partial {\mathit{\theta }}^{\mathrm{T}}}\right\}{n}_1^{1/2}(\widehat{\mathit{\theta }}-{\mathit{\theta }}_0)+o_p(1).$$

This yields $n_1^{1/2}(\widehat{\mathit{\theta }}-{\mathit{\theta }}_0)\to \text{Normal}\{\mathbf{0},{\mathbf{A}}^{-1}\mathbf{B}{({\mathbf{A}}^{-1})}^{\mathrm{T}}\}$, and hence

$$N^{1/2}(\widehat{\mathit{\theta }}-{\mathit{\theta }}_0)\to \text{Normal}\{\mathbf{0},{\mathbf{A}}^{-1}\mathbf{B}{({\mathbf{A}}^{-1})}^{\mathrm{T}}\}$$

when N → ∞.