High Resolution Prediction of Calcium-Binding Sites in 3D Protein Structures Using FEATURE

Abstract

Metal-binding proteins are ubiquitous in biological systems ranging from enzymes to cell surface receptors. Among the various biologically active metal ions, calcium plays a large role in regulating cellular and physiological changes. With the increasing number of high-quality crystal structures of proteins associated with their metal ion ligands, many groups have built models to identify Ca²⁺ sites in proteins, utilizing information such as structure, geometry, or homology to do the inference. We present a FEATURE-based approach in building such a model and show that our model is able to discriminate between nonsites and calcium-binding sites with a very high precision of more than 98%. We demonstrate the high specificity of our model by applying it to test sets constructed from other ions. We also introduce an algorithm to convert high scoring regions into specific site predictions and demonstrate the usage by scanning a test set of 91 calcium-binding protein structures (190 calcium sites). The algorithm has a recall of more than 93% on the test set with predictions found within 3 Å of the actual sites.

Introduction

Calcium ions (Ca²⁺) participate in a diverse range of biological activities ranging from ventricular contractions to cell motility. Mass movement of Ca²⁺ across membranes causes electrical polarization and underlies neuronal synaptic transmission and cardiovascular contractions. As a second messenger in signaling pathways, Ca²⁺ activates regulatory proteins such as calmodulin, which then act on other proteins to cause large-scale physiological changes. Ca²⁺ is also directly involved in the activities of many enzymes,¹ where the metal ion functions as a cofactor (prothrombinase) or plays a role in thermostability (mammalian trypsin).² The involvement of Ca²⁺ in a range of biological activities has led to interest in identifying calcium-binding proteins and also in designing proteins that can bind to calcium.^3,4

Although the EF-hand motif is common in many calcium-binding proteins, there exist a significant number of calcium binding sites with differing coordinating residues and structures.⁵ Prediction of calcium binding sites has therefore been mostly reliant on structure-based methods rather than 2D sequence motifs. Yamashita et al.⁶ used hydrophobicity to identify metal-binding sites and noted that long-range properties of the protein, such as electrostatics, did not work as well. Nayal and Di Cera⁷ subsequently presented a method to predict calcium sites with higher accuracy using the estimated valence of a point as a predictor of local presence of calcium. Wei and Altman⁸ suggested the use of protein microenvironments as statistical predictors of calcium sites (FEATURE) and showed that a Naïve Bayes model trained on just 16 sites and 100 nonsites had a high recall on a small test set of 33 sites. Developing further along the idea of a FEATURE-based model, Liang et al. incorporated information from binding motifs to increase the classification power,⁹ while Halperin et al. increased the computational efficiency to make the FEATURE method tractable.¹⁰ Glazer et al. and Liu et al. used molecular dynamics¹¹ and loop-modeling,¹² respectively, to improve the performance of previous FEATURE models. Additionally, Sodhi et al. developed a neural network classifier¹³ to detect calcium sites (MetSite) using sequence profile information and approximate structural data. A random forest classifier was trained by Bordner et al. on various protein sequences and structure properties (SitePredict)¹⁴ but explicitly avoided the reliance on exact positions of residue atoms. Deng et al. also demonstrated the use of graph theory in a geometry-based approach¹⁵ to the site-prediction problem. Many of these methods returned protein regions that are likely to contain sites, rather than specific site positions within the protein. Although the prediction of site regions may be sufficient to infer protein function, prediction of specific site locations is often desirable when designing peptides or re-engineering calcium-binding sites. There is unfortunately no standard method to directly infer exact site locations from predicted regions. The difficulty in doing so is that unless a perfect scoring function (where a high score is given to the exact site location and nowhere else nearby) is used, significant regions around each site would also have relatively high scores, leading to a large number of false positives when aggregation is performed.

While varying levels of success have been reported with earlier methods, many of them do not take full advantage of the large number of calcium sites available in current structure repositories. The exponential growth in the number of crystal structures deposited in the Protein Data Bank (PDB) repository over the past two decades has provided an opportunity to build models with better predictive power. Furthermore, the increase in computing power over the years has allowed previously computationally intensive methods to now be feasibly accomplished on a personal computer. In this paper, we revisit the FEATURE-based calcium model first introduced by Wei and Altman,⁸ using a 20-fold increase in training size and performing a more rigorous analysis of the model. We evaluated our model’s performance against a range of data sets used in other papers and also on curated alternative ion data sets and show that our current model performs significantly better at site classification than the earlier FEATURE-based calcium model.⁸ We also studied our model’s sensitivity as a function of distance of a query point from the location of the known calcium sites and showed that the relationship to distance is similar to a logistic function. Finally, we develop an algorithm that utilizes the FEATURE scores obtained from a grid scan of a protein to predict exact site positions. We applied the algorithm on a set of 91 PDB structures with 190 sites and were able to recover more than 90% of the sites, with more than half of the predictions made within 0.5 Å from actual sites. The site recall using the algorithm was higher than comparable methods published previously.^7,15

Methods

Training Set Construction

Our training set for the calcium model consisted of 314 calcium sites and 2735 nonsites from 312 protein structures taken from the RCSB Protein Data Bank (PDB),¹⁶ and the full list of calcium sites is provided in Table S1 of the Supporting Information. We first queried Uniprot¹⁷ for only reviewed protein entries that had an annotation for a calcium ligand and restricted the results to those that had an associated PDB and chain identifier. The protein chains were assigned to clusters based on precomputed BLASTClust¹⁸ results downloaded from the RCSB PDB server (ftp://resources.rcsb.org/sequence/clusters/; 11 January 2013 snapshot), with the sequence similarity threshold set to 70%. The PDB structures with the best resolution in each cluster were chosen, and structures with a resolution of more than 3.5 Å were rejected. PDB’s BLASTClust results do not cluster proteins with significantly different lengths together and may therefore over-represent the actual number of clusters. To address this, we recomputed the BLAST score between the protein chains using BLAST+,¹⁹ with an identity cutoff of 70% for the best scoring local alignment between each pair. The pairs of chains with more than 70% identity were then aligned structurally, and only the chain from the structure with the highest resolution was retained if the associated calcium site for both chains were found to be in the same relative position. In the case where the associated calcium sites in both chains were in different relative positions, both calcium sites were retained in the training set. We characterized two physical properties of the sites in the training set, specifically the number of protein atoms within 1.25 and 5 Å of a site, in order to generate matched nonsites.

We consider points in protein regions more than 10 Å from metal ions as potential candidates for nonsites. The nonsites were obtained by first generating protein surface points with PyMOL²⁰ from the 312 calcium-binding protein structures, excluding points that were within 10 Å from any calcium, zinc, sodium, and magnesium ions. For each of the PDB structures, a subset of 1000 surface points were selected randomly, to which vectors of length 1.5 Å were then added in a random direction to generate nonsites with diverse distances from protein atoms. The perturbed points were retained if the number of protein atoms found within 1.25 and 5 Å matched that of the training sites. To avoid any possible sequence-based bias in the nonsites, no more than 10 out of the 1000 points generated were accepted for each protein structure.

Test Set Construction

To evaluate the performance of the model, we used three different data sets (Table S2) from previous studies as test sets, similar to work done by Deng et al.¹⁵ Data set I consist of 62 calcium sites from 32 PDBs and was previously compiled and studied by Nayal and Di Cera.⁷ One of the protein structures in Data set I (PDB ID: 2MSB) was also used in our training set. Data set II from Liang et al.⁹ consist of 14 noncalcium-binding proteins and 92 calcium sites from 40 calcium-binding proteins. Four of the calcium-binding structures were repeated in Data set I (PDB IDs: 1OVA, 1SNC, 2POR, 4SBV), containing a total of eight calcium sites. Twelve of the calcium-binding protein structures were also used in our training set (PDB IDs: 1AXN, 1CLC, 1KIT, 1KUH, 1MHL, 1POC, 1SCM, 1SRA, 1TCO, 2AAA, 2SCP, 3DNI), containing a total of 33 calcium sites. Data set III consists of 60 calcium sites from 44 PDBs and was compiled and studied by Pidcock and Moore.²¹ Six of the protein structures (PDB IDs: 1KIT, 2FIB, 1MMQ, 1BJR, 1SRA, 1BF2) were also used in our training set, containing a total of nine calcium sites. Four of the calcium-binding structures in Data set III also appeared in Data set II (PDB IDs: 1CEL, 1ESL, 1KIT, 1SRA). The three data sets yielded a total of 154 unique calcium sites from 91 calcium-binding protein structures, excluding all duplicated structures (and their sites) from our training set. In reporting the performance metrics, we refer to this set of 154 calcium sites as the “Combined Data set”. A total of 788 nonsites were generated from the 91 calcium-binding protein structures in the Combined Data set, using the same method that generated the nonsites for the training set.

Additionally, alternative (noncalcium) ion test sets were similarly obtained by querying Uniprot for desired ion-binding sites and then clustering the results using BLASTClust. Using a threshold of 70% sequence similarity, we obtained 651 zinc sites, 349 magnesium sites, 59 copper sites, 14 chloride sites, and 19 potassium sites for the test sets.

FEATURE Microenvironments

The FEATURE software¹⁰ was used to characterize the microenvironment of a given point. Briefly, the microenvironment of the point is partitioned into six 1.25 Å-thick concentric shell; 80 physiochemical properties such as hydrophobicity, electrostatic and the number of protein atoms are evaluated within each of those six shells, ultimately returning a combined numeric vector of length 480 for the given point (6 shells × 80 properties/shell). All heteroatoms, such as water molecules, are ignored. All sites and nonsites were converted into their respective FEATURE vectors. FEATURE has been described in detail previously.^8,10,22

Calcium Model

A Naïve Bayesian classifier was built using the FEATURE software, with the FEATURE vectors corresponding to the calcium sites and nonsites used as the training data. The prior probability for calcium site classification was set at 0.01, and for each of the 480 properties in the vector, the range of values was divided into five bins (query values beyond the range obtained from the training data were assigned to the nearest bin), as per a previous version of the calcium model.⁸ For each property p, the conditional probability of a value v_p falling in bin b_p, given that the query was a site, is simply:

We then used Bayes’ Rule to calculate the posterior probability that v_p was drawn from the distribution of the site values rather than the nonsite values:

The reported FEATURE score of a model is the summation of the log-odds ratio across all 480 properties and is an indication of the likelihood that a given query is a site.

The full set of training data (314 calcium sites and 2735 nonsites) was used to build the calcium model. To determine the score cutoffs corresponding to the desired precision thresholds (95% and 99%) for the calcium model, we performed 10-fold cross-validation. Briefly, the full training data set was partitioned into 10 nonoverlapping, equal-sized subsets, and in each fold, a model was trained on nine subsets and tested on the left-out subset. The precision was collected over a range of cutoff values on each left-out subset. The lowest score at which both the mean and median precision (of the 10 models) reached the desired threshold was designated the score cutoff (Figure S1). The precision-recall curves for each of the 10 models were plotted, and the area under the curves (AUC) computed in order to detect the presence of anomalous data.

Score Function’s Sensitivity to Distance from Actual Site

In order to determine the sensitivity of the model’s scoring function to distance from actual sites, we studied the distribution of scores at various distances from the sites. A series of spherical grid shells were generated for each calcium site in our training data with 0.05 Å spacing (up to 5 Å), where ψ and φ angles were sampled at 22.5 degree increments. This yielded a total of 16 ψ angles ×16 φ angles × 100 shells = 25,600 grid points per calcium site. The set of all grid points from the various calcium sites were scored using the calcium model and then grouped together based on distance from the calcium sites. For a given distance, we computed the proportion of scores that were above the score cutoff corresponding to the model’s precision threshold, i.e., the fraction of points (at that distance from actual calcium sites) that would still have been classified as sites.

External Validation of Calcium Model

To evaluate the performance of the calcium model independently, we applied the calcium model on Data sets I–III and an alternative ions data set. For Data sets I–III and the Combined Data set, a true positive (TP) was defined as a calcium site that had a score above the determined score cutoff (based on the model’s precision threshold). Conversely, a calcium site that scored below the score cutoff was determined as a false negative (FN). A nonsite that scored above the score cutoff was determined as a false positive (FP) and a true negative (TN) otherwise. The precision and recall of the calcium model were calculated as

For the alternative ion test sets, a true negative (TN_ion) was defined as a point that scored below the score cutoff, and a false positive (FP_ion) was defined as a point that scored above the score cutoff. The specificity of the calcium model in each ion test set was calculated as

Calcium Site Prediction Algorithm

As a simulation of actual use scenario, we scanned across the structures from Data set I–III and scored the points in order to predict the location of calcium sites. A cubic grid with a spacing of 0.48 Å was constructed for each PDB structure, extending by 1 Å beyond the extreme Cartesian coordinates of the structure. The grid spacing was determined by the evaluating the score function’s sensitivity to distance from actual site. The grid points were converted into FEATURE vectors and then scored using the calcium model. We retained only the points that were above the score cutoff determined by the model’s precision threshold. The following was then done recursively to obtain aggregate numerous high scoring grid points into a more compact set of site predictions:

While (number of remaining points >0):

• (i)Take the top scoring point as an initial guess of the site’s position.
• (ii)Weigh all points within 3.5 Å of the initial guess by the exponential of their FEATURE score, and refine the site position by taking the weighted mean of those points.
• (iii)Return the refined position as a predicted site, and remove all points within 3.5 Å of the refined predicted site.

A true prediction (TPRED) is defined as a prediction that lies within 3.5 Å (similar to comparable work by Deng et al.¹⁵) from an actual calcium site, and a predicted site (PS) is defined as a calcium site with at least one prediction within 3.5 Å. Note that for site predictions, all annotated calcium sites in a structure are retained as actual sites since the scanning was done across the entire structure. The Combined Data set for site prediction thus contains 190 calcium sites.

The performance of the site prediction algorithm was determined by the site recall (SR), redundancy (RE), median relative rank (MRR), first rank percentage (FRP), and the median distances between TPRED and the actual calcium sites (MD). The site recall represents the proportion of true calcium sites that were detected by our method and is calculated as the proportion of calcium sites that had at least one prediction within 3.5 Å. The redundancy is the average number of predictions found within 3.5 Å in the PS.

Due to the design of the algorithm, each prediction is associated with a cluster of points within 3.5 Å, and in nearly all cases, the predictions are ordered by the magnitude of the highest score found within each respective cluster. This natural ranking of predicted sites lends itself to the notion of a relative rank, whereby the relative rank of a particular true prediction, going down the list of prediction in descending order, is the difference between the ranks of the previous true prediction and the current prediction. That is, if only the second and fifth predictions for a protein structure were found to be TPRED, the second and fifth predictions have relative ranks 2 and 3, respectively. Ideally, the median relative rank should be close to 1. We note that it is possible for a structure with multiple PS to have the respective predictions all ranked sequentially so that the relative rank for all except the first PS (the site with the highest absolute rank prediction in the structure) is 1 but with the highest-ranked TPRED having an absolute rank much greater than 1. If this pathological example was sufficiently common, the MRR would be 1 even though a large number of false positives would be made before the first TPRED is encountered. To account for this, we also report the FRP, which is the percentage of highest rank TPRED for a structure, out of all highest rank TPRED for structures in the data set, which has an absolute rank of 1.

To calculate the MD, we consider the distance between the PS and the highest-ranked prediction for that site. The MD is the median of all such distances across the data set.

Results

Characterization of Sites

We found that there were no protein atoms within 1.25 Å in all 283 calcium sites. The number of protein atoms within 5 Å of a site ranged from 10 to 50, with a median of around 30 protein atoms. The number of water molecules found in a resolved crystal structure depended on the crystallization techniques employed and was thus not a good physical property to generate matched nonsites. Nonetheless, we found that the sites generally had less than eight water molecules within 5 Å, with most sites having none or less than three water molecules.

Calcium Model’s Internal Evaluation

We initially trained a model using only 70% of the full training set (220 sites and 1914 nonsites), leaving the remaining 94 sites and 821 nonsites as the test set. We observed a clear separation in FEATURE scores between the test sites and nonsites and an area under precision-recall curve of 0.98 (Figure S2). The full model (hereafter referred to as the calcium model), which was trained on all 314 sites and 2735 nonsites, was used to perform the site predictions and also scoring of the validation data sets. The calcium model discriminates well between the sites and nonsites (Figure 1) in the training set. The 10 cross-validation models were also in good agreement with one another, with a mean area under the precision-recall curve (AUPRC) of 0.989 and a standard deviation of 0.01.

Figure 1.

(Left) Histogram of the FEATURE scores corresponding to the training set when the full calcium model was applied. The red bars correspond to the scores of the sites, while the blue bars correspond to the scores of nonsites. (Right) Precision-recall curves obtained by using a range of score cutoffs in each of the 10-fold CV test set. AUPRC is the area under the precision-recall curve. Note that while recall is a strictly increasing function with respect to decreasing score cutoff, precision is not.

The FEATURE score cutoffs for the calcium model, as determined by the 10-fold cross-validation (Figure S1), were 2.08 and 25.67 at the 95% and 99% precision thresholds, respectively. We refer to these two score cutoffs as “low” and “high”, respectively. The corresponding recalls estimated for those two precision levels were 96% and 88% (Figure 2).

Figure 2.

For each of the two score cutoffs, the corresponding precision and recall values in each of the 10-fold models is plotted. Triangular points (both upward- and downward-pointing) represent two circular points at that position of the same color. Top and right margins: Boxplots for the precision and recall of both score cutoffs are plotted using the corresponding colors. The diamond peg and line segment inside the box are the mean and median of the values, respectively. The whiskers extend 1.5 × interquartile-ranges beyond the first and third quartiles. Any points beyond the whiskers are represented by empty circles.

Among the 480 FEATURE properties, we find some trends that are well expected (Figure S3). Oxygen atoms are enriched in shells 2 and 6 (1.25–2.5 Å and 6.25–7.5 Å from sites, respectively), which is within the ligand distance (1.6–3.3 Å) previously reported by Nayal and Di Cera.⁷ Polar and charged residues that are known to ligate calcium, such as aspartic acid, asparagine, and glutamic acid, are also found to be enriched in those shells. The training calcium sites showed significantly lower hydrophobicity between shells 2 to 6 (1.25–7.5 Å from sites) than the nonsites, which concurs with the observations made by Yamashita et al.⁶

Calcium Model’s Performance on Test Sets

A generally high recall was obtained across the Data sets I–III and the Combined Data set, with a recall of 94% in the latter when the low score cutoff was used (Table 1). At that cutoff, the precision and specificity obtain on the Combined Data set was 98% and 99.6%, respectively. When the high score cutoff (corresponding to the model’s precision threshold of 99%) was used, the recall on the Combined Data set decreased to 84%, while the precision and specificity both attained a full 100%.

Table 1. Calcium Model’s Recall (Sensitivity) on Test Datasets.

		Recall
		Data set I (N = 62)	Data set II (N = 92)	Data set III (N = 60)	Combined Data set (N = 154)
model’s precision threshold	99%	0.90	0.84	0.75	0.84
	95%	0.95	0.95	0.88	0.94

FEATURE score cutoffs were determined by the model’s precision threshold. N is the number of calcium sites reported in the respective data sets.

The model also displayed generally high specificity when applied to the alternative ion test sets, with the exception of Mg²⁺ and K⁺ (Table 2). Notably, the specificity reported on the K⁺ data set improves sharply to 95% when the model’s precision threshold was increased from 95% to 99%.

Table 2. Calcium Model’s Specificity in Alternative Ions Datasets.

		Specificity
		Cl– (N = 14)	Cu2+ (N = 59)	Mg2+ (N = 349)	K+ (N = 19)	Zn2+ (N = 651)
model’s precision threshold	99%	1.00	1.00	0.54	0.95	0.95
	95%	1.00	1.00	0.36	0.58	0.84

FEATURE score cutoffs were determined by the precision threshold. N is the number of ion sites in the data set.

Calcium Model Scores Are Sensitive to Distance from Calcium Sites

After establishing the performance of the calcium model in classifying sites and nonsites, we evaluated the distribution of FEATURE scores with respect to distance from documented calcium sites. As shown in Figure 3, the proportion of points classified as a site decreases sharply with distance from the actual calcium sites, exhibiting a logistic behavior. The greatest decrease in the site classification occurs after 1 Å from the actual calcium site, and at 2 Å away, less than 50% of the points were still classified as sites. At a distance of 0.414 Å from a calcium site, a point has a 95% chance of being classified as a site under the score cutoff for 99% precision. This is the maximum distance that a grid point can be from an actual site in order to still pick up the site information reliably. We therefore determined the appropriate grid spacing for the scanning box to be (4 × 0.414²/3)^1/2 = 0.48 Å.

Figure 3.

(Left) Proportion of points classified as sites, at various distances from actual calcium sites for 95% and 99% precision cutoffs. (Right) Zoom-in image of the brown box in the left plot.

Calcium Site Prediction Algorithm

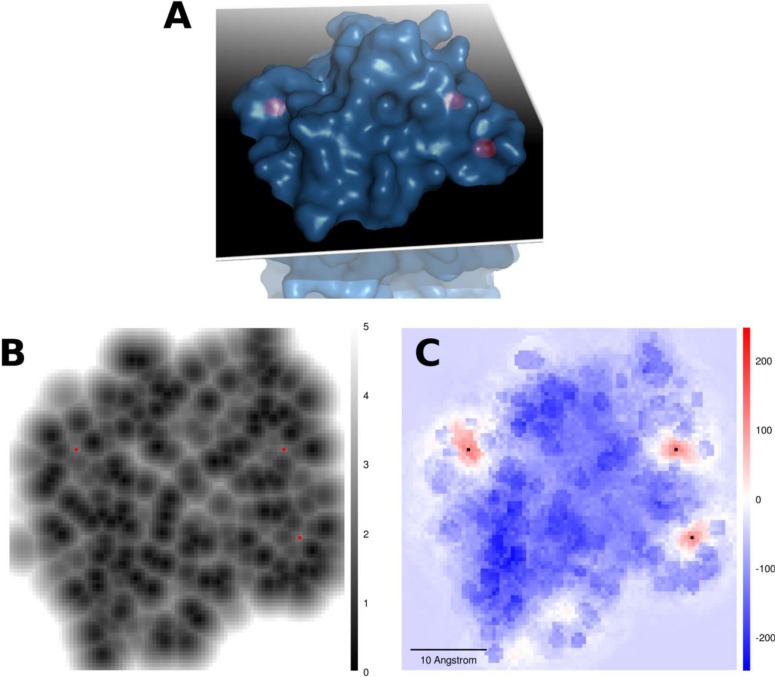
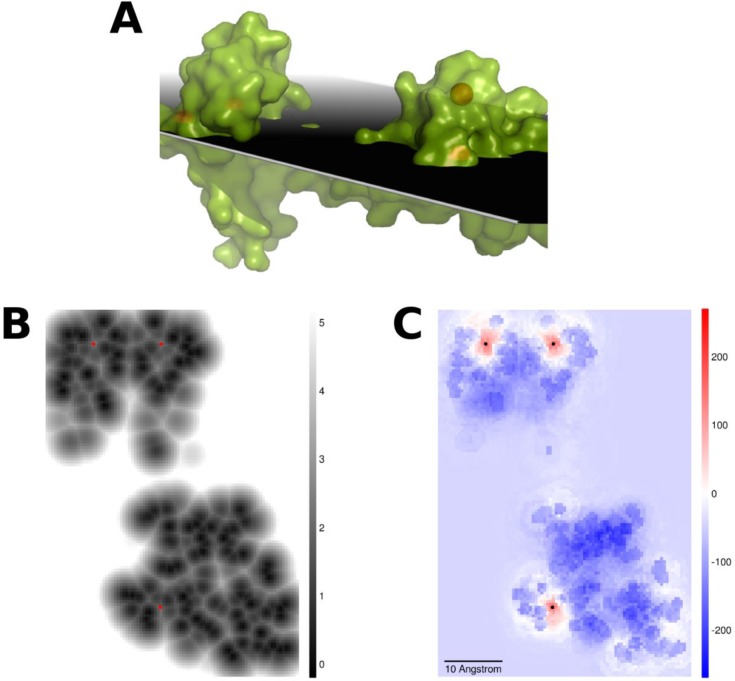
Our site prediction algorithm reports a very high site recall of more than 90%, even when the high score cutoff (model’s 99% precision threshold) was used for the calcium model (Table 3). The algorithm has a slightly better site recall when the precision threshold is set lower at 95%. The median relative rank across all three data sets is 1, and approximately 80% of the highest ranked TPRED for each structure in the data sets was also rank 1 (Table 4). An average of less than two predictions was made for each site (Table 5), and the median distance between the best prediction and the site was less than 0.5 Å in the Combined Data set (Table 6). Grid points that were more than 4 Å from protein atoms had a generally uniform negative score, and points that were in steric clashes with protein atoms scored even more negatively (Figures 4 and 5).

Table 3. Site Recall (SR) Using the Calcium Site Prediction Algorithm.

		Site Recall (SR)
		Data set I (N = 66)	Data set II (N = 92)	Data set III (N = 94)	Combined Data set (N = 190)
model’s precision threshold	99%	0.954	0.902	0.904	0.932
	95%	0.984	0.978	0.968	0.979

FEATURE score cutoffs were determined by the precision threshold. N here is the total number of calcium ions annotated in the crystal structures from the data set.

Table 4. Median Relative Rank (MRR) and First Rank Percentage (FRP).

		MRR (FRP)
		Data set I (N = 66)	Data set II (N = 92)	Data set III (N = 94)	Combined Data set (N = 190)
model’s precision threshold	99%	1 (90.0)	1 (76.3)	1 (78.6)	1 (80.5)
	95%	1 (87.1)	1 (74.4)	1 (75.0)	1 (77.8)

N here is the total number of calcium ions annotated in the crystal structures from the data set. Each prediction has a relative rank, and the MRR is the median of these relative ranks across the data set. The FRP calculates the percentage of predictions in the data set with relative rank 1.

Table 5. Site Prediction Redundancy (RE).

		Site Prediction Redundancy (RE)
		Data set I (N = 66)	Data set II (N = 92)	Data set III (N = 94)	Combined Data set (N = 190)
model’s precision threshold	99%	1.63	1.40	1.26	1.41
	95%	2.10	1.91	1.72	1.89

N here is the total number of calcium ions annotated in the crystal structures from the data set. The RE is the ratio of true predictions to the number of predicted sites.

Table 6. Median Distance (MD) of Predictions from Actual Sites.

		Median Distance (Å)
		Data set I (N = 66)	Data set II (N = 92)	Data set III (N = 94)	Combined Data set (N = 190)
model’s precision threshold	99%	0.458	0.573	0.446	0.476
	95%	0.459	0.631	0.487	0.495

N here is the total number of calcium ions annotated in the crystal structures from the data set.

Figure 4.

A sectional-plane through three calcium sites in a sarcoplasmic calcium-binding protein from Nereis diversicolor (PDB ID: 2SCP). The three calcium sites are located in (B) and (C) with red and black dots, respectively. (A) Structural view of 2SCP and the plane. (B) Minimum distance (in Å) to protein atoms at each grid point in the plane. All points with no protein atoms within 5 Å are colored white. (C) FEATURE scores for the corresponding grid points when our model is applied.

Figure 5.

Sectional-plane through three calcium sites in calmodulin from Rattus rattus (PDB ID: 3CLN). Three calcium sites are located in (B) and (C) with red and black dots, respectively. (A) Structural view of 3CLN and the plane. (B) Minimum distance (in Å) to protein atoms at each grid point in the plane. All points with no protein atoms within 5 Å are colored white. (C) FEATURE scores for the corresponding grid points when our model is applied.

Discussion

In this work, we built a FEATURE-based calcium model for scoring points in 3D structures and also developed an algorithm that utilizes the model for automated calcium site prediction in protein structures. We evaluated the FEATURE-based calcium model on various test sets and showed that the model exhibited high recall for calcium ions across all Data sets I–III, with a recall of 94% and 84% on the Combined Data set when the low and high score cutoff were used, respectively. This is a significant improvement from the 75% recall obtained when Wei’s calcium model⁸ was applied to the same data set. Using random points close to the protein surface as nonsites for evaluation, the model achieved a precision of 98% and 100% at the low and high score cutoffs, respectively. The improved performance is expected given that Naïve Bayes models tend to perform better with increased training set size, and our current training set is approximately 20-fold larger than the one used in Wei’s FEATURE calcium model.

In order to determine if our calcium model was sensitive to the choice of sequence similarity threshold used to define the training set, we also built an additional model with identical methods, but using 30% sequence similarity threshold to create the training sets. We found that this “smaller” model had comparable performance with the model used in this paper (Figure S4). Consequently, we chose the model with the larger training set as the calcium model.

Although the nonsites in the training set were derived from protein surface points, the model was able to correctly reject most other cationic and anionic sites, displaying a high level of specificity (Table 2). The exceptions to this are the K⁺ and Mg²⁺ data sets, for which the model performs poorly in recognizing them as nonsites. It is known that a number of calcium sites can accommodate potassium, sodium, and magnesium ions,²³ and many metal-binding sites are known to bind to multiple metal ions.²⁴ In particular, magnesium ions have been previously reported to bind to the EF-hand motif, which underlies many calcium-binding sites.²⁵ In fact, crystallographers often take advantage of the high affinity of calcium sites for magnesium ions by using magnesium ions during the crystallization process. The difficulty in discriminating calcium and magnesium sites has also been documented by other groups. In a recent attempt by Wei et al. to discriminate different metal-binding sites computationally,²⁶ a low AUC score of close to 0.5 was obtained when discriminating the two different binding sites. Nonetheless, we show that when a higher precision threshold for the model was used the specificity of our model increases across the alternative ion data sets and significantly improves the specificity in the K⁺ data set from 58% to a respectable 95%.

Although sodium and calcium ions have very similar ionic radii, the coordination spheres of both ions are quite different given that the former is an alkaline earth metal, whereas the latter is an alkali metal. The similarity in electron density of sodium ions and water molecules often result in sodium ions being misassigned as water molecules in crystal structures.^27,28 Additionally, rubidium ions are also often used for protein phasing in place of sodium, making it difficult to find well-documented sodium sites in the PDB repository. We attempted to construct a sodium ion test set using the same criteria for the other ions but found that the test set was too small (only six distinct sites) to make any meaningful discussion on the absolute specificity. However, we did observe that the specificity improved from 16.7% to 66.7% when the higher precision threshold for the model was used, consistent with the trend reported on the other ions.

We also report an algorithm to predict calcium sites in a query protein structure using our FEATURE-based calcium model. Although previous work by our group⁸ had also shown good performance in classifying points as sites and nonsites, direct application of the model to actual site prediction had not been attempted on a large scale. This is because of the difficulty in transforming high-scoring regions reliably to exact site predictions, given that a significant region around each site may all be classified as sites by the FEATURE model. To reduce the difficulty of the problem, we first ensured that the distribution of FEATURE scores decayed with increasing distance from the calcium site. In our evaluation, we found that the FEATURE scores obtained by our model do indeed show a complete decorrelation with the calcium site when separated by more than 5 Å and that the greatest drop in signal occurred at 1 to 3 Å from the calcium site. We showed that the relationship is similar to a logistic curve and that points sampled within 1 Å of a calcium site would almost always be classified as a true positive (Figure 3). This makes our calcium model well-suited for subsequent incorporation into exact site prediction algorithms. Using the curve obtained in Figure 3, we also determined that the maximum grid spacing required for the 95% and 99% precision thresholds were 0.94 and 0.48 Å, respectively. Although the 95% precision threshold allowed for the larger grid spacing and was thus less computationally expensive to scan across a protein, we found that this resulted in a slightly lower site recall compared to that obtained using the finer grid size of 0.48 Å. In particular, we found that the finer grid size combined with the lower score cutoff corresponding to the 95% precision threshold resulted in the highest site recall but also with the most number of predictions per structure. Many of these predictions are likely false positives, given their proximity to each other. The combination of finer grid size and higher score cutoff corresponding to the 99% precision threshold provided a balance, reducing the site recall by around 5–8% while also reducing the number of predictions made per structure. In this paper, we report the results using both score cutoffs on only the finer grid size.

Many groups have suggested various methods to reduce the redundancy of predictions. Deng et al. employed a merging algorithm that builds on properties of their geometry-based approach to calcium site prediction.¹⁵ Nayal and Di Cera⁷ proposed a more general, iterative method by ranking the predictions by valences and taking only the top rank prediction. Each time a prediction was accepted, all predictions within 3.5 Å were removed, and the process was continued until no predictions remained. We adapted this algorithm by refining the predicted site position at each step using the weighted means of all predictions within 3.5 Å of the top rank prediction. We found that the exponential of the FEATURE scores as weights reduced the noise in the data and led to an overall refinement in the predicted site location. Our algorithm outputs a reduced list of predictions that were naturally ranked by the highest FEATURE score within each prediction’s cluster. We demonstrated that this algorithm can be used to accurately predict calcium sites with root-mean squared distances (RMSD) of less than 1 Å. In particular, we observed a high site recall (using a distance cutoff of 3.5 Å) of more than 90% across all the data sets with our algorithm and with nearly four-fifths of the highest ranked TPRED of each structure corresponding to an actual calcium site. In at least eight of the structures with two or more calcium sites (PDB IDs: 1TF4, 2AMG, 3CLN, 2TAA, 2TEP, 1JS4, 1CLX and 1SAC), we observed that not only were all sites predicted by our algorithm, but the relative rank was also 1 for all the predictions. Notably, the median relative rank is 1 for all the data sets, and the prediction redundancy was less than 2, suggesting that if a priori knowledge of the number of calcium sites in a structure (e.g., via stoichiometry) was used to determine the number of top predictions to retain, the precision of our site prediction algorithm would be close to 100%. We also found that our predictions were extremely close to the sites themselves, with the median distance being less than 0.5 Å. It is important to note that these results were obtained using a much stricter criterion for predicted sites (PS) compared to previous work from our group. In particular, we now define a site as PS if and only if there is a prediction within 3.5 Å, compared to the 6 Å used by Liang et al.⁹ and 7 Å used by Wei and Altman.⁸ If we had used the 7 Å criteria in this work, our site recall would increase by 1.5–3% across the data sets.

By considering a rich variety of physiochemical properties, the calcium model also shows better sensitivity than some of the previously published models used for calcium site prediction. The GG algorithm¹⁵ by Deng et al. reported a site recall of 91% and 87% for Data sets II and III, respectively (using a distance cutoff of 3.5 Å), while our algorithm reports a site recall of 90.2% and 90.4% for those two data sets, respectively, at the precision threshold of 99%. When the lower precision threshold of 95% was used, our model reports a site recall of 97.8% and 96.8%, respectively. In either case, our algorithm shows comparable, if not better, recall than the GG algorithm on those data sets. Deng et al.¹⁵ noted that the GG algorithm had difficulty identifying calcium sites with abnormal Ca–O distances, and identified six structures (PDB IDs: 1OVA, 1CEL, 1DJX, 1SCM, 1BJR and 1AG9) in which the GG algorithm failed to detect the presence of sites. Our algorithm was not able to identify sites for 1OVA as well but performed with varying levels of success for the rest. For 1CEL, a prediction for the calcium site was made within 1.29 Å but had a large relative rank of 18. For 1DJX, all four calcium sites were predicted with RMSD of less than 1 Å and with relative ranks 3, 4, 4, and 8. Our algorithm performed excellently on 1SCM, with predictions for both sites having relative rank 1 and a low RMSD of around 1 Å. The two calcium sites in 1BJR were predicted by our algorithm at the 95% precision threshold but not at the 99% precision threshold due to the low FEATURE scores of the sites themselves. The calcium site of 1AG9 (Ca350) that Deng et al.¹⁵ failed to predict was also not predicted by our algorithm due to the ion being chelated by nonprotein oxygen atoms from the cofactor BTB (bis-2-hydroxy-imino-tris-hydroxymethylmethane). It is worth pointing out here that the FEATURE software ignores all heteroatoms in structures, making this a potential weakness in detecting sites that depend heavily on nonprotein ligands. Although the GG algorithm also ignores oxygen from water molecules, it retains information from other chelating ligands. In the particular case of 1AG9, however, both algorithms were unable to recover the calcium site.

We also report a slightly higher site recall (95.4% and 98.4%) on Data set I as compared to the 95% reported by the GG algorithm and the 93% reported by Nayal and Di Cera’s method⁷. In a few cases, the ranks of our predictions were also higher than those from Nayal’s algorithm. For instance, the documented calcium ion in Con A (PDB ID: 3CNA, estimated valence 1.41) was detected by Nayal’s method as the 67th rank prediction, with an RMSD of 2 Å. Our method returned a prediction within 0.44 Å of the site as our first prediction for the structure (using the 99% precision cutoff). Similarly, the calcium ion in Taka amylase A (PDB ID: 2TAA, estimated valence 1.40) was detected by Nayal’s method in the 61st ranked prediction, with an RMSD of 3.2 Å. Our method returned a prediction within 1.95 Å of the site as our sixth prediction for the structure (using the 99% precision cutoff). In general, we observed that the performance of Nayal’s method diminishes when the estimated valence of the calcium site is close to or less than the threshold of 1.4.

Nonetheless, our site prediction algorithm suffers the same pitfalls as all scoring-function based models do; if the calcium site itself does not score above the calcium model’s score cutoff, the algorithm typically fails to correctly predict the presence of the site. For instance, the calcium site in tobacco mosaic virus protein (PDB ID: 2TMV, estimated valence 1.70) was recovered by Nayal’s method, but not our model, which had assigned the site a low FEATURE score of −3.90. Analysis of the calcium site in 2TMV reveals very different FEATURE properties from the other calcium-binding sites in the Combined Data set (Figure S5). In particular, the site in 2TMV was lacking in some features that were enriched in the calcium model for calcium sites and was instead enriched for other features that were expected to be diminished. Additionally, the binding of calcium to the viral protein is enabled by the chelation of RNA bases, which are not incorporated into the default FEATURE properties as previously noted. Similarly, the second calcium site in flavodoxin (PDB ID: 1AG9, A350) from Data set III is chelated by BTB (2-[bis(2-hydroxyl-ethyl)-amino]-2-hydoxymethylpropane-1,3-diol) and at least three water molecules, all of which were not used in the FEATURE vector. As a result, the site had a negative score and was not recovered by our method. We note, however, that the generally high recall of our calcium model suggests that such occurrences are not a major problem.

While many of the methods currently available for calcium site prediction are often rule-based and dependent on properties such as the presence of glutamate or aspartate or sequence similarities, these methods immediately preclude the possibility of discovering novel calcium sites that do not resemble known calcium sites. A statistical-based method like the one used in our model relaxes the conditions for classification and may be more suitable for evaluating engineered or newly discovered proteins.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jcim.5b00367.

• The FEATURE calcium model file and the R script used to implement the algorithm is available on http://simtk.org/home/feature. Table S1: Calcium sites used for training model. Table S2: Calcium sites in Data set I, II, and III. Figure S1: Precision thresholds from cross-validation. Figure S2: Performance metrics of initial model 17. Figure S3: Visualization of model’s properties. Figure S4: Performance of model at 30% sequence similarity. Figure S5: Composite graphs of 2TMV properties. (PDF)

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

This work is funded by LM05652 and GM102365. W.Z. is supported by the National Science Scholarship from A*STAR, Singapore.

The authors declare no competing financial interest.