Mid-Space-Independent Symmetric Data Term for Pairwise Deformable Image Registration

Abstract

Aligning a pair of images in a mid-space is a common approach to ensuring that deformable image registration is symmetric – that it does not depend on the arbitrary ordering of the input images. The results are, however, generally dependent on the choice of the mid-space. In particular, the set of possible solutions is typically affected by the constraints that are enforced on the two transformations (that deform the two images), which are to prevent the mid-space from drifting too far from the native image spaces. The use of an implicit atlas has been proposed to define the mid-space for pairwise registration. In this work, we show that by aligning the atlas to each image in the native image space, implicit-atlas-based pairwise registration can be made independent of the mid-space, thereby eliminating the need for anti-drift constraints. We derive a new symmetric cost function that only depends on a single transformation morphing one image to the other, and validate it through diffeomorphic registration experiments on brain magnetic resonance images.

1 Introduction

Image registration – i.e., computation of a set of dense spatial correspondences among images – is a central step in most population and longitudinal imaging studies. Since linear transformation is usually not sufficient to account for cross-subject variation and temporal changes in the anatomy, deformable image registration often becomes a necessary part of the analysis pipeline. In pairwise deformable registration, the choice of the reference space in which the two images are compared affects the registration, making the resulting deformation field dependent on this choice. When the native space of one of the input images (say, the first image) is chosen as the reference, the registration becomes asymmetric, meaning that reversing the order of the input images will produce different spatial correspondences [1-11]. Pairwise registration has been proposed to be symmetrized by minimizing the average of two cost functions, each using one input image as the reference space [1-4], yet integrating the mismatch measure non-uniformly in the native space of the interpolated image [11].

In a different approach to achieve symmetry, both images are deformed and compared in a mid-space, thereby making registration invariant with respect to the ordering of the images [5-10]. Such approaches essentially minimize their cost functions with respect to two transformations T₁ and T₂ that take the two input images to the mid-space. However, without additional constraints, this increases the degrees of freedom of the problem twofold, compared to the end result of pairwise registration that is the one transformation, $T=T_2\circ T_1^{-1}$, taking the second input image to the first. Furthermore, if the images are compared in the mid-space (that depends on T₁ and T₂), the optimization algorithm is given the liberty to update the mid-space so as to decrease the cost function without necessarily changing the final result T. For example, the algorithm can shrink the regions with mismatching image intensities to make the deformed images look more similar in the mid-space, without necessarily making them more similar in the two native spaces. To alleviate these issues, additional constraints are used to keep the mid-space “in between” the native spaces of the two images. These anti-drift constraints, which are different from those regularizing the transformations, define the mid-space. They typically either restrict the space of possible T₁ and T₂ (resulting in fewer degrees of freedom), or penalize those values of T₁ and T₂ that move the mid-space away from the native spaces. The most common such constraints, proposed in the mid-space registration and atlas construction literature, are restrictions on T₁ and T₂ to have opposite displacement [7, 8, 12-14] or velocity [9, 10, 15] fields. In large deformation models, geodesic averaging of the deformations has also been proposed, which preserves the properties of the transformations [5, 6, 16]. The choice of the anti-drift constraints may bias the registration algorithm towards favoring a particular set of transformations, thereby affecting the resulting T.

Unbiased atlas construction techniques, when applied to a pair of images, can constitute mid-space pairwise registration, since the images are both deformed to the atlas space (i.e., the mid-space) [10, 16, 17]. In such a case, given that the desired output of pairwise image registration is the deformation field, but not the auxiliary atlas, one can substitute the atlas in the cost function with an analytical expression of the two deformed images, leading to an implicit-atlas cost function that is minimized with respect to the deformations. To that end, it was initially proposed to compare the deformed images to the atlas in the abstract mid-space [16]. A better justified generative model, however, progresses from the atlas to the images and compares the deformed atlas to the images (i.e., in the native image spaces) [18, 19], computing the atlas as a weighted average of the images [18]. Taking advantage of this native-space atlas construction resolves the issue of susceptibility to shrinkage-type problems, leading to a proper implicit-atlas cost function for mid-space pairwise registration [10]. Nevertheless, the registration still remains a function of two transformations taking the images to a mathematically defined mid-space.

In this work, we point out for the first time the key fact that implicit-atlas pairwise registration is inherently independent of the mid-space. We show that the cost function only depends on the overall image-to-image transformation T, implying that the individual image-to-atlas transformations T₁ and T₂ are redundant and unnecessary to keep, and that anti-drift constraints are indeed not needed. We derive a new cost function that, in contrast to the existing mid-space approaches, can be minimized directly with respect to T, with no anti-drift constraints. The proposed cost function is general and can be used with any transformation model, such as the displacement and velocity fields.

We describe our methodology in Section 2, experimentally evaluate our approach on brain magnetic resonance images in Section 3, and conclude the paper in Section 4.

2 Methods

2.1 Mid-Space Approach to Registration Symmetry

Let $I_1,I_2:\Omega \to \mathbb{R}$ be the two d -dimensional input images to be registered, where $\Omega \subseteq {\mathbb{R}}^d$. We want to compute the regular transformation T: Ω → Ω that deforms I₂ so as to make I₁ and I₂ ○ T most similar to each other; a task that is often done by minimizing a cost function with respect to T. The data term of the common sum of squared differences (SSD) cost function can be formulated for instance as ${\Vert I_1-I_2\circ T\Vert }_2^2$ or ${\Vert I_1\circ T^{-1}-I_2\Vert }_2^2$. These two forms are not equivalent though, because the transformed image – which is different in each case – is integrated non-uniformly [1-4, 11], resulting in the registration asymmetry.

In a popular approach to derive a symmetric cost function, both images are deformed to a mid-space [5-10]. Consequently, these cost functions depend on two transformations, T₁, T₂: Ω → Ω, deforming images I₁ and I₂, respectively. The deformed images are then often compared in the mid-space through a cost function such as ${\Vert I_1\circ T_1-I_2\circ T_2\Vert }_2^2$, and the output is eventually computed as $T=T_2\circ T_1^{-1}$. The mid-space cost function is by definition invariant with respect to the ordering of the images.

With no additional constraints, the dimension of the mid-space registration problem (solving for T₁ and T₂) is twice as big as the standard asymmetric problem (solving for T). Also, the mid-space can drift arbitrarily far away from the native spaces of the images due to large changes in T₁ and T₂, for instance through combination with a transformation h, as T₁ ○ h and T₂ ○ h, which decreases the mid-space cost function without changing the final $T=T_2\circ h\circ h^{-1}\circ T_1^{-1}=T_2\circ T_1^{-1}$. An example of this phenomenon is the situation where the optimization algorithm modifies T₁ and T₂ in order to shrink the regions where the two deformed images do not match, resulting in a decrease in the mid-space cost function, without necessarily changing the end result, T. To avoid these issues, additional constraints are often employed to keep the mid-space “in between” the native spaces. For instance, the two transformations may be forced to have opposite-sign displacement fields, as T₁(x) = x + u(x) and T₂(x) = x – u(x), resulting in the constraint T₁(x) + T₂(x) = 2x (or similarly $T_1^{-1}\left(x\right)+T_2^{-1}\left(x\right)=2x$) [7, 8, 12-14]. This reduces the degrees of freedom and to some extent prevents the mid-space drift, however, at the expense of limiting our ability to model all possible transformations T. An extreme example of this limitation would be the 2D case with the true transformation T being a 180° rotation about the origin, i.e. T(x) = –x, where no T₁ and T₂ will simultaneously satisfy both T₁(x) + T₂(x) = 2x and T₂(x) = T ○ T₁(x). For large deformations, opposite-sign velocity fields [9, 10, 15] and geodesic averaging are used to preserve the properties of the transformations [5, 6, 16]. Since there is no unique way to define the mid-space, the registration results can depend on the choice of the constraints imposed on T₁ and T₂.

Mid-space pairwise registration can also be performed by constructing an unbiased atlas from two images [10, 16, 17]. In atlas construction, the observed images are assumed to be instances generated from an atlas image with some geometrical and intensity variation. Therefore, the problem boils down to finding an atlas, $A:\Omega \to \mathbb{R}$, and regular transformations $T_1^{-1}$ and $T_2^{-1}$ that take the atlas from the mid-space to the native spaces of the two images, in such a way that the deformed versions of the atlas resemble the observed images. Using the SSD metric, the data term for such an optimization is the sum of two (asymmetric [18, 19]) subject-atlas distance terms, as in:¹

$${\widehat{T}}_1,{\widehat{T}}_2,\widehat{A}=\underset{T_1,T_2,A}{\mathrm{argmin}}\left[{\int }_{\Omega }{(I_1\left(x\right)-A\circ T_1^{-1}\left(x\right))}^2\mathrm{d}x+{\int }_{\Omega }{(I_2\left(z\right)-A\circ T_2^{-1}\left(z\right))}^2\mathrm{d}z\right].$$ (1)

Comparing the images to the atlas in the physically meaningful native image spaces complies with the generative model assumption that the image is generated as a deformed version of the atlas (not vice versa), and that the Gaussian noise is added to the deformed atlas [18, 19]. The changes of variables x = T₁(y) and z = T₂(y) leads to:

$$\underset{T_1,T_2,A}{\mathrm{argmin}}{\int }_{\Omega }[{(I_1\circ T_1\left(y\right)-A\left(y\right))}^2{J}_1\left(y\right)+{(I_2\circ T_2\left(y\right)-A\left(y\right))}^2{J}_2\left(y\right)]\mathrm{d}y,$$ (2)

where J₁(y) ≔ det ∂T₁(y) and J₂(y) ≔ det ∂T₂(y) are the Jacobian determinants of the two transformations. The Â(y) minimizing the cost function is derived as [18]:

$$\widehat{A}\left(y\right)=\frac{J_1\left(y\right)I_1\circ T_1\left(y\right)+J_2\left(y\right)I_2\circ T_2\left(y\right)}{J_1\left(y\right)+J_2\left(y\right)}.$$ (3)

In an explicit-atlas scheme, the transformations and the atlas can be iteratively computed from Eq. (1) and Eq. (3) [17]. However, the atlas can indeed be eliminated in Eq. (2) by substituting A(y) with Â(y), leading to an implicit-atlas data term [10]:

$${\widehat{T}}_1,{\widehat{T}}_2=\underset{T_1,T_2}{\mathrm{argmin}}{\int }_{\Omega }\frac{{(I_1\circ T_1\left(y\right)-I_2\circ T_2\left(y\right))}^2}{J_1^{-1}\left(y\right)+J_2^{-1}\left(y\right)}\mathrm{d}y.$$ (4)

2.2 Independence from the Mid-Space

Equation (4) is an optimization over both T₁ and T₂, which define the mid-space. Even so, further simplification reveals that the two transformations are redundant. The change of variables $y=T_1^{-1}\left(x\right)$, with $\mathrm{d}y=\mathrm{d}x∕J_1\circ T_1^{-1}\left(x\right)$, results in:

$${\widehat{T}}_1,{\widehat{T}}_2=\underset{T_1,T_2}{\mathrm{argmin}}{\int }_{\Omega }\frac{{(I_1\left(x\right)-I_2\circ T_2\circ T_1^{-1}\left(x\right))}^2}{1+\frac{J_1\circ T_1^{-1}\left(x\right)}{J_2\circ T_1^{-1}\left(x\right)}}\mathrm{d}x.$$ (5)

Recall that the output transformation T is computed as $T\left(x\right)=T_2\circ T_1^{-1}\left(x\right)$, the Jacobian determinant of which is $J\left(x\right)≔\det \partial T\left(x\right)=J_2\circ T_1^{-1}\left(x\right)∕J_1\circ T_1^{-1}\left(x\right)$. It now becomes clear that the above integral is, remarkably, only a function of T, and that the optimization can be written independently of the individual T₁ and T₂, as:

$$\begin{array}{c}\hfill \widehat{T}=\underset{T}{\mathrm{argmin}}D(I_1,I_2,T),\hfill \\ \hfill D(I_1,I_2,T)≔{\int }_{\Omega }{(I_1\left(x\right)-I_2\circ T\left(x\right))}^2\frac{J\left(x\right)}{1+J\left(x\right)}\mathrm{d}x.\hfill \end{array}$$ (6)

Thus, we can minimize this cost-function data term directly with respect to T, as opposed to the previous methods that optimize their cost functions with respect to both T₁ and T₂, conditioned to constraints that prevent the mid-space drift.

With D(I₁, I₂, T) being independent of T₁ and T₂, the mid-space disappears, eliminating the problem of the mid-space drift as well. We do not need to enforce any anti-drift constraints anymore, hence not biasing the space of possible transformations T by the particular choice of such constraints. This is all while keeping the degrees of freedom of the optimization half of that of the unconstrained problem of solving for both T₁ and T₂. In addition, no transformation needs to be inverted to compute T, as opposed to most existing mid-space approaches that need to invert T₁ to compute $T=T_2\circ T_1^{-1}$. These advantages are especially valuable for displacement-field parameterized transformations, inverting which is a difficult and inexact task. Lastly, one can verify the expected symmetry of the proposed data term, i.e. D(I₁, I₂, T) = D(I₂, I₁, T^–1). Note that this symmetry holds only in the continuous domain. In the discrete case, where one image is resampled and the other is not, discretization artifacts produce a bias [19-21].

Equation (6) might seem like a non-uniform integral in the native space of I₁. However, this cost function originates from Eq. (1), which is the sum of two integrals taken uniformly in the native spaces of images, and non-uniformly only in the abstract mid-space. Therefore, the pitfalls associated with non-uniform integration in native spaces [11] are not expected to arise. We subsequently showed that Eq. (1) can be written independently of not only the atlas (Eq. (4) [10]), but also the mid-space itself (Eq. (6)).

2.3 Implementation

We implement the proposed registration method via the diffeomorphic demons scheme [22], and minimize D(I₁, I₂, T) of Eq. (6) by gradient descent with line search. Similar to the demons algorithm, T is regularized by Gaussian blurring between each two descent iterations. We use a compositive scheme and update T by composing it with a transformation S, chosen to be the exponential of the update field. At each iteration, we fix T and J, and compute the variation of D(I₁, I₂, T ○ S) with respect to S, with S currently assumed to be the identity transformation. Then, to preserve the diffeomorphism, we initialize $S\left(x\right)=x-2^{-M}\Delta {\frac{\delta D}{\delta S}\mid }_{S=\mathbb{I}}$ (for a large enough M), with Δ the step size, and compose it with itself (S ← S ○ S) M times, before updating T as T ← T ○ S [22]. The variation is computed as follows (derivations omitted):

$${\phantom{\mid }\frac{\delta }{\delta S}D(I_1,I_2,T\circ S)\mid }_{S=\mathbb{I}}=-\frac{2(I_1-I_2\circ T)J}{{(1+J)}^2}(\nabla I_1+J\nabla (I_2\circ T))+\frac{2{(I_1-I_2\circ T)}^{2}J}{{(1+J)}^3}\sum _{k=1}^d{H}^k.{\left(C_{k,:}\right)}^{\mathrm{T}},$$ (7)

where C is the cofactor matrix of ∂T with C_k,: its k^th row, and H^k is the Hessian matrix of the k^th element of T. The notation (x) has been dropped for brevity. The last term of Eq. (7) involves the Hessian tensor of the deformation field, which can introduce large discretization error. In fact, the imprecision due to the discretization of the second derivative may outweigh the accuracy that this term is expected to bring about. In our experiments, ignoring this second-order term improved the optimization of Eq. (6).

3 Experimental Results

We tested the proposed deformable registration method on 2D slices of brain magnetic resonance images, using our in-house Matlab implementation of the diffeomorphic demons with the compositive scheme [22] (see Section 2.3). We compared our symmetric mid-space-independent registration method with the popular symmetrization approach that minimizes the average of the forward and backward cost functions [1-4], simplified in the form of ${\int }_{\Omega }{(I_1\left(x\right)-I_2\circ T\left(x\right))}^2\frac{1+J\left(x\right)}{2}\mathrm{d}x$, with –(I₁ – I₂ ○ T)(J∇I₁ + ∇(I₂ ○ T)) being its compositive gradient. Each registration experiment consisted of 2000 gradient descent iterations, and was repeated with the demons regularization parameter taking a range of 22 different values.

3.1 Retrieval of Synthetic Deformations

In the first set of experiments, we compared the two algorithms on the mid-sagittal planes of 20 brain images taken from the publicly available OASIS database [23], which were pre-processed in FreeSurfer [24]. From each intensity-normalized and resampled volume (1-mm³ isotropic voxel), the sagittal slice located four voxels to the right of the mid-sagittal plane was extracted, and resampled to the size 128×128 (Figure 1a). For each subject, two random deformation fields $T_1^{\mathrm{synth}}$ and $T_2^{\mathrm{synth}}$ were synthesized, spatially low-pass filtered, and applied to the sagittal slice, I, to produce two synthetically deformed images, $I_1=I\circ T_1^{\mathrm{synth}}$ and $I_2=I\circ T_2^{\mathrm{synth}}$ (Figure 1b,c), which were then registered with each other using both methods (Figure 1d,e). Ideally, we would expect to retrieve a transformation T satisfying $T_1^{\mathrm{synth}}\approx T_2^{\mathrm{synth}}\circ T$. Accordingly, we computed the error ${\int }_{\Omega }{\Vert T_1^{\mathrm{synth}}\left(x\right)-T_2^{\mathrm{synth}}\circ T\left(x\right)\Vert }_2^2\mathrm{d}x$, and for each subject and method, chose the best result (with the smallest error) across the experiments with different demons regularization values. Our mid-space-independent registration resulted in a lower error than the symmetrization method did in 14 out of the 20 subjects. On average, the error was 0.2% ± (SE) 0.2% lower for our method. We also ran the experiments in the reverse direction, and computed the inverse-consistency error, ${\int }_{\Omega }{\Vert T_{\text{forward}}\circ T_{\text{backward}}\left(x\right)-x\Vert }_2^2\mathrm{d}x$, which was 4% ± 2% lower for our method than for the symmetrization method.

Figure 1.

The original image (a) was deformed by two synthetic random transformations (b,c). The deformed images were then registered with each other, resulting in deformation fields by the proposed (d) and the symmetrization (e) methods.

3.2 Cross-Subject Registration of Labeled Images

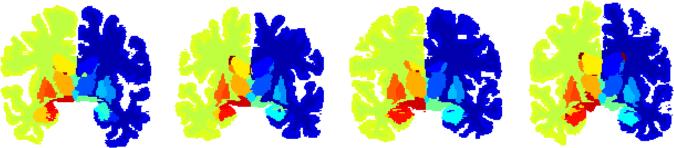
We performed a second set of experiments on a dataset of brain images with 37 neuroanatomical structures manually labeled [25]. We chose a fixed coronal slice maximizing the number of included distinct labels across the subjects (Figure 2). We randomly selected 40 pairs of subjects, and registered the chosen slices using the two methods. Although cross-sections of labels of 3D structures are not so precise for empirical validation, slice registration, being much faster than volumetric registration, allowed us to run many more experiments with a wide range of regularization.

Figure 2.

Examples of the labeled coronal slices used in Section 3.2.

We first considered 12 key subcortical regions: left/right amygdala, caudate, hippocampus, pallidum, putamen, and thalamus. As a similarity score for comparing the two methods, we computed in the union of these regions the portion of the voxels with matching labels between the two images. For each method and pair of subjects, we chose the maximum score achieved across different values of the demons regularization parameter. When the labels were compared in the native space of I₁, the two methods achieved on average similar scores (difference: 0.0% ± 0.2%). On the other hand, when the scores were computed in the native space of I₂ (by nearest-neighbor interpolation), the proposed method resulted in 0.10% ± 0.16% higher score than the symmetrization approach did.

In a different comparison, we computed the similarity score for each experiment by averaging the Dice's similarity coefficient across all of the labels. When the label overlaps were computed in the native space of I₁, the symmetrization approach produced a significant 0.7% ± 0.2% higher similarity score compared to the proposed method. When the scores were computed in the native space of I₂, however, the two algorithms performed similarly (0.0% ± 0.2%).

4 Conclusions

We have demonstrated for the first time that implicit-atlas pairwise registration is inherently independent of the mid-space, which led to deriving a new symmetric data term for deformable image registration. The independence of the cost function from the two image-to-atlas transformations alleviates the need for enforcing anti-drift constraints that can potentially bias the results. Our method is especially advantageous for the displacement-field transformation models, since inverting a velocity-field transformation is straightforward. We validated our method through experiments on two brain image datasets. Future work includes: a comprehensive evaluation of the proposed method on 3D labeled data; investigating the practicality of the proposed framework for group-wise registration; and devising a suitable symmetric regularization scheme.