A multi-objective optimization approach accurately resolves protein domain architectures

Abstract

Motivation: Given a protein sequence and a number of potential domains matching it, what are the domain content and the most likely domain architecture for the sequence? This problem is of fundamental importance in protein annotation, constituting one of the main steps of all predictive annotation strategies. On the other hand, when potential domains are several and in conflict because of overlapping domain boundaries, finding a solution for the problem might become difficult. An accurate prediction of the domain architecture of a multi-domain protein provides important information for function prediction, comparative genomics and molecular evolution.

Results: We developed DAMA (Domain Annotation by a Multi-objective Approach), a novel approach that identifies architectures through a multi-objective optimization algorithm combining scores of domain matches, previously observed multi-domain co-occurrence and domain overlapping. DAMA has been validated on a known benchmark dataset based on CATH structural domain assignments and on the set of Plasmodium falciparum proteins. When compared with existing tools on both datasets, it outperforms all of them.

Availability and implementation: DAMA software is implemented in C++ and the source code can be found at http://www.lcqb.upmc.fr/DAMA.

Contact: juliana.silva_bernardes@upmc.fr or alessandra.carbone@lip6.fr

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Sequence-based domain recognition represents one of the most convenient and practical approaches to understand evolution and function of proteins. Domains are sequence fragments that can be independently stable and folded, they have a shape and a function, they occur alone or in groups and are the building blocks of all proteins. To account for the great diversity of domain contexts, several efforts were made in categorizing coding regions into protein domains and domain families. Some resources, like SCOP (Murzin et al., 1995) and CATH (Sillitoe et al., 2013), organize domains according to their structural classes, while others, such as Pfam (Finn et al., 2010) and PROSITE (Sigrist et al., 2013), are purely sequence based. These databases are the starting point of annotation pipelines that are commonly organized into three steps: (i) a probabilistic model or a set of models is built to represent each functional domain; (ii) the model library representing all domains in the database is used to scan query sequences identifying potential domains and (iii) conflicting predictions are resolved to propose a domain architecture (domain arrangement) for each protein to be annotated. Domain architecture prediction (step iii) can be used to improve the performance of annotation methods, since homologous proteins might share their architectural context. The problem though can be complex when a query sequence matches several models, producing a set of conflicting predictions with overlapping domain boundaries. A simple strategy to resolve domain architecture in multi-domain proteins is to consider highest confidence domains without overlapping (Finn et al., 2010). However, some overlapping must be admitted to increase the number of correct domain predictions, as demonstrated by the Multi-Domain Architecture (MDA) approach (Yeats et al., 2010). In this approach, the set of potential domains in a query sequence is represented as a weighted graph (where nodes are domains and edges connect non-overlapping domains) and the heavier clique-finding algorithm is used to detect the most probable domain architecture. More recently, other approaches have explored domain combinations (co-occurrences) to improve architecture prediction. They all consider domains to be co-occurring on the same protein, not necessarily as consecutive one of the other. Domain co-occurrence is expected to enhance the level of confidence in a prediction (Geer et al., 2002; Vogel et al., 2004) mainly because (i) the majority of proteins are multi-domain and (ii) we observe fewer combinations than the statistically expected ones (Coin et al., 2003; Moore et al., 2008; Vogel et al., 2004). Intuitively, co-occurrence suggests functional cooperation, i.e. two or more domains can interact to determine the protein function (Apic et al., 2001; Marcotte et al., 1999; Wuchty and Almaas, 2005). Domain co-occurrence has been explored by two methods: CODD (Co-Occurrence Domain Discovery) (Terrapon et al., 2009) and dPUC (domain Prediction Using Context) (Ochoa et al., 2011). Both methods are based on the Pfam database and, for a given protein sequence, they detect a set of potential domains by setting a permissive Pfam threshold and by allowing overlaps. They also compute and use a list of known domain architectures from UniProtKB sequences (Leinonen et al., 2004). CODD starts by assigning to the query sequence non-overlapping domains detected with a restrictive Pfam threshold. Then, it iteratively tries to add new non-overlapping domains that co-occur with the old ones according to the list of known architectures. dPUC differs in strategy from CODD. It represents potential domains as nodes of a graph, where edges connect non-overlapping domains. It weights each node with normalized Pfam scores, and it weights edge with a special context score that captures the propensity of pairwise domain combinations in the list of known architectures. Then, similar to MDA approach, dPUC finds a domain architecture for a given query sequence by looking for the maximum-weighted clique in the graph.

dPUC presents two advantages over CODD: it takes into account co-occurrence of repeated domains and penalizes higher confidence domains with no co-occurrence. However, we believe that there are two points into dPUC’s approach that could be improved. First, it did not consider multi-domain co-occurrence to compute domain architectures. Second, dPUC combines individual domain scores and co-occurrence information into a very simplified function, which is then optimized. We argue that this combination is non-trivial and that the function could be more complex or alternatively, could be split into several sub-functions to be optimized.

Here, we present DAMA (Domain Annotation by a Multi-objective Approach), a novel algorithm that treats protein domain architecture prediction as a multi-objective optimization problem. DAMA combines a number of criteria including multi-(possibly pairwise-) domain co-occurrence and domain overlapping. By taking into account known architectural solutions, DAMA identifies them within the protein sequence and integrates new domains into them whenever possible. DAMA has been evaluated over a benchmark containing protein sequences extracted from the Protein DataBank (PDB), over the genome of the poorly annotated malaria parasite Plasmodium falciparum and over two datasets collecting known sequences characterized by large domain architectures and repeated blocks of domains. Our results show that, for all datasets, DAMA outperforms existing computational methods and detects domain architectures presenting co-occurrences.

2 Methods

2.1 Data

2.1.1 The PDB benchmark

To evaluate DAMA performance, we have used the benchmark constructed for the evaluation of MDA. It contains 2523 multi-domain proteins extracted from the PDB, where each domain is classified in a CATH superfamily. The dataset is available at ftp://ftp.biochem.ucl.ac.uk/pub/gene3d_data/DomainFinder3/RC1/Benchmark/. Since this dataset is based on CATH superfamilies, we have extracted the list of known domain architectures by parsing the file CathDomainDescriptionFile containing CATH superfamilies (domains) for all proteins in PDB database. This file is available at ftp://ftp.biochem.ucl.ac.uk/pub/cath/latest_release/.

2.1.2 The P. falciparum protein dataset

All data were extracted from PlasmoDB (http://PlasmoDB.org), the official repository of the P. falciparum proteins used as a reference database by malaria researchers (Aurrecoechea et al., 2009; Bahl et al., 2003). PlasmoDB v11 contains 5542 proteins. To provide a list of potential domains for P. falciparum protein sequences, we used Pfam v27 (downloaded from http://pfam.sanger.ac.uk), containing 14 831 domains. The list of known domain architectures was extracted from Pfam-A.full, as well as the list of allowed domain overlaps. HMM profiles, required to produce the list of potential domains for P. falciparum, were downloaded directly from the Pfam web site. To identify potential domains, we run HMMER 3.0 (hmmscan) on all protein sequences (Eddy, 2011). See Section 2.5. The distribution of the number of domains in P. falciparum proteins is reported in Supplementary Figure S1.

2.1.3 DAMA time complexity on P. falciparum protein sequences

We computed the run time of DAMA, MDA, CODD and dPUC on the set of domain hits provided by HMMER 3.0 and selected with an E value $\le 1e$-3. All experiments run time have been obtained on a one core single-user linux (kernel 2.6.32-431.11.2.el6.x86_64 - Red Hat 4.4.7-4) Intel(R) Xeon(R) CPU E5-2650 v2 2.60 GHz, with 64 GB of RAM. Single user mode was used to minimize the number of system activities.

2.1.4 Three benchmarks to test DAMA time complexity on long proteins

The TitinLikeDB was constructed by considering three Pfam families (PF00041: fn3, PF09042: Titin_Z, PF07679: I-set; Titin_Z is known to strongly co-occur with I-set and fn3 with I-set). From these families, we selected proteins with at least 1000 amino acids: we included all Titin_Z proteins (53), randomly selected 750 proteins from fn3 and 750 from I-set. The number of proteins (1553) was determined by disk space limitations, since, on these large sequences, hmmscan was executed with permissive parameters and it produced a large amount of domain hits. The SilkWormSet was constructed from the SilkWormDB (Xia et al., 2005) and it collects 324 proteins whose architecture is characterized by consecutive domain block repeats. For instance, these are proteins of the form DE[ABC]₁₃FD, where ABCDEF are domains and where the block of domains ABC is repeated 13 times consecutively (Moore et al., 2013). SilkWormSet contains all proteins with such repeated patterns found among the 14 623 proteins of the silkworm genome. A third dataset is constituted by long generated sequences. From the 14 831 domain families constituting Pfam₂₇, we built hundred random sequences with n domains, for each $n=3\dots 99$ taken by steps of 3. Namely, for each random sequence to be generated, we randomly selected n domains within the Pfam₂₇ set, used HMMEmit (Eddy, 1998) to generate n sequences close to the original ones and concatenated the n generated sequences following the order of domain extraction. For each n, DAMA has been run on the concatenated random sequences, the average computational time has been evaluated for each n and plot in Supplementary Figure S4. Over the three datasets, experiments were performed on a one core single-user machine as indicated in Section 2.1.3.

2.2 Parameter settings for the optimization step

To find the best domain architecture for a given query sequence, the algorithm (described in Section 3) generates a set of feasible architectures based on domain co-occurrence constraints and finds the most likely one by optimizing the five objective functions $F_1\dots F_5$ above. The tolerance values δ_j for each function F_j ($j\le 4$) in Equation (6) are set by the user depending on the dataset considered. For the δ₁ value, aimed to introduce some flexibility on the selection of the domains, the idea is to evaluate not only domains with best E-value score but also those with good E-value score that are well supported by known co-occurrence. This required to set ${\delta }_1=0$ for the two datasets we analyzed, one based on CATH and the other on Pfam. Then, for each domain database, the notion of ‘higher confidence domain’ for the optimization function F₁ was modeled accordingly. For CATH, we wanted the model to fit the spirit of the database by allowing a selection of several potential hits for the final architecture, among the ones suggested by multiple probabilistic models (for a given domain, these hits overlap and are characterized by different boundaries and E-value scores), and we set ${\delta }_1=40$ to expand the region of optimal solutions for our PDB benchmark. This permissive δ₁ value allows to select a large number of overlapping hits with acceptable E value among which to find the one that accommodates best the other domains of the architecture. In contrast, for Pfam, the higher confidence domain is modeled by the domain hit with the best score. Because of this, we set a much less permissive ${\delta }_1=10$ to assure hits with the highest E-value scores to belong to the final architecture for the P. falciparum annotation. To maximize the number of domain co-occurrences and the number of distinct domains, we set ${\delta }_j=0$ for j > 1 for both datasets.

2.3 Measuring prediction accuracy

As was done for MDA in Yeats et al. (2010), a predicted MDA is considered correct if the superfamily types and the number of occurrences of domains are predicted correctly, irrespective of whether the boundary positions are correct. The overall accuracy is then calculated over the whole dataset. If too many domains of the correct superfamilies (the CATH level H corresponding to Homologous superfamilies is used) are predicted then this is termed a ‘semi-false positive’, while if the extra domains belong to an incorrect superfamily, it is termed a ‘false positive’; if DAMA is missing a domain, it is a ‘false negative’. Note that the false negative rate is due to the E-value cut-off 0.001, used both in DAMA and MDA. A single predicted MDA can potentially contain errors in all three classes.

2.4 Estimating false discovery rate

The estimation of the number of false predictions is an essential step for evaluating the performance of domain identification methods. The two strategies that we used to estimate the false discovery rate (FDR) were both employed before. The first one estimates the probability that a potential domain has been randomly predicted, and it was employed for the evaluation of dPUC (Section 2.4.1). The second strategy estimates the number of false co-occurrence certifications in architectures and it was proposed in the evaluation of CODD (Section 2.4.3).

2.4.1 FDR over domain prediction

The FDR over domain predictions was estimated by comparing the number of predictions on real and shuffled sequences. Intuitively, domain predictions on shuffled sequences arise by chance alone, whereas predictions on real sequences provide the total number of domains (true or false). Therefore, the ratio between these two values should approximate the FDR. To compute FDRs, real sequences were concatenated to shuffled ones, where these latter were generated according to two different hypothesis or random models. The first random model (1-mer) takes a real sequence and generates a reshuffled one that has the same residue content of the original sequence and the same length. The second random model (4-mer) takes a real sequence but generates reshuffled sequences of successive k-mers, for k = 4. This implies that the same residue content and the same length are preserved. The idea behind this last model is that protein sequences are made by small fragments of residues playing a relevant structural and functional role and that small k-mers approximate these potential patterns in a protein. Both random models were applied to each sequence 20 times, and the random reshuffling was realized with the perl function List::Util::shuffle(). If P is the original set of protein sequences and S its associated shuffled sequence, let P + S be the set of concatenated sequences. Note that the set P + S is a set containing 20 times more sequences than P because from each sequence in P, we generated 20 sequences. Then, we computed the number of domain predictions within the P-portion (saying R) and the number of predictions within S-portion (saying A) of the P + S sequences and set the FDR $=A/R$ for the dataset. The same strategy was used in (Ochoa et al., 2011) (see Section 2.4.2 and the legend of Supplementary Fig. S6).

2.4.2 FDR curves

The FDR can be controlled by modulating the E-value threshold used to filter potential domains. To construct the FDR curve, we followed the method in Ochoa et al. (2011). Namely, we consider several input sets of domain hits produced by HMMER 3.0 with a threshold $<M$, for different E-value thresholds M. Then we run each tool on each set and compute FDR and number of domains per protein for the resulting sets of architectures. This calculation allows the construction of the curves in the figure. Best performing methods present higher curves. In each plot, the FDR curves of all methods were computed by using the same set of shuffled sequences.

2.4.3 FDR over domain architectures

The FDR over domain architectures estimates the probability of detecting co-occurrent domains by chance. Given the list of known architectures, a set of validated domains (obtained by applying hmmscan with restrictive thresholds) and a set of potential domains (i.e. new domains detected by a tool with permissive threshold), we wished to ‘certify’ a potential domain based on the co-occurrence of the domain with ‘validated’ ones. Then, intuitively, the FDR will express how many times an architecture made of validated domains and certified domains will arise at random. To compute the FDR, first, we randomly permuted all potential domains across proteins. This means that the identities of the potential domains (not their locations) are randomly reassigned. Then, we computed the number of random domains that were ‘certified’ after randomization over all proteins. The FDR of the certification procedure is computed as A/R, where A is the number of certified domains after randomization and R is the number of ‘certified’ domains on the original data. This procedure is repeated 1000 times and the average FDR is reported. The same strategy was used in Terrapon et al. (2009).

2.5 Computational tools used for comparisons

We compare DAMA to four domain architecture prediction tools: hmmscan, CODD, dPUC and MDA. hmmscan was run with default parameters and curated inclusion thresholds. The option –cut_ga, for model-specific thresholding (using profile’s GA gathering cutoffs to set all thresholding), was used. hmmscan is included in the HMMER 3.0 package (http://hmmer.janelia.org/software). We also used hmmscan (with permissive thresholds) to generate the set of potential domains required as input for DAMA, CODD, dPUC and MDA. For that, we used the following command line: hmmscan –F1 0.1 –F2 0.1 –F3 0.1 –domZ 1 -Z 1 -E 0.1 –domE 0.1 -o dev/null –domtblout output. All tools were tested starting from the same reference set of known architectures and the same domain context information, for each comparison. CODD, dPUC and MDA were run with default parameters. MDA was downloaded from ftp://ftp.biochem.ucl.ac.uk/pub/gene3d_data/DomainFinder3/. CODD and dPUC were not publicly available at the time our analysis (on Pfam₂₇) was realized and we obtained them from the authors. A version of dPUC, compatible with Pfam₂₇, is now available at http://viiia.org/dpuc2/.

2.6 Implementation and input files

DAMA package is written in C++, and it is available at http://www.lcqb.upmc.fr/DAMA/. Parameters and options are described in the website.

DAMA takes as input two files. The first describes the set of annotated sequences. For each domain, a line reports the sequence identifier, the domain identifier, start and end positions of the domain match on the probabilistic model used for annotation, start and end positions of the domain along the sequence. The localization of the domain match against the probabilistic model is used only for computing the coverage of the match against the model. Depending on the set of sequences to annotate, different coverage thresholds might be best appropriate. For the evaluation of DAMA on P. falciparum sequences, we asked domain matches to cover at least 40% of their probabilistic models. This option allows DAMA to construct architectures with domains that match sufficiently well their model. It can be disabled by setting the domain coverage parameter at 0.

The second input file contains the list of known domain architectures. In our tests, we used the lists produced by CATH and Pfam but any choice is possible.

DAMA leads to a unique solution. In case multiple architectures would display the same best F₅ value, all architectures would be proposed as solutions. (This case is unlikely to happen.) Note that a DAMA option provides the user with the whole set of feasible architectures $\mathcal{L}\prime$.

3 The algorithm

DAMA is a combinatorial search algorithm designed to resolve domain architectures in multi-domain proteins. Two main steps underpin DAMA approach: (i) the enumeration of all possible architectures, subject to domain co-occurrence constraints and (ii) the selection of the architecture that maximizes a set of objective functions.

3.1 Step 1: enumeration of the architectures

Let s be a query sequence, $\mathcal{P}$ be the set of its potential domains provided with an E-value (also called ‘hits’; Fig. 1A) and $\mathcal{L}$ be the list of all known architectures sharing domains with $\mathcal{P}$ (Fig. 1C).

Fig. 1.

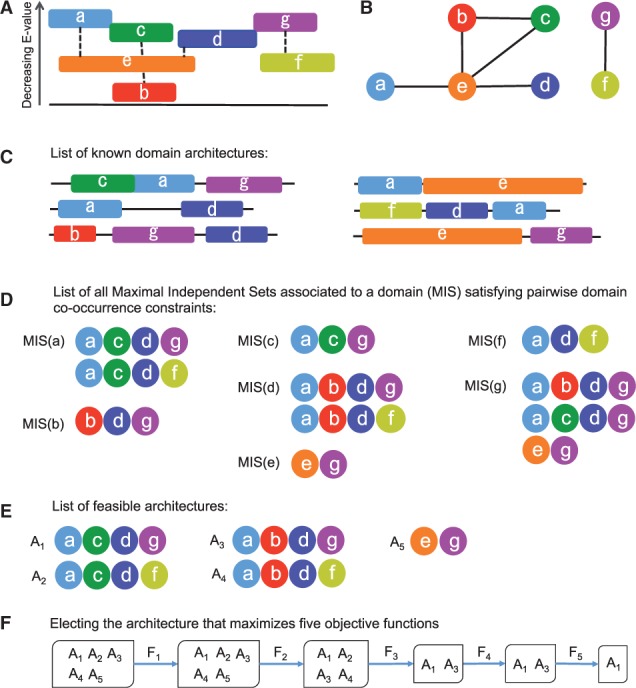
Main steps in DAMA algorithm. (A) Potential domains ($\mathcal{P}$) for a query sequence are ranked from bottom to top by their decreasing E value. Overlaps between domains are allowed (see domains de or dg). Domains are denoted with different letters. The same letter code is used in (B–E). (B) Domains in (A) are represented as nodes of an ‘interval’ graph, where edges connect all overlapping domains with the exception of domains with a very small overlap or domains that appear as overlapping in the list of known protein architectures in (C) (see the overlapping condition). Edges not included in G are (g, d) because the overlap is too small and (a, c) because the overlap is known (see C). (C) List of known domain architectures sharing domains with $\mathcal{P}$. (D) List of all Maximal Independent Subsets associated to some domain (MSI) for the graph in B satisfying pairwise domain constraints according to the list in (C). (E) List of feasible architectures obtained by crossing information coming from (C) and (D). (F) Filtering of the architectures in E with 5 optimization functions and selection of the best architecture

To enumerate a set of potential architectures for s, we first construct the interval graph G whose nodes represent domains in $\mathcal{P}$ and edges connect overlapping domains (Fig. 1B). Note that domain overlap is allowed if it is made of less than 30 amino acids and it comprises at most 50% of the match, as done in Yeats et al. (2010), or if it has been observed before as indicated in the list of known architectures $\mathcal{L}$, as done in Ochoa et al. (2011). We refer to it as ‘overlapping condition’.

Second, we read off from the interval graph G a list of potential architectures. To do so, let us recall that an independent set is a set of nodes in G, such that no edge connects two vertices in the set and that a maximal independent set is a set that is not a proper subset of any independent set. Inspired by these classical notions, given a domain $D_i\in \mathcal{P}$, we say that an independent set associated to a domain D_i is an independent set of nodes in G, such that for each pair of domains D_i, D_j in the set, there exists an architecture in $\mathcal{L}$ that contains D_i, D_j where both the sequential order and the number of times each domain occurs are ignored (Fig. 1D). We also say that a Maximal Independent Set associated to a domain D_i (in short $MIS(D_i)$) is an independent set of nodes in G that is maximal for D_i, in the sense that it is not a proper subset of any independent set associated to D_i. Hence, on the basis of these definitions, for each domain D_i, we define the potential architectures for s to be the maximal independent sets associated to D_i. Note that there might be several maximal independent sets associated to D_i, as illustrated in Figure 1D.

Finally, the list of architectures associated to domains in $\mathcal{P}$ is enriched with new domains having an E-value $<1e$-10, possibly overlapping with those domains that are already present in the architecture (see the overlapping condition above). Note that these new domains added to an architecture do not co-occur with the existing ones. All possible maximal enrichments are generated, in the sense that an enriched architecture is not a proper subset of any other architecture. We call this set of architectures $\mathcal{L}\prime$ (Fig. 1E).

3.2 Step 2: selection of the optimal architecture

We wish to find the optimal architecture in $\mathcal{L}\prime$. For this, we define five objective functions, and we treat this problem as a multi-objective optimization problem. There exist many methods to search for an optimal solution (Marler and Arora, 2004), and we used a variation of the lexicographic approach proposed in (Waltz, 1967), where objective functions are arranged in order of importance, constraints are formulated on these functions and the optimization problems are solved one at a time. The five functions were designed according to several objectives:

1. To ensure that higher confidence domains (not necessarily the highest) are in the final architecture, we define

   $$F_1(x)=\underset{a_i}{\arg \hspace{0.17em}max}\hspace{0.17em}\text{E}-\text{valueExp}(a_i)$$ (1)

   where a_i is a domain contained in the feasible architecture $x\in \mathcal{L}\prime$, and $\mathrm{E}-\text{valueExp}(a_i)$ is the function that taken a score $1e\text{-}k\le \mathrm{E}-\text{value}(a_i)\le 1e\text{-}k+1$ associated to the match of the domain a_i in x, returns the exponent k.
2. To maximize the number of multi-domain co-occurrences, we define

   $$F_2(x)=\text{MDCO}(x),$$ (2)

   where MDCO(x) is the multi-domain co-occurrence factor, that is the number of domains in x that co-occur together in $\mathcal{L}$. For instance, $F_2(bdg)=3$ if the domains b, d, g are found in some architecture in $\mathcal{L}$, while $F_2(acd)=2$ if only pairs of domains a, c and a, d are found in architectures of $\mathcal{L}$ (Fig. 1C and D).
3. To choose, based on pairwise domain combinations, between two architectures presenting the same MDCO, we define

   $$F_3(x)=\text{pairDCO}(x),$$ (3)

   where pairDCO(x) counts the number of distinguished domain pairs in x (possibly non-consecutive) that co-occur in $\mathcal{L}$. For an architecture abb, this means to consider all combinations of domain pairs ab, ab and bb and check the co-occurrence in the list of architectures. For example, $F_3(abb)=3,F_3(abc)=1$ for the list of architectures ${\mathcal{L}}_1$ in Figure 2B, and $F_3(abb)=F_3(abc)=3$ for ${\mathcal{L}}_2$ in 2C.
4. To privilege architectures with distinct domains, we define

   $$F_4(x)=\text{diff}(x),$$ (4)

   where $\text{diff}(x)$ returns the number of distinct domains in x that co-occur in $\mathcal{L}$. For example, $F_4(abb)=F_4(abc)=2$ for the list of architectures ${\mathcal{L}}_1$ in Figure 2B and $F_4(abb)=2,F_4(abc)=3$ for ${\mathcal{L}}_2$ in 2C.
5. To select the architecture with highest score domains, we define

   $$F_5(x)=\frac{1}{N}{\displaystyle \sum _{i=1}^N-}\log (\text{E}\mathrm{-}\text{value}(a_i))$$ (5)

   where N is the number of domains in x, a_i is the ith domain in x. For example, among the two architectures A₁ and A₃ in Figure 1E, F₅ selects A₁ because domain c has higher E-value than domain b, as illustrated in Figure 1A.

Fig. 2.

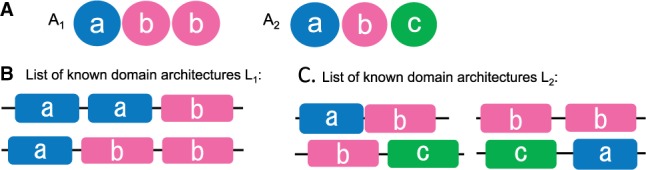
Selection of architectures with a multiple domain co-occurrence. (A) Two architectures, A₁, A₂, where A₁ is composed by a double occurrence of domain b. Domains are denoted with different letters, and the same letter code is used in (B) and (C). (B) List of architectures that allow for the selection of A₁ with the objective function F₂, because $F_2(abb)=3$ and $F_2(abc)=2$. (C) List of architectures that allow for the selection of A₂ with the objective function F₄, because $F_4(abb)=2$ and $F_4(abc)=3$. Note that $F_2(abb)=F_2(abc)=2,\hspace{0.17em}{F}_3(abb)=F_3(abc)=3$

For each protein sequence and its set of feasible architectures $\mathcal{L}\prime$, we run the optimization problems defined by the five functions above and solve them one at a time:

$$\begin{array}{l}{\displaystyle \underset{x\in \mathcal{L}\prime }{\text{Maximize}}}{F}_i(x)\\ \text{subject}\hspace{0.17em}\text{to}\hspace{0.17em}{F}_j(x)\ge F_j(x_j^{*})-{\delta }_j\hspace{0.17em}for\hspace{0.17em}j=1,\dots ,i-1\hspace{0.17em}\text{and}\hspace{0.17em}i>1\end{array}$$ (6)

where $i=1,2,\dots ,5$ indexes the order of the objective functions F_is, $F_j(x)\ge F_j(x_j^{*})-{\delta }_j$ is a constraint on the jth function where $F_j(x_j^{*})$ represents the optimum of the jth objective function found in the jth iteration and δ_j is a tolerance constant. Note that, after the first function F₁ is applied, $F_j(x_j^{*})$ is not necessarily the same as the independent maximum of $F_j(x)$, because constraints dependent on δ_j might have been applied. In fact, the parameter δ_j is a non-negative constant that defines a non-negative tolerance for each objective function (values for it are discussed in Section 2.2; note that the last function, F₅, is not dependent on a tolerance value and will provide a unique solution). If ${\delta }_j=0$ then the optimal solution is dictated by F_j and if ${\delta }_j=0$ then the ‘region’ of optimal solutions dictated by F_j expands. This reduces the sensitivity of the final solution to the initial objective function ranking process. In Figure 1, the role of tolerance constants is illustrated by domains a and g that match the sequence with close E values; because of the parameter ${\delta }_1=0$, the optimization function F₁ selects the architecture, e.g. where the E value of g is strictly smaller than the E value of a. It should be remarked that the lexicographic approach (Waltz, 1967) makes sense only if $x_i^{*}$ can be computed for all F_i’s, and we ensure this by applying our objective functions to the list of feasible architectures $\mathcal{L}\prime$, where the functions are well-defined.

In practice, the algorithm starts with the set of architectures ${\mathcal{L}}_0=\mathcal{L}\prime$ and maximizes the list of objective functions, one after the other, by selecting, after the optimization of the first j functions, a set of optimal architectures ${\mathcal{L}}_{j+1}\subset {\mathcal{L}}_j$ satisfying the (j + 1)th function. Such optimal architectures are required to satisfy all j objective functions evaluated until that point, up to some tolerance constant. The final selected architecture is the one that satisfies all optimization functions (Fig. 1F).

The algorithm returns a single architecture as the best one. In case multiple architectures happen to maximize F₅, they will all be provided as best solutions.

4 Results

We evaluated the performance of DAMA on two datasets: a benchmark containing multi-domain proteins and the genome of the malaria parasite P. falciparum. The PDB benchmark was proposed in Yeats et al. (2010) to measure the performance of the MDA approach, and we used it to compare DAMA and MDA (Section 4.1). This benchmark is useful for optimizing parameters and evaluate the robustness of the algorithm, but it does not constitute a realistic case study, made of a large set of highly divergent sequences, as often encountered in the annotation of new genomes. To address these difficulties, we considered the set of P. falciparum proteins, known to be hard to annotate and we compared the performance of DAMA, MDA, dPUC and CODD on its domain annotation (Section 4.2).

4.1 The PDB benchmark

The PDB benchmark contains only multi-domain proteins extracted from the PDB (see Section 2) and was proposed to measure the performance of MDA (Yeats et al., 2010). We have reproduced the same experiment and compared DAMA with MDA. Table 1 lists precision, recall and F-measure for DAMA and MDA on the PDB benchmark. Both tools present high accuracy being DAMA slightly better. The table also shows the number of true positives, false positives, false negatives and semi-false positives obtained for each tool. Semi-false positives are additional domains that were detected by DAMA or MDA and that belong to the same CATH superfamilies. DAMA seems to be more permissive than MDA detecting more true positives and a high number of semi-false positives. The high accuracy obtained by both methods is due to the high similarity between the query sequences and the seed sequences used to construct CATH models. In fact, we expect each domain in a query sequence to be identified by a model constructed from close sequences, since query sequences and CATH superfamilies are both extracted from the PDB.

Table 1.

Performance of MDA and DAMA on a PDB benchmark

Performance measures	MDA	DAMA
Precision	0.99	0.99
Recall	0.96	0.98
F measure	0.97	0.99
True positives	5914	6044
False positives	25	52
Semi-false positives	67	1030
False negatives	262	132

4.2 Annotation of the P. falciparum proteins

To account for a realistic dataset, made of a large pool of highly divergent sequences, we tested DAMA, MDA and two more available tools, CODD (Terrapon et al., 2009) and dPUC (Ochoa et al., 2011), on the P. falciparum genome. Since we do not know the exact number of domains present in proteins of P. falciparum, it is not possible to measure the rate of true positives, false positives and false negatives for computing standard measures (precision, recall and F-measure) as done for the PDB benchmark. However, we can estimate the proportion of false positives, i.e. the FDR, among domain predictions obtained for P. falciparum and then plot the number of domain predictions against the FDR at various thresholds. We have computed the FDRs according to two different strategies, over domain predictions (Section 2.4.1) and over domain architecture predictions (Section 2.4.3). We expect the best methods to detect more domains at the same ‘noise’ level and with ‘noise’ increase. The distribution of the number of domains per protein of the P. falciparum sequences is reported in Supplementary Figure S1, where most of the sequences have no domain or one domain.

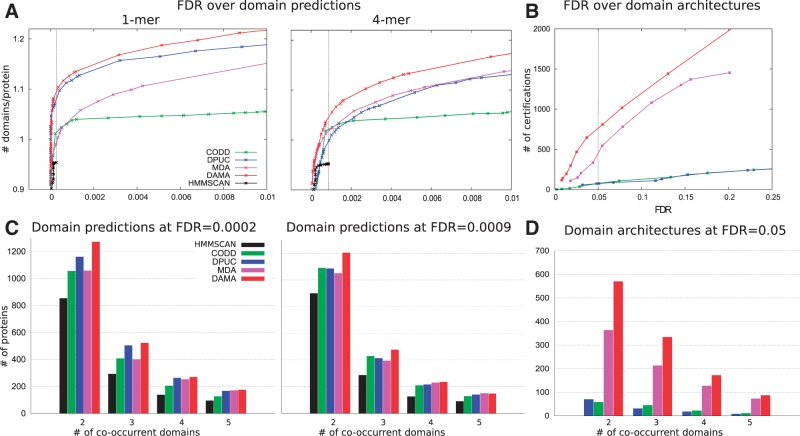
The first strategy computes the FDR as the ratio between predictions obtained on shuffled sequences concatenated to real sequences and predictions obtained on real sequences only. Shuffled sequences were generated according to two different hypotheses both preserving the same amino-acids composition of the original sequence. The first hypothesis, named 1-mer, reshuffles all amino-acid positions in a sequence, while the second one reshuffles consecutive 4-mers in a sequence. Figure 3A shows that DAMA predicts more domains over a large range of FDRs for both the 1-mer (Fig. 3A, left) and the 4-mer (Fig. 3A, right) hypotheses than the other tools. Note that dPUC outperforms MDA on 1-mer, while on 4-mer the opposite holds. This is due to MDA better handling of false positives (see legend of Supplementary Fig. S6AB). CODD displays a stable behavior on both cases, but its performance remains poor. We also report hmmscan behavior and its poor results are due to the fact that over Pfam, it adopts a Pfam curated ‘gathering’ threshold (GA) cutoff to control the rate of false positives (see Section 2.5). (See Supplementary Fig. S6 for an alternative evaluation strategy reconfirming DAMA behavior.)

Fig. 3.

Performance of DAMA and other tools on the P. falciparum proteins annotation. (A) The y-axis is the number of predicted domains per protein (‘signal’), while the x-axis is the FDR (‘noise’), so better performing methods have higher curves (more signal for a given noise threshold). On the 1-mer and the 4-mer hypotheses, DAMA (red) outperforms all hmmscan variations tested (black) and the methods MDA (pink), dPUC (blue) and CODD (green). (B) The y-axis is the number of certified domains (‘signal’) obtained by a method, while the x-axis is the FDR (‘noise’) computed over domain architectures. Colors as in (A). (C) Distribution of the number of proteins with a fixed number of predicted domains, for each tool at FDR $=2e$-4 (see vertical bar in A) for 1-mer and at FDR $=9e$-4 for 4-mer. (D) Distribution of number of proteins with a fixed number of predicted domains, for each tool at FDR $=0.05$ (see vertical bar in B)

The second strategy measures the FDR over domain architectures by computing the probability of obtaining them randomly. For this, we assume that the architectures provided by hmmscan are the true ones. (As highlighted above, hmmscan uses restrictive domain-dependent thresholds guaranteeing a low false-positive rate.) Therefore, domains in an annotated protein sequence are split into two groups: domains assigned by hmmscan (true domains) and domains detected by another tool (potential domains). We randomly permute the potential domains of all proteins preserving the number of domains in each protein. Then, the FDR is the number of certified random domains over the number of certified true domains, where a certified domain is a potential domain that co-occurs with a true domain according to the list of known architectures (see details of FDR computation in Section 2.4.3). It is noteworthy to say that although the shuffling leads to ‘random’ contexts, the nature of this FDR definition might disadvantage methods that use domain scores in picking a best set of domains (including DAMA and dPUC) as opposed to just considering contexts (such as CODD). However, as shown in Figure 3B, DAMA predicts more certified domains than the other tools for the same FDR value. Also, note that MDA, a method that does not explore domain co-occurrence, achieves a better performance than dPUC and CODD.

We verified whether DAMA detects architectures having more co-occurrent domains than other tools. For this and for a given FDR, we have computed the number of proteins having 2, 3, 4 and at least 5 co-occurrent domains. Figure 3C shows the number of proteins having co-occurrents domains at FDR $=2e\text{-}4$ for 1-mer (Fig. 3C, left) and at FDR $=9e\text{-}4$ for 4-mer (Fig. 3C, right), where the values correspond to the highest FDR value obtained by hmmscan. We observe that DAMA predicts more co-occurrents domains for all values (i.e. 2, 3, 4 and more). Figure 3D shows the number of proteins having co-occurrent domains at FDR $=0.05$ computed over domain architectures. DAMA predicts much more co-occurrent domains than any other tool, and this confirms that it is an accurate method for prediction of MDAs. Some examples are illustrated in Figure 4. They are all supported by known co-occurrence and they highlight the identification of domains with different functionalities (Fig. 4A and C) and of repeated domains with identical function (Fig. 4B and C).

Fig. 4.

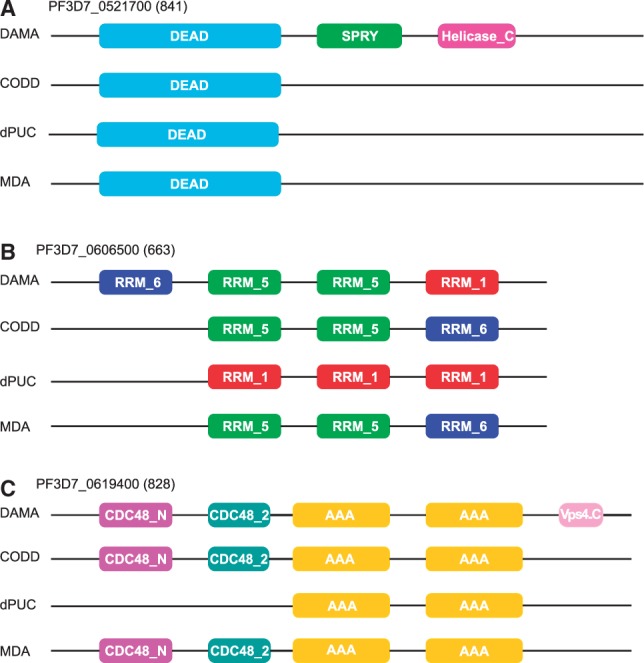
Three examples of domain predictions on P. falciparum proteins. Architectures of P. falciparum proteins identified by DAMA, CODD, dPUC, MDA run with default parameters. DAMA shows to identify more domains that other tools and predictions are based on known co-occurrence in Pfam₂₇: (A) DEAD, SPRY, Helicase_C co-occur in 113 proteins; (B) RRM_5 (2 occurrences), RRM_1, RRM_6 co-occur in 34 proteins; (C) CDC48_N, CDC48_2, AAA x 2, Vps4_C co-occur in 159 proteins. The name of the protein (PlasmDB id) is followed by its length (number of amino-acids). DAMA was used fixing a FDR threshold at 2e–04, as in the 1-mer experiment reported in Figure 3C

One more test was done on domain architectures that were selected as best ones by MDA, CODD and dPUC and that were filtered out by one of the five DAMA functions (Supplementary Fig. S2). About half of these architectures are filtered out by the F1 function and progressively by F2, F3, F4 and F5. All functions contribute in DAMA selection, for the three subsets. The majority of the architectures selected by the three tools are subsets of DAMA best architecture (as illustrated in Fig. 4), but there are 20% of the architectures that contain domains that are not present in DAMA best architecture and F1, F3 and F4 play a key role in their selection.

4.3 Role of the optimization functions in DAMA

Several tests have been performed to establish the importance of each optimization function in domain filtering. When taken alone (the other four functions are ignored by the algorithm), the five functions do not perform as well as taken together, on both 1-mer and 4-mer. In particular, F1 and F5 appear to contribute the most and the least to DAMA performance, respectively. (Note that the corresponding performance curves approximate from the top and the bottom the curves associated to the other functions; see Supplementary Fig. S3c and d). Also, the absence of either F1 or F5 in DAMA is associated to a decreased performance (Supplementary Fig. 3g and h). Assuming the presence of F1 and F5, all other functions were tested alone (Supplementary Fig. S3e and f) or in pairs (Supplementary Fig. S3g and h) and in all cases, DAMA (defined by the five functions together) appeared to provide the best results. The filtering order suggested in DAMA is supported by these results.

It has been previously shown that some domain are more versatile than others (Basu et al., 2008; Weiner et al., 2008). For this, we redefined function F3 as the probability that a distinguished domain pair in a sequence x co-occurs in $\mathcal{L}$ to test whether this recognized bias could improve DAMA prediction. This alternative definition does not improve the performance obtained with the original F3 function, based on counting. Moreover, when tested alone, F3 appears to perform better than F3 based on probabilities. See Supplementary Figure S3a and b. This finding suggests that the maximization of the number of known co-occurrences in a domain arrangement, is the main trend guiding architecture evolution and not most probable domain co-occurrence.

Function F4 was also redefined by letting $diff(x)$ to return the number of distinct domains in a sequence x that co-occur in $\mathcal{L}$ and do not belong to the same clan. Replacing this new version of F4 in DAMA did not improve the performance obtained with the original F4 function. When tested alone, the new version performs worse than the original one. See Supplementary Figure S3a and b.

4.4 DAMA time complexity and large domain architectures

We evaluated DAMA time complexity and compared it with other methods, on three benchmarks: the set of P. falciparum protein sequences contains 5542 proteins; TitinLikeDB contains 1553 proteins with an average length of 11 820 aa (spanning from 211 to 36 507 aa) and with a very large number of domains (up to 942, with an average of 22 domains per protein): fibronectin type III domains (fn3), Titin_Z and immunoglobulin I-set domains (I-set); SilkWormSet contains 324 proteins with consecutive repetitions of blocks of domains (Moore et al., 2013), where block size spans from 2 to 18 domains and repetitions might reach 28 block occurrences. These proteins span from 114 up to 13 509 aa in length, with an average of 1031 aa and they contain up to 92 domains with an average of 13 domains per protein.

Results for the three experiments are reported in Table 2. See also Supplementary Figure S5 for boxplots of run time on P. falciparum proteins. For TitinLikeDB and SilkWormSet, all known domain architectures could correctly (for domain positioning and number of repeated domains) be reconstructed by all systems in a very reasonable computational time, starting from the same set of domain hits. DAMA is the fastest, yet comparable to MDA and CODD.

Table 2.

Time performance comparison

Tools	P. falciparum dataset	TitinLikeDB	SilkWormSet
DAMA	16.064 s	24.437 s	3.72 s
MDA	36.9 s	27.672 s	4.96 s
dPUC	212.601 s	132.133 s	22.08 s
CODD	53.317 s	29.417 s	5.37 s
No. proteins	5542	1553	324
No. domain hits	3 850 992	2 278 497	504 936

To investigate further DAMA behavior on small and large architectures, we constructed a dataset of generated sequences containing a progressively large number of domains, from 3 up to 99. DAMA time performance is reported in Supplementary Figure S4. Note that, this performance evaluation agrees with the one reported in Table 2, and it provides an estimation for much larger protein architectures.

5 Discussion

Accurate prediction of MDAs is extremely useful for function and network prediction, including phylogenetic profiling, gene fusion detection, protein–protein interaction inheritance and annotation by homology transfert (Yeats et al., 2010). Moreover, the amount of accurate information that can be generated by tools like DAMA on new genomes and metagenomes will be useful to answer evolutionary questions on the dynamics of architecture formation across species. The way protein architectures form is an important factor to understand protein evolution. A quantification of the elementary events affecting protein architectures, such as domain(s) insertion/ deletion, duplication and exchange, was done (Björklund et al., 2005) but, yet, little is known about the relationships between these elementary events (Pasek et al., 2006) and the molecular mechanisms they originate from. Finer domain mapping on entire sets of proteins for completely sequenced genomes will contribute precise information on the evolution of these architectures. This means, for instance, a more precise estimation of the rate of insertion, deletion, duplication and exchange of domains within proteins in a given species. In general, it would be interesting (i) to establish whether the process of generation of an architecture follows constraints or not, (ii) to pinpoint such constraints, if they exist and (iii) to verify whether they are species specific or not. Along a phylogenetic tree, domains might have been lost, permuted, combined with other domains, they might be integrated within an architecture and lost again. On the other hand, architectures might have been duplicated, recombined, broke up again. In summary, the process of architectures formation appears to follow evolutionary rules that need yet to be unraveled.

To test the performance of DAMA and other tools in architecture reconstruction, we looked for a realistic dataset of sequences that could represent well the difficulties encountered in genome and metagenome annotation. We decided to consider the set of P. falciparum protein sequences, knowing that these sequences diverged sufficiently from those that were used to construct probabilistic models employed for domain identification. This set of sequences represent in a fine way the protein world, compared with the benchmark based on CATH domains used in the first evaluation. Other genomes could be used instead.

On comparable FDRs, computed from the two artificial datasets (1-mer and 4-mer) constructed by reshuffling sequences of the P. falciparum genome, MDA showed to behave very well despite the fact that it was not explicitly tested over the P. falciparum genome before, while CODD and dPUC were. DAMA overperforms all tools and its excellent performance is due to several reasons. First, in DAMA, domain overlapping is considered by combining the strategies introduced in MDA (Yeats et al., 2010) and in dPUC (Ochoa et al., 2011). Second, DAMA exploits knowledge on multi-domain co-occurrence by combining individual domain scores with co-occurrence information in five different optimization functions. This multi-objective optimization strategy is a refinement of the simplified function proposed in dPUC, while domain co-occurrence was not considered at all in MDA.

We also considered the likeliness to find co-occurring domains by chance on randomly shuffled domain architectures. The artificial dataset that we constructed from P. falciparum sequences, allowed to verify again that DAMA performs the best followed by MDA. The difference between MDA and DAMA with CODD and dPUC is striking, especially when considering the high number of domains certified by the tools.

New improvements, leading to a higher accuracy, might be envisageable by looking at specific failures of DAMA, by replacing some of the optimization functions F_i with some alternative definition, by redefining tolerance parameters δ_i as functions of specific architecture characteristics (as the number of domains) or by integrating other architecture characteristics like the high frequency of certain pairs of domains that was ignored in this version of the tool.

Funding

This work was undertaken (partially) in the framework of CALSIMLAB, supported by the public grant ANR-11-LABX-0037-0 from the ‘Investissements d’Avenir’ program (ANR-11-IDEX-0004-02) (to A.C. and J.S.B.); Institut Universitaire de France (A.C.) and Brazilian National Research Agencies CNPq, CAPES, FAPERJ and FACEPE (to F.R.J.V. and G.Z.).

Conflict of Interest: none declared.