Abstract
Tuning the lattice strain (εL) is a novel approach to manipulate the magnetic, electronic, and transport properties of spintronic materials. Achievable εL in thin film samples induced by traditional ferroelectric or flexible substrates is usually volatile and well below 1%. Such limits in the tuning capability cannot meet the requirements for nonvolatile applications of spintronic materials. This study answers to the challenge of introducing significant amount of elastic strain in deposited thin films so that noticeable tuning of the spintronic characteristics can be realized. Based on subtle elastic strain engineering of depositing L10-FePt films on pre-stretched NiTi(Nb) shape memory alloy substrates, steerable and nonvolatile lattice strain up to 2.18% has been achieved in the L10-FePt films by thermally controlling the shape memory effect of the substrates. Introduced strains at this level significantly modify the electronic density of state, orbital overlap, and spin-orbit coupling (SOC) strength in the FePt film, leading to nonvolatile modulation of magnetic anisotropy and magnetization reversal characteristics. This finding not only opens an efficient avenue for the nonvolatile tuning of SOC based magnetism and spintronic effects, but also helps to clarify the physical nature of pure strain effect.
Magnetic1,2,3,4, electronic5,6,7, and coupled magneto-transportation8,9,10,11,12,13,14,15,16,17,18,19 properties of spintronic materials and heterostructures are sensitive to their intrinsic and/or interfacial electronic structures. Studies have shown that spin distribution, charge density, orbital occupancy, and spin-orbit coupling (SOC) strength of these materials can be modified through a local electrical field or a spin polarized current, resulting in tunibility in magnetic responses1,2,3,4, magnetization switching8,9,10,11, and spin dependent transport6,12,13,14,18 properties. However, most of the electrical modulation methods are volatile thus not suitable for nonvolatile applications. And it is still challenging to realize effective and nonvolatile modulation of electronic and related characteristics in spintronic materials.
Lattice strain (εL) is known to be closely related to the physical or chemical properties of a material. It has been shown by ab initio calculation that when the lattice constant of a semiconductor changes by 1%, there can be a change in bandgapas as much as 100 meV20. Thus, there is increasing interest in using lattice strain to manipulate spintronic materials properties15,19,21,22,23,24,25,26,27,28,29,30,31,32,33. Recent studies show that by incorporating piezo/ferroelectric materials as substrates, it is possible to use external electric field to influence the magnetic properties of deposited magnetic films through the inverse magnetoelectric coupling effect21,22,23,24,25,26. However, such strain introduction is volatile unless the magnetic domain structures can be altered25,26. Furthermore, the transferrable lattice strain in such heterostructures is normally limited to be less than 0.5%21,22,23,24, which restricts the tuning effectiveness in magnetic properties. Further studies also show that when appropriate buffer layers are used, it is possible to obtain a lattice strain as large as 3% in a deposited magnetic film, but there is little tunability in film electronic structure and magnetic properties once the strain is set27,28,29. More recently, the use of polymer substrates with high ductility has been explored to modulate the magnetic properties of grown films. Although polymer strain can exceed 30%30,31, mismatch in Young’s modulus between magnetic film and polymer substrate limits the possible film strain to be below 1%32,33. Thus, it is of great importance to able to generate and control a significant amount of elastic strain in spintronic films so that electronic structure and related magnetic/transport properties can be tuned.
In previous work, we demonstrate the achievement of a revertible strain as large as 6.5% in a NiTi(Nb) shape memory alloy (SMA) by coupling the pseudoelasticity of NiTi matrix with the elasticity of Nb nanowires34. Such a large strain output has the potential to effectively modulate the lattice strain in magnetic thin films deposited on top of it. In such a system, simple thermal treatment can introduce significant shape recovery in the SMA substrate through the inverse martensitic phase transformation, and because the elastic modulus of the SMA is on the same order as many metallic films, significantly large lattice strains can be introduced in the magnetic films (as shown in the Fig. 1). This approach allows easy strain modulation in the thin film by controlling the pre-deformation and heat treatment of the SMA substrate. Moreover, the elastic lattice strain in the film is nonvolatile because the elastic deformation of substrate can be maintained in a broad temperature range (−20 °C ∼ 100 °C). Thus, this subtle heterostructure design can help to realize large, steerable, and nonvolatile elastic strains which are desirable for effectively modifying the electronic structure and magnetic property of magnetic films. To verify this hypothesis, we deposited L10-FePt films on pre-stretched NiTi(Nb) SMA substrates. L10-FePt alloy is a spintronic material with high magnetocrystalline anisotropy and strong SOC strength. But effective magnetism tunability in the L10-FePt films via elastic strain engineering was scarcely reported due to the difficulty of introducing significant elastic strain in such large magnetocrystalline anisotropy materials. In the current study, an in-plane compressive lattice strain as high as 2.18% was obtained in the L10-FePt film, leading to prominent changes in density of state (DOS) and SOC strength, and consequently resulted in noticeable and nonvolatile change in magnetic anisotropy (up to 75%).
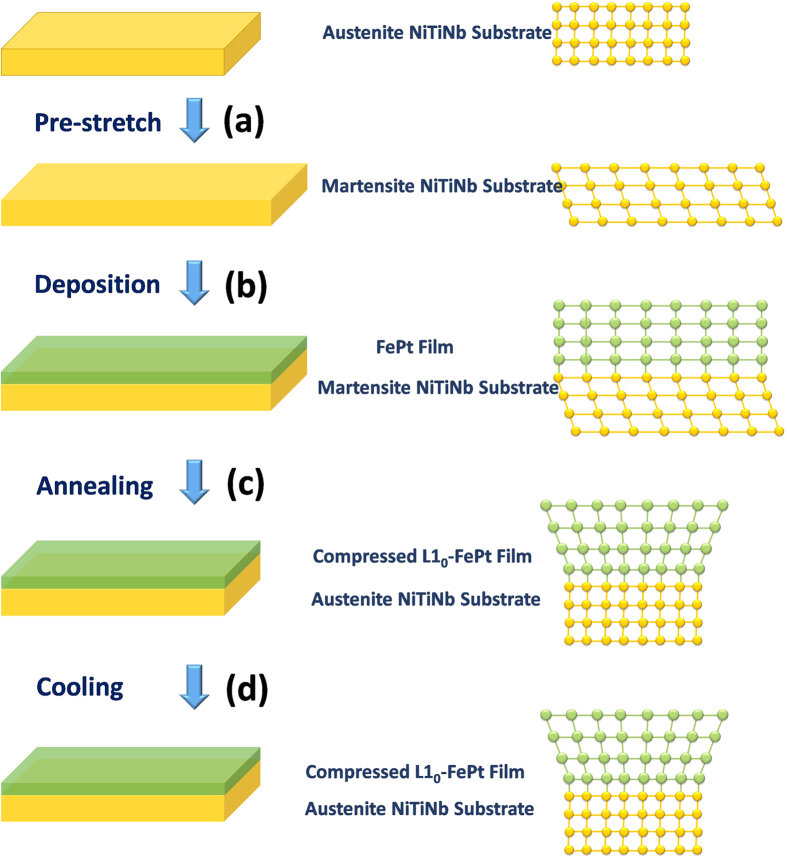
Figure 1. Schematics of sample preparation and corresponding atomic structure change during sample deformation.
(a) Pre-treatment of NiTi(Nb) substrate: A NiTi(Nb) sheet was pre-stretched to induces reorientation of the martensitic phase. Then, the surface of the NiTi(Nb) sheet was cleaned and polished to achieve a surface roughness around 1 nm. (b) Film deposition: the FePt film was deposited on the polished SMA substrate by magnetron sputtering. (c) Sample annealing: the as-deposited sample was annealed to introduce both the L10 ordering in the FePt film and the shape recovery in the substrate through an inverse martensitic phase transformation, resulting in a nonvolatile lattice strain in the L10-FePt film. (d) Sample cooling: the compressive strain maintained in the film even after cooling down to room temperature.
Results
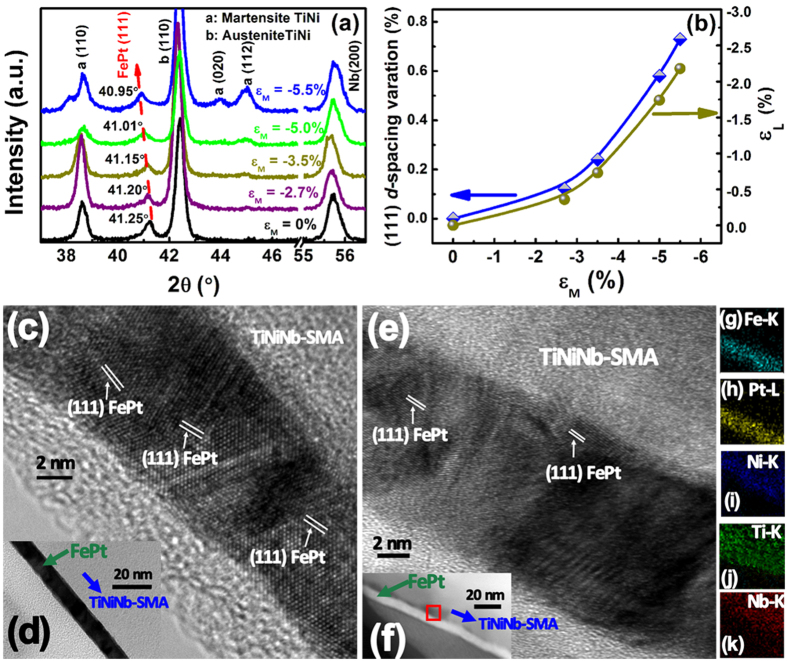
In this work, the revertible macro-strain (εM) of the NiTi(Nb) substrates were tuned between 0% to 5.5% through the control of the pre-deformation amount (seen in Figure S1). The samples were first studied by X-ray diffractometer (XRD) and high-resolution electron microscopy (HRTEM). The TEM local images (Fig. 2c–f) and elemental mapping pictures (Fig. 2g–k) indicate strong adhesion between the film and the substrate. Sharp interface with no apparent atomic diffusion can be observed. Such favorable interfacial condition ensures the strain transfer from the substrate to the film. Lattice strain in the FePt film is quantified using XRD spectra (Fig. 2a). All FePt samples exhibit (111) texture, implying that the (111) plane lies parallel to the film plane. When εM in the NiTi(Nb) substrate increases from 0% to 5.5%, the attached FePt(111) diffraction peak (2θ) gradually shifts from 41.25° to 40.95°, indicating an increasing in the (111) plane-spacing. The (111) d-spacing variation ratio was used to evaluate the out-of-plane tensile strain in the film, as shown by the blue line in Fig. 2b. Assuming a FePt Poisson’s ratio υ of 0.3335, the in-plane compressive lattice strain (εL) in the film can be calculated, as shown by the yellow line in Fig. 2b. A maximum εL value of 2.18% has been achieved, which is at least 4–5 times larger than the lattice strain that can be achieved by ferroelectric substrates (<0.5%)21,22,23,24,25,26. It should be noticed that the lattice strain in the film is not uniform across the film thickness and the calculated εL is an average value.
Figure 2. Microstructure and strain evolution in L10-FePt(10 nm) films grown on shape memory alloy substrates with different amount of pre-deformation.
(a) XRD patterns of the samples with different macro-strain (εM) in the SMA substrates. (b)Variations of the FePt(111) d-spacing and the in-plane compressive lattice strain (εL) with εM. Cross-sectional HRTEM images of the samples: (c,d) εM = 0%; (e,f) εM = −3.5%. (g–k) Elemental mapping obtained from EDX scan of the area marked by the red square in Fig. 2f.
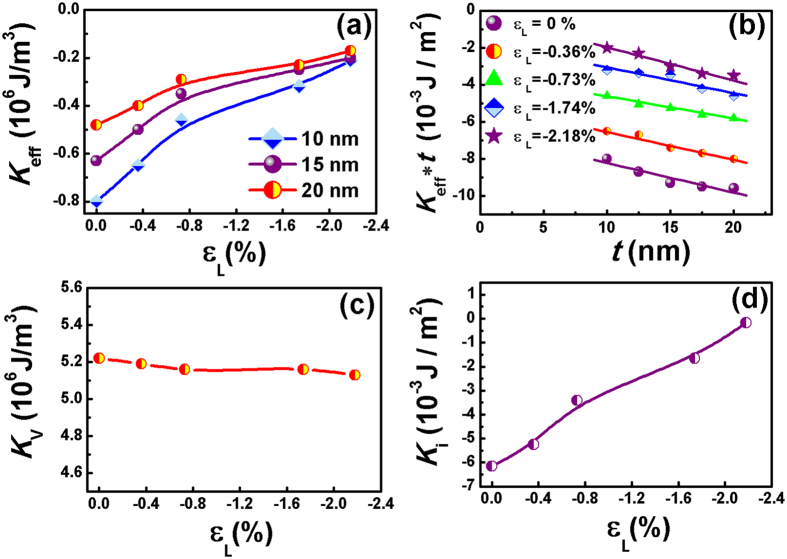
Under such large elastic strain, how do magnetic properties of the film change? From the in-plane (along the strain) and out-of-plane hysteresis loop (Figures S2–S4) measurements, the dependence of the FePt effective magnetic anisotropy (Keff) on εL is determined and shown in Fig. 3a. Here, Keff, the energy difference when the FePt film is magnetized along the in-plane and out-of-plane directions, is used to describe magnetic anisotropy of a film. When Keff is positive, a sample possesses the so-called perpendicular anisotropy (PMA). In this work, all of the FePt films on NiTi(Nb) substrates possess in-plane anisotropy (as shown in the Figs S2–S4,) because of the (111) texture. Figure 3a clearly shows that the magnetic anisotropy of the FePt film grown on NiTi(Nb) is very sensitive to both the lattice strain εL and the film thickness (t). Small variation in εL can lead to noticeable change in the Keff, suggesting that the modification of lattice strain is indeed an effective method to manipulate the magnetic properties of thin films. The thinner the film, the larger the tunability in FePt magnetic responses. For a 10 nm FePt thin film, Keff increases from −0.8 × 106 J/m3 at zero strain to −0.2 × 106 J/m3 when εL = −2.18%. Such significant change in the magnetic anisotropy (up to 75%) was rarely reported in hard magnetic materials used for logic storage devices, which is very important for reducing device power consumption36. When t increases from 10 nm to 15 nm or 20 nm, the tunability of magnetic property decreases. Thus, the strain effect can be considered as interfacial effect which exhibits stronger effects in smaller film thickness. For a magnetic film, the total anisotropy energy includes bulk anisotropy (Kv), shape anisotropy (Ks = −2πMs2), and interfacial anisotropy (Ki), as shown in formula 137:
Figure 3. Magnetic property tunability induced by lattice strain in the L10-FePt (t = 10, 15, 20 nm) films.
(a) Keff dependence on εL (from 0% to −2.18%). (b) Dependence of Keff*t on t as a function of strain. (c,d) Modification of bulk anisotropy (Kv) and interfacial anisotropy (Ki) by εL, where Kv and Ki are obtained from the slope and the y axis interception of the curves in Fig. 3b, respectively.
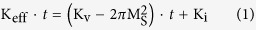 |
Where MS is the saturation magnetization of FePt. By plotting the variation of Keff ·t with t (Fig. 3b), we can tell from the relative contributions of Kv (the slope of the curves) and Ki (the y axis interception) to Keff. As shown in Fig. 3c, with increasing εL, Kv only changes slightly, but Ki rises at a much higher rate. For ordered L10-FePt, Kv (i.e. intrinsic magnetocystalline anisotropy) is dominated by the ordering degree of the structure38. Thus, it is possible that the strain has not significant influence on the ordering of the FePt atomic structure and ordering degree effect on magnetism modification is not dominant. On the other hand, the drastic increase of Ki in Fig. 3d suggests that the in-plane compressive strain in the FePt film introduces additional magnetic anisotropy with the easy magnetization direction perpendicular to the film plane, resulting in the tilting of magnetization easy axis away from in-plane direction and consequent increase of Keff. These results indicate that the Keff manipulation observed here are mainly resulted from the interfacial anisotropy induced by the large elastic strain.
Discussion
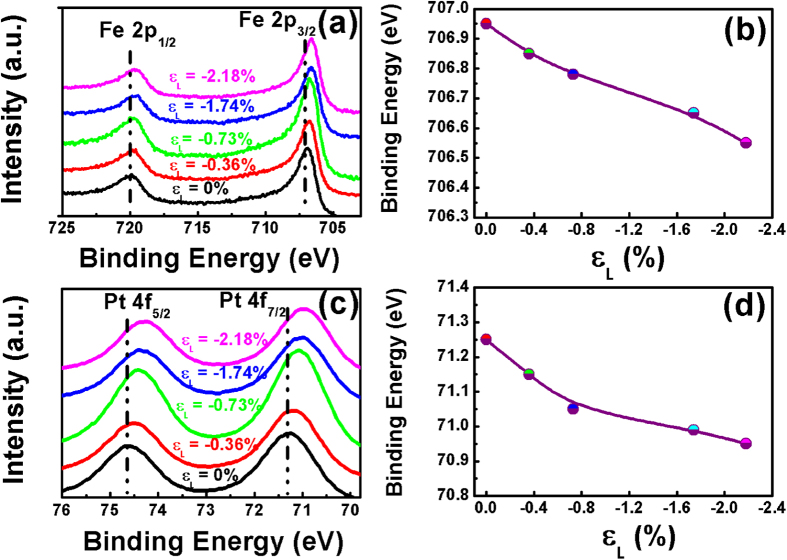
The interfacial strain modulation effect is hypothesized to directly link to the evolution of interfacial electronic structure of the spintronic materials. To reveal the electronic structure changes, X-ray photoelectron spectroscopy (XPS) analyses were conducted on NiTi(Nb)-SMA/L10-FePt(3 nm)/Ta(5 nm) films with different amount of lattice strain. The binding energy evolution of the characteristic Fe2p and Pt4f electrons at the NiTi(Nb)/FePt interfaces, which reflects the effect of elastic strain on the interfacial electronic structure, is shown in Fig. 4. All of the Fe and Pt atoms at the interface remain in metallic states (the standard binding energy for Fe 2p3/2 and Pt 4f7/2 electrons are 706.75 eV and 70.9 eV, respectively). However, as the compressive strain increases, Fe 2p3/2 and Pt 4f7/2 peaks shift by 0.3 ∼ 0.4 eV towards the low binding energy. Actually, increasing compressive strains in the film enhances the overlap of outer electron orbits in the Fe and Pt atoms and strengthens the shielding effect to the core electrons. This is equivalent to the reduction of nuclear charge, and will consequently lead to the decline of binding energy of core electrons, and thus shifts the XPS peaks. The noticeable peak shift provides direct proof of substantial modification of the electronic structure due to elastic strain.
Figure 4. Effect of elastic strain on the interfacial electronic structure of the L10-FePt film.
(a,c) High resolution XPS spectra of characteristic Fe2p and Pt4f electrons at the NiTi(Nb)/FePt interface of the NiTi(Nb)-SMA/L10-FePt (3 nm)/Ta(5 nm) sample; and (b,d) Binding energy evolutions of Fe2p3/2 and Pt4f7/2 electrons with different εL.
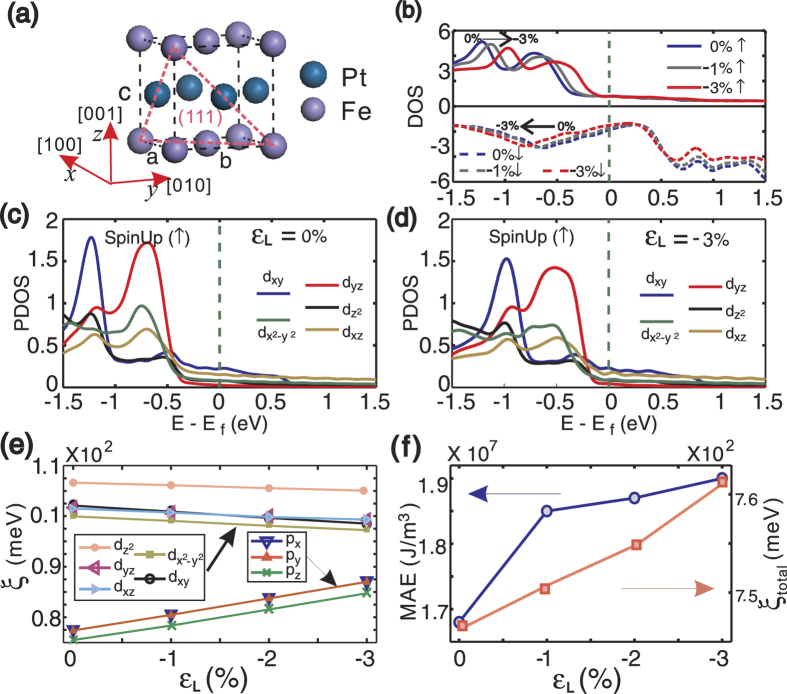
To theoretically reveal the elastic strain effect on electronic structures of FePt, we conducted first-principle calculations based on the density functional theory (DFT). Since we focus on the role of externally induced elastic stresses on FePt in the calculation, ideal bulk L10-FePt is assumed, as shown in Fig. 5a. Considering the FePt films deposited on the NiTi(Nb) substrate are (111) oriented (seen in Fig. 2a), the elastic stress induced by NiTi(Nb) substrates is assumed to act on FePt (111) uniformly. On the other words, the [100], [010] and [001] axis of FePt crystal have the same compression ratio, seen in Fig. 5a. To show the strain effect, 4 different compressive strains, εL = 0%, −1%, −2%, −3%, along the three axis, were calculated.
Figure 5. First-principles calculations on modifications of interfacial electronic structure and related physical properties due to the lattice strain in L10-FePt.
(a) Unstrained unit cell of L10-FePt with lattice constants of a = b = 3.86 Å and c/a = 0.98. (b) Representative DOS of the spin-up (↑) and spin-down (↓) electrons in L10-FePt films with three different strains. (c,d) Comparison of the PDOS of L10-FePt films with and without a compressive lattice strain (εL = −3%). (e) Calculated SOC strengths (ξ) for different orbitals in L10-FePt with a εL of −3%. (f) Dependences of total SOC strength (ξ total) and MAE of L10-FePt on the εL.
As shown in the calculated total density of state (DOS) in Fig. 5b, the spin distribution of spin-up electrons shifts toward fermi level with respect to increasing compressive lattice strains. Typically, when εL = −3%, the spin distribution shift by 0.3eV. On the contrary, the spin distribution of spin-down electrons shifts away from Fermi level when we increase the straining. As a consequence, the magnetic moment of L10-FePt decreases from 6.60 μB for εL = 0% to 6.27 μB for εL = −3% (seen in Figure S5b), which is consistent with our experimental observations (shown in Figure S6). Meanwhile, we also calculated the partial density of states (PDOS) of L10-FePt, shown in Fig. 5c for εL = 0% and Fig. 5d for εL = −3%, respectively. For simplification, we only plot the PDOS of d orbital because it dominates near the Fermi level for both Fe and Pt atoms. As shown in Fig. 5a, the closest atoms in x-y plane is along the xy direction, so dxy orbital has the largest DOS near the Fermi level (indicated by the blue line in Fig. 5c,d). Therefore, when we compress the FePt crystal along x, y and z axis, the dxy orbitals have the most overlap in Fe or Pt atoms, meanwhile, the dyz and dxz orbitals have the most overlap between Fe and Pt atoms. Comparing with Fig. 5c, the peaks of dxy and dyz orbitals in Fig. 5d have the biggest drop, resulting in a largest bandwidth for dxy and dyz orbitals.
With increasing the bandwidth, what happens to the SOC of L10-FePt systems? Here the well-known Thomas SOC formula has been used for analyses:
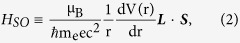 |
Where me is the electron mass, c is the speed of light, V(r) is the electrostatic potential at r, L and S are the orbital moment and spin moment, respectively. According to the spin-orbital matrix element analysis39, we project the SOC on each of the p and d orbital, plotted in Fig. 5e. Since the Pt atom is much heavier than the Fe atom, the SOC of Pt atoms dominates the total FePt SOC, and only the SOC strength (ξ) of Pt atoms is shown in Fig. 5e. As previously mentioned, with increasing compressive strain in the FePt (111) plane, the overlap of d orbitals between nearest atoms becomes larger, which reduces the localization of d orbital40 and results in a decrease in angular momentum Lz of the d orbital. From equation (2), we can see that the ξ of d orbitals will decrease with Lz, especially for the dxy orbital which have the largest overlap, as shown in Fig. 5e. On the other hand, the nearest 5p orbital of Pt is localized and does not have any overlaps, even during compression. So opposite to the d orbital, the Lz of 5p orbital only changes slightly during straining, leading to an increase of ξ for 5p orbitals. More importantly, the lattice compression makes the outer orbital charge density to have a quick increase. Therefore, the gradient of the electrostatic potential (dV(r)/dr) and ξ of 5p orbitals will increase considerably based on equation (2). Consequently, the ξ of 5p orbitals increases at a much faster rate than the decrease of ξ for the d orbital, which results in the total SOC strength (ξtotal) increase with the induced in-plane strain. As seen in Fig. 5f, ξtotal goes up from 746 meV for εL = 0% to 761 meV for εL = −3%. In-depth study of Fig. 5e shows that px and py orbitals have much larger contributions to the increase of ξtotal than the other orbitals. Since px and py are in the (001) plane, and the angular moments L are perpendicular to (001) plane, i.e. along the [001] direction. Equation (2) shows that the spin moment S in the [001] orientation will have the largest SOC, leading to the largest energy level splitting along the [001] direction for FePt. As a result, when external magnetic field is applied along the [001] axis, FePt will be stabilized with the lowest total energy. On the other words, inducing the compressive strain in FePt(111) plane makes the magnetization easy axis orientated along the [001] direction and increases the magnetic anisotropic energy (MAE) of L10-FePt. In Fig. 5f, when the compressive straining εL increases from 0% to −3%, the MAE of FePt system goes up from 1.68 to 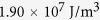 . This tendency is consistent with our experimental data of Keff as shown in Fig. 3a.
. This tendency is consistent with our experimental data of Keff as shown in Fig. 3a.
These results indicate large and nonvolatile lattice strain (maximum of 2.18% in this paper) can be achieved in FePt films through the nonvolatile shape memory effect of the SMA substrate, which can lead to effective tuning of the interfacial electronic structures such as electronic density of state and SOC strength, and results in noticeable and nonvolatile modulations of magnetic properties. This property modulation mechanism should also be applicable to other spintronic materials because no lattice match between film and SMA substrate is required. Since many spintronic effects are closely related to the SOC strength, including the anomalous hall effect12,13,18, spin hall effect8,14,15, spin transfer torque effect9,10,11, magnetic proximity effect16,17, and magnetic damping effect41, the importance of this work is not only to open an efficient avenue for magnetism tunability of spintronic materials, but also to provide a possible opportunity for the manipulation of SOC based spintronic effects by the elastic strain engineering. It should be mentioned that much larger recoverable strain (about 8%) has been achieved in SMA materials42, which gives us more possibility for unprecedented manipulations on electronic structure and property (our calculated results are shown in Figure S5).
Methods
Sample preparation process is shown in the schematic Fig. 1. (A) Preparation of NiTi(Nb) substrates. A cold rolled NiTi(Nb) sheet (0.5 mm thickness) was annealed at 400 °C for 20 min followed by an air cooling process. Then, the NiTi(Nb) sheet was cut into 3 mm × 100 mm pieces by electrical discharge machining. These pieces were then stretched in a tensile machine to introduce reorientation of martensitic phase in the sheets. The pre-loading amounts were chosen to be 6%, 8%, 10%, 12% which can produce revertible macro-strain (εM) of 2.7%, 3.5%, 5.0%, 5.5%, respectively, as verified by dynamic thermomechanical analysis (DMA) curves (Figure S1). After unloading, the sheets were cut into our desirable size for film deposition and characterization. Finally, the surface of the sheets was cleaned and polished until the surface roughness is around 1 nm by using both rough grinding (choosing abrasive paper from 600 Mo to 3000 Mo in sequence) and elaborated polishing (using 5 μm, 1 μm and 0.05 μm alumina suspension as the polishing agent). (B) Film Deposition. FePt alloy films (3–20 nm) were deposited on the polished SMA substrates by magnetron sputtering with a base pressure of 5 × 10−5 Pa and an Ar working pressure of 0.45 Pa. The FePt film composition was confirmed to be Fe52Pt48 by inductively coupled plasma atomic emission spectrometry. (C) Annealing of samples. The as-deposited samples were annealed at 350 °C in a vacuum of 3 × 10−5 Pa for 20 min. Thermal treatment introduces both the L10 ordering in the FePt film and shape recovery in the substrate through an inverse martensitic phase transformation. This process also introduces macro-strain transfer from the substrate to L10-FePt film, constructing the nonvolatile lattice strain in the film. (D) Cooling the samples down to room temperature for subsequent characterizations.
All of the property measurements and microstructure characterizations were conducted at room temperature. Magnetic properties were measured using a physical property measurement system (Quantum Design) with applied in-plane (along the strain) or out-of-plane fields up to 20kOe. The lattice strain development in the films was measured by XRD using Cu Kα radiation. The microstructure evolution after strain treatments was studied by the HRTEM (Tecnai F20). The electronic structure change at the NiTi(Nb)/FePt interface was revealed by the XPS measurements. Mg Kα radiation was used with the X-ray source that was run at 14.5 kV. The energy analyzer operated at a constant pass energy of 50 eV. Since the XPS detectable depth for Fe 2p and Pt 4f electrons are only 5.19 nm and 4.17 nm43, the NiTi(Nb)-SMA/L10-FePt(3 nm)/Ta(5 nm) samples with different elastic strain treatments were designed for the XPS tests. The Ta protection layer was etched off with Ar+ ion before collecting XPS signals from the NiTi(Nb)/FePt interface with a detecting angle of 90°. The etching rate was about 0.25 Å/s. Our DFT calculations were carried out with the projector augmented plane wave (PAW) method44 and Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional45, as implemented in the Vienna ab initio simulation package (VASP)46. For simplicity, it includes 2 Fe atoms and 2 Pt atoms per unit FePt cell. As shown in Fig. 5a, we took the experimental data for uncompressed system (εL = 0%), lattice constant a = b = 3.86 Å and c/a = 0.98. A fine K-mesh at 16 × 16 × 16 and energy cutoff at 500 eV were used to ensure numerical accuracy.
Additional Information
How to cite this article: Feng, C. et al. Nonvolatile modulation of electronic structure and correlative magnetism of L10-FePt films using significant strain induced by shape memory substrates. Sci. Rep. 6, 20199; doi: 10.1038/srep20199 (2016).
Supplementary Material
Acknowledgments
This work was supported by the National Science Foundation of China (Grant No. 11174020, 51271211, 51331002, 51471028, 51101170, 51231008), the National Key Scientific Research Projects of China (2015CB921502), the Beijing Nova programme (Grant No. Z141103001814039), the Beijing Natural Science Foundation (Grant No. 2132021), Beijing Laboratory of Metallic Materials and Processing for Modern Transportation, and the Beijing Higher Education Young Elite Teacher Project (Grant No. YETP0358). We thank CLUMEQ, Calcul Quebec, and Compute Canada for providing computation facilities.
Footnotes
Author Contributions C.F. conceived the work and wrote the paper. J.C.Z. fabricated the samples and performed the PPMS and XPS measurements. K.G. conducted the DFT calculations and corresponding interpretations. F.Y., Z.Q.W., L.C. and S.R.L. carried out studies of the SMA substrates and the HRTEM. S.J.H., Y.C., C.H. and J.Y.Z. gave many fruitful suggestions on the introduction. L.S. gave advice on the mechanism analyze and grammar modification. L.S.C. and G.H.Y. supervised the work. All authors discussed the results and commented on the manuscript.
References
- Weisheit M. et al. Electric field–induced modification of magnetism in thin-film ferromagnets. Science 315, 349–351 (2007). [DOI] [PubMed] [Google Scholar]
- Maruyama T. et al. Large voltage-induced magnetic anisotropy change in a few atomic layers of iron. Nat. Nanotechno. 4, 158–161 (2009). [DOI] [PubMed] [Google Scholar]
- Seki T., Kohda M., Nitta J. & Takanashi K. Coercivity change in an FePt thin layer in a Hall device by voltage application. Appl. Phys. Lett. 98, 212505 (2011). [Google Scholar]
- Cui B. et al. Electrical manipulation of orbital occupancy and magnetic anisotropy in manganites. Adv. Funct. Mater. 25, 864–870 (2014). [Google Scholar]
- Bauer U. et al. Magneto-ionic control of interfacial magnetism. Nat. Mater. 14, 174–181 (2015). [DOI] [PubMed] [Google Scholar]
- Cui B. et al. Reversible Ferromagnetic Phase Transition in Electrode-Gated Manganites. Adv. Funct. Mater. 24, 7233–7240 (2014). [Google Scholar]
- Qiu X. P. et al. Spin-orbit-torque engineering via oxygen manipulation. Nat. Nanotechno. 10, 333–338 (2015). [DOI] [PubMed] [Google Scholar]
- Fan X. et al. Observation of the nonlocal spin-orbital effective field. Nat. Commun. 4, 1799 (2013). [DOI] [PubMed] [Google Scholar]
- Liu L. Q. et al. Spin-torque switching with the giant spin hall effect of tantalum. Science 336, 555–558 (2012). [DOI] [PubMed] [Google Scholar]
- Myers E. B., Ralph D. C., Katine J. A., Louie R. N. & Buhrman R. A. Current-induced switching of domains in magnetic multilayer devices. Science 285, 867–870 (1999). [DOI] [PubMed] [Google Scholar]
- Tsoi M. et al. Excitation of a magnetic multilayer by an electric current. Phys. Rev. Lett. 80, 4281–4284 (1998). [Google Scholar]
- Nagaosa N., Sinova J., Onoda S., MacDonald A. H. & Ong N. P. Anomalous hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010). [Google Scholar]
- Seemann K. M. et al. Spin-orbit strength driven crossover between intrinsic and extrinsic mechanisms of the anomalous hall effect in the epitaxial L10-ordered ferromagnets FePd and FePt. Phys. Rev. Lett. 104, 076402 (2010). [DOI] [PubMed] [Google Scholar]
- Jungwirth T., Wunderlich J. & Olejník K. Spin hall effect devices. Nat. Mater. 11, 382–390 (2012). [DOI] [PubMed] [Google Scholar]
- Loong L. M. et al. Strain-enhanced tunneling magnetoresistance in MgO magnetic tunnel junctions. Sci. Rep. 4, 6505 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miao B. F., Huang S. Y., Qu D. & Chien C. L. Physical origins of the new magnetoresistance in Pt/YIG. Phys. Rev. Lett. 112, 236601 (2014). [DOI] [PubMed] [Google Scholar]
- Lin T., Tang C., Alyahayaei H. M. & Shi J. Experimental investigation of the nature of the magnetoresistance effects in Pd-YIG hybrid structures. Phys. Rev. Lett. 113, 037203 (2014). [DOI] [PubMed] [Google Scholar]
- He P. et al. Chemical composition tuning of the anomalous hall effect in isoelectronic L10-FePd1-xPtx alloy films. Phys. Rev. Lett. 109, 066402 (2012). [DOI] [PubMed] [Google Scholar]
- Sahadevan A. M., Tiwari R. K., Kalon G., Bhatia C. S., Saeys M. & Yang H. Biaxial strain effect of spin dependent tunneling in MgO magnetic tunnel junctions. Appl. Phys. Lett. 101, 042407 (2012). [Google Scholar]
- Feng J., Qian X. F., Huang C. W. & Li J. Strain-engineered artificial atom as a broad-spectrum solar energy funnel. Nat. Photonics 6, 865–871 (2012). [Google Scholar]
- Jo W. et al. Giant electric-field-induced strains in lead-free ceramics for actuator applications — status and perspective. J. Electroceram. 29, 71–93 (2012). [Google Scholar]
- Ehmke M. C. et al. Stress, temperature and electric field effects in the lead-free (Ba,Ca)(Ti,Zr)O3 piezoelectric system. Acta Mater. 78, 37–45 (2014). [Google Scholar]
- Zhu G. D. et al. Quantitative analysis of electric field induced change in anisotropy field in Co60Fe20B20/(011)xPb(Mg1/3Nb2/3)O3-(1-x)PbTiO3 (x~0.68). Appl. Phys. Lett. 101, 202404 (2012). [Google Scholar]
- Hsu C.-J., Hockel J. L. & Carman G. P. Magnetoelectric manipulation of domain wall configuration in thin film Ni/[Pb(Mn1/3Nb2/3)O3]0.68-[PbTiO3]0.32 (001) heterostructure. Appl. Phys. Lett. 100, 092902 (2012). [Google Scholar]
- Tsai W. C., Liao S. C., Huang K. F., Wang D. S. & Lai C. H. Nonvolatile electric-field modulation of magnetic anisotropyin perpendicularly magnetized L10-FePt/(001)[Pb(Mg1/3Nb2/3)]0.7-(PbTiO3)0.3 heterostructures. Appl. Phys. Lett. 103, 252405 (2013). [Google Scholar]
- Zhang S. et al. Electric-Field Control of Nonvolatile Magnetization in Co40Fe40B20 /Pb(Mg1/3Nb2/3)0.7Ti0.3O3 Structure at Room Temperature. Phys. Rev. Lett. 108, 137203 (2012). [DOI] [PubMed] [Google Scholar]
- Chen J. S., Lim B. C., Ding Y. F. & Chow G. M. Low-temperature deposition of L10-FePt films for ultra-high density magnetic recording. J. Magn. Magn. Mater. 303, 309–317 (2006). [Google Scholar]
- Jacobsen R. S. et al. Strained silicon as a new electro-optic material. Nature 441, 199–202 (2006). [DOI] [PubMed] [Google Scholar]
- Zeches R. J. et al. A Strain-Driven morphotropic phase boundary in BiFeO3. Science 326, 977–980 (2009). [DOI] [PubMed] [Google Scholar]
- Melzer M., Lin G. G., Makarov D. & Schmidt O. G. Stretchable spin valves on elastomer membranes by predetermined periodic fracture and random wrinkling. Adv. Mater. 24, 6468–6472 (2012). [DOI] [PubMed] [Google Scholar]
- Melzer M. et al. Stretchable magnetoelectronics. Nano Lett. 11, 2522–2526 (2011). [DOI] [PubMed] [Google Scholar]
- Tang Z. H. et al. Magneto-mechanical coupling effect in amorphous Co40Fe40B20 films grown on flexible substrates. Appl. Phys. Lett. 105, 103504 (2014). [Google Scholar]
- Dai G. H. et al. Mechanically tunable magnetic properties of Fe81Ga19 films grown on flexible substrates. Appl. Phys. Lett. 100, 122407 (2012). [Google Scholar]
- Hao S. J. et al. A transforming metal nanocomposite with large elastic strain, low modulus, and high strength. Science 339, 1191–1194 (2013). [DOI] [PubMed] [Google Scholar]
- Hsu C. J., Chen S. K., Liao W. M., Yuan F. T., Chang W. C. & Tsai J. L. Effect of Pt underlayer on the coercivity of FePt sputtered film. J. Alloy & Comp. 449, 52–55 (2008). [Google Scholar]
- Meng H. & Wang J.-P. Spin transfer in nanomagnetic devices with perpendicular anisotropy. Appl. Phys. Lett. 88, 172506 (2006). [Google Scholar]
- Kyuno K., Ha J.-G., Yamamoto R. & Asano S. Theoretical study on the strain dependence of the magnetic anisotropy of X/Co (X = Pt, Cu, Ag, and Au) metallic multilayers. J. Appl. Phys. 79, 7084–7089 (1996). [Google Scholar]
- Kota Y. & Sakuma A. Magnetocrystalline anisotropy in FePt with L10 ordering and tetragonal distortion. J. Appl. Phys. 111, 07A310 (2012). [Google Scholar]
- Laan G. V. D. Microscopic origin of magnetocrystalline anisotropy in transition metal thin films. J. Phys.: Condens. Matter. 10, 3239–3253 (1998). [Google Scholar]
- Stöhr J. Exploring the microscopic origin of magnetic anisotropies with X-ray magnetic circular dichroism (XMCD) spectroscopy. J. Magn. Magn. Mater. 200, 470–497 (1999). [Google Scholar]
- He P. et al. Quadratic Scaling of Intrinsic Gilbert Damping with Spin-Orbital Coupling in L10 FePdPt Films: Experiments and Ab Initio Calculations. Phys. Rev. Lett. 110, 077203 (2013). [DOI] [PubMed] [Google Scholar]
- Otsuka K. & Ren X. Physical metallurgy of Ti-Ni-based shape memory alloys. Prog. Mater. Sci. 50, 511–678 (2005). [Google Scholar]
- Tanuma S., Powell C. J. & Penn D. R. Calculations of electron inelastic mean free paths for 31 materials. Surf. Interface Anal. 11, 577–589 (1988). [Google Scholar]
- Blochl P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994). [DOI] [PubMed] [Google Scholar]
- Perdew J. P., Burke K. & Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
- Kresse G. & Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.