HEALER: homomorphic computation of ExAct Logistic rEgRession for secure rare disease variants analysis in GWAS

Abstract

Motivation: Genome-wide association studies (GWAS) have been widely used in discovering the association between genotypes and phenotypes. Human genome data contain valuable but highly sensitive information. Unprotected disclosure of such information might put individual’s privacy at risk. It is important to protect human genome data. Exact logistic regression is a bias-reduction method based on a penalized likelihood to discover rare variants that are associated with disease susceptibility. We propose the HEALER framework to facilitate secure rare variants analysis with a small sample size.

Results: We target at the algorithm design aiming at reducing the computational and storage costs to learn a homomorphic exact logistic regression model (i.e. evaluate P-values of coefficients), where the circuit depth is proportional to the logarithmic scale of data size. We evaluate the algorithm performance using rare Kawasaki Disease datasets.

Availability and implementation: Download HEALER at http://research.ucsd-dbmi.org/HEALER/

Contact: shw070@ucsd.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Genome-wide association studies (GWAS) (Visscher et al., 2012) have largely focused on the common disease gene discovery, which often involves large sample sizes. In GWAS, many common variations [e.g. Single-Nucleotide Polymorphisms (SNPs) with frequencies  > 1%] have been studied to uncover the risk of complex genetic disorders. One controversy in GWAS is whether multiple rare variations (with frequencies much <1%) may also result in certain risk. These unknown associations might be very important, as they could reveal the biologic cause of diseases and provide useful suggestions for treatments (Cantor et al., 2010). For example, Hamosh et al. (2005) show that rare variants (e.g. protein-modifying rare risk alleles) play a clear role in Mendelian disorders. There is increasing interest in the rare variants studies (Rivas et al., 2011; Styrkarsdottir et al., 2014) in GWAS. However, rare variations must have much higher effects (e.g. odds ratios) than that of common SNPs in order to be detected by ordinary GWAS methods (e.g. logistic regression) (Stram, 2014). These variants may be too rare, such that there are not enough participants with these rare alleles that could be identified in a study. When variants are very rare (i.e. lacking of enough samples), ordinary tests [e.g. Wald-test (Hauck and Donner, 1977) in GWAS fail to capture true significant alleles, as the asymptotic approximation assumption might be no longer valid. For example, in a recent study (Haiman et al., 2013) with unbalanced case-control population, (i.e. the number of case patients is about 10 times less than that of the control population), the ordinary method identified hundreds of significantly rare SNPs that is related to breast cancer. However, a later study (Stram, 2014) shows that most of these significant rare SNPs are false positive after applying exact logistic regression (Mehta et al., 2000). The exact logistic regression is more robust in computing P-values for rare variants analysis with limited sample size (Mehta and Patel, 1995). The studies of rare variants also raise significant privacy concerns of participants. Rare variants can be highly unique to the specific population, which makes them more vulnerable to re-identification attacks. As discussed in a previous study, Lin et al. (2004) show that an individual can be uniquely identified by using as few as 75 independent SNPs. Recent studies (Gymrek et al., 2013; Sweeney et al., 2013) demonstrated that even anonymized genome data can leak signification personal information (e.g. name) of the participants. Moreover, even aggregated genome information (e.g. test statistics) can be used to recover sensitive personal information (Homer et al., 2008; Wang et al., 2009). As genome data are vulnerable to various attacks (Humbert et al., 2013; Malin and Sweeney, 2001, 2004), it is imperative to develop protection methods to secure genome analysis.

A number of technical solutions (Ayday et al., 2013; Bos et al., 2014; Cheon et al., 2015; Jiang et al., 2014; Kamm et al., 2013; Lauter et al., 2014; Naveed et al., 2014; Wang et al., 2014; Xie et al., 2014; Yu and Ji, 2014) have been proposed to protect genome privacy in data analysis. Existing studies can be categorized into two groups: (i) protecting the computation process (Cheon et al., 2015; Humbert et al., 2013; Lauter et al., 2014) in genome data analysis, and (ii) protecting the genome data before computation (Wang et al., 2014; Zhao et al., 2015) or research outcomes after computation (Yu and Ji, 2014). In this work, we focus on the protection of the computation process of rare variants analysis in GWAS. In particular, we consider the use of homomorphic encryption techniques in designing secure protocols to learn an exact logistic regression model from encrypted data, which allow researchers to securely outsource the storage and computation of sensitive data (e.g. to commercial cloud computing services like Microsoft Azure or Amazon EC2). The development of homomorphic encryption-based methods to support secure genome data computation has been studied in (Bos et al., 2014; Cheon et al., 2015; Graepel et al., 2013; Lauter et al., 2014; Naehrig et al., 2011), where certain computation can be directly carried out over homomorphic-encrypted data. The resulting encrypted outcomes, when decrypted, match the result of the same operations performed on the plaintext. However, none of the aforementioned studies has addressed the problem of rare variants analysis in GWAS. In addition, Verle et al. (2015) recently proposed to tackle the secure rare-variants analysis using multi-party computation techniques. Their approach assumes multiple data owners and active participation of the owners in data storage and computation, which is completely different to our model as illustrated below.

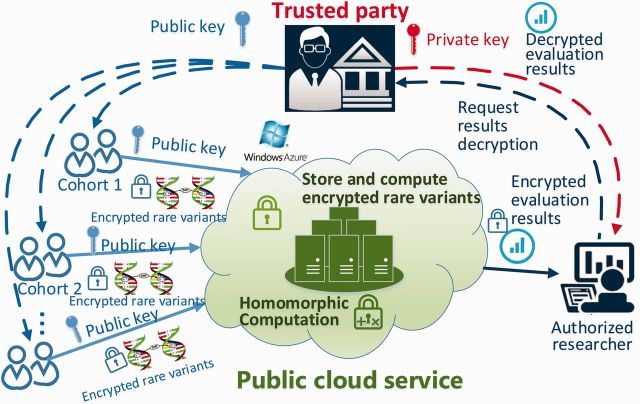
Figure 1 illustrates the application scenario of the proposed HEALER framework. Homomorphic encryption allows the encrypted rare disease variants to be stored and computed in a cloud server without requiring the participation of data owners, e.g. request for decryption keys. By encrypting rare variants with public key, data owners can directly upload them to the cloud service. Thus, the genetic association of rare disease variants with a phenotype can be securely evaluated with homomorphic computation over different cohorts. The final encrypted evaluation results are accessible to researchers, but it requires the private key for decryption from the trusted party. Remarkably, there is no interaction between the trusted party and the cloud service, which guarantees the confidentiality of uploaded sensitive information. Therefore, the proposed scheme enables secure outsourcing of the computation of rare disease variants to commercial cloud services, by which individuals could contribute to the rare disease analysis in GWAS in a secure manner protected by the homomorphic encryption schemes.

Fig. 1.

Application scenario of the proposed HEALER framework. By encrypting rare disease variants with public key, data owners can securely upload them to the cloud service, where the genetic association of rare variants with a phenotype can be securely evaluated with homomorphic computation without requiring the participation of data owners. Authorized researchers can obtain final evaluation results by requiring result decryption from the trusted party with the private key (Color version of this figure is available at Bioinformatics online.)

To enable HEALER framework, we developed novel methods including: (i) secure rejection sampling and (ii) secure and efficient integer comparison to compute a homomorphic exact logistic regression model, (iii) parallel computation over homomorphic-encrypted data to accelerate the proposed algorithm, (iv) a compression scheme to reduce the storage cost of homomorphic-encrypted data. We also compared the HEALER framework with other competing alternatives and conducted performance analysis of the proposed protocols in this article and the supplementary, including the acceptance rate of rejection sampling, circuit depth, and number of homomorphic operations. The rest of this article is organized as follows. In Section 2, we will introduce the exact logistic regression method and presents the implementation of homomorphic computation of exact logistic regression. Section 3 reports experimental results and Section 4 provides the discussion of the article. Section 5 concludes this article.

2 Methods

In this section, we introduce the exact logistic regression model and the proposed homomorphic encryption algorithm to secure the analysis, where a list of frequently used symbols can be found in the Supplementary Materials.

2.1 Exact logistic regression

Let us denote by $\mathbf{Y}=\{Y_1,Y_2,\dots Y_n|Y_i\in \{0,1\},i=1,\dots ,n\}$ a set of independent binary random variables and $\mathbf{y}={(y_1,y_2,\dots y_n)}^{\mathbf{T}}$ the realization of Y with n records. For clarity, we use bold and regular symbols to represent vector and scalar variables, respectively. In the logistic regression model, the response probability π_i for the ith record is formulated by

$$\log \left(\frac{{\pi }_i}{1-{\pi }_i}\right)={\mathit{\omega }}^{\mathit{T}}{\mathit{z}}_{\mathit{i}}+{\mathit{\beta }}^{\mathit{T}}{\mathit{x}}_{\mathit{i}}$$ (1)

where $\mathit{\omega }={{(\omega }_1,{\omega }_2,\dots ,{\omega }_{h_1})}^{\text{T}}$ and $\mathit{\beta }={{(\beta }_1,{\beta }_2,\dots ,{\beta }_{h_2})}^{\text{T}}$ are h₁ and h₂ dimensional model parameters with respect to the covariates ${\mathit{z}}_i=(z_i{}_1,z_i{}_2,\dots ,z_i{}_{h1})$ and ${\mathit{x}}_i=(x_i{}_1,x_i{}_2,\dots ,x_i{}_{h2})$, respectively. The likelihood function given the observations y, and parameters $\mathit{\omega }$ and $\mathit{\beta }$ can be expressed as

$$L(\mathit{Y}=\mathit{y}|\mathit{\omega },\mathit{\beta })=\frac{\exp \left({\displaystyle {\sum }_{i=1}^n{y}_i({\mathit{\omega }}^{\text{T}}{\mathit{z}}_i+{\mathit{\beta }}^{\text{T}}{\mathit{x}}_i)}\right)}{{\displaystyle {\prod }_{i=1}^n(1+\exp ({\mathit{\omega }}^{\text{T}}{\mathit{z}}_i+{\mathit{\beta }}^{\text{T}}{\mathit{x}}_i))}}$$ (2)

Here ${\mathit{z}}_{\mathit{i}}$ is a nuisance variable, which is correlated to the explanatory variable ${\mathit{x}}_{\mathit{i}}$, but may not be of direct interest. We can eliminate the model parameter $\mathit{\omega }$ by conditioning on the sufficient statistics ${\mathit{t}}_{\mathbf{\text{N}}}={\sum }_{i=1}^n{y}_i{\mathit{z}}_{\mathit{i}}$. Let us denote ${\mathit{t}}_{\mathbf{\text{I}}}={\sum }_{i=1}^n{y}_i{\mathit{x}}_i$ as the sufficient statistics of parameters of interest (i.e. β) and define $t_0={\sum }_{i=1}^n{y}_i$. The exact inference of β is based on the permutation distribution of its sufficient statistics. The conditional likelihood function of T_I given T_N = t_N can be expressed as

$$L({\mathit{T}}_{\mathbf{\text{I}}}={\mathit{t}}_{\mathbf{\text{I}}}|{\mathit{T}}_{\mathit{\text{N}}}={\mathit{t}}_{\mathit{\text{N}}}\mathit{\beta })=\frac{C({\mathit{t}}_{\text{I}},{\mathit{t}}_{\mathbf{\text{N}}})\exp ({\mathit{\beta }}^{{}_T}{\mathit{t}}_{\text{I}})}{{\displaystyle {\sum }_{\text{u}}C(\mathit{u},{\mathit{t}}_{\mathit{\text{N}}})\exp ({\mathit{\beta }}^{{}_T}\mathit{u})}}$$ (3)

where C(u, t_N) is the number of vectors ${\mathit{y}}^{*}={(y_1^{*},y_2^{*},\dots y_n^{*})}^{\text{T}}$, such that ${\sum }_{i=1}^n{y}_i^{*}=t_0$, ${\sum }_{i=1}^n{y}_i^{*}{\mathit{x}}_{\mathit{i}}=\mathit{u}$ and ${\sum }_{i=1}^n{y}_i^{*}{\mathit{z}}_i={\mathit{t}}_{\mathbf{\text{N}}}$. Note that y* is just a permutation of y. We define two vectors are equal, if their pair-wise elements are identical. Without loss of generality, we would like to make inferences about a single parameter $\beta$ with respect to the explanatory variable x_i. For the case of multiple parameter (i.e. $\mathit{\beta }={({\beta }_1,{\beta }_2,\dots {\beta }_{h2})}^{\text{T}}$ with h₂ > 1), one can eliminate the rest h₂ − 1 parameter by conditioning on their sufficient statistics in Equation (3). In this study, we limit our discussion of the problem with considering a single parameter at a time. Suppose we are interested in the following hypothesis test with null hypothesis against its two-sided alternative.

$${\text{H}}_0:\beta =0$$ (4)

One can calculate the exact P-value by summing the following conditional probability over a certain critical region R

$$P\text{value}={\displaystyle {\sum }_{v\in R}L(T_{\text{I}}=v|{\mathit{T}}_{\mathit{\text{N}}}={\mathit{t}}_{\mathit{\text{N}}},\beta =0)=}{\displaystyle {\sum }_{v\in R}\frac{C(v,{\mathit{t}}_{\mathit{\text{N}}})}{{\Sigma }_{\text{u}}C(u,{\mathit{t}}_{\mathit{N}})}}$$ (5)

For example, the critical region can be defined as $R=\{v:L(T_{\text{I}}=v|{\mathit{T}}_{\mathit{\text{N}}}={\mathit{t}}_{\mathit{\text{N}}},\beta =0\}\le L(T_{\mathit{\text{I}}}={\mathit{t}}_{\mathit{\text{I}}}|{\mathit{T}}_{\mathit{\text{N}}}={\mathit{t}}_{\mathit{\text{N}}},\beta =0)\}$. This region includes all possible values of the test statistic at which the above conditional probability is equal or less than that at the observed value of t_I. Sampling methods (Mehta and Patel, 1995; Mehta et al., 2000) are widely used to efficiently evaluate the P-value, where a detailed discussion can be found in Section S1 in Supplementary Materials.

2.2 Homomorphic encryption-based exact logistic regression

2.2.1 Homomorphic encryption

Homomorphic encryption is a form of encryption technique, which allows certain operations (e.g. addition and/or multiplication) to be conducted directly over ciphertext. Existing homomorphic encryption techniques can be categorized as follows (Fontaine and Galand, 2007): (i) partially homomorphic cryptosystems (PHCs) that support a single type of operation (i.e. either addition or multiplication) over ciphertext (Boneh and Shacham, 2002; Gjøsteen, 2006), (ii) fully homomorphic cryptosystems (FHCs) that support arbitrary number of addition and multiplication operations but less efficient (Brakerski and Vaikuntanathan, 2011; Gentry and Halevi, 2011) and (iii) somewhat homomorphic cryptosystems (SHCs) that is specified by a limited number of accumulated operations (Brakerski et al., 2012). PHCs like Paillier cryptosystems (Paillier, 1999): E(x) = g^xr^m mod m² (with modulus m and base g as the public key, and a random number $r\in \{1,\dots ,m-1\}$ to ensure the randomness of ciphertext) are very efficient: $E(x_1)E(x_2)=(g^{x_1}{r}_1^{\text{m}})(g^{x_2}{r}_2^{\text{m}}){\text{mod\hspace{0.17em}m}}^2=(g^{x_1+x_2}{(r_1{r}_2)}^{\text{m}}){\text{mod m}}^2=E(x_1+x_2)$. However, PHCs have limitation, as they cannot combine both addition and multiplication operations to securely solve complex problems. FHCs are more powerful than PHCs, as they support both operations without limitation. However, the complexity of FHCs is still formidable in solving practical problem. SHCs, which support a specific number of both accumulated operations, provide a better trade-off between the flexibility and efficiency. In this article, we will leverage SHCs to build basic functions to securely compute exact logistic regression. For the sake of simplicity, the rest of this article will use homomorphic encryption to denote somewhat homomorphic encryption.

2.2.2 The proposed HEALER framework

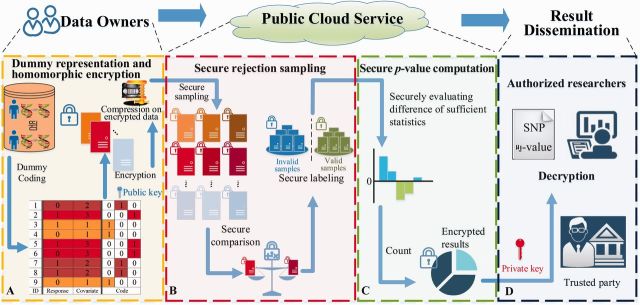
Figure 2 illustrated the four key steps of the proposed HEALER framework, which includes Step A: Data preparation and encryption by data owners, Step B: Secure rejection sampling in public cloud, Step C: Secure P-value computation in public cloud, and Step D: Result dissemination to authorized researchers. In step A, data owners can generate the encrypted dummy vector representations (see Supplementary Section S4) of the input data using homomorphic public key. Then, they can securely outsource both computation and storage of homomorphic-encrypted data to the public cloud service, where a compression scheme is proposed to reduce both storage and communication costs of homomorphic-encrypted data. In step B, the public cloud can securely generate samples by performing random permutations over encrypted data. Then, the proposed secure rejection sampling algorithm (see Supplementary Section S2) can be applied to securely label valid samples. In step C, the public cloud first securely computes the statistics based on the permuted samples and the corresponding labels. Then, the cloud securely counts the number of sample statistics that are greater than these from the originally encrypted dummy vector representations (see Supplementary Section S3). Finally, in step D, the authorized researcher can request the decrypted result to obtain the P-value as defined in Equation (S2) in Supplementary Materials. A detailed description of each step and the corresponding mathematical formulas can be found in Supplementary Sections S1–S6.

Fig. 2.

The workflow of the proposed HEALER framework involving four key steps: Step A: Data preparation and encryption by data owners, Step B: Secure rejection sampling in public cloud, Step C: Secure-value computation in public cloud, and Step D: Result dissemination to authorized researchers (Color version of this figure is available at Bioinformatics online.)

2.3 Parallel computation using multiple slots

In this section, we will discuss how to perform parallel computation using encryption schemes to support single instruction multiple data (SIMD) with L_S slots. It is worth mentioning that packing multiple ciphertexts into multiple slots have no impact on the size of encrypted data. We can utilize the multiple slots by packing (see Supplementary Fig. S3): (i) pre-permuted vectors of the same observation $\mathit{y}={(y_1,y_2,\dots ,y_n)}^{\text{T}}$or (ii) covariates from different models. In the scenario (i), we need to encrypt a few pre-permuted vectors 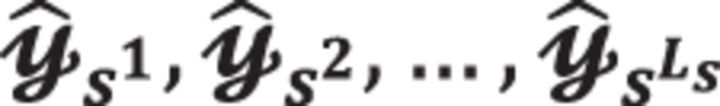where 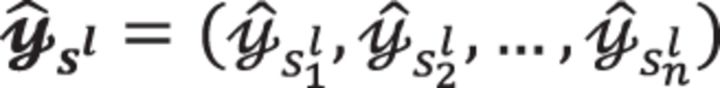is the lth permutation instance of the vector y indicated by the permutation index ${\mathit{S}}^l=({\text{S}}_1^l,{\text{S}}_2^l\dots ,{\text{S}}_n^l)$ with l = 1, 2,…,L_S. In this scenario, each slot can generate different samples for the same model using SIMD in parallel. Given multiple samples across multiple ciphertext slots, we can apply the proposed HEALER framework over the same covariate ${\widehat{\mathit{x}}}^{\mathit{l}}$ (e.g. the lth encrypted SNP) with different samples. Finally, the user can aggregate multiple counts to learn the P-value. The use case of the scenario (i) is that the data owner possesses all the observations in y (as it requires pre-permutation in multiple slots during the encryption phase) and would like to minimize the computational time of analyzing a single model. In contrast, the scenario (ii) allows cloud to learn multiple models in parallel. We can apply the HEALER framework over multiple covariate ${\widehat{\mathit{x}}}^1,{\widehat{\mathit{x}}}^2,\dots ,{\widehat{\mathit{x}}}^{{\text{L}}_{\text{S}}}$ with the same sample , where ${\widehat{\mathit{x}}}^l={({\widehat{\mathit{x}}}_1^l,{\widehat{\mathit{x}}}_2^l,\dots ,{\widehat{\mathit{x}}}_n^l)}^{\text{T}}$ with l = 1, 2,…, L is the covariate in lth model (e.g. different independent SNPs). Then, the aggregated counts in each slot can be used to evaluate the P-values in different models (e.g. independent SNPs). The use case of the scenario (ii) is that different data owners can securely contribute to the same rare disease study using the same public key (as the pre-permutation is no longer required) and the cloud can maximize the number of concurrent tasks for different model learning. It is quite favorable for rare disease analysis in GWAS, as data in such studies are usually from different sources and involve a large number of SNPs for analysis. Besides SMID parallelization, our framework supports multi-core and multi-node computation, as different computing nodes can access and compute the same encrypted data in parallel.

2.4 Storage and communication optimization of homomorphic-encrypted data through compression

Ciphertext in homomorphic encryption requires larger storage and communication costs than these of plaintext. It is important to reduce the size of homomorphic-encrypted data through compression, which would significantly improve the efficiency of the proposed framework in practical scenarios. One evidence supporting the motivation is that the ciphertext mainly consists of 10 numeric symbols (i.e. ‘0’–’9’), which implies that only four bits are required to represent each symbol. Therefore, the ciphertext size can be reduced by at least 50% with substitution-based compression schemes e.g. gzip (Deutsch, 1996) or 7zip (Pavlov, 2007).

In our framework, we adopt a Variable-order Markov Model (VoMM) (Begleiter et al., 2004) based compression scheme to further compress the homomorphic-encrypted data. Unlike the substitution based schemes (e.g. gzip or 7zip), VoMM-based methods establish mappings between the emergence frequency of the combination of finite numbers and probabilistic models. As a result, it can provide a more effective compression using the arithmetic coding. In our framework, we employed the PPMd scheme (Barr and Asanović, 2006) version-j1 to achieve a better compression.

3 Results

3.1 Experimental setups

Our HEALER framework was implemented in the HElib (https://github.com/shaih/HElib) and evaluated in the iDASH cloud (Ohno-Machado et al., 2012) at UCSD, where three virtual machines (VMs), each equipped with 96 GB memory and 8 cores, were used. Real rare Kawasaki Disease (KD) Coronary Artery Aneurysm (CAA) datasets with 15 and 30 records were obtained from three different institutions (i.e. UCSD, University of Emory, and Genome Institute of Singapore). Both datasets include one categorical nuisance variable [i.e. Percent C-reactive Protein (PCRP) expression level] with m = 3 categorical groups. Moreover, we selected 180 and 372 SNPs to fit slot size L_S in ciphertexts to maximize the computational throughput for both datasets based on the parameters shown in Supplementary Table S5. It is worth mentioning that the HEALER framework does not limit the number of supported SNPs. Readers can find more details of datasets and computing environment descriptions in Supplementary Section S8. The goal of this study is to evaluate the feasibility of using homomorphic computation of exact logistic regression to securely identify SNPs susceptible for KD CAA adjusted for different PCRP groups. The time and storage costs of key generation for both datasets are described in Supplementary Table S5.

3.2 Experimental results

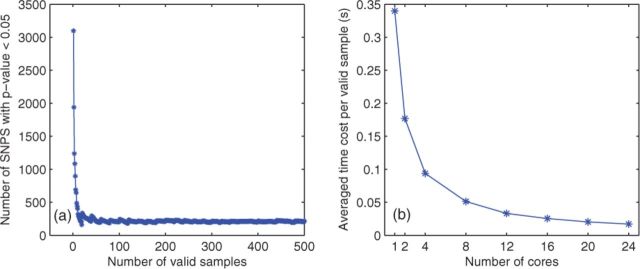
We evaluated the number of valid samples required to obtain the stable number of SNPs with P-value < 0.05 among 10 000 SNPs over plaintext (non-encrypted data) in Figure 3(a). We can see the number of SNPs with P-value < 0.05 varying with the number of valid samples, where the number decreases rapidly when the number of valid samples is over 80, and tends to be stable for 400 valid samples or more. For secure rejection sampling, Figure 3(b) depicts the average time cost for securely generating one valid sample over the encrypted KD dataset with 15 records, where we used up to 24 cores (8 cores × 3 VMs) in parallel. The time cost is measured by computing 180 SNPs in parallel based on the scenario (ii) in Section 2.3, where a total of 1440 number of samples were drawn for each SNPs with an acceptance rate of 17.397%. We can find that the time cost using 24 (8 × 3) cores is about one-fifth of the one using 4 cores, which demonstrates the scalability of the HEALER framework in the secure cloud computing. The remaining reported experimental results were all based on 24 cores (8 cores × 3 VMs).

Fig. 3.

(a) Number of SNPs with P-value < 0.05 versus number of valid samples over 10 000 SNPs, where the number of SNPs become stable when there are more than 400 valid samples. (b) Average time cost to securely generate a valid sample versus different number of cores using the KD dataset with 15 records. The time cost is for the computation of 180 SNPs in parallel based on the scenario (ii) in Section 2.3, where a total of 1440 samples were drawn for each SNPs with an acceptance rate of 17.397% (Color version of this figure is available at Bioinformatics online.)

Table 1 shows the time cost and sampling performance obtained by packing pre-permuted vectors of the same observation $\widehat{\mathit{y}}$ with multiple slots (see scenarios (i) in Section 2.3) for both KD datasets. Here, data encryption and decryption are one-time costs, which took up to 20 s as shown in Table 1. Remarkably, the time cost of P-value calculation for a single SNP was significantly reduced by parallel computation. The algorithm can securely evaluate the P-value of a single SNP within 3 min based on a total of 2262 number of valid samples for the larger KD dataset. Table 1 shows that the acceptance rates of 19.127 and 6.2687% were achieved for two KD datasets, respectively.

Table 1.

The performance to securely compute $p$-value for a single SNP based on scenarios (i) in Section 2.3 for both KD datasets

No. of records	Encryption time	Decryption time	P-value calculation	No. of valid samples	Acceptance rate
15	8.24 s	1.034 s	54.817 s	1928	19.127%
30	19.49 s	1.33 s	175.35 s	2262	6.2687%

In Table 2, we simultaneously computed 180 and 372 SNPs for both KD datasets, respectively (see scenarios (ii) in Section 2.3). Ciphertext slots were used to pack covariates from multiple models. Our algorithm generated 1677 and 1864 valid samples for the small and large KD datasets, respectively. Table 2 shows that the total time cost for P-value calculation is proportional to the number of SNPs and the number of records. However, comparing Tables 1 and 2, we can find that the average time cost for each SNP is mainly related to the number of records. Because the exact logistic regression is targeted to handle rare disease variants analysis, which typically involves a small number of records, the average time cost can be controlled in an acceptable level. In addition, the performance can be further improved by allocating more computational resources (e.g. in the case of could computing).

Table 2.

The performance to securely compute P-value for multiple SNPs (180 and 372) based on scenarios (ii) in Section 2.3 for both KD datasets

No. of records	Encryption time	Decryption time	Average computing time per SNP	No. of valid samples	Acceptance rate
15	7.53 s	7.947 s	46.489 s	1677	17.47%
30	17.04 s	25.356 s	171.25 s	1864	5.18%

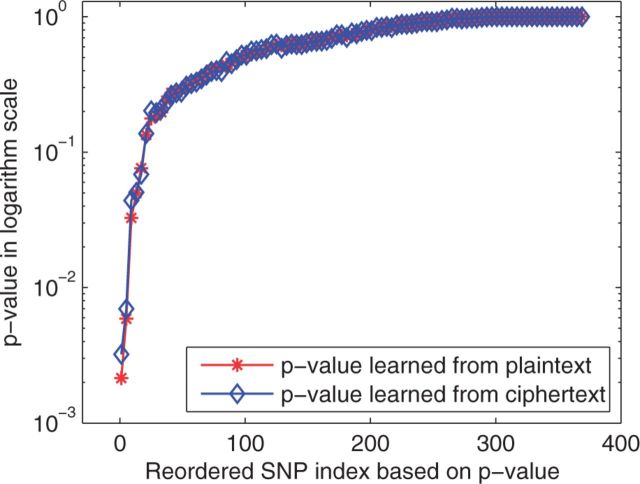
Finally, we validate the $p$-values calculated based on ciphertext (blue line with diamond marker) with those learned from plaintext (red line with asterisk marker) as shown in Figure 4, which includes P-values of 372 SNPs for the KD dataset with 30 records. We sorted the results learned from plaintext in ascending order, and ordered P-values learned from ciphertext accordingly. Figure 4 shows that the two curves are mostly matched, which validates the results obtained with the proposed HEALER framework. The differences in Figure 4 are due to the randomness in sampling algorithm. Table 3 lists the SNP IDs and P-values of the top five SNPs identified in the HEALER framework.

Fig. 4.

Sorted P-values for all the 372 SNPs, where the blue line with diamond marker and red line with asterisk marker are computed over ciphertext and the corresponding plaintext based on 1864 valid samples, where we found 13 SNPs with P-value < 0.05 (Color version of this figure is available at Bioinformatics online.)

Table 3.

The top five SNPs with the smallest P-values in all 372 SNPs

SNP ID	rs332822	rs332818	rs11121354	rs2977272	rs2764900
P-value	0.000536	0.0032	0.0038	0.0070	0.0123

4 Discussions

4.1 Performance analysis

We first analyze the acceptance rate of the proposed protocol. Let us denote n_j the number of records with covariate z_i = j and $n_j^1$ the number of records with y_j = 1 in the jth group with j = 1,…, m for a total of m categories. As samples are drawn by the random permutation of the vector $\widehat{\mathit{y}}$ with a total of $n$ records, the acceptance rate can be expressed as

$$p^{\text{accept}}={\displaystyle \prod _{j=1}^m\frac{\left(\begin{array}{c}{n}_j\\ n_j^1\end{array}\right)}{\left(\begin{array}{c}n\\ {\Sigma }_{j=1}^m{n}_j^1\end{array}\right)}}$$ (6)

Equation (6) shows that on average there will be a valid sample by drawing 1/p^accept samples. In other words, the algorithm can accept p^accept·r number of valid samples for drawing r samples.

Moreover, we conducted the complexity analysis of secure rejection sampling (Algorithm 1 in Supplementary Materials) and secure P-value computation (Algorithm 2 in Supplementary Materials) in terms of circuit depth, number of homomorphic multiplications (HMs), and homomorphic additions (HAs). The detailed step-by-step analysis is provided in Supplementary Materials. For Algorithm 1, Supplementary Table S3 shows that the circuit depth is log(2n(m − 1)). Given r samples, Algorithm 2 requires a circuit depth of log(4n(m − 1)), which is shown in Supplementary Table S4. Finally, the number of HAs and HMs could be reduced by a factor of L_S using L_S-slot in SIMD parallel computation or further reduced by a factor cL_S when using $c$ number of computing cores.

4.2 Comparison with other homomorphic encryption applications to protect computation process

In Table 4, we first discuss the storage cost among our proposed HEALER framework and three other homomorphic encryption-based applications (Bos et al., 2014; Cheon et al., 2015; Lauter et al., 2014) in terms of the size of a single encrypted value (SSEV) and the number of accumulated homomorphic multiplication (NAHM), where NAHM reflects the depth of a circuit and SSEV represents the average size of each encrypted integer. In addition, we can encrypted a total of L_S integers into one ciphertext with L_S slots, without increasing the ciphertext size. For example, we use 372 slots to store the KD dataset with 30 records, which yields an average cost of 4.68 KB to store a single encrypted integer without compression. Table 4 shows that the proposed method requires a much smaller ciphertext than that of the other schemes. When compared with the homomorphic edit distance application (Cheon et al., 2015), which represents an integer as a binary vector (BV), the proposed method can directly handle secure integer comparison. For example, at least four ciphertexts are required to represent an integer ranging from 0 to 15 in a BV representation. Thus, BV-based method usually results in a larger ciphertext. The SSEV and NAHMs for the applications of expectation maximization (with different number of iterations) and model evaluation (using logistic regression and cox regression) under various length of ciphertext modulus (in the parentheses) are also listed in Table 4, where our method shows the least cost of ciphertext size. Unlike HEALER, which is designed to securely learn an exact logistic regression model over a data set, the applications of model evaluation only take a pre-learned model parameter and a single record as inputs and evaluate the prediction result.

Table 4.

Comparison among HEALER and other homomorphic encryption applications in terms of the SSEV and the number of accumulated NAHM

Application scenarios			SSEV	NAHM
Exact logistic regression (HEALER)			4.38 KB	8
Edit distance (Cheon et al., 2015)			17.95 KB	13
Expectation maximization (Lauter et al., 2014)		2 iterations (192 bits)	96 KB	5
		3 iterations (384 bits)	384 KB	8
Model evaluation (Bos et al., 2014)		Logistic regression (128 bits)	64 KB	1
		Cox regression (512 bits)	1.0 MB	3

To further demonstrate the advantage of the proposed HEALER framework, we discuss the storage costs between HEALER and Binary HEALER in Table 5. Unlike HEALER using secure integer comparison, Binary HEALER is based on the idea of using BVs to represent integers (Cheon et al., 2015). Table 5 shows that Binary HEALER always requires larger circuit depths (i.e. larger levels L′ in modulus chain) due to the accumulated HMs required in the BV-based integer addition. BV representation of integers also results in both larger plaintext and ciphertext sizes, as each binary component in the vector needs to be encrypted as a ciphertext. The number of integers in ciphertexts that is required to compute the same dataset in both methods are also listed in Table 5, where HEALER requires much less redundant information (i.e. less number of integers). It is worth mentioning that the ciphertext can be further compressed to reduce the storage cost, as discussed in Section 2.4. Table 5 shows that the ciphertext size can be reduced by >55%, when the PPMd scheme (Barr and Asanović, 2006) was employed.

Table 5.

Comparison of storage costs between HEALER and Binary HEALER

Methods	No. of records	p	L′	Ciphertext size	Compressed ciphertext size	Plaintext size	No. of integers
HEALER	15	31	10	1.18MB	0.53MB	1.41KB	180
	30		11	1.59MB	0.71MB	2.91KB	372
Binary HEALER	15	2	13	9.97MB	4.43MB	15.75KB	504
	30		16	14.95MB	6.67MB	26.64KB	682

Where p is plaintext base and L′ is levels in modulus chain.

4.3 Comparison with perturbation-based protection methods

We compare HEALER with perturbation-based methods [i.e. Differential Privacy (DP)] for genome information protection. DP (Dwork, 2008) has emerged as one of the strongest privacy guarantees for sensitive data release. DP ensures that the risk incurred by changing any single individual’s information in a particular database is bounded by a quantifiable probability, where a higher protection can be achieved by choosing a smaller privacy budget ε. In practice, DP protections can be applied either to the original genome data (e.g. SNPs) before computation (Wang et al., 2014) or to the research outcomes (e.g. P-value or test statistics) obtained after computation (Yu and Ji, 2014). To compare with the methods of applying DP before computation (DPBC) and DP after computation (DPAC), we select a KD dataset with 30 records and 744 SNPs.

On the basis of the DPBC method by Wang et al. (2014), we grouped 744 SNPs into 18 blocks and set the number of specialization as 5. Then, we apply exact logistic regression over the DPBC protected data (short for the anonymized data that are generated by the DPBC method). We selected the P-value cutoff as 0.05 to evaluate how many significant SNPs can be correctly preserved in the DPBC protected data (in terms of Recall and Precision) under different privacy budgets (i.e. ε = 1 and 0.5). The number of significant SNPs based on the raw data under the P-value cutoff is also provided in Table 6. Table 6 shows that the recalls of DPBC method are <0.05 for all setups, which means that <5% of the originally significant SNPs with P-value < 0.05 can be preserved.

Table 6.

Comparison among HEALER, DPBC and DPAC methods in term of Recall and Precision in preserving significant SNPs with P-value cutoff 0.05, and privacy budget ε = 1 and 0.5

Methods	Recall		Precision		No. of significant SNPs
HEALER	1	1	1	1	70
DPBC	ε = 1	ε = 0.5	ε = 1	ε = 0.5
	0.0428	0.0286	0.1034	0.0556
DPAC	ε = 1	ε = 0.5	ε = 1	ε = 0.5
	0.0714	0.0571	0.2174	0.1481

Based on the idea of DPAC in (Yu and Ji, 2014), we also derived the corresponding DP algorithm for exact logistic regression in Supplementary Section S9. The results in terms of recall and precision in DPAC are better than those of DPBC in Table 6. Table 6 implies that it is hard to preserve significant SNPs after applying either DPBC or DPAC methods when record number is small. In contrast, the proposed HEALER framework can provide accurate results as well as protect the computation. A more detailed comparison among HEALER, DPBC and DPAC can be found in the Supplementary Section S11.

4.4 Comparison with secure multiparty computing

Homomorphic encryption methods are highly generalizable and promising for secure outsourcing to meet individual data custodians’ need in terms of privacy and utility (Check Hayden, 2015). But homomorphic encryption methods are also computation and storage intensive. In contrast, secure multiparty computing protocols are customized for certain data analysis tasks and allow multiple parties to collaborate. In these cases, participating parties jointly compute a function over their inputs, and keep these inputs private. Each party can perform certain computation locally over the controlled-access (private) data, and only exchange intermediary results to synthesize a global model. However, these protocols often require synchronization and involve a large amount of peer-to-peer communication. In contrast, homomorphic-encrypted data allow flexible on-demand analysis requests in an untrusted cloud environment. Given the homomorphic-encrypted data, authorized users are able to repeat existing analysis or conduct new analysis by outsourcing both storage and computation in the cloud.

4.5 Limitation

There are several limitations to the HEALER framework in the current designs. First, the HEALER framework is based on the rejection sampling scheme, where the acceptance rate would be low if a suitable proposal distribution is not available in the encrypted domain (Bishop, 2006). Second, the computational and storage costs over homomorphic-encrypted data are still very significant, which is several order of magnitudes higher than these over plaintext. Although, a compression scheme is employed to reduce the storage cost of homomorphic-encrypted data, further investigation is still needed to improve the storage efficiency. Third, as it is still challenging to efficiently handle homomorphic division operations (Naehrig et al., 2011), HEALER framework requires users to perform one division operation between two integers [see Equation (S2) in Supplementary Materials]. Finally, HEALER framework only considered the P-value evaluation. The estimation of the parameter β and the predictive inference of a response at x_i could be also possible (Mehta and Patel, 1995). However, they were not studied in our current implementation. There is still room to improve our algorithm by redesigning the sampling method to increase acceptance rate or making better use of the HELib and cloud computing parallel capacity. Besides obtaining P-values, we also plan to investigate parameter estimation and predictive inference on encrypted data in our future work.

4.6 Potential extension to whole genome sequencing and whole exome sequencing

Whole genome sequencing (WGS) and whole exome sequencing (WES) have been widely used to identify rare disease-associated variants (Cirulli and Goldstein, 2010; Lohmueller et al., 2013). However, many sources of false positive detections (O’Rawe et al., 2013) have been identified in discovering rare disease-associated variants in both WGS and WES. Recent study shows that a logistic regression-based filtering method (Hwang et al., 2014) can be applied to variant call files to reduce false positive detection. We speculate that homomorphic encryption techniques with proper optimizations (e.g. advanced algorithm designs with reduced circuit depth, acceleration with parallel computation, compression on encrypted data, etc.) could be applied to build a secure logistic regression-based filtering method to protect WGS or WES data. These warrant our future studies in homomorphic encryption-based methods.

5 Conclusion

This article presented a novel HEALER framework for estimating the P-value of exact logistic regression parameters over homomorphic-encrypted data. Our algorithm supports secure outsourcing and mitigates the risk of analyzing sensitive data in an untrusted cloud environment (e.g. Amazon EC2 or Microsoft Azure). We proposed a new rejection sampling approach, secure integer comparison methods and parallelizable mechanisms to accelerate the execution of these algorithms, which make the computation of homomorphic encrypted exact logistic regression practical. We also employed a compression scheme to reduce the storage and communication cost of homomorphic-encrypted data. We demonstrated the computational feasibility of our proposed framework, which takes about 3 min to compute over 30 records in parallel.

Funding

This work has been supported by the NHGRI (K99HG008175), NLM (R00LM011392, R21LM012060), NHLBI (U54HL108460), NSFC (61425011, 61271218 and U1201255) and ‘Shu Guang’ project (13SG13), NRF (No. 2014R1A2A 1A11050917).

Conflict of Interest: none declared.