QuantFusion: Novel Unified Methodology for Enhanced Coverage and Precision in Quantifying Global Proteomic Changes in Whole Tissues

Abstract

Single quantitative platforms such as label-based or label-free quantitation (LFQ) present compromises in accuracy, precision, protein sequence coverage, and speed of quantifiable proteomic measurements. To maximize the quantitative precision and the number of quantifiable proteins or the quantifiable coverage of tissue proteomes, we have developed a unified approach, termed QuantFusion, that combines the quantitative ratios of all peptides measured by both LFQ and label-based methodologies. Here, we demonstrate the use of QuantFusion in determining the proteins differentially expressed in a pair of patient-derived tumor xenografts (PDXs) representing two major breast cancer (BC) subtypes, basal and luminal. Label-based in-spectra quantitative peptides derived from amino acid-coded tagging (AACT, also known as SILAC) of a non-malignant mammary cell line were uniformly added to each xenograft with a constant predefined ratio, from which Ratio-of-Ratio estimates were obtained for the label-free peptides paired with AACT peptides in each PDX tumor. A mixed model statistical analysis was used to determine global differential protein expression by combining complementary quantifiable peptide ratios measured by LFQ and Ratio-of-Ratios, respectively. With minimum number of replicates required for obtaining the statistically significant ratios, QuantFusion uses the distinct mechanisms to “rescue” the missing data inherent to both LFQ and label-based quantitation. Combined quantifiable peptide data from both quantitative schemes increased the overall number of peptide level measurements and protein level estimates. In our analysis of the PDX tumor proteomes, QuantFusion increased the number of distinct peptide ratios by 65%, representing differentially expressed proteins between the BC subtypes. This quantifiable coverage improvement, in turn, not only increased the number of measurable protein fold-changes by 8% but also increased the average precision of quantitative estimates by 181% so that some BC subtypically expressed proteins were rescued by QuantFusion. Thus, incorporating data from multiple quantitative approaches while accounting for measurement variability at both the peptide and global protein levels make QuantFusion unique for obtaining increased coverage and quantitative precision for tissue proteomes.

The past decade has witnessed rapid progress in mass spectrometry (MS)-based quantitative proteomics with the development of software and data analysis tools to interrogate large amounts of MS data. Quantitative proteomic technologies have shown great potential in delineating dysregulated proteomes in diseases such as cancer (1–4). Quantitative schemes via either stable isotope labeling or label-free quantitation (LFQ)¹ are used widely to assist MS for quantitative assessments of the changes in protein expression, post-translational modifications (5), and protein-protein interactions (6) in many biological systems, including tumor samples (7–11). However, the integration of accuracy, sensitivity, and totality in the analysis of tumor-specific proteoforms from individual patients still remains challenging with the current quantitative platforms. For example, strategies to increase analytical throughput (12) for tumor analysis have utilized the multiplexing advantage of isobaric mass tags such as tandem mass tags or isotope tagging for relative and absolute quantitation (13, 14). However, for routine quantitative analysis of large scale peptides/proteins, tandem mass tags and isotope tagging for relative and absolute quantitation reagents are prohibitively expensive due to the requirement of large amounts of protein as input. The use of added internal peptide standards, derived from isotope-labeled cell lines, or ¹⁸O labeling to quantify peptides (15) allows for quantitation of proteome expression changes; however, these methods require high resolution in both LC separation and MS acquisition for accurate quantitation of overlapping isotopes. The metabolic incorporation of in-spectra quantitative markers through cell culture (16, 17), in vivo quantitation strategies involving amino acid-coded tags (AACT, also known as SILAC or stable isotope labeling by amino acids in cell culture (18)), is still considered the gold standard for accurate quantitation of relative changes in protein abundance across different biological states. However, for tissue proteomics, neither a single cell line as an add-in SILAC standard (19) nor a library of cell lines (a super-SILAC mix (20)) is close to being a universal standard due to peptides that are either missing or present at low levels. The missing internal standards that fail to cover tissue-peptide counterparts, referred to as orphan peptides, preclude quantitative estimation of tissue proteome differences, an issue that has been addressed recently by the addition of peptide standards (21). A more universal labeling strategy such as complete labeling of the equivalent tissue of the organism of interest via stable isotope labeling of mammals (SILAM) has found limited utility (22, 23). The relatively high cost and laborious procedures associated with animal feeding and labeling prevent widespread use of SILAM.

Conversely, quantitation of tissue and tumor proteins is very amenable to LFQ and has gained traction recently as an alternative to spiked-in labeled standards (24, 25). Despite the inherent low precision and low throughput of LFQ methods (i.e. multiple separate or independent LC-MS runs as opposed to interdependent, multiplexed LC-MS runs), LFQ does offer some advantages. Running each sample separately provides a higher number of peptide identifications, whereas LFQ avoids issues inherent to multiplexing, such as low or discrepant labeling efficiencies, inaccuracies in sample mixing, and the need for scrambling/switching the isotope-labeled samples to test whether conversion of isotopically labeled arginine to proline impacts results (26). Also LFQ using MS1 peak intensities can significantly improve the sensitivity as much as 60% compared with label-based quantitative methods such as AACT that rely on the MS1 peak intensities (18).

We therefore reasoned that the integration of multiple quantitative schemes would provide synergy, higher throughput, and effectiveness to more precisely determine the changes of protein expressions with a larger coverage of given tissue proteome across different tumor subtypes. Specifically, combining peptide abundance differences using both LFQ and AACT label-based, Ratio-of-Ratio (RoR) estimations would greatly increase the overall number of quantifiable peptide/protein changes to distinguish various tumors. When a common set of peptide features cannot be matched and quantitated between two independent LFQ LC-MS runs due to the frequently occurring issues of retention-time misalignment, the labeled-based quantification strategy could provide complementary peptide ratio estimation. Conversely, when LFQ provides quantitation ratios between samples after retention-time alignment of features, a situation may also exist wherein, at minimum, one of the samples lacks a labeled peptide counterpart, making the label-based estimate impossible. To achieve a complementary quantitative scheme, here we report our development of a unified quantitative approach, termed QuantFusion, that uses a multivariate mixed model to interrogate quantifiable peptide data derived from both LFQ and label-based AACT methods from a single MS experimental run. As stated above, LFQ and RoR measurements share complementary information and therefore can be integrated to reduce the number of replicates required for generating the statistically significant LFQ ratios.

The complexity of combining dependent outcomes with heterogeneous error structures and varying sample sizes within each protein necessitated the use of a statistical model. We demonstrate the merit of the mixed model-based approach on the integration of the global-scale proteome characteristics implicated in two major breast cancer (BC) subtypes. QuantFusion increased by 65% the number of distinct peptide ratios to highlight BC-subtypic proteome differences. This increase of quantifiable peptide coverage, in turn, increased the number of measurable protein fold-changes by 8% and increased the average precision of quantitative peptide estimates by 181%. The Statistical Analysis Software code used to implement the statistical model along with a test data set used in this study are available to investigators who wish to perform QuantFusion experiments.

MATERIALS AND METHODS

Tumor Sample Generation and Protein Extraction

Patient-derived xenograft (PDX) breast tumors were established (27, 28) and processed to cryopulverized powders (4, 14). The powders (100 mg wet weight) were subjected to lysis and protein extraction using a buffer composed of 8 m urea, 50 mm Tris, pH 8.0, 75 mm NaCl, 1 mm MgCl₂, and 500 units Benzonase. Approximately 1 mg of total protein extracted was reduced with DTT and subsequently alkylated with iodoacetamide. The proteins were then subjected to proteolysis with endoproteinase Lys-C (Wako Chemicals, USA, Richmond, VA) for ∼4 h at 37 °C. The solution was diluted 4-fold with 25 mm Tris, pH 8.0, 1 mm CaCl₂ and further digested with trypsin (Promega, Madison, WI) for ∼12 h at 37 °C. Digestion was stopped by the addition of TFA to 0.4%, and the precipitate was removed by centrifugation. The peptide solutions were desalted on Sep-Pak Light C18 cartridges (Waters, Milford, MA) and dissolved in 30% acetonitrile, 0.1% TFA before loading on a 300-μm Source 15S (GE Healthcare, Pittsburgh, PA) column for basic reversed phase chromatography (bRPLC). A linear LC gradient was performed by increasing buffer B from 0 to 70% within 60 min, where buffer A was aqueous 10 mm ammonium formate, and buffer B was 90% AcCN (Acetonitrile) in 10 mm ammonium formate. A total of 30 fractions were collected for each of the basal (WHIM2) and luminal (WHIM16) samples and non-contiguously recombined to five fractions per sample. The fractions were dried and desalted using a stop-and-go-extraction tip (StageTip) protocol containing 4 × 1-mm C18 extraction disk (3 m).

Liquid Chromatography-Tandem Mass Spectrometry and Protein Identification

Samples were desalted using PepClean C18 spin columns (Pierce) according to the manufacturer's directions and resuspended in aqueous 0.1% formic acid. Sample analysis was performed via reversed phase LC-MS/MS using a Proxeon 1000 nano-LC system coupled to a Q Exactive mass spectrometer (Thermo Scientific, San Jose, CA). The Proxeon system was configured to trap peptides using a 3-cm long, 100-μm inner diameter C18 column at 5 μl/min liquid flow that was diverted from the analytical column via a vent valve, whereas elution was performed by switching the valve to place the trap column in line with a 15-cm long, 75-μm inner diameter, 3.5-μm, 300-Å particle C18 analytical column. Analytical separation of all the tryptic peptides was achieved with a linear gradient of 2–30% buffer B over 240 min at a 250 nl/min flow rate, where buffer A was aqueous 0.1% formic acid, and buffer B was acetonitrile in 0.1% formic acid.

LC-MS experiments were also performed in a data-dependent mode with full MS (externally calibrated to a mass accuracy of <5 ppm and a resolution of 70,000 at m/z 200) followed by high energy collision-activated dissociation-MS/MS of the top 20 most intense ions. High energy collision-activated dissociation-MS/MS was used to dissociate peptides at a normalized collision energy of 27 eV in the presence of nitrogen bath gas atoms. All five bRPLC fractions were derived from three process technical replicates of each tumor sample and were subjected to two independent LC-MS runs resulting in the production of 20 LC-MS runs for global peptide analysis. Mass spectra were processed, and peptide identification was performed using the Andromeda search engine found in MaxQuant software version 1.3.0.5 (Max Planck Institute, Germany). All protein database searches were performed against the UniProt human and mouse protein sequence database downloaded from the Clinical Proteomic Tumor Analysis Consortium Data Portal (29). This database contains 105,001 annotated proteins, and the sequences were derived from the UniProt December 2012 assembly. Peptides were identified with a target-decoy approach using a combined database consisting of reverse protein sequences of the UniProt human, mouse, and common repository of adventitious proteins. The common repository of adventitious proteins database was obtained from the Global Proteome Machine. Peptide inference was made with a false discovery rate (FDR) of 1%, and peptides were assigned to proteins with a protein FDR of 5%. A precursor ion mass tolerance of 20 ppm was used for the first search that allowed for m/z retention time recalibration of precursor ions that were then subjected to a main search using a precursor ion mass tolerance of 6 ppm and a product ion mass tolerance 0.5 Da. Search parameters included up to two missed cleavages at Lys/Arg on the sequence, oxidation of methionine, and protein N-terminal acetylation as a dynamic modification. Carbamidomethylation of cysteine residues was considered as a static modification. Peptide identifications are reported by filtering of reverse and contaminant entries and assigning to their leading razor protein. All of the mass spectrometry data on PDX tumor samples were deposited at the CPTAC Data Coordinating Center as raw and mzML files for public access.

Peptide and Protein Quantitation

LFQ was performed based on peak area. The measured area under the curve of m/z and the retention time-aligned extracted ion chromatogram of a peptide were performed via the label-free quantitation module found in MaxQuant version 1.3.0.5 (30). All replicates for each PDX were included in the LFQ experimental design with peptide-level quantitation performed using unique and razor peptide features corresponding to identifications filtered with a posterior error probability of 0.06, peptide FDR of 0.01, and protein FDR of 0.05. The MaxQuant peptide and protein groups files were processed and stored in an Oracle database, and statistical analysis, model building, and visualization of a majority of data were performed based on Statistical Analysis Software code and R script that was developed in-house. All of the processed results are found in supplemental Table S1, and single peptide identifications are provided in supplemental Table S2 with annotated MS/MS spectra in supplemental file spectra.zip.

QuantFusion for Comprehensive Quantitation of BC-subtypic Differences in Global Protein Expression in PDX Tissues

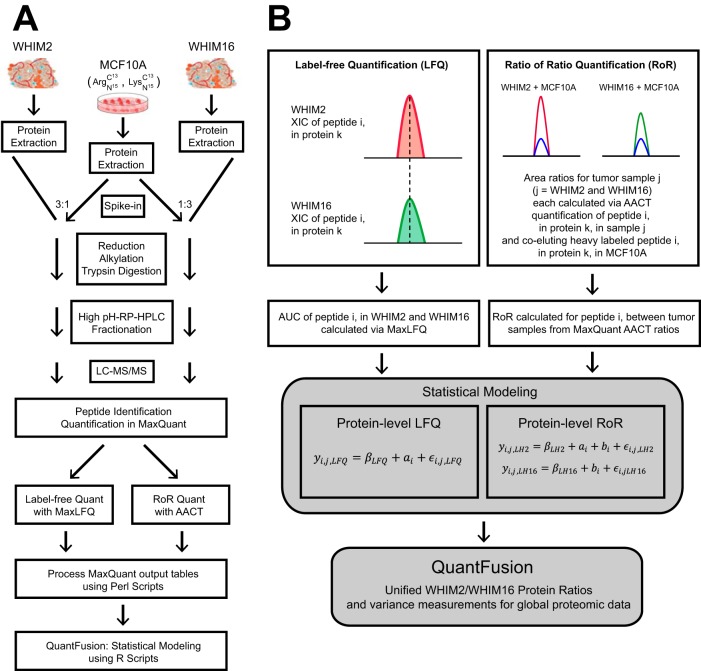
Fig. 1A illustrates the proteomic workflow used for obtaining quantitative comparisons of the two PDX tumor samples, WHIM2 and WHIM16, with addition of AACT-labeled, non-malignant mammary epithelial cell line MCF10A used for generating in-spectra quantitation-reference peptides. The cell line was grown in a culture medium with ¹³C₆¹⁵N₄-enriched arginine and ¹³C₆,¹⁵N₂-lysine (AACT-labeled or “heavy”). The workflow starts with protein extraction from the cryopulverized PDX tissues, followed by addition of heavy-labeled proteins from MCF10A into the WHIM tissue tumor protein lysates at approximately a 1:3 stoichiometric ratio. The peptide mixtures were then subjected to reduction, alkylation and digestion to obtain tryptic peptides. To reduce the complexity of the peptides in MS/MS analysis, the protein mixture was fractionated into 30 fractions by a high-pH bRPLC. Based on the distribution of HPLC-separated peptides, noncontiguous fractions were selected and combined into five fraction pools that allowed for the optimization of the chromatographic separation and detection of peptides by LC-MS. Fig. 1B illustrates the tiered workflow where the spectra are first assigned identities at the global peptide level, and then each identified feature was quantified, respectively, using either LFQ of unlabeled spectra across both samples or by obtaining an AACT ratio from the added in heavy labeled MCF10A cells and the corresponding peptide counterpart on individual tissue samples. It should be noted that both ratio measurements by LFQ and AACT-derived ROR were obtained from the same raw dataset of each single LC-MS/MS run, i.e. one LC-MS run for WHIM2 with MCF10A added in (3:1) and another LC-MS run with WHIM16 with MCF10A added in (3:1), respectively.

Fig. 1.

Proteomic workflow and QuantFusion model. A, proteomics workflow to analyze PDX tumors with heavy labeled added-in standard peptides derived from an MCF10A cell line. The cell line proteins were added to each tumor lysate at a protein mass ratio of 1:3, reduced, alkylated, and subjected to dual digestion with an endoproteinase Lys-C-trypsin enzyme combination. The resulting peptides were fractionated by high pH reversed phase liquid chromatography into 30 fractions that were non-contiguously recombined into five fractions and used for global LC-MS proteomic analysis. All data were subjected to LFQ analysis and AACT ratio determination. The LFQ and AACT outputs were processed using a Perl script and subjected to statistical modeling. B, graphical depiction of LFQ and RoR quantitation schemes and statistical model that merges LFQ and RoR estimates into a unified estimate.

Statistical Analysis

Analysis at the peptide level began with the assumption that identification and spectral groupings are correct. LC-MS/MS was performed on the WHIM2-MCF10A added in sample, and the WHIM16-MCF10A added in sample with two replicates each, respectively. MaxQuant was then used to process both the WHIM raw spectra data together with an LFQ analysis and another AACT-based quantitative analysis respectively, resulting in 3 separate datasets for each replicate. These datasets were then merged into one file and the outcomes were converted into log ratios. Note, that many different methods exist to measure LFQ data and an analysis of these methods is beyond the scope of this paper. We simply used the ratios of the peptide level measurements as reported by MaxQuant but our model would certainly permit different types of LFQ ratios to be substituted here. We conducted a complete case analysis where only peptide ratios are examined. For LFQ data, a single peptide ratio can be used as a measure of the protein fold-change. However, a protein fold-change from light to heavy in WHIM2 and from light to heavy in WHIM16 is required for a RoR protein estimate. Thus, our analysis was performed using only LFQ intensities that have matching intensities in both samples and light to heavy ratios (LH) that belong to proteins that can be feasibly RoR-estimated. In other words, a single LH ratio in WHIM2 that belongs to a protein with no LH ratio in WHIM16 must be discarded. With the data reduction complete, we computed the appropriate ratios and their base 2 logarithms. For each peptide, itself within a protein, there are now three ratios that can be observed. In protein i, each LFQ peptide ratio should equal the protein ratio, and we call this quantity a_i, whereas b_i and c_i represent log protein ratios between the light and the heavy protein ratio in WHIM16 and WHIM2, respectively. Then, based on the RoR model assumptions, we expect that c_i − b_i = a_i. This relationship leads to the following model definition (Equation 1) for the log scale intensity ratios,

where y_i,j,T is the type T (either LFQ or RoR) ratio of the jth peptide within the ith protein, so that y_i,j,LH2 is the log LH intensity ratio in WHIM2 for the jth peptide from protein i (i.e. type LH16 denotes a LH ratio in WHIM16, and type LFQ denotes the LFQ peptide intensity ratio from WHIM2 to WHIM16). β_T is a fixed effect representing the average ratio across all proteins within type T. b_i is a random effect that represents the light to heavy ratio in WHIM16 for protein i. a_i is a random effect representing the log fold-change for protein i between WHIM2 and WHIM16 (a_i is the parameter of interest). Experimental variability (ε) is represented Equations 2 and 3,

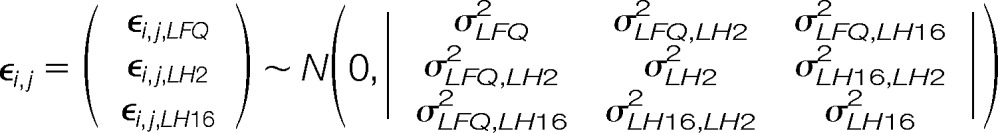and it is independent of

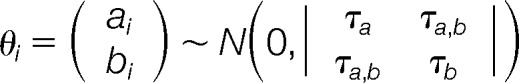which represents the natural variability among proteins. It is common in proteomics experiments to center at zero the average log fold-changes across all proteins. This practice has been performed here by defining a_i as a mean zero random variable. In this setting, the parameters (β_LH2 − (β_LH16) and β_LFQ represent experimental effects that have shifted the protein ratio profiles away from one for the RoR and LFQ experiments, respectively. Notice that the asymmetry of these equations is determined by the comparison of interest. Our LH2 equation contains an extra parameter so that an LH2 peptide minus an LH16 peptide will leave us with the same parameter obtained from our LFQ equation, a_i. If a user wanted to reverse this relationship, study LH16/LH2, then the parameterization would have to be switched and the LFQ ratios would have to be inverted. Following only one of these steps would be a mistake.

In this model, the predicted log protein fold-change â_i is informed from both the LFQ ratios and the LH ratios. For this reason, we refer to â_i as our Unified Estimate. Because we have made the primary parameters of interest random effects, our estimates of these quantities are in the form of Best Linear Unbiased Predictors (31). This approach yields greatly improved computational efficiency. A fixed effects model would likely have forced us to break up the analysis into separate partitions, as was done by Oberg and Mahoney (12). Our random effects formulation allows us to analyze all the data at once on any modern computer. The Best Linear Unbiased Predictors also provides some built-in protection against outliers. When a protein is estimated from a small number of peptide ratios, the estimate will be “shrunk” toward the average of all protein ratios. This shrinkage estimate provides improved accuracy and repeatability in highly unbalanced situations (32). Problems that arise from the stochastic missingness inherent to mass spectrometry experiments and the potential for misidentifications are mitigated by the shrinkage estimates.

Empirical Best Linear Unbiased Predictors were calculated for each protein random effect (â_i), and the error of the predictor was estimated as var(â_i − a). To select proteins of interest, we divided the fold-change estimates by their variance estimates. These values are similar to z scores in a fixed effects analysis, and the values can be used to generate q-values as described by Storey (33). All proteins with a q-value of less than 0.05 were considered “significant.” Statistical Analysis Software code for fitting the model QuantFusion.sas and sample data file SampleDat.csv are provided in the supplemental material.

RESULTS AND DISCUSSION

Overview of QuantFusion, A 'Ratio-based' Statistical Model for the Integration of LFQ and RoR

To recover peptide pairs missed for quantitation when either LFQ or RoR is used alone, we developed a data-dependent statistical model, termed QuantFusion, to unify data obtained via each method. Fig. 1 shows a workflow integrating MS data from two methods as follows: label-free peptide intensities of both tumor samples, and ratios derived using the corresponding peptide intensity of the added-in cell line. Note that the use of the MCF10A-derived heavy peptides at lower concentrations provides a common quantitative standard in both tumors without compromising the sensitivity of detecting endogenous peptides from the WHIM tissues.

Protein abundances in MS data are computed from either the mean or median of the corresponding peptide intensity ratios (34) instead of from raw intensity values, because each amino acid sequence potentially has a different probability of ionization. Measuring average intensities provides an estimate of the number of ions that make their way into a mass spectrometer, but to make inferences about protein concentrations, one must note that the ionization probabilities are the same for matching peptides across samples. As a result, the ionization probabilities in a ratio will cancel out, leaving a ratio of the concentrations in each sample. Furthermore, assuming that the trypsin digestion efficiencies are the same for all samples, these peptide ratios should be equivalent to the protein ratio(s) found in the sample. Hence, estimating the protein ratio by computing the average peptide ratio is reasonable.

Many statistical models exist that provide similar estimates to the average ratio method just described (12, 35, 36). These models do not attempt to take into account any missing values and when “peptide” is included as a covariate, model based estimates of protein fold changes will be very similar to the median ratio estimate. The primary advantage to the model based approach lies in the estimation of a single experimental variance parameter, obtained from information across different proteins.

Attempting to account for missing data bias is a worthy objective but not one that we address here. However, our method does provide a way to decrease the number of missing ratios. In the LFQ framework, a peptide ratio will be missing if a measured peptide in sample A has no corresponding intensity aligned in sample B. Conversely, in the RoR framework, a peptide ratio will be missing if the intensity in sample A cannot be matched to the heavy-labeled peptide also found in sample A. These missing data mechanisms are distinct, which means that if we combine both quantitative estimate schemes we can increase the amount of peptide ratios available in either scheme for use in our analysis. However, combining both methods requires some thought. Consider the case where we observe all of the possible data for a given peptide. We will have raw intensity measurements for the peptide in samples A and B, y_A and y_B, respectively. We will also have the corresponding heavy-labeled intensities h_A and h_B. y_A and y_B will be processed according to the LFQ protocol (30), which will create LFQ intensity values l_A and l_B. Thus, three ratios will be formed as follows: the LFQ ratio l_A/l_B, the light-to-heavy ratio within A, y_A/h_A, and the light-to-heavy ratio within B, y_B/h_B. The RoR estimate for a peptide would then be computed as y_A/h_B·h_B/y_B, which should equal y_A/y_B because the heavy-labeled peptides were mixed in constant/equal proportions in each sample. It might be tempting at this point to simply average the RoR and LFQ ratios. However, such averaging would be a significant mistake for two reasons. First, the values are not independent. l_A and l_B come from a transformation of y_A and y_B, which means that treating them as two separate pieces of data to be used in estimating the protein ratio will lead to anti-conservative estimates of variability. Second, the methods have substantially different error processes. If the variation of the LFQ estimates is much greater than in the RoR estimates, then it will make more sense to weight their contributions accordingly. To account for the complications of this situation, we have developed a statistical model that estimates and incorporates the covariance structure of the data. This model is explained in detail under “Materials and Methods.”

QuantFusion Is Superior to Any Single Quantitation Scheme, Either LFQ or AACT-derived RoR, for Estimating BC-subtypic Global Proteomic Differences

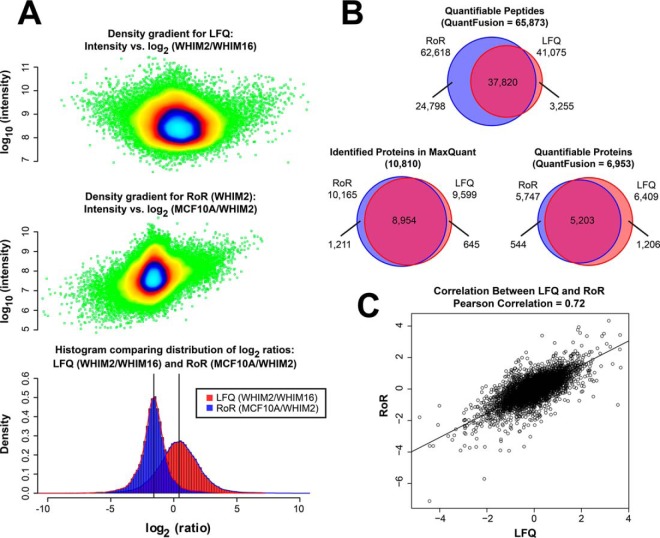
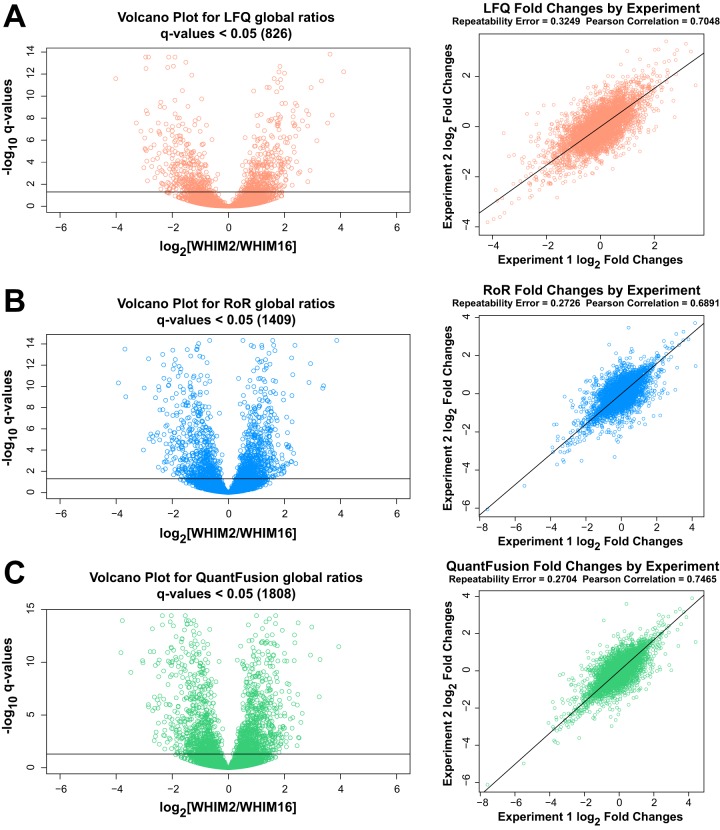
Fig. 2A shows the overlaid histogram of all global peptides for WHIM2/WHIM16 LFQ-ratios and MCF10A/WHIM2 AACT-ratios. It is noteworthy that the LFQ ratio and AACT ratio are shifted by 1:3 and mirror the experimental added-in total protein ratio of 1:3 between MCF10A cells and WHIM2 tumor cells. The corresponding intensity (in log scale) is shown for each distribution with colors representing the density gradients. Analogously, we obtained the MCF10A/WHIM16 AACT ratio centered at 1:3 for global peptides, and by combining both ratios, we obtained RoR estimates that quantified differences in the expression of individual proteins between WHIM2 and WHIM16 tumors with label added-in standards from the MCF10A cell line as the common reference. Fig. 2B shows the overall number of peptides and proteins quantified using LFQ, RoR, and the QuantFusion method. The number of quantifiable peptides was 41,075, 62,618, and 65,873, respectively, for LFQ, RoR, and QuantFusion. The number of quantifiable protein groups was 6,409, 5,747, and 6,953, respectively, for LFQ, RoR, and QuantFusion (these proteins are listed in supplemental Table S3). This demonstrates the benefit of using the unified approach to increase the number of assignments of quantifiable peptides to the corresponding proteins. Fig. 2B also shows a comparison of the number of LFQ (9,599) and RoR (10,165) protein groups initially identified in the MaxQuant search. Compared with an analysis that used only LFQ data, the QuantFusion method increased by 65% the number of unique peptides used for measurements of protein abundance changes, which, in turn, led to an 8% increase in the number of unique proteins quantified. More importantly, the average estimate precision was increased by 181%. Fig. 2C shows the correlation between LFQ and RoR for the global scale overlapping protein quantification values with a Pearson Correlation of 0.72. The unquantifiable protein groups are not addressed in the context of missingness, where a missing value can either be imputed, obtained by additional measurements, or obtained by targeted quantification methods such as selected ion monitoring (37) or data-independent acquisition (38). Our QuantFusion method provides an opportunity to recover true quantification values as a unified estimate when present in either LFQ or RoR separately. The unified quantification values for all missing values highlighted in either LFQ or RoR are presented in supplemental Table S4. We selected significant proteins based on a q-value of less than 0.05. This criterion is basically arbitrary. One could reasonably look at q-values of less than 0.001 or one might even prefer to analyze the posterior probability of being near zero instead of using q-values. Any decision rule based on both fold-change magnitude and the variability of the estimate yields similar results. Fig. 3 shows precision versus fold-change magnitude with the color scheme based on two different criteria. In Fig. 3, we color in green the points where the q-value was less than 0.05. Points representing the posterior probability that a ∈ (−.1,.1) <0.05 are in blue, and points where both “significance” conditions are met are in red in Fig. 3. Fig. 4 compares the volcano plots and corresponding correlation plots for LFQ, RoR, and QuantFusion. The volcano plots show 826, 1,409, and 1,808 biologically significant protein groups that are differentially expressed between WHIM2 and WHIM16 determined by LFQ, RoR, and QuantFusion, respectively, for a q-value cutoff of 0.05. Applying the q-value criteria to the two reduced models, which use only LFQ or RoR values, respectively, the QuantFusion estimate increases the number of biologically significant fold-changes by 119% from that obtained by LFQ. The corresponding volcano plots were obtained when applying a posterior probability to obtain significant changes between WHIM2 and WHIM16 (supplemental Fig. S1). The volcano plots show 1,976, 2,088, and 2,615 significant protein groups differentially expressed between WHIM2 and WHIM16 in LFQ, RoR, and QuantFusion, where the posterior probability that a ∈ (−.1,.1) <0.05. The dramatic improvement in the number of biologically significant protein differences between WHIM2 and WHIM16 makes the QuantFusion method an attractive option for discovery proteomics experiments, as it provides the largest protein candidate list for follow-up biological exploration or verification. In addition to the improved quantitative coverage, QuantFusion demonstrated substantial variance reduction and improved repeatability. Repeatability error is used to measure the experimental precision obtained with each method. In our primary analysis, we had two replicates from each sample. To analyze repeatability, as shown on the right of Fig. 4, we analyzed each replicate separately with LFQ only, RoR only, and QuantFusion, giving us a total of six sets of protein estimates. The repeatability error was computed by taking the within-protein variance (across experiments) and then computing the average of these variances. The repeatability error was 0.3249, 0.2726, and 0.2704 for LFQ, RoR, and QuantFusion, respectively. The Pearson correlation coefficient is the retest correlation that provides a measure of how well the ranking of protein estimates is preserved across experiments. The Pearson correlation between two process/technical replicate runs was 0.7048, 0.6891, and 0.7465 for LFQ, RoR, and QuantFusion, respectively. Our results demonstrate that QuantFusion provides the best retest correlation, and RoR shows the best precision measurement. These results demonstrate that, despite the higher precision of RoR estimates, QuantFusion still provides greater repeatability. This outcome should not be surprising because the QuantFusion estimate comes from a substantially larger set of data, suggesting that the advantages gained from the additional data of quantifiable peptides used in QuantFusion analysis outweigh the disadvantage of incorporating into the model the noisier LFQ data.

Fig. 2.

Comparison of LFQ and RoR methods. A, histograms of the LFQ measurements between the PDX tumors (red) and ratio measurements via the added-in heavy-labeled cell lines to obtain RoR (blue). The LFQ ratios of peptides between WHIM2 and WHIM16 are median-centered on zero fold-change, although the RoR distributions of peptides between each WHIM and MCF10A (results shown only for MCF10A/WHIM2) are medians centered at 1.58 (3-fold). Note that all the data points in each distribution are shown as density gradient plots above each distribution. B, Venn diagrams showing the number of quantifications obtained for LFQ, RoR, and QuantFusion methods for global peptides and global protein groups. With QuantFusion, the number of quantifiable peptides is 65,873, and the number of quantifiable protein groups is 6,953. A Venn diagram showing the number of protein groups identified in the initial MaxQuant search is also displayed. C, scatter plot showing the correlation between LFQ- and RoR-derived estimates for WHIM2/WHIM16 ratios.

Fig. 3.

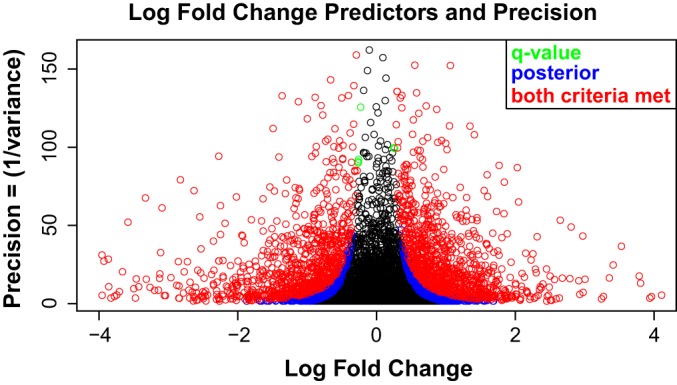
Scatterplot of every QuantFusion estimate of log2 fold-changes plotted against the square root of the precision estimates (1/(variance)). Points plotted toward the upper right and upper left corners have the highest precision and greatest absolute fold-change estimates. Selecting significant proteins should always be based on both the magnitude of a fold-change and the precision of the estimate. This plot demonstrates the results from two different methods for selecting significant fold-changes. The first criterion for significance is a q-value less than 0.05. The second criterion examines the posterior probability that the log2 fold-change falls in the interval (−.1,.1). If this probability is less than 0.05, then the protein is considered significant. Points that are significant according to both criteria are plotted in red; points that are exclusively q-value significant are plotted in green, and points that are exclusively significant using posterior probabilities are plotted in blue. Black points were not significant under either criterion. Both of these methods are similar, as expected of any method that utilizes both magnitude and precision.

Fig. 4.

Volcano plots and corresponding repeatability plot. The volcano plot shows −log10 of q-value that each protein fold-change is ≤0.05 plotted against the log2 fold-changes. Here, we consider multiple ways to analyze the same data. On the left, we have the results from measuring both replicates together with each of three methods. On the right, we are splitting up the data and analyzing each replicate separately. This enables us to measure the repeatability error for each method. Repeatability error is used to measure the experimental precision obtained with each method. This error was computed by taking the within-protein variance (across experiments) and then computing the average of these variances. The Pearson correlation coefficient is the retest correlation that provides a measure of how well the ranking of protein estimates is preserved across experiments. A, LFQ analysis. B, RoR analysis. C, QuantFusion analysis. Note that our results demonstrate that the QuantFusion method provides both the best retest correlation and the best precision. Note that the RoR method has the least variability, which suggests that the advantages gained from the extra data used in the QuantFusion method outweigh the disadvantage of incorporating into the model the noisier LFQ data.

When comparing QuantFusion to an analysis using LFQ alone, the benefits are substantial. Fig. 5A shows log2 fold-change estimates using QuantFusion (x axis) and LFQ (y axis). The fold-change estimates are very similar between methods with a Pearson correlation coefficient of 0.82. QuantFusion reduced the prediction variance by 40%. For comparison, we found that running an entire replicate experiment reduced the variance by 35%. This reduction was estimated by comparing estimates from the LFQ model with both replicates and to estimates from the LFQ model that only utilize one replicate. The variances obtained in this fashion are plotted in Fig. 5B. Average standard prediction variances for LFQ, RoR, and QuantFusion models are 0.35, 0.17, and 0.21, respectively. Prediction variances for all three methods are displayed in Fig. 5C. These error values confirmed our hypothesis that the RoR estimates would be the most precise but the LFQ estimates would be greater in number. The combined effect of increasing the number of estimates and decreasing estimate variability has a synergistic effect on the biological significance of quantified protein ratios.

Fig. 5.

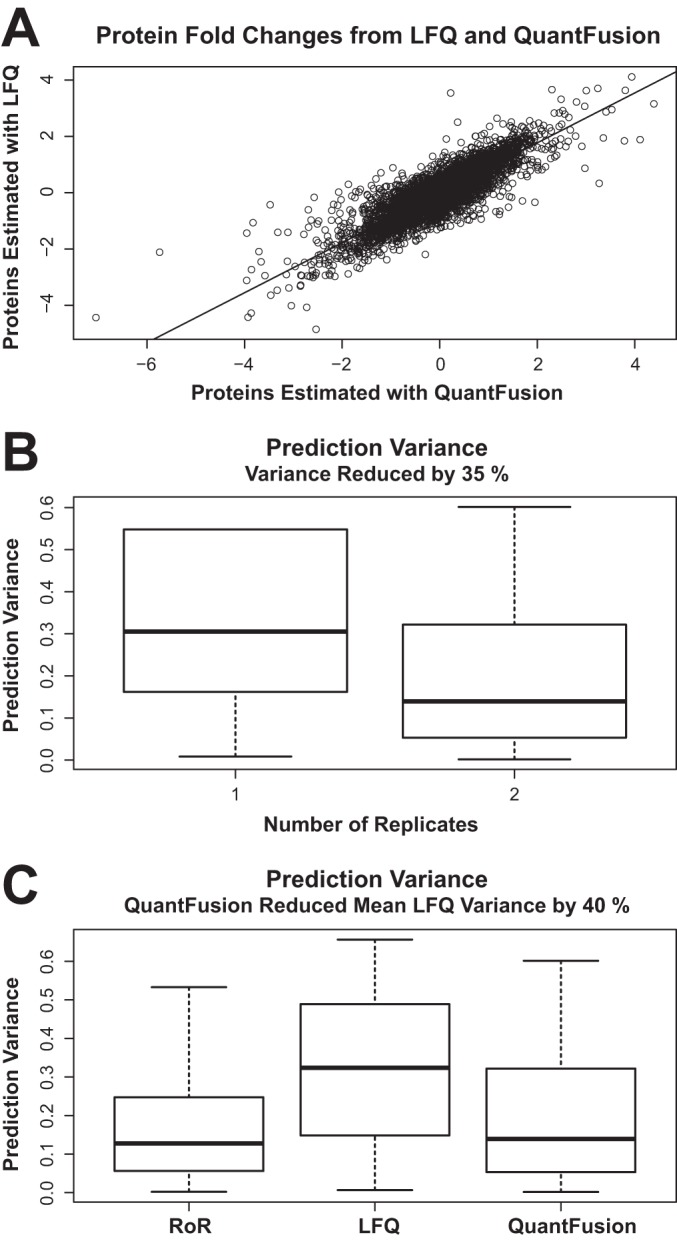
Comparing protein estimates and prediction of variances. A, scatter plot of log2 fold-change estimates using QuantFusion (x axis) and LFQ (y axis), with data from both replicates combined. The fold-change estimates are very similar between methods with a Pearson correlation coefficient of 0.82. B, estimates of prediction variances of the log2 fold-changes obtained by using only LFQ results with one replicate are compared with the variance estimates from performing LFQ with two replicates. Adding a full experimental replicate reduces the average variance by 35%. C, boxplots of the prediction variances for each method. Label-free fold-change estimates exhibit the highest variability. Using QuantFusion to combine the noisier LFQ data with the more precise RoR data results in a 40% reduction of average variability.

The relationship between prediction error and detectable effect size is displayed in supplemental Fig. S2, showing the relationship between power, effect size, and prediction error that would be found in experiments with prediction errors similar to what we found. The average prediction standard error across proteins (σ_type²) was computed for each model type and used as the true process variation to calculate power as follows. Let Φ be the CDF (Cumulative Distribution Function) of N(0,1) random variable; let X be the prediction of our protein fold-change, and let Δ be the true log2 fold-change of the protein. Then the test statistic formed under the null hypothesis is distributed as shown in Equation 5,

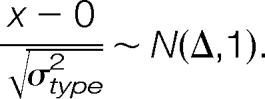Power for a given Δ is calculated as the probability of this statistic being greater than 2.326 or less than −2.326. These cutoff points were selected because the FDR corrected p value of 0.05, in these experiments, was close to 0.01 that has associated Z score cutoff values of −2.326 and 2.326.

Results show that, on average, true log-scale fold-changes of ±1.88, ±1.31, and ±1.46 are needed to have a 0.8 probability of detecting the difference with LFQ, RoR, and QuantFusion, respectively. Although RoR provides the lowest prediction variability, far fewer total protein estimates could be obtained by RoR compared with estimates obtained by QuantFusion.

QuantFusion Identifies or Rescues More Breast Cancer Subtype-specific Proteins

We then examined how QuantFusion increases the number of the quantifiable proteins that show the statistically significant BC subtype-specific changes in their expressions, which in the case of this study will provide a larger proteome coverage for distinguishing the biological differences between basal and luminal breast cancer tumors. As shown in the volcano plot in Fig. 4C, QuantFusion identified 1,808 differentially expressed proteins. After applying QuantFusion, 1,035 proteins that were not significantly differentially expressed (or in a few cases not quantifiable or identified) in LFQ were promoted to differentially expressed status. For RoR, 447 proteins were promoted to differentially expressed status. When considering proteins that were not significantly differentially expressed (or not quantifiable or identified) in both LFQ and RoR, 272 proteins were promoted to differentially expressed status. Fig. 6 indicates were these rescued proteins are located in the QuantFusion volcano plot of q-value plotted against WHIM2/WHIM16-fold-changes. A look at the volcano plots shows that in terms of proteins promoted with increased significance and differential expression values, LFQ benefits the most from QuantFusion. A list of these promoted proteins can be found in supplemental Table S5 (LFQ), supplemental Table S6 (RoR), and supplemental Table S7 (both LFQ and RoR). For example, we found a number of QuantFusion-rescued proteins up-regulated in WHIM2 (basal) that are described to be associated with the more aggressive basal/triple-negative subtype of breast cancer. SHC1 (SHC-transforming protein 1, UniProt P29353) is associated with tumor aggressiveness (39). For both LFQ and RoR, the q-values for P29353 are not significant. With QuantFusion, the q-value becomes significant. Likewise, MORC2 (MORC (microrchidia) family CW (cysteine-tryptophan)-type zinc finger protein 2, UniProt Q9Y6X9) is a predictor of recurrence of triple-negative breast cancer (40) and was not significantly differentially expressed in both LFQ and RoR but was in QuantFusion. STAT3 (signal transducer and activator of transcription 3, UniProt P40763) was not differentially expressed in LFQ but was in QuantFusion and RoR. STAT3 signaling has been shown to play a distinct role in basal breasts cancers (41). Another protein promoted from both LFQ and RoR is SENP3 (Sentrin-specific protease 3, UniProt Q9H4L4). SENP3 has been shown to be overexpressed and to promote epithelial-mesenchymal transition in gastric cancer (42). Because epithelial-mesenchymal transition plays a role in metastasis, SENP3 could be a candidate for additional studies to see whether it plays a similar role in basal breast cancer.

Fig. 6.

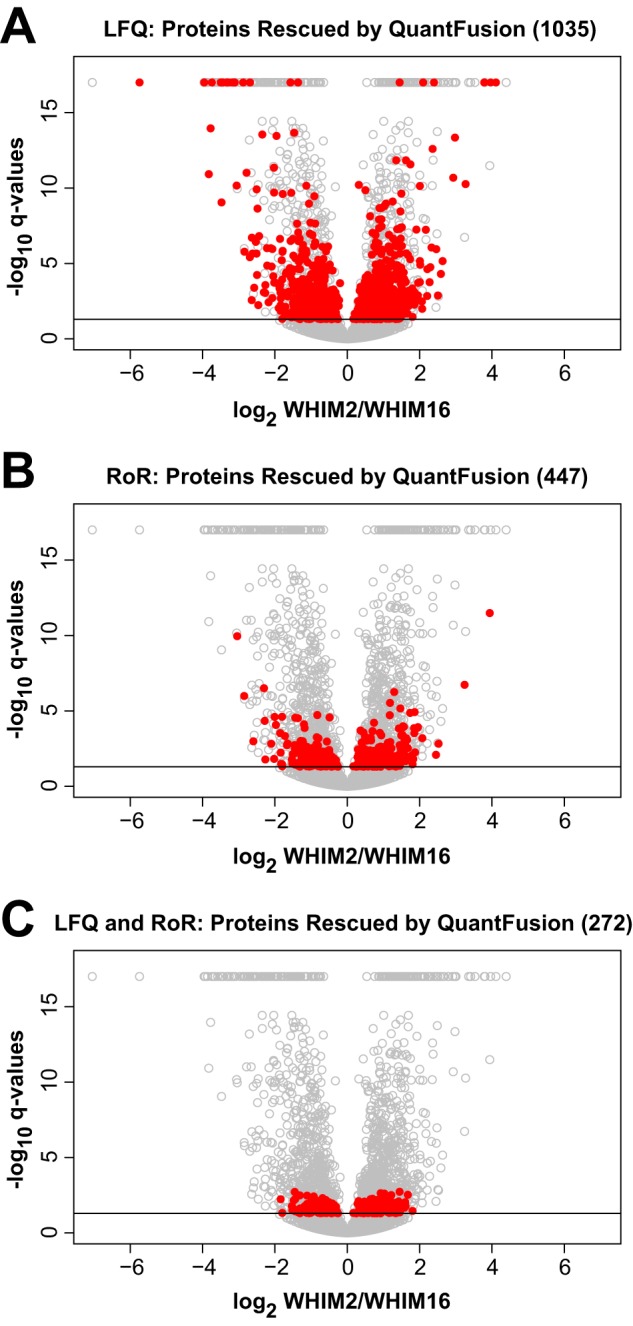
Volcano plots indicating significantly differentially expressed proteins rescued by QuantFusion. Similar to Fig. 4C, the volcano plots show −log10 of q-value plotted against the log2 WHIM2/WHIM16 fold-changes for each protein in the QuantFusion analysis. Significantly differentially expressed proteins are shown above the cutoff q-value (−log10(0.05) equals about 1.3). Proteins rescued by QuantFusion are indicated as red circles for not significantly differentially expressed (or not quantifiable or not identified) in LFQ (A), in RoR (B), and in both LFQ and RoR (C). Proteins with a q-value of 0 are plotted as a group at the top of each plot.

CONCLUSIONS

Here, we present the development of a unified quantitative approach, QuantFusion, for maximizing the number of peptides to determine global protein expression differences between tissues. Our approach combines direct measures of peak intensities via LFQ and MS1 ratios between tumor peptides and corresponding added-in stable isotope-labeled peptide standards. QuantFusion indirectly facilitates the quantitative estimation of differences between tumor subtypes by obtaining an RoR measurement. We have analyzed all data with a random effects model that frequently augments missing data in either LFQ or RoR, allowing for more comprehensive unified estimates for protein expression changes. The analytical workflow and the data modeling approach we have used for combining two different quantitative measurements into a single unified estimate we call “QuantFusion.” QuantFusion provided more significant assignments of global protein expression differences in WHIM2 (basal) and WHIM16 (luminal) PDX tumor subtypes when compared with each individual method (i.e. LFQ or RoR). Although the missing values present in both LFQ and RoR methods have not been addressed from an imputation standpoint or collection of additional replicates, the unified approach addresses the missing values to some degree by using all the data from both methods in estimating global protein expression differences between the WHIM tumors. QuantFusion increased by 65% the number of distinct peptide ratios used in our analysis. This increase, in turn, increased the number of measurable protein fold-changes by 8% and increased the average precision of our estimates by 181%. The Statistical Analysis Software code used to implement the statistical model along with test data set used in this study are made available to investigators who wish to perform QuantFusion experiments. In principle, QuantFusion can be extremely useful for other types of proteomic workflows such as affinity enrichment and label-free interaction proteomics experiments, where reproducibility in pulldowns can impact the ability to detect bona fide interactors. The use of QuantFusion in other proteomic workflows will be reported in a future study.