Quantile Regression Analysis of Censored Longitudinal Data with Irregular Outcome-Dependent Follow-Up

Summary

In many observational longitudinal studies, the outcome of interest presents a skewed distribution, is subject to censoring due to detection limit or other reasons, and is observed at irregular times that may follow a outcome-dependent pattern. In this work, we consider quantile regression modeling of such longitudinal data, because quantile regression is generally robust in handling skewed and censored outcomes and is flexible to accommodate dynamic covariate-outcome relationships. Specifically, we study a longitudinal quantile regression model that specifies covariate effects on the marginal quantiles of the longitudinal outcome. Such a model is easy to interpret and can accommodate dynamic outcome profile changes over time. We propose estimation and inference procedures that can appropriately account for censoring and irregular outcome-dependent follow-up. Our proposals can be readily implemented based on existing software for quantile regression. We establish the asymptotic properties of the proposed estimator, including uniform consistency and weak convergence. Extensive simulations suggest good finite-sample performance of the new method. We also present an analysis of data from a long-term study of a population exposed to Polybrominated Biphenyls (PBB), which uncovers an inhomogeneous PBB elimination pattern that would not be detected by traditional longitudinal data analysis.

1. Introduction

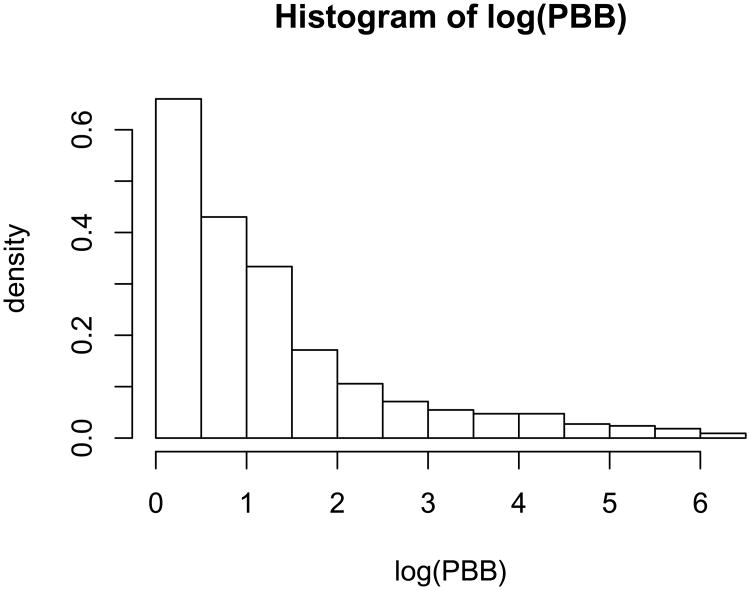
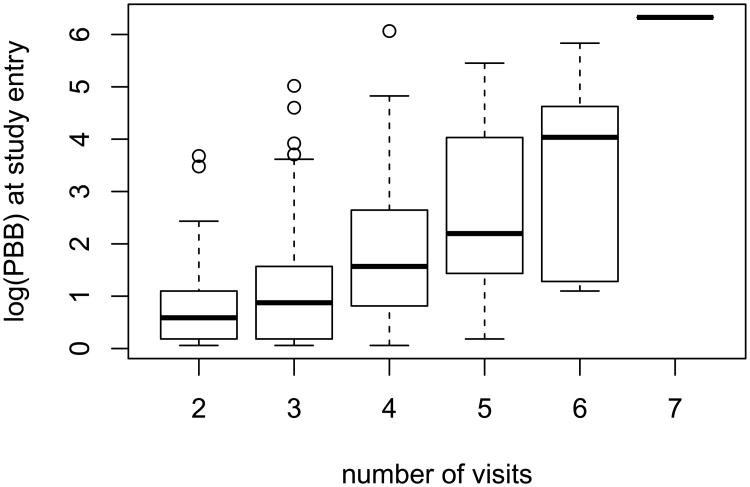
Epidemiological follow-up studies often present various features that can complicate statistical analysis, such as censoring, skewness, and irregular outcome-dependent follow-up. Our motivating example is the Michigan Long-Term Polybrominated Biphenyls (PBBs) Study, which was established following the PBB exposures of residents of Michigan farms and neighboring communities after their consumption of PBB contaminated food products in the early 1970s. With over 20 years of follow-up, PBB study provides a rich database for investigating the elimination of PBB from the human body. However, there exist several challenges with the analysis of the PBB data. First, due to laboratory assay detection limit, PBB concentration was not detectable when it was less than 1 part per billion (p.p.b.). This caused some left censored PBB measurements. Secondly, the distribution of PBB concentration is highly skewed, as evidenced by the histogram of log-transformed PBB measurements; see Figure 1. Thirdly, serum samples from each subject were not taken at a set of common time points or intervals. Furthermore, visit/sample-taking times may be outcome dependent. In Figure 2, we present the box-plots of log PBB levels measured at study entry by the number of visits. It is shown that subjects with high initial PBB levels contributed more serum samples, or equivalently speaking, made more follow-up visits, than those with low initial PBB levels. Similar data situations are encountered in many other epidemiological studies.

Figure 1.

Distribution of PBB concentration measurements after logarithm transformation.

Figure 2.

Distribution of observed log (PBB) at the first visit versus number of measurements.

Many standard longitudinal methods (Diggle et al., 2002) assumed the follow-up visit times to be pre-determined or outcome-independent given covariates. When the follow-up visit times are irregular and are correlated with outcomes, one intuitive approach is to group irregular visit times into a common set of time intervals and formulate the data as longitudinal data with informative intermittent missing. Methods, such as Robins et al. (1995), can be applied; however they may be sensitive to arbitrary divisions of time intervals. Without involving discretizing the visit time scale, Lipsitz et al. (2002) developed a likelihood-based approach assuming the outcome process follows a Gaussian process with mean and covariance parametrically specified. Under reasonable conditions on the dependency between visit times and outcomes, they showed that the likelihood for the longitudinal outcomes is separable from that for the follow-up times, and thus the estimation of the outcome process parameters can be carried out without modeling the follow-up times. Fitzmaurice et al. (2006) extended Lipsitz et al. (2002)'s method to longitudinal binary data. Ryu et al. (2007) presented a Bayesian regression method, which jointly modeled the follow-up time process and the longitudinal outcome process through introducing a subject-specific latent variable.

Marginal semiparametric regression has also been studied for longitudinal data with irregular outcome-dependent follow-up. This type of approach avoids strong parametric assumptions on the joint distribution of longitudinal outcomes, but as a trade-off, requires a model for the follow-up time process to facilitate correcting the bias resulted from outcome-dependent follow-up. For example, Lin et al. (2004) investigated the marginal mean regression of the longitudinal outcome, while modeling the follow-up time process by a proportional intensity model (Andersen and Gill, 1982). They proposed an inverse intensity weighting strategy to adjust for the effect of outcome-dependent follow-up on the observed outcomes. To avoid directly estimating the baseline intensity function of the follow-up visit process, which usually requires smoothing, Buzkova and Lumley (2007) justified the use of intensity-ratio as the inverse weight in Lin et al. (2004)'s approach. The resulting estimator does not require smoothing, and thus is simpler to compute. Furthermore, it can be applied under a mixture of continuous and discrete follow-up visit times.

With skewed and censored outcomes, quantile regression is naturally advantageous over either Gaussian regression modeling or marginal mean regression because quantiles are more robust and informative summary statistics for a skewed distribution and have better identifiability than mean when censoring is present. This motivates us to consider quantile regression modeling for longitudinal data with irregular outcome-dependent follow-up. With a proper formulation of outcome process and follow-up time process as in Lipsitz et al. (2002), our model specifies how the quantiles of the outcome at time t relates to the covariates observed up to time t. This type of marginal quantile regression model has been exploited in literature by many authors in various aspects (Jung, 1996; Lipsitz et al., 1997; Koenker, 2004; Wang and Fygenson, 2009; Yi and He, 2009; Yuan and Yin, 2010; Lee and Kong, 2013, among others). For example, Lipsitz et al. (1997) proposed a GEE-type estimating equation and adopted the technique of inverse probability weighting to handle missing outcomes due to random dropouts. Koenker (2004) considered subject-specific fixed effects which are intended to capture unobserved individual heterogeneity, and proposed an ℓ₁-regularization estimating method to modify the inflation effect caused by the introduction of individual fixed effects. Wang and Fygenson (2009) investigated the case with longitudinal outcomes left censored by fixed constants and developed inference procedures that properly account for censoring and intra-subject dependency. Lee and Kong (2013) recently presented an adaptation of Wang and Fygenson (2009)'s method to handle longitudinal data subject to both left censoring and random dropouts. However, all these methods are generally focused on standard longitudinal settings with common visit times or outcome-independent follow-up times.

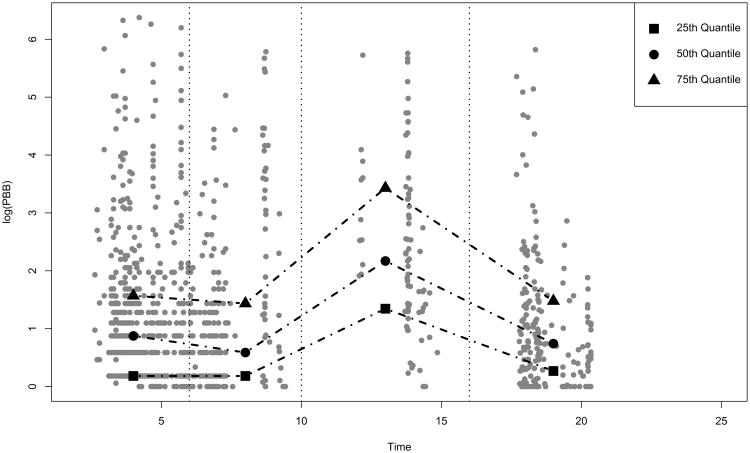
For marginal quantile regression inference, ignoring the dependency between irregular follow-up times and outcomes can lead to biased estimation. This is well demonstrated by an exploratory analysis of the PBB example. In Figure 3, we plot the 25th, 50th, 75th empirical quantiles of PBB measurements collected in each of four follow-up time intervals. Each gray dot represents one PBB measurement. Without accounting for outcome-dependent follow-up, a naive interpretation of Figure 3 would be that the distribution of PBB would first shift up and then go down over the time course. This is not scientifically plausible, and in fact, manifests the data distortion resulted from outcome-dependent follow-up. A further data examination reveals that the cohort participants who had PBB levels measured 10 to 16 years after PBB exposure are mostly those who had high PBB levels at the initial study visit. Thus, the PBB samples collected during this time period are not representative of the PBB concentrations of the whole study cohort, but rather reflect the PBB distribution for a subcohort that is likely to have high PBB levels. This explains the unexpected rise in empirical PBB quantiles observed in Figure 3, and more importantly indicates the need to appropriately address outcome-dependent follow-up in quantile regression analysis of longitudinal data.

Figure 3.

An intuitive data illustration of PBB study.

In this paper, we develop a marginal quantile regression approach to analyzing longitudinal data with censored and skewed outcomes as well as irregular outcome-dependent follow-up. We propose an estimation procedure that properly accommodates these realistic data features. More specifically, we employ Powell (1986)'s censored quantile regression technique to handle fixed or known random left censoring to longitudinal outcomes. To address outcome-dependent follow-up, we model the follow-up time process via a proportional intensity model, viewing each follow-up visit as a recurrent event. As one of the most popular models for recurrent events, a proportional intensity model can be conveniently implemented by standard statistical software such as SAS and R. It also allows us to specify how the intensity for the counting process of visits at time t depends on the past observed data, including visit history, outcomes, and covariates; thus it is an appropriate device for characterizing outcome-dependent follow-up. The adopted proportional intensity model forms the basis to correct the bias induced by outcome-dependent follow-up through inverse intensity-ratio weighting. It can also help understand the factors influencing the follow-up behaviors. We properly design our estimation and inference procedures so that they can be implemented via existing statistical software for quantile regression. Algorithmic issues are carefully addressed.

The rest of this paper is organized as follows. In Section 2, we introduce models and present the proposed estimation procedure and algorithm. We outline asymptotic studies in Section 3, and develop bootstrap and sample-based inference procedures in Section 4. In Section 5, we evaluate the proposed method by simulation studies. In Section 6, we present an analysis of PBB data, which demonstrates the importance and practical utility of the new method. We conclude with some remarks in Section 7.

2. Methods

2.1 Data and Notation

Let $Y_i^{\ast }(t)$ denote the outcome process of interest, namely the outcome at time t, and likewise let Z_i(t) denote a vector of external covariate processes for the ith subject. Let [L_i, R_i] be a time interval indicating when the ith subject is under study. We assume that L_i and R_i are independent of $Y_i^{\ast }(·)$ given Z_i(·). Note that $Y_i^{\ast }(·)$ and Z_i(·) are only observed at L_i, when the subject enters the study, and at a sequence of follow-up visit times, $\{t_i^{(j)}:j=1,2,\dots ,m_i\}$ within (L_i, R_i]. Here m_i is the total number of follow-up visits for the ith subject.

Define a counting process for study entry as $N_i^L(t)=I(L_i\le t)$ and a counting process for follow-up visits as $N_i(t)={\sum }_{j=1}^{m_i}I(t_i^{(j)}\le t)$. Outcome $Y_i^{\ast }(t)$ is subject to left censoring at a fixed constant c. As explained in a remark in Section 7, the constant c can be replaced by a random variable which is observed for all subjects. Define $Y_i(t)=max(c,Y_i^{\ast }(t))$. The observed data consist of ${\{L_i,{\mathbf{Z}}_i(L_i),Y_i(L_i),t_i^{(j)},{\mathbf{Z}}_i(t_i^{(j)}),Y_i(t_i^{(j)}),R_i,m_i:j=1,2,\dots ,m_i\}}_{i=1}^n$. Notation with subscript i removed stands for the corresponding population analogue.

2.2 Models

Define the τth conditional quantile of a random variable Y given Z as Q_Y(τ|Z) = inf{y : Pr(Y ≤ y|Z) ≥ τ}. We consider a marginal quantile regression model that takes the form,

$$Q_{Y_i^{\ast }(t)}(\tau |{\mathbf{Z}}_i(t))={\mathbf{X}}_i{(t)}^{\mathrm{\top }}{\mathit{\beta }}_0(\tau ),\text{for all}t>0,$$ (1)

where X_i(t) = (1,Z_i(t)^⊤)^⊤ and β₀(τ) is a vector of unknown regression coefficients. This model marginally specifies the relationship between outcome quantiles and covariates at time t. The coefficients in β₀(τ) are formulated as functions of τ, thereby allowing for inhomogeneous covariate effects across different segments of the outcome distribution. Model (1) covers some commonly used models for longitudinal data. For example, one special case is the linear random intercept model, $Y_i^{\ast }(t)=\mu +{\mathbf{b}}^{\mathrm{\top }}{\mathbf{Z}}_i(t)+a_i+{\epsilon }_i(t)$, where for subject i, a_i is the random intercept effect, and ε_i(t) is the random error term at time t that follows a common distribution over t. With (a_i, ε_i(t)) assumed to be independent of Z_i(t), it can shown that Q_Y*(t)(τ|Z_i(t)) = {μ + Q_a+ε(τ)} + b^⊤Z_i(t), where Q_a+ε(τ) denotes the τth quantile of a_i + ε_i(t). Thus model (1) holds in this special case.

Model (1) is also flexible in characterizing the profile change of the longitudinal outcome over time, which is of particular interest in the PBB study. For instance, with Z_i(t) = t, model (1) becomes $Q_{Y_i^{\ast }(t)}(\tau )=b_0(\tau )+t·b_1(\tau )$. In this case, the coefficient b₀(τ) represents the τth quantile of baseline outcome (i.e. Y_i(0)) and b₁(τ) represents the change rate of the τth outcome quantile over time. Clearly, this model can be expanded to adjust for relevant baseline covariates or covariates collected during follow-up.

We further model follow-up visit times, and give some special attention to the subtle difference between the initial study visit and follow-up visits. This is motivated by the PBB study, in which, the commonly adopted time origin is the PBB exposure date set as July 1, 1973, rather than the date at study entry. Since study participants had little or no knowledge about how much they were exposed to PBB until they received results from their initial visit, we expect little dependency between the initial visit time and outcomes. In fact, we assume that $L_i\perp Y_i^{\ast }(·)|{\mathbf{Z}}_i(·)$ and L_i is not necessarily fixed. Consequently, our modeling of the follow-up process starts after the initial study visit. That is, defining a history function ℋ_i(t) as all observed data before time t of the ith subject, we assume a proportional intensity model (Andersen and Gill, 1982) that takes the form,

$$\lambda (t|{\mathcal{H}}_i(t))=I(L_i<t\le R_i){\lambda }_0(t)exp({\mathbf{h}}_i{(t)}^{\mathrm{\top }}{\mathit{\alpha }}_0),$$ (2)

where $\lambda (t|{\mathcal{H}}_i(t))={lim}_{\mathrm{\Delta }t\to 0}\frac{1}{\mathrm{\Delta }t}P\{N_i(t+\mathrm{\Delta }t)-N_i(t)=1|{\mathcal{H}}_i(t)\}$ and α₀ is a vector of unknown coefficients. Here h_i(t) is a vector of time-dependent covariates belonging to ℋ_i(t), which may be flexibly set to contain prior outcomes or covariates observed before time t.

2.3 Estimation

The primary estimation goal is to estimate the β₀(τ) in model (1), which captures the covariate effects on the τth marginal quantile of the outcome of interest, Y*(t). When the follow-up process is independent of the outcome process, one may follow Wang and Fygenson (2009)'s method to estimate β₀(τ) through minimizing the objective function,

$$n^{-1/2}\sum _{i=1}^n[\underset{0}{\overset{\infty }{\int }}{\rho }_{\tau }\{Y_i(t)-max(c,{\mathbf{X}}_i{(t)}^{\mathrm{\top }}\mathit{\beta })\}(d{N}_i^L(t)+d{N}_i(t))],$$ (3)

where ρ_τ(u) = u · {τ − I(u < 0)}. The basic idea underlying objective function (3) is derived from an application of the equivariance property of quantiles to monotone transformation (Koenker, 2005). A similar strategy was used by Powell (1986)'s method for censored quantile regression. More specifically, by the equivariance property, under model (1), quantiles of the observed outcome, Y_i(t), satisfy,

$$Q_{Y_i(t)}(\tau |{\mathbf{Z}}_i(t))=max(c,{\mathbf{X}}_i{(t)}^{\mathrm{\top }}{\mathit{\beta }}_0(\tau )).$$

Such a relationship between the observed outcomes and covariates lays the key justification for objective function (3).

However, in the presence of outcome-dependent follow-up, minimizing (3) does not render a valid approach because Y_i(t) and dN_i(t) are not independent given X_i(t). To correct the bias resulted from outcome-dependent follow-up, we adopt the strategy of inverse intensity-ratio weighting (Buzkova and Lumley, 2007) with separate handling of the initial study visit and follow-up visits. That is, we intend to weigh the outcomes observed at follow-up visits by the reciprocal of the intensity ratios, which, according to the follow-up time model (2), take the form w_i(t; α₀) = I (L_i < t ≤ R_i) exp {h_i(t)^⊤α₀}. At the same time, we do not weigh the data collected at the initial study visit because the study entry time L_i is assumed to be conditionally independent of outcomes given covariates. Since α₀ is usually unknown, we employ weights w_i(t; α̂) instead of w_i(t; α₀), where α̂ is a consistent estimate for α₀ obtained by Andersen and Gill (1982)'s method, which maximizes a partial likelihood function of model (2).

We propose to estimate β₀(τ) by the minimizer of Ψ_τ(β; α̂) with respect to β, where

$${\mathrm{\Psi }}_{\tau }(\mathit{\beta };\mathit{\alpha })=n^{-1/2}\sum _{i=1}^n[\underset{0}{\overset{\infty }{\int }}{\rho }_{\tau }\{Y_i(t)-max(c,{\mathbf{X}}_i{(t)}^{\mathrm{\top }}\mathit{\beta })\}(d{N}_i^L(t)+\frac{1}{w_i(t;\mathit{\alpha })}d{N}_i(t)\left)\right].$$ (4)

The resulting estimator is denoted by β̂(τ). We recommend calculating w_i(t; α̂) based on centered covariates. Doing so would lead to a better interpretation of the weight and also naturally confine the weight to take values in a reasonable range. For example, suppose g_i(t) is a covariate included in h_i(t). A centered covariate $g_i^{\ast }(t)$ is defined as g_i(t) – ḡ, where $\overline{g}={\sum }_{i=1}^n{\sum }_{j=1}^{m_i}{g}_i(t_i^{(j)})/{\sum }_{i=1}^n{m}_i$.

To find the minimizer of Ψ_τ(β; α̂), we note that Ψ_τ(β; α̂) has an equivalent form of

$$n^{-1/2}\sum _{i=1}^n[{\rho }_{\tau }\{Y_i(L_i)-max(c,{\mathbf{X}}_i{(L_i)}^{\mathrm{\top }}\mathit{\beta })\}+\sum _{j=1}^{m_i}\frac{1}{w_i(t_i^{(j)};\widehat{\mathit{\alpha }})}{\rho }_{\tau }\{Y_i(t_i^{(j)})-max(c,{\mathbf{X}}_i{(t_i^{(j)})}^{\mathrm{\top }}\mathit{\beta })\left\}\right].$$

This shows that, by treating observed outcomes as independent and properly assigning weights as one or the reciprocal of estimated intensity-ratio, we can solve the minimization problem for objective function (4) by using the existing crq() function in R package quantreg via the option for Powell's censored regression quantiles.

To justify the proposed weighting strategy, we examine the gradient of Ψ_τ(β; α) with respect to β, denoted by U_τ{β; α}, which equals

$$n^{-1/2}\sum _{i=1}^n[\underset{0}{\overset{\infty }{\int }}{\mathbf{X}}_i(t)I({\mathbf{X}}_i{(t)}^{\mathrm{\top }}\mathit{\beta }>c)\{I(Y_i(t)\le {\mathbf{X}}_i{(t)}^{\mathrm{\top }}\mathit{\beta })-\tau \}(d{N}_i^L(t)+\frac{1}{w_i(t;\mathit{\alpha })}d{N}_i(t)\left)\right].$$

Assuming $d{N}_i(t)\perp \{Y_i^{\ast }(t),{\mathbf{Z}}_i(t)\}|{\mathcal{H}}_i(t)$, or in words, dN_i(t) is independent of current outcome and covariates given the history, we can show that under model assumptions (1) and (2),

$$E[{\int }_0^{\infty }\frac{1}{w_i(t;{\mathit{\alpha }}_0)}{\mathbf{X}}_i(t)I({\mathbf{X}}_i{(t)}^{\mathrm{\top }}\mathit{\beta }>c)\{I(Y_i(t)\le {\mathbf{X}}_i{(t)}^{\mathrm{\top }}\mathit{\beta })-\tau \}d{N}_i(t)]=0.$$

At the same time, provided that $d{N}_i^L(t)$ is independent of Y_i(t) given X_i(t), it is easy to see that

$$E[{\int }_0^{\infty }{\mathbf{X}}_i(t)I({\mathbf{X}}_i{(t)}^{\mathrm{\top }}\mathit{\beta }>c)\{I(Y_i(t)\le {\mathbf{X}}_i{(t)}^{\mathrm{\top }}\mathit{\beta })-\tau \}d{N}_i^L(t)]=0.$$

Combining these results immediately gives E[U_τ{β₀(τ); α₀}] = 0, which endorses the proposed idea for estimating β₀(τ). As commented by Lin et al. (2004), the assumption, $d{N}_i(t)\perp \{Y_i^{\ast }(t),{\mathbf{Z}}_i(t)\}|{\mathcal{H}}_i(t)$, is weaker than those imposed by Lipsitz et al. (2002), and is reasonable for the follow-up mechanisms of many real studies, including the PBB study.

3. Asymptotic Properties

We study the asymptotic properties of the proposed estimator, β̂(τ). Due to space limit, we relegate regularity conditions and proofs of theorems to Web Appendices A–C.

The asymptotic properties of β̂ (τ) are stated in the following theorems.

Theorem 1: Under conditions C1-C4, sup_{τ∈[γ, γ′]} ║β̂(τ) − β₀(τ)║ → 0, a.s..

Theorem 2: Under conditions C1-C6, {n^1/2 [β̂(τ) − β₀(τ)] : τ ∈ [γ, γ′]} converges weakly to a Gaussian process with mean 0 and covariance matrix Σ, which is defined in (C.3) in Web Appendix C.

Note that Theorems 1 and 2 provide the asymptotic properties of {β̂(τ), τ ∈ [γ,γ′]}, with 0 < γ < γ′ < 1. In principle, the choice of [γ,γ′] should reflect the range of the quantile levels of interest. In theory, we assume that γ and γ′ satisfy the technical constraints imposed by the regularity conditions. These constraints are necessitated by considerations relating to the tail identifiability and estimation stability. For example, with γ′ < 1, we can avoid the complication with extreme quantile inference. When Y_i(t) is subject to left censoring by a positive constant, the lower tail quantiles may not be identifiable, and thus requiring γ > 0 may be necessary. In practice, there is usually no definite way to verify whether these technical constraints are met or not. Our recommendation is to first select γ and γ′ based on the scientific interest and then adjust γ and γ′ in an adaptive manner. That is, when β̂(τ) turns out to be an infeasible solution at τ = γ (or γ′), we would reset γ (or γ′) to a larger (or smaller) value. Based on our numerical experience, such an empirical adaptive rule performances very well.

4. Inference

Bootstrap procedures can be used to make inference on β₀(τ). For example, one may generate a bootstrap sample by randomly selecting n subjects with replacement. Based on each bootstrap sample, the proposed estimation procedure can be applied to obtain a bootstrap estimator, denoted by β̂* (τ). With many bootstrap samples generated, the asymptotic distribution of √n{β ^(τ) − β₀(τ)} can be approximated by the empirical distribution of √n{β̂*(τ) − β̂(τ)}.

We also develop a sample-based inference procedure, which is expected to be more computationally efficient. One challenge is about how to estimate the asymptotic variance matrix of √n{β ^(τ) − β₀(τ)}, which involves the unknown density function f_Yi(t)(X_i(t)^⊤ β₀(τ)|X_i(t)) according to our asymptotic studies. To tackle this difficulty, we adopt the technique of Huang (2002) and Peng and Fine (2009). More specifically, we perturb U_τ(β̂; α̂) and then utilize the functional linearity of U_τ(·) to derive a sample-based consistent estimate for B_τ(β₀(τ); α₀) in condition C5. Then we can obtain a consistent estimate for the asymptotic variance of √n{β̂(τ) − β₀(τ)} based on its closed form derived in the proof of Theorem 2. The specific procedure is outlined as follows.

Step 1. Define ${\mathcal{l}}_j^{\tau }(\mathit{\beta };\mathit{\alpha })={\int }_0^{\infty }{\mathbf{X}}_j(t)I({\mathbf{X}}_j{(t)}^{\mathrm{\top }}\mathit{\beta }>c)\{I(Y_j(t)\le {\mathbf{X}}_j{(t)}^{\mathrm{\top }}\mathit{\beta })-\tau \}(d{N}_j^L(t)+\frac{1}{w_j(t;\mathit{\alpha })}d{N}_j(t))$ and $\mathbf{\Omega }(\tau )=n^{-1}{\sum }_{j=1}^n{\{{\mathcal{l}}_j^{\tau }(\widehat{\mathit{\beta }}(\tau );\tau ,\widehat{\mathit{\alpha }})\}}^{\mathrm{\otimes }2}$, where v^⊗2 = vv^⊤. Find a symmetric and nonsingular (p + 1) × (p + 1) matrix E(τ) such that Ω(τ) = E²(τ). Let e_j(τ) denote the jth column of E(τ).

Step 2. Solve the equation

$${\mathbf{U}}_{\tau }(\mathbf{b};\widehat{\mathit{\alpha }})={\mathbf{e}}_j(\tau )$$ (5)

for b, and denote the solution by β̌_j(τ) (j = 1,…, p + 1).

Step 3. Calculate D(τ) = (β̌₁(τ) − β̌(τ),…, β̌_p+1(τ) − β̂(τ)).

Step 4. Compute n^−1/2E(τ)D(τ)⁻¹, which provides a consistent estimate for B_τ(β₀(τ); α₀).

It is, however, not straightforward to employ the crq() function in R to solve equation (5) in Step 2. In order to take the advantage of existing software package, we propose an alternative solution-finding strategy for equation (5). That is, we first solve the equation,

$$\sum _{i=1}^n{\int }_0^{\infty }{\mathbf{X}}_i(t)I({\mathbf{X}}_i{(t)}^{\mathrm{\top }}\mathbf{b}>c)\{I(Y_i(t)\le {\mathbf{X}}_i{(t)}^{\mathrm{\top }}\mathbf{b})-\tau \}(d{N}_i^L(t)+\frac{1}{w_i(t;\widehat{\mathit{\alpha }})}d{N}_i(t))+I({\mathbf{X}}_j^{\ast \mathrm{\top }}\mathbf{b}>0){\mathbf{X}}_j^{\ast }\{I({\mathbf{X}}_j^{\ast \mathrm{\top }}\mathbf{b}>0)-\tau \}=0,$$ (6)

where ${\mathbf{X}}_j^{\ast }=-n^{1/2}{\mathbf{e}}_j(\tau )/(1-\tau )$. Mimicking the proposed algorithm for β₀(τ), we can solve equation (6) using the crq() function. It is easy to show that equation (6), coupled with condition $X_j^{\ast \mathrm{\top }}\mathbf{b}>0$, is equivalent to equation (5). Therefore, we check whether the solution to equation (6), b̃, satisfies the condition $X_j^{\ast \mathrm{\top }}\stackrel{\sim }{\mathbf{b}}>0$. If yes, we let β̌_j(τ) = b̃. Otherwise, we solve equation (6) switching the sign of e_j(τ). In this case, solving equation (6) would serve to locate a solution to a variant of equation (5), which is given by

$${\mathbf{U}}_{\tau }(\mathbf{b};\widehat{\mathit{\alpha }})=-{\mathbf{e}}_j(\tau ).$$ (5′)

Note that the perturbations to U_τ(b;α̂) posed by equation (5) and equation (5′), namely e_j(τ) and −e_j(τ), have the same asymptotic order. Following the theory presented in Huang (2002) and Peng and Fine (2009), we can show that the proposed inference procedure remains valid when one replaces equation (5) by (5′). When (5′) is adopted for some j, E(τ) in Step 4 needs to be updated by (e₁(τ),…, − e_j(τ), …, e_p+1(τ)) accordingly.

Let B̂(τ) denote the proposed sample-based estimate for B_τ(β₀(τ); α₀). A consistent sample-based covariance estimator for β̂(τ) may be given by

$$n^{-1}\sum _{i=0}^n{[-\widehat{\mathbf{B}}{(\tau )}^{-1}\{{\mathcal{l}}_i^{\tau }(\widehat{\mathit{\beta }}(\tau );\widehat{\mathit{\alpha }})-{\widehat{\mathbf{A}}}_{\tau }{\widehat{\mathbf{J}}}^{-1}{\iota }_i(\widehat{\mathit{\alpha }})\left\}\right]}^{\mathrm{\otimes }2},$$

where ι_i(·) is an influence function defined in Web Appendix A (see (A.2)), and Â_τ and Ĵ are plug-in estimators of A_τ(β₀; α₀) and J(α₀) defined in (C.2) in Web Appendix C and (A.1) in Appendix A respectively.

5. Simulations

Simulation studies were conducted to assess finite-sample performance of the proposed method. We considered two time-independent covariates, Z_i1 ∼ Uniform(0, 1) and Z_i2 ∼ Bernoulli(0.5), and one time-dependent covariate Z_i3(t) = t. For the study visit times, we generated the study entry time L_i from Uniform(0, 1), and the time at the end of follow-up R_i from Uniform(4, 5). Between L_i and R_i, follow-up visit times were generated according to a proportional intensity model:

$$P\{d{N}_i(t)=1|{\mathcal{H}}_i(t)\}=I(L_i<t\le R_i)0.2texp\{a_0{Y}_i(t^{-})\}dt,$$ (7)

where Y(t⁻) represents the last observed outcome before time t and a₀ = 0.2. A positive coefficient for Y(t⁻) would indicate that subjects with larger previous outcomes have higher intensity of making subsequent visits.

We adopted Normal distribution and Gamma distribution for generating outcomes. More specifically,

Case 1: Y_i(t) = max(0, 4.5+d_i − Z_i1+Z_i2−t+ε_i(t)), where $d_i\sim N(0,\frac{1}{4}\{{(Z_{i1}+Z_{i2}+1)}^2-\frac{1}{2}\})$ and ${\epsilon }_i(t)\sim N(0,\frac{1}{8})$ and they are independent. In this set-up, data follow a marginal quantile regression model,

$$Q_{Y_i(t)}(\tau |Z_{i1},Z_{i2})=max(0,4.5+{\mathrm{\Phi }}^{-1}(\tau )+\{-1+{\mathrm{\Phi }}^{-1}(\tau )\}{Z}_{i1}+\{1+{\mathrm{\Phi }}^{-1}(\tau )\}{Z}_{i,2}-t).$$

Case 2: Y_i(t) = max(0, 3.5 + d_i − 2Z_i1 − t + ε_i(t)), where $d_i\sim \mathit{\text{Gamma}}(3,\frac{1}{4}(Z_{i1}+Z_{i2}+1))$ and ${\epsilon }_i(t)\sim \mathit{\text{Gamma}}(1,\frac{1}{4}(Z_{i1}+Z_{i2}+1))$, and they are independent. In this set-up, data follow a marginal quantile regression model,

$$Q_{Y_i(t)}(\tau |Z_{i1},Z_{i2})=max(0,3.5+F_{\mathit{\text{Gamma}}(4,1)}^{-1}(\tau )+\{-2+F_{\mathit{\text{Gamma}}(4,1)}^{-1}(\tau )\}{Z}_{i1}+F_{\mathit{\text{Gamma}}(4,1)}^{-1}(\tau )Z_{i2}-t).$$

Under the set-ups described above, c is specified as 0, the average number of visits is 4.4, and the average left censoring rate is 10% in both case 1 and case 2. Note that fitting model (1) to a dateset with responses Y_i(t) subject to left censoring by c can be equivalently formulated as fitting model (1) to a transformed dataset with shifted responses, Y_i(t) − c, subject to left censoring by the constant 0. Therefore, the cases we considered here with c = 0 are representative for the general scenarios with nonzero c's.

For each set-up, we generated 1000 data sets of sample size n = 200. For each simulated dataset, we applied the proposed method to estimate covariate effects on the 25th, 50th, and 75th outcome quantiles. We also compared our method with a naive approach, which implements Wang and Fygenson (2009)'s method by obtaining the coefficient estimator as the minimizer of objective function (3). Empirical bias and standard deviations of estimators from both methods are presented in Table 1. It is shown that the proposed estimator is virtually unbiased. The bias from the naive method is quite evident; the magnitude of bias can be over half of the magnitude of standard deviation in some cases. The empirical standard deviations of the proposed estimator are reasonable for the sample size n = 200 and are fairly close to estimated standard deviations. The agreement between empirical and estimated standard deviations improves as the sample size is increased to n = 400. We also examined the estimates at higher quantiles, corresponding to τ = 0.85, 0.90, 0.95. The results are presented in Table D.1 of Web Appendix D, indicating satisfactory performance of our proposals. The simulation results with n = 400 are presented Table D.2 of Web Appendix D.

Table 1.

Simulation studies that compared the proposed method and the naive approach: EmpSD – empirical standard deviation; AvgSD – the average of standard deviation estimates; Cov95 – the coverage rate of a 95% confidence interval.

		Naive		Proposed
						Bootstrapping		Sample-based
Effect	True	Bias	EmpSD	Bias	EmpSD	AvgSD	Cov95	AvgSD	Cov95
Case 1
τ = 0.25
Intercept	4.163	-0.077	0.157	-0.011	0.162	0.172	0.97	0.194	0.95
Z1	-1.337	0.149	0.284	0.028	0.307	0.323	0.96	0.348	0.94
Z2	0.663	0.131	0.175	0.011	0.190	0.189	0.95	0.201	0.94
t	-1	0.033	0.032	0.0007	0.035	0.041	0.97	0.054	0.96
τ = 0.5
Intercept	4.5	-0.066	0.145	-0.007	0.144	0.153	0.95	0.162	0.95
Z1	-1	0.134	0.269	0.015	0.269	0.287	0.96	0.301	0.95
Z2	1	0.130	0.169	0.002	0.171	0.173	0.95	0.174	0.93
t	-1	0.028	0.027	-0.0006	0.028	0.031	0.97	0.036	0.97
τ = 0.75
Intercept	4.837	-0.061	0.155	0.002	0.149	0.159	0.96	0.165	0.95
Z1	-0.663	0.117	0.300	-0.010	0.278	0.298	0.96	0.300	0.94
Z2	1.337	0.142	0.191	0.0008	0.178	0.185	0.96	0.184	0.94
t	-1	0.025	0.027	-0.002	0.027	0.030	0.97	0.033	0.96
Case 2
τ = 0.25
Intercept	4.134	-0.029	0.121	0.006	0.121	0.125	0.94	0.135	0.93
Z1	-1.366	0.062	0.218	-0.003	0.211	0.225	0.96	0.235	0.95
Z2	0.634	0.065	0.127	-0.001	0.129	0.132	0.95	0.135	0.94
t	-1	0.022	0.026	0.001	0.027	0.031	0.97	0.038	0.97
τ = 0.5
Intercept	4.418	-0.043	0.142	0.006	0.136	0.146	0.96	0.155	0.94
Z1	-1.082	0.097	0.261	-0.005	0.244	0.263	0.96	0.275	0.95
Z2	0.918	0.093	0.166	-0.007	0.154	0.155	0.94	0.157	0.93
t	-1	0.027	0.028	0.001	0.028	0.031	0.97	0.035	0.96
τ = 0.75
Intercept	4.777	-0.060	0.195	0.002	0.178	0.190	0.96	0.199	0.95
Z1	-0.723	0.134	0.383	0.001	0.327	0.339	0.94	0.352	0.93
Z2	1.277	0.151	0.241	-0.008	0.209	0.210	0.94	0.205	0.92
t	-1	0.033	0.035	0.0004	0.034	0.037	0.97	0.040	0.96

In our simulations, we evaluated both bootstrap and sample-based inference procedures. The bootstrap size was chosen as 500. In Table 1, we report the averages of standard deviation (SD) estimates and the empirical coverage rates of 95% confidence intervals obtained from both inference approaches. Generally, both types of SD estimates are acceptably close to the empirical standard deviations. The bootstrap-based SD estimates are slightly better than the sample-based SD estimates. The computation of the sample-based approach is about 50 times faster than that of the bootstrapping procedure. Both bootstrap and sample-based inference procedures yield confidence intervals with accurate coverage rates.

We also investigated the robustness of the proposed estimation of model (1) to the potential mis-specification of the model for the follow-up time process. We consider three different scenarios of model mis-specification. The details about the set-ups and the results are relegated to Web Appendix D due to space limit.

From our simulations, we find that the proposed estimator always has much smaller bias compared to that of the naive estimator. When only a moderate model misspecification presents, the bias of the proposed estimator is only slightly larger than the empirical bias observed in the case with correctly specified follow-up model. The bias increases as the departure from the true model increases. Overall, the proposed method demonstrates quite robust performance when the follow-up time model is misspecified.

6. Application to PBB study

Polybrominated biphenyls (PBBs) are manufactured chemicals added as flame retardants to electrical devices, plastics, and various textiles. A widespread contamination with PBBs occurred in Michigan during 1973 - 1974 when PBB was accidently substituted for a nutritional supplement manufactured at the same chemical plant. The PBB was then mixed with animal feed. Farmers and Michigan residents throughout the state were exposed to PBB by consuming contaminated animal food products (e.g. milk, beef, pork, chicken, eggs). The Michigan Department of Public (now Community) Health (MDCH), in collaboration with the US Public Health Service, established a registry of individuals exposed to the contaminated food products. Since the initial enrollment period (1976 - 1978), the MDCH has periodically contacted cohort members to obtain additional serum samples. Serum samples from cohort members were collected from 1976–1993.

Our analysis was focused on understanding the elimination of PBB from the body by examining repeated measurements of PBB in serum. The current analysis is limited to women. PBBs are stable, persistent halogenated organic pollutants with extremely long half-lives. Participants may continue to have measurable PBB levels in serum after more than 20 years. We included females who were born before the contamination incident (July, 1973) if they had at least two serum PBB measurements at least 6 months apart, and if they had an initial serum PBB measurement greater than 2 parts per billion (p.p.b.) and taken after age 16. We required an initial serum PBB measurement of at least 2 p.p.b. to ensure that their levels were above the limit of detection of 1 p.p.b. This imposed “artificial” truncation which would limit the interpretation of our analysis results to the population with initial visit PBB measurements greater than 2 p.p.b. We excluded females who were younger than age 16 at initial measurement because childhood growth could potentially affect the compartment mobility and thus the equilibrium of serum PBB concentration levels. We also excluded measurements taken during pregnancy or during any period of breast-feeding because of the potential mobilization of PBB into the bloodstream during these times (Eyster et al., 1983; Kreuzer et al., 1997).

The final dataset used for our analysis included 364 women. There are between 2 and 7 serum measurements of PBB per woman. Initial PBB concentration level ranges from 1 to 559.80 p.p.b. (mean=11.44, median=2.40). Outcome Y*(t) is defined as log(PBB) at time t, with the time origin set as July 1, 1973, the time when the PBB contamination started. Study entry time L is defined as the time from PBB exposure date to the first study visit. Similarly, R is defined as the time from PBB exposure to the most recent PBB serum measurements available, December 31, 1993. The initial visit time L ranges from 2.67 to 8.04 years with mean=3.74, median=3.71, and interquartile range=(3.38, 3.96). A histogram of the gap times between adjacent visits is presented in Web Appendix F.

When we modeled follow-up visit times, we excised separate attentions to the three time periods, 1976-1981, 1982-1989, and 1990-1993, to accommodate the special design of the PBB study. During 1982-1989, a substudy focused on those with high PBB levels to examine the health of those who had been more severely exposed. As a result, serum samples available during this time period were mostly contributed by participants of this substudy, who tended to have higher PBB levels than a member randomly selected from the whole study cohort. After 1990, all participants of the PBB study were aggressively contacted for serum samples. Giving a careful consideration of such a study design and conjecturing that a high initial PBB level may lead to more frequent follow-up visits, we assume the following model for the follow-up visit time process:

$$P(d{N}_i(t)|{\mathcal{H}}_i(t))=I(L_i<t\le R_i){\lambda }_0(t)\times exp\{{\alpha }_{1}I(t\le 8.5)·Y_i(L_i)+{\alpha }_2·I(8.5<t\le 16.5)Y_i(L_i)+{\alpha }_3·I(t>16.5)Y_i(L_i)\}.$$ (8)

Note that in model (8), we convert the three calendar time intervals stated above into time intervals starting from the assigned time origin. The coefficients, α₁, α₂ and α₃, represent the effects of the initial outcome on the follow-up time process in these three time intervals respectively.

Table 2 presents the coefficient estimates for the assumed proportional intensity model (8). All coefficient estimates are positive. The estimated α₂ has the largest magnitude, 0.584, and is significantly different from zero with p < 0.01. This result indicates that one unit larger in the initial log(PBB) level may be associated with 79% higher intensity of making a follow-up visit during 1982-1989. This is consistent with our observation in Figure 2, which demonstrates participants with higher initial PBB levels have more follow-up visits. In contrast, the coefficient estimates for α₁ and α₃ are close to zero. This may reflect a rather uniform visit patterns across all study cohort member during the cohort recruiting and during the most recent time periods.

Table 2. Parameter estimates of the proportional intensity model for PBB study.

Coeff	Estimate	exp(Estimate)	p-value
α1	0.027	1.03	0.61
α2	0.584	1.79	< 0.01
α3	0.039	1.04	0.52

We modeled the outcome log(PBB) by marginal quantile regression models taking the form,

$$Q_{Y_i(t)}(\tau )={\beta }_0(\tau )+{\beta }_1(\tau )\times t,t>0,$$ (9)

where 0 < τ < 1. Here, the intercept, β₀(τ), represents the τth quantile of log(PBB) level at time origin. The time effect, β₁(τ), represents the elimination rate of the population τth quantile of log(PBB) level over time, and thus is the key quantity of interest in this analysis. We applied the proposed method to estimate model (9) with τ = 0.25, 0.50, 0.75, 0.85, 0.90 and 0.95. We also fit these models by naively applying Wang and Fygenson (2009)'s method, which would ignore the dependency between follow-up and outcome. For inference, we adopted the bootstrap procedure to obtain standard deviation estimates and 95% confidence intervals. The bootstrap size was chosen as 500.

In Table 3, we present the coefficient estimates and 95% confidence intervals obtained from the proposed method and the naive approach. Based on the naive approach, we obtain positive time coefficient estimates at all considered quantile levels. In particular, the 95% confidence interval for the time effect on the 75th percentile of PBB concentration is (0.001, 0.054). This result can lead to a conclusion that among individuals at the 75th percentile of PBB distribution the amount of PBB in their blood increases with time. It contradicts with the biologic fact that human bodies can not produce chemical PBB (and the exposure did not continue). As we explain in Section 1 on Figure 3, these positive time effect estimates are probably artifacts caused by ignoring the dependency between outcome and follow-up.

Table 3. Parameter estimates and 95% confidence interval for PBB study.

	Naive		Proposed
Quantile	Estimate	95% CI	Estimate	95% CI
Intercept
25th	0.150	(0.092, 0.208)	0.182	(0.155, 0.210)
50th	0.852	(0.707, 0.997)	0.904	(0.609, 1.199)
75th	1.496	(1.246, 1.745)	1.435	(1.171, 1.699)
85th	2.298	(1.763, 2.833)	2.057	(1.635, 2.479)
90th	2.829	(2.182, 3.475)	2.956	(2.357, 3.555)
95th	3.813	(3.112, 4.514)	4.047	(3.379, 4.716)
Time
25th	0.009	(2e-4, 0.018)	6e-17	(-0.008, 0.008)
50th	0.006	(-0.007, 0.018)	-0.009	(-0.024, 0.007)
75th	0.028	(0.001, 0.054)	-4e-17	(-0.012, 0.012)
85th	0.019	(-0.027, 0.064)	-8e-4	(-0.024, 0.022)
90th	0.036	(-0.017, 0.090)	-0.026	(-0.056, 0.005)
95th	0.046	(-0.003, 0.096)	-0.052	(-0.097, -0.007)

On the other hand, the estimates for β₁(τ) from the proposed approach are all negative except for the β₁(τ) estimate with τ = 0.25, which is extremely close to zero. The negative estimates for the time effect are consistent with the biological evidence that PBB concentration in blood should decrease over time. By taking into account that subjects with lower initial PBB levels tend to contribute fewer serum samples, our inverse intensity-ratio weighting strategy assigned larger weights for these subjects and hence correct the bias due to outcome-dependent follow-up.

In addition, the estimated time coefficients demonstrate an overall trend of increasing with τ. The time effect on lower percentiles, such as τ = 0.25, 0.50, 0.75, are not significant while the time effect on the 95th quantile is significantly less than zero. Our estimates may be interpreted as that the 95th percentile of PBB distribution decreases 5.1% (= 1 − exp(−0.052)) per year with 95% confidence interval between 0.7% and 9.2%. The faster elimination rates of upper quantiles (compared to those of lower quantiles) provide some confirmation to the conjecture that subjects with higher PBB levels may demonstrate faster PBB elimination over time. The interesting and sensible varying pattern of time effect on different quantiles cannot be uncovered by traditional longitudinal models that are focused on modeling mean outcomes.

We also performed sensitivity analyses, in which we fit two different models for follow-up visit times. In one case (Case A), we assume that the proportional intensity model for visit times include one additional covariate, BMI, which represents the body mass index of study participants at study enrollment. In the other case (Case B), we fit the proportional intensity model (8) with Y_i(L_i) replaced by its discrete version with cutoff points chosen as exp(1) and exp(3). The results from adopting these different visit time models are presented in Web Appendix E; please see Table E.1–Table E.4. From Tables E.1 and E.3, we note that fitting the three different visit time models consistently evidences the presence of outcome-dependent following during 1982-1989, which conforms to the design of the PBB study. Moreover, it renders quite similar estimates for β₀(τ). This demonstrates the robustness of the proposed method.

In summary, our analysis shows that the PBB concentration distribution shifts down slowly over time. Upper quantiles decrease faster than lower quantiles. A significant decreasing trend over time has been shown by the data for the 95th quantile of PBB distribution. Ignoring outcome-dependent follow-up would result in very biased estimates of β₁(τ) leading to implausible scientific conclusions.

7. Remarks

Quantile regression offers a robust and flexible approach to analyzing longitudinal data with skewed outcomes. Irregular outcome-dependent follow-up is a common data feature but can be easily overlooked in practice. The proposed inverse intensity-ratio weighted estimator can effectively correct the bias due to irregular outcome-dependent follow-up, with reasonable modeling of the follow-up time process.

The current method exposition takes the assumption that the left censoring variable is a fixed constant. Nevertheless, the new method can be readily adapted to cases where the left censoring variable is random but always observed. Moreover, it is straightforward to extend the proposed method to deal with doubly censored longitudinal outcomes, for example, measurements subject to a upper detection limit as well as a lower detection limit.

Like Powell (1986)'s censored quantile regression method, our approach can be readily extended to cases where the left censoring variable is not just a fixed constant but a random variable which is always observed. More specifically, when the outcome Y_i(t) is subject to left censoring by an observed random variable C_i(t), the proposed method would remain valid if one replaces the constant c by C_i(t) and C_i(t) is independent of Y_i(t) given X_i(t). Such an extension of the proposed method can accommodate more general practical settings, for example, a long-term follow-up study where the assay detection limit changes over time.

The proposed method can be revised to accommodate other types of models for the follow-up time process, such as proportional mean/rate model (Lin et al., 2000). Our simulations suggest that the proposed estimation of the marginal quantile regression model is reasonably robust to mis-specifications of the follow-up time model. Even when the adopted proportional intensity model departs from the true model, our approach can still achieve considerable bias reductions compared to the naive approach that does not make any adjustment for outcome dependent follow-up.