Skip to main content
PMC home page
Nature Communications logoLink to Nature Communications
. 2016 Feb 4;7:10452. doi: 10.1038/ncomms10452

Origin of the spin Seebeck effect in compensated ferrimagnets

Stephan Geprägs 1,a, Andreas Kehlberger 2,3, Francesco Della Coletta 1,4, Zhiyong Qiu 5,6, Er-Jia Guo 2, Tomek Schulz 2, Christian Mix 2,3, Sibylle Meyer 1,4, Akashdeep Kamra 1,7,*, Matthias Althammer 1, Hans Huebl 1,8, Gerhard Jakob 2,3, Yuichi Ohnuma 9,10, Hiroto Adachi 6,10, Joseph Barker 9, Sadamichi Maekawa 6,10, Gerrit E W Bauer 5,7,9, Eiji Saitoh 5,9,10,11, Rudolf Gross 1,4,8, Sebastian T B Goennenwein 1,8,b, Mathias Kläui 2,3,c
PMCID: PMC4742853  PMID: 26842873

Abstract

Magnons are the elementary excitations of a magnetically ordered system. In ferromagnets, only a single band of low-energy magnons needs to be considered, but in ferrimagnets the situation is more complex owing to different magnetic sublattices involved. In this case, low lying optical modes exist that can affect the dynamical response. Here we show that the spin Seebeck effect (SSE) is sensitive to the complexities of the magnon spectrum. The SSE is caused by thermally excited spin dynamics that are converted to a voltage by the inverse spin Hall effect at the interface to a heavy metal contact. By investigating the temperature dependence of the SSE in the ferrimagnet gadolinium iron garnet, with a magnetic compensation point near room temperature, we demonstrate that higher-energy exchange magnons play a key role in the SSE.

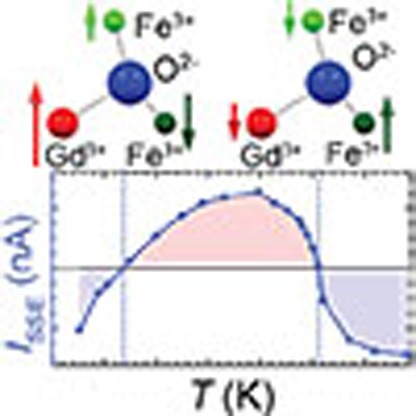Inline graphicFerrimagnets possess multiple spin sub-lattices resulting in a complex magnon band structure and subtle spin transport across interfaces. Here, the authors show how the spin Seebeck effect, the thermal generation of pure spin current, may be an effective tool to study these magnetic excitations.

Recently, the spin Seebeck effect (SSE)1,2,3,4 has attracted much attention, due to open fundamental physics questions1,2,3,5,6,7,8,9,10,11,12,13, and also because of the potential for practical applications14. It is now widely accepted that the thermopower signals measured in ferromagnetic insulator/normal metal (FMI/NM) bilayers in the longitudinal SSE geometry are indeed a consequence of magnonic spin currents generated by a temperature gradient2,5,6,7,8,15. However, the exact mechanism of the SSE and the contribution of different magnon modes to the spin current are still under discussion3,9,10,11,12,13. So far, the detection of the magnonic spin currents via the inverse spin Hall effect (ISHE) in the adjacent normal metal layer has been analysed based on an effective spin current combined with an effective spin mixing conductance that governs the spin current transport across the interface. Experimental data have typically been described within a simple spin wave model, neglecting higher energy magnon bands3,15. This approach is reasonable for the SSE in ferromagnets/normal metal hybrids, where one only has to consider low-energy magnons. However, owing to the presence of different magnetic sublattices, ferrimagnets exhibit more complex magnon spectra, much like acoustic and optical phonon modes in crystals with more than one atom per unit cell16,17. For Gd3Fe5O12/Pt (GdIG/Pt) bilayers as a test bed, we demonstrate that the SSE in complex ferrimagnets results from the balance of thermal spin pumping between multiple magnon modes where distinct magnetic moments might contribute differently to the spin mixing conductance. This leads to different efficiencies for the spin transport across the GdIG/Pt interface. In particular, we measure the magneto-thermopower (the longitudinal SSE) as a function of temperature. We observe an abrupt sign change in the SSE close to the magnetic compensation point, followed by another, more gradual sign change at lower temperatures demonstrating that the SSE is qualitatively different to the temperature dependence of the net magnetization. Our theoretical analysis reveals that the thermally generated net spin current giving the SSE signal reflects the complex interplay of two magnon branches and possibly the exchange coupling at the interface. This shows that the description of the SSE needs to take into account the magnon dispersion relation including the polarization of spin waves as well as interface effects that have previously been neglected.

Results

Magnetic properties of GdIG thin films

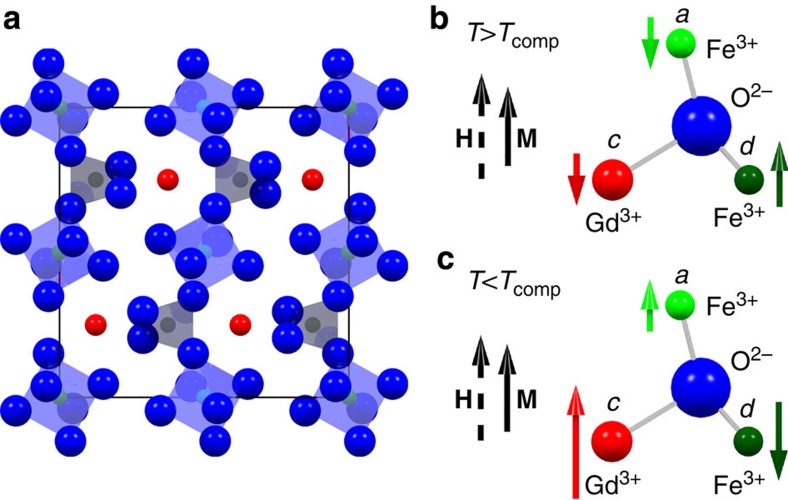
First, we discuss the magnetic properties of GdIG as a function of temperature. As sketched in Fig. 1, GdIG is a ferrimagnetic insulator with three magnetic sublattices. Each unit cell consists of 12 trivalent Fe atoms that are tetrahedrally coordinated with oxygen atoms (d sites), 8 Fe atoms that are octahedrally coordinated (a sites) and 12 dodecahedrally coordinated Gd atoms (c sites). The two Fe sublattices are strongly coupled via antiferromagnetic superexchange (exchange constant Jad≃32 cm−1)16, with a Néel temperature of TN≃550 K. Since the Gd moments are weakly exchange coupled to the Fe a sublattices (Jac≃7 cm−1)16 they experience an effective magnetic field below TN and can be treated as an ‘exchange-enhanced' paramagnetic moment18, which is strongly temperature dependent. The magnetization of GdIG is thus determined by the d site Fe ions at high temperatures (Fig. 1b). With decreasing temperature, the magnetization of the Gd sublattice strongly increases, and together with the Fe magnetization at the a site eventually overcomes the Fe magnetization at the d site. At the magnetic compensation temperature Tcomp≃288 K (bulk value)19,20, the total magnetization of the a (Fe) and c (Gd) sublattices is equal in magnitude but antiparallel to the magnetization of the d (Fe) sublattice, such that the net remanent magnetization of GdIG vanishes. In a finite external magnetic field the net GdIG magnetization exhibits a minimum at Tcomp, caused by a reorientation of the sublattice magnetizations (Fig. 1c).

Figure 1. Magnetic sublattices of GdIG.

Figure 1

Open in a new tab

(a) Iron garnet crystal structure. The tetrahedrally and octahedrally coordinated Fe3+ ions are highlighted. (b,c) The three different magnetic sublattices of GdIG shown for temperatures above (T>Tcomp) and below (T<Tcomp) the magnetic compensation temperature Tcomp. Due to the strong temperature dependence of the magnetic Gd sublattice (c sites), the Gd sublattice dominates the magnetic behaviour for T<Tcomp, while for T>Tcomp it is mainly caused by the antiferromagnetically coupled Fe sublattices (d and a sites). In the presence of a finite magnetic field, the net magnetization M points along the external magnetic field H. The direction and length of the coloured arrows represent the direction and magnitude of the magnetizations of the three magnetic sublattices.

We investigate the SSE in three samples with different crystallographic orientations and thicknesses (sample A, sample B, and sample C) (Fig. 2). As evident from Fig. 3b,d,f, the magnetic properties of these GdIG thin films recorded by SQUID magnetometry show the characteristics expected for a ferrimagnet with a magnetization compensation point21. The magnetization first decreases with decreasing temperature, reaches a minimum at Tcomp and then increases again. The compensation temperature of sample A is around 285 K (Fig. 3b), in line with literature19,20. For sample B and sample C, Tcomp is somewhat lower (Fig. 3d,f), most likely due to a small reduction of the magnetic exchange strength due to strain effects, Fe deficiency or interdiffusion of Al in GdIG thin films22.

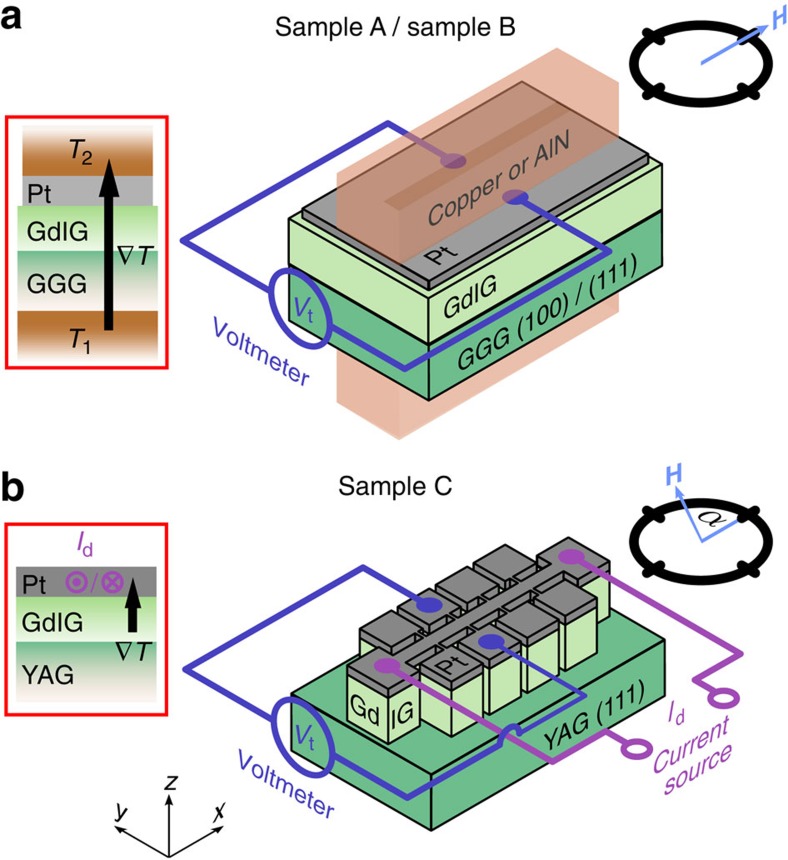
Figure 2. Experimental set-up.

Figure 2

Open in a new tab

(a,b) Sketches of the experimental configurations used to record the longitudinal spin Seebeck effect (SSE). Three different samples were investigated: Sample A and sample B consist of a GdIG(100 nm)/Pt(8 nm) and a GdIG(1 μm)/Pt(10 nm) bilayer fabricated on a (100)- and a (111)-oriented gadolinium gallium garnet (Gd3Ga5O12, GGG) substrate, respectively. Sample C is composed of a GdIG(26 nm)/Pt(10 nm) bilayer fabricated on a (111)-oriented yttrium aluminium garnet (Y3Al5O12, YAG) substrate. For sample A and B, the longitudinal SSE signal is determined by measuring the transverse voltage Vt perpendicular to an external magnetic field while modifying the magnetic field magnitude at a fixed magnetic field orientation 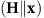Inline graphic. The temperature gradient required for SSE measurements is generated by two independently heated copper blocks or AlN ceramics, respectively. The longitudinal SSE signal of sample C is obtained by recording Vt as a function of the in-plane orientation of the external magnetic field α at a fixed magnetic field magnitude of 2 T. Here the temperature gradient across the GdIG/Pt interface is generated by driving a large current Id along the Pt microstructure. The temperature-dependent resistance of the Pt is exploited for on-chip thermometry.

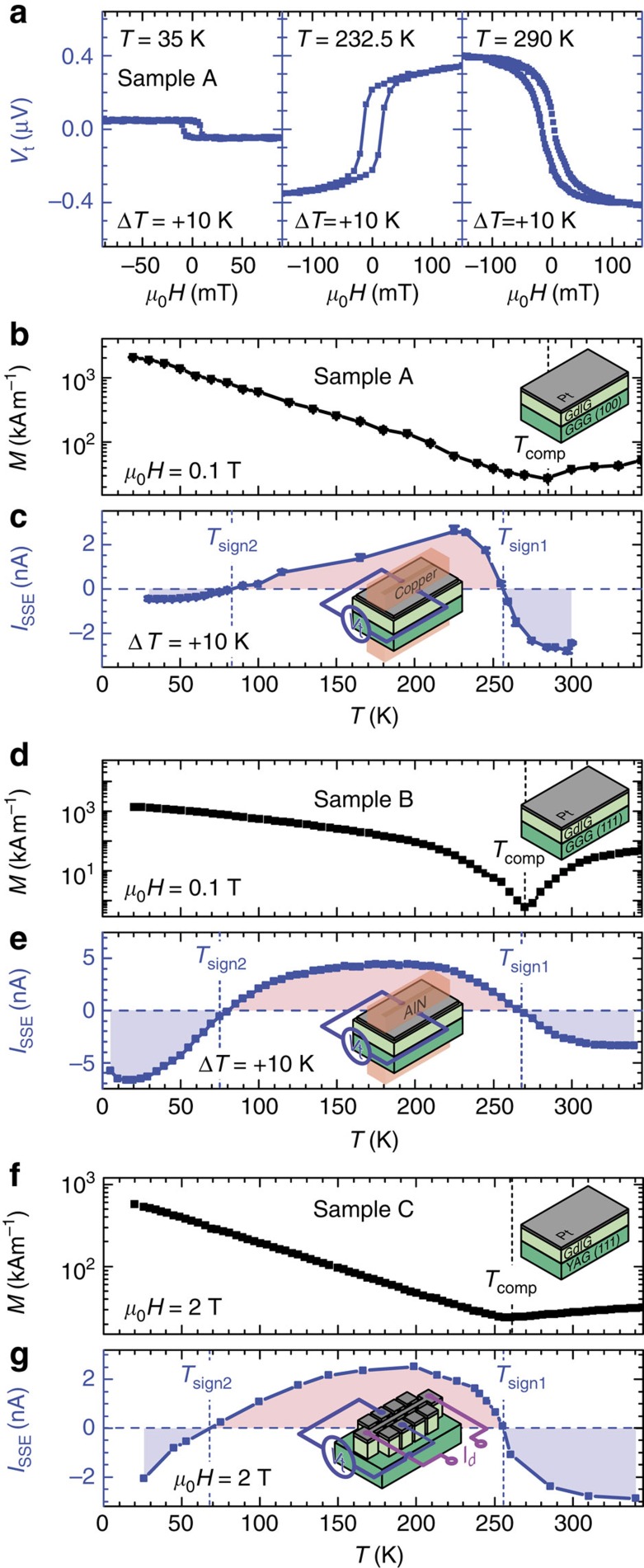
Figure 3. Magnetization and spin Seebeck effect in GdIG/Pt hybrids.

Figure 3

Open in a new tab

(a) Transverse voltage Vt of sample A plotted versus the applied magnetic field for selected temperatures. The hysteresis loop flips sign twice with decreasing temperature. (b) Temperature-dependent magnetization of sample A recorded at a magnetic field of 0.1 T. (c) Corresponding SSE signal ISSE obtained from the difference in Vt at positive and negative saturation taking the temperature dependence of the Pt resistance R(T) into account. (d,f) Magnetization as a function of temperature of sample B and sample C measured at μ0H=0.1 T and μ0H=2 T, respectively. (e) ISSE signal of sample B. (g) ISSE signal of sample C obtained by recording the transverse voltage Vt as a function of the in-plane orientation of the external magnetic field with constant magnitude of 2 T while applying a heating current Id of 6 mA across the Hall bar. The SSE signal ISSE is then calculated from 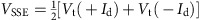Inline graphic. The blue dashed lines mark the zero-crossing temperatures Tsign1 and Tsign2 of the ISSE signal. The temperatures Tcomp of the magnetic compensation points are indicated by the black dashed lines.

Temperature-dependent spin Seebeck experiments

We now turn to the results of the SSE experiments shown in Fig. 3. The longitudinal SSE was recorded as a function of temperature using two complementary methods. Sample A and sample B are sandwiched between two copper blocks and two AlN ceramics, respectively (Fig. 2a)6. A resistive heater as well as a temperature sensor within each block allow the temperature to be independently set and stabilized. To determine the longitudinal SSE signal, the transverse voltage Vt perpendicular to an external magnetic field is measured while modifying the magnetic field magnitude at a fixed magnetic field orientation 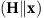Inline graphic. The GdIG/Pt bilayer of sample C is micropatterned into a Hall bar structure using optical lithography and Argon ion beam milling (Fig. 2b). The temperature gradient across the GdIG/Pt interface required for SSE experiments is generated by driving a large current Id along the Pt microstructure itself, while simultaneously exploiting the temperature-dependent resistance of the Pt for on-chip thermometry23. Here Vt is recorded as a function of the in-plane external magnetic field direction α at a fixed magnetic field magnitude of 2 T. The SSE data shown in Fig. 3a were taken on sample A at three different base temperatures with a temperature difference of ΔT=+10 K applied across the sample. Positive temperature difference hereby means that the Pt is warmer than the GdIG and the GGG substrate. As expected for the SSE, a hysteretic voltage signal Vt is obtained on sweeping the magnetic field2. Interestingly, however, the Vt hysteresis loop flips sign twice with decreasing temperature: while Vt(H) is ‘regular' (that is, the Vt(H) recorded in GdIG/Pt hybrids has the same sign as the established SSE signal of YIG/Pt; ref. 24) for T=280 K, the Vt(H) loop recorded for T=232.5 K is ‘inverted', while the loop at T=35 K is ‘regular' again.

To analyse the temperature-dependent evolution of the SSE signal in more detail, we define the SSE amplitude VSSE as the difference 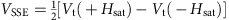Inline graphic, recorded at external magnetic field strengths μ0Hsat large enough to saturate the GdIG magnetization. Taking the temperature dependence of the Pt resistance R(T) into account, Fig. 3c shows the ISSE(T)=VSSE(T)/R(T) curve from sample A. At first, the SSE signal is negative at high temperatures, then becomes positive in a temperature interval Tsign2≲T≲Tsign1 with Tsign2≈80 K, and is negative again for T≲Tsign2. The first sign change around Tsign1≈256.5 K is rather abrupt, while the second around Tsign2 is much more gradual. As evident from Fig. 3e,g the SSE signal ISSE of sample B and sample C confirm the SSE temperature dependence observed in sample A. Interestingly, the temperature dependence of the SSE is very similar to the Faraday response of GdIG single crystals25, demonstrating that the measured SSE is dominated by GdIG bulk properties. However, interface effects might also have an influence on the SSE signal. For example, a layer with modified magnetic properties might form at the interface due to reduced exchange interaction strength at the GdIG surface. However, so far, there is no experimental evidence for the existence of such a magnetic surface layer in other temperature-dependent measurements of the SSE26,27.

Theory of SSE in compensated ferrimagnets

To understand and explain the temperature dependence of the SSE signal in GdIG/Pt hybrids in more detail, we carried out theoretical calculations. Using two approaches, one based on a detailed atomistic model of GdIG and the other on a two sublattice linear response formalism, two possible effects can be identified contributing to the observed behaviour: (a) the temperature dependence of the different branches of the magnon dispersion and (b) different spin transport efficiencies across the GdIG/Pt interface, owing to a difference in the exchange coupling strength between the GdIG constituent ions and the Pt conduction electrons.

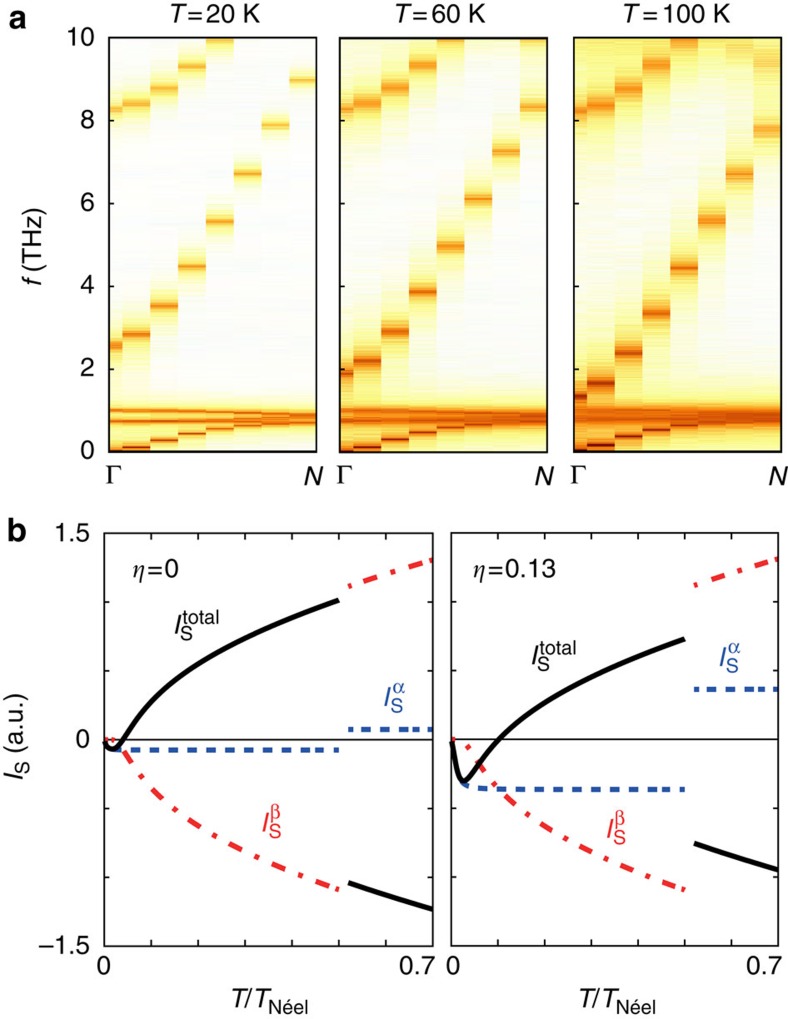
First, we discuss the atomistic spin model, which is described in detail in the Supplementary Note 1. The approach is based on the classical Heisenberg model and the Landau–Lifshitz–Gilbert equation, which describes the dynamical behaviour. By including a Langevin thermostat, numerical calculations using the parameters summarized in Supplementary Table 1 yield the spin dynamics including statistical thermal properties (see Supplementary Figures 1 and 2). From the space–time Fourier transform of the real time dynamics, the spin wave spectrum is obtained. Since the model does not involve a magnon ansatz, it includes all non-linear effects such as the magnon–magnon interactions, which are important for the understanding of the relative contributions of each sublattice to the SSE. By analysing the spin wave spectrum we gain insight into the temperature dependence of the frequency, amplitude, as well as the linewidth of the modes, which goes beyond mean-field theories and the random phase approximation. The thus obtained low-frequency spin wave spectra of GdIG are shown in Fig. 4a. The first band in the GHz regime corresponds to the ferrimagnetic resonance mode (α-mode), followed by two nearly dispersionless modes at 1 THz. These two optical modes are the Gd moments precessing in the exchange field of the Fe moments16. The next approximately parabolic band is a gapped, optical mode (β-mode) precessing in opposite sense as compared with the α-mode, where the gap at k=0 depends on the Fe–Gd exchange couplings. The higher frequency spin wave modes have only small amplitudes below room temperature (see Supplementary Figure 3) and are disregarded in the further discussion. At low temperature, the α-mode dominates the SSE signal. With increasing temperature the two Gd-modes close to 1 THz decrease in power spectral intensity and broaden (see Supplementary Figure 4), reducing their contribution to the SSE due to the decrease in coherence of the associated spin waves. Significantly, the optical β-mode red shifts due to the loss of order of the Gd moments, reducing the magnon gap at k=0. At a certain temperature the contribution of the β-mode overwhelms that of the α-mode resulting in a sign change of the SSE due to the different polarization of the α-mode compared with the β-mode. Therefore, the temperature dependence of the SSE is determined predominantly by just two magnon bands and the shrinking of the magnon gap at k=0.

Figure 4. Calculated spin wave spectra of GdIG and sublattice spin currents injected by the SSE.

Figure 4

Open in a new tab

(a) Low-frequency spin wave spectra of GdIG calculated from an atomistic model for three different temperatures. The colour code indicates the power spectral density. For temperatures lower than 300 K, the SSE is dominated by two modes: a uniform precession mode in the GHz regime (α-mode) and a gapped, optical mode (β-mode). The two nearly dispersionless modes around 1 THz are the Gd moments precessing in the exchange field of the Fe moments. (b) Temperature dependence of the spin current 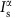Inline graphic (red) and 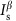Inline graphic (blue) caused by the respective magnon modes. The total spin current 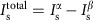Inline graphic (black) determines the SSE. 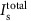Inline graphic takes the different interface exchange couplings at the GdIG/Pt interface into account. The ratio between these couplings is given by η.

The atomistic model does not address possible interface effects such as a temperature-dependent exchange coupling at the GdIG/Pt interface. Since the measured SSE signal is based on the spin currents injected from the ferrimagnet GdIG into the normal metal Pt, magnon-mode-dependent interface exchange couplings can be important. We carried out theoretical calculations of the SSE using a linear response formalism based on a two spin-lattice model with parametrized interface exchange couplings. As detailed in the Supplementary Note 2, the linear response theory results in two non-degenerate magnon modes5: the α-mode exhibits a gapless dispersion with a narrow bandwidth, while the magnon spectrum of the other mode (β-mode) is gapped by the exchange coupling energy between the Gd and the Fe sublattices. Thus, the two sublattice model is an effective model employed to understand the physics at play. The resulting temperature-dependent spin currents of both modes are shown in Fig. 4b. The total SSE signal in the GdIG/Pt hybrid is given by 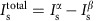Inline graphic. We make the assumption that the interface exchange coupling of the Gd 4f-spin with the Pt conduction electrons is weaker than that of the Fe 3d-spin. The ratio between these interface couplings is given by η. Figure 4b reveals that the temperature of the SSE sign change Tsign2 increases with increasing η. Using η=0.13 the experimentally obtained temperature Tsign2≈68 K can be reproduced.

Discussion

We experimentally and theoretically investigated the temperature dependence of the longitudinal SSE in GdIG/Pt bilayers grown on different substrates and with different layer thicknesses. Using two complementary experimental approaches, we find two sign changes of the SSE signal as a function of temperature. The first sign change at Tsign1 close to the magnetic compensation temperature Tcomp can be understood in terms of the reversal of the sublattice magnetizations at Tcomp, which preserves the net magnetization along the external magnetic field (Fig. 1). Since the spin current polarization is determined by the (sublattice) magnetization orientation, this leads to a sign change in the SSE current (Fig. 4b), as predicted by Ohnuma et al.5. The second sign change at Tsign2 can arise from the different temperature dependences of the spin wave power spectral densities and/or different exchange coupling strengths of these modes at the GdIG/Pt interface. Spin wave spectra based on a classical atomistic spin model as a function of temperature reveal that the temperature dependence of the SSE in GdIG is determined predominantly by two modes: a soft-mode with a gapless dispersion and narrow bandwidth (α-mode) as well as a gapped, optical mode (β-mode), where the gap at k=0 depends on the Fe–Gd exchange coupling. Due to the reduced order of the Gd moments, the magnon gap closes with increasing temperature. This causes a sign inversion of the SSE signal at a certain temperature, above which the contribution of the β-mode to the SSE becomes larger than that of the α-mode. However, the temperature Tsign2 of this SSE sign change might be influenced by different exchange couplings at the GdIG/Pt interface, that is, by different relative weights of the α- and β-mode spin current transfer into the Pt layer. By assuming a weaker exchange coupling of the α-magnons compared with the β-magnons at the interface 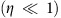Inline graphic, not only the magnitude of Tsign2 but also the gradual change of the SSE signal as a function of temperature can be reproduced (Fig. 4b). Concluding, the origin of the second SSE sign change results from an increased contribution of the gapped β-mode with increasing temperature. In addition, the temperature at which the second sign change occurs might be affected by mode-dependent exchange coupling strengths at the GdIG/Pt interface. Thus, the SSE probes the complex spin wave dynamics in ferrimagnets.

Methods

Sample fabrication

Three different sets of samples were fabricated and investigated: at Mainz, GdIG films were deposited on single crystalline, (100)-oriented gadolinium gallium garnet (Gd3Ga5O12, GGG) substrates by pulsed laser deposition using a KrF excimer laser with a laser fluence of 1.2 J cm−2. We here focus on a 100-nm-thick GdIG film (sample A) grown with optimized parameters, that is, in an oxygen atmosphere at 2 × 10−2 mbar and at a substrate temperature of 650 °C. No parasitic phases were detected using x-ray diffraction. Furthermore, an out-of-plane lattice constant of (1.254±0.005) nm, which is comparable to the bulk value of 1.247 nm, is calculated using the GdIG (400) film reflection. Moreover, the rocking curve around the GdIG (400) reflection has a full width at half maximum (FWHM) of 0.036°, indicating a high crystalline quality and low mosaicity. The 8 nm-thick Pt layer, used for the ISHE measurements, was deposited by DC-magnetron sputtering after in situ cleaning of the interface. At Sendai, a GdIG/Pt bilayer was fabricated by liquid phase epitaxy of GdIG with a thickness of around 1 μm on a (111)-oriented GGG substrate and subsequently depositing a 10 nm-thick Pt layer by DC-magnetron sputtering on the GdIG thin film (sample B). The FWHM of the rocking curve around the GdIG (444) reflection is comparable to the FWHM value of the rocking curve around the GGG (444) substrate reflection, demonstrating the high crystalline quality of the GdIG thin film. At Garching, the GdIG films were deposited onto single crystalline, (111)-oriented yttrium aluminium garnet (Y3Al5O12, YAG) substrates via pulsed laser deposition. Best structural and magnetic properties of the GdIG films were obtained by using a substrate temperature of 500 °C, an oxygen atmosphere of 1.25 × 10−2 mbar and an energy fluence of the KrF excimer laser of 2.0 J cm−2 at the target surface. The crystalline quality of the GdIG films demonstrated by the FWHM of the rocking curves around the GdIG (444) reflection of around 0.04° is comparable to the GdIG thin films fabricated at Mainz and at Sendai. We here discuss a 26 nm-thick GdIG film with a lattice constant of (1.252±0.005) nm, covered in situ, without breaking the vacuum, with 4 nm of Pt deposited via electron beam evaporation (sample C).

Longitudinal SSE experiments

The longitudinal SSE was recorded as a function of temperature, using two complementary methods. At Mainz and at Sendai, the sample is sandwiched between two heat reservoirs (copper blocks and AlN ceramics, respectively). A resistive heater within each block allows to independently set and stabilize its temperature. In particular, it thus is possible to invert the temperature difference between the heat baths, allowing to exclude spurious effects due to asymmetric sample mounting. In case of the copper blocks, thin single crystalline sapphire plates combined with thermo-conductive foil ensure good thermal contact as well as electric insulation between the copper blocks and the sample. Here the transverse voltage Vt perpendicular to an external magnetic field is measured as a function of the external magnetic field magnitude at a fixed magnetic field orientation Inline graphic. In Garching, the GdIG/Pt bilayer is micropatterned into a Hall bar structure using optical lithography and Argon ion beam milling. The sample is then inserted into a three-dimensional vector magnet cryostat, in which He exchange gas in a variable temperature insert allows us to adjust the sample base temperature. We generate the temperature gradient across the GdIG/Pt interface by sourcing a large current Id along the Pt microstructure itself, and exploit the temperature-dependent resistance of the Pt for on-chip thermometry. Here Vt is recorded as a function of the in-plane external magnetic field direction α using a fixed magnetic field magnitude.

Additional information

How to cite this article: Geprägs, S. et al. Origin of the spin Seebeck effect in compensated ferrimagnets. Nat. Commun. 7:10452 doi: 10.1038/ncomms10452 (2016).

Supplementary Material

Supplementary Information

Supplementary Figures 1-4, Supplementary Table 1, Supplementary Notes 1-2 and Supplementary References

ncomms10452-s1.pdf (893.2KB, pdf)

Acknowledgments

We would like to thank the Deutsche Forschungsgemeinschaft (DFG) for financial support via SPP 1538 ‘Spin Caloric Transport' (Project No. GO 944/4-1, BA 2954/2 and KL 1811/7-1), JSPS Grants-in-Aid for Scientific Research (Nos. 25247056, 25220910, and 26103006) and the Graduate School of Excellence Materials Science in Mainz (MAINZ) GSC 266, the EU (IFOX, NMP3-LA-2012 246102; MASPIC, ERC-2007-StG 208162; InSpin FP7-ICT-2013-X 612759), the SpinNet project, and the Research Center of Innovative and Emerging Materials. At Garching, we thank T. Brenninger for technical support, A. Habel and K. Helm-Knapp for the fabrication of the stoichiometric GdIG targets, and M. Schreier as well as J. Lotze for fruitful discussions.

Footnotes

Author contributions S.G., A. Kehlberger, F.D.C. and Z.Q. performed the measurements with support from S. Meyer, T.S., M.A. and E.-J.G., Y.O., H.A., A. Kamra and J.B. developed the theory under supervision of S. Maekawa and G.E.W.B., A. Kehlberger, F.D.C., C.M., S.G. and G.J. were responsible for sample fabrication. S.G., H.H., R.G., S.T.B.G., E.S. and M.K. supervised the project. S.G., A. Kehlberger, S.T.B.G. and M.K. analysed the data and prepared the manuscript. All authors discussed the results and commented on the manuscript.

References

  1. Uchida K. et al. Observation of the spin Seebeck effect. Nature 455, 778–781 (2008). [DOI] [PubMed] [Google Scholar]
  2. Uchida K., Nonaka T., Ota T. & Saitoh E. Longitudinal spin-Seebeck effect in sintered polycrystalline (Mn,Zn)Fe2O4. Appl. Phys. Lett. 97, 262504 (2010). [Google Scholar]
  3. Xiao J., Bauer G. E. W., Uchida K., Saitoh E. & Maekawa S. Theory of magnon-driven spin Seebeck effect. Phys. Rev. B 81, 214418 (2010). [Google Scholar]
  4. Bauer G. E. W., Saitoh E. & van Wees B. J. Spin caloritronics. Nat. Mater. 11, 391–399 (2012). [DOI] [PubMed] [Google Scholar]
  5. Ohnuma Y., Adachi H., Saitoh E. & Maekawa S. Spin Seebeck effect in antiferromagnets and compensated ferrimagnets. Phys. Rev. B 87, 014423 (2013). [Google Scholar]
  6. Kehlberger A. et al. Length scale of the spin Seebeck effect. Phys. Rev. Lett. 115, 096602 (2015). [DOI] [PubMed] [Google Scholar]
  7. Schreier M. et al. Magnon, phonon, and electron temperature profiles and the spin Seebeck effect in magnetic insulator/normal metal hybrid structures. Phys. Rev. B 88, 094410 (2013). [Google Scholar]
  8. Siegel G., Prestgard M. C., Teng S. & Tiwari A. Robust longitudinal spin-Seebeck effect in Bi-YIG thin films. Sci. Rep. 4, 4429 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Sandweg C. W. et al. Spin pumping by parametrically excited exchange magnons. Phys. Rev. Lett. 106, 216601 (2011). [DOI] [PubMed] [Google Scholar]
  10. Tikhonov K. S., Sinova J. & Finkel'stein A. M. Spectral non-uniform temperature and non-local heat transfer in the spin Seebeck effect. Nat. Commun. 4, 1945 (2013). [DOI] [PubMed] [Google Scholar]
  11. Agrawal M. et al. Direct measurement of magnon temperature: new insight into magnon-phonon coupling in magnetic insulators. Phys. Rev. Lett. 111, 107204 (2013). [DOI] [PubMed] [Google Scholar]
  12. Agrawal M. et al. Role of bulk-magnon transport in the temporal evolution of the longitudinal spin-Seebeck effect. Phys. Rev. B 89, 224414 (2014). [Google Scholar]
  13. Roschewsky N. et al. Time resolved spin Seebeck effect experiments. Appl. Phys. Lett. 104, 202410 (2014). [Google Scholar]
  14. Kirihara A. et al. Spin-current-driven thermoelectric coating. Nat. Mater. 11, 686–689 (2012). [DOI] [PubMed] [Google Scholar]
  15. Adachi H., Ohe J.-i., Takahashi S. & Maekawa S. Linear-response theory of spin Seebeck effect in ferromagnetic insulators. Phys. Rev. B 83, 094410 (2011). [Google Scholar]
  16. Harris A. B. Spin-wave spectra of yttrium and gadolinium iron garnet. Phys. Rev. 132, 2398–2409 (1963). [Google Scholar]
  17. Cherepanov V., Kolokolov I. & L'vov V. The saga of YIG: Spectra, thermodynamics, interaction and relaxation of magnons in a complex magnet. Phys. Rep. 229, 81–144 (1993). [Google Scholar]
  18. Belov K. P. Ferrimagnets with a ‘weak' magnetic sublattice. Phys. Usp. 39, 623–634 (1996). [Google Scholar]
  19. Pauthenet R. Spontaneous magnetization of some garnet ferrites and the aluminum substituted garnet ferrites. J. Appl. Phys. 29, 253–255 (1958). [Google Scholar]
  20. Rodić D., Tomkowicz Z., Novakovi L., Szytula A. & Napijalo M. L. The initial magnetic susceptibilities of Gd3Fe5O12 and Tb3Fe5O12 in the compensation point region. Solid State Commun. 73, 243–246 (1990). [Google Scholar]
  21. Dionne G. F. Magnetic oxides Springer (2009). [Google Scholar]
  22. Sawatzky E. & Kay E. Some magnetic and structural properties of epitaxial garnet films prepared by rf sputtering. J. Appl. Phys. 40, 1460–1462 (1969). [Google Scholar]
  23. Schreier M. et al. Current heating induced spin Seebeck effect. Appl. Phys. Lett. 103, 242404 (2013). [Google Scholar]
  24. Schreier M. et al. Sign of inverse spin hall voltages generated by ferromagnetic resonance and temperature gradients in yttrium iron garnet platinum bilayers. J. Phys. D Appl. Phys. 48, 025001 (2015). [Google Scholar]
  25. Ostorero J., Le Gall H., Guillot M. & Marchand A. Faraday effect in gadolinium iron garnet. IEEE Trans. Magn. 22, 1242–1244 (1986). [Google Scholar]
  26. Guo E.-J., Kehlberger A., Cramer J., Jakob G. & Kläui M. Origin of the thickness-dependent low-temperature enhancement of spin Seebeck effect in YIG films. Preprint at http://arxiv.org/abs/1506.06037 (2015).
  27. Uchida K., Kikkawa T., Miura A., Shiomi J. & Saitoh E. Quantitative temperature dependence of longitudinal spin Seebeck effect at high temperatures. Phys. Rev. X 4, 041023 (2014). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures 1-4, Supplementary Table 1, Supplementary Notes 1-2 and Supplementary References

ncomms10452-s1.pdf (893.2KB, pdf)

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES