Functional mixed effects spectral analysis

SUMMARY

In many experiments, time series data can be collected from multiple units and multiple time series segments can be collected from the same unit. This article introduces a mixed effects Cramér spectral representation which can be used to model the effects of design covariates on the second-order power spectrum while accounting for potential correlations among the time series segments collected from the same unit. The transfer function is composed of a deterministic component to account for the population-average effects and a random component to account for the unit-specific deviations. The resulting log-spectrum has a functional mixed effects representation where both the fixed effects and random effects are functions in the frequency domain. It is shown that, when the replicate-specific spectra are smooth, the log-periodograms converge to a functional mixed effects model. A data-driven iterative estimation procedure is offered for the periodic smoothing spline estimation of the fixed effects, penalized estimation of the functional covariance of the random effects, and unit-specific random effects prediction via the best linear unbiased predictor.

1. INTRODUCTION

In biomedical experiments, it is common to collect time series data from multiple subjects and use the time series as the basic unit in the analysis to study the effects of design covariates. These studies can include multiple time series segments collected from the same unit, which can be potentially correlated. The motivating study considered in this article measures three epochs of heart rate variability from subjects during three stages of sleep where it is believed that the heart rate variability spectra are associated with sleep and the presence of disease (Malik et al., 1996; Hall et al., 2004). When the focus of the analysis is on the effects of the design covariates on the first moment, such data can be modelled by mixed effects models. However, few methods exist when the interest is on the second-order spectra.

A model for replicate time series collected from independent units was introduced by Diggle & Al Wasel (1997) which models unit-specific spectra through a log-linear mixed effects model. Iannaccone & Coles (2001) generalize this model by allowing for the nonparametric spline estimation of the fixed effects. More recently, Freyermuth et al. (2010) introduced a tree-structured wavelet method for the estimation of the spectra of replicated time series. These models are designed exclusively for the analysis of a collection of time series under a very simple nested structure, where the individual time series are mutually independent. A novel contribution of our article is the introduction of the mixed effects Cramér representation for modelling a collection of stationary time series that exploits the flexibility of the linear mixed effects model (Laird & Ware, 1982) where many designs can be handled by correctly specifying the design matrices. This model can take into account potential correlations among the spectra of time series segments from a common unit.

The asymptotic properties of periodograms for deterministic spectra are well known and are the foundation for most nonparametric spectral estimation procedures. We investigate the asymptotic properties of the periodograms of collections of time series that can be modelled through a mixed effects Cramér spectral representation and show that when the replicate-specific spectra almost surely lie in a Sobolev space, the log-periodograms uniformly converge to a functional mixed effects model that is comprised of the log-spectral fixed effects, the log-spectral random effects and additive noise with known variance.

Mixed effects models with functional random and fixed effects have been the focus of considerable research including Rice & Silverman (1991), Brumback & Rice (1998), Staniswalis & Lee (1998), Rice & Wu (2001), Guo (2002), Wu & Zhang (2002), Morris & Carroll (2006), Qin & Guo (2006) and Zhang & Chen (2007). The functional models of Guo (2002), Morris & Carroll (2006) and Qin & Guo (2006) can flexibly encompass a variety of designs through the specification of design matrices for both the random and fixed effects in a manner similar to the traditional linear mixed effects model. Guo (2002) and Qin & Guo (2006) define the covariance kernels of the random effects as the reproducing kernel of a Sobolev space while Morris & Carroll (2006) parametrically define the covariance kernels through a small number of covariance parameters. Our proposed mixed effects model for the log-periodograms is similar to these three models in that design matrices can be specified to flexibly incorporate a variety of designs, but differs in that the only assumptions made of the covariance kernels of the log-spectral random effects are inherited from the assumption that the random effects are independent second-order stochastic processes with trajectories almost surely in a Sobolev space (Lukic & Beder, 2001). Another distinction between our proposed model and the models of Guo (2002), Morris & Carroll (2006) and Qin & Guo (2006) is that they assume that the random effects are Gaussian whereas our model does not assume a distribution for the log-spectral random effects.

To fit the mixed effects model for the log-periodograms, we propose an iterative algorithm that begins with an initial smoothing spline estimator of the log-spectral fixed effects. This initial estimator is obtained by approximating the minimizer of a penalized sum-of-squares which ignores the within-unit log-spectral correlation and can be viewed as an extension of the estimators of Cogburn & Davis (1974) and Wahba (1980) to the regression setting. Despite the empirical findings of Qin & Wang (2008), which show that the negative penalized Whittle-likelihood under the proper selection of smoothing parameters can produce more efficient spectral estimates than the penalized sum-of-squares for a single deterministic spectrum, we base our fixed effects estimator on a penalized sum-of-squares because of its computational feasibility and transparent form as a multivariate low-pass filter applied to the ordinary least squares estimates of the log-periodograms at each frequency.

Smoothing spline estimates of fixed effects from correlated data are consistent if the within-unit correlation is ignored but they are not efficient (Welsh et al., 2002; Lin et al., 2004). Iterative procedures for functional models that nonparametrically account for the within-replicate correlation when unique replicates are independent are offered by Yao & Lee (2006) and by Krafty et al. (2008). We extend these ideas to formulate an iterative procedure for the log-periodogram mixed effects model. First, the log-spectral fixed effects are estimated. Conditional on estimates of the fixed effects, the functional covariances of the random effects are estimated as the outer product of smoothed deviations of unit-specific log-periodograms from their estimated mean with smoothing parameters selected for the optimal estimation of the covariance functions via a Kullback–Leibler criterion (Krafty et al., 2008). The estimates of the first two moments of the log-spectra are used to estimate the unit-specific random effects through plug-in estimates of the best linear unbiased predictors. Fixed effects are then re-estimated by approximating the minimizer of the penalized sum-of-squares after removing the estimated unit-specific random effects from the log-periodograms.

2. MODEL

2.1. Mixed effects Cramér spectral representation

We introduce the mixed effects Cramér spectral representation for modelling a collection of $n={\sum }_{j=1}^N{n}_j$ time series from N independent units, where n_j time series are observed from the jth unit. This model consists of a stochastic transfer function that is composed of population fixed effects and unit-specific random effects. Let U_jk = (u_jk1,..., u_jkP)^T ∈ 𝒰 and V_jk = (v_jk1,...,v_jkQ)^T ∈ 𝒱 be vectors of covariates for the kth replicate of the jth independent unit which index the fixed effects and the unit-specific random effects, respectively. These covariates can include continuous covariates as well as indicator variables for categorical variables. Our motivating study of heart rate variability, discussed in greater detail in § 5, consists of n = 375 epochs of heart rate variability measured at n_j = 3 different sleep stages from N = 125 independent subjects. In addition to its dependence on sleep stage, the expected spectrum of heart rate variability is hypothesized to be associated with the presence of insomnia. The fixed covariates are modelled with P = 6 by indicator variables to indicate the presence of insomnia and stage of sleep. The covariates of the random effects are modelled with Q = 2 to capture the variation in the across-the-night average heart rate variability between different subjects and the correlation in the heart rate variability from the same subject at different stages of sleep.

The transfer function of the kth replicate of the jth independent unit is decomposed into A₀(ω; U_jk)A_j (ω; V_jk), where A₀ is a fixed effects term and A_j is a random effects term. To formally define our model, let the population fixed effects term A₀ be a complex valued function over ℝ × 𝒰 such that for every U_jk ∈ 𝒰, A₀(·; U_jk) is Hermitian, square-integrable over [−1/2, 1/2], and has period 1 as a function of frequency. The unit-specific random terms are defined for j = 1,..., N as the complex valued random functions A_j over ℝ × 𝒱 such that for every V_jk ∈ 𝒱, A_j (·; V_jk) are Hermitian, square-integrable over [−1/2, 1/2], and have period 1 as trajectories over frequency. Additionally, A_j and A_j′ for j, j′ ≠ 0 are independent and identically distributed conditional on V_jk when j ≠ j′, and it is assumed that sup_{ω∈ℝ, Vjk∈𝒱} E{|A_j (ω; V_jk)|²} < ∞.

The mixed effects Cramér spectral representation defines the kth replicate time series of the jth independent unit {X_jkt} as

$$X_{jkt}={\int }_{-1/2}^{1/2}{A}_0(\omega ;U_{jk})A_j(\omega ;V_{jk})e^{2\pi i\omega t}d{Z}_{jk}(\omega )\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(k=1,\dots ,n_j;\hspace{0.17em}\hspace{0.17em}j=1,\dots ,N),$$ (1)

where Z_jk are mutually independent identically distributed mean-zero orthogonal increment processes over [−1/2, 1/2] that are independent of A_j′ for all j and j′, and E{|dZ_jk (ω)|²} = dω. The time series {X_jkt} exists with probability one, is mean zero second-order stationary and has spectral density |A₀(ω; U_jk)|² E{|A_j (ω; V_jk)|²}. Additionally, any second-order stationary time series with a spectral density possesses a mixed effects Cramér spectral representation. Conditional on A_j, the time series {X_jkt} is also mean zero second-order stationary and we define the replicate-specific spectra and the population average spectrum as

$$f_{jk}(\omega ;U_{jk},V_{jk})={\left|A_0(\omega ;U_{jk})\right|}^2{\left|A_j(\omega ;V_{jk})\right|}^2,\hspace{0.17em}\hspace{0.17em}f(\omega ;U_{jk})={\left|A_0(\omega ;U_{jk})\right|}^2.$$

We focus on inference on the log-spectral scale and without loss of generality assume that the replicate-specific spectra are parameterized such that E{log |A_j (ω; V_jk)|²} = 0 for all ω ∈ ℝ and V_jk ∈ 𝒱.

2.2. Semiparametric log-spectral model

We will assume semiparametric models for both the fixed and random components of the transfer functions. The semiparametric model of the fixed effects component of the transfer function is defined for U_jk = (u_jk1,..., u_jkP)^T as $A_0(\omega ;U_{jk})={\prod }_{p=1}^P{h}_p^0{\left(\omega \right)}^{u_{jkp}}$, where the $h_p^0$ are deterministic Hermitian functions over ℝ with period 1 that are bounded away from zero. The random components of the unit-specific transfer functions are defined for V_jk = (v_jk1,...,v_jkQ)^T ∈ 𝒱 as $A_j(\omega ;V_{jk})={\prod }_{q=1}^Q{h}_{jq}{\left(\omega \right)}^{{\upsilon }_{jkq}}$ where h_jq are mutually independent Hermitian random functions with period 1 that are bounded away from zero, h_jq and h_j′q are independent and identically distributed for j ≠ j′, and E{|h_jq (ω)|⁴} < ∞. Define the functions ${\beta }_p(\omega )=\text{log}{\left|h_p^0(\omega )\right|}^2$ and α_jq (ω) = log |h_jq (ω)|² as well as the p-dimensional vectors β (ω) = {β₁(ω), . . . , β_P (ω)}^T and the q-dimensional vectors α_j (ω) = {α_j1(ω), . . . , α_jQ (ω)}^T. This transfer function model induces the semiparametric mixed effects model on the replicate-specific log-spectra

$$\text{log}{f}_{jk}(\omega ;U_{jk},V_{jk})=U_{jk}^{\text{T}}\beta (\omega )+V_{jk}^{\text{T}}{\alpha }_j(\omega ).$$ (2)

If we define the covariance function for the qth log-spectral random effect as Γ_q (ω, ν) = E{α_jq (ω)α_jq (ν)} and let Γ(ω, ν) = diag{Γ₁(ω, ν), . . . , Γ_Q (ω, ν)} be the diagonal Q × Q matrix of these covariances, the first two central moments of log-spectra are

$$\begin{array}{c}E\left\{\text{log}{f}_{jk}(\omega ;U_{jk},V_{jk})\right\}=U_{jk}^{\text{T}}\beta (\omega )\\ \text{cov}\left\{\text{log}{f}_{jk}(\omega ;U_{jk},V_{jk}),\hspace{0.17em}\hspace{0.17em}\text{log}{f}_{j\ell }(v,U_{j\ell },V_{j\ell })\right\}=V_{jk}^{\text{T}}\mathrm{\Gamma }(\omega ,v)V_{j\ell }.\end{array}$$

2.3. Modelling log-spectral effects in a Sobolev space

The mixed effects Cramér spectral representation (1) and semiparametric log-spectral model (2) offer a general model for collections of time series data that can be potentially correlated. Many applications, such as the study of heart rate variability explored in § 5, involve unit-specific log-spectra which are smooth. Section 3 develops a data-driven estimation procedure when the unit-specific log-spectra are real-valued periodic functions that are absolutely continuous, have absolutely continuous first derivatives and L₂ integrable second derivatives. Although the space of such functions can be expanded in a cosine series, we find it advantageous for later theoretic exposition to represent this space as

$$W_{2,\text{per}}^2=\left\{\sum _{m=-\infty }^{\infty }{a}_m{e}^{2\pi \text{i}m\omega }:a_m\in ℂ,\hspace{0.17em}{a}_m=\overline{a_{-m}},\hspace{0.17em}\hspace{0.17em}\sum _{m=-\infty }^{\infty }{m}^4{\left|a_m\right|}^2\right\}.$$

Penalized estimation procedures will be developed by viewing this space as the reproducing kernel Hilbert space under the well-studied periodic Sobolev norm which is examined in Cogburn & Davis (1974) and in § 4.2 of Gu (2002). Consider the decomposition $W_{2,\text{per}}^2=W_0\oplus W_1$ where $W_0=\left\{f\in W_{2,\text{per}}^2:{\int }_{-1/2}^{1/2}{f}^{″}(\omega )d\omega =0\right\}$ and $W_1=\left\{f\in W_{2,\text{per}}^2:{\int }_{-1/2}^{1/2}f(\omega )d\omega =0\right\}$ are viewed as Hilbert spaces under the respective inner products ${\langle f,g\rangle }_0=\left\{{\int }_{-1/2}^{1/2}f(\omega )d\omega \right\}\left\{{\int }_{-1/2}^{1/2}g(\omega )d\omega \right\}$ and ${\langle f,g\rangle }_1={\int }_{-1/2}^{1/2}{f}^{″}(\omega )g^{″}(\omega )d\omega$. The spaces W₀ and W₁ are reproducing kernel Hilbert spaces with reproducing kernels R₀(ω, ν) = 1 and $R_1(\omega ,\nu )=2{\sum }_{m=1}^{\infty }{\left(2\pi m\right)}^{-4}\text{cos}\left\{2\pi m(\omega -\nu )\right\}$ so that $W_{2,\text{per}}^2$ is a reproducing kernel Hilbert space with reproducing kernel 1 + R₁(ω, ν).

3. ESTIMATION

3.1. Log-periodogram mixed effects model

Let T = 2L for a positive integer L and assume that we observe epochs of length T of a collection of time series {X_jk1,..., X_jkT} that follow a mixed effects Cramér spectral representation for k = 1,..., n_j and j = 1,..., N. Let ω_ℓ = ℓ/T for ℓ = (1 − L),..., L be the Fourier frequencies and define the finite Fourier transforms as $d_{jk\ell }=T^{-1/2}{\sum }_{t=1}^{\text{T}}{X}_{jkt}{e}^{-2\pi \text{i}{\omega }_{\ell }t}$ and subsequent periodograms as I_jkℓ =|d_jkℓ|². Theorem 1 establishes asymptotic properties of the log-periodograms when the replicate-specific spectra are in $W_{2,\text{per}}^2$ and allows the log-periodograms to be approximated by a functional mixed effects model.

Theorem 1. Assume that $h_p^0\in W_{2,\mathit{per}}^2$ for p = 1,..., P, $h_{jq}\in W_{2,\mathit{per}}^2$ almost surely for q = 1,..., Q, and Assumptions A1–A5 in the Appendix. Let κ_jkℓ = log I_jkℓ − log f_jk (ω_ℓ; U_jk, V_jk) and note that κ_jkℓ = κ_jk−ℓ. As T → ∞, κ_jkℓ are asymptotically independent for ℓ = 0,..., L, the κ_jkℓ are asymptotically distributed as log(ψ) for ℓ = 1,...,(L − 1) where $\psi ~{\chi }_2^2/2$, and κ_jk0 and κ_jkL are asymptotically distributed as log(ϕ) where $\varphi ~{\chi }_1^2$.

Let γ ≈ 0.577 be the Euler–Mascheroni constant. For ℓ ≠ 0, L, let γ_ℓ = E{log(ψ)} = γ and ${\sigma }_{\ell }^2=\mathit{var}\left\{\text{log}(\psi )\right\}={\pi }^2/6$. Define γ₀ = γ_L = E{log(ϕ)}= (log 2 + γ)/π and ${\sigma }_0^2={\sigma }_L^2=\mathit{var}\left\{\text{log}(\varphi )\right\}\approx 4.935$. Uniformly in j, k and ℓ, as T → ∞

$$\begin{array}{ll}\text{E}({\kappa }_{jk\ell })\hfill & =-{\gamma }_{\ell }+O(T^{-1}),\hfill \\ \mathit{var}({\kappa }_{jk\ell })\hfill & ={\sigma }_{\ell }^2+O(T^{-1}),\hfill \\ \mathit{cov}\left({\kappa }_{jk\ell },{\kappa }_{j^{\prime }{k}^{\prime }{\ell }^{\prime }}\right)\hfill & =O(T^{-1})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(j\ne j^{\prime },\hspace{0.17em}\hspace{0.17em}k\ne k^{\prime },\hspace{0.17em}\hspace{0.17em}\left|\ell \right|\ne \left|{\ell }^{\prime }\right|\right).\hfill \end{array}$$

The first part of Theorem 1 demonstrates that analogous distributional properties to the well-studied properties of log-periodograms for deterministic transfer functions exist for the Cramér spectral representation model. Letting y_jkℓ = log I_jkℓ + γ_ℓ, the log-periodograms approximately follow the functional mixed effects model

$$y_{jk\ell }\approx U_{jk}^{\text{T}}\beta ({\omega }_{\ell })+V_{jk}^{\text{T}}{\alpha }_j({\omega }_{\ell })+{∊}_{jk\ell }$$ (3)

where ∊_jkℓ are zero mean independent random variables for ℓ = 0,..., L with $\text{var}({∊}_{jk\ell })={\sigma }_{\ell }^2$. The second part of Theorem 1 provides the uniform convergence of the first two moments of this smooth signal plus noise model and subsequently allows functional mixed effects modelling techniques to be applied to (3) to obtain consistent estimates of β_p, Γ_q and α_jq.

3.2. Fixed effects

The proposed estimator of β is based on minimizing the penalized sums-of-squares

$$\frac{1}{nT}\sum _{j=1}^N\sum _{k=1}^{n_j}\sum _{\ell =1-L}^L{\left\{y_{jk\ell }-U_{jk}^{\text{T}}\beta ({\omega }_{\ell })\right\}}^2+\sum _{p=1}^P{\lambda }_p{\int }_{-1/2}^{1/2}{\beta }_p^{″}{\left(\omega \right)}^{2}d\omega$$ (4)

over ${\otimes }^P{W}_{2,\text{per}}^2$ given smoothing parameters λ_p ⩾ 0. By the representer lemma for smoothing splines, if U_j are the n_j × P matrices with kpth elements u_jkp and $U={\left(U_1^{\text{T}},\dots ,U_N^{\text{T}}\right)}^{\text{T}}$ is full rank, then a unique solution exists. To find this solution, let $Y_{\ell }={\left(Y_{1\ell }^{\text{T}},\dots ,Y_{N\ell }^{\text{T}}\right)}^{\text{T}}$, $Y={\left(Y_{1-L}^T,\dots ,Y_L^{\text{T}}\right)}^{\text{T}}$. Further, let R be the T × T matrix of the reproducing kernel R₁ of W₁ evaluated the Fourier frequencies. The matrix R has the singular value decomposition F^T DF, where F is the matrix of the discrete Fourier transform that has ℓmth element T^−1/2 exp{−2πi(m − L) (ℓ − L)/T} (Gu, 2002, § 4.2). The minimizer of (4) over ${\otimes }^P{W}_{2,\text{per}}^2$ is defined for ω ∈ ℝ as d̂ + [{R₁(ω, ω_1−L),..., R₁(ω, ω_L)} ⊗ I_P]ĉ for d̂ ∈ ℝ^P and ĉ ∈ ℝ^PT that satisfy

$$\begin{array}{l}{T}^{1/2}\left(e_o\otimes U^{\text{T}}U\right)d+\left\{\left(DF\otimes U^{\text{T}}U\right)+nT\left(I_T\otimes \mathrm{\Lambda }\right)\right\}c=\left\{F\otimes {\left(U^{\text{T}}U\right)}^{-1}{U}^{\text{T}}\right\}Y,\hspace{0.17em}\hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(e_o^{T}F\otimes I_p\right)c=0_P,\end{array}$$

where Λ = diag(λ₁,...,λ_P), e₀ is the T-vector of zeros except for a one in the (L + 1)st element, and 0_p is the P-vector of zeros. Cogburn & Davis (1974) developed and Wahba (1980) popularized an approximation to the minimizer of the penalized sums-of-squares over $W_{2,\text{per}}^2$ that results in an estimator that is equivalent to applying the classical Butterworth filter to the log-periodograms. We apply this approximation to the minimizer (4) and estimate β (ω) with

$$\widehat{\beta }(\omega )=\frac{1}{T}\sum _{\ell =1-L}^L\sum _{m=1-L}^L{\left\{U^{\text{T}}U+n{\left(2\pi m\right)}^4\mathrm{\Lambda }\right\}}^{-1}{U}^{\text{T}}{Y}_{\ell }{e}^{2\pi \text{i}m(\omega -{\omega }_{\ell })}.$$ (5)

When n = 1 and P = 1, the proposed estimator is equivalent to the estimator proposed by Wahba (1980) and is subsequently a generalization of this well-studied estimator to the regression setting with multiple log-spectra. Using simple algebra to express

$${\left\{U^{\text{T}}U+n{\left(2\pi m\right)}^4\mathrm{\Lambda }\right\}}^{-1}{U}^{\text{T}}{Y}_{\ell }={\left\{I_P+n{\left(2\pi m\right)}^4{\left(U^{\text{T}}U\right)}^{-1}\mathrm{\Lambda }\right\}}^{-1}\left\{{\left(U^{\text{T}}U\right)}^{-1}{U}^{\text{T}}{Y}_{\ell }\right\}$$

illuminates that the proposed estimate is a type of multivariate low-pass filter applied to the ordinary least squares estimates at each frequency. It is dependent on the smoothing parameters such that as max λ_j → 0, β̂ approaches a spline interpolation of the ordinary least squares estimates. Theorem 2 establishes the optimal decay of λ_j if both the number of independent units and the number of time-points is large, as well as the point-wise consistency of β̂.

Theorem 2. Assume the conditions of Theorem 1, regularity assumptions on the covariate design given by Assumptions A6 and A7, and that n_j is bounded away from zero and infinity through Assumption A8. Let λ = max_p λ_p, and assume that there exists a constant C such that min_p λ_p/λ > C. As N, T →∞, the optimal mean-square convergence rate is achieved when λ ∼ (NT)^−4/5, under which

$$\underset{p=1,\dots ,P;\omega \in ℝ}{\text{sup}}E\left\{{\left|{\widehat{\beta }}_p(\omega )-{\beta }_p(\omega )\right|}^2\right\}=O\left(N^{-4/5}{T}^{-4/5}\right)+O\left(T^{-1}\right)+O\left(N^{-1}\right).$$

Traditionally, the large sample properties of smoothing splines are explored either when the number of independent units is bounded, most famously in the estimation of a single curve when N = 1 and n₁ = 1 (Wahba, 1990), or in the longitudinal data setting where N may be large but the number of observations per individual unit are bounded (Lin et al., 2004). Theorem 2 shows that the amount of smoothing for the estimation of fixed effects depends on both N and T and consequently smoothing parameter selection procedures directed towards the prediction of individual log-spectra, i.e., ignoring N, will behave suboptimally. One popular approach to the data-driven selection of smoothing parameters for linear smoothers is generalized crossvalidation (Gu, 2002). The generalized crossvalidation procedure to select the parameters indexing the estimate β̂ as a linear smoother of the ordinary least squares estimates of β at each Fourier frequency minimizes

$$𝒢(\mathrm{\Lambda })=\frac{{\sum }_{\ell =1-L}^L{\left\{{\left(U^{\text{T}}U\right)}^{-1}{U}^{\text{T}}{Y}_{\ell }-\widehat{\beta }({\omega }_{\ell })\right\}}^{\text{T}}\left\{{\left(U^{\text{T}}U\right)}^{-1}{U}^{\text{T}}{Y}_{\ell }-\widehat{\beta }({\omega }_{\ell })\right\}}{\mathit{PT}{\left[1-{\sum }_{m=1-L}^L\text{trace}{\left\{I_P+n{\left(2\pi m\right)}^4{\left(U^{\text{T}}U\right)}^{-1}\mathrm{\Lambda }\right\}}^{-1}/P\right]}^2}.$$

3.3. Functional covariance

We propose an estimate of the functional covariance of the log-spectral random effects conditional on the estimate β̂ through the outer product of smoothed unit-specific quantities. Define the residuals $y_{jkl}^{*}=y_{jk\ell }-U_{jk}^{\text{T}}\widehat{\beta }({\omega }_{\ell })$ and $Y_{j\ell }^{*}={\left(y_{j1\ell }^{*},\dots ,y_{j{n}_j\ell }^{*}\right)}^{\text{T}}$. We propose to estimate Γ_q (ω, ν) for ω, ν ∈ ℝ as

$${\widehat{\mathrm{\Gamma }}}_q(\omega ,v)=N^{-1}\sum _{j=1}^N{\tilde{\alpha }}_{jq}(\omega ){\tilde{\alpha }}_{jq}(\nu ),$$ (6)

where α̃_j = (α̃_j1,..., α̃_jQ)^T is based on minimizing

$$\frac{1}{n_{j}T}\sum _{k=1}^{n_j}\sum _{\ell =1-L}^L{\left\{y_{jk\ell }^{*}-V_{jk}^{\text{T}}{\alpha }_j({\omega }_{\ell })\right\}}^2+\sum _{q=1}^Q{\theta }_q{\int }_{-1/2}^{1/2}{\alpha }_{jq}^{″}{\left(\omega \right)}^{2}d\omega$$

over ${\otimes }^Q{W}_{2,\text{per}}^2$ given the smoothing parameters θ_q ⩾ 0. Approximating the solution to the penalized sums-of-squares, we estimate Γ̂_q (ω, ν) as the qth diagonal element of the Q × Q matrix

$$\begin{array}{c}\frac{1}{{\mathit{NT}}^2}\sum _{j=1}^N\sum _{\ell ,m,r,s=1-L}^L{\left\{V_j^{\text{T}}{V}_j+n_j{\left(2\pi m\right)}^4\mathrm{\Theta }\right\}}^{-1}{V}_j^{\text{T}}{Y}_{j\ell }^{*}{Y}_{jr}^{*\text{T}}{V}_j\\ \times {\left\{V_j^{\text{T}}{V}_j+n_j{\left(2\pi s\right)}^4\mathrm{\Theta }\right\}}^{-1}{e}^{2\pi \text{i}m(\omega -{\omega }_{\ell })+2\pi \text{i}s(\nu -{\omega }_r)}\end{array}$$

where V_j is the n_j × Q matrix with kqth element v_jkq and Θ = diag(θ₁,...,θ_Q). Theorem 3 finds the optimal decay of the smoothing parameters θ_q for the estimation of Γ_q as well as the point-wise mean-squared consistency of the estimate of Γ_q.

Theorem 3. Assume the conditions of Theorem 2 and the existence of the first eight moments of X_jkt given in Assumption A9. Let θ = max_q θ_q, and assume that there exists a constant C such that min_q θ_q/θ > C. As N, T → ∞, the optimal mean-square convergence is achieved when θ ∼ (N^−2/3 + T^−4/3), under which

$$\underset{q=1,\dots ,Q;\hspace{0.17em}\omega ,\nu \in ℝ}{\text{sup}}E\left\{{\left|{\widehat{\mathrm{\Gamma }}}_q(\omega ,\nu )-{\mathrm{\Gamma }}_q(\omega ,\nu )\right|}^2\right\}=O\left(N^{-2/3}+T^{-1}\right).$$

The amount of smoothing for method-of-moments type estimation of Γ_q requires a smoothing parameter that decays with respect to the number of time-points at a rate of T^−4/3, whereas the amount of smoothing for α̃_jq to predict the unit-specific log-spectra α_jq would decay at a rate of T^−4/5 (Wahba, 1980). Consequently, selecting smoothing parameters to optimally predict unit-specific random effects when forming a method-of-moments estimate for the functional covariance will result in over-smoothing. This result partially motivates the development of an iterative procedure in § 3.5 for the estimation of β_p and Γ_q that allows for different amounts of smoothing to be used for the estimation of the fixed effect coefficients and the covariance of the random effects. The functions α̃_j will be thought of as nuisance parameters for the estimation of the functional covariance and not estimates of the unit-specific random effects.

Krafty et al. (2008) offer a crossvalidation procedure for the data-driven selection of smoothing parameters θ_q that uses the quasi Kullback–Leibler distance conditional on fixed effect estimates as a measure of lack-of-fit over the functional covariance space. To approximate the first two moments of all data from an independent-unit, let W be the QT × QT block matrix with ℓmth Q × Q block Γ(ω_ℓ−L, ω_m−L), and Σ_∊ be the T × T matrix with ℓmth element ${\sigma }_{\ell }^2{\delta }_{\left|\ell -L\right|,\left|m-L\right|}$. Theorem 1 implies that $\text{E}\left(Y_j^{*}\right)\approx 0_{n_{j}T}$ and $\text{var}\left(Y_j^{*}\right)\approx \left(I_T\otimes V_j\right)W\left(I_T\otimes V_j^{\text{T}}\right)+\left({\mathrm{\Sigma }}_{∊}\otimes I_{n_j}\right)$ where $Y_j^{*}={\left(Y_{j(1-L)}^{*\text{T}},\dots ,Y_{jL}^{*\text{T}}\right)}^{\text{T}}$. We use a leave-out-one procedure to estimate the quasi Kullback–Leibler distance of $Y_j^{*}$ conditional on β̂ between the within-unit covariance obtained by using smoothing parameters Θ and the true within-unit covariance. Letting Γ̂^(−j)(ω, ν : Θ) be the estimate of the matrix Γ(ω, ν) using smoothing parameters Θ and excluding data from the jth independent unit, Ŵ^(−j)(Θ) be the corresponding QT × QT block matrix with ℓmth Q × Q block Γ̂^(−j)(ω_ℓ−L, ω_m−L : Θ), and ${\widehat{\mathrm{\Sigma }}}_j(\mathrm{\Theta })=\left(I_T\otimes V_j\right){\widehat{W}}^{(-j)}(\mathrm{\Theta })\left(I_T\otimes V_j^{\text{T}}\right)+\left({\mathrm{\Sigma }}_{∊}\otimes I_{n_j}\right)$, we select Θ to minimize

$$𝒦(\mathrm{\Theta })=\sum _{j=1}^N\text{log}{\left|{\widehat{\mathrm{\Sigma }}}_j(\mathrm{\Theta })\right|}_{+}+Y_j^{*T}{\widehat{\mathrm{\Sigma }}}_j{\left(\mathrm{\Theta }\right)}^{-}{Y}_j^{*},$$

where |Σ̂_j (Θ)|₊ is the product of the positive eigenvalues of Σ̂_j (Θ) and Σ̂_j (Θ)⁻ is its Moore–Penrose inverse.

3.4. Unit-specific random effects

Estimates of the best linear unbiased predictors of unit-specific random effects allows for the pooling of information across units and serves as the cornerstone of unit-specific random effect estimation (Robinson, 1991). The plug-in estimate of the best linear unbiased estimate of α_j (ω) for ω ∈ ℝ based on $Y_j^{*}$ is

$${\widehat{\alpha }}_j(\omega )=\left\{\widehat{\mathrm{\Gamma }}(\omega ,{\omega }_{1-L}),\dots ,\widehat{\mathrm{\Gamma }}(\omega ,{\omega }_L)\right\}\left(I_L\otimes V_j^{\text{T}}\right){\left\{\left(I_T\otimes V_j\right)\widehat{W}\left(I_L\otimes V_j^{\text{T}}\right)+\left({\mathrm{\Sigma }}_{∊}\otimes I_{n_j}\right)\right\}}^{-}{Y}_j^{*}$$ (7)

where Γ̂(ω, ν) and Ŵ are the estimates of Γ(ω, ν) and W with their dependence on smoothing parameters suppressed for notational simplicity.

3.5. Iterative estimation of β_p and α_jq

The estimates obtained by first estimating β through (5) then estimating Γ_q through (6) are consistent. However, Welsh et al. (2002) and Lin et al. (2004) showed that failing to account for within-unit correlation in the smoothing spline estimation of fixed effects results in suboptimal estimates. Adapting the ideas proposed by Yao & Lee (2006) for principal component-based penalized spline models to our periodic spline model for log-periodograms, we propose to increase the efficiency by iterating between the estimation of the random effects after removing estimates of the fixed effects and the estimation of the fixed effects after removing estimates of the random effects. Formally, if we set ${\alpha }_{jq}^{(0)}(\omega )=0$, the estimates β^(m), ${\mathrm{\Gamma }}_q^{(m)}$ and ${\alpha }_j^{(m)}$ are defined for iteration m = 1, 2,... by

1. letting $y_{jk\ell }^{(m)}=y_{jk\ell }-V_{jk}^{\text{T}}{\alpha }_{jq}^{(m-1)}({\omega }_{\ell })$ and $Y_{\ell }^{(m)}={\left\{\left(y_{11\ell }^{(m)},\dots ,y_{1n_1\ell }^{(m)}\right),\dots ,\left(y_{N1\ell }^{(m)},\dots ,y_{N{n}_N\ell }^{(m)}\right)\right\}}^{\text{T}}$, define β̂^(m) through (5) with Y_ℓ replaced with $Y_{\ell }^{(m)}$;

2. defining ${\widehat{\mathrm{\Gamma }}}_q^{(m)}$ and ${\widehat{\alpha }}_j^{(m)}$ for j = 1,..., N through (6) and (7) with β̂ replaced with β̂^(m) in the definition of $y_{jk\ell }^{*}$.

This algorithm can be repeated until same convergence criteria are met and, if M is the final iteration of the algorithm, set β̂ = β̂^(M), ${\widehat{\mathrm{\Gamma }}}_q={\widehat{\mathrm{\Gamma }}}_q^{(M)}$ and $\widehat{{\alpha }_j}={\widehat{{\alpha }_j}}^{(M)}$.

3.6. Point-wise confidence intervals for fixed effects

We propose a parametric bootstrap procedure for obtaining point-wise confidence intervals for the log-spectral fixed effects. Although the proposed model in (2) and iterative procedure for obtaining point estimates given in § 3.5 do not assume a distribution for the log-spectral random effects, we propose parametric Gaussian bootstrap sampling of the log-spectral random effects. Morris (2002) discusses the underestimation of variability in nonparametric bootstrap sampling of mixed effects models.

The bth bootstrap sample of the collection of time series for b = 1,..., B is generated by first generating the log-spectral random effects ${\alpha }_{jq}^{[b]}$ for j = 1,..., N and q = 1,..., Q as independent mean zero Gaussian random processes with covariance kernel Γ̂_q. These random effects are used to compute the replicate specific spectra $f_{jk}^{[b]}(\omega )=\text{exp}\left[U_{jk}^{\text{T}}(\widehat{\beta }(\omega )+V_{jk}^{\text{T}}{\left\{{\alpha }_{j1}^{[b]}(\omega ),\dots ,{\alpha }_{jQ}^{[b]}(\omega )\right\}}^{\text{T}}\right]$. Dai & Guo (2004, Theorem 2) allow for the approximate simulation of time series epochs with a given spectrum and we use this to simulate time series epochs $X_{jkt}^{[b]}$ for t = 1,..., T with spectrum $f_{jk}^{[b]}$. The log-periodograms of the time series $X_{jkt}^{[b]}$ are computed and used in the data-driven iterative algorithm to obtain the fixed effects coefficient estimates from the bth bootstrap sample, ${\widehat{\beta }}_1^{[b]},\dots ,{\widehat{\beta }}_P^{[b]}$. We estimate the (1 − α)% confidence interval for β_p (ω) as {ξ_p (ω; α/2), ξ_p (ω; 1 − α/2)}, where ξ_p (ω; α) is the α percentile of the set ${\left\{{\widehat{\beta }}_p^{[b]}(\omega )-{\text{Bias}}_p(\omega )\right\}}_{b=1}^B$ and ${\text{Bias}}_p(\omega )=B^{-1}{\sum }_{b=1}^B{\widehat{\beta }}_p^{[b]}(\omega )-{\widehat{\beta }}_p(\omega )$.

4. SIMULATIONS

Simulation studies were conducted to investigate the empirical performance of the proposed iterative estimation procedure and to compare it to the performance of three alternative procedures. The first alternative estimation procedure is the noniterative procedure, or the procedure proposed in § 3.5 with M = 1, which is implemented to allow for the empirical assessment of the benefits in iterating. The proposed iterative estimation procedure can be viewed as a data-driven smoother applied to the collection of log-periodograms which is formulated to exploit the dependence structure across time series. A naive approach would be to obtain replicate-specific log-spectral estimates by applying a smoothing procedure to replicate specific log-periodograms while ignoring the dependence structure among time series. Fixed effect estimates can then be obtained through ordinary least squares at each frequency. The second alternative estimation procedure considered examines the empirical properties of this approach, which we will refer to as presmoothing, by applying the generalized crossvalidated spline smoother of Wahba (1980) to each replicate-specific log-spectra. Estimation procedures that smooth across frequency are essential in the consistent estimation of a spectrum from a single time series. However, consistent estimates of log-spectrum fixed effects can be obtained from the log-periodograms of a collection of time series without smoothing across frequency when N is large. The third alternative estimation procedure explores the empirical properties of estimating the log-spectral fixed effects without smoothing across frequency by computing the ordinary least square estimates of the log-spectral fixed effects at each Fourier frequency.

The simulation settings consider n_j = 5, P = 2 and Q = 1. Replicate-specific log-spectra are obtained as g_jk (ω) = β₁(ω) + u_jk β₂(ω) + α_j (ω) for β₁(ω) = 2 cos(2πω), β₂(ω) = 2 cos(4πω) and α_j = ξ_j1 + ξ_j2 cos(2πω) + ξ_j3 cos(4πω), where (ξ_j1, ξ_j2, ξ_j3)^T are independent mean zero normal random vectors with variance matrix diag(2.5, 2, 1), and u_jk are independent uniform random variables over [0, 1]. After a replicate-specific log-spectrum is simulated, the square-root of the spectrum is calculated and used as the replicate-specific transfer function to simulate the time series X_jkt in accordance with Dai & Guo (2004, Theorem 2). Five hundred random samples of N independent units of time series epochs of length T are drawn for the six possible combinations of N = 50, 100 and T = 50, 100, 200. Ninety-five per cent bootstrap confidence intervals for the log-spectral fixed effects from B = 1000 bootstrap samples are computed for each simulated random sample.

The performance of the estimation procedures are evaluated through the square error of the log-spectral fixed effects over the Fourier frequencies, of the replicate-specific log-spectral estimates and of the estimates of the covariance kernel as displayed in Table 1. The average across the curve coverage of the 95% point-wise bootstrap confidence intervals for the six settings ranged from 90.4 to 95.5%. In each of the six settings, the proposed iterative procedure has smaller square error than the other methods for the estimation of the log-spectral fixed effects, the prediction of replicated-specific log-spectra, and for the estimation of the covariance kernel. Although the errors of the estimates of the replicate-specific spectra via the proposed iterative estimation procedure decreased as either N or T increased, the error of the estimates of the replicate-specific spectra obtained through presmoothing did not change with N. This finding, which is a consequence of the fact that the estimated best linear unbiased estimate of a subject-specific log-spectrum requires the estimation of the covariance kernels that depends on N whereas the performance of presmoothing the data for the estimation of a the replicate-specific log-spectrum only depends on T, implies that the relative gain in efficiency for the estimation of the replicate-specific spectra between the proposed iterative procedure and presmoothing decreases as the ratio of T to N increases.

Table 1.

Results of the simulation studies. Square error averaged over the Fourier frequencies are displayed for the estimation of β₁, β₂, g_jk, and Γ from 500 random samples per setting

T	Method	Square error ×102
		N = 50				N = 100
		β̂1	β̂2	ĝjk	Γ̂	β̂1	β̂2	ĝjk	Γ̂
50	Iterative	7.9	11.0	22.8	57.3	3.9	9.3	21.3	32.8
	Noniterative	13.9	29.1	24.5	58.9	7.9	17.8	22.5	34.0
	Presmooth	15.0	34.8	275.6	—	9.6	28.0	286.9	—
	OLS	17.2	26.7	—	—	11.2	17.2	—	—
100	Iterative	7.3	2.1	7.2	51.2	3.8	1.5	5.9	24.8
	Noniterative	12.4	19.8	8.5	51.9	6.6	11.7	6.8	25.1
	Presmooth	12.2	20.0	49.5	—	7.1	14.6	48.1	—
	OLS	15.5	25.3	—	—	10.1	15.1	—	—
200	Iterative	5.3	0.7	2.8	33.4	2.8	0.4	1.5	20.5
	Noniterative	9.4	13.2	3.6	36.2	4.6	8.0	2.2	26.2
	Presmooth	9.3	13.7	9.4	—	4.6	8.7	9.4	—
	OLS	12.8	21.3	—	—	7.3	12.3	—	—

OLA, ordinary least squares.

5. ANALYSIS OF HEART RATE VARIABILITY

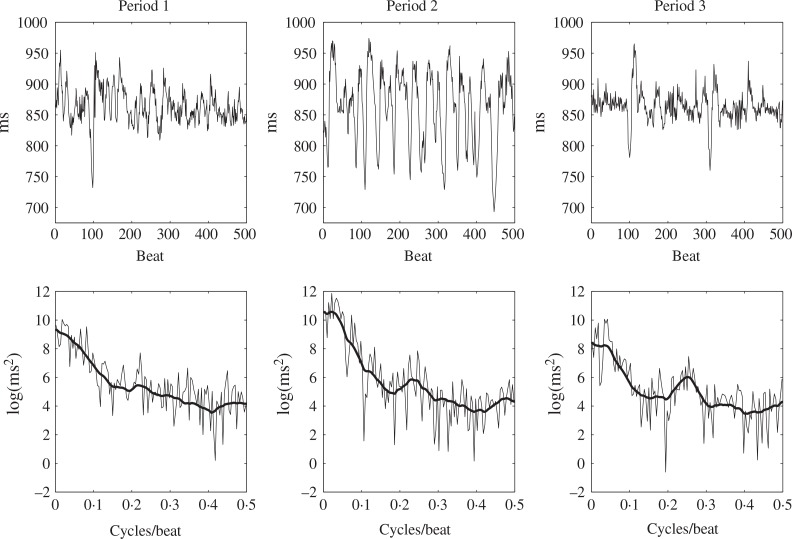
Heart rate variability is the measure of variability in the elapsed time between consecutive heart beats. The spectral analysis of heart rate variability is important in the study of various physiological outcomes and provides indirect measures of autonomic nervous system activity (Malik et al., 1996). Researchers have devised methods to assess heart rate variability continuously and non-invasively throughout sleep (Hall et al., 2004, 2007). In the present study, sleep and heart rate variability were concurrently assessed in a sample of N = 125 men and women between the ages of 60 and 89 years. Data were collected in participants’ homes to enhance the ecological validity of study measures. Of these participants, 76 were poor sleepers due to insomnia while 49 were poor sleepers due to emotional strain of caregiving for a spouse with advanced dementia. The present analysis uses epochs of heart rate variability tachograms, or the series of the elapsed time between consecutive heart beats indexed by beat number, of the first 500 continuous heart beats during each of the first three periods of non-rapid eye movement. The data for each subject are comprised of patient type, either insomnia or caregiver and three time series, heart rate variability for the first three periods. Heart rate variability during the first three periods, their associated log-periodograms and estimated best linear unbiased predictors of the log-spectra for a caregiver participant are displayed in Fig. 1.

Fig. 1.

Data from a sample caregiver subject in the heart rate variability study. Displayed are the heart rate variability, log-periodogram and estimated best linear unbiased log-spectral predictor from the first three periods of non-rapid eye movement.

The goal of our analysis is to quantify the expected differences in heart rate variability spectra between individuals with insomnia and caregivers during different periods. We model the heart rate variability log-spectrum for the j = 1,..., 129 subjects at the first k = 1, 2, 3 periods as $\text{log}{f}_{jk}(\omega ;U_{jk},V_{jk})=U_{jk}^{\text{T}}\beta (\omega )+V_{jk}^{\text{T}}{\alpha }_j(\omega )$, where

$$\left[\begin{array}{c}{U}_{j1}^{\text{T}}\\ U_{j2}^{\text{T}}\\ U_{j3}^{\text{T}}\end{array}\right]=\left[\begin{array}{cccccc}1& 0& 0& S_j& 0& 0\\ 0& 1& 0& 0& S_j& 0\\ 0& 0& 1& 0& 0& S_j\end{array}\right],\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left[\begin{array}{c}{V}_{j1}^{\text{T}}\\ V_{j2}^{\text{T}}\\ V_{j3}^{\text{T}}\end{array}\right]=\left[\begin{array}{cc}1& -1\\ 1& 0\\ 1& 1\end{array}\right],$$

and S_j is the indicator variable for the jth subject being an insomniac. The fixed effects β₁, β₂, β₃ are the mean log-spectrum at periods 1, 2 and 3, respectively, for caregivers, β₄, β₅, β₆ are the differences in the mean log-spectra between individuals with insomnia and caregivers at periods 1, 2 and 3 respectively, Γ₁ accounts for the variability in the across-the-night average log-spectra among subjects and Γ₂ is the covariance kernel among adjacent periods within a subject.

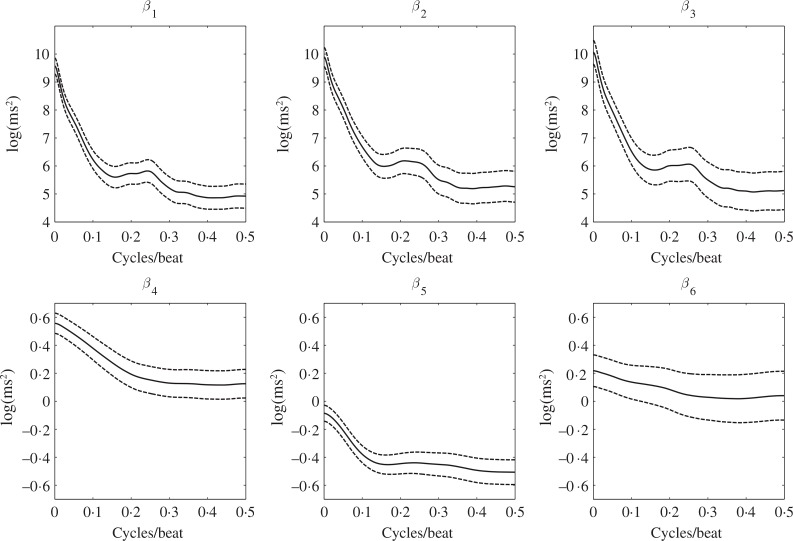
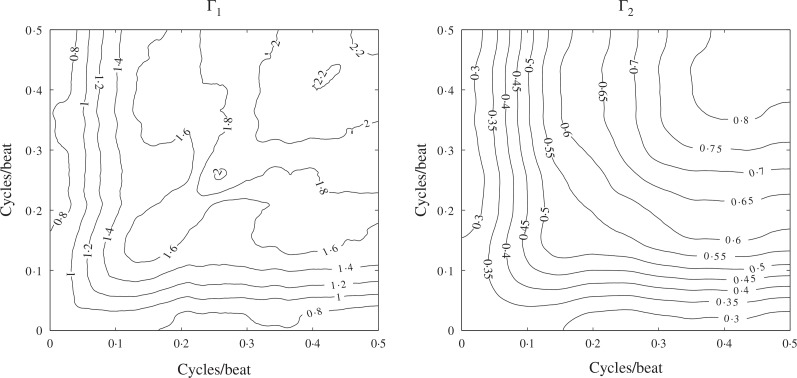
The estimated fixed effects are displayed in Fig. 2 along with point-wise 95% bootstrap confidence intervals from B = 1000 random bootstrap samples. The mean log-spectrum for caregivers over different periods, reflected in β̂₁, β̂₂ and β̂₃, are very similar with a slight gain in power at frequencies <0.05 cylces/beat as the night progresses. The expected log-power at all frequencies for individuals with insomnia is greater than that for caregivers at the first and third periods, reflected through β̂₄ and β̂₆, but less than that for caregivers during the second period, reflected in β̂₅. The monotonic decrease in β̂₄, β̂₅ and β̂₆ reveals that the ratio of power from low frequencies when compared with high frequencies is exaggerated for each of the first three periods among individuals with insomnia compared to caregivers. Clinically, this increase in the ratio of power in low to high frequencies is an indirect measure of an increase in the sympathetical balance and has been shown to be associated with acute stress (Hall et al., 2007). Figure 3 shows that both the estimated variability in the across-the-night average log-spectrum among subjects from Γ̂₁ and the estimated within-subject variability between adjacent periods from Γ̂₂ are larger for higher frequencies.

Fig. 2.

Estimated log-spectral fixed effects and 95% point-wise bootstrap confidence intervals from 1000 bootstrap samples for the analysis of heart rate variability.

Fig. 3.

Contour plots the estimated covariance kernels of the log-spectral random effects in the mixed effects Cramér spectral representation model for heart rate variability.

6. DISCUSSION

The model and estimation procedure introduced in this article offer tools for analysing collections of time series from designed studies and can be extended in several directions to encompass other popular settings. We have focused on estimation based on the first two moments of the log-spectra. It is possible to extend our procedure to Whittle-likelihood-based inference. In addition, many applications involve the analysis of replicated time series that are not stationary. The incorporation of the tensor-product design employed by Guo et al. (2003) into our proposed model to allow for the spectral analysis of replicated nonstationary time series could provide a useful tool for the analysis of replicated locally stationary time series. We hypothesize that the computational burden associated with Whittle-likelihood-based inference and the tensor-product analysis of locally stationary time series for a collection of time series could make these two extensions nontrivial. Although the mixed effects Cramér spectral representation holds when unit-specific spectra are not smooth, our estimation procedure is formulated for applications such as the analysis of heart rate variability where a global smoothness criterion is appropriate. Extending the iterative estimation procedure to utilize tools that can capture local properties, such as free knot splines or wavelet bases, could prove useful in many applications.

SUPPLEMENTARY MATERIAL

Supplementary material available at Biometrika online provides proofs of the theorems; Supplementary PDF file supplied by authors.

APPENDIX. Regularity assumptions

The properties established in the theorems are dependent on regularity assumptions about the distributions of Z_jk and f_jk (ω; U_jk, V_jk) and on the covariate design. For the noise process, we will make Assumption A1 which assures that X_jkt can be written as a linear process, the Cramér type condition in Assumption A2 which guarantees that the distribution of the Fourier transform of z_jkt is absolutely continuous, and the existence of the fourth moment in Assumption A3.

• Assumption A1. Let z_jkt = ∫ e^2πiωt dZ_jk (ω). The random variables z_jkt are white noise with mean zero and unit variance.

• Assumption A2. There exists an integer ρ > 0 such that ∫ |E (e^isz_jkt)|^ρ ds < ∞.

• Assumption A3. Fourth moments of z_jkt exist such that sup_ω E{|Z_jk (ω)|⁴} < ∞.

Assumption A2, which excludes z_jkt with discrete distributions, is satisfied when z_jkt possesses a differentiable density. Regularity on f_jk (ω; U_jk, V_jk) will be induced through regularity assumptions on A_j, 𝒰 and 𝒱. Assumption A4 assures that the unit-specific spectra are bounded away from zero while Assumptions A5–A7 place regularity conditions on the covariate design.

• Assumption A4. There exists an ∊ > 0 such that sup_{ω, Vjk} pr{|A_j (ω; V_jk)|² < ∊} = 0.

• Assumption A5. The sets 𝒰 and 𝒱 are compact.

For a square matrix M, let σ₋(M) and σ₊(M) be its smallest and largest eigenvalues. We will assume the following.

• Assumption A6. There exist positive constants D₁ and D₂ such that lim_N→∞ σ₋(U^TU/n) = D₁ and lim_N→∞ σ₊(U^TU/n) = D₂.

• Assumption A7. There exist positive constants D₃ and D₄ such that ${\sigma }_{-}\left(V_j^{\text{T}}{V}_j\right)\ge D_3$ and ${\sigma }_{+}\left(V_j^T{V}_j\right)\le D_4$ for all j.

The asymptotic properties are explored when the number of replicates per unit are bounded through Assumption A8.

• Assumption A8. There exists positive n₋ and n₊ such that n₋ ⩽ n_j ⩽ n₊ for all j.

The consistency of the covariance kernel of the log-spectral random effects requires the existence of the first eight moments of X_jkt through Assumption A9.

• Assumption A9. The first eight moments of h_jq and Z_jk are bounded such that sup_{ω, q} E{|h_jq (ω)|⁸} < ∞ and sup_ω E{|Z_jk (ω)|⁸} < ∞.